Two-stage deep learning network-based few-view image reconstruction for parallel-beam projection tomography

Introduction

Projection tomography (PT), such as computed tomography (CT), optical projection tomography (OPT), photoacoustic tomography (PAT), and stimulated Raman projection tomography (SRPT), is an emerging technology that provides a novel approach to recreating three-dimensional (3D) images of biological specimens (1-5). It plays a vital role in biomedical imaging because it can realize fast volumetric imaging with isotropic spatial resolution and has displayed tremendous applicability in several disciplines, including gene expression, protein-protein interaction, and clinical drug evaluation (6-8). It is used to record the attenuation of collimated light beams passing through an object or the signal (fluorescence or Raman) excited by the collimated light beams. A reconstruction algorithm is then used to recover the spatial distribution of the light attenuation or the optical signal emission source (4,9,10). Traditionally, intensive acquisition of projection images in full-angle is required for PT to achieve high-precision, high-quality images. For example, using analytic reconstruction algorithms such as the filtered back-projection (FBP) algorithm, no fewer than 360 projection images within a full-angle, or 180 projection images within a semicircle-angle need to be collected to obtain reasonable imaging results (11-13). Furthermore, the higher the number of projection images used, the higher the quality and accuracy of the reconstructed images will be (14). However, this processing has serious drawbacks as it involves long data-acquisition time, leading to increased sample damage from the accumulation of light dose and a high degree of sample fixation (15). Moreover, these algorithms are highly sensitive to noise (16,17). With sparse-view or limited-angle view data, iterative algorithms based on complex physical imaging models and noise-computing models can be used to reconstruct high-quality images. These techniques can reduce the total data-acquisition time, lower light damage to the sample, and reduce the need for sample fixation to a certain degree. Classical iterative algorithms include the algebraic reconstruction technique (ART) algorithm, simultaneous ART (SART) algorithm, multiplicative ART (MART) algorithm, simultaneous iterative reconstruction technique (SIRT), fast-iterative shrinkage thresholding algorithm (FISTA), two-step iterative shrinkage/thresholding (TwIST) algorithm, and other iterative algorithms based on reduced penalized weighted least-squares (PWLS) cost functions (18-23). Especially when integrated with a regularization strategy, such as the total variation (TV) and lp (0<P≤1, or P=2) norm terms (24-30), these iterative algorithms can reconstruct sparse-view images with a quality close to that of analytic reconstruction algorithms using a complete dataset. However, there is a limit to how far these algorithms can reduce the required number of projection images. Generally, when the number of projection images is reduced to one-sixth of the complete full-angle data used in analytic reconstruction algorithms, an acceptable reconstructed image quality can be obtained (27-29). In the case of a lower number of projection images, such as in few-view reconstruction (PT reconstruction with data acquired from less than 10 views), which is in high demand in in vivo imaging applications for living systems, it is difficult to guarantee the quality of the reconstructed images. Moreover, these algorithms need to establish an accurate projection model to ensure the quality of the reconstructed images. Calculations can be time-consuming, and the reconstruction-related parameters need to be optimized for different applications (30). These factors limit the applicability of such algorithms in living-system imaging (31). However, a deep learning network may provide a solution to these problems.

Deep learning is playing an increasingly important role in PT image reconstruction (32,33). Deep learning networks improve tomographic image degradation caused by insufficient contrast agent, low radiation dose, or sparse-view measurements, such as few-view or limited-angle measurements (34-54). For example, Chen et al. proposed an updated residual encoder-decoder convolutional neural network (RED-CNN) integrating the autoencoder, deconvolution, and shortcut connections for low-dose CT imaging, which exhibited good performance in reducing noise, preserving structural details, and detecting lesions (44). Huang et al. proposed a cycle-consistent generative adversarial network (GAN) with the aim of suppressing noise and reducing artifacts caused by low-dose X-ray (45). Much work has been done on deep learning-based reconstructions using sparse-view measurements for CT, PAT, and OPT. With the help of deep learning networks, such as U-net and GAN, high-quality images with a much clearer edge and fine structural information can be obtained using sparse-view data, thus achieving faster imaging speeds (37-40,46-50). For example, Davis et al. used U-net to remove artifacts, reducing the processing time for an undersampled OPT dataset. Their results showed that it was possible to obtain reconstructed images, whose quality was comparable to those obtained from a compressed sensing-based iterative algorithm, with 40% fewer projections (46). Zhang et al. presented a new deep learning network that combined direct inversion and DenseNet to solve the inverse problem, and combined multi-resolution deconvolution and residual learning to achieve image structure preservation and artifact removal. This method was able to reduce the projection number to 60 (47). In another study, Zhang et al. proposed a hybrid-domain CNN to remove artifacts from limited-angle CT imaging. Their results showed good performance in artifact removal (49). Tong et al. developed a domain transformation network for PAT to achieve high-quality image reconstruction from limited-view and sparsely sampled data (50). These methods showed excellent performance in reconstruction based on a small number of measurements. Some researchers have also developed a priori knowledge-based deep learning networks for few-view projection data-based reconstruction (55-60). Shen et al. proposed a patient-specific reconstruction framework that achieved CT image reconstruction from a single-view projection image (55). However, they trained the network parameters and predicted the diagnostic result using images from the same patient. Ying et al. achieved 3D CT image reconstruction from 2 orthogonal 2D images of the human chest with the help of GAN (56); however, the network was trained and validated using data from the same modality, without exploring the migration capabilities of their methods.

Like CT, PAT, and OPT, PT requires a rotating sample or a source-detector pair to collect multi-angle projection data to obtain high-quality images. Data-acquisition time in these cases is prohibitively long, and the samples need special fixation, which is unfavorable to the dynamic imaging of living organisms. Therefore, image reconstruction based on few-view projection data has great significance for in vivo PT. With the aim of addressing the above problems, we developed a 2-stage deep learning network (TSDLN)-based reconstruction framework for parallel-beam PT. In this framework, the TSDLN is comprised of two parts: a reconstruction network (R-net) and a correction network (C-net). The measurements are first sent to the R-net and then to the C-net to obtain high-quality reconstructed images. We trained the TSDLN-based framework and evaluated its performance with CT data from a public database (DeepLesion; Yan et al., NIHCC, Bethesda, MD, USA). The framework exhibited better reconstruction performance than traditional analytic reconstruction algorithms, iterative algorithms, and the cascade U-Net of U2E4C2K32 (52), especially in cases using sparse-view projection images. It should be emphasized that with few-view projection data, the TSDLN-based framework reconstructed high-quality images very close to the original images. By using the previously acquired OPT data in the TSDLN trained on CT data, we further exemplified the migration capabilities of the framework. Our results collectively showed that the TSDLN-based framework has strong capabilities in the reconstruction of sparse-view projection images and exhibited great applicability potential for in vivo PT.

We present the following article in accordance with the Materials Design Analysis Reporting (MDAR) checklist (available at https://qims.amegroups.com/article/view/10.21037/qims-21-778/rc).

Methods

TSDLN-based reconstruction framework for image reconstruction

This study was conducted in accordance with the Declaration of Helsinki (as revised in 2013). A diagram of the TSDLN-based framework is shown in Figure 1. We first built an initial TSDLN. Then, CT datasets from a public database, developed by Yan et al. at the National Institute of Health Clinical Center (NIHCC) (51), were selected to train and optimize the TSDLN. Finally, we evaluated the ability of the optimized TSDLN to reconstruct high-quality volumetric images from few-view projection data. In order not to lose the original projection information, instead of filtering the signal, we used the direct inverse projection method to turn the sinusoidal signal of the few-view projection into an n×n image. In the experiments, previously acquired few-view OPT images were transformed into a corresponding series of sparse sinograms, which were used to obtain the BP images of the object to be reconstructed. Finally, these BP images were used as input data for the TSDLN.

Figure 1 Diagram of the TSDLN-based framework for image reconstruction. The goal of this framework was to reconstruct the chemical distribution of a 3D volume using previously acquired few-view projection data. In the framework, the TSDLN was first trained and optimized using a public CT dataset. Then, the few-view projection images were acquired using an experimental system and converted into a sparse sinogram. The sparse sinogram was then converted into a BP down-sampled image, which was used as the input data for the well-trained TSDLN to finally obtain the high-quality volumetric image. 3D, three-dimensional; TSDLN, 2-stage deep learning network; CT, computed tomography; BP, back-projection.

The TSDLN

The structure of the proposed TSDLN is shown in Figure 2. The BP image, obtained from the BP of the sparse sinogram, was used as input data for the TSDLN. The BP image was fed to the R-net for image reconstruction, and the resulting reconstructed image was fed to the C-net for denoising to finally obtain a high-quality reconstructed image. The R-net was a GAN framework, in which the generator was composed of U-net++ (RG-net) and the discriminator was a CNN with 4 blocks (RD-net). The C-net was a U-net array, responsible for denoising the R-net output.

Figure 2 Diagram of the TSDLN. In the first stage, an R-net was used to generate a WSA image from a BPFDS image. The R-net was built on a GAN framework, with a U-net++-based generator (RG-net) and a discriminator with 4 residual blocks (RD-net). The loss function used in the GAN framework included the L_RD for the generator and L_RG for the discriminator. In the second stage, the U-net-based C-net was used to correct the WSA image, converting it into an RBCPD image, whose loss function was L_C. TSDLN, 2-stage deep learning network; WSA, without stellate artifacts; BPFDS, back-projection from down-sampled sinogram; GAN, generative adversarial network; RBCPD, reconstructed by complete projection dataset.

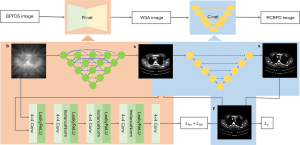
The training process aimed to seek the optimal parameters for the TSDLN that would help it map a BP from a down-sampled sinogram image (BPFDS image) onto an image reconstructed by a complete projection dataset (RBCPD image). Process [1], presented below, summarizes the 2-stage training process, which comprised an initial mapping of a BPFDS image to a WSA image and the subsequent mapping of the WSA image to an RBCPD image. In the process, if b∈ℝN×N is a BPFDS image, s∈ℝN×N denotes an image without stellate artifact (a WSA image). Stellate artifact refers to the fact that FBP reconstruction will produce polygonal artifacts if few projection images are used. x∈ℝN×N is the corresponding RBCPD image, and y∈ℝN×N is the corresponding ground truth. In the process diagram [1], →R−net is training R-net, and →C−net is training C-net.

TSN:b→R−nets→C−netx[1]

The R-net

The R-net was built on a GAN-based framework. We used U-net++ as the generator and referred to it as the RG-net, while the CNN acted as the discriminator and was referred to as the RD-net. To map the BPFDS image to the WSA image, the following minimax problem was raised:

minRGmaxRDLR(RG,RD)[2]

where the first term is the loss function of the RG-net and the second is the loss function of the RD-net.

The loss functions were defined as follows:

LRG=1N∑i=1N[α1(1−RD(RG(bi)))2+α2(RG(bi)−yi)2−α3SSIM(RG(bi),yi)][3]

LRD=1N∑i=1N(1−RG(bi))2+(RD(RG(bi)))2[4]

where α₁, α₂ and α₃ are constant weighting coefficients; N is the mini-batch size; RG(b_i) maps the BPFDS image b_i to the WSA image. RD(·) aims to distinguish between s_i and the corresponding ground truth y_i; SSIM(s_i,y_i) is the error summation of the structural similarity (SSIM) (61) between s_i and y_i; and

SSIM(si,yi)=2μsiμyi+C1μsi2+μyi2+C2⋅2σsiyi+C2σsi2+σyi2+C2[5]

where μ and σ denote the means and standard deviations (the square roots of the variances) of the images, respectively. C₁=(k₁L)² and C₂=(k₂L)², where L is the maximum pixel value in the image, and k₁ and k₂ are small constants to avoid the denominator being close to zero.

The C-net

The second stage involved mapping the WSA image to an RBCPD image. The loss function of this network was defined as follows:

LC=1N∑i=1N(xi−yi)2[6]

It is a mean squared error (MSE) loss function, where x_i is the RBCPD image that is determined from the WSA image s_i via the C-net.

Dataset and pre-processing

The DeepLesion dataset is the largest open-access dataset of multi-category, level-of-focus clinical CT images to date (51). The images in the dataset include a variety of lesion types, such as renal lesions, bone lesions, pulmonary nodules, and lymphadenopathy. The DeepLesion dataset contains 14,601 folders, and we selected the first image from each folder to generate our TSDLN training and testing dataset with a total of 14,601 images, containing lesion information from 4,427 patients. From this dataset, we selected the first 12,000 images from 3,225 patients to train our network. A further 1,818 images from 1,202 patients were selected from the remaining 2,601 images, according to image quality, and used to test our training results. The experimental dataset, collected by our homebuilt OPT system, had been acquired and published in a previous study (14). Full-angle projection images of Drosophilia and Arabidopsis silique samples were collected and down-sampled to obtain sparsely sampled sinusoidal signals.

Each selected image from the DeepLesion dataset was first downscaled to 128×128 pixels. The downscaled images were then rotated to obtain projection data using a method similar to ray tracing technique. First, 180 projections were generated at equal full-view intervals of 180°. Each projection was the linear integral of all the pixels along the direction of the simulated light source. Then, all the projection data (180 projections) were converted into a sinogram which was used to reconstruct the down-sampled image using a BP operator. Finally, the sinogram was sampled at equal intervals to generate sparse-view sinograms that approximated different numbers of sparse-view projection images. The selected sparse views included 2, 3, 4, 5, 6, 9, 10, 12, 15, 30, 36, 45, 60, and 90 projections. The sparse-view sinograms were also used to reconstruct down-sampled images using a BP operator. Finally, all the reconstructed down-sampled images, including those using the complete-view data and the sparse-view data, were included in the training and testing datasets. All images were scaled to the same size 128×128 and the Hounsfield unit (HU) values were normalized to between −175 and 275.

The training dataset obtained by using the above process was employed to train the R-net. The goal was to find a correlation between the direct BP operation and the ground truth. The output of the trained R-net was used as the training dataset for the C-net. The C-net was trained for better reconstruction by using few-view projections, specifically 2, 3, 4, 5, 6, and 9 projections.

Training parameters and environment

Since a sample can produce 18 pairs of data, we expected a minimum of 18 pairs per batch. The R-net parameters were set as: α₁=0.1, α₂=10, α₃=0.03, the learning rate was 10⁻⁴, and the batch size of RlU, RlU,SSIM and U-net++ were 20, 22, and 44. The batch size of the C-net was 100, and the learning rate was 10-4. These parameters were empirically determined in the experiments. The networks were implemented and trained using Pytorch 1.2.0 (https://pytorch.org/) on a personal computer with Intel Core i7-8700 CPU @ 3.20 GHz (Intel, Santa Clara, CA, USA) and an NVIDIA GeForce RTX 2080 Ti (11G) GPU (Nvidia, Santa Clara, CA, USA). The large amount of training data resulted in the R-net already starting to converge at the first epoch, and we eventually selected the parameters of the 20^th epoch as the result, for a total of 12 hours. Each C-net was trained for 2 hours. In the experiments, the processing time of the R-net was 41.13 seconds, and that of the C-net was 32.72 seconds. Thus, the total reconstruction time was 73.85 seconds.

Evaluation indicator

To evaluate the quality of the reconstructed images, 3 commonly used evaluation indictors in sparse-view CT reconstruction were introduced into the experiment, including the peak signal to noise ratio (PSNR) (28), feature similarity (FSIM) (62), and the normalized root mean square error (NRMSE) (63). The PSNR was used as the metric factor and had the following expression:

PSNR(I1,I2)=10log10((MAXI)2‖I1−I2‖22)[7]

where MAX_I was the maximum possible pixel value of the image, I₁ was the sparsely reconstructed image, and I₂ was the reference image that acts as the ground truth.

The FSIM was calculated using the following formula:

FSIM=∑p∈ΩSL(p)⋅PCm(p)∑p∈ΩPCm(p)[8]

where the components of Ω, S_L, and PC_m can be found in the detailed expression in (62). The FSIM values were expressed in a range of 0 to 1. The larger the FSIM and PSNR, the better the quality of the reconstructed image.

The NRMSE was defined using the square root of the mean square error (RMSE), with the following expressions:

RMSE=1mn∑i=0m−1∑j=0n−1[Y(i,j)−X(i,j)]2[9]

NRMSE=RMSEMAXY−MINY[10]

where Y represented the ground truth image, X denoted the reconstructed image from the noisy input, m and n were dimensions of the image, and MAX_Y and MIN_Y were the maximum and minimum values of Y.

Results

Performance evaluation of the TSDLN-based framework

The performance of the TSDLN-based framework was first evaluated with simulations using the DeepLesion dataset. The experiments were divided into two parts. In the first part, the accuracy of the TSDLN-based framework was evaluated by comparing it with the popular FBP, pixel vertex driven model (PVDM)-based TV regularized SART algorithm (PVDM-SART), and the cascade U-Net of U2E4C2K32 (52). In the second part, we evaluated the role of the network structure and parameters and their influence on reconstruction results.

Accuracy verification

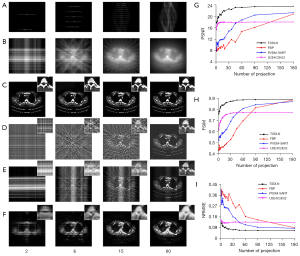
In the accuracy verification experiments, sample images were randomly selected from the test dataset and reconstructed using FBP, PVDM-SART, and the TSDLN-based framework. The PVDM-SART parameters were set as N=20, N_grad=10 and λ=0.05. The results of the representative test data are shown in Figure 3A-3F. For ease of reference, we did not include the reconstructed results for all the projection numbers examined, but for a representative number (2, 6, 15, and 60) of projections. Results including those of 2, 4, 6, 9, 15, 45, 60, and 180 projections are presented in Figure S1. The sinogram and corresponding BP images are shown in Figure 3A and Figure 3B, and Figure 3C-3F present the reconstructed results using the TSDLN, FBP, PVDM-SART, and the cascade U-Net of U2E4C2K32. We found that the reconstructed results using the proposed TSDLN were better than those using FBP, PVDM-SART, and U2E4C2K32 in all investigated cases. As observed visually from the reconstructed images, FBP results were affected when the number of projections was reduced to 60 and were greatly affected when the number was reduced to 45 (Figure S1D). For the PVDM-SART, these numbers were 60 and 15. When there were 6 projections, the U2E4C2K32 results were blurred. When the number was reduced to 2, it could not resolve the details. However, for the proposed TSDLN, all results were free of artifact noise, and when the number of projections was reduced to fewer than 10, we still obtained reconstructed images that were very similar to those of FBP and PVDM reconstructions using 180 projections. We further calculated the difference images by subtracting the reconstructed images from the original ones, and observing the missing information from the difference images for the different projection numbers. The lower the number of projections, the greater the information loss in the reconstructed images (Figure S2). To evaluate these reconstruction algorithms quantitatively, we calculated evaluation indicators for the PSNR, FSIM, and NRMSE (Figure 3G-3I). We found that as the number of projections increased, the PSNR and FSIM also increased, while the NRMSE values decreased for all results. When the number of projections was more than 9, the PSNR value provided by the TSDLN was higher than that of the U2E4C2K32 and the FBP and PVDM-SART using 180 projections. When the projection number was greater than 20, the FSIM value of the TSDLN was greater than that of the PVDM-SART with 180 projections (Figure S1). To further observe the anatomical details, we extracted partially-enlarged views (images shown in the upper right corner of Figure 3C-3F), and drew the same conclusions. These results verified the accuracy of the proposed TSDLN-based framework for few-view projection image reconstruction.

Figure 3 Accuracy verification of the proposed TSDLN-based framework. (A,B) Sinograms and input BP images corresponding to 2, 6, 15, and 60 projections; (C-F) reconstructed results using the TSDLN, FBP, PVDM-SART, and U2E4C2K32, respectively; (G-I) PSNR, FSIM, and NRMSE values as a function of the projection number. The images in the upper right corner of (C-F) are partially-enlarged views of the reconstructed image. TSDLN, 2-stage deep learning network; BP, back-projection; FBP, filtered back-projection; PVDM-SART, pixel vertex driven model-based total variation regularized simultaneous algebra reconstruction technique algorithm; PSNR, peak signal to noise ratio; FSIM, feature similarity; NRMSE, normalized root mean square error.

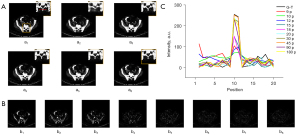
We found that the proposed TSDLN-based framework had good reconstruction abilities in few-view projections-based PT. With an increase in the number of projections, the overall imaging quality did not change significantly, although some details were lost (Figure 4A). When the number of projections was greater than 30, the detailed parts of the image were still well-reconstructed. However, when the number of projections was reduced to 9, tiny details were difficult to reconstruct and there was a big difference in detail compared to the ground truth. To thoroughly investigate the relationship between the loss of information and the reduction in projections, we subtracted the reconstructed images from the originals and correlated the difference images to the number of the projections (Figure 4B). As the number of projections decreased, more information was lost. When the number of projections was greater than 9, relatively little information was lost in the reconstructed images, and the variability of the difference images using different numbers of projections was not obvious. When the projection number was reduced to 6, the contour information and internal details of the reconstructed images almost disappeared. When the projection number was further reduced to 2, the significant and relatively large internal features of the reconstructed image were also lost. To observe this phenomenon more clearly, we selected localized regions of the reconstructed images for comparison of the intensity profiles (Figure 4C), and our observations supported the same conclusions.

Figure 4 Analysis of detailed resolution ability. (A) Ground truth selected from the DeepLesion dataset (a₁) and images reconstructed using the proposed TSDLN-based framework with 9, 30, 45, 90, and 180 projections (a₂-a₆, respectively); (B) difference images between the original and reconstructed images corresponding to (A); (C) intensity profiles extracted from the reconstructed images and the ground truth along the selected line, shown with a red line in (a₁). TSDLN, 2-stage deep learning network.

Performance analysis

To analyze the reconstruction performance of the proposed TSDLN-based framework with few-view projection data and discuss the necessity for the TSDLN architecture, we disassembled the R-net layer of the proposed TSDLN and discussed the reconstruction performance of the different networks. The R-net was disassembled into a U-net++ that contained only generators, a network of RlU that contained generator and discriminator but did not use SSIM as a loss function, and a network of RlU,SSIM that contained generator and discriminator and used SSIM as a loss function. Similarly, we used the DeepLesion dataset to train and test these 4 reconstruction networks. Representative testing results are shown in Figure 5, and Figure 5A-5D present the reconstructed results of U-net++, RlU, RlU,SSIM, and TSDLN using 2, 4, 6, and 9 projections. Intuitive analysis of the reconstructed images yielded several conclusions, as follows: First, when using few-view projection for reconstruction, U-net++ can reconstruct the high-brightness portion of the image, but not the low-brightness portion very well. Second, the reconstructed results of RlU and RlU,SSIM are similar and closer to the ground truth than those of U-net++. Third, as the number of projections increases, so does the ability of all networks to reconstruct details. Finally, the addition of a correction function for the RlU,SSIM (i.e., the TSDLN) is a good way to remove the noise present in the RlU,SSIM results, bringing the reconstruction results closer to the ground truth.

Figure 5 Performance analysis of the different reconstruction networks. (A-D) Reconstructed results of U-net++, RlU, RlU,SSIM, and TSDLN using 2, 4, 6, and 9 projections, respectively; (E-G) evaluation indicators for the PSNR, FSIM, and NRMSE values as a function of the projection number. The images in the upper right corner of (A-D) are the partially-enlarged views of the reconstructed images. TSDLN, 2-stage deep learning network; PSNR, peak signal to noise ratio; FSIM, feature similarity; NRMSE, normalized root mean square error.

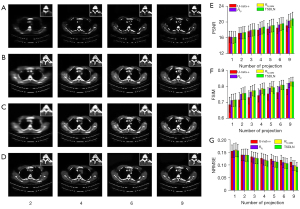
For soft tissue with a relatively low signal intensity, U-net++, RlU and RlU,SSIM could not provide good reconstruction quality when using few-view projections. The addition of the C-net could remove the artificial noise and achieve resolution similar to the ground truth. In general, U-net++ had the worst reconstruction results, and RlU and RlU,SSIM provided similar reconstruction results. In applying the correction effect, the C-net reduced the noise in the reconstruction results of RlU,SSIM. To observe the differences with low numbers of projections, we calculated the difference images by subtracting the reconstructed images from the original images and observed the missing information from the difference images for various projection numbers (Figure S3). We could observe some differences in detail on these difference images. For example, in the bottom third of the reconstructed images, clear white lines can be observed in Figure S3A, which do not appear in Figure S3B-S3D. This indicated that there was significant information loss in the images reconstructed by U-net++. While there were no obvious differences between Figure S3B-S3D in the difference images, there was smoothing in Figure S3B and Figure S3C at a low number of projections in the reconstructed images.

We quantitatively analyzed the reconstructed results of all the samples of the testing dataset by calculating evaluation indicators for the PSNR, FSIM, and NRMSE. The quantitative analysis results are shown in Figure 5E-5G. In most cases, U-net++ provided the poorest reconstruction quality, while the TSDLN provided the best reconstruction quality, as seen from the evaluation factor values. Although U-net++ provided a slightly higher mean PSNR value than the TSDLN when using few-view projection for reconstruction, the TSDLN had a slightly smaller variance. This indicated better algorithmic stability in the TSDLN. The PSNR values of RlU,SSIM were better than those of RlU in most cases of few-view projections reconstruction, while the FSIM values were always better. This indicated that RlU,SSIM was able to retain more detailed information. We also calculated other evaluation indicators for the MSE, RMSE, and NMSE values (Table S1). Therefore, we used RlU,SSIM to generate the training data for the C-net. It is also interesting to note from the quantitative FSIM results that the lower the number of projections used in the reconstruction, the more pronounced the correction effect of the C-net. This indicated that when the number of projections that can be acquired is small, i.e., fewer than 4 projections, the use of the C-net allows better recovery of detailed information.

Taking these results collectively, we reached the following conclusions. First, U-net++ does not perform well in few-view projection-based reconstruction problems. Secondly, the reconstruction quality of RlU,SSIM is better than that of RlU, indicating that the SSIM loss has a substantial impact on the reconstruction. Thirdly, C-net has a corrective effect on the output of the R-net, which provides better noise suppression in the low-brightness portions of images, such as areas of soft tissue. These results showed that the proposed TSDLN is a valid method for obtaining better reconstruction results using few-view projections.

Verification of the migration capability of the TSDLN-based framework

We further verified the migration capabilities of the TSDLN with the experimental OPT dataset. It should be noted that the TSDLN training only used data from the DeepLesion dataset and not from the experimental OPT dataset. The down-sampled OPT data of Drosophila and Arabidopsis silique were selected as the test dataset for the trained TSDLN. Since the actual OPT data collected did not include a true image of the sample, we used the reconstructed results of the PVDM-SART with 180 projections data as the ground truth. In Figure 6A,6B, the reconstructed results of the Drosophila and Arabidopsis silique are shown, respectively, using the TSDLN with 2, 4, 9, 15, and 60 projections, and the PVDM-SART and FBP with 180 projections. More results, including 2, 3, 4, 5, 6, and 9 projections, are presented in Figure S4. We found that when the projection number was reduced to 9, the contours and distribution information of the investigated samples could still be seen in the reconstructed images. The images could not resolve the structure when the projection number was decreased to 2. Similarly, we calculated quantitative evaluation indicators for the PSNR, FSIM, and NRMSE (Figure 6C-6E), with the following results. Firstly, for both the Drosophila and Arabidopsis silique samples, the TSDLN-based framework recovered the sample image information well and had a high degree of agreement with the results obtained by the PVDM-SART algorithm. This indicated that the TSDLN has good migration ability.

Figure 6 Verification of the migration capabilities of the proposed TSDLN-based reconstruction framework. (A,B) Reconstructed results of the Drosophila and Arabidopsis silique, respectively, using the TSDLN with 2, 4, 6, 9, and 15 projections, and the PVDM-SART and FBP with 180 projections; (C-E) corresponding evaluation indicators of the PSNR, FSIM, and NRMSE values as a function of the number of projections, where the red columns represent the results of the Drosophila samples, and the blue columns denote those of the Arabidopsis silique samples. TSDLN, 2-stage deep learning network; FBP, filtered back-projection; PVDM-SART, pixel vertex driven model based total variation regularized simultaneous algebra reconstruction technique algorithm; PSNR, peak signal to noise ratio; FSIM, feature similarity; NRMSE, normalized root means square error.

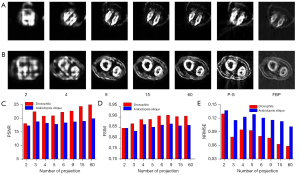
Secondly, the reconstructed results of the Drosophila samples were slightly better than those of the Arabidopsis silique. For example, at 3 projections, the Drosophila sample had a PSNR greater than 18, and an FSIM greater than 0.85. When the projection number was greater than 2, the NRMSE values of the Drosophila were lower than those of the Arabidopsis silique. However, to achieve such values, a minimum of 4 projections were required for the Arabidopsis silique sample, and the results fluctuated. This may be due to the somewhat simple morphology and distribution of the Drosophila samples. The results in this section showed that our proposed TSDLN had good migration ability in OPT imaging.

The proposed framework was further evaluated to determine how much it relied on a priori knowledge of what medical samples typically look like. We conducted a simulation of the reconstruction of an unnatural digital phantom (Figure S5). The results showed that when the projection number was reduced from 180 to 10, the structure of the phantom could be well resolved. However, when the projection number was fewer than 10, the reconstructed images became blurred.

Discussion

Image reconstruction based on few-view projection data will be of great significance for in vivo PT of living organisms. To this end, a TSDLN-based framework was developed for reconstructing parallel-beam PT images. Combining R-net and C-net in two steps, the TSDLN-based framework performed well in few-view projections-based reconstruction. The TSDLN was trained using down-sampled data from a public dataset. We then verified the accuracy of the TSDLN-based framework with test data extracted from the public dataset. Results showed that the TSDLN-based framework could obtain a much higher accuracy with few projections than FBP, iterative algorithms, and the cascade U-Net of U2E4C2K32. Then, we demonstrated the advantages of and necessity for a 2-stage network for few-view projection reconstruction by decomposing the network structure. Finally, we demonstrated the good migration capabilities of the proposed TSDLN-based framework in few-view projection reconstruction using previously acquired OPT data as the experimental dataset. The overall experimental results showed that by using the proposed TSDLN-based framework, we were able to reconstruct useful information about the investigated sample with few-view projections. These findings could potentially increase the applicability of PT for imaging living organisms. The TSDLN had 2 loss functions that separately constrained the network. The constraint was stronger than that of a single-layer network, and the reconstruction result was closer to the actual object. Furthermore, training the TSDLN was easier than training a single-stage network, which reduced computer performance requirements.

Although some details were lost, especially when sparse-view projection images were used, the TSDLN-based framework still reconstructed high-quality images that were very close to the originals when the projection number was reduced to 6, with an FSIM larger than 0.827. This value was equivalent to that obtained in reconstruction using a traditional FBP algorithm and 90 projections (FSIM =0.814). The FSIM value for the proposed TSDLN-based framework was 0.848 when the projection number was reduced to 15, which was comparable to that obtained by the SART-PVDM algorithm at 90 projections (FSIM =0.842). In this case, reconstructions using a small number of projections had a high morphological similarity to the original images, which also showed that the loss of information was relatively small. However, exactly how many angles are needed to ensure that no useful information is lost depends on the details of the region of interest. We also need to consider a combination of quantitative evaluation metrics for the reconstructed image and the amount of information lost. If just the contour information of the reconstructed sample is required, 2 projections are sufficient. If detailed inner information is required, the number of projections depends on the detail to be observed. There may be cases where a reconstruction framework with a small number of projections is simply not appropriate. We further analyzed the difference images by selecting the region of interest and calculating the number of lost pixels in the reconstructed image (Figure S2A). The results showed that the values became larger as the number of projections decreased, which is consistent with and complementary to the quantitative analysis indices. Such information loss, which may impact clinical pathological analysis, could be due to 2 possible reasons. First, the training data we used to train the TSDLN had a low resolution (128×128), which impacted the image details. Secondly, the TSDLN framework was too large, which resulted in gradient disappearance and loss of detailed information. These issues can be improved in follow-up studies in two ways. First, we can increase the number of dimensions of the training dataset and add high-resolution images into it. Secondly, we can employ a super-resolution network in the second stage of the TSDLN framework and perform super-resolution operations on the images reconstructed from the first-stage network to obtain images with sharp detail resolution.

We also investigated the robustness of the proposed TSDLN framework with regard to mechanical or sample drift by performing two sets of simulations. In these simulations, we artificially misaligned sinograms to mimic mechanical or sample drift. In the first group, the 1°–45° and 91°–135° sinograms were moved up by 5 pixels, while those of the other angles remained unchanged. In the second group, the 1°–30°, 61°–90°, and 121°–150° sinograms were moved up by 5 pixels, and those of the other angles remained unchanged. Obvious misalignment appeared in the reconstructed images as the projection number increased (Figure 7 and Figure S6). Furthermore, the fewer the number of projections, the less information was lost in the reconstructed image. For example, when the projection number was 45, the reconstructed images exhibited obvious misalignment, but when the number of projections was 2 and 4, there was relatively little lost information. From these results, we concluded that the misalignment of sinograms caused by mechanical or sample drift could affect the performance of the proposed TSDLN-based framework, especially when more projections were used in the reconstruction.

Figure 7 Reconstructed images with a misalignment in the sinogram. (A,B) Sinograms and corresponding input BP images for 2, 4, 6, 9, 15, 45, 60, and 180 projections; (C) reconstructed images using the TSDLN; (D) difference images between the original and reconstructed images. BP, back-projection; TSDLN, 2-stage deep learning network.

We conducted another simulation to observe the quality of the reconstructed images using 2 projections from incorrect angles. One of the projections was fixed at the 90° angle while the other projection was selected at the 180°, 175°, 170°, 160°, 150°, and 140° angle. The reconstructed images and corresponding difference images are shown in Figure S7. When the interval of the two projections was 90°, the anatomical details in the reconstructed images were well resolved. When the interval was reduced to 70° or less, the image became blurred and it was difficult to distinguish useful information. In addition, as the interval decreased, the reconstructed image rotated and became distorted, with increasing severity. These results showed that the proposed TSDLN-based framework is able to generate high-quality images when the projection interval was consistent with the training dataset.

Conclusions

In conclusion, a reconstruction framework based on a TSDLN was developed for parallel-beam PT. We demonstrated the accuracy and feasibility of the framework for few-view projection-based reconstruction with simulations, and further explored its migration capabilities using previously acquired OPT data. Our results showed that by using the deep learning technique, it is possible to achieve high-quality PT using few-view projections. We believe that this work will facilitate basic, preclinical, and clinical applications of PT techniques, such as obtaining a patient’s 3D CT image from a single 2D projection, a challenge we will be working on in the future.

Acknowledgments

Funding: This work was supported in part by the National Natural Science Foundation of China (Nos. 81871397, 81627807, 62101439, 62105255, 91959208, and 62007026), the Fundamental Research Funds for Central Universities (No. QTZX2185), the National Young Top-notch Talent of “Ten Thousand Talents Program”, Shaanxi Science Fund for Distinguished Young Scholars (No. 2020JC-27), the Fok Ying-Tung Education Foundation of China (No. 161104), the Program for the Young Top-notch Talent of Shaanxi Province, and the National Key R&D Program of China (No. 2018YFC0910600).

Footnote

Reporting Checklist: The authors have completed the MDAR checklist. Available at https://qims.amegroups.com/article/view/10.21037/qims-21-778/rc

Conflicts of Interest: All authors have completed the ICMJE uniform disclosure form (available at https://qims.amegroups.com/article/view/10.21037/qims-21-778/coif). The authors have no conflicts of interest to declare.

Ethical Statement: The authors are accountable for all aspects of the work in ensuring that questions related to the accuracy or integrity of any part of the work are appropriately investigated and resolved. The study was conducted in accordance with the Declaration of Helsinki (as revised in 2013).

Open Access Statement: This is an Open Access article distributed in accordance with the Creative Commons Attribution-NonCommercial-NoDerivs 4.0 International License (CC BY-NC-ND 4.0), which permits the non-commercial replication and distribution of the article with the strict proviso that no changes or edits are made and the original work is properly cited (including links to both the formal publication through the relevant DOI and the license). See: https://creativecommons.org/licenses/by-nc-nd/4.0/.

References

1. McCullough EC, Payne JT. X-ray-transmission computed tomography. Med Phys 1977;4:85-98. [Crossref] [PubMed]
2. Sharpe J, Ahlgren U, Perry P, Hill B, Ross A, Hecksher-Sørensen J, Baldock R, Davidson D. Optical projection tomography as a tool for 3D microscopy and gene expression studies. Science 2002;296:541-5. [Crossref] [PubMed]
3. Martinez-Ramirez JD, Quispe-Siccha R, Garcia-Segundo C, Gonzalez FJ, Espinosa-Luna R, Gutierrez-Juarez G. Photoacoustic tomography system. J Appl Res Technol 2012;10:14-9. [Crossref]
4. Chen X, Zhang C, Lin P, Huang KC, Liang J, Tian J, Cheng JX. Volumetric chemical imaging by stimulated Raman projection microscopy and tomography. Nat Commun 2017;8:15117. [Crossref] [PubMed]
5. Shi L, Fung AA, Zhou A. Advances in stimulated Raman scattering imaging for tissues and animals. Quant Imaging Med Surg 2021;11:1078-101. [Crossref] [PubMed]
6. Louie AY, Hüber MM, Ahrens ET, Rothbächer U, Moats R, Jacobs RE, Fraser SE, Meade TJ. In vivo visualization of gene expression using magnetic resonance imaging. Nat Biotechnol 2000;18:321-5. [Crossref] [PubMed]
7. Alanentalo T, Lorén CE, Larefalk A, Sharpe J, Holmberg D, Ahlgren U. High-resolution three-dimensional imaging of islet-infiltrate interactions based on optical projection tomography assessments of the intact adult mouse pancreas. J Biomed Opt 2008;13:054070. [Crossref] [PubMed]
8. Bassi A, Fieramonti L, D'Andrea C, Mione M, Valentini G. In vivo label-free three-dimensional imaging of zebrafish vasculature with optical projection tomography. J Biomed Opt 2011;16:100502. [Crossref] [PubMed]
9. McGinty J, Tahir KB, Laine R, Talbot CB, Dunsby C, Neil MA, Quintana L, Swoger J, Sharpe J, French PM. Fluorescence lifetime optical projection tomography. J Biophotonics 2008;1:390-4. [Crossref] [PubMed]
10. Darrell A, Marias K, Broadoy M, Meyer H, Ripoll J. Noise reduction in fluorescence optical projection tomography. IEEE International Workshop on Imaging Systems and Techniques. Chania, Greece, 2008.
11. Lasser T, Ntziachristos V. Optimization of 360 degrees projection fluorescence molecular tomography. Med Image Anal 2007;11:389-99. [Crossref] [PubMed]
12. Deliolanis N, Lasser T, Hyde D, Soubret A, Ripoll J, Ntziachristos V. Free-space fluorescence molecular tomography utilizing 360 degrees geometry projections. Opt Lett 2007;32:382-4. [Crossref] [PubMed]
13. Ge J, Erickson SJ, Godavarty A. Multi-projection based fluorescence optical tomography using a hand-held probe based optical imager. Conference on optical tomography and spectroscopy of tissue VIII, San Jose, USA, 2009.
14. Chen X, Zhu S, Wang H, Bao C, Yang D, Zhang C, Lin P, Cheng JX, Zhan Y, Liang J, Tian J. Accelerated Stimulated Raman Projection Tomography by Sparse Reconstruction From Sparse-View Data. IEEE Trans Biomed Eng 2020;67:1293-302. [Crossref] [PubMed]
15. De AK, Goswami D. Exploring the nature of photo-damage in two-photon excitation by fluorescence intensity modulation. J Fluoresc 2009;19:381-6. [Crossref] [PubMed]
16. Yao HB, Xia Y, Jun Z, Anzhi H. Orthogonal projection sampling method used in reconstruction of incomplete data field. Microw Opt Techn Let 2006;48:2333-6. [Crossref]
17. Mishra D, Longtin JP, Singh RP, Prasad V. Performance evaluation of iterative tomography algorithms for incomplete projection data. Appl Opt 2004;43:1522-32. [Crossref] [PubMed]
18. Gordon R, Bender R, Herman GT. Algebraic reconstruction techniques (ART) for three-dimensional electron microscopy and x-ray photography. J Theor Biol 1970;29:471-81. [Crossref] [PubMed]
19. Andersen AH, Kak AC. Simultaneous algebraic reconstruction technique (SART): a superior implementation of the art algorithm. Ultrason Imaging 1984;6:81-94. [Crossref] [PubMed]
20. Badea C, Gordon R. Experiments with the nonlinear and chaotic behaviour of the multiplicative algebraic reconstruction technique (MART) algorithm for computed tomography. Phys Med Biol 2004;49:1455-74. [Crossref] [PubMed]
21. Bappy DM, Jeon I. Modified simultaneous iterative reconstruction technique for fast, high-quality CT reconstruction. IET Image Process 2017;11:701-8. [Crossref]
22. Xu Q, Yang D, Tan J, Sawatzky A, Anastasio MA. Accelerated fast iterative shrinkage thresholding algorithms for sparsity-regularized cone-beam CT image reconstruction. Med Phys 2016;43:1849. [Crossref] [PubMed]
23. Chae BG, Lee S. Sparse-view CT image recovery using two-step iterative shrinkage-thresholding algorithm. ETRI J 2015;37:1251-8. [Crossref]
24. Hu Y, Xie L, Luo L, Nunes JC, Toumoulin C. L0 constrained sparse reconstruction for multi-slice helical CT reconstruction. Phys Med Biol 2011;56:1173-89. [Crossref] [PubMed]
25. Zhang C, Zhang T, Li M, Peng C, Liu Z, Zheng J. Low-dose CT reconstruction via L1 dictionary learning regularization using iteratively reweighted least-squares. Biomed Eng Online 2016;15:66. [Crossref] [PubMed]
26. Lu W, Li L, Cai A, Zhang H, Wang L, Yan B. A weighted difference of L1 and L2 on the gradient minimization based on alternating direction method for circular computed tomography. J Xray Sci Technol 2017;25:813-29. [Crossref] [PubMed]
27. Du Y, Wang X, Xiang X, Wei Z. Evaluation of hybrid SART + OS + TV iterative reconstruction algorithm for optical-CT gel dosimeter imaging. Phys Med Biol 2016;61:8425-39. [Crossref] [PubMed]
28. Luo XQ, Yu W, Wang CX. An image reconstruction method based on total variation and wavelet tight frame for limited-angle CT. IEEE Access 2018;6:1461-70.
29. Correia T, Lockwood N, Kumar S, Yin J, Ramel MC, Andrews N, Katan M, Bugeon L, Dallman MJ, McGinty J, Frankel P, French PM, Arridge S. Accelerated Optical Projection Tomography Applied to In Vivo Imaging of Zebrafish. PLoS One 2015;10:e0136213. [Crossref] [PubMed]
30. Xie H, Wang HY, Wang L, Wang N, Liang JM, Zhan YH, Chen XL. Comparative studies of total-variation-regularized sparse reconstruction algorithms in projection tomography. AIP Adv 2019;9:085122. [Crossref]
31. Wang N, Chen DF, Chen D, Bao CP, Liang JM, Chen XL, Zhu SP. Feasibility study of limited-angle reconstruction for in vivo optical projection tomography based on novel sample fixation. IEEE Access 2019;7:87681-91.
32. Wang G. A perspective on deep imaging. IEEE Access 2016;4:8914-24.
33. Ge Y, Su T, Zhu J, Deng X, Zhang Q, Chen J, Hu Z, Zheng H, Liang D. ADAPTIVE-NET: deep computed tomography reconstruction network with analytical domain transformation knowledge. Quant Imaging Med Surg 2020;10:415-27. [Crossref] [PubMed]
34. Chen H, Zhang Y, Chen Y, Zhang J, Zhang W, Sun H, Lv Y, Liao P, Zhou J, Wang G. LEARN: Learned Experts' Assessment-Based Reconstruction Network for Sparse-Data CT. IEEE Trans Med Imaging 2018;37:1333-47. [Crossref] [PubMed]
35. Huang Y, Lu Y, Taubmann O, Lauritsch G, Maier A. Traditional machine learning for limited angle tomography. Int J Comput Assist Radiol Surg 2019;14:11-9. [Crossref] [PubMed]
36. Yang Q, Yan P, Zhang Y, Yu H, Shi Y, Mou X, Kalra MK, Zhang Y, Sun L, Wang G, Low-Dose CT. Image Denoising Using a Generative Adversarial Network With Wasserstein Distance and Perceptual Loss. IEEE Trans Med Imaging 2018;37:1348-57. [Crossref] [PubMed]
37. Dai XB, Bai JN, Liu TL, Xie LZ. Limited-view cone-beam CT reconstruction based on an adversarial autoencoder network with joint loss. IEEE Access 2019;7:7104-16.
38. Zhao J, Chen Z, Zhang L, Jin X. Unsupervised learnable sinogram inpainting network (SIN) for limited angle CT reconstruction. arXiv preprint arXiv:1811.03911.
39. Anirudh R, Kim H, Thiagarajan JJ, Mohan KA, Champley K, Bremer T. Lose the views: limited angle CT reconstruction via implicit sinogram completion. IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, USA, 2018.
40. Han Y, Ye JC. Framing U-Net via Deep Convolutional Framelets: Application to Sparse-View CT. IEEE Trans Med Imaging 2018;37:1418-29. [Crossref] [PubMed]
41. Ronneberger O, Fischer P, Brox T. U-Net: convolutional networks for biomedical image segmentation. In: Navab N, Hornegger J, Wells W, et al. editors. MICCAI 2015: International Conference on Medical Image Computing and Computer-Assisted Intervention. 2015 Nov 18; Munich, Germany, Springer, 2015:234-41.
42. Goodfellow J, Pouget-Abadie J, Mirza M, Xu B, Warde-Farley D, Ozair S, Courville A, Bengio Y. Generative adversarial nets. arXiv preprint arXiv; 1406.2661.
43. Mirza M, Osindero S. Conditional generative adversarial nets. arXiv preprint arXiv:1411.1784.
44. Chen H, Zhang Y, Kalra MK, Lin F, Chen Y, Liao P, Zhou J, Wang G, Low-Dose CT. With a Residual Encoder-Decoder Convolutional Neural Network. IEEE Trans Med Imaging 2017;36:2524-35. [Crossref] [PubMed]
45. Huang ZY, Chen ZX, Zhang QY, Quan GT, Ji M, Zhang CJ, Yang YF, Liu X, Liang D, Zheng HR, Hu ZL. CaGAN: a cycle-consistent generative adversarial network with attention for low-dose CT imaging. IEEE Trans Comput Imaging 2020;6:1203-18. [Crossref]
46. Davis SPX, Kumar S, Alexandrov Y, Bhargava A, da Silva Xavier G, Rutter GA, Frankel P, Sahai E, Flaxman S, French PMW, McGinty J. Convolutional neural networks for reconstruction of undersampled optical projection tomography data applied to in vivo imaging of zebrafish. J Biophotonics 2019;12:e201900128. [Crossref] [PubMed]
47. Zhang Z, Liang X, Dong X, Xie Y, Cao G. A Sparse-View CT Reconstruction Method Based on Combination of DenseNet and Deconvolution. IEEE Trans Med Imaging 2018;37:1407-17. [Crossref] [PubMed]
48. Zhou Z, Siddiquee MMR, Tajbakhsh N, Liang J. UNet++: Redesigning Skip Connections to Exploit Multiscale Features in Image Segmentation. IEEE Trans Med Imaging 2020;39:1856-67. [Crossref] [PubMed]
49. Zhang Q, Hu Z, Jiang C, Zheng H, Ge Y, Liang D. Artifact removal using a hybrid-domain convolutional neural network for limited-angle computed tomography imaging. Phys Med Biol 2020;65:155010. [Crossref] [PubMed]
50. Tong T, Huang W, Wang K, He Z, Yin L, Yang X, Zhang S, Tian J. Domain Transform Network for Photoacoustic Tomography from Limited-view and Sparsely Sampled Data. Photoacoustics 2020;19:100190. [Crossref] [PubMed]
51. Yan K, Wang X, Lu L, Summers RM. DeepLesion: automated mining of large-scale lesion annotations and universal lesion detection with deep learning. J Med Imaging (Bellingham) 2018;5:036501. [Crossref] [PubMed]
52. Kofler A, Haltmeier M, Kolbitsch C, Kachelrieß M, Dewey M. A U-Nets cascade for sparse view computed tomography. International Workshop on Machine Learning for Medical Image Reconstruction. Springer, 2018:91-9.
53. Schlemper J, Caballero J, Hajnal JV, Price AN, Rueckert D. A Deep Cascade of Convolutional Neural Networks for Dynamic MR Image Reconstruction. IEEE Trans Med Imaging 2018;37:491-503. [Crossref] [PubMed]
54. Zhang H, Xu T, Li H, Zhang S, Wang X, Huang X, Metaxas DN. Stackgan: Text to photo-realistic image synthesis with stacked generative adversarial networks. IEEE International Conference on Computer Vision 2017:5907-15.
55. Shen L, Zhao W, Xing L. Patient-specific reconstruction of volumetric computed tomography images from a single projection view via deep learning. Nat Biomed Eng 2019;3:880-8. [Crossref] [PubMed]
56. Ying X, Guo H, Ma K, Wu J, Weng Z, Zheng Y. X2CT-GAN: reconstructing CT from biplanar X-rays with generative adversarial networks. IEEE/CVF Conference on Computer Vision and Pattern Recognition 2019:10619-28.
57. Henzler P, Rasche V, Ropinski T, Ritschel T. Single-image Tomography: 3D Volumes from 2D Cranial X-Rays. Computer Graphics Forum 2018;37:377-88. [Crossref]
58. Xu Y, Yan H, Ouyang L, Wang J, Zhou L, Cervino L, Jiang SB, Jia X. A method for volumetric imaging in radiotherapy using single x-ray projection. Med Phys 2015;42:2498-509. [Crossref] [PubMed]
59. Jiang Y, Li P, Zhang Y, Pei Y, Yuan X. 3D volume reconstruction from single lateral X-ray image via cross-modal discrete embedding transition. In: Liu M, Yan P, Lian C, et al. editors. MLMI 2020: International Workshop on Machine Learning in Medical Imaging. Springer, 2020:322-31.
60. Wang Y, Zhong Z, Hua J. DeepOrganNet: On-the-Fly Reconstruction and Visualization of 3D / 4D Lung Models from Single-View Projections by Deep Deformation Network. IEEE Trans Vis Comput Graph 2020;26:960-70. [PubMed]
61. Wang Z, Bovik AC, Sheikh HR, Simoncelli EP. Image quality assessment: from error visibility to structural similarity. IEEE Trans Image Process 2004;13:600-12. [Crossref] [PubMed]
62. Zhang L, Zhang L, Mou X, Zhang D. FSIM: a feature similarity index for image quality assessment. IEEE Trans Image Process 2011;20:2378-86. [Crossref] [PubMed]
63. Kang E, Min J, Ye JC. A deep convolutional neural network using directional wavelets for low-dose X-ray CT reconstruction. Med Phys 2017;44:e360-75. [Crossref] [PubMed]