Translation and rotation analysis based on stress MRI for the diagnosis of anterior cruciate ligament tears
Introduction
The anterior cruciate ligament (ACL) is one of the most important structures responsible for proper movement control and stabilization of the knee joint. Injury to the anterior cruciate ligament leads to complex knee instability, including disruption of tibial translation and rotation. Evaluation of knee stability after injury of the anterior cruciate ligament should be performed based both on physical examination [Lachman test (1) and Pivot Shift test (2)] and standard magnetic resonance imaging (MRI). After the Lachman test was described over 30 years ago (1), many of the clinical examination devices were developed, such as the instrumented version of the Lachman test performed on a KT 1000 (3) device or a Rolimeter (4). However, the general rules of calculation of tibia translation remained unchanged: anterior translation of tibia was achieved by the anteriorly directed force applied to the calf on 30° knee flexion, and tibia anterior translation in the sagittal plane was recorded using various devices (4-6).
Several devices have been described to test the anterior tibial translation by MRI (7-10), but none have been validated. The previously described devices were not used for the purpose of three-dimensional calculations. Moreover, the devices were not available for distribution with the possibility of adapting the device to our MRI laboratory. For this reason, a prototype of the device was developed.
When performing the anterior translation of the tibia in general, the resulting displacement is not just one plane movement. The result comprises both translation and rotation, which is defined as a three-dimensional transformation. Several methods based on transformation calculations have been described (11). The reference points used for calculations in these methods were attached to the skin and were mobile during the examination (12,13). To perform accurate 3D transformation calculations, landmarks should be precisely correlated with the anatomical regions and remain unchanged during tibial translation to reduce measurement error. In several papers, bony landmarks for the knee joint were developed (14), but all these anatomical references were dedicated to CT imaging techniques (11,15-19).
When performing a CT scan, the contrast between bone and soft tissues is high, which makes it easy to identify landmarks on the bone. Also, methods that enable automatic alignment of bone contours, called automatic registration, allow for greater accuracy, as the software aligns the entire bone volume. For MRI, the levels of bone-soft tissue contrast are not sufficient to manually define landmarks the same as in CT. The software is also unable to determine the contours of the bones with automatic registration. Nowadays, MRI is a gold standard technique for a ligamentous knee injury, and the landmarks for 3D transformation calculations should be easy to find and establish during the MRI examination (20).
The purpose of the study was to develop a reproducible model of calculations of 3D tibia translation in ACL-injured knees using an Arthroholder device during the MRI examination.
Methods
Participants
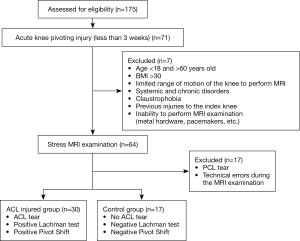
After obtaining IRB approval from the Local Ethical Committee of Bielsko-Biała, 175 patients admitted to our clinic between January 2018 and December 2019 with possible ACL injury were screened (Figure 1). The study was conducted in accordance with the Declaration of Helsinki (as revised in 2013). The informed consent was taken from all the patients. Seventy-one patients who had an acute knee pivoting injury (less than three weeks) were included in the study. Exclusion criteria for both groups were: age <18 and >60 years old, BMI >30, limited range of motion of the knee to perform MRI, systemic and chronic disorders, claustrophobia, previous injuries to the index knee, and inability to perform MRI examination (metal hardware, pacemakers, etc.). Sixty-four patients who met the study criteria had a stress MRI examination. After the examination, two patients were excluded from the study due to PCL damage, and 15 patients were excluded due to technical errors during MRI examination, such as improper setting of the device or MRI parameters. They were then divided into two groups: the ACL injured group and the control group. Inclusion criteria for the ACL-injured group were ACL tear and positive Lachman and Pivot-Shift tests.
In 14 patients in the research group, ACL damage was confirmed arthroscopically.
The stress MRI examination
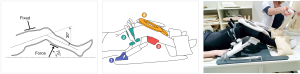
All participants had an MRI examination using the Arthroholder device prototype manufactured by IDD Medical Startup, Bielsko-Biała, Poland. The device is a knee mounting system with force applied to the calf directed anteriorly, perpendicular to the tibia. It uses a calibrated air pump system to determine the value of the translation force.
After positioning the Arthroholder on the MRI table, the knee flexion was adjusted to 30 degrees, which was verified with a goniometer. A tight at an angle of 75° to the ground plane was fixed to the Arthroholder base using a wide strap. The first MRI was initially performed with the knee resting on the Arthroholder without touching the tibial support to the skin. Then, without changing the patient’s position, a second study was performed using a force of 80 N applied to the calf. The direction of the force vector applied to the calf was set at an angle of 75° to the ground plane (Figure 2). The loading force of 80 N was generated by a piston, which was connected to a pump and controlled by the calibrated pressure gauge.
The protocol of MRI knee examination used for calculations is based on axial and sagittal ACL oblique plane orientation. All MRI planes were obtained in PD sequences on a Philips Ingenia 3.0T MR (Philips, The Netherlands), and a dStream Flex L (Philips, The Netherlands) coil was used. The tibial plateau was positioned by the technician to be perpendicular to the XY plane. The detailed technical parameters of the MRI protocol used were as follows:
- Oblique sagittal ACL PD TSE (TR: 2,800 ms; TE: 40 ms; FOV: 140 mm × 140 mm rectangular; Matrix: 704×704; Pixel size: 0.198864 mm × 0.198864 mm; NSA: 1.5; Slice thickness: 1.6 mm; Slice spacing: 1.76 mm; Number of slices: ~40; Fat saturation: none; Acquisition duration: ~2 min 30 s).
- Axial PD TSE (TR: 2,400 ms; TE: 45 ms; FOV: 160 mm × 160 mm rectangular; Matrix: 640×640; Pixel size: 0.25 mm × 0.25 mm; NSA: 1; Slice thickness: 3 mm; Slice spacing: 3.3 mm; Number of slices: ~36; Fat saturation: mSPIR; Acquisition duration: ~2 min 30 s).
In addition, the following 3D volume isotropic protocol was used to validate the registration method:
- PD 3D TSE (TR: 1,300 ms; TE: 22 ms; FOV: 160 mm × 160 mm × 140 mm; Matrix: 576×576; Pixel size: 0.277778 mm × 0.277778 mm; NSA: 2; Slice thickness: 0.698; Slice spacing: 0.349; Number of slices: ~400; Fat saturation: SPAIR; Acquisition duration: ~6 min).
Point marking and registration
The PDW sagittal and axial series were examined using Osirix 10.0 (Pixmeo, Switzerland) software.
The set of landmarks proposed by Xue (18) and ISB (21) were initially considered; however, due to the difficulty of automatic registration based on MRI images, those landmarks were not used. The new landmarks were selected based on areas of high contrast differences in the sagittal oblique and axial sections. For each examination, six points were marked as described (Table 1).
Table 1
| Symbol | Name | Description | Schematic |
|---|---|---|---|
| Flc | Femoral lateral condyle point | Inner top edge of the lateral condyle |  |
| Fmc | Femoral medial condyle point | Inner top edge of the medial condyle |  |
| Fin | Intercondylar notch point | Center of the intercondylar notch in line through a femoral physeal scar |  |
| Ff | Proximal fibula point | The top of the fibula |  |
| Fpl | Posterior cruciate ligament point | PCL tibial attachment |  |
| Flc | Patella ligament point | Top central edge of the patellar ligament attachment |  |
Two orthopedic surgeons with several years of experience in interpreting MRI images marked landmarks three times for each examination.
Selected points were redefined using Slicer 4.10 (The Slicer Community, USA) Landmark Registration with small region SimpleITK v4.13.3 (Insight Software Consortium, USA) automatic registration algorithms (22). Point locations based on the XYZ coordinate system were exported for further analysis. Femoral points were used for registration using the CloudCompare software (EDF, France) (23). Points exported from MRI examination without the use of force (Flc, Fmc, Fin) were used as reference points. Points exported from MRI examination with the use of force were used as the aligned set of points (Flc', Fmc', Fin').
Automatic registration
SimpleITK v4.13.3 registration algorithms were used to redefine registration points in small regions. Fully automated registration algorithms such as BRAINS v3.0.0 (NITRC, USA) (24), General Registration ITK v4.13.3 (22) (Insight Software Consortium, USA) and Elastix v5.0.0 (25) (LUMC, Netherlands) with ROI masks were tested; however, none of them provided accurate registration due to shifting landmarks during the performed MRI examinations. Only marking the points with the use of semiautomatic registration gave measurable results.
Translation and rotation calculations
Two sets of tibial points (Pf, P_pl, P_pcl and Pf', Ppl', Ppcl') were prepared for seven parameters of Helmert transformation model calculations. The general form can be written as (26):
where i is the number of points that have known coordinates in the two XYZ systems, pi, and qi, d is a scale factor, R is the product of three elementary rotation matrices around XYZ axes, and t is the translation vector in the XYZ space. The R3×3 matrix can be written as (26-28):
where:
The given parameters allow transforming a set of points qi, into another set pi. To determine translation t and rotation R parameters of given sets of points pi,qi, a least-squares solution should be applied (26,29):
The solution should be independent of d, which can be obtained by (26):
Detailed calculations and unit conversions were performed using 3D-Transformation-Matrix-Calculator v1.0 (Wojtin, Poland) software (30) based on the open-source singular value decomposition of 4×4 transformation matrix algorithms (31-33). These algorithms are based on the general principles of the Helmert transformation explained above.
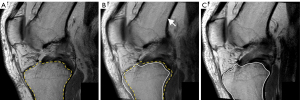
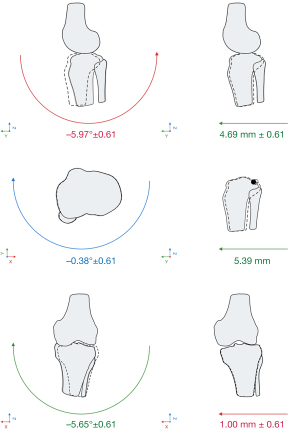
The registration of landmarks was visually verified (Figure 3), and individual patient data was presented in graphics (Figure 4).
Statistical analysis
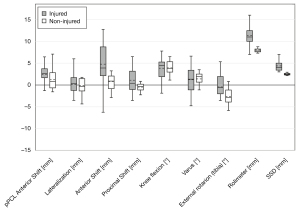
All data were collected and analyzed using the PQStat v1.6 (PQStat Software, Poland) software. The normal distribution of each parameter was tested with the Shapiro–Wilk test. For all parameters, the median ± interquartile range was calculated and presented (Figure 5). The Mann-Whitney test was used to compare the groups. Spearman’s rank correlation coefficient was calculated to achieve a relationship between translation and rotation values. The intraclass correlation coefficient (ICC) was calculated for the purpose of assessing the reliability of measurements. Statistical significance was set at P<0.05.
Validation and calibration
Calibrating the tibial translation force, 30 measurements were made with a dynamometer applied to the tibial element of the device, and then the pressure values were determined on a standardized pressure gauge connected to the pump. On the basis of the performed calibration, the translation force was set to 80±5 N each time during the examination.
To validate the tibia translation with the device, a Rolimeter was used (Table 2). In each test performed by two experienced orthopedic surgeons, the Rolimeter measurement was taken with a knee flexion of 30 degrees in the Lachman test. Then, after mounting the knee in the Arthroholder device, the measurement was taken again with the use of the Rolimeter. The Rolimeter’s zero state was set without using tibial translation force, then the Rolimeter measurement was taken using 80 N force applied to the calf. The Side-to-Side Difference (SSD) of the Rolimeter measurement was also calculated.
Table 2
| Lateralization (mm) | Anterior shift (mm) | Proximal shift (mm) | Knee flexion (°) | Varus (°) | External rotation (°) | |
|---|---|---|---|---|---|---|
| Pooled SD | ||||||
| Rolimeter | – | 1.22 | – | – | – | – |
| PD | 0.85 | 0.51 | 1.22 | 0.68 | 0.98 | 1.2 |
| 3D VISTA | 0.75 | 0.40 | 1.11 | 0.63 | 0.78 | 0.95 |
| ICC | ||||||
| Rolimeter | – | 0.994205 | – | – | – | – |
| PD/3D VISTA | 0.959001 | 0.993994 | 0.984733 | 0.998301 | 0.983295 | 0.985244 |
For all results, P<0.000001. SD, standard deviation; ICC, intraclass correlation coefficient.
To validate the landmark registration method, an additional 3D VISTA sequence was performed in 10 patients. The landmarks were marked three times by two experienced orthopedic surgeons in both the 3D VISTA sequence (0.7 mm slice thickness) and the standard PD sequence (2 mm slice thickness). Then, a semiautomatic landmark registration was performed and transition parameters were compared (Table 2). Both MRI sequences were performed during one examination.
Results
The mean ± SD age of the ACL injured group was 37±9.8 years (27% women, 73% men), The mean ± SD age of the control group was 36±9.4 years (30% women, 70% men), ranging in booth groups from 19 to 54 years.
When the group with the damaged ACL was compared to the control group, statistically significant differences were found in the evaluation of all point distances, anterior shift, external rotation, Rolimeter, and SSD; these are presented in Figure 5.
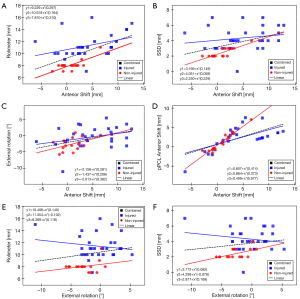
Several dependencies between particular translation and rotation parameters were noticed. Statistically significant correlations between Anterior Shift and parameters such as Rolimeter measurement, SSD, External Rotation, pPCL Anterior Shift, between the External Rotation and the Rolimeter measurement, and SSD were observed in combined groups (Figure 6A-6F).
Discussion
The most important finding of this study was the development of a 3D translation and rotation computation method based on semi-automatic registration and its implementation for stress MRI.
Fully-automated registration is widely used in the various fields of radiology (34,35); in this case, however, its use caused complications because of the repositioning of the bones and soft tissue compression by the device, even when area masks were used (36). Previously published CT (21) landmarks are not suitable for MRI registration due to difficulty in localizing bone regions on MRI PD sequences. For these reasons, new landmark locations adapted for semiautomated MRI registration were proposed. Registration of small areas around landmarks was used, which to be effective must rely on the analysis of contrasts between the bone and the surrounding tissue (34). Therefore, the location of the points was chosen so that the smallest possible cross-section would have as many areas of contrast as possible. It is also important that the location of landmarks cannot change during the translation and rotation of the tibia relative to the thigh (37).
Stress MRI examination allows for achieving parametric results, which can lead to a detailed analysis of the mechanics of the tested knee. The natural muscle tension during stress MRI allows distinguishing this method from those previously used, which were performed on cadavers (20) or under anesthesia (38). Muscle tension plays an important role in the stability of the knee, and this is taken into account when this method is used (39).
The tibia transition stress imaging calculation methods such as stress MRI or stress radiography cannot rely only on the 2D anterior shift parameter (40). The tibial transformation values must be presented as a combination of translation and rotation in which the rotation plays an important role in the tibial movement (40). This was also confirmed in this study by showing correlations between the individual components of the three-dimensional translation and rotation and differences in these values compared to the control group.
The presented results showed differences compared to the control group not only in the case of anterior translation, but also in the rotation of the tibia. The correlations between external rotation and anterior shift, as well as between the values of the Rolimeter measurements, are particularly noteworthy. It is known that damage to individual bundles affects the rotation of the tibia (41). The importance of rotation is especially relevant in the case of diagnosis of knee laxity (42), but the assessment of this parameter has not been widely used so far.
The complex analysis of tibial translation and rotation introduces new precise numerical parameters in the clinical evaluation of knee instability. This gives new possibilities of biomechanical analysis of the knee joint as well as the quality of the performed ACL repair procedures, which require further research.
It should be noted that a small group of patients and the low diversity of the research group were limitations of this research, which should be improved in future studies. Moreover, patients with limited range of knee mobility were not examined using stress MRI due to the assumed discomfort during the examination.
Conclusions
The semiautomatic registration method allows for a detailed analysis of the tibial translation and rotation parameters during stress MRI in the knees with damaged ACL. Particularly noteworthy is the strong correlation of external rotation parameters to the anterior tibia translation, as well as to the value of the Rolimeter measurement. The described method has clinical application in the accurate diagnosis of ACL lesions, but it requires further research.
Acknowledgments
Funding: None.
Footnote
Conflicts of Interest: All authors have completed the ICMJE uniform disclosure form (available at https://dx.doi.org/10.21037/qims-21-153). BS reported his participation in the patent, which is pending. The other authors have no conflicts of interest to declare.
Ethical Statement: The authors are accountable for all aspects of the work in ensuring that questions related to the accuracy or integrity of any part of the work are appropriately investigated and resolved. The study was approved by the Local Ethical Committee of Bielsko-Biała. The study was conducted in accordance with the Declaration of Helsinki (as revised in 2013). Informed consent was taken from all the patients.
Open Access Statement: This is an Open Access article distributed in accordance with the Creative Commons Attribution-NonCommercial-NoDerivs 4.0 International License (CC BY-NC-ND 4.0), which permits the non-commercial replication and distribution of the article with the strict proviso that no changes or edits are made and the original work is properly cited (including links to both the formal publication through the relevant DOI and the license). See: https://creativecommons.org/licenses/by-nc-nd/4.0/.
References
- Gurtler RA, Stine R, Torg JS. Lachman test evaluated. Quantification of a clinical observation. Clin Orthop Relat Res 1987;141-50. [PubMed]
- Lane CG, Warren R, Pearle AD. The pivot shift. J Am Acad Orthop Surg 2008;16:679-88. [Crossref] [PubMed]
- Daniel DM, Stone ML, Sachs R, Malcom L. Instrumented measurement of anterior knee laxity in patients with acute anterior cruciate ligament disruption. Am J Sports Med 1985;13:401-7. [Crossref] [PubMed]
- Balasch H, Schiller M, Friebel H, Hoffmann F. Evaluation of anterior knee joint instability with the Rolimeter. Knee Surg Sports Traumatol Arthrosc 1999;7:204-8. [Crossref] [PubMed]
- Jenny JY, Puliero B, Schockmel G, Harnoist S, Clavert P. Experimental validation of the GNRB® for measuring anterior tibial translation. Orthop Traumatol Surg Res 2017;103:363-6. [Crossref] [PubMed]
- Garcés GL, Perdomo E, Guerra A, Cabrera-Bonilla R. Stress radiography in the diagnosis of anterior cruciate ligament deficiency. Int Orthop 1995;19:86-8. [Crossref] [PubMed]
- Shefelbine SJ, Ma CB, Lee KY, Schrumpf MA, Patel P, Safran MR, Slavinsky JP, Majumdar S. MRI analysis of in vivo meniscal and tibiofemoral kinematics in ACL-deficient and normal knees. J Orthop Res 2006;24:1208-17. [Crossref] [PubMed]
- Espregueira-Mendes J, Pereira H, Sevivas N, Passos C, Vasconcelos JC, Monteiro A, Oliveira JM, Reis RL. Assessment of rotatory laxity in anterior cruciate ligament-deficient knees using magnetic resonance imaging with Porto-knee testing device. Knee Surg Sports Traumatol Arthrosc 2012;20:671-8. [Crossref] [PubMed]
- Al-Dadah O, Shepstone L, Marshall TJ, Donell ST. Secondary signs on static stress MRI in anterior cruciate ligament rupture. Knee 2011;18:235-41. [Crossref] [PubMed]
- Schneider M, Pinskerova V, Breusch SJ, Noe V, Freeman MA. Observations of normal and ACL-deficient knee joints after stress MRI. Orthopade 2006;35:337-46. [Crossref] [PubMed]
- Wang H, Zheng NN. Knee joint secondary motion accuracy improved by quaternion-based optimizer with bony landmark constraints. J Biomech Eng 2010;132:124502 [Crossref] [PubMed]
- Kundra RK, Moorehead JD, Barton-Hanson N, Montgomery SC. Magnetic tracking: a novel method of assessing anterior cruciate ligament deficiency. Ann R Coll Surg Engl 2006;88:16-7. [Crossref] [PubMed]
- Arilla FV, Rahnemai-Azar AA, Yacuzzi C, Guenther D, Engel BS, Fu FH, Musahl V, Debski RE. Correlation between a 2D simple image analysis method and 3D bony motion during the pivot shift test. Knee 2016;23:1059-63. [Crossref] [PubMed]
- Guenoun D, Vaccaro J, Le Corroller T, Barral PA, Lagier A, Pauly V, Coquart B, Coste J, Champsaur P. A dynamic study of the anterior cruciate ligament of the knee using an open MRI. Surg Radiol Anat 2017;39:307-14. [Crossref] [PubMed]
- Sandau M, Heimbürger RV, Villa C, Jensen KE, Moeslund TB, Aanæs H, Alkjær T, Simonsen EB. New equations to calculate 3D joint centres in the lower extremities. Med Eng Phys 2015;37:948-55. [Crossref] [PubMed]
- Zhang N, Jiang Z, Wen X, Sugamoto K, Yang C. The triangle zone as a femoral attachment location in medial patellofemoral ligament reconstruction: An in vivo three-dimensional analysis using an open MRI scanner. Knee 2015;22:585-90. [Crossref] [PubMed]
- Murayama T, Sato T, Watanabe S, Kobayashi K, Tanifuji O, Mochizuki T, Yamagiwa H, Koga Y, Omori G, Endo N. Three-dimensional in vivo dynamic motion analysis of anterior cruciate ligament-deficient knees during squatting using geometric center axis of the femur. J Orthop Sci 2016;21:159-65. [Crossref] [PubMed]
- Xue N, Doellinger M, Fripp J, Ho CP, Surowiec RK, Schwarz R. Automatic model-based semantic registration of multimodal MRI knee data. J Magn Reson Imaging 2015;41:633-44. [Crossref] [PubMed]
- Miranda DL, Rainbow MJ, Leventhal EL, Crisco JJ, Fleming BC. Automatic determination of anatomical coordinate systems for three-dimensional bone models of the isolated human knee. J Biomech 2010;43:1623-6. [Crossref] [PubMed]
- Englander ZA, Martin JT, Ganapathy PK, Garrett WE, DeFrate LE. Automatic registration of MRI-based joint models to high-speed biplanar radiographs for precise quantification of in vivo anterior cruciate ligament deformation during gait. J Biomech 2018;81:36-44. [Crossref] [PubMed]
- Wu G, Siegler S, Allard P, Kirtley C, Leardini A, Rosenbaum D, Whittle M, D'Lima DD, Cristofolini L, Witte H, Schmid O, Stokes IStandardization and Terminology Committee of the International Society of Biomechanics. ISB recommendation on definitions of joint coordinate system of various joints for the reporting of human joint motion--part I: ankle, hip, and spine. International Society of Biomechanics. J Biomech 2002;35:543-8. [Crossref] [PubMed]
- Yaniv Z, Lowekamp BC, Johnson HJ, Beare R. SimpleITK Image-Analysis Notebooks: a Collaborative Environment for Education and Reproducible Research. J Digit Imaging 2018;31:290-303. [Crossref] [PubMed]
- Oniga EV, Savu A, Negrilă A. The Evaluation of Cloudcompare Software in the Process of Tls Point Clouds Registration. RevCAD J Geod Cadastre 2016;21:117-24.
- Johnson H, Harris G, Williams K. BRAINSFit: mutual information rigid registrations of whole-brain 3D images, using the insight toolkit. Insight J 2007;57:1-10.
- Bron EE, van Tiel J, Smit H, Poot DH, Niessen WJ, Krestin GP, Weinans H, Oei EH, Kotek G, Klein S. Image registration improves human knee cartilage T1 mapping with delayed gadolinium-enhanced MRI of cartilage (dGEMRIC). Eur Radiol 2013;23:246-52. [Crossref] [PubMed]
- Watson GA. Computing Helmert transformations. J Comput Appl Math 2006;197:387-94. [Crossref]
- Islam MT. Least Square Approach to Estimate 3D Coordinate Transformation Parameters : A Case of Three Reference Systems in Sweden. International Journal of Remote Sensing and GIS 2014;3:30-8.
- Brazeal R. Three Dimensional Coordinate Transformations for Registering Terrestrial Laser Scanning Datasets Based on Tie Points. 2008;107:236-41.
- Horn BKP, Hilden HM, Negahdaripour S. Closed-form solution of absolute orientation using orthonormal matrices. J Opt Soc Am A 1988;5:1127. [Crossref]
- 3D-Transformation-Matrix-Calculator: Find CloudOfPoints 3D BestFit transformation matrix. Transform CloudOfPoints by matrix. Matrices multiplification [Internet]. [cited 2020 Jan 8]. Available online: https://github.com/wojtin/3D-Transformation-Matrix-Calculator
- GitHub - danielorf/Transform3DBestFit: Transform3D class used to calculate best fit 3D transform between two sets of cartesian (X,Y,Z) points [Internet]. [cited 2019 Dec 2]. Available online: https://github.com/danielorf/Transform3DBestFit
- Eggert DW, Lorusso A, Fisher RB. Estimating 3-D rigid body transformations: a comparison of four major algorithms [Internet]. Vol. 9, Machine Vision and Applications. 1997 [cited 2019 Feb 19]. Available online: http://graphics.stanford.edu/~smr/ICP/comparison/eggert_comparison_mva97.pdf
- Sorkine-Hornung O, Rabinovich M. Least-Squares Rigid Motion Using SVD [Internet]. 2017 [cited 2019 Feb 19]. Available online: http://igl.ethz.ch/projects/ARAP/svd_rot.pdf
- Wang L, Chitiboi T, Meine H, Günther M, Hahn HK. Principles and methods for automatic and semi-automatic tissue segmentation in MRI data. MAGMA 2016;29:95-110. [Crossref] [PubMed]
- Luu HM, Klink C, Niessen W, Moelker A, van Walsum T. An automatic registration method for pre- and post-interventional CT images for assessing treatment success in liver RFA treatment. Med Phys 2015;42:5559-67. [Crossref] [PubMed]
- Kamojima S, Miyata N, Ota J. Identification of position and orientation of hand bones from MR images by bone model registration. 2004 IEEE/RSJ Int Conf Intell Robot Syst 2004;2:2021-7.
- Rhee T, Lewis JP, Nayak K, Neumann U. Adaptive non-rigid registration of 3D knee MRI in different pose spaces. 2008 5th IEEE Int Symp Biomed Imaging From Nano to Macro, Proceedings, ISBI. 2008;(May):1111-4. Available online: https://ieeexplore.ieee.org/document/4541195
- Martelli S, Zaffagnini S, Bignozzi S, Lopomo N, Marcacci M. Description and validation of a navigation system for intra-operative evaluation of knee laxity. Comput Aided Surg 2007;12:181-8. [Crossref] [PubMed]
- Davarinos N, O’Neill BJ, Curtin W. A Brief History of Anterior Cruciate Ligament Reconstruction. Adv Orthop Surg 2014;2014:1-6. [Crossref]
- Noyes FR, Grood ES. Scientific Basis for Examination and Classification of Knee Ligament Injuries. In: Noyes’ Knee Disorders: Surgery, Rehabilitation, Clinical Outcomes [Internet]. Second Edition. Elsevier; 2017:37-82. Available online:
10.1016/B978-0-323-32903-3.00003-2 10.1016/B978-0-323-32903-3.00003-2 - DeFranco MJ, Bach BR Jr. A comprehensive review of partial anterior cruciate ligament tears. J Bone Joint Surg Am 2009;91:198-208. [Crossref] [PubMed]
- Girgis FG, Marshall JL, Monajem A. The cruciate ligaments of the knee joint. Anatomical, functional and experimental analysis. Clin Orthop Relat Res 1975;216-31. [Crossref] [PubMed]