A medical image enhancement based on generalized class of fractional partial differential equations
Introduction
Fractional partial differential equations (FPDEs) with different types of fractional operators have been successfully applied as a novel direction in image processing. For example, the analytic approximated solution of conforming model problems using FPDE methods was applied as an image denoising algorithm (1,2). More recently, an image denoising and enhancement algorithm that employs stability and convergence was proposed based on the numerical method of FPDE (3). Another FPDEs model was proposed for image denoising and texture enhancement of images (4). Fractional calculus is regularly used as an image enhancement model due to its good performance (5). The fractional order allows for the superior enhancement of the quality of input images, however, there is still room for improvement since the results are not always satisfactory. Here, we introduce a new method for solving FPDEs analytically. We focus on a class of heat equations of fractional order that utilize a hybrid fractional integral-differential operator.
Magnetic resonance imaging (MRI) and computed tomography (CT) scans contribute essential information during the clinical diagnosis of several diseases. This is achieved by presenting the visceral tissues in a clear manner so that clinicians are able to make suitable diagnosis.
Medical imaging techniques sometimes generate images that: have artifacts, are low in contrast, and/or don’t clearly show the boundaries of the visceral organs. To mitigate these issues, we propose a new mathematical model that is based on the class of FPDEs to enhance the low contrast intensities of medical images. We aim to provide an enhancement method for medical images so that doctors can give clinical diagnoses faster and more confidently.
The logic behind using FPDEs as medical image enhancement lies in its capability to enhance the low contrast intensities through the proposed fractional enhanced operator. For each pixel in the image, the proposed model derives the coefficient estimates of FPDE according to the details of image pixels’ frequency. As a result, the proposed FPDE model enhances the low the gray-level of each pixel in which without affecting high frequency details.
The performance of the proposed image enhancement model was assessed using relevant image quality metrics, and compared with state-of-the art of image enhancement techniques.
The main contributions of this study are as follows:
- We present a unique low-light image enhancement method which can achieve better contrast enhancement on real low-light medical images.
- We propose a FPDEs model that is based on the spatial domain method, and utilizes a hybrid fractional integral-differential operator for real low-light medical images enhancement.
- The proposed FPDEs can be applied as an efficient pre-processing step for any image processing approach.
The rest of this paper is organized as follows. The related work section highlights the relevant studies. The method section describes the class of FPDEs with some properties of the geometric functions in the unit disk. In the results section, we present the details of the experiments we conducted for the evaluation of the proposed method. The conclusions section is the final part of the study.
Related work
Image enhancement methods are designed to enhance the visual appearance of an image such that the details of the image are significantly improved without altering the information of the image. This is done through different ways, such as blur removal and denoising (6). In the literature, image enhancement can be classified into spatial and frequency domain. Spatial domain image enhancement works on pixel values, while the image enhancement in frequency domain uses a transform approach of the images.
Most image enhancement algorithms are based on spatial processes implemented on image pixels to produce more appropriate images compared to the input image.
Multiple image enhancement methods based on spatial domain algorithms have been reported in the literature. The most common concept among image enhancement methods is the modification of the image histogram (7). This concept is common due to its simplicity and robustness under different scenarios. However, images enhanced using this concept may suffer from a washed-out effect due to normalized image intensities. To solve this issue, a novel joint histogram equalization (JHE) based technique was proposed. The motivation is to use the pixels and its neighbor’s information to improve the image contrast (8).
Guo et al. 2017 (9), used the brightness of the image as the initial illumination component and optimized the illumination component iteratively. The use of this approach leads to a better image enhancement with good visual appearance.
The above-mentioned techniques may produce images with over saturation artifacts due to the stretching of the gray levels over the full gray level range. To resolve this issue, as well as to enhance the contrast and the brightness, a dynamic fuzzy histogram equalization with brightness preserving has been proposed by Sheet et al. 2010 (10). The fuzzy set theory has been used in the aforementioned work to deal with the imprecision of the gray values in a histogram that is partitioned according to local maxima.
Another image enhancement approach based on the fuzzy set theory was proposed by Hasikin et al. 2014 (11). This approach achieved better image quality with minimum processing time. In their work, the authors proposed a contrast factor that is based on the differences in the gray-level values of image pixels in the local neighborhood. This approach has successfully improved the quality of the image while preserving the details. However, the fuzzy histogram is challenging to implement on non-uniform illumination images because the overexposed and underexposed areas could occur in the same region of the image.
Recently, a few image enhancement algorithms based on the concept of fractional calculus have been proposed. The fractional operators have the ability to keep the high frequency contour features, and to enhance the texture details. Roy et al. 2016 (12) proposed a new fractional calculus enhancement algorithm based on Laplacian operations. The method was proposed to remove the generated Laplacian noise from text inside video frames.
Similarly, a fractional-based image enhancement model was proposed by Al-Shamasneh et al. 2018 (13). The proposed model relies on pixel probability of the neighboring pixels to enhance kidney images obtained from self-collected MRI dataset. Raghunandan et al. 2017 (14) proposed a low contrast license plate image enhancement model based on Riesz fractional operator. The model achieved good results for the text images only. Alternatively, Al-Ameen and Sulong 2016 (15) proposed a tuned single-scale Retinex algorithm for improving the dynamic range of MRI scans. The proposed enhancement model is able to improve the brightness and contrast of the input MRI scans, but the preservation of fine details was not achieved. For poorly illuminated images, Fu et al. 2016 (16) proposed the fusion-based image enhancement method by applying different techniques to adjust the image illumination. This approach effectively improved the images illumination. However, the aim of the method is restricted to weakly illuminated images but not for images that suffer from degradations, and poor quality. In the same way, Zhang et al. 2019 (17) proposed an automatic image exposure correction method by using dual illumination estimation. In this method, the multi-exposure image fusion technique is employed to improve the input image with both under and over exposed regions into a globally well-exposed image. Despite the good results of this method, it was not shown to be able to preserve the fine details of medical images, which is required for the diagnosis process. Likewise, more image enhancement methods have been proposed deep learning approaches. Li et al. 2018 (18) proposed a deep learning approach to enhance dark images. This approach operated well without any paired training data for low-light enhancement jobs. The experimental results on various low light datasets show the effectiveness of this method. The partial differential equations (PDEs) based methods have been used in many research fields. Sharma et al. 2019 (6) have proposed a FPDE based image enhancement model. The proposed model decreased the image noise and enhanced the image contrast. However, it is found that the model used the iterations approach to enhance the image which increased the complexity of the algorithm.
In the same approach, Zhang et al. 2019 (19) have developed an adaptive fractional order image enhancement method based on the information of fractional order differential and the image segmentation. The image enhancement depends on the result of the image segmentation algorithm which is used to segment the image into the objects and the background, which makes it not able to preserve contrast information of the image efficiently.
The above-mentioned methods explored different approaches for enhancing images. These methods work well in improving the whole image, but not for the sub-regions enhancement. Therefore, in this study, the image enhancement model proposed in this study is based on a class of heat equations of fractional order utilizing a hybrid fractional integral-differential operator, which can enhance the image to a certain extent, and the display effect of image information is better than the traditional image enhancement model.
Methods
First, we define the pixel energy based on proportional-Caputo hybrid operator (PCHO) for each image pixel (i, j) on spatial domain. Then, in terms of the hypergeometric functions, we will introduce the convex solution as compensation to get the enhanced MRI image.
PCHO
In this section, we introduce the technique of the PCHO. Let S be the class of analytic functions in the open unit disk D(|z|<1). Let ℵ be the subclass of S admitting the function f(z)=z+a2z2+... [see (20)]. Here, we give the definitions of the fractional operators in the complex plane C followed by the interpretations of the Srivastava and Owa fractional operators of fractional calculus (21).
Definition 1: the integral of arbitrary order α, where R(α)>0 for a function g(z), is
Here, g is analytic in D and the multiplicity of is terminated by letting when .
Definition 2: the Srivastava and Owa fractional derivative of order 0≤α<1 [see (21)]:
such that g is analytic in D and the multiplicity of is terminated by consuming when .
Definition 3: let k=1,2,…. Then for k−1<α<k and analytic function g(z); the Caputo derivative of order α is formulated by
where g and its k-derivatives are analytic in D and the multiplication of (z−ζ)k−α−1 is ignored by supposing log(z−ζ) when R(z−ζ)>0.
Remark 4: the properties of and are as follows: , .
Lately, Ibrahim and Jahangiri 2019 (22) introduced a definition of a proportional (conformable) differential operator (PDO) in a complex domain, specifically for function as follows:
Definition 5: for , the PDO () of order α∈[0,1] in defined by
where the functions κ1,κ0:[0,1] ×D→D are analytic in D and thus κ1(α,z)≠−κ0(α,z), , , κ1(α,z)≠0, ∀z∈D, α∈(0,1), and , , κ0(α,z)≠0, ∀z∈D, α∈(0,1).
It is clear that for , we have , ∀z∈D. Applying the next property of , we define the combined operator as follows: .
Now, by substituting Eq. [4] in the derivative f'(z), we receive the following operator
A special case of Eq. [5] can be considered, when κ1 and κ0 are constants formulating by α. We have the following construction of a linear operator:
It is clear that represents a linear combination of the Srivastava-Owa operator f and the complex Caputo operator for zf. For example, when κ1=1−α and κ0=α, we have the operator .
Define a conformable operator Θαf(z), f∈ℵ by the formula
Note that the real case of PCHO is studied in (23) , where and indicate the Riemann-Liouville integral and the Caputo derivative respectively. Note that achieves the property [(23), theorem 2] , h(0)=0.
The generalized PDE
In this approach, we deal with the PDE of the form
where f:D×J→D is analytic parametric function such that f(0,0)=0. Our aim is to construct a real solution of Eq. [8] in terms of the hypergeometric functions. It is well known that the source of the heat is near the origin in the open unit disk. Consequently, the delivery of the heat is in a homogeneous formal; in this situation, we receive a convex shape; or it is a non-homogeneous then we get the starlike (univalent) shape (24). For this purpose, we check the upper bound solution of Eq. [8] by using convex and starlike functions respectively.
Upper bound solution (optimal solution)
In this subsection, we approximate the solution of Eq. [8] by using the hypergeometric function.
Proposition 6: suppose that f(z,t) in the class of convex functions in the open unit disk (C). Then
where F indicates the hypergeometric function. The equality occurs for the parametric (rotated) Koebe function of the first type .
Proof: let f∈C then the coefficients satisfy |an|<1 for all n. Moreover, we have the following limit .
A calculation implies
where is the Pochhammer symbol. Lastly, by assuming the Koebe function K(tz), with an=1 in the above conclusion, we can indicate the sharp outcome.
Next, we show the maximal solution of Eq. [8].
Proposition 7: consider Eq. [8] with a convex solution f(z,t). Then
By using Proposition 6, Eq. [8] becomes
Operating Eq. [11] by , and since f(0,0)=0, then we have
Now by letting a:=α−1 and b:=κ1(α)/κ0(α) then we have .
In general, assume that .
But, is a decreasing function in α such that for t∈J and α∈(0,1); thus, we have
(|z|=r<1, κ0(α)=α, t∈J=[0,1], 0<α<1).
The connect values (coefficient estimates)
Here, we deal with the connect values (coefficient estimates), which are convoluted with the images. In our application, the value of r<1 is indicated the probability of the pixel of the image for all t∈J and α∈(0,1). Moreover, the value of ϕ(i, j) is calculated for each image pixel(i, j) on spatial domain using the following expressions:
Proposition 8: the value of ϕn is approximated in the following formula
The enhanced image is given by:
Where I(i,j) is the input image, Ien(i, j) is the result enhanced image, and α is the fractional parameter.
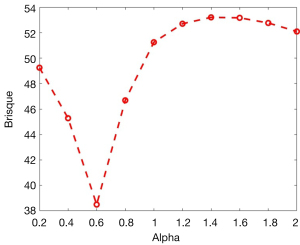
In the proposed enhancement model, the fractional parameter α is the parameter for the fine detail enhancement, and it is fixed experimentally as shown in Figure 1. It is observed that when the value of α is equal to 0.6, the best score for Brisque is obtained (lower is better). Therefore, we consider 0.6 as the experimental value of α in this study.
The proposed algorithm is based on the spatial domain method, utilizing a hybrid fractional integral-differential operator. The algorithm steps are described as follows:
- Set the fractional parameter α=0.6;
- For each input image, calculate the pixel probability (r) in
Eq. [15]; - Calculate ϕ(i,j) using
Eq. [11], where (i,j) denotes the pixel position; - Calculate the Ien(i,j) using
Eq. [16].
Figure 2 shows the input and their enhanced images as well as their histogram components. The lack of image details of the input images is clearly being noted as shown in Figure 2A. However, the image contrast of the input images is stretched when comparing them to the proposed method as shown in Figure 2C. Moreover, areas lacking details become brighter with well-defined detail after the enhancement process. The histogram analysis illustrates the variations in the features of the input and the enhanced images. The histogram analysis of the input and the enhanced images are shown in Figure 2B,2D respectively. It is apparent from Figure 2B, that the probability distribution of the input image pixels looks compact, while the probability distribution of the pixels in the enhanced image Figure 2D looks more scattered. This implies that the image quality as well as its contract have been improved.

Results
The code of the proposed image enhancement algorithm was developed using MATLAB 2020b, while both Matlab and Python have been used to conduct the comparative analysis with other methods. In this study the following datasets are used:
- The CT scan dataset created by the Italian Society of Medical and Interventional Radiology, which is named as COVID-19 DATABASE dataset (25).
- Brain MRI dataset, comprising 154 MRI brain images (26).
To evaluate the proposed image enhancement model, we use four, no-reference image quality assessment metrics, which are:
- “The blind referenceless image spatial quality evaluator (Brisque)”, which calculates the perceptual quality of images (27).
- “Perception based image quality evaluator (Piqe)”, which calculates the image quality affected by arbitrary distortion (28).
- “Spatial-spectral entropy-based quality (SSEQ) index”, which assesses the quality of a distorted image across multiple distortion categories (29).
- “The blind image sharpness assessment based on maximum gradient and variability of gradients” (SAMGVG), in which the maximum gradient represents the sharpest spot in an image, and the variability of gradients shows variations within the content of the image (30). Sharpness represents the amount of details in an image. Accordingly, motion blur, out-of-focus, de-noising filtering reduce the amount of details in an image, and therefore, reduce the perceived sharpness.
It is noted that lower scores of Brisque, Piqe and SSEQ indicate better quality of the enhanced images.
To demonstrate that the proposed enhancement model is efficient as a medical image enhancement tool, we implemented the following existing methods for the comparative study: The fractional entropy based enhancement method of kidney images by Al-Shamasneh et al. 2018 (13). The image enhancement method for license plate by Raghunandan et al. 2017 (14) that is based on the Riesz fractional operator. The MRI brain images enhancement method by Al-Ameen and Sulong 2016 (15). The fusion-based enhancement method of poorly illuminated images by Fu et al. 2016 (16). The CNN-based image enhancement method by Li et al. 2018 (18) for weakly illuminated images. And finally, the automatic exposure correction method by Zhang et al. 2019 (19). All of the aforementioned methods were executed on the same machine (Windows 10 64-bit, Intel Core i7, SSD storage, and 8 GB of RAM) for consistency.
The qualitative results of the proposed and the existing methods for input images of two image datasets are illustrated in Figure 3, in which all of the images have different trends with the dark and bright areas. When we compare the enhancement results of existing methods with the proposed method, the proposed method shows better enhancement results than the existing methods in terms of image quality. The reason is that the proposed method uses the fractional partial differential enhanced operator which captures the high frequency image details in, regardless of noise, blur, and distortion created by image capturing systems. In the case of the existing method, it could be seen that the Fu et al. (16) Figure 3E, and Zhang et al. (19) Figure 3G methods produce over-enhanced images, while the proposed method produces natural appearance by enhancing the dark areas and maintaining the bright areas of input images.

Overall, the brightening caused by the proposed model makes the structures of the medical images which usually represent edges well-defined and clear. This is accredited to the model’s capability to capture high frequency details efficiently. The proposed method introduces fair visual results for the weakly illuminated images. This is the contribution of the fractional integral entropy in this study.
The achieved quantitative results of the proposed enhancement method and the existing image enhancement models are stated in Table 1. Most of the image enhancement methods reported in the literature use the no-reference image quality metrics, therefore, the Brisque and Piqe scores have been used for the quantitative comparisons as presented in Table 1. The proposed method achieves the best Brisque and Piqe for almost all of the images from the two datasets. However, for the brain MRI images, the performance of the proposed method degrades slightly compared to the Zhang et al. (19) method. This might be caused by the increased complexity of the said images compared to the ones found in the other two datasets, and might constitute a primary limitation of the present study.
Table 1
| Methods | Brain MRI images | CT lungs images | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Brisque | Piqe | SSEQ | SAMGVG | Brisque | Piqe | SSEQ | SAMGVG | ||
| Al-Shamasneh et al., 2018 (13) | 42.77 | 78.29 | 68.65 | 32.08 | 41.74 | 45.55 | 36.62 | 168.03 | |
| Raghunandan et al., 2017 (14) | 41.04 | 59.03 | 66.85 | 31.02 | 39.67 | 41.51 | 34.52 | 158.68 | |
| Al-Ameen and Sulong, 2016 (15) | 42.30 | 69.05 | 69.41 | 31.72 | 41.09 | 43.98 | 35.165 | 164.36 | |
| Fu et al., 2016 (16) | 41.96 | 65.52 | 65.60 | 29.37 | 44.64 | 39.53 | 35.20 | 178.56 | |
| Li et al., 2018 (18) | 41.39 | 55.98 | 65.60 | 31.04 | 42.98 | 42.07 | 33.60 | 171.92 | |
| Zhang et al., 2019 (19) | 43.92 | 42.59 | 68.80 | 32.94 | 43.09 | 42.98 | 34.40 | 172.36 | |
| Proposed method | 40.93 | 41.13 | 66.09 | 31.04 | 39.07 | 41.33 | 30.97 | 159.24 | |
MRI, magnetic resonance imaging; CT, computed tomography; Brisque, blind referenceless image spatial quality evaluator; Piqe, perception based image quality evaluator; SSEQ, spatial-spectral entropy-based quality; SAMGVG, sharpness assessment based on maximum gradient and variability of gradients.
Discussion
The proposed image enhancement method is better than the existing methods in terms of Brisque and Piqe score as reported in Table 1. The proposed method achieves the best Brisque and Piqe for almost all of the images from the two datasets. However, for the CT lungs images, the Piqe score of the proposed method degrades slightly compared to the Raghunandan et al. (14). The reason is that the method (14) is developed for enhancing license plates for detection and recognition. Overall, the proposed method achieves the best of Brisque and Piqe scores (lower is better), regardless of dataset and content. In summary, for the two image datasets of different visual complexities, the proposed method achieves the best results compared to the rest of the mentioned methods due to its consistent results across the different datasets. However, some existing methods may produce better results when used under particular conditions since they were designed with a specific application in mind.
Conclusions
In this study, a novel method for medical image enhancement based on the class of FPDEs has been proposed. The proposed method embraces the fractional calculus and geometric functions in the unit disk. This model applied the fractional operator, which dynamically enhanced the fine details of the medical images. The proposed enhancement model enhanced the fine details in images of the two image datasets efficiently. The experimental results on two medical image datasets indicated that the proposed approach outperforms the existing methods under the general application of image enhancement. This gives the proposed model the advantage of being more scalable for medical image enhancement than the existing methods. Future works may adapt the present model for specific applications to achieve maximum enhancement benefit.
Acknowledgments
Funding: This research is supported by Faculty Program Grant (GPF096C-2020), Universiti Malaya, Malaysia.
Footnote
Conflicts of Interest: All authors have completed the ICMJE uniform disclosure form (available at https://dx.doi.org/10.21037/qims-21-15). The authors have no conflicts of interest to declare.
Ethical Statement: The authors are accountable for all aspects of the work in ensuring that questions related to the accuracy or integrity of any part of the work are appropriately investigated and resolved.
Open Access Statement: This is an Open Access article distributed in accordance with the Creative Commons Attribution-NonCommercial-NoDerivs 4.0 International License (CC BY-NC-ND 4.0), which permits the non-commercial replication and distribution of the article with the strict proviso that no changes or edits are made and the original work is properly cited (including links to both the formal publication through the relevant DOI and the license). See: https://creativecommons.org/licenses/by-nc-nd/4.0/.
References
- Jalab HA. Regularized fractional power parameters for image denoising based on convex solution of fractional heat equation. Abstract and Applied Analysis 2014; [Crossref]
- Yang Q, Chen D, Zhao T, Chen Y. Fractional calculus in image processing: a review. Fractional Calculus and Applied Analysis 2016;19:1222-49. [Crossref]
- Cai Y, Yu X. Convergence and Stability of a Fractional Differential System in Image Processing. Revista Argentina de Clínica Psicológica 2020;29:579.
- Xu L, Huang G, Chen Q, Qin H, Men T, Pu Y. An improved method for image denoising based on fractional-order integration. Frontiers of Information Technology & Electronic Engineering 2020;21:1485-93. [Crossref]
- Wang Y, Wang Z. Image denoising method based on variable exponential fractional-integer-order total variation and tight frame sparse regularization. IET Image Processing 2021;15:101-14. [Crossref]
- Sharma D, Chandra SK, Bajpai MK. Image Enhancement Using Fractional Partial Differential Equation. In: 2019 Second International Conference on Advanced Computational and Communication Paradigms (ICACCP). IEEE, 2019. doi:
10.1109/ICACCP.2019.8882979 .10.1109/ICACCP.2019.8882979 - Janan F, Brady M. RICE: A method for quantitative mammographic image enhancement. Med Image Anal 2021;71:102043 [Crossref] [PubMed]
- Agrawal S, Panda R, Mishro P, Abraham A. A novel joint histogram equalization based image contrast enhancement. Journal of King Saud University-Computer and Information Sciences 2019. doi:
10.1016/j.jksuci.2019.05.010 .10.1016/j.jksuci.2019.05.010 - Xiaojie Guo, Yu Li, Haibin Ling. LIME: Low-light image enhancement via illumination map estimation. IEEE Trans Image Process 2017;26:982-93. [Crossref] [PubMed]
- Sheet D, Garud H, Suveer A, Mahadevappa M, Chatterjee J. Brightness preserving dynamic fuzzy histogram equalization. IEEE Transactions on Consumer Electronics 2010;56:2475-80. [Crossref]
- Hasikin K, Isa NAM. Adaptive fuzzy contrast factor enhancement technique for low contrast and nonuniform illumination images. Signal, Image and Video Processing 2014;8:1591-603. [Crossref]
- Roy S, Shivakumara P, Jalab HA, Ibrahim RW, Pal U, Lu T. Fractional poisson enhancement model for text detection and recognition in video frames. Pattern Recognition 2016;52:433-47. [Crossref]
- Al-Shamasneh AaR. Jalab HA, Palaiahnakote S, Obaidellah UH, Ibrahim RW, El-Melegy MT. A new local fractional entropy-based model for kidney MRI image enhancement. Entropy 2018;20:344. [Crossref]
- Raghunandan KS, Shivakumara P, Jalab HA, Ibrahim RW, Kumar GH, Pal U, Lu T. Riesz fractional based model for enhancing license plate detection and recognition. IEEE Transactions on Circuits and Systems for Video Technology 2017;28:2276-88. [Crossref]
- Al-Ameen Z, Sulong G. Ameliorating the Dynamic Range of Magnetic Resonance Images Using a Tuned Single-Scale Retinex Algorithm. International Journal of Signal Processing Image Processing and Pattern Recognition 2016;9:285-92. [Crossref]
- Fu X, Zeng D, Huang Y, Liao Y, Ding X, Paisley J. A fusion-based enhancing method for weakly illuminated images. Signal Processing 2016;129:82-96. [Crossref]
- Zhang Q, Nie Y, Zheng WS. Dual illumination estimation for robust exposure correction. Computer Graphics Forum. 2019;38:243-52. [Crossref]
- Li C, Guo J, Porikli F, Pang Y. LightenNet: A convolutional neural network for weakly illuminated image enhancement. Pattern Recognition Letters 2018;104:15-22. [Crossref]
- Zhang X, Yan H. Image enhancement algorithm using adaptive fractional differential mask technique. Mathematical Foundations of Computing 2019;2:347. [Crossref]
- Duren PL. Univalent functions. New York: Springer Science & Business Media, 2001.
- Srivastava HM, Owa S. Univalent functions, fractional calculus, and their applications. Chichester: Ellis Horwood; New York; Toronto: Halsted Press, 1989.
- Ibrahim RW, Jahangiri JM. Conformable differential operator generalizes the Briot-Bouquet differential equation in a complex domain. AIMS Math 2019;4:1582-95. [Crossref]
- Baleanu D, Fernandez A, Akgül A. On a fractional operator combining proportional and classical differintegrals. Mathematics 2020;8:360. [Crossref]
- Ibrahim RW, Jalab HA. Time-space fractional heat equation in the unit disk. Abstract and Applied Analysis 2013; [Crossref]
- Radiology ISoMaI. COVID-19 CT Scans. 2020. Available online: https://www.sirm.org/category/senza-categoria/covid-19/ (accessed on 10 August 2020).
- Menze BH, Jakab A, Bauer S, Kalpathy-Cramer J, Farahani K, Kirby J, et al. The Multimodal Brain Tumor Image Segmentation Benchmark (BRATS). IEEE Trans Med Imaging 2015;34:1993-2024. [Crossref] [PubMed]
- Mittal A, Moorthy AK, Bovik AC. Blind/referenceless image spatial quality evaluator. In: 2011 Conference Record of the Forty Fifth Asilomar Conference on Signals, Systems and Computers (ASILOMAR). IEEE, 2011. doi:
10.1109/ACSSC.2011.6190099 .10.1109/ACSSC.2011.6190099 - Venkatanath N, Praneeth D, Bh MC, Channappayya SS, Medasani SS. Blind image quality evaluation using perception based features. In: 2015 Twenty First National Conference on Communications (NCC). IEEE, 2015. doi:
10.1109/NCC.2015.7084843 .10.1109/NCC.2015.7084843 - Liu L, Liu B, Huang H, Bovik AC. No-reference image quality assessment based on spatial and spectral entropies. Signal Processing: Image Communication 2014;29:856-63. [Crossref]
- Zhan Y, Zhang R. No-reference image sharpness assessment based on maximum gradient and variability of gradients. IEEE Transactions on Multimedia 2017;20:1796-808. [Crossref]