
A novel automatic segmentation method directly based on magnetic resonance imaging K-space data for auxiliary diagnosis of glioma
Introduction
Brain tumors, especially gliomas, seriously endanger the function of the human nervous system and are one of the most harmful diseases to human health. Pre-operative imaging examinations, especially magnetic resonance imaging (MRI), can provide detailed images of the brain, which are essential for glioma diagnosis and prognostic evaluations. Moreover, the accurate segmentation of brain tumors on MRI images is helpful for surgery planning.
Brain tumor segmentation (BraTS) is achieved by identifying abnormal areas that are different from normal tissue signals. Its main task is to detect the boundary between the tumor area and the surrounding normal tissues. Tumors, especially gliomas, are often diffused, with poor contrast and tentacle-like structures that make them difficult to segment. As a solution, some studies have used automatic segmentation models based on deep-learning methods, such as DeepMedic (1), fully convolutional networks (2), and the U-net (3), to complete this challenging task. These networks adopt the encoder-decoder structure of convolutional neural networks, and use an asymmetrically large encoder to extract image features, and a decoder to reconstruct the segmentation masks (4). The encoder extracts and computes increasingly complex features that are beyond the realm of human comprehension using convolution operations. The decoder then analyzes the complex features and reconstructs the features back into the in-domain data form. However, all such image-based networks are affected by a tedious image reconstruction process.
The reconstruction of diagnosable images from K-space data collected by MRI requires fast Fourier transformation (FFT) and image reconstruction algorithms. The quantitative error caused by FFT usually leads to image information loss and even image distortion. Previous studies by James (5), Weinstein (6), Tasche (7), and Kaneko (8) revealed this issue. These studies not only showed the error characteristics of the performance of FFT on white noise or sine wave inputs but also showed the coefficient rounding errors of FFT.
Further, different image reconstruction algorithms also cause various degrees of image quality loss, especially in highly under-sampled K-space data (9,10). All these factors significantly affect the image quality of reconstructed MRI images and the accuracy of image-based segmentation. In addition, to ensure accurate segmentation results, patients must be scanned for a relatively long time to collect enough K-space data to obtain high-quality reconstructed MRI images for segmentation, making disease diagnosis time consuming and costly. Additionally, some patients may not be able to tolerate the long imaging time due to their diseases, which may also cause motion artifacts in MRI images (11-13).
Thus, we hypothesized that performing lesion segmentation directly from K-space data would improve segmentation accuracy compared to traditional image-based segmentation. In this study, we proposed a new architecture that can accomplish the challenging task of automatically segmenting brain tumors directly based on K-space data. The architecture mainly uses the K-space data of two-dimensional (2D) MRI images as the input of the semantic segmentation neural networks, eliminating the time-consuming and tedious image reconstruction process. This significantly simplified segmentation process, which can be compared with the traditional image-based segmentation method, is shown in Figure 1.
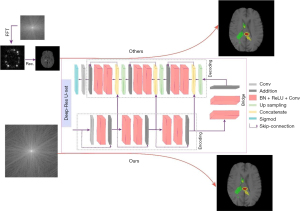
In this study, we employed the BraTS data set, a widely recognized open-source data set in the medical imaging field. The BraTS data set comprises MRI scans of brain tumors sourced from multiple institutions. It is important to note that this data set was assembled under strict ethical guidelines (14-16), and comprises the following four types of contrast images: T1-weighted images (T1WIs), contrast-enhanced T1WIs (cT1WIs), T2-weighted images (T2WIs), and fluid-attenuated inversion recovery (FLAIR) images, which enabled us to directly and quantitatively compare our method with a number of other methods.
Methods
BraTS data set
The primary MRI data set used in this study was the 2018 BraTS Challenge data set. The data set comprised the following three sub-data sets: the training data set, test data set, and leaderboard data set. The training data set included 285 gliomas, comprising 210 patients with high-grade gliomas and 75 patients with low-grade gliomas. The data of each patient included four contrast images (i.e., a T1WI, cT1WI, T2WI, and FLAIR image), which were rigidly aligned, re-sampled to an isotropic resolution of 1 mm × 1 mm × 1 mm, and skull-stripped. All the patients had pixel-wise actual ground truth with the following four segmentation labels: non-tumor, edema [whole tumor (WT)], enhanced tumor (ET), and necrosis. As we did not participate in the 2018 BraTS Challenge, the test data set was unavailable. Thus, we divided the training data set into a smaller training data set and a test data set at a ratio of 8 to 2 for this study.
We trained multiple models to accommodate different K-space input proportions; each model underwent the same single training phase. In the training phase, each example consistently included all four modalities (i.e., cT1WI, cT1WI, T2, and FLAIR images) to ensure the uniform representation of each modality and maintain data consistency throughout. Adopting the approach of Menze et al. (15,16), the tumor regions were categorized into three distinct classes: (I) WT, which encompassed all tumor structures; (II) tumor core (TC), which comprised all tumor structures with the exclusion of edema; and (III) ET, which included ET structures only. The study was conducted in accordance with the Declaration of Helsinki (as revised in 2013).
Data preparation
The 2D MRI scan slices were generated from the three-dimensional (3D) MRI scans of gliomas. First, we transformed the 2D MRI scans into 2D K-space data using FFT, which did not change the data size; thus, all slices kept the size of 160×160×4. The four channels of the input image indicate the four multi-contrast images: T1WI, cT1WI, T2WI, and FLAIR images. After the image data were transformed into K-space data through FFT, the image data became a complex number, including the real and imaginary parts. Thus, one image input channel corresponded to two K-space input channels (i.e., the real and the imaginary parts). We then composited the real and imaginary parts of the K-space data, setting the data size to 160×160×8. The eight channels of the input K-space data indicate the real and imaginary parts of the four multi-contrast images. We did not use any augmentation methods, as the K-space data did not have the same properties as the image data. Finally, the simulated under-sampled K-space data were generated by linearly eliminating part of the data. In this way, we were able to test the clinical application of our architecture.
Deep-residual U-net architecture
The primary architecture employed in this study was the deep-residual U-net (17), which was originally designed for road extraction tasks. This architecture combines the U-net’s encoder-decoder structure with residual blocks, offering dual advantages: ease of training and efficient information propagation (3,18).
The U-net’s architecture replaces fully-connected layers with convolutional layers (2,3) enhancing its performance on medical images. Its encoder consists of sequential layers of convolution, max-pooling, and rectified linear unit (ReLU) blocks, while the decoder employs deconvolution blocks for up-sampling. Skip connections between corresponding layers in the encoder and decoder facilitate backpropagation and preserve finer details.
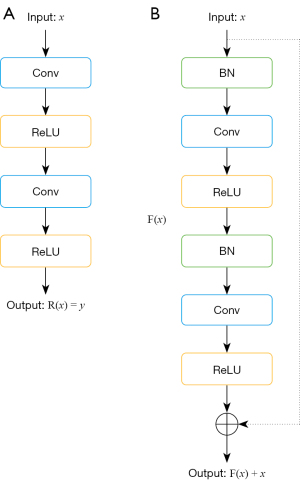
Deeper neural networks generally yield better performance than shallow neural networks, but they also complicate training and may lead to performance degradation. To address this issue, He et al. introduced residual networks that ease training by reformulating information flow (18). In a standard neural network block (Figure 2A), the output R(x) = y maps input x to output y through layers like convolution and ReLU. Conversely, a residual block (Figure 2B) includes batch normalization and ReLU layers, producing an output F(x). The final output is F(x) + x, which combines the identity mapping, x, with the specialized mapping, F(x).
Our deep-residual U-net combines these strengths. It comprises three main parts: an encoder, a bridge, and a decoder. The encoder and decoder each contain three residual units, while the bridge serves as a connecting layer. Up-sampling layers in the decoder and skip connections throughout the architecture, as shown by the dashed line in Figure 3, ensure efficient information flow. The details of the network layers are provided in Table 1.
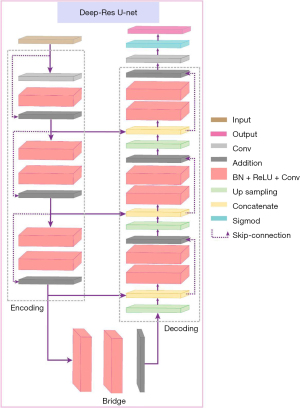
Table 1
| Unit level | Operations | Output size |
|---|---|---|
| Input | – | 8×160×160 |
| L1 | Conv + BN + ReLU + Conv + Add | 64×160×160 |
| Encoder | ||
| L2 | Conv + BN + ReLU + Conv + Conv + BN + ReLU + Conv + Add | 128×80×80 |
| L3 | Conv + BN + ReLU + Conv + Conv + BN + ReLU + Conv + Add | 256×40×40 |
| Bridge | ||
| L4 | Conv + BN + ReLU + Conv + Conv + BN + ReLU + Conv + Add | 512×20×20 |
| L5 | Upsample + concatenation + BN + ReLU + Conv + BN + ReLU + Conv + Add | 256×40×40 |
| Decoder | ||
| L6 | Upsample + concatenation + BN + ReLU + Conv + BN + ReLU + Conv + Add | 128×80×80 |
| L7 | Upsample + concatenation + BN + ReLU + Conv + BN + ReLU + Conv + Add | 64×160×160 |
| Output | 1×1 Conv + sigmoid | 3×160×160 |
The encoder part contains L1, L2, and L3 levels. The bridge part is the L4 level. The decoder part contains L5, L6, and L7 parts. Conv, convolution; BN, batch normalization; ReLU, rectified linear unit; Add, addition.
Robustness assessment with varying under-sampling rates
In our evaluation, we compared the proposed architecture against traditional segmentation tasks using both the K-space data and corresponding image data. The K-space data were subjected to different under-sampling rates to assess the robustness of the segmentation methods. The traditional segmentation methods were found to be susceptible to information loss, particularly as the under-sampling rate increased. Conversely, our architecture showed signs of stabilization even with the reduced K-space data, indicating its relative independence from data loss.
Segmentation performance evaluation
We compared our segmentation results with the ground-truth masks to assess the performance of our architecture. To quantify the comparison precisely, we used four different evaluation metrics; that is, the Dice similarity coefficient (DSC), sensitivity rate, positive predictive value (PPV), and Hausdorff_95 distance. These metrics are represented below: TP means true positive, TN means true negative, FP means false positive, and FN means false negative.
The DSC is the spatial overlap index and represents the quantitative similarity between two samples. It is expressed as:
The sensitivity is the percentage of pixels correctly classified as brain tumor pixels, and is expressed as:
The PPV represents the percentage of pixels classified correctly over the total number of pixels classified as brain tumor pixels, and is expressed as:
The Hausdorff_95 distance refers to the difference between the borders of samples, and is expressed as:
Loss function
In our study, we adopted a hybrid loss function that integrates both binary cross-entropy (BCE) and Dice loss, which were tailored for our segmentation task. This combination was adopted to harness the stability offered by BCE, while also leveraging the unique advantages of Dice loss for segmentation. By using both BCE and Dice loss, we sought to achieve a more effective optimization process tailored to our specific task.
BCE loss was defined as:
Dice loss was defined as:
where y is our results, and is the ground-true masks.
Thus, the BCE Dice loss was the average of BCE loss and Dice loss, and was defined as:
where α is defined as 0.5 in our work.
Experiment settings
In our experiments, the network was designed to produce segmentations 3×160×160 in size, where 3 indicates the channels and 160×160 represents the spatial dimensions. Of our data set, 20% was reserved for testing, while the remaining data underwent a 10-fold cross-validation. The deep-residual U-net employed for the task was initialized using the He Initializer, with a weight decay rate of 0.0001. Optimization was carried out using the Adam optimizer, with an initial learning rate of 0.0003, a batch size of 18, and a momentum of 0.9. To address potential overfitting, we incorporated a dynamic early stopping method (19), setting the initial number of epochs to 10,000. This method was used to monitor the performance metrics and halt the training if no improvement was observed over a predefined interval. Training was executed on an NVIDIA RTX 8000 GPU, with each epoch taking approximately four minutes for both the training and validation. For testing, the same GPU was used, and the predictions for the entire data set were completed in 30 minutes (on average).
Results
To evaluate the performance of our proposed method, a total of 285 patients from the 2018 BraTS Challenge data set were used in the training and testing processes. Among the corresponding 285 lesions, 210 were high-grade gliomas, and 75 were low-grade gliomas, according to the pathological results.
Segmentation results based on fully sampled K-space data
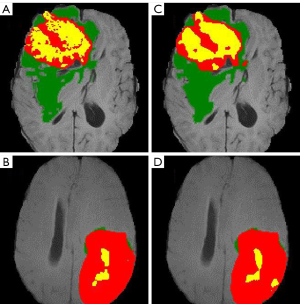
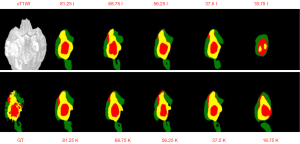
The image data were first transformed into fully sampled K-space data, and the fully sampled K-space data were then used as the input for the deep-residual U-net. The training time was approximately 3 days. The training details are provided in Appendix 1. The training process is depicted in Figure S1. The results of the proposed method and the best results of the 2018 BraTS Challenge are shown in Table 2 (20). The mean Dice scores of the proposed method were 0.8573, 0.8789, and 0.7765 for the segmentation of the WT, TC, and ET regions, respectively. With the exception of the results for the WT region, our results were always better than the state-of-the-art (SOTA) of the 2018 BraTS Challenge, which had mean Dice scores of 0.8154, and 0.7664 for the segmentation of the TC and ET regions, respectively. However, for the segmentation of the WT region, the mean Dice score (0.8839) of the best results of the 2018 BraTS Challenge was slightly higher than our mean Dice score. However, the lower Hausdorff distance of our results indicates that our proposed architecture performed better than the best results of the 2018 BraTS Challenge on segmenting details and edges. Figure 4 provides two examples of our segmentation results compared to the ground truth.
Table 2
| Testing data set | Dice | Hausdorff (mm) | |||||
|---|---|---|---|---|---|---|---|
| WT | TC | ET | WT | TC | ET | ||
| Deep-residual U-net | 0.8573 | 0.8789 | 0.7765 | 2.5649 | 1.6146 | 2.7187 | |
| Best results in 2018 | 0.8839 | 0.8154 | 0.7664 | 5.9044 | 4.8091 | 3.7731 | |
BraTS, brain tumor segmentation; WT, whole tumor; TC, tumor core; ET, enhanced tumor.
Segmentation results based on under-sampled K-space data
Our proposed architecture’s performance was assessed on K-space data that were under-sampled using a specific pattern: certain rows of the K-space data were zero-padded to emulate the effects of under-sampling. The quantitative results of the segmentations (for the WT, TC, and ET regions) are presented in Tables 3-5. As the results revealed, our architecture remained robust even in the face of K-space data loss. It consistently surpassed traditional segmentation methods, which involve first transforming the under-sampled K-space data into the image domain using the FFT and then segmenting the reconstructed images. This superiority was particularly pronounced when the K-space data retention rate was below 68.75%. For example, at an under-sampling rate of 18.75%, our method achieved a Dice value that was 25% higher than that of the traditional approach. This trend was consistent across sensitivity and PPV metrics. The Hausdorff distances between the two techniques were somewhat similar; however, our architecture’s segmentations were more closely aligned with the ground-truth masks, suggesting a higher fidelity in representation. Visual evidence supporting these claims can be found in Figures S2-S4, with a representative segmentation displayed in Figure 5.
Table 3
| Under-sample | Dice | Sensitivity | PPV | Hausdorff | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Image | K-space | Image | K-space | Image | K-space | Image | K-space | ||||
| 81.25% | 0.8065 | 0.8309 | 0.8454 | 0.8345 | 0.8242 | 0.8654 | 2.9091 | 2.8328 | |||
| 75% | 0.8306 | 0.8407 | 0.886 | 0.8506 | 0.836 | 0.8688 | 2.7182 | 2.7619 | |||
| 68.75% | 0.8269 | 0.8491 | 0.8778 | 0.8607 | 0.8377 | 0.8714 | 2.7409 | 2.7074 | |||
| 62.50% | 0.8152 | 0.8355 | 0.8526 | 0.8529 | 0.8335 | 0.8564 | 2.8636 | 2.8008 | |||
| 56.25% | 0.7941 | 0.8475 | 0.8393 | 0.8621 | 0.8077 | 0.8695 | 2.9953 | 2.6925 | |||
| 50% | 0.7724 | 0.8443 | 0.8339 | 0.8595 | 0.7849 | 0.8653 | 3.0678 | 2.7275 | |||
| 43.75% | 0.7858 | 0.8357 | 0.8241 | 0.8539 | 0.8101 | 0.8575 | 3.024 | 2.7855 | |||
| 37.50% | 0.783 | 0.8268 | 0.8465 | 0.8444 | 0.7928 | 0.85 | 3.0056 | 2.833 | |||
| 33.30% | 0.7331 | 0.8242 | 0.7898 | 0.8324 | 0.7552 | 0.8565 | 3.2782 | 2.8954 | |||
| 25% | 0.7523 | 0.7803 | 0.8454 | 0.7743 | 0.7576 | 0.8398 | 3.107 | 3.133 | |||
| 18.75% | 0.5232 | 0.7721 | 0.5694 | 0.7744 | 0.6064 | 0.8286 | 4.3101 | 3.1739 | |||
WT, whole tumor; PPV, positive predictive value.
Table 4
| Under-sample | Dice | Sensitivity | PPV | Hausdorff | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Image | K-space | Image | K-space | Image | K-space | Image | K-space | ||||
| 81.25% | 0.8541 | 0.8424 | 0.9045 | 0.8941 | 0.8671 | 0.8875 | 1.7754 | 1.7472 | |||
| 75% | 0.8598 | 0.8656 | 0.9233 | 0.9047 | 0.8801 | 0.8845 | 1.664 | 1.7161 | |||
| 68.75% | 0.8639 | 0.8607 | 0.9218 | 0.9041 | 0.8763 | 0.8921 | 1.6858 | 1.6803 | |||
| 62.50% | 0.8562 | 0.8497 | 0.9179 | 0.9032 | 0.8634 | 0.8805 | 1.733 | 1.7251 | |||
| 56.25% | 0.8702 | 0.8242 | 0.8947 | 0.9116 | 0.8539 | 0.8908 | 1.8422 | 1.6662 | |||
| 50% | 0.8619 | 0.8134 | 0.9037 | 0.9126 | 0.8338 | 0.8801 | 1.8803 | 1.6895 | |||
| 43.75% | 0.8563 | 0.8207 | 0.8961 | 0.9047 | 0.8454 | 0.8817 | 1.856 | 1.7234 | |||
| 37.50% | 0.8477 | 0.8226 | 0.9108 | 0.8942 | 0.8386 | 0.8798 | 1.8364 | 1.7514 | |||
| 33.30% | 0.8434 | 0.7678 | 0.878 | 0.9079 | 0.7957 | 0.8593 | 2.0506 | 1.7719 | |||
| 25% | 0.8007 | 0.7996 | 0.9036 | 0.8728 | 0.8222 | 0.8399 | 1.9121 | 1.9547 | |||
| 18.75% | 0.7948 | 0.5334 | 0.6981 | 0.8664 | 0.6635 | 0.8402 | 3.0091 | 1.9657 | |||
BraTS; brain tumor segmentation; TC, tumor core; PPV, positive predictive value.
Table 5
| Under-sample | Dice | Sensitivity | PPV | Hausdorff | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Image | K-space | Image | K-space | Image | K-space | Image | K-space | ||||
| 81.25% | 0.6928 | 0.7154 | 0.7319 | 0.7228 | 0.7217 | 0.7573 | 3.0639 | 3.008 | |||
| 75% | 0.7385 | 0.735 | 0.7943 | 0.7436 | 0.7518 | 0.7754 | 2.8508 | 2.9288 | |||
| 68.75% | 0.734 | 0.7492 | 0.7854 | 0.7665 | 0.7528 | 0.7779 | 2.8788 | 2.8538 | |||
| 62.50% | 0.7073 | 0.7245 | 0.7405 | 0.7457 | 0.7395 | 0.7526 | 3.019 | 2.9656 | |||
| 56.25% | 0.6668 | 0.7499 | 0.7138 | 0.7626 | 0.687 | 0.7847 | 3.1446 | 2.8545 | |||
| 50% | 0.6441 | 0.744 | 0.7016 | 0.758 | 0.6686 | 0.7769 | 3.2298 | 2.8832 | |||
| 43.75% | 0.6604 | 0.7258 | 0.694 | 0.7476 | 0.6989 | 0.7548 | 3.1863 | 2.9465 | |||
| 37.50% | 0.6649 | 0.7116 | 0.7207 | 0.7363 | 0.6895 | 0.7389 | 3.1482 | 2.9907 | |||
| 33.30% | 0.587 | 0.705 | 0.6331 | 0.7133 | 0.6267 | 0.7492 | 3.4362 | 3.0559 | |||
| 25% | 0.6332 | 0.631 | 0.7191 | 0.6243 | 0.6505 | 0.7024 | 3.2105 | 3.3281 | |||
| 18.75% | 0.3408 | 0.6208 | 0.3832 | 0.6269 | 0.4168 | 0.685 | 4.3552 | 3.3619 | |||
ET, enhanced tumor; PPV, positive predictive value.
Discussion
This study highlights the feasibility of using K-space data for tumor segmentation. Our method shows promise in identifying borders between smaller malignant tissues and normal brain tissue, and thus may have potential in enhancing microscopic lesion detection. A noteworthy feature of our architecture is that directly solving the K-space data does not distort the image information, which makes our method more reliable for landmark detection, registration, brain lesion segmentation, and diagnosis prediction. Our findings also show that our method is adaptable to various rates of under-sampling, a crucial factor in accelerating MRI processes. This adaptability indicates the practical applicability of our approach in diverse MRI scenarios. In summary, our findings suggest that our architecture has the potential to complement traditional lesion segmentation methods, providing radiologists with an additional tool for more accurately assessing glioma severity. This approach, subject to further validation, could enhance diagnostic accuracy in clinical settings.
Our analysis indicates that segmentation using fully sampled K-space data is potentially better than segmentation using image data. This suggests that direct K-space analyses might provide a more precise understanding of tumor characteristics. Our study reinforces the concept that tumor segmentation tasks can be effectively conducted independently of traditional image reconstruction processes, highlighting the innovative potential of K-space data analysis in MRI diagnostics. Using K-space data as input for our network appeared to minimize issues typically associated with the FFT and reconstruction processes, such as artifact generation and data loss. This approach may set new benchmarks in the precision of segmentation tasks, as evidenced by our comparative performance in the Medical Image Computing and Computer Assisted Interventions (MICCAI)-2018 BraTS Challenge.
Further, our method reduced the effect of image distortion caused by the FFT and reconstruction processes or super-resolution networks. Traditional segmentation methods that are reliant on processed image data carry the risk of introducing artificial anomalies. Conversely, using K-space data, our approach potentially offers a more accurate representation of actual tissue characteristics. Further research needs to be conducted to delve further into K-space data analysis to address its challenges and harness its unique advantages for MRI diagnostics.
Fully sampled methods are standard in many clinical contexts; however, there are challenges in consistently obtaining such data, especially given how difficult it is for patients to remain completely still during the imaging process. This has prompted investigations into under-sampling techniques. Reconstructed images from under-sampled K-space data are frequently marred by artifacts, which in turn affect the segmentation accuracy.
In our study, we examined the effects of linearly eliminating portions of K-space data using Cartesian sampling. This method aimed to investigate the balance between under-sampling and segmentation fidelity (10,21). Some K-space reconstruction methods, such as compressed sensing (22) and reconstruction network exist; however, the image data still face the difficulty of image information distortion or loss. As a solution, we also investigated the influence of the under-sampling method on our architecture. We eliminated part of the K-space data linearly, and then applied the Cartesian sampling method. We then compared the segmentation results from the under-sampled K-space data and the under-sampled image data. Our findings indicate that segmentation from under-sampled K-space data using our architecture can closely approximate the results from fully sampled K-space data. This is notable, as it reduces the extensive time required for K-space reconstruction, a significant factor in MRI processing (10,23).
Our analysis suggests that for tumor segmentation tasks, K-space data may be more suitable than traditional imaging data. The primary reasons for this include the preservation of complete information within each point of the K-space data and the absence of FFT in our architecture, which often leads to data loss in image processing. There are two main reasons of implementing our new architecture. First, any point of the K-space data contains the complete information of one image data slice (21,24). Thus, the under-sampling method does not greatly reduce the data information during the computation process. As for the image data, the reduction of K-space data causes artifacts that significantly lower the precision of segmentation tasks (24). Second, FFT is not part of our architecture. As mentioned above, FFT also causes image data loss.
Conclusions
Our results demonstrate the efficacy of a novel segmentation architecture that not only enhances the precision of segmentation tasks but also preserves image information integrity. This approach underscores both the feasibility and potential superiority of our methods, particularly in the context of clinical applications. We rigorously tested our method using emulated K-space data to establish its feasibility in MRI segmentation tasks. Our initial test results are promising and suggest a new avenue for segmentation approaches in medical imaging. However, it is crucial to acknowledge the limitations of our current approach. We did not use true K-space data in our experiments, and factors such as coil numbers and their sensitivity, which can significantly influence K-space data quality, were not considered. These limitations highlight important areas for future research.
Building on the insights gained from our current study, we are exploring the development of a 3D segmentation technique based on the V-net (25). This is a natural progression, given the 3D nature of most medical imaging data sets (26). Our aim is to extend the applicability of our architecture to more complex and clinically relevant 3D data.
Acknowledgments
Funding: The study was partially support by
Footnote
Conflicts of Interest: All authors have completed the ICMJE uniform disclosure form (available at https://qims.amegroups.com/article/view/10.21037/qims-23-946/coif). Y.X.J.W. serves as the Editor-In-Chief of Quantitative Imaging in Medicine and Surgery. D.L. serves as an unpaid editorial board member of Quantitative Imaging in Medicine and Surgery. The other authors have no conflicts of interest to declare.
Ethical Statement: The authors are accountable for all aspects of the work in ensuring that questions related to the accuracy or integrity of any part of the work are appropriately investigated and resolved. The study was conducted in accordance with the Declaration of Helsinki (as revised in 2013).
Open Access Statement: This is an Open Access article distributed in accordance with the Creative Commons Attribution-NonCommercial-NoDerivs 4.0 International License (CC BY-NC-ND 4.0), which permits the non-commercial replication and distribution of the article with the strict proviso that no changes or edits are made and the original work is properly cited (including links to both the formal publication through the relevant DOI and the license). See: https://creativecommons.org/licenses/by-nc-nd/4.0/.
References
- Kamnitsas K, Ferrante E, Parisot S, et al. DeepMedic for brain tumor segmentation. In: Brainlesion: Glioma, Multiple Sclerosis, Stroke and Traumatic Brain Injuries: Second International Workshop, BrainLes 2016, with the Challenges on BRATS, ISLES and mTOP 2016, Held in Conjunction with MICCAI 2016, Athens, Greece, October 17, 2016, Revised Selected Papers 2. Springer International Publishing; 2016:138-49.
- Shelhamer E, Long J, Darrell T. Fully Convolutional Networks for Semantic Segmentation. IEEE Trans Pattern Anal Mach Intell 2017;39:640-51. [Crossref] [PubMed]
- Ronneberger O, Fischer P, Brox T. U-net: Convolutional networks for biomedical image segmentation. In: Medical Image Computing and Computer-Assisted Intervention-MICCAI 2015: 18th International Conference, Munich, Germany, October 5-9, 2015, Proceedings, Part III 18. Springer International Publishing; 2015:234-41.
- Chen LC, Zhu Y, Papandreou G, et al. Encoder-decoder with atrous separable convolution for semantic image segmentation. In: Proceedings of the European Conference on Computer Vision (ECCV). 2018:801-18.
- James D. Quantization errors in the fast Fourier transform. IEEE Transactions on Acoustics, Speech, and Signal Processing 1975;23:277-83.
- Weinstein C. Roundoff noise in floating point fast Fourier transform computation. IEEE Transactions on Audio and Electroacoustics 1969;17:209-15.
- Tasche M, Zeuner H. Worst and average case roundoff error analysis for FFT. BIT Numerical Mathematics 2001;41:563-81.
- Kaneko T, Liu B. Accumulation of round-off error in fast Fourier transforms. Journal of the ACM 1970;17:637-54. (JACM).
- Jeelani H, Martin J, Vasquez F, et al. Image quality affects deep learning reconstruction of MRI. In: 2018 IEEE 15th International Symposium on Biomedical Imaging (ISBI 2018). IEEE; 2018:357-60.
- Zeng G, Guo Y, Zhan J, Wang Z, Lai Z, Du X, Qu X, Guo D. A review on deep learning MRI reconstruction without fully sampled k-space. BMC Med Imaging 2021;21:195. [Crossref] [PubMed]
- Wijethilake N, Islam M, Ren H. Radiogenomics model for overall survival prediction of glioblastoma. Med Biol Eng Comput 2020;58:1767-77. [Crossref] [PubMed]
- Lustig M, Donoho D, Pauly JM. Sparse MRI: The application of compressed sensing for rapid MR imaging. Magn Reson Med 2007;58:1182-95. [Crossref] [PubMed]
- Hollingsworth KG. Reducing acquisition time in clinical MRI by data undersampling and compressed sensing reconstruction. Phys Med Biol 2015;60:R297-322. [Crossref] [PubMed]
- Bakas S, Akbari H, Sotiras A, Bilello M, Rozycki M, Kirby JS, Freymann JB, Farahani K, Davatzikos C. Advancing The Cancer Genome Atlas glioma MRI collections with expert segmentation labels and radiomic features. Sci Data 2017;4:170117. [Crossref] [PubMed]
- Bakas S, Reyes M, Jakab A, et al. Identifying the best machine learning algorithms for brain tumor segmentation, progression assessment, and overall survival prediction in the BRATS challenge. arXiv:1811.02629 [Preprint]. 2018. Available online: https://arxiv.org/abs/1811.02629
- Menze BH, Jakab A, Bauer S, Kalpathy-Cramer J, Farahani K, Kirby J, et al. The Multimodal Brain Tumor Image Segmentation Benchmark (BRATS). IEEE Trans Med Imaging 2015;34:1993-2024. [Crossref] [PubMed]
- Zhang Z, Liu Q, Wang Y. Road extraction by deep residual u-net. IEEE Geosci Remote Sens Lett 2018;15:749-53.
- He K, Zhang X, Ren S, et al. Identity mappings in deep residual networks. In: Computer Vision-ECCV 2016: 14th European Conference, Amsterdam, The Netherlands, October 11-14, 2016, Proceedings, Part IV 14. Springer International Publishing; 2016:630-45.
- Prechelt L. Early stopping-but when? In: Orr GB, Müller KR. editors. Neural Networks: Tricks of the trade. Berlin, Heidelberg: Springer Berlin Heidelberg; 2002:55-69.
- Myronenko A. 3D MRI brain tumor segmentation using autoencoder regularization. In: Brainlesion: Glioma, Multiple Sclerosis, Stroke and Traumatic Brain Injuries: 4th International Workshop, BrainLes 2018, Held in Conjunction with MICCAI 2018, Granada, Spain, September 16, 2018, Revised Selected Papers, Part II 4. Springer International Publishing; 2019:311-20.
- Kojima S, Shinohara H, Hashimoto T, Suzuki S. Undersampling patterns in k-space for compressed sensing MRI using two-dimensional Cartesian sampling. Radiol Phys Technol 2018;11:303-19. [Crossref] [PubMed]
- Jaspan ON, Fleysher R, Lipton ML. Compressed sensing MRI: a review of the clinical literature. Br J Radiol 2015;88:20150487. [Crossref] [PubMed]
- Liu J, Saloner D. Accelerated MRI with CIRcular Cartesian UnderSampling (CIRCUS): a variable density Cartesian sampling strategy for compressed sensing and parallel imaging. Quant Imaging Med Surg 2014;4:57-67. [Crossref] [PubMed]
- Moratal D, Vallés-Luch A, Martí-Bonmatí L, Brummer M. k-Space tutorial: an MRI educational tool for a better understanding of k-space. Biomed Imaging Interv J 2008;4:e15. [Crossref] [PubMed]
- Milletari F, Navab N, Ahmadi SA. V-net: Fully convolutional neural networks for volumetric medical image segmentation. In: 2016 Fourth International Conference on 3D Vision (3DV). IEEE; 2016:565-71.
- Sun Y, Xu S, Ortíz-Ledón CA, Zhu J, Chen S, Duan J. Biomimetic assembly to superplastic metal-organic framework aerogels for hydrogen evolution from seawater electrolysis. Exploration (Beijing) 2021;1:20210021. [Crossref] [PubMed]


