
Validation of biomechanical assessment of coronary plaque vulnerability based on intravascular optical coherence tomography and digital subtraction angiography
Introduction
Cardiovascular diseases (CVDs) are the number one cause of mortality, and are projected to remain the single leading cause of death globally until 2030 (1,2). CVDs have been shown to be caused by silent atherosclerotic plaque progression, leading to sudden plaque rupture, occlusive thrombosis, and acute coronary syndrome (3). Therefore, the early identification and treatment of plaque prone to catastrophic rupture is an essential approach to decreasing cardiovascular morbidity and mortality.
Pathology-based studies (4-6) and multi-modality imaging (7,8) have been used to explore the potential features related to plaque vulnerability. Morphological characteristics, such as the fibrous cap thickness (FCT) and the extent of the necrotic lipid core, have been identified as the main determinants predisposing plaque to rupture (9-11). In vivo intravascular studies have shown that the thin fibrous cap is the most common predisposing lesion (12,13). This is reasonable, as the fibrous cap is the last barrier to resist the stress exerted on the atheroma and thus prevent plaque rupture. However, over a 3-year follow-up period, intravascular imaging histology only identified <10% of CVDs associated with the thin fibrous cap (12,13). In addition, there is still no consensus as to the exact cut-off value of the thin fibrous cap that can be used to identify vulnerable plaque (4,14,15). In one study of 72 patients with acute coronary syndrome, only 67% of patients with ruptured plaques were identified as having a thin fibrous cap (15). Thus, the FCT should not be the only determinant for predicting plaque rupture, which occurs due to the difference between the protection exerted by the fibrous cap and its disrupting forces.
Plaques develop at specific areas of coronary arteries where flow is disturbed, and plaque rupture occurs when the intraplaque stress exceeds the material strength of the overlying fibrous cap. Thus, biomechanical factors may be used to assess plaque status. The coupling of morphological and functional metrics could also provide novel insights into the detection of vulnerable plaques in advance, and thus prevent major adverse cardiovascular events. However, accurate biomechanical computation greatly depends on the precise reconstruction of vessels and plaque geometry.
Intravascular optical coherence tomography (IV-OCT) is a high-resolution imaging technology (up to 10–20 µm) based on near-infrared interferometry that could provide the best estimation for plaque configurations. In this study, a finite-element analysis (FEA) was conducted based on two-dimensional (2D) slice models, including plaque component and vessel wall reconstruction, to explore the mechanical fields. However, it is preferable to create three-dimensional (3D) vessel and plaque configurations via the fusion of IV-OCT and biplane angiography or coronary computed tomography angiography to guarantee the true tortuosity of the reconstructed models. Hence, hemodynamics, such as wall shear stress (WSS), which plays a key role in atherosclerotic disease development, can be calculated accurately (16).
This study aimed to develop a framework to fully evaluate the rationality of using biomechanical features to assess plaque stability based on both 2D FEA and 3D fluid-structure interaction (FSI) simulations. Our findings might provide a viable foundation for high-risk plaque prediction and thus prevent major adverse cardiovascular events. In this study:
- An IV-OCT-based morpho-mechanic analysis was performed to assess the vulnerability of coronary plaque;
- IV-OCT and digital subtraction angiography (DSA) images were fused to achieve accurate 3D model reconstruction;
- 3D FSI computation was performed to investigate the role of both the structural and hemodynamic parameters in assessing plaque stability.
Figure 1 summarizes the approach of this study.
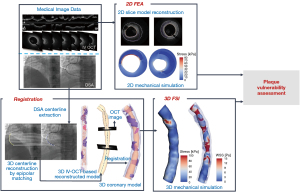
Methods
Data acquisition
A 54-year-old male with a history of hypertension and a diagnosis of acute coronary syndrome was enrolled in this study. A set of right coronary artery imaging data, including coronary IV-OCT and DSA imaging data, were acquired from the Catheterization Laboratory of the Anzhen Hospital. The study was conducted in accordance with the Declaration of Helsinki (as revised in 2013). This study was approved by the Institutional Review Board of Beijing Anzhen Hospital (No. ks2020002), and written informed consent was obtained from the patient before the study.
2D geometry reconstruction and morphometric analysis
Image segmentation was conducted on each frame of every IV-OCT pullback to obtain a patient-specific coronary plaque model. Plaque composition was analyzed according to the Consensus Standards (17). The vessel lumen was first segmented via the automatic IV-OCT processing module, which is further described in Appendix 1. Next, the boundaries of different plaque compositions, including the fibrous cap, necrotic lipid pool, and calcification, were identified and manually segmented. The external border of the coronary outer wall was also traced and shaped from the IV-OCT image. In relation to any borders that could not be detected due to artifacts or the limited penetration of light, an estimation based on the visible characteristics near the non-detectable regions was made. Figure 2A,2B show the IV-OCT image and contour extraction, respectively. All the segmentations were conducted using the 3D slicer (v4.13.0) by an expert with extensive experience in reading IV-OCT images. Two experienced cardiologists were engaged to review and correct the segmentation results. Both the segmentation expert and cardiologist were blinded to the patient’s demographic and clinical characteristics. The 2D structures were finally formed (Figure 2C). In this study, 250 slices were reconstructed, and slices that contained lipid plaque were selected for the parameter calculation and analysis. Five lipid plaques were identified, resulting in 103 slices in total. Subsequently, two experienced cardiologists conducted the plaque identification. Both the cardiologists identified plaque-1 and plaque-4 as vulnerable plaques in 32 slices, and classified plaque-2, plaque-3, and plaque-5 as stable plaques in 71 slices.
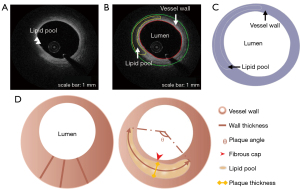
The morphological parameters were computed for each slice on the basis of the 2D-reconstructed geometry. The area of the vessel lumen was then calculated. The geometric features of the outer wall were quantified, including the area, the maximal wall thickness (MWT), and the normalized wall index (NWI), which was defined as the ratio between the area of the wall and the overall area of the vessel. The structural characteristics of the plaque, including the area, angle, maximal plaque thickness (MPT), minimum FCT (FCTmin), and average FCT (FCTave), were computed. Figure 2D shows the details of the geometric features.
3D model reconstruction
3D model reconstruction was performed for the FSI simulation. The contours of the vessel lumen, outer wall boundary, and plaque component for each slice were the same as those for the 2D geometry reconstruction (Figure 3A). As the IV-OCT is a catheter-based imaging modality, each slice had to be stacked and aligned with the catheter path-line to form a 3D coronary model. This 3D path-line was generated from the DSA data. Specifically, two angiographic images with projections ≥25° apart, and with minimum vessel overlap and foreshortening were first selected. Among which, at least one DSA image with a visible IV-OCT catheter was chosen to guarantee the coherence of the starting and ending points between the DSA and IV-OCT images. The 2D centerline of the coronary artery in each DSA image was extracted using the Medical Imaging Interaction Toolkit (MITK) Workbench. The 3D centerline was subsequently reconstructed via epipolar geometry and the stereo matching algorithm and exported as discrete points as shown in Figure 3B.
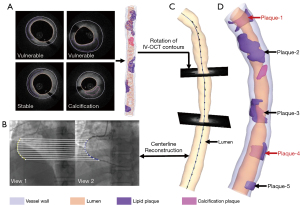
To ensure more accurate 3D model reconstruction, the interpolation was first used to increase the number of slices using the Visualization Toolkit (VTK) package in Python 3.93 (https://vtk.org). The number of discrete points of the 3D angiographic centerline was determined by the final slice number. The registration process between the IV-OCT slices and 3D angiographic centerline comprised several sub-steps. First, the scale was converted into millimeter units for the points from the IV-OCT and the DSA to eliminate the resolution difference between the two image modalities. Second, the large side branches in both the DSA and IV-OCT images were identified as the key landmarks. Those landmarks were used to determine the coordinate axis direction. Third, the centroid of each IV-OCT slice was obtained and defined as the midpoint on the perpendicular bisector of the longest line segment between the two points on the lumen contour. The 2D IV-OCT slice was then moved to their position to the space of 3D angiographic centerline by applying the translation and rotation operations. Next, the IV-OCT slices orthogonal to the 3D angiographic centerline were generated as shown in Figure 3C. The transferred model was finally exported in triangulation mesh in STereoLithography (STL) format to facilitate the computational analysis (Figure 3D). The details of the co-registration process between the IV-OCT and 3D angiographic centerline are provided in Appendix 2.
2D FEA
The FEA was performed with ABAQUS (version 2020, Dassault Systemes Simulia Corp., Providence, RI, USA). The model was meshed with three-node and four-node linear, hybrid elements. In this study, the element sizes for the vessel wall and plaque were set at 0.02 and 0.01 mm, respectively. Ultimately, the models contained about 50k–60k elements. The material properties used for the vessel wall and the different components of the plaque are set out in Table 1. A pulsatile waveform of pressure with the peak value of 130 mmHg was applied to the luminal side as the external load as detailed in Appendix 3. A four-point constraint was employed in the outer vessel wall to suppress rigid translation and rotation. Further, the self-contact interaction was set for the intraluminal surface of the vessel lumen, and the bonded contact was given at the contact region between the vessel wall and the plaque. The constraint and contact settings for the 2D FEA computation are detailed in Appendix 4. The temporal discretization of the computational models was assigned as 100 steps with the time step of 0.01 seconds. Grid and temporal independency analyses were conducted (Appendix 5) to prove that the base mesh resolution and time step settings were adequate in this study. The maximal and average values of displacement and stress for each slice were analyzed after the simulation.
Table 1
| Material | Young’s modulus | Poisson’s ratio |
|---|---|---|
| Vessel wall | 0.6 MPa | 0.48 |
| Lipid plaque | 0.02 MPa | 0.48 |
| Calcification plaque | 10 GPa | 0.3 |
FSI simulation
The FSI simulation was performed on the Ansys Workbench platform (ANSYS Inc., Canonsburg, PA, USA). The outer face of the vessel lumen was selected as the fluid-solid interface for the data transfer in the simulation. The fluid domain was meshed with the tetrahedral elements in the core region and prismatic cells (five layers) in the boundary layer near the vessel wall, resulting in 683,035 elements. A velocity boundary condition was imposed at the inlet with a value of 0.43 m/s, and a pressure value of 130 mmHg was given to the outlet as the pressure boundary condition. The blood was assumed to be incompressible with a density of 1,050 kg/m3 and a dynamic viscosity of 0.00365 kg·m−1·s−1. The Newtonian and laminar model was applied in this study. No-slip condition was assumed at the fluid-solid interface. The structural analysis of this model was made of 517,987 elements. The mesh independent test was performed for both the fluid and solid domains as detailed in Appendix 6 to show that the base mesh resolution was sufficient for this study. Table 1 shows the material properties of the coronary vessel and plaques. Two small surfaces at the coronary wall ends were fixed to suppress rigid displacement and rotation. The self-contact interaction was set for the intraluminal surface of the vessel lumen, and the bonded contact was given at the contact region between the vessel wall and the plaque. No extra load was applied to the structural participant, and the wall only received the pressure transferred from the fluid participant.
Statistical analysis
The statistical analyses were conducted with Python 3.93 and R software (v4.1.3). The Shapiro-Wilk test was used to test the normality of the continuous variables. The differences between the variables in the two groups were analyzed using the Student t-test for the normally distributed data and the Wilcoxon rank-sum test for the non-normally distributed data. The reported statistical importance levels were all two-sided, and a P value <0.05 was considered statistically significant. The correlation test was performed using the Pearson method for the normally distributed data or the Spearman method for the non-normally distributed data. The R value indicated the strength of the linear relationship between the variables. The weighted least absolute shrinkage and selection operator (LASSO) method was used to identify significant features related to plaque vulnerability (18) with penalty parameter tuning adjusted by 10-time cross-validation.
Results
Morphological and mechanical analyses
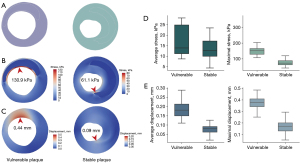
The morphological and mechanical analyses of the 103 lipid plaque slices revealed 13 candidate factors for vulnerable plaque assessment (Table 2). The geometric features, including the lumen area, NWI, plaque area, MPT, FCTmin, and FCTave, differed significantly between the vulnerable and stable groups. Further, all the mechanical parameters differed significantly between the two groups. As Figure 4 shows, the slices with vulnerable plaque had higher stress and displacement than those with stable plaque. The box-plots also depict higher concentrations of both stress and displacement in the vulnerable plaque group (Figure 4D,4E).
Table 2
| Variables | Vulnerable (n=32) | Stable (n=71) | P value |
|---|---|---|---|
| Lumen data | |||
| Lumen area (mm2)† | 6.08±2.85 | 5.68±2.04 | <0.05 |
| Outer wall data | |||
| Wall area (mm2) | 11.47±5.27 | 9.93±3.47 | 0.083 |
| NWI† | 0.66±0.24 | 0.68±0.14 | <0.05 |
| MWT (mm) | 1.19±0.54 | 1.33±0.51 | 0.103 |
| Plaque data | |||
| Plaque area (mm2)† | 2.19±1.86 | 1.63±1.21 | <0.05 |
| MPT (mm)† | 0.74±0.52 | 0.60±0.38 | <0.05 |
| Plaque angle (°) | 137.00±34.00 | 100.00±78.00 | 0.064 |
| Fibrous cap data | |||
| FCTmin (mm)† | 0.10±0.05 | 0.28±0.14 | <0.05 |
| FCTave (mm)† | 0.19±0.04 | 0.39±0.16 | <0.05 |
| Mechanical data | |||
| Average stress (kPa)† | 13.96±13.82 | 12.78±7.50 | <0.05 |
| Maximal stress (kPa)† | 151.38±39.75 | 72.91±26.90 | <0.05 |
| Average displacement (mm)† | 0.18±0.07 | 0.08±0.03 | <0.05 |
| Maximal displacement (mm)† | 0.37±0.07 | 0.16±0.05 | <0.05 |
Continuous and normal data are presented as the mean ± standard deviation; continuous and non-normal data are presented as the median ± interquartile range. †, the variables showing a significant difference (with a P value <0.05) between the vulnerable and stable groups. NWI, normalized wall index; MWT, maximal wall thickness; MPT, maximal plaque thickness; FCTmin, minimum fibrous cap thickness; FCTave, average fibrous cap thickness.
Correlation between the geometric features and FEA-derived parameters
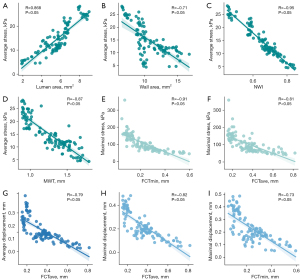
The correlation between four FEA-derived parameters (average and maximal value of stress and displacement) and nine morphological features were investigated (Table 3). The univariate linear regression analysis showed that four geometric parameters, including the lumen area, wall area, NWI, and MWT, were significantly correlated with the average stress (with R values >0.70) (Figure 5A-5D). Further, the average stress was positively related to the lumen area, but negatively correlated with the wall area, NWI, and MWT. As Figure 5E,5F show, the maximal stress in all the analyzed slices decreased as the FCTmin and FCTave increased. The displacement was negatively correlated with the FCTmin (with maximal displacement) and FCTave (with both average and maximal displacement) (Figure 5G-5I).
Table 3
| Variables | Value | Average stress | Maximal stress | Average displacement | Maximal displacement | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| R | P value | R | P value | R | P value | R | P value | |||||
| Lumen area (mm2) | 5.72±1.92 | 0.868† | <0.05 | 0.289 | 0.003 | 0.688 | <0.05 | 0.482 | <0.05 | |||
| Wall area (mm2) | 9.96±3.51 | −0.71† | <0.05 | 0.028 | 0.781 | −0.25 | 0.011 | 0.036 | 0.722 | |||
| NWI | 0.67±0.14 | −0.95† | <0.05 | −0.25 | 0.012 | −0.61 | <0.05 | −0.35 | <0.05 | |||
| MWT (mm) | 1.30±0.50 | −0.87† | <0.05 | −0.08 | 0.422 | −0.44 | <0.05 | −0.17 | 0.088 | |||
| Plaque area (mm2) | 1.78±1.45 | −0.66 | <0.05 | 0.434 | <0.05 | 0.235 | 0.017 | 0.407 | <0.05 | |||
| MPT (mm) | 0.63±0.39 | −0.62 | <0.05 | 0.484 | <0.05 | 0.131 | 0.188 | 0.353 | <0.05 | |||
| Plaque angle (°) | 120.00±58.00 | −0.28 | 0.004 | 0.112 | 0.26 | 0.171 | 0.083 | 0.1 | 0.317 | |||
| FCTmin (mm) | 0.24±0.19 | −0.04 | 0.662 | −0.91† | <0.05 | −0.66 | <0.05 | −0.73† | <0.05 | |||
| FCTave (mm) | 0.35±0.22 | −0.21 | 0.034 | −0.81† | <0.05 | −0.79† | <0.05 | −0.82† | <0.05 | |||
Continuous and normal data are presented as the mean ± standard deviation; continuous and non-normal data are presented as the median ± interquartile range. †, the correlation coefficient of morphological and FEA-derived parameters is >0.7. FEA, finite-element analysis; NWI, normalized wall index; MWT, maximal wall thickness; MPT, maximal plaque thickness; FCTmin, minimum fibrous cap thickness; FCTave, average fibrous cap thickness.
Influential parameter selection for vulnerable plaque
The intercorrelations among the candidate factors were examined (Figure S7, Appendix 7). A weighted LASSO regression analysis was subsequently employed to identify the most influential plaque parameters from the nine morphological parameters and four mechanical parameters (13 parameters in total) using the tuning parameter (λ), which was determined using a 10-fold cross-validation based on the mean-squared prediction error. The optimized lambda values (λ) were commonly determined using the criteria that minimizes the mean-squared prediction error, indicated as λ-min, while the tuning parameter (λ), λ-1se, was selected using the one-standard error rule (18,19). Figure 6A,6B display the plots of the mean-square error versus log(λ) and the LASSO coefficient paths, respectively. Five factors were selected by λ-min with the value of 0.00114 [log(λ-min) =−6.77688], which included the FCTmin, average displacement, maximal displacement, average stress, and maximal stress. Their coefficients were −41.852, 34.748, 38.5, 429.878, and 3.791, respectively. Three core features were identified by λ-1se with the value of 0.02958 [log(λ-1se) =−3.52070], including the FCTmin, average displacement, and maximal displacement. Their coefficients were −7.709, 33.361, and 6.708, respectively (Table 4).
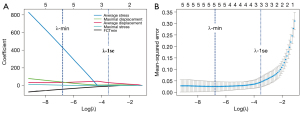
Table 4
| Criteria | Variable | LASSO coefficient |
|---|---|---|
| λ-min | Intercept | −10.144 |
| FCTmin | −41.852 | |
| Average displacement | 34.748 | |
| Maximal displacement | 38.5 | |
| Average stress | 429.878 | |
| Maximal stress | 3.791 | |
| λ-1se | Intercept | −4.678 |
| FCTmin | −7.709 | |
| Average displacement | 33.361 | |
| Maximal displacement | 6.708 |
LASSO, least absolute shrinkage and selection operator; λ-min, minimum criteria; FCTmin, minimum fibrous cap thickness; λ-1se, one-standard error criteria.
WSS analysis based on FSI simulation
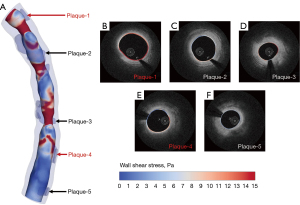
The identification of high WSS over vulnerable atheroma might improve the detection of plaques prone to rupture. Figure 7A shows the spatial distribution of WSS in the vessel lumen. To further explore the localization of the WSS patterns, slices orthogonal to the 3D angiographic centerline were extracted and the WSS distribution of each slice was also displayed. One representative slice for each lipid plaque was randomly selected (Figure 7B-7F). Plaque-1 and plaque-4, which were identified as vulnerable plaques, had more elevated WSS than the other plaques (Figure 7B,7E).
Discussion
This study verified that biomechanical features play a crucial role in evaluation of plaque stability based on 2D FEA and 3D FSI simulations using IV-OCT and DSA data sets. A total of 103 IV-OCT slices containing lipid plaque were used for the 2D geometry reconstruction and structural analysis. Experienced cardiologists classified plaque status by combining the FCT, the features of the plaque, including the area, angle, and thickness, and the features of the vessel wall, as no consistent criteria had been established for vulnerable plaque identification in previous studies (4,14,15,20). IV-OCT is excellent for penetrating vessel walls to identify vulnerable plaques with high resolution (21). However, it might be insufficient to confirm the plaque status relying solely on IV-OCT images. Histopathological studies should be conducted in the future to enable more accurate grouping. In addition, the model was reconstructed in a semi-automatic way due to the imprecise segmentations of the current automatic frameworks for coronary plaque (22-26) as summarized in Appendix 8. The boundaries of different plaque compositions were identified and manually segmented to achieve accurate geometry creation. However, the limited ranging depth of the IV-OCT images (1–2.5 mm) might introduce bias into the reconstruction of the outer wall especially in poor lipid-rich tissue (27). The co-registration with more image modalities, such as intravascular ultrasound images and near-infrared spectroscopy (13,28-35), or advanced computational techniques (36) should be employed to achieve more accurate model reconstruction.
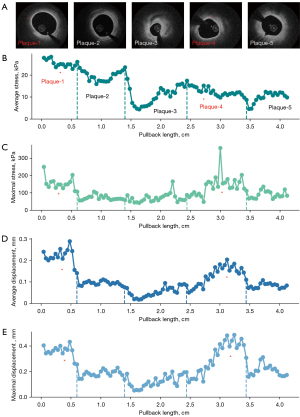
In this study, 2D FEA computation was conducted with the assignment of linear material properties for the vessel wall and plaques. The average displacement for each slice at the early, peak, and late systole was calculated. All the slices displayed a “small enough” displacement of approximately 0.2 mm, 5% of the original dimensions of the considered vessel (4 mm), confirming the rationality of employing the linear equation to depict the behavior of the material (Appendix 9). The hyperelastic behavior of certain plaque components have been described in previous studies (37,38). However, the settings of hyperelastic behaviors might be suitable for circumstances with large displacements (>20–30% of the initial dimensions) (37,39,40), which was greatly over the average displacements reported in our study. In addition, with a single central processing unit (CPU) time of 3 minutes, which is much faster than simulations based on 3D models, 2D FEA is time-saving. The analysis based on the 2D slice models could also contribute to the accurate tracking of critical lesion sites (Figure 8). Therefore, this approach has the potential to serve as a clinical tool for the comprehensive biomechanical profiling of coronary plaques due to its accuracy and time efficacy (41). We also compared the 2D and 3D computation results and found that the 2D FEA had a larger maximal stress value than the 3D FSI. The average absolute difference between the two simulation methods was 35.6% (as detailed in Appendix 10). Our results showed that the 2D and 3D computation results displayed a similar trend, even if the 2D FEA tends to overestimate the stresses (42,43). It is evident that both 2D and 3D simulations can provide additive information to assist in plaque vulnerability assessment.
Detailed morpho-mechanic analyses were subsequently conducted based on the 2D FEA computation. The thin fibrous cap is the most commonly assessed predisposing lesion in vivo intravascular studies (12,13); however, to date no consensus as to an exact cut-off value has been reached. We conducted a correlation analysis to examine the relationship between the mechanical parameters and morphological features and found that maximal stress and maximal displacement were significantly correlated to the FCTmin and FCTave, which is consistent with the findings of previous studies (44-46). The results indicated that the biomechanical features are closely related to the clinical event. The LASSO method was used to select factors to optimize the prediction accuracy. FEA-derived parameters were included either via the λ-min or λ-1se criteria, which also highlighted the necessity of including the biomechanical factors. Previous studies have shown that plaque vulnerability is not a static process; stable plaques may process towards morphologically more vulnerable plaques in a proportion of patients (10,47), and up to three-quarters of vulnerable plaques can lose vulnerability features over time with appropriate optimal medical therapy (48). Therefore, adding information reflecting the mechanical response could enable more accurate evaluation.
3D model reconstruction based on the fusion of the IV-OCT and DSA images was conducted for the FSI simulation. Plaque-1 and plaque-4, which were identified as vulnerable plaques, displayed higher WSS. A strong correlation between the focal elevation in WSS and the site of the plaque rupture has been reported in previous studies (49-51). Therefore, this patient needs to be closely monitored and careful attention needs to be paid to the regions with high WSS. Moreover, plaque-3, which was one of the stable plaques, also showed elevated WSS. This might have been induced by the luminal narrowing near plaque-3. This plaque also requires frequent monitoring. A FSI simulation was employed in a previous study of coronary diseases (7), and its accuracy was also evaluated. In this study, a structural-only simulation was performed and compared with the FSI computation to facilitate the necessity of FSI simulations (as detailed in Appendix 11). However, the FSI simulation took around 6 hours to obtain the functional parameters in this study, and thus is time-consuming and not suitable for real-time analysis. Automatic frameworks should be applied in the future to enable the integration of plaque stress analysis in the clinic (52,53).
Despite the excellent resolution of IV-OCT images near the field, limited light penetration to the deeper vessel wall might introduce imprecisions into model reconstructions. Other imaging modalities, such as intravascular ultrasound, should be co-registered to overcome this limitation. In this study, manual segmentation was used for the geometry creation; however, it is time-consuming. A precise automatic segmentation framework should be established to relieve human experts of having to engage in repetitive tasks and enable real-time analysis.
The small deformation of the vessel wall confirmed the rationality of using the linear material property; however, a uniaxial test is needed to obtain more precise material properties for the simulation. A computational modeling of residual stress for in vivo-based models should be implemented in future research to provide more accurate stress distributions. The current study modeled a single component; however, multi-material interaction effects should be further investigated (54).
3D model reconstruction was achieved by fusing the IV-OCT and DSA images using a rigid registration method and based on an assumption of a constant speed of pullback. Interpolation operations and key landmarks were used in this study to reduce imprecisions; however, non-rigid registration should be adopted (55,56). The one-way steady FSI simulation failed to consider the influence of the pulse pressure wave and the deformation of the vessel wall, which might have led to mis-estimates of the functional parameters. Two-way transient FSI simulation should be performed to provide more information on detailed and accurate functional indicators in the future to serve plaque vulnerability assessment.
Weighted LASSO was performed in the current study for the multicollinear and imbalanced scenarios to identify crucial features that could improve predictive accuracy. However, the prediction model was not established in the current study, as the data sets of only one patient were used. Analyses based on large cohorts of patients with more follow-up data should be conducted in the future to enable more reliable conclusions to be drawn. Further, the employment of advanced computational strategies, such as machine learning, might provide efficient evaluations. A prediction tool that integrates the morphological and functional metrics should be established, thus providing better guidance for clinical practice.
Conclusions
In this study, both 2D FEA and 3D FSI simulations were conducted to examine the use of biomechanical assessments of plaque status. The results showed that stress, displacement, and WSS were crucial features that were closely related to plaque vulnerability. In vivo biomechanical simulation might be a powerful tool to provide key information for plaque risk assessment, and thus might contribute to CVD therapy in the future.
Acknowledgments
The authors would like to thank Shukun (Beijing) Network Technology Co., Ltd. for providing additional computing resources and technical support.
Funding: This study was supported by
Footnote
Conflicts of Interest: All authors have completed the ICMJE uniform disclosure form (available at https://qims.amegroups.com/article/view/10.21037/qims-23-1094/coif). The authors have no conflicts of interest to declare.
Ethical Statement: The authors are accountable for all aspects of the work in ensuring that questions related to the accuracy or integrity of any part of the work are appropriately investigated and resolved. The study was conducted in accordance with the Declaration of Helsinki (as revised in 2013). This study was approved by the Institutional Review Board of Beijing Anzhen Hospital (No. ks2020002). Written informed consent was obtained from the patient before the study.
Open Access Statement: This is an Open Access article distributed in accordance with the Creative Commons Attribution-NonCommercial-NoDerivs 4.0 International License (CC BY-NC-ND 4.0), which permits the non-commercial replication and distribution of the article with the strict proviso that no changes or edits are made and the original work is properly cited (including links to both the formal publication through the relevant DOI and the license). See: https://creativecommons.org/licenses/by-nc-nd/4.0/.
References
- Mathers CD, Loncar D. Projections of global mortality and burden of disease from 2002 to 2030. PLoS Med 2006;3:e442. [Crossref] [PubMed]
- Mendis S, Puska P, Norrving B. Global atlas on cardiovascular disease prevention and control. Geneva: World Health Organization; 2011.
- Badimon L, Vilahur G. Thrombosis formation on atherosclerotic lesions and plaque rupture. J Intern Med 2014;276:618-32. [Crossref] [PubMed]
- Burke AP, Farb A, Malcom GT, Liang YH, Smialek J, Virmani R. Coronary risk factors and plaque morphology in men with coronary disease who died suddenly. N Engl J Med 1997;336:1276-82. [Crossref] [PubMed]
- Virmani R, Kolodgie FD, Burke AP, Farb A, Schwartz SM. Lessons from sudden coronary death: a comprehensive morphological classification scheme for atherosclerotic lesions. Arterioscler Thromb Vasc Biol 2000;20:1262-75. [Crossref] [PubMed]
- Virmani R, Burke AP, Kolodgie FD, Farb A. Pathology of the thin-cap fibroatheroma: a type of vulnerable plaque. J Interv Cardiol 2003;16:267-72. [Crossref] [PubMed]
- Wang J, Paritala PK, Mendieta JB, Komori Y, Raffel OC, Gu Y, Li Z. Optical coherence tomography-based patient-specific coronary artery reconstruction and fluid-structure interaction simulation. Biomech Model Mechanobiol 2020;19:7-20. [Crossref] [PubMed]
- Maurovich-Horvat P, Ferencik M, Voros S, Merkely B, Hoffmann U. Comprehensive plaque assessment by coronary CT angiography. Nat Rev Cardiol 2014;11:390-402. [Crossref] [PubMed]
- Reith S, Battermann S, Hoffmann R, Marx N, Burgmaier M. Optical coherence tomography derived differences of plaque characteristics in coronary culprit lesions between type 2 diabetic patients with and without acute coronary syndrome. Catheter Cardiovasc Interv 2014;84:700-7. [Crossref] [PubMed]
- Uemura S, Ishigami K, Soeda T, Okayama S, Sung JH, Nakagawa H, Somekawa S, Takeda Y, Kawata H, Horii M, Saito Y. Thin-cap fibroatheroma and microchannel findings in optical coherence tomography correlate with subsequent progression of coronary atheromatous plaques. Eur Heart J 2012;33:78-85. [Crossref] [PubMed]
- Kato K, Yonetsu T, Kim SJ, Xing L, Lee H, McNulty I, Yeh RW, Sakhuja R, Zhang S, Uemura S, Yu B, Mizuno K, Jang IK. Nonculprit plaques in patients with acute coronary syndromes have more vulnerable features compared with those with non-acute coronary syndromes: a 3-vessel optical coherence tomography study. Circ Cardiovasc Imaging 2012;5:433-40. [Crossref] [PubMed]
- Stone GW, Maehara A, Lansky AJ, de Bruyne B, Cristea E, Mintz GS, Mehran R, McPherson J, Farhat N, Marso SP, Parise H, Templin B, White R, Zhang Z, Serruys PW. PROSPECT Investigators. A prospective natural-history study of coronary atherosclerosis. N Engl J Med 2011;364:226-35. Erratum in: N Engl J Med 2011;365:2040. [Crossref] [PubMed]
- Calvert PA, Obaid DR, O'Sullivan M, Shapiro LM, McNab D, Densem CG, Schofield PM, Braganza D, Clarke SC, Ray KK, West NE, Bennett MR. Association between IVUS findings and adverse outcomes in patients with coronary artery disease: the VIVA (VH-IVUS in Vulnerable Atherosclerosis) Study. JACC Cardiovasc Imaging 2011;4:894-901. [Crossref] [PubMed]
- Schaar JA, Muller JE, Falk E, Virmani R, Fuster V, Serruys PW, Colombo A, Stefanadis C, Ward Casscells S, Moreno PR, Maseri A, van der Steen AF. Terminology for high-risk and vulnerable coronary artery plaques. Report of a meeting on the vulnerable plaque, June 17 and 18, 2003, Santorini, Greece. Eur Heart J 2004;25:1077-82. [Crossref] [PubMed]
- Tanaka A, Imanishi T, Kitabata H, Kubo T, Takarada S, Tanimoto T, Kuroi A, Tsujioka H, Ikejima H, Ueno S, Kataiwa H, Okouchi K, Kashiwaghi M, Matsumoto H, Takemoto K, Nakamura N, Hirata K, Mizukoshi M, Akasaka T. Morphology of exertion-triggered plaque rupture in patients with acute coronary syndrome: an optical coherence tomography study. Circulation 2008;118:2368-73. [Crossref] [PubMed]
- Gijsen F, Katagiri Y, Barlis P, Bourantas C, Collet C, Coskun U, et al. Expert recommendations on the assessment of wall shear stress in human coronary arteries: existing methodologies, technical considerations, and clinical applications. Eur Heart J 2019;40:3421-33. [Crossref] [PubMed]
- Tearney GJ, Regar E, Akasaka T, Adriaenssens T, Barlis P, Bezerra HG, et al. Consensus standards for acquisition, measurement, and reporting of intravascular optical coherence tomography studies: a report from the International Working Group for Intravascular Optical Coherence Tomography Standardization and Validation. J Am Coll Cardiol 2012;59:1058-72. [Crossref] [PubMed]
- Sauerbrei W, Royston P, Binder H. Selection of important variables and determination of functional form for continuous predictors in multivariable model building. Stat Med 2007;26:5512-28. [Crossref] [PubMed]
- Wu Y, Wang L. A survey of tuning parameter selection for high-dimensional regression. Annu Rev Stat Appl 2020;7:209-26.
- Farb A, Burke AP, Tang AL, Liang TY, Mannan P, Smialek J, Virmani R. Coronary plaque erosion without rupture into a lipid core. A frequent cause of coronary thrombosis in sudden coronary death. Circulation 1996;93:1354-63. [Crossref] [PubMed]
- Tearney GJ, Jang IK, Bouma BE. Optical coherence tomography for imaging the vulnerable plaque. J Biomed Opt 2006;11:021002. [Crossref] [PubMed]
- Lee J, Prabhu D, Kolluru C, Gharaibeh Y, Zimin VN, Bezerra HG, Wilson DL. Automated plaque characterization using deep learning on coronary intravascular optical coherence tomographic images. Biomed Opt Express 2019;10:6497-515. [Crossref] [PubMed]
- Gharaibeh Y, Prabhu D, Kolluru C, Lee J, Zimin V, Bezerra H, Wilson D. Coronary calcification segmentation in intravascular OCT images using deep learning: application to calcification scoring. J Med Imaging (Bellingham) 2019;6:045002. [Crossref] [PubMed]
- Kolluru C, Prabhu D, Gharaibeh Y, Bezerra H, Guagliumi G, Wilson D. Deep neural networks for A-line-based plaque classification in coronary intravascular optical coherence tomography images. J Med Imaging (Bellingham) 2018;5:044504. [Crossref] [PubMed]
- Rico-Jimenez JJ, Campos-Delgado DU, Villiger M, Otsuka K, Bouma BE, Jo JA. Automatic classification of atherosclerotic plaques imaged with intravascular OCT. Biomed Opt Express 2016;7:4069-85. [Crossref] [PubMed]
- Athanasiou LS, Bourantas CV, Rigas G, Sakellarios AI, Exarchos TP, Siogkas PK, Ricciardi A, Naka KK, Papafaklis MI, Michalis LK, Prati F, Fotiadis DI. Methodology for fully automated segmentation and plaque characterization in intracoronary optical coherence tomography images. J Biomed Opt 2014;19:026009. [Crossref] [PubMed]
- Lowe HC, Narula J, Fujimoto JG, Jang IK. Intracoronary optical diagnostics current status, limitations, and potential. JACC Cardiovasc Interv 2011;4:1257-70. [Crossref] [PubMed]
- Pinilla-Echeverri N, Mehta SR, Wang J, Lavi S, Schampaert E, Cantor WJ, Bainey KR, Welsh RC, Kassam S, Mehran R, Storey RF, Nguyen H, Meeks B, Wood DA, Cairns JA, Sheth T. Nonculprit Lesion Plaque Morphology in Patients With ST-Segment-Elevation Myocardial Infarction: Results From the COMPLETE Trial Optical Coherence Tomography Substudys. Circ Cardiovasc Interv 2020;13:e008768. [Crossref] [PubMed]
- Cheng JM, Garcia-Garcia HM, de Boer SP, Kardys I, Heo JH, Akkerhuis KM, Oemrawsingh RM, van Domburg RT, Ligthart J, Witberg KT, Regar E, Serruys PW, van Geuns RJ, Boersma E. In vivo detection of high-risk coronary plaques by radiofrequency intravascular ultrasound and cardiovascular outcome: results of the ATHEROREMO-IVUS study. Eur Heart J 2014;35:639-47. [Crossref] [PubMed]
- Prati F, Romagnoli E, Gatto L, La Manna A, Burzotta F, Ozaki Y, et al. Relationship between coronary plaque morphology of the left anterior descending artery and 12 months clinical outcome: the CLIMA study. Eur Heart J 2020;41:383-91. [Crossref] [PubMed]
- Karlsson S, Anesäter E, Fransson K, Andell P, Persson J, Erlinge D. Intracoronary near-infrared spectroscopy and the risk of future cardiovascular events. Open Heart 2019;6:e000917. [Crossref] [PubMed]
- Waksman R, Di Mario C, Torguson R, Ali ZA, Singh V, Skinner WH, et al. Identification of patients and plaques vulnerable to future coronary events with near-infrared spectroscopy intravascular ultrasound imaging: a prospective, cohort study. Lancet 2019;394:1629-37. [Crossref] [PubMed]
- Erlinge D. Near-infrared spectroscopy for intracoronary detection of lipid-rich plaques to understand atherosclerotic plaque biology in man and guide clinical therapy. J Intern Med 2015;278:110-25. [Crossref] [PubMed]
- Madder RD, Goldstein JA, Madden SP, Puri R, Wolski K, Hendricks M, Sum ST, Kini A, Sharma S, Rizik D, Brilakis ES, Shunk KA, Petersen J, Weisz G, Virmani R, Nicholls SJ, Maehara A, Mintz GS, Stone GW, Muller JE. Detection by near-infrared spectroscopy of large lipid core plaques at culprit sites in patients with acute ST-segment elevation myocardial infarction. JACC Cardiovasc Interv 2013;6:838-46. [Crossref] [PubMed]
- Li J, Li X, Mohar D, Raney A, Jing J, Zhang J, Johnston A, Liang S, Ma T, Shung KK, Mahon S, Brenner M, Narula J, Zhou Q, Patel PM, Chen Z. Integrated IVUS-OCT for real-time imaging of coronary atherosclerosis. JACC Cardiovasc Imaging 2014;7:101-3. [Crossref] [PubMed]
- Olender ML, Athanasiou LS, de la Torre Hernandez JM, Ben-Assa E, Nezami FR, Edelman ER. A Mechanical Approach for Smooth Surface Fitting to Delineate Vessel Walls in Optical Coherence Tomography Images. IEEE Trans Med Imaging 2019;38:1384-97. [Crossref] [PubMed]
- Yang C, Bach RG, Zheng J, Naqa IE, Woodard PK, Teng Z, Billiar K, Tang D. In vivo IVUS-based 3-D fluid-structure interaction models with cyclic bending and anisotropic vessel properties for human atherosclerotic coronary plaque mechanical analysis. IEEE Trans Biomed Eng 2009;56:2420-8. [Crossref] [PubMed]
- Cardoso L, Kelly-Arnold A, Maldonado N, Laudier D, Weinbaum S. Effect of tissue properties, shape and orientation of microcalcifications on vulnerable cap stability using different hyperelastic constitutive models. J Biomech 2014;47:870-7. [Crossref] [PubMed]
- Kobielarz M, Kozuń M, Gąsior-Głogowska M, Chwiłkowska A. Mechanical and structural properties of different types of human aortic atherosclerotic plaques. J Mech Behav Biomed Mater 2020;109:103837. [Crossref] [PubMed]
- Milzi A, Lemma ED, Dettori R, Burgmaier K, Marx N, Reith S, Burgmaier M. Coronary plaque composition influences biomechanical stress and predicts plaque rupture in a morpho-mechanic OCT analysis. Elife 2021;10:e64020. [Crossref] [PubMed]
- Doradla P, Otsuka K, Nadkarni A, Villiger M, Karanasos A, Zandvoort LJCV, Dijkstra J, Zijlstra F, Soest GV, Daemen J, Regar E, Bouma BE, Nadkarni SK. Biomechanical Stress Profiling of Coronary Atherosclerosis: Identifying a Multifactorial Metric to Evaluate Plaque Rupture Risk. JACC Cardiovasc Imaging 2020;13:804-16. [Crossref] [PubMed]
- Nieuwstadt HA, Akyildiz AC, Speelman L, Virmani R, van der Lugt A, van der Steen AF, Wentzel JJ, Gijsen FJ. The influence of axial image resolution on atherosclerotic plaque stress computations. J Biomech 2013;46:689-95. [Crossref] [PubMed]
- Anantula K, Vankayala B, Yadav SS. A three-dimensional finite element analysis of stress distribution in maxillary central incisor with a horizontal mid root fracture after various management protocols. J Conserv Dent 2021;24:470-4. [Crossref] [PubMed]
- Loree HM, Kamm RD, Stringfellow RG, Lee RT. Effects of fibrous cap thickness on peak circumferential stress in model atherosclerotic vessels. Circ Res 1992;71:850-8. [Crossref] [PubMed]
- Sadat U, Teng Z, Gillard JH. Biomechanical structural stresses of atherosclerotic plaques. Expert Rev Cardiovasc Ther 2010;8:1469-81. [Crossref] [PubMed]
- Ohayon J, Finet G, Gharib AM, Herzka DA, Tracqui P, Heroux J, Rioufol G, Kotys MS, Elagha A, Pettigrew RI. Necrotic core thickness and positive arterial remodeling index: emergent biomechanical factors for evaluating the risk of plaque rupture. Am J Physiol Heart Circ Physiol 2008;295:H717-27. [Crossref] [PubMed]
- Kubo T, Maehara A, Mintz GS, Doi H, Tsujita K, Choi SY, Katoh O, Nasu K, Koenig A, Pieper M, Rogers JH, Wijns W, Böse D, Margolis MP, Moses JW, Stone GW, Leon MB. The dynamic nature of coronary artery lesion morphology assessed by serial virtual histology intravascular ultrasound tissue characterization. J Am Coll Cardiol 2010;55:1590-7. [Crossref] [PubMed]
- Räber L, Koskinas KC, Yamaji K, Taniwaki M, Roffi M, Holmvang L, Garcia Garcia HM, Zanchin T, Maldonado R, Moschovitis A, Pedrazzini G, Zaugg S, Dijkstra J, Matter CM, Serruys PW, Lüscher TF, Kelbaek H, Karagiannis A, Radu MD, Windecker S. Changes in Coronary Plaque Composition in Patients With Acute Myocardial Infarction Treated With High-Intensity Statin Therapy (IBIS-4): A Serial Optical Coherence Tomography Study. JACC Cardiovasc Imaging 2019;12:1518-28. [Crossref] [PubMed]
- Fukumoto Y, Hiro T, Fujii T, Hashimoto G, Fujimura T, Yamada J, Okamura T, Matsuzaki M. Localized elevation of shear stress is related to coronary plaque rupture: a 3-dimensional intravascular ultrasound study with in-vivo color mapping of shear stress distribution. J Am Coll Cardiol 2008;51:645-50. [Crossref] [PubMed]
- Gijsen F, van der Giessen A, van der Steen A, Wentzel J. Shear stress and advanced atherosclerosis in human coronary arteries. J Biomech 2013;46:240-7. [Crossref] [PubMed]
- Vergallo R, Papafaklis MI, Yonetsu T, Bourantas CV, Andreou I, Wang Z, Fujimoto JG, McNulty I, Lee H, Biasucci LM, Crea F, Feldman CL, Michalis LK, Stone PH, Jang IK. Endothelial shear stress and coronary plaque characteristics in humans: combined frequency-domain optical coherence tomography and computational fluid dynamics study. Circ Cardiovasc Imaging 2014;7:905-11. [Crossref] [PubMed]
- Straughan R, Kadry K, Parikh SA, Edelman ER, Nezami FR. Fully automated construction of three-dimensional finite element simulations from Optical Coherence Tomography. Comput Biol Med 2023;165:107341. [Crossref] [PubMed]
- Lee J, Gharaibeh Y, Kolluru C, Zimin VN, Dallan LAP, Kim JN, Bezerra HG, Wilson DL. Segmentation of Coronary Calcified Plaque in Intravascular OCT Images Using a Two-Step Deep Learning Approach. IEEE Access 2020;8:225581-93.
- Kadry K, Olender ML, Marlevi D, Edelman ER, Nezami FR. A platform for high-fidelity patient-specific structural modelling of atherosclerotic arteries: from intravascular imaging to three-dimensional stress distributions. J R Soc Interface 2021;18:20210436. [Crossref] [PubMed]
- Kadry K, Karmakar A, Schuh A, Peterson K, Schaap M, Marlevi D, Taylor C, Edelman E, Nezami F. Morphology-based non-rigid registration of coronary computed tomography and intravascular images through virtual catheter path optimization. arXiv:2301.00060 [Preprint]. 2022. Available online: https://arxiv.org/abs/2301.00060
- Karmakar A, Olender ML, Marlevi D, Shlofmitz E, Shlofmitz RA, Edelman ER, Nezami FR. Framework for lumen-based nonrigid tomographic coregistration of intravascular images. J Med Imaging (Bellingham) 2022;9:044006. [Crossref] [PubMed]


