
A two-step neural network-based guiding system for obtaining reliable radiographs for critical shoulder angle measurement
Introduction
Rotator cuff tears (RCTs) are a prevalent condition linked to shoulder discomfort and impaired function (1,2). According to one study (3), 20.7% of patients had full-thickness RCTs. Further, it has been noted that the likelihood of developing this particular ailment tends to increase as age advances. Thus, the early and accurate diagnosis of RCTs is critical.
Various acromion morphological parameters, such as the critical shoulder angle (CSA), lateral acromial angle, and acromial index, have been widely reported to have great value in the etiological analysis of RCTs and in assessing patient prognosis (4). Among these parameters, higher CSA values have been reported to be the most closely associated with full-thickness RCTs and a high risk of rotator cuff re-tears (5). However, the CSA measurement is significantly affected by the malpositioning of the shoulder, which has led to concerns about the reliability of measurements taken on non-standard anteroposterior (AP) radiographs (6). A previous study (6) reported that a ratio of the transverse to longitudinal diameter of the glenoid projection (RTL) ≤0.25 is a reliable CSA measurement with excellent diagnostic efficacy in identifying adequate images for the accurate measurement of CSA.
However, it is not easy to acquire AP radiographs with RTLs ≤0.25 in real-world settings, as (I) it takes much time to manually adjust patients’ position in radiography, which increases the workloads of radiologists and is against ethical guidelines; and (II). it is challenging for radiologists to determine RTL values ≤0.25 or >0.25 with the naked eye in real-time. Thus, it would be beneficial to have an automated classification system that could assist radiologists to accurately recognize reliable CSA radiographs and guide patient position adjustments in a timely manner.
In the field of computer vision, research has shown that deep learning has the ability to classify images with high accuracy (7,8). Deep learning can capture the complex relationships between images and diagnostics by extracting features from the raw data (9,10). Several studies (11-13) have shown that the application of deep learning could minimize the effects of experience and other external factors in the decision-making processes of radiologists. Thus, we proposed a two-step neural network-based guiding system and evaluated its feasibility and accuracy in detecting and classifying reliable CSA radiographs. To the best of our knowledge, this study was the first to use a hierarchical deep-learning algorithm to classify reliable CSA radiographs. The model’s performance was assessed using an offline, prospective approach and compared with the diagnoses of a radiologist. We present this article in accordance with the STARD reporting checklist (available at https://qims.amegroups.com/article/view/10.21037/qims-23-610/rc).
Methods
Source of data
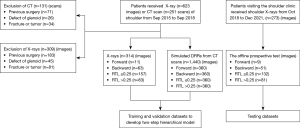
A sequential series of patients who had undergone shoulder imaging, including X-ray radiographs and/or computed tomography (CT) scans, from September 2015 to September 2018 were included in this single-center retrospective diagnostic study. The study was conducted in accordance with the guidelines set out in the Declaration of Helsinki (as revised in 2013). The study was granted approval by the Research Ethics Committee of Sun Yat-sen Memorial Hospital of Sun Yat-sen University (No. SYSEC-ky-ks-2018-036). No informed consent was required for this retrospective study, and the data were anonymized.
The shoulder CT scans were performed at 120 kVp, 275 mAs, and 1.25 mm slice thickness with a fourth-generation scanner (GE Healthcare, Chicago, IL, USA). A standard digital radiography system (Ysio, Siemens Healthcare, Erlangen, Germany) was used to perform the shoulder AP radiographs. As part of the routine examination, the acquisition settings were automatically modified based on each patient’s exposure. The primary authors (Y.A. and C.L.) reviewed each CT scan and X-ray radiograph before its inclusion in the study. The study included patients aged 18 years or older who underwent X-rays and/or CT scans of the shoulder. Patients who had undergone shoulder surgery, had a confirmed fracture, or were diagnosed with a musculoskeletal tumor or glenoid defect were excluded from the study (Figure 1).
Generate digitally reconstructed radiographs (DRRs)
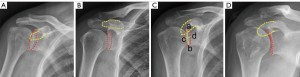
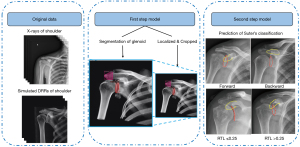
Based on Suter’s classification system and other previous studies (14,15), shoulder AP radiographs can be classified into the following types: ‘forward’ when the non-overlapping coracoid process is above the glenoid rim, ‘backward’ when the non-overlapping coracoid process is below or aligned with the glenoid rim, RTL ≤0.25, and RTL >0.25 (Figure 2). As the distribution of these four types of radiographs was unbalanced in the real-world setting, simulations of the DRRs were used to augment the training data for the network (16). First, Suter’s classification method was used to produce 12 DRRs from each CT scan of each patient following a regular procedure (16). Next, the generated DRRs were used as extra input data to feed the network (Figure 3).
Two‑step hierarchical model
Once the data generation was completed, a one-step classification model was established. This model operates directly on the complete radiograph, without localization or cropping. To improve the classification efficacy and optimize the algorithms, we implemented a two-step hierarchical model. The two-step hierarchical approach has been effectively employed in previous studies related to medical imaging. For example, Pham et al. used a comparable technique to identify abnormalities in chest X-rays (17). Specially, Pham et al. used YOLOv5 (You Only Look Once model version 5) to swiftly localize anomalies across the entire image, and ResNet50 (50-layer deep Residual Network model) to classify the detected regions with more precision, thereby minimizing the false positives identified by YOLOv5. The hierarchical integration of the two models was better able to detect medical anomalies.
In the present study, the first step was to generate a 512×512 pixel crop from each AP radiograph. The second step was to classify the shoulder AP radiographs into the forward, backward, RTL ≤0.25, or RTL >0.25 groups based on downscaled 512×512 inputs from the first network. To reduce the risk of overfitting the model to the training data, five-fold cross-validation was used to select the optimal hyperparameter setting and estimate the expected accuracy for each model. All the networks were trained on an Intel Xeon Platinum (8260 M, 2.4 GHz) computer with a Nvidia Tesla P100-PCIE16GB GPU. The framework used included Python 3.7 based on Python, PyTorch 1.8, CUDA 11.1, and cuDNN 8.0.4, which can be downloaded for free from https://pytorch.org/ and https://developer.nvidia.com/.
The first step: localization of the glenoid and acromion contours
First, the training data set was manually labeled to provide the training ground truth. The data set was divided into the two following different regions of interest (ROIs): the glenoid and the acromion contours. In the annotation labeling process, specialists used the VGG Image Annotator (version 2.0.1 download from https://www.robots.ox.ac.uk/~vgg/software/via/) to label the shoulder radiographs by drawing polylines and/or polygons. The determination of the medial border of the acromion ROI included the creation of a line originating from the most prominent point and extending at a right angle to the lower boundary of the acromion contour. To ensure uniformity and correctness, we sought the assistance of five senior clinical specialists who had expertise in establishing criteria for the original shoulder and associated information in accordance with the annotation requirements. To ensure quality control, each assessment underwent a thorough review process by senior specialists.
Augmentation techniques, including horizontal flips, affine transformations, and contrast adjustments, were used to generate sufficient labeled data from the original data. To reduce the redundancy and inconsistency of the X-rays and DRRs, the intensity range of the X-rays and DRRs was normalized between 0 and 1. The Mask Region-based Convolutional Neural Networks (Mask-RCNN) model using a ResNet-50 backbone and a Feature Pyramid Network, trained with a ‘1x’ learning schedule (Mask-RCNN R50-FPN-1x) from the Detectron2 Model Zoo was chosen to initialize our recognition backbone because it improves accuracy and significantly decreases the number of network parameters (18). The dice similarity coefficient was used to evaluate segmentation accuracy in this process (19) by quantifying the spatial overlap between the predicted segmentation and the ground-truth segmentation. The coefficient ranged from 0 to 1, with a value of 0 indicating no overlap, and a value of 1 indicating perfect agreement between the segmentations. Typically, a dice coefficient above 0.7 is considered acceptable for medical image segmentation tasks (20). Once the segmentation was completed, the acromion and glenoid contours were automatically localized as the center of the images and cropped to 255×255 pixels for further classification.
The second step: classification of shoulder AP radiographs
To classify the radiographs based on Suter’s classification, EfficientNet was selected because of its superior recognition performance (21). The EfficientNet network has been well described previously by Tan et al. (19). In this study, the network was trained to classify the radiographs into four classes: forward, backward, RTL ≤0.25, and RTL >0.25. The selection of the pre-trained model EfficientNet-B3 was based on its performance with a shoulder radiography data set in a previous study (22). We trained the network using an Adam optimizer and saved the model that achieved the best accuracy in every 15 epochs. The batch size and the initial learning rate were set at 16 and 0.02, respectively. These values were selected based on our previous experience, taking into consideration their respective advantages and trade-offs. A batch size of 16 provides a good trade-off between speed and accuracy for this model, while an initial learning rate of 0.02 is a reasonable starting point for optimization. Higher batch sizes can be faster but prone to overfitting, while lower learning rates can be more stable but slower to converge. The last model was saved after 200 epochs, and the network training stopped when there was no improvement in the validation. Finally, to segregate each input image into one of the classes, probabilities for each class were calculated by the classification layer of the network.
Offline prospective test data set
Patients with suspected RCTs who visited the hospital for shoulder AP radiographs between October 1, 2018, and December 30, 2021 were included in the offline prospective test data set. The inclusion and exclusion criteria were similar to those mentioned above. The two-step hierarchical model was employed to test all shoulder AP radiograph images in an offline setting (Figure 1). Radiological diagnoses of shoulder AP radiographs by two radiology experts were used as the ground truths.
Statistical analysis
The mean (standard deviation) is used to represent the continuous data, and the number is used to represent the categorical variables. The dice similarity coefficient was used to assess the performance of the network’s segmentation.
During the five-fold cross-validation, we used various metrics, such as the area under the receiver operating characteristic curve (AUROC), sensitivity, specificity, positive predicted value (PPV), negative predicted value (NPV), and accuracy, to present comprehensive results for both the one-step and two-step approaches. To evaluate the functional performance of the two-step hierarchical model, we conducted an offline prospective test and represented the outcomes using a 4×4 confusion matrix. This matrix provided measurements of the sensitivity, specificity, PPV, NPV, and classification rate for each class. The following abbreviations were used for these metrics: SensF, B, −, + for sensitivity; SpecF, B, −, + for specificity; PPVF, B, −, + for the PPV; and NPVF, B, −, + for the NPV. The classification rate was determined by calculating the ratio of correctly classified patients in all categories to the total number of test patients. To assess the agreement between the two-step hierarchical model and radiologists, we employed Cohen’s kappa index. A two-sided P value <0.05 indicated a statistically significant difference, and we also calculated the 95% confidence interval (CI). All the statistical analyses were performed using IBM SPSS Statistics for Windows Version 21.0 (IBM Corp., Armonk, NY, USA) for Windows.
Results
Clinical characteristics of the training and validation data set
A total of 1,754 shoulder AP radiographs (314 X-rays and 1,440 CT-based DRRs generated from 120 patients) were collected and used for the training and validation data sets (Table 1). The average age of the patients was 43±16 years for the X-rays and 45±13 years for the CT-based DRRs. The original training data set comprised 314 shoulder X-ray images, with an imbalanced distribution across the classes: forward (11 images), backward (63 images), RTL ≤0.25 (157 images), and RTL >0.25 (83 images). To address the class imbalance and enhance model training, we used DRRs to generate additional synthetic images. Specifically, we produced 1,440 DRRs, with 360 DRRs created per class, distributed as follows: forward (360 DRRs), backward (360 DRRs), RTL ≤0.25 (360 DRRs), and RTL >0.25 (360 DRRs). After augmenting the original 314 images with the 1,440 DRRs, our final training data set comprised 1,754 images, with a more balanced distribution across the classes: forward (371 images, including 11 original and 360 DRRs), backward (423 images, including 63 original and 360 DRRs), RTL ≤0.25 (517 images, including 157 original and 360 DRRs), and RTL >0.25 (443 images, including 83 original and 360 DRRs) (Figure 1).
Table 1
| Characteristic | X-rays | CT-based DRRs |
|---|---|---|
| Patients | 314 | 120 |
| Age (years), mean ± SD | 43±16 | 45±13 |
| Sex | ||
| Male | 171 | 67 |
| Female | 143 | 53 |
| Shoulder disease | ||
| Normal | 127 | 43 |
| Shoulder dislocation without bony Bankart | 35 | 16 |
| Rotator cuff tear | 86 | 29 |
| Frozen shoulder | 39 | 15 |
| Acromioclavicular arthritis | 16 | 7 |
| Impingement syndrome | 6 | 6 |
| Mild osteoarthritis | 5 | 4 |
| Radiographs | 314 | 1,440 |
| Forward | 11 | 360 |
| Backward | 63 | 360 |
| RTL ≤0.25 | 157 | 360 |
| RTL >0.25 | 83 | 360 |
CT, computed tomography; DRRs, digitally reconstructed radiographs; SD, standard deviation; RTL, ratio of the transverse to longitudinal diameter of the glenoid projection.
Five-fold cross-validation results
The one-step model
In the five-fold cross-validation, the accuracy of 90.48% (95% CI: 82.41–96.77%). The AUROC was 0.873 (95% CI: 0.844–0.902), sensitivity 80.95% (95% CI: 75.68–85.33%), specificity 93.65% (95% CI: 91.70–95.17%), PPV 80.95% (95% CI: 75.68–85.33%), and NPV 93.65% (95% CI: 91.70–95.17%) (Table 2).
Table 2
| Five-fold cross-validation | One-step model (95% CI) | Two-step model (95% CI) |
|---|---|---|
| AUROC | 0.873 (0.844–0.902) | 0.958 (0.941–0.976) |
| Sensitivity, % | 80.95 (75.68–85.33) | 93.77 (90.03–96.21) |
| Specificity, % | 93.65 (91.70–95.17) | 97.92 (96.62–98.74) |
| PPV, % | 80.95 (75.68–85.33) | 93.77 (90.03–96.21) |
| NPV, % | 93.65 (91.70–95.17) | 97.92 (96.62–98.74) |
| Accuracy, % | 90.48 (82.41–96.77) | 96.88 (88.72–98.36) |
CI, confidence interval; AUROC, area under the receiver operating characteristic curve; PPV, positive predicted value; NPV, negative predicted value.
The two-step model
In the five-fold cross-validation, the two-step model had an average dice score of 0.912, an accuracy of 96.88% (95% CI: 88.72–98.36%), an AUROC of 0.958 (95% CI: 0.941–0.976), a sensitivity of 93.77% (95% CI: 90.03–96.21%), a specificity of 97.92% (95% CI: 96.62–98.74%), a PPV of 93.77% (95% CI: 90.03–96.21%), and a NPV of 97.92% (95% CI: 96.62–98.74%) (Table 2).
Results of the offline prospective test
A total of 273 shoulder AP radiographs were acquired for the offline prospective test. including 9 imaging sets with forward, 51 imaging sets with backward, 132 imaging sets with an RTL ≤0.25, and 81 imaging sets with an RTL >0.25. Figure 4 shows the four-by-four confusion matrix displaying the results of the model’s predictions compared to the radiologists’ final diagnoses. The SensF, SensB, Sens−, and Sens+ were 88.88% (95% CI: 50.67–99.41%), 94.11% (95% CI: 82.77–98.47%), 96.96% (95% CI: 91.94–99.02%), and 95.06% (95% CI: 87.15–98.40%), respectively. The SpecF, SpecB, Spec−, and Spec+ were 98.48% (95% CI: 95.90–99.51%), 99.55% (95% CI: 97.12–99.97%), 95.04% (95% CI: 89.65–97.81%), and 97.39% (93.69–99.03%), respectively. The PPVF, PPVB, PPV−, and PPV+ were 66.67% (95% CI: 35.44–88.73%), 97.95% (95% CI: 87.63–99.89%), 94.81% (95% CI: 89.21–97.71%), and 93.90% (95% CI: 85.72–97.73%), respectively. The NPVF, NPVB, NPV−, and NPV+ were 99.62% (95% CI: 97.55–99.98%), 98.66% (95% CI: 95.81–99.65%), 97.10% (95% CI: 92.89–99.07%), and 97.90% (95% CI: 94.37–99.32%), respectively (Table 3). The classification rate was 93.41% (95% CI: 89.14–96.24%). The probability cut-off points for classifying the types of forward, backward, RTL ≤0.25, and RTL >0.25 films were 0.295, 0.289, 0.301, and 0.278, respectively. The Cohen’s kappa was 0.903 (95% CI: 0.86–0.95; P<0.001), which revealed almost perfect agreement between the two-step hierarchical model and radiologists (Table 3).
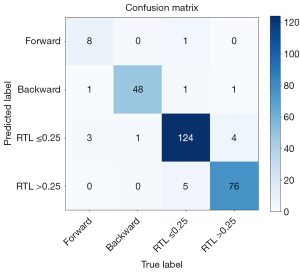
Table 3
| Image classification | Sensitivity, % (95% CI) |
Specificity, % (95% CI) |
PPV, % (95% CI) |
NPV, % (95% CI) |
Accuracy, % (95% CI) |
Classification rate (95% CI) |
Cohen’s kappa | |
|---|---|---|---|---|---|---|---|---|
| Value (95% CI) |
P value | |||||||
| Forward (n=9) | 88.88 (50.67–99.41) |
98.48 (95.90–99.51) |
66.67 (35.44–88.73) |
99.62 (97.55–99.98) |
66.67 (63.13–68.45) |
93.41 (89.14–96.24) |
0.903 (0.86–0.95) |
<0.001 |
| Backward (n=51) | 94.11 (82.77–98.47) |
99.55 (97.12–99.97) |
97.95 (87.63–99.89) |
98.66 (95.81–99.65) |
97.92 (89.04–95.32) |
|||
| RTL ≤0.25 (n=132) | 96.96 (91.94–99.02) |
95.04 (89.65–97.81) |
94.81 (89.21–97.71) |
97.10 (92.89–99.07) |
93.62 (90.22–96.12) |
|||
| RTL >0.25 (n=81) | 95.06 (87.15–98.40) |
97.39 (93.69–99.03) |
93.90 (85.72–97.73) |
97.90 (94.37–99.32) |
98.32 (96.13–99.45) |
|||
CI, confidence interval; PPV, positive predicted value; NPV, negative predicted value; RTL, ratio of the transverse to longitudinal diameter of the glenoid projection.
Discussion
The measurement of CSA, which has great value in the prediction of RCTs, should be applied to reliable CSA radiographs (with an RTL ≤0.25). However, in clinical practice, obtaining satisfactory AP radiographs of the shoulder is time consuming and carries the risk of increasing a patient’s radiation exposure. In this study, our two-stage hierarchical approach effectively identified and categorized the important anatomic structure in the shoulder AP radiograph into four classes: forward, backward, RTL ≤0.25, and RTL >0.25. In addition, the offline prospective test showed that our two-step hierarchical model had a high classification rate (93.41%). We were able to show that the two‑step neural network could be trained to automatically localize the glenoid structure on raw input AP radiographs and classify radiographs according to the Suter’s classification system. Our findings indicate that our two-step model for reliable CSA radiographs (i.e., those with an RTL ≤0.25) might provide precise and reliable acromion morphological parameter assessments due to its high sensitivity and specificity.
Most earlier studies used medical data sets that were not balanced in terms of the class labels, which resulted in low predictive accuracy for the minority class (23,24). In our study, the types of forward (3–5%) and backward (20–26%) shoulder AP radiographs were uncommon in our real-world environment. Multiple data-augmentation techniques have been reported, including horizontal image flips, and contrast adjustments. However, the data augmented using these strategies were obtained from a limited number of individuals and were prone to overfitting (25). To address these issues, we used an advanced DRR technique that could generate additional radiographs as extra input features for the network training and validation, together with real X-rays. Our results showed that the two-step network developed from 1,754 mixed input radiographs had a classification accuracy of 93.41% (95% CI: 89.14–96.24%) in the offline prospective test.
Recently, several deep-learning methods have been used for shoulder X-ray classification (26-28). Unlike in our study, previous methods focused on the classification performances of various networks for shoulder fractures or implants. Chung et al. achieved a classification accuracy of 96% in 1,376 shoulder bone fracture cases with four different types (29). The highest classification accuracy (94.74%) was achieved using Yılmaz’s NASNet model that was based on 597 X-ray images of shoulders with four different types of implants (26). In the current study, the classification rate of our network (93.41%) was lower than those reported in the studies of Chung et al. and Yılmaz (26,29). This might be attributed to the significant overlap between the anterior and posterior edges of the glenoid structure, particularly in the RTL ≤0.25 type. In addition, we included two different types of input (DRRs and X-rays) for network training. Ying et al. noted that while DRRs are quite photo-realistic, there are still differences between real X-rays and DRRs that influence network training (30). However, our network achieved comparable performance to that of Sasidhar, who reported a classification accuracy of 92.16% on three types of greater tuberosity fractures based on the Mutch classification (31).
The two-step model performed better than the one-step model in terms of the AUROC, sensitivity, and specificity (Table 2). This suggests that different input strategies influence network performance. We opted to incorporate a localizer neural network as the initial step in the two-step model, specifically targeting the center of the glenoid structure, instead of using the full AP radiograph in the one-step model. This decision was based on two key factors. First, our experience has shown that the network can avoid unnecessary computations by disregarding extraneous features, such as the rib and distal part of the humeral. By automatically detecting and cropping to the glenoid structure, we effectively minimized the effects of these irrelevant details on the model, allowing the neural network to concentrate on the essential aspects of glenoid texture and morphology. As expected, the performances of the two-step model were higher than those in the one-step model (accuracy: 96.88% vs. 90.48%, respectively).
For the classification of the shoulder AP radiographs, the network had a classification rate of 93.41% (95% CI: 89.14–96.24%) in the offline prospective test. However, we found that its accuracy in classifying the RTL ≤0.25 type was lower than that for the RTL >0.25 type (93.62% vs. 98.32%, respectively). This may be due to the significant overlap between the anterior and posterior edges of the glenoid structure in the RTL ≤0.25 type, which can influence network recognition performance. Similarly, most radiologists cannot distinguish between the RTL ≤0.25 and RTL >0.25 types in capturing shoulder AP radiographs in a clinical setting. Thus, the two-step model might provide a second option that complements the radiologist’s assessment. Further, the classification accuracy might be improved by training the model on a larger input matrix and using external data sets from different individual medical centers in the future. Nevertheless, the two-step model achieved an almost perfect agreement with the two radiology experts with a Cohen’s Kappa agreement score of 0.903 (95% CI: 0.86–0.95). Hence, the two-step model shows promise for potential application in future clinical settings.
It should be noted that our study had several limitations. First, as the included data sets were from one institute, the network performance might be influenced by the various technical differences and imaging protocols of different medical centers. Thus, the generalizability of the model needs to be validated using a separate external cohort in the future. Second, the sample size of the training data set was relatively small. In this study, we attempted to avoid overfitting by employing an advanced technique that merged the extra input features from DRRs and real X-rays. A more extensive data set comprising shoulder AP radiographs from multiple medical centers might increase the robustness of the network. Third, only the Mask-RCNN detection algorithm and EfficientNet neural network were used in this study. Other potential deep-learning algorithms might result in higher classification performance. However, the purpose of this study was not to determine which algorithm works the best in classification but to demonstrate in principle that a deep-learning algorithm could be trained to assist radiologists to recognize that reliable CSA radiographs have a potential role in guiding patient position adjustment in radiology.
The importance of this work is twofold. First, the recognition of reliable CSA radiographs is crucial as an initial step in obtaining accurate radiographic images for measuring the CSA. Unfortunately, no automated approach for shoulder radiography currently exists. Our proposed two-step neural network could enhance the work of radiologists by identifying reliable CSA radiographs. It could serve as a reliable secondary tool that would be particularly beneficial for inexperienced readers. Second, the developed guiding system has potential applications in future integrated automatic radiology repositioning systems. It could play a critical role in transitioning from the manual to automatic adjustment of patient positioning to acquire desired radiographs. This would lead to a significant reduction in radiation exposure time.
Conclusions
Our results demonstrated that our two-step neural network-based guiding system could rapidly and accurately classify different types of shoulder radiographs. Our system could improve the recognition of reliable CSA radiographs and reduce the workload of radiologists. The results obtained from the two-step hierarchical model demonstrate that the neural network had a high level of sensitivity and specificity. This indicates that the neural network has the capacity to provide precise and dependable measurements of diverse acromion morphological features. However, additional external validation is necessary to evaluate the model’s generalizability beyond the current study.
Acknowledgments
Funding: This study received funding from
Footnote
Reporting Checklist: The authors have completed the STARD reporting checklist. Available at https://qims.amegroups.com/article/view/10.21037/qims-23-610/rc
Conflicts of Interest: All authors have completed the ICMJE uniform disclosure form (available at https://qims.amegroups.com/article/view/10.21037/qims-23-610/coif). R.Y. reports that this study received funding from the National Natural Science Foundation of China (No. 81972067), the Fundamental Research Funds for the Central Universities, Sun Yat-sen University (No. 2020004), and the National Natural Science Foundation of China (No. 82002342). The other authors have no conflicts of interest to declare.
Ethical Statement: The authors are accountable for all aspects of the work in ensuring that questions related to the accuracy or integrity of any part of the work are appropriately investigated and resolved. The study was conducted in accordance with the Declaration of Helsinki (as revised in 2013) and approved by the Research Ethics Committee of Sun Yat-sen Memorial Hospital of Sun Yat-sen University (No. SYSEC-ky-ks-2018-036). No informed consent was required for this retrospective study, and the data were anonymized.
Open Access Statement: This is an Open Access article distributed in accordance with the Creative Commons Attribution-NonCommercial-NoDerivs 4.0 International License (CC BY-NC-ND 4.0), which permits the non-commercial replication and distribution of the article with the strict proviso that no changes or edits are made and the original work is properly cited (including links to both the formal publication through the relevant DOI and the license). See: https://creativecommons.org/licenses/by-nc-nd/4.0/.
References
- Agarwalla A, Cvetanovich GL, Gowd AK, Romeo AA, Cole BJ, Verma NN, Forsythe B. Epidemiological Analysis of Changes in Clinical Practice for Full-Thickness Rotator Cuff Tears From 2010 to 2015. Orthop J Sports Med 2019;7:2325967119845912. [Crossref] [PubMed]
- Sarasua SM, Floyd S, Bridges WC, Pill SG. The epidemiology and etiology of adhesive capsulitis in the U.S. Medicare population. BMC Musculoskelet Disord 2021;22:828. [Crossref] [PubMed]
- Yamamoto A, Takagishi K, Osawa T, Yanagawa T, Nakajima D, Shitara H, Kobayashi T. Prevalence and risk factors of a rotator cuff tear in the general population. J Shoulder Elbow Surg 2010;19:116-20. [Crossref] [PubMed]
- İncesoy MA, Yıldız KI, Türk ÖI, Akıncı Ş, Turgut E, Aycan OE, Bayhan IA. The critical shoulder angle, the acromial index, the glenoid version angle and the acromial angulation are associated with rotator cuff tears. Knee Surg Sports Traumatol Arthrosc 2021;29:2257-63. [Crossref] [PubMed]
- Smith GCS, Liu V, Lam PH. The Critical Shoulder Angle Shows a Reciprocal Change in Magnitude When Evaluating Symptomatic Full-Thickness Rotator Cuff Tears Versus Primary Glenohumeral Osteoarthritis as Compared With Control Subjects: A Systematic Review and Meta-analysis. Arthroscopy 2020;36:566-75. [Crossref] [PubMed]
- Tang Y, Hou J, Li Q, Li F, Zhang C, Li W, Yang R. The Effectiveness of Using the Critical Shoulder Angle and Acromion Index for Predicting Rotator Cuff Tears: Accurate Diagnosis Based on Standard and Nonstandard Anteroposterior Radiographs. Arthroscopy 2019;35:2553-61. [Crossref] [PubMed]
- O‘Mahony N, Campbell S, Carvalho A, Harapanahalli S, Hernandez GV, Krpalkova L, Riordan D, Walsh J. Deep Learning vs. Traditional Computer Vision. In: Arai K, Kapoor S. editors. Advances in Computer Vision. Cham: Springer; 2019.
- Radford A, Kim JW, Hallacy C, Ramesh A, Goh G, Agarwal S, Sastry G, Askell A, Mishkin P, Clark J, Krueger G, Sutskever I. Learning Transferable Visual Models From Natural Language Supervision. Proc Mach Learn Res 2021;139:8748-63.
- Jia F, Lei Y, Lin J, Zhou X, Lu N. Deep neural networks: A promising tool for fault characteristic mining and intelligent diagnosis of rotating machinery with massive data. Mechanical Systems and Signal Processing 2016;72-73:303-15.
- Liu Z, Jia Z, Vong CM, Bu S, Han J, Tang X. Capturing High-Discriminative Fault Features for Electronics-Rich Analog System via Deep Learning. IEEE Trans Industr Inform 2017;13:1213-26.
- Seah JCY, Tang CHM, Buchlak QD, Holt XG, Wardman JB, Aimoldin A, Esmaili N, Ahmad H, Pham H, Lambert JF, Hachey B, Hogg SJF, Johnston BP, Bennett C, Oakden-Rayner L, Brotchie P, Jones CM. Effect of a comprehensive deep-learning model on the accuracy of chest x-ray interpretation by radiologists: a retrospective, multireader multicase study. Lancet Digit Health 2021;3:e496-506. [Crossref] [PubMed]
- Rezazade Mehrizi MH, Mol F, Peter M, Ranschaert E, Dos Santos DP, Shahidi R, Fatehi M, Dratsch T. The impact of AI suggestions on radiologists’ decisions: a pilot study of explainability and attitudinal priming interventions in mammography examination. Sci Rep 2023;13:9230. [Crossref] [PubMed]
- Najjar R. Redefining Radiology: A Review of Artificial Intelligence Integration in Medical Imaging. Diagnostics (Basel) 2023;13:2760. [Crossref] [PubMed]
- Hou J, Li F, Zhang X, Zhang Y, Yang Y, Tang Y, Yang R. The Ratio of the Transverse to Longitudinal Diameter of the Glenoid Projection Is of Good Predictive Value for Defining the Reliability of Critical Shoulder Angle in Nonstandard Anteroposterior Radiographs. Arthroscopy 2021;37:438-46. [Crossref] [PubMed]
- Suter T, Gerber Popp A, Zhang Y, Zhang C, Tashjian RZ, Henninger HB. The influence of radiographic viewing perspective and demographics on the critical shoulder angle. J Shoulder Elbow Surg 2015;24:e149-58. [Crossref] [PubMed]
- Milickovic N, Baltast D, Giannouli S, Lahanas M, Zamboglou N. CT imaging based digitally reconstructed radiographs and their application in brachytherapy. Phys Med Biol 2000;45:2787-800. [Crossref] [PubMed]
- Pham VTN, Nguyen QC, Nguyen QV. Chest X-Rays Abnormalities Localization and Classification Using an Ensemble Framework of Deep Convolutional Neural Networks. Vietnam Journal of Computer Science 2023;10:55-73.
- Hernández ÓG, Morell V, Ramon JL, Jara CA. Human Pose Detection for Robotic-Assisted and Rehabilitation Environments. Appl Sci 2021;11:4183.
- Tan M, Le Q. EfficientNet: Rethinking Model Scaling for Convolutional Neural Networks. Proc Mach Learn Res 2019;97:6105-14.
- Thada V, Jaglan V. Comparison of Jaccard, Dice, Cosine Similarity Coefficient To Find Best Fitness Value for Web Retrieved Documents Using Genetic Algorithm. International Journal of Innovations in Engineering and Technology 2013;2:202-5.
- Pachade S, Porwal P, Kokare M, Giancardo L, Mériaudeau F. NENet: Nested EfficientNet and adversarial learning for joint optic disc and cup segmentation. Med Image Anal 2021;74:102253. [Crossref] [PubMed]
- Shariatnia MM, Ramazanian T, Sanchez-Sotelo J, Maradit Kremers H. Deep learning model for measurement of shoulder critical angle and acromion index on shoulder radiographs. JSES Rev Rep Tech 2022;2:297-301. [Crossref] [PubMed]
- Shao Y. Imbalance Learning and Its Application on Medical Datasets. 2021.
- Deng Y, Lu L, Aponte L, Angelidi AM, Novak V, Karniadakis GE, Mantzoros CS. Deep transfer learning and data augmentation improve glucose levels prediction in type 2 diabetes patients. NPJ Digit Med 2021;4:109. [Crossref] [PubMed]
- Chao X, Zhang L. Few-shot imbalanced classification based on data augmentation. Multimedia Systems 2021;29:2843-51.
- Yılmaz A. Shoulder Implant Manufacturer Detection by Using Deep Learning: Proposed Channel Selection Layer. Coatings 2021;11:346.
- Vo MT, Vo AH, Le T. A robust framework for shoulder implant X-ray image classification. Data Technologies and Applications 2021;56:447-60.
-
Uysal F Hardalaç F Peker O Tolunay T Tokgöz N. Classification of Fracture and Normal Shoulder Bone X-Ray Images Using Ensemble and Transfer Learning With Deep Learning Models Based on Convolutional Neural Networks. arXiv:2102.00515. - Chung SW, Han SS, Lee JW, Oh KS, Kim NR, Yoon JP, Kim JY, Moon SH, Kwon J, Lee HJ, Noh YM, Kim Y. Automated detection and classification of the proximal humerus fracture by using deep learning algorithm. Acta Orthop 2018;89:468-73. [Crossref] [PubMed]
-
Ying X Guo H Ma K Wu J Weng Z Zheng Y. X2CT-GAN: Reconstructing CT from Biplanar X-Rays with Generative Adversarial Networks. arXiv:1905.06902. - Sasidhar A, Thanabal MS. Comparative Analysis of Deep Convolutional Neural Network Models for Humerus Bone Fracture Detection. Journal of Medical Imaging and Health Informatics 2021;11:3117-22.


