
UMRFormer-net: a three-dimensional U-shaped pancreas segmentation method based on a double-layer bridged transformer network
Introduction
Computer vision and artificial intelligence applications are becoming increasingly important, especially in the field of medical imaging technology (1). In medical imaging, accurate organ segmentation is a prerequisite and an important factor in many subsequent image computing-based analyses. With the rapid development of deep neural networks, automatic segmentation has achieved good results in many organs and tissues, including the brain, lung, liver, and heart (2). For the pancreas, however, the segmentation accuracy is still relatively low, despite considerable improvements in results during the pre-deep learning era (3).
In recent years, deep learning methods based on convolutional neural networks (CNNs) have achieved remarkable success in medical image segmentation. Based on the original two-dimensional (2D) U-Net and three-dimensional (3D) U-Net architectures, Isensee et al. (4) proposed nnU-Net, a robust and adaptive deep learning framework. This method focuses on the configuration of preprocessing (resampling and normalization), training strategy, inference, and post-processing, which allows the network to achieve a good improvement in segmentation accuracy. The network provides an efficient and accurate solution for solving any new task in the biomedical field, including automatic segmentation of the pancreas and pancreatic tumors in clinical medicine, and has also been applied in the pancreatic segmentation competition of the Medical Segmentation Decathlon (MSD) (5). Further, Chen et al. (6) proposed a model-driven deep learning segmentation method for the pancreas based on helical transformation. They investigated a uniformly sampled helical transformation algorithm that maps a 3D image onto a 2D plane and preserves the spatial relationship between textures. The method effectively deals with 3D context information in 2D models. Salanitri et al. (7) proposed a novel 3D CNN for automatic segmentation of the pancreas from magnetic resonance and computed tomography (CT) images which learns to extract and decode volumetric features at different scales in the encoder-decoder structure. Most of the models in the abovementioned pancreatic segmentation-related studies were conducted from the perspective of spatial locality features.
Recently, transformer-based models (8,9) have attracted much attention in computer vision after achieving state-of-the-art benchmarks in natural language and text processing areas. They have a strong ability to model long-range dependencies and capture global context. However, unlike the local formulation of convolutions, the transformer focuses more on global semantic information as it encodes images as a sequence of one-dimensional (1D) patch embeddings and utilizes self-attention modules to learn a weighted sum of values calculated from hidden layers (10). For example, vision transformer architecture achieved outstanding performances in image classification via pre-training on large-scale datasets (11,12). Subsequently, many transformer-based architectures (13,14) have been explored for dense prediction tasks. Peiris et al. (15) proposed the transformer architecture VT-Unet for volumetric medical image segmentation. The encoder has two consecutive self-attention layers to simultaneously encode local and global cues, and the decoder has novel parallel shifted window-based self- and cross-attention blocks to capture fine details.
Although the aforementioned methods provide reliable technical guidance, pancreas segmentation remains a challenging task. The difficulty is mainly due to the following aspects: (I) the shape, size, and position of the pancreas in the abdomen varies greatly among patients, which makes it difficult to use reliable prior to improve the delineation procedure; (II) the contrast between the pancreas and surrounding tissue is weak; (III) the pancreas occupies only a very small portion of the CT image; and (IV) the pancreas is relatively soft and can easily be pushed by surrounding tissues with similar intensities, which could result in significant deformation. Although CNN-based methods for automatic pancreas segmentation have excellent representational capabilities, it is difficult to build an explicit long-distance dependence due to the limited receptive fields of convolution kernels. This limitation of convolution operation poses challenges to the learning of global semantic information, which is critical for dense prediction tasks such as segmentation. Existing models utilize convolution to focus more on local features of the pancreatic region, ignoring the global features associated with the pancreas and surrounding tissues; this obfuscates the border between the pancreas and surrounding tissues.
To overcome these challenges, learning from the transformer idea, we contemplated whether it is possible to design a module that pays deep attention to global long-range dependencies and local feature information to be embedded in the CNN network. Therefore, we proposed a model-driven deep learning method based on UMRFormer-Net for pancreas segmentation. A double transformer-like module named MRFormer was designed to help extract the deep feature information generated by the encoder. We connected two layers of residual units, composed of a 3×3 depthwise convolutional block and a post-layer normalization block after the multi-head self-attention (MHSA) layer inside the module, to achieve the advantage of endogenously integrating the local features of the convolution and the global long-range dependence features of the transformer. This method models the local and global dependencies between features of different scales in the bridging encoder. Furthermore, an MHSA mechanism and a residual depthwise convolution combination block was introduced on the path from the encoder's deep feature input to the skip connection to facilitate feature aggregation at different semantic scales on the decoder sub-network and subsequently, highly flexible feature fusion schemes for differences in coarseness and fine grains.
The main contributions of this paper are as follows:
- For the 3D deep learning segmentation model, we propose a transformer-like module that extracts feature information at different scales on the last two deep layer features of U-Net, which can obtain more effective deep feature context information in the 3D model.
- We propose an MRFormer module that aims to extract spatially fine-grained local information from long sequence feature outputs. It has the advantage of maintaining long-range dependencies, as well as feature recognition and local context capabilities.
- Compared with existing transformer-related methods, our method achieved good segmentation results in CT pancreas datasets from the Clinical Proteomic Tumor Analysis Consortium Pancreatic Ductal Adenocarcinoma (CPTAC-PDA) Pancreas dataset (16) and the public MSD dataset (self-division) (5), which showed it to be superior to the existing methods.
Methods
The study was conducted in accordance with the Declaration of Helsinki (as revised in 2013). In this section, we first describe the overall pipeline and specific structure of UMRFormer-Net, and then show the details of the basic unit (MRFormer) of UMRFormer-Net.
Architecture
As shown in Figure 1, the proposed UMRFormer-Net has a U-shaped encoder-decoder architecture with a hybrid CNN and transformer, and adopts a double MRFormer context bridge module at the bottom of the whole network. Specifically, we generally assume that input a 3D image with a spatial resolution of H×W, depth dimension of D (# of slices), and C channels (# of modalities). UMRFormer-Net first utilizes a five-layer 3D CNN to generate feature maps at different scales to capture spatial and deep features, and then utilizes a double transformer-like module to encode the long-range dependencies semantic information of the fourth- and fifth-layer feature maps in a global space. Next, the upsampling layer and the convolution layer are repeatedly stacked to gradually obtain high-resolution segmentation results. Next, we describe the components of UMRFormer-Net in detail.
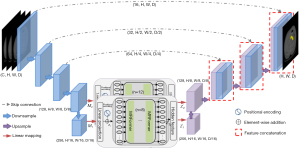
Network encoder
Feature embedding of the double MRFormer encoder
Given the feature maps M1 and M2 are output by the fourth and fifth layers of the network encoder. We used linear projection (3×3×3 convolution layers) to increase the channel size of the fourth and fifth layers from K1=128 and K2=256 to d1=512 and d2=1024. Since the double MRFormer module requires a sequence as input separately, we uniformly compressed the spatial and depth dimensions of the input 3D feature map into 1D, and obtained d1 × Q1 () and d2 × Q2 () feature maps (f1 and f2, respectively), which can be regarded as Q1d1-dimensional and Q2d2-dimensional labels, respectively. The input 3D feature map was compressed into 1D and then added to a learnable positional encoding, creating feature embedding, as follows:
where LP1 and LP2 are the linear projection operation, and denote the positional encoding, and and refer to the feature embedding.
MRFormer block
As shown in Figure 2, the MRFormer block consists of MHSA (8,17) and RDCB modules. The RDCB module mainly consists of two depthwise convolutions (18,19) with layer normalization after each layer. We also added a dense residual connection between each layer. Compared with the original transformer, which used only a feed-forward network, we proposed to use an additional two depthwise convolution layers. This was conducted with the aim of focusing on local receptive fields and to attract 2D or 3D spatial features which cannot be captured by 1D vectors. The layer normalization operations produced milder activation value at the network layers, facilitating more stable model training. The output of the transformer layer can be calculated by:
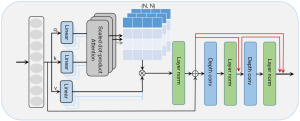
where LN(*) denotes the layer normalization, is the output of the MRFormer layer, and DConv(*) denotes the depthwise convolution. Similar to previous works (20,21), the calculation formula of self-attention in MHSA (8,17) is as follows:
where denote the query, key, and value matrices, respectively; M2 and d(*) represent the number of patches in a window and the dimension of the query or key, respectively; and represents the weight matrix of the dot product.
Network decoder
In order to match the input size of the decoder, it was necessary to map the feature sequence output by the double MRFormer module into a 3D feature map. Specifically, the double MRFormer and were reshaped to and , respectively. After feature mapping, upsampling and convolution were performed on the outputs of and , respectively, and then fused with encoder features via long-range skip connections in order to capture finer semantic and fine-grained information as well as richer spatial details.
Results
MSD Pancreas and CPTAC-PDA Pancreas Datasets
The model was validated in pancreas segmentation experiments. For a fair comparison with previous transformer-based architectures, we evaluated our methods on the public MSD dataset (self-division) and the CPTAC-PDA Pancreas dataset.
For the MSD dataset, the original training datasets with open ground truth segmentation consist of 281 3D CT volumes, divided into 169, 56, and 56 at a 6:2:2 ratio, and is used for training, validation, and testing of pancreas segmentation. The number of slices ranges from 36 to 174, and the CT images are 512×512 in size. The labels contain two categories: background (label 0) and pancreas (label 1).
CPTAC-PDA Pancreas dataset consists of reference segmentations for 91 abdominal CT images delineating the pancreas and pancreas adenocarcinoma (PDA). The 91 CT images are divided into 55, 18, and 18 for training, validation, and testing, respectively. The labels contain two categories: background (label 0) and pancreas (label 1).
Evaluation metrics
To compare the performance between different models in our experiments, the evaluation metrics used to measure the segmentation effect of medical images included the Dice coefficient (22) and 95% Hausdorff distance (23). Mean and standard deviation (SD) indicate the dispersion of the results of the sample data, respectively. With Isegand IGT representing the segmentation image and the ground truth segmentation, respectively, the Dice formula can be written as follows:
Regarding set X and set Y, the maximum Hausdorff distance represents the maximum distance of one point set to the nearest point of another point set, defined as:
The 95% Hausdorff distance is the 95th percentile of the distances between the points of sets X and Y.
Implementation details
We performed all experiments using Python 3.8 (Guido van Rossum, Netherlands) and Pytorch 1.8.0 (FAIR, Menlo Park, USA) on Ubuntu 18.04 (Canonical, Mann, UK). All training procedures were performed on a single NVIDIA RTX 3090 GPU (Nvidia, Santa Clara, CA, USA) with 24 GB memory for 1000 epochs using a batch size of 2. The initial learning rate was set to 0.002 with a poly learning rate strategy, in which the initial rate decayed by each iteration with power 0.9. To train the model, the SGD optimizer was adopted (24). The weight decay was set to 1e-5. We utilized the sum of the Dice loss and cross-entropy loss.
Pre-processing and augmentation strategies
All CT images were resampled to the same spacing (0.73 mm × 0.73 mm × 3.0 mm). During the training process, the augmentation strategy was implemented in the following order: rotation, scaling, Gaussian blurring, brightness and contrast adjustment, simulation of low resolution, gamma augmentation, and mirroring.
Network configurations
In Table 1, we show experimental network configurations on the CPTAC-PDA Pancreas dataset and the Public MSD dataset.
Table 1
| Data processing mode | UMRFormer-Net |
|---|---|
| Target spacing | 0.73 mm × 0.73 mm × 3.0 mm |
| Median image size | 145×512×512 |
| Crop size | 64×128×128 |
| Batch size | 2 |
| Stride of downsampling | [2 2 2], [2 2 1], [2 2 2], [2 2 2], [2 2 2] |
Experiments on the MSD Pancreas dataset
To investigate the segmentation performance of our model, we conducted experiments on the MSD Pancreas dataset, comparing our model’s performance with those of the 3D U-Net (25), Swin-Unet (26), Trans-UNet (27), nnFormer (28), and VT-UNet (15) models. The best-performing existing engineering method, nnU-Net (4), was also used as a reference for segmentation accuracy. We directly used the results obtained using these methods for comparison. For a fair comparison, we divided the datasets according to VT-UNet-B (15). At the time of inference, we generated multi-class predictions using a sliding window technique used in previous papers (29,30). As shown in Table 2, the quantitative experimental results of this model suggest that our approach obtained a better segmentation performance than all the baselines, as measured by either the Dice coefficient or 95% Hausdorff distance. The differences were statistically significant. Additionally, UMRFormer-Net obtained dominance over the 95% Hausdorff distance of the pancreas with our redesigned MRFormer block.
Table 2
| Method | Pancreas | |
|---|---|---|
| Dice score ↑ | 95% HD ↓ | |
| 3D U-Net | 72.69±0.08*** | 9.45±8.68** |
| Trans UNet | 62.84±0.13** | 16.22±11.75 |
| Swin UNet | 63.72±0.32 | 14.89±10.24* |
| nnFormer | 65.86±0.18** | 13.92±9.05** |
| VT-UNet-B | 70.04±0.26 | 10.13±5.24*** |
| nnU-Net | 76.88±0.09* | 8.62±7.26** |
| UMRFormer-Net (ours) | 77.36±0.11 | 8.34±6.69 |
Data were presented as mean ± SD. Paired t-test was used to test for the difference between our method and other methods in Dice score, 95% HD individually, *P<0.05, **P<0.01, ***P<0.001. MSD, Medical Segmentation Decathlon; SD, standard deviation; HD, Hausdorff distance.
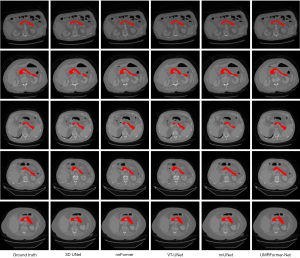
For qualitative analysis, Figure 3 displays a visual comparison of the pancreas segmentation results of various methods. UMRFomer-Net obtained more matched and accurate segmentation boundary and region information, which improved the accuracy of pancreas segmentation.
Experiments on CPTAC-PDA Pancreas dataset
To better demonstrate the generalization ability and efficiency of our model, we further evaluated its performance in another public dataset, CPTAC-PDA Pancreas. We also compared our method with other existing methods including 3D U-Net (25), Swin-Unet (26), Trans-Unet (27), nnFormer (28), VT-UNet (15), and nnU-Net (4), as shown in Table 3. The results showed that our proposed UMRFormer-Net achieved state-of-the-art accuracy compared with the classical 3D U-Net and other transformer-based methods.
Table 3
| Method | Pancreas | |
|---|---|---|
| Dice score ↑ | 95% HD ↓ | |
| 3D U-Net | 81.43±0.03** | 7.31±6.52* |
| Trans UNet | 79.95±0.07* | 9.40±10.36 |
| Swin UNet | 80.92±0.08 | 8.24±9.65** |
| nnFormer | 82.46±0.05** | 6.35±8.34 |
| VT-UNet-B | 83.21±0.06** | 5.78±6.42*** |
| nnU-Net | 85.06±0.02** | 4.63±5.84* |
| UMRFormer-Net (ours) | 85.54±0.04 | 4.05±5.15 |
Data were presented as mean ± SD. Paired t-test was used to test for differences between our method and other methods in Dice score and 95% HD individually, *P<0.05, **P<0.01, ***P<0.001. CPTAC-PDA, Clinical Proteomic Tumor Analysis Consortium Pancreatic Ductal Adenocarcinoma; SD, standard deviation; HD, Hausdorff distance.
Ablation study
We conducted extensive ablation experiments to validate the effectiveness of the proposed transformer-like decoder layers and the necessity of using transformer-like at the skip connections of the last two layers of the encoder and decoder. The experimental results were yielded by five cross-validation evaluations on the CPTAC-PDA Pancreas dataset. First, we analyzed the impact of different layers of MRFormer decoders. Further, we studied the effect of the original transformer and the improved MRFormer module on the segmentation performance. Different from the native transformer module, the MRFormer module is composed of a multi-head attention module and two convolution layers. Finally, we studied and compared the impact of the addition of MRFormer on the segmentation performance of the base 3D CNN network.
Depth of the double MRFormer (n)
As shown in Figure 1, we conducted ablation experiments to verify the effect of the depth of the double-layer MRFormer (n) on the segmentation performance.
As shown in Table 4, the optimal depth for the MRFormer module was 12 and 8 for the fourth and fifth layers, respectively. A greater depth did not necessarily improve the performance.
Table 4
| Depth of double MRFormer (n) | Pancreas | |
|---|---|---|
| Dice score ↑ | 95% HD ↓ | |
| {[fourth,14], [fifth,10]} | 81.86±0.05 | 7.28±8.34 |
| {[fourth,12], [fifth,8]} | 85.54±0.04 | 4.05±5.15 |
| {[fourth,10], [fifth,6]} | 84.88±0.03 | 6.15±6.92 |
| {[fourth,8], [fifth,4]} | 83.01±0.04 | 7.13±7.96 |
Data were presented as mean ± SD. HD, Hausdorff distance; SD, standard deviation.
Additionally, we investigated the effects of the original transformer and the improved MRFormer module on the segmentation performance. Different from the native transformer module, the MRFormer module is composed of a multi-head self-attention module and two convolution layers. We set the convolution layers in MRFormer to two layers, considering the memory constraints and computational efficiency.
Comparison of the native and improved MRFormer module
We compared the impact of the double native transformer and the double improved transformer in performing network segmentation. The embedded dimensions input to the double transformer-like module in a given network were as follows: the fourth and fifth layers of the network were set to 512 and 1024, respectively. Of note, replacing the feed-forward network layer with two residual units combined with depthwise convolution and layer normalization made the network pay more attention to its local feature information while ensuring global semantic information of long feature sequences, which significantly improved the model’s performance. The specific results are shown in Table 5. Compared with the native transformer module, our MRFormer module had better segmentation accuracy in the CPTAC-PDA Pancreas dataset.
Table 5
| Native and improved transformer |
Configuration of double-layer embedded | Pancreas | |
|---|---|---|---|
| Dice score ↑ | 95% HD ↓ | ||
| Transformer | {[fourth,512], [fifth, 1024]} | 84.31±0.06 | 5.65±6.74 |
| MRFormer | 85.54±0.04 | 4.05±5.15 | |
Data were presented as mean ± SD. HD, Hausdorff distance; SD, standard deviation.
Transformer-like decoder layers
Our method is based on a five-layer symmetric 3D CNN encoder-decoder architecture. Table 6 presents a comparison of transformer-like ablation experiments for different layers. It counts from the bottom layer of the network and compares the segmentation performance with one and two decoding layers connected to transformer-like layers. As the results show, after the network decoding layer was connected to a double-layer transformer, the segmentation performance showed an improvement compared to that with a single-layer transformer. We also set up an experiment which aimed to simultaneously access the transformer-like layer to the feature sequences output by more than three decoding layers. The result showed that as the computational efficiency decreased, the time complexity increased, and the computational memory footprint became too large during training. The final segmentation accuracy also decreased compared to that with the two-layer transformer-like method.
Table 6
| Transfomer-like decoder types | Position of transformer-like module | Pancreas | |
|---|---|---|---|
| Dice score ↑ | 95% HD ↓ | ||
| Zero | – | 81.43±0.03 | 7.31±6.52 |
| One | Fifth layer | 83.17±0.05 | 5.17±6.68 |
| Two | Fourth and fifth layers | 85.54±0.04 | 4.05±5.15 |
| Three | Fourth, fifth, and third layers | 84.08±0.02 | 4.79±5.92 |
Data were presented as mean ± SD. HD, Hausdorff distance; SD, standard deviation.
Discussion
Accurate segmentation of the pancreas is crucial in the quantitative analysis of radiology and surgery, as it can assist radiologists and surgeons in achieving the best diagnosis and treatment strategies for patients. To this end, we proposed a model-driven deep learning method based on UMRFormer-Net for pancreas segmentation. Our segmentation experiments demonstrated that the model has high segmentation accuracy and outperforms some existing methods in segmentation.
Our proposed model has the following two characteristics. First, a novel double MRFormer was proposed to enable a 3D network to efficiently apply 3D contextual information for 3D CT image segmentation. The UMFormer-Net method embedded in the double MRFormer module can be used to more effectively obtain deep feature contextual information in 3D models. It forms a spatially local and global unified framework to directly optimize 3D segmentation results, thereby improving model performance; Second, the proposed MRFormer module aims to focus on spatial local information in long sequence features. It has the advantage of maintaining long-range dependencies, as well as feature recognition and local context capabilities. It helps to solve the problem of unclear boundary texture segmentation of targets such as the pancreas. As shown in Table 2 and Table 3, we can clearly see that the UMRFormer-Net using MRFormer is superior to other methods (4,15,25,26,27,28) in terms of the Dice score and 95% Hausdorff distance.
However, our proposed model still has a few limitations. First, the performance of the model depends on the accuracy of manual annotation during training, and manual annotation by doctors is based on their existing clinical knowledge. The size of pancreatic organ tissue varies with age (e.g., between children and adults), and the subjective standards of doctors for pancreas delineation differ slightly, which affects the performance of the model for pancreas segmentation. Therefore, it is necessary to fine-tune the model parameters according to the data characteristics of the case.
Image quality and annotation quality are critical in artificial intelligence application research. Suman et al. (31) studied the MSD dataset and found that there were numerous biliary stents and post-chemotherapy cases in the training datasets, which may impact the overall segmentation performance. It is therefore essential to further optimize the model structure or adopt a more effective way of enhancing data to improve the model’s segmentation performance.
Conclusions
This paper has presented a novel medical segmentation framework named UMRFormer-Net and applied it in pancreatic segmentation of CT images. The model effectively integrates the transformer-like structure into the CNN, which not only retains the advantages of the CNN in modeling local receptive field information, but also fully utilizes and innovates the advantages of the transformer module’s learnable global dependence semantic information. Our experimental results from two datasets (the CPTAC-PDA Pancreas dataset and the MSD Pancreas dataset) fully demonstrate the effectiveness of the proposed UMRFormer-Net. Based on this endogenous hybrid architecture, UMRFormer-Net achieves better segmentation accuracy in pancreas than previous transformer-based segmentation models. In the future, we will test UMRFormer-Net in other medical segmentation tasks.
Acknowledgments
Funding: This work was supported by grants from the NSFC Grant Program (Nos. 12026602 and 62172401), the Key-Area Research and Development Program of Guangdong Province (No. 2020B010165004), the National Key R&D Program, China (No. 2019YFC0118100), the Natural Science Foundation of Guangdong Province (No. 2022A1515010439), the Shenzhen Key Basic Science Program (No. JCYJ20180507182437217), and the Shenzhen Key Laboratory Program (No. ZDSYS201707271637577).
Footnote
Conflicts of Interest: All authors have completed the ICMJE uniform disclosure form (available at https://qims.amegroups.com/article/view/10.21037/qims-22-544/coif). CF and FJ report that this work was supported in part by the NSFC Grant Program (No. 12026602). FJ also reports that this work was supported in part by grants from the NSFC Grant Program (No. 62172401), the Key-Area Research and Development Program of Guangdong Province (No. 2020B010165004), the National Key R&D Program, China (No. 2019YFC0118100), the Natural Science Foundation of Guangdong Province (No. 2022A1515010439), the Shenzhen Key Basic Science Program (No. JCYJ20180507182437217), and the Shenzhen Key Laboratory Program (No. ZDSYS201707271637577). The other authors have no conflicts of interest to declare.
Ethical Statement: The authors are accountable for all aspects of the work in ensuring that questions related to the accuracy or integrity of any part of the work are appropriately investigated and resolved. The study was conducted in accordance with the Declaration of Helsinki (as revised in 2013).
Open Access Statement: This is an Open Access article distributed in accordance with the Creative Commons Attribution-NonCommercial-NoDerivs 4.0 International License (CC BY-NC-ND 4.0), which permits the non-commercial replication and distribution of the article with the strict proviso that no changes or edits are made and the original work is properly cited (including links to both the formal publication through the relevant DOI and the license). See: https://creativecommons.org/licenses/by-nc-nd/4.0/.
References
- Olveres J, González G, Torres F, Moreno-Tagle JC, Carbajal-Degante E, Valencia-Rodríguez A, Méndez-Sánchez N, Escalante-Ramírez B. What is new in computer vision and artificial intelligence in medical image analysis applications. Quant Imaging Med Surg 2021;11:3830-53. [Crossref] [PubMed]
- Wang R, Lei T, Cui R, Zhang B, Meng H, Nandi AK. Medical image segmentation using deep learning: A survey. IET Image Process 2022;16:1243-67. [Crossref]
- Jiang J, Elguindi S, Berry SL, Onochie I, Cervino L, Deasy JO, Veeraraghavan H. Nested block self-attention multiple resolution residual network for multiorgan segmentation from CT. Med Phys 2022;49:5244-57. [Crossref] [PubMed]
- Isensee F, Jaeger PF, Kohl SAA, Petersen J, Maier-Hein KH. nnU-Net: a self-configuring method for deep learning-based biomedical image segmentation. Nat Methods 2021;18:203-11. [Crossref] [PubMed]
- Antonelli M, Reinke A, Bakas S, Farahani K, Kopp-Schneider A, Landman BA, et al. The Medical Segmentation Decathlon. Nat Commun 2022;13:4128. [Crossref] [PubMed]
- Chen X, Chen Z, Li J, Zhang YD, Lin X, Qian X. Model-Driven Deep Learning Method for Pancreatic Cancer Segmentation Based on Spiral-Transformation. IEEE Trans Med Imaging 2022;41:75-87. [Crossref] [PubMed]
- Salanitri FP, Bellitto G, Irmakci I, Palazzo S, Bagci U, Spampinato C. Hierarchical 3D feature learning for pancreas segmentation. In: Lian C, Cao X, Rekik I, Xu X, Yan P. editors. Machine Learning in Medical Imaging. Springer, Cham; 2021;238-47.
- Vaswani A, Shazeer N, Parmar N, Uszkoreit J, Jones L, Gomez AN, Kaiser Ł, Polosukhin I. Attention is all you need. In: Proceedings of the 31st International Conference on Neural Information Processing Systems 2017;6000-6010.
- Devlin J, Chang MW, Lee K, Toutanova K. BERT: Pre-training of deep bidirectional transformers for language understanding. 2018. arXiv preprint arXiv:181004805.
- Hatamizadeh A, Tang Y, Nath V, Yang D, Myronenko A, Landman B, Roth HR, Xu D. UNETR: Transformers for 3D medical image segmentation. In: Proceedings of the IEEE/CVF Winter Conference on Applications of Computer Vision (WACV) 2022:1748-58.
- Dosovitskiy A, Beyer L, Kolesnikov A, Weissenborn D, Zhai X, Unterthiner T, Dehghani M, Minderer M, Heigold G, Gelly S, Uszkoreit J, Houlsby N. An image is worth 16x16 words: Transformers for image recognition at scale. 2020. arXiv preprint arXiv:201011929.
- Touvron H, Cord M, Douze M, Massa F, Sablayrolles A, Jégou H. Training data-efficient image transformers & distillation through attention. In: Proceedings of the 38th International Conference on Machine Learning 2021. PMLR 139:10347-57.
- Zhang Y, Liu H, Hu Q. TransFuse: Fusing transformers and CNNs for medical image segmentation. In: de Bruijne M, Cattin PC, Cotin S, Padoy N, Speidel S, Zheng Y, Essert C. editors. Medical Image Computing and Computer-Assisted Intervention - MICCAI. Springer, Cham; 2021;12901;14-24.
- Wang W, Xie E, Li X, Fan DP, Song K, Liang D, Lu T, Luo P, Shao L. Pyramid vision transformer: A versatile backbone for dense prediction without convolutions. In: Proceedings of the IEEE/CVF International Conference on Computer Vision 2021:548-58.
- Peiris H, Hayat M, Chen Z, Egan G, Harandi M. A volumetric transformer for accurate 3D tumor segmentation. 2021. arXiv preprint arXiv:211113300.
- National Cancer Institute Clinical Proteomic Tumor Analysis Consortium (CPTAC). The Clinical Proteomic Tumor Analysis Consortium Pancreatic Ductal Adenocarcinoma Collection (CPTAC-PDA) (Version 11) [Data set]. The Cancer Imaging Archive 2018. doi:
10.7937/K9/TCIA.2018.SC20FO18 .10.7937/K9/TCIA.2018.SC20FO18 - Ahmed K, Keskar NS, Socher R. Weighted transformer network for machine translation. arXiv preprint 2017. arXiv:171102132.
- Howard AG, Zhu M, Chen B, Kalenichenko D, Wang W, Weyand T, Andreetto M, Adam H. MobileNets: Efficient convolutional neural networks for mobile vision applications. 2017. arXiv preprint arXiv:170404861.
- Chollet F. Xception: Deep learning with depthwise separable convolutions. In: Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition 2017:1800-7.
- Hu H, Gu J, Zhang Z, Dai J, Wei Y. Relation networks for object detection. In: Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition 2018;3588-97.
- Hu H, Zhang Z, Xie Z, Lin S. Local relation networks for image recognition. In: Proceedings of the IEEE/CVF International Conference on Computer Vision 2019:3463-72.
- Dice LR. Measures of the amount of ecologic association between species. Ecology 1945;26:297-302. [Crossref]
- Huttenlocher DP, Klanderman GA, Rucklidge WJ. Comparing images using the Hausdorff distance. IEEE Trans Pattern Anal Mach Intell 1993;15:850-63. [Crossref]
- Ruder S. An overview of gradient descent optimization algorithms. 2016. arXiv preprint arXiv:160904747.
- Çiçek Ö, Abdulkadir A, Lienkamp SS, Brox T, Ronneberger O. 3D U-Net: learning dense volumetric segmentation from sparse annotation. In: Medical Image Computing and Computer-Assisted Intervention - MICCAI. Springer, Cham; 2016;424-32.
- Cao H, Wang Y, Chen J, Jiang D, Zhang X, Tian Q, Wang M. Swin-Unet: Unet-like pure transformer for medical image segmentation. 2021. arXiv preprint arXiv:210505537
- Chen J, Lu Y, Yu Q, Luo X, Adeli E, Wang Y, Lu L, Yuille AL, Zhou Y. TransUNet: Transformers make strong encoders for medical image segmentation. 2021. arXiv preprint arXiv:210204306.
- Zhou HY, Guo J, Zhang Y, Yu L, Wang L, Yu Y. nnFormer: Interleaved transformer for volumetric segmentation. 2021. arXiv preprint arXiv:210903201.
- Giusti A, Cireşan DC, Masci J, Gambardella LM, Schmidhuber J. Fast image scanning with deep max-pooling convolutional neural networks. In: IEEE International Conference on Image Processing (ICIP) 2013;4034-8.
- Gouk HG, Blake AM. Fast sliding window classification with convolutional neural networks. In: Proceedings of the 29th International Conference on Image and Vision Computing New Zealand 2014;114-8.
- Suman G, Patra A, Korfiatis P, Majumder S, Chari ST, Truty MJ, Fletcher JG, Goenka AH. Quality gaps in public pancreas imaging datasets: Implications & challenges for AI applications. Pancreatology 2021;21:1001-8. [Crossref] [PubMed]


