
High-resolution and high-speed 3D tracking of microrobots using a fluorescent light field microscope
Introduction
Recently, considerable development of microrobots for biomedical applications has been achieved. Those devices in micro and nano scales are expected to navigate through complex environments and perform various tasks, such as unclogging blood vessels or making targeted drug delivery (1-4). In order to facilitate the biomedical applications of microrobots, imaging and tracking of these tiny agents are crucial. To date, a variety of imaging techniques have been proposed (5) for the localization and tracking of microrobots, mainly including magnetic resonance imaging (MRI) (6-8), ultrasonic (US) imaging (9-11), computed tomography (CT) (12), positron emission tomography (PET) (13) and single-photon emission computed tomography (SPECT) (14). Owing to the high penetration capability of the probe material, most of the methods allow a wide range of ex vivo or even in vivo tracking without any harm to the human body (15,16). However, the resolutions of the above methods are poor (5). To our knowledge, the highest resolution of such methods can only reach about 100 µm (MRI) (17), which is insufficient for the precise tracking of microrobots at micrometer scales. Moreover, some of the methods, such as PET and SPECT, may cause harmful ionizing radiation to organs (18,19). Photoacoustic (PA) imaging is another emerging imaging modality for microrobots (20,21). Taking benefits from both optical and US, PA is a high spatial and temporal resolution imaging technique. However, this imaging technique contains only in-plane information that cannot be used in 3D tracking.
Fluorescent imaging (FI) by microscope is a highly scalable tool for micro-imaging and has been widely used to study the properties of microrobots (22-24). Typically, fluorescent modifiers label the microrobots, and a fluorescent microscope captures the image of the samples (25,26). It has advantages of high imaging sensitivity and good lateral resolution, typically about 100–300 nm, depending on the numerical aperture (NA) of the system (27-29). However, the conventional fluorescent microscope suffers from the shallow depth of field (DOF), which is not greater than 100 µm, and lacks the capability of 3D imaging (5,30-32). The 3D imaging capability could be improved using through-focus scanning or binocular microscopy. However, the former requires an extra acquisition time for the sequential measurements, while the latter is troubled with its bulky experimental setup (33-35).
A light field microscope (LFM), which could be built by placing a micro lenslet array (MLA) at the native image plane of a microscope, is able to simultaneously capture both the 2D spatial and 2D angular information of light (31). The measurement of the 4D information allows digital refocusing and reconstruction of the full 3D volume of a fluorescent specimen. The DOF of the system is extended (31,36-38) without any reduction of the field of view (FOV). LFM has been widely used in many applications (39), including depth estimation (40), volumetric imaging (41-43), precise volumetric illumination (44,45), and neural activity observation (46-48). Moreover, the advantage of single-shot enables 3D imaging of moving samples, with the temporal resolution depending on the framerate of the camera.
In this paper, we proposed a high-resolution and high-speed 3D tracking method for microrobots using a fluorescent light field microscope (FLFM). First, we designed the FLFM system according to the size of a representative helical microrobot (150 µm body length, 50 µm screw diameter) and studied the system’s performance. Second, we proposed a 3D tracking algorithm for microrobots by applying digital refocusing on the measured fluorescent light field images. Finally, we verified the accuracy of the method by simulations and built the FLFM system to perform the tracking of microrobots with representative size. The method achieves 30 frame per second (fps) 3D tracking over a 1,200×1,200×326 µm3 volume (1,200 µm × 1,200 µm FOV and 326 µm DOF), with the lateral resolution of 10 µm and the axial resolution of approximately 40 µm. The results indicate that the accuracy can reach about 9 µm. Compared with the FI by a conventional microscope, our method gains wider DOF and higher axial resolution with a single-shot image, and succeeds the high imaging sensitivity and good lateral resolution.
Methods
Experimental setup
The optical layout of the FLFM is shown in Figure 1A. The system was built on a fluorescent microscope (Olympus, IX73) using a bright field objective lens (OL, Olympus, UPLFLN10X2). A magnetic helical microrobots sample, with a body length about 150 µm and a screw diameter about 50µm, was placed at the native object plane (NOP) of the objective lens. The definition of the coordinates in the object space is shown at the left side in Figure 1A, and the origin is at the center of the NOP. To gain a better contrast, the sample was dyed with Rhodamine B (627 nm central absorption wavelength) in advance. The corresponding emitted fluorescence was generated using an excitation filter (EX, ET560/40×), a dichroic mirror (DM, T585lpxr) and an emission filter (EM, ET630/75m). An MLA (RPC Photonics, MLA-S100-f15) was placed at the native image plane of the fluorescent microscope to capture the 4D light field. The lenslet of the MLA is a square with a side length of 100 µm. As shown in Figure 1B, the incident light was encoded as a 2D spatial (x, y coordinates) and 2D angular (u, v coordinates) light field [marked as L (x, y, u, v)]. The light field was imaged using a 1:1 relay imaging lens (Nikon, AF-S DX 40 mm f/2.8G) and recorded on a complementary metal-oxide-semiconductor (CMOS) camera (PCO Edge 5.5) at the back focal plane of the MLA. Table 1 lists the detailed parameters of the FLFM system, which are used for theoretical calculation and simulation in the following sections.
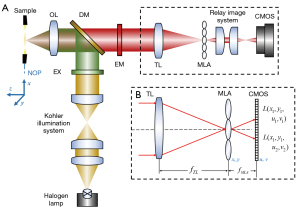
Table 1
| Definition | Symbol | Value |
|---|---|---|
| Spatial coordinate | x, y, z | – |
| Angular coordinate | u, v | – |
| Optical wavelength | λ | 627 nm |
| Refractive index of air | n | 1.00 |
| Magnification of OL | Mobj | 10× |
| NA of OL | NMobj | 0.3 |
| Magnification of relay image system | MR | 1× |
| Focal length of relay image system | fR | 40 mm |
| F number of relay image system | FR | 2.8 |
| Focal length of MLA | fMLA | 1,500 μm |
| Pitch size of MLA | p | 100 μm |
| Resolution of CMOS | W×H | 2,560×2,160 |
| Pixel size of CMOS | s | 6.5 μm |
| Magnification of FLFM | M | Mobj·MR |
FLFM, fluorescent light field microscope; OL, objective lens; NA, numerical aperture; MLA, micro lenslet array; CMOS, complementary metaloxide- semiconductor.
Based on the parameters listed in Table 1, Table 2 summarizes the key performances of the system, including FOV, DOF, diffraction limit, lateral resolution, angular resolution, axial resolution and recording rate. The central absorption wavelength of Rhodamine B (627 nm) is taken as the optical wavelength of the system. The immersed medium in which the microrobot floats is air. The formulas for calculating the achieved performances are also listed in Table 2 (49,50), which can be used as the scheme for the system design of the FLFM. The FLFM system can reach a lateral resolution of 10 µm and an axial resolution about 40 µm over a 1,200×1,200×326 µm3 volume (1,200 µm × 1,200 µm FOV and 326 µm DOF). Besides, the system records fluorescent light field images at 30 fps, allowing 3D tracking of microrobots with camera videorate.
Table 2
| Definition | Symbol | Formula (49,50) | Value |
|---|---|---|---|
| FOV | FOV | 1,200 μm × 1,200 μm | |
| Angular resolution | Nu, Nv | 9.57 | |
| DOF | DOF | 325.95 μm | |
| Diffraction limit | Δ | 1.04 μm | |
| Laterally resolution | rL | 10 μm | |
| Axial resolution | rA | 40.30 μm | |
| Recording rate | – | – | 30 fps |
max() and min() respectively extract the greater value and the smaller value in brackets. Assumed that Nu= Nv according to the square lenslet of the MLA. FLFM, fluorescent light field microscope; FOV, field of view; DOF, depth of field.
3D tracking algorithm for microrobots
The flowchart of the proposed 3D tracking algorithm is shown in Figure 2A. It includes the following steps. First, we extract the sub-aperture (SA) images from the light field image of a fluorescent microrobot. Next, we generate a focal stack of refocused images by digital refocusing, and the depth of the microrobot is obtained by sharpness evaluation (40,51). Last, the lateral position of the microrobot is estimated from the best focus image.
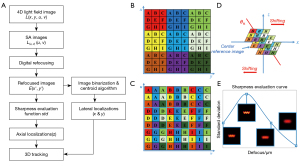
The light field image, denoted as L (x, y, u, v), captures both spatial and angular information of light. The subimage behind each lenslet locally measures the angular distribution of light. By taking the pixel corresponding to the same angle from each subimage, we can extract SA images [denoted as L(u, v) (x, y)] from the original light field image. Each SA image can be considered as the image captured from the view angle, which corresponds to the sampled angle on the lenlet’s subimage. Figure 2B shows an example of a light field image captured by the FLFM. The image consists of 3×3 lenslets, and each lenslet covers 3×3 pixels. By rearranging the pixels according to different view angles, a light field image can be reformed into 3×3 SA images shown in Figure 2C.
Figure 2D shows the process of digital refocusing using SA images (49,52). The digital refocusing was achieved with a shift-and-add scheme. Defocus causes the SA images of different view angles shift laterally. By shifting the SA images and summing them up, a defocus image can be obtained. Applying the digital refocusing scheme to multiple refocusing distances gives a focal stack of intensity images. The process can also be expressed as (53):
where E (x', y') is the refocused image, and Δxu and Δyv are the shifting distance along x and y direction, respectively. The shifting distance along x direction (similar for the case along y direction) is calculated as:
where Δz is the axial refocusing distance from the NOP, and n is the refractive index of the immersed medium. For a certain sub-aperture image L(u, v) (x, y), the shifting slope θu is only determined by the view angle u, and can be calculated as (similar for the y dimension):
where M is the magnification of the system, Δuis the number of pixels, and s is the pixel size of the CMOS.
The lateral shifting distances of SA images in digital refocusing depend on the effective axial refocusing distance, nΔz. Only when the refocusing distance matches the true depth of the sample, the SA images overlap with each other after shifting, resulting in a refocusing image with the best sharpness. By using a sharpness evaluation function, the image with the best sharpness can be detected from the focal stack. Thus, the depth of the microrobot could be obtained from the corresponding effective defocusing distance. Note that the effective defocusing distance is proportional to the refractive index of the immersed medium. Since the standard deviation function reaches the maximum when the image has the best sharpness, it is used as the sharpness evaluation function in our method (as shown in Figure 2E). Thus, the depth can be obtained by seeking the peak of the function.
The lateral localization of the microrobot is based on the best focus result of the previous step of digital refocusing and sharpness evaluation. The center position of the microrobot in the focal plane can be obtained by applying the image binarization process and centroid algorithm to the refocusing image with the best sharpness. The focal plane coincides with the real depth, so that the center position can be considered as the lateral position of the microrobot. Finally, by applying the 3D localization algorithm to each frame of the light field video, the 3D tracking of the microrobot can be achieved.
Results
Simulation results
In this part, the 3D tracking method for microrobots was validated by simulations. First, we built the forward model of the FLFM system and generated simulated light field images of a helical microrobot. Next, we demonstrated the 3D tracking algorithm based on digital refocusing and applied it to the simulated light field images to estimate the location of the microrobot. Last, we simulated several cases of the 3D motions of the microrobot and validated the tracking results of the proposed 3D tracking algorithm. The immersed medium of the microrobot used in the simulations was air. The simulations were done on a laptop PC (AMD Ryzen 5900HX, 16GB RAM) using MATLAB 2021b software.
Forward model of the FLFM and digital refocusing process
The forward model of the FLFM is based on the wave optics theory proposed by Broxton (37). The micro lenslet array is treated as a phase object, which modulates the complex field impinged on the micro lenslet array. The camera sensor measures the intensity after free-space propagation. Figure 3A shows the light field images of a point source at different defocus depths (0, −25, −50 and −75 µm from the NOP, respectively). The depth information of the point sources is recorded in the diffraction patterns of the light field images.
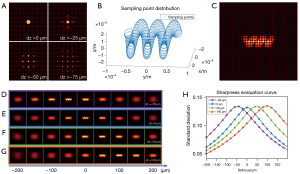
The light field image of a 3D fluorescent object can be obtained by summing over the images generated by all of the point sources in the 3D volume. The sampling point distribution of the designed helical microrobot is shown in Figure 3B. As the fluorescent substrate covers the surface of the microrobot, the sample points were designed to distribute only on the surface of the microrobot (54). By varying the 3D displacement and the rotation of the microrobot, the microrobot of arbitrary positions and 3D motion can be simulated (55). The measured light field image is a summation of all of the intensity images of the sampled points. The light field image (pseudo-color) of a microrobot on NOP (dz =0 µm) is shown in Figure 3C.
After we obtained the measured light field image, we can get a through-focus intensity stack by digital refocusing. The digital refocusing results of the microrobot at different depths (dz =0, 50, 100 and −50 µm) are shown in Figure 3D-3G, respectively. The sharpness of the refocusing images varies from blurred to sharp, and then changes back to blurred when the refocusing distance changes from −200 to 200 µm. It reaches the best sharpness when the refocusing distance matches the depth of the microrobot. Figure 3H shows the sharpness evaluation curves for the microrobot at different depths. The evaluations reach maximums at the distances near −50, 0, 50 and 100 µm, respectively, which match the groundtruth depths (dz). Thus, it indicates the validity of the 3D localization algorithm based on the digital refocusing of the light field image of a microrobot.
3D tracking results
In order to evaluate the 3D tracking algorithm, we simulated four motion paths (marked as 1, 2, 3 and 4, respectively) of the helical microrobot. In Path 1, the microrobot solely floats along the z axis. Without lateral motion and the rotation of the microrobot, the axial movement acts as the main factor which affects the accuracy of the tracking algorithm. In Path 2 and Path 3, the microrobot spins forward along the y axis and z axis, respectively. By simulating the lateral and axial motions separately, it allows individually evaluating the motion along each axis. Path 4 consists of two lateral motions at different depths, which are connected by axial movements. Detailed information about the motion paths is listed in Table 3. The digital refocusing distance ranges from −200 to 200 µm with a step size of 1 µm. The locations of the microrobot in the designed paths are the groundtruth values of the tracking results.
Table 3
| Path | Motion type | dx (μm) | dy (μm) | dz (μm) | α (deg) | β (deg) | γ (deg) |
|---|---|---|---|---|---|---|---|
| 1 | Axial (static) | 0 | 0 | −150 to 150 | 0 | 0 | 0 |
| 2 | Lateral | 0 | −120 to 120 | 0 | 0 | 0 | −180 to 180 |
| 3 | Axial | 0 | 0 | −120 to 120 | 90 | 0 | −180 to 180 |
| 4 | Lateral & axial | −240 to 240 | −240 to 240 | −60 to 60 | 0 to 90 | −90 to 180 | −180 to 180 |
The origin point of the 3D space is the center point of the NOP. The pose of the microrobots is defined by the six motion parameters as follows, x displacement (dx), y displacement (dy), z displacement (dz), z rotating angle (α), x rotating angle (β) and y rotating angle (γ). The definition of the coordinates is same to that in Figure 1A. NOP, native object plane.
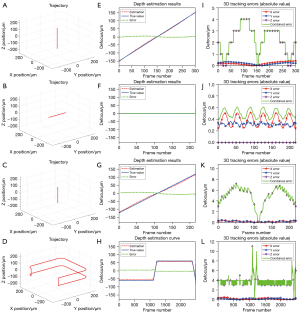
For each path, we generated the light field images of the microrobot, and then recovered the 3D locations of the microrobot from these images using the 3D tracking algorithm. Figure 4 shows the estimated depths and the 3D tracking errors. For the motions only in lateral direction (Path 2, Figure 4F), the estimated depths maintain as zero, which matches the groundtruth values. For the other paths which include axial motions, the errors of depth estimation exist, and the rotation of the microrobot exacerbates the error (Figure 4G,4H vs. Figure 4E). The step-like errors are caused by the digital refocusing process, and can be smoothed by reducing the step size of refocusing distance. As the combined errors nearly overlap with the z errors, we could conclude that the accuracy of 3D tracking mainly depends on the error of the depth estimation. The maximum combined tracking error in the simulation is about 11 µm (Figure 4L).
The dynamic tracking results of the paths are demonstrated in Videos 1-4, respectively. Each video consists of 4 synchronized parts, including the 3D motion of the microrobots, the corresponding light field image, the sharpness evaluation curve, and the recovered real-time 3D trajectory.
Experimental results
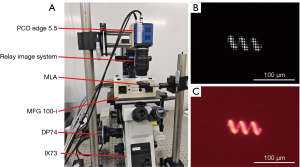
The experimental setup of the FLFM is shown in Figure 5A. We fabricated helical microrobots using a two-photon polymerization printing system (Nanoscribe, Photonic Professional GT2) with photoresist IP-L 780, and employed a physical vapor deposition device (KYKY-300, KYKY Technology) to deposit magnetic layer (nickel) and protection layer (titanium) on the helices. The CMOS camera installed at the top port of the microscope was used to capture the light field images of the moving microrobot, from which the 3D locations of the microrobot were estimated by post-processing. We added an extra CMOS camera (DP74) at the side port to simultaneously capture the image of the microrobot. The lateral locations estimated from the side port images provide reference for the lateral locations estimated from the light field images. Figure 5B and Figure 5C show the light field image (gray-scale) of a microrobot on the NOP and its corresponding side port image (RGB colored).
Validation of the 3D locations estimated from the fluorescent light field image
Although the side port image of the experimental setup in Figure 5 provides the reference for the lateral locations of the microrobot, it still lacks references for the depths. We performed a separate experiment to validate the accuracy of the 3D locations estimated by the proposed tracking method. A microrobot, dyed by immersing into Rhodamine B solution, was placed at the bottom of a flat holder on the stage of the light field microscope. The immersed medium the microrobot floated in was air. We axially moved the microrobot on the stage by adjusting the focusing knob. The defocus distance ranged from −150 to 150 µm with a step size of 5 µm. The defocus distances from the focusing knob provided the groundtruth for the depth estimations. The lateral position of the microrobot on the NOP estimated from the side port image acted as the reference for the lateral locations. Thus, the groundtruth value of the 3D locations of the microrobot was obtained.
The tracking algorithm recovered the location of the microrobot from the light field image measured at each of the defocus distances. Figure 6A shows the whole estimated 3D motion trajectory, and Video 5 demonstrates the dynamic tracking results. The estimated depths and the 3D tracking error are shown in Figure 6B and Figure 6C, respectively. The maximum depth tracking error is about 7 µm, which appears near the NOP of the system. The lateral tracking errors along x and y directions range from 0 µm to about 8 µm. The errors are greater than that in the simulation. It could be possibly caused by the background noises and the fluorescent fragments near the microrobot in the experiment. The maximum combined tracking error is about 9 µm, and it is the claimed accuracy of the FLFM system in this work.

3D tracking of the magnetically driven microrobot
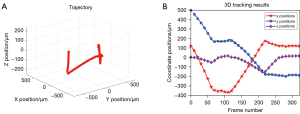
To demonstrate the capability of high-speed tracking, we fabricated a fluorescent magnetic microrobot based on the method proposed by Wang (56). In the experiment, a magnetic field generator (Magnebotix MFG 100-i) was used to control the 3D motions of the microrobot, and the CMOS (PCO Edge 5.5) was used to capture the light field images at 30 fps during the motion. The motion of the microrobot was carried out in distilled water (refractive index n=1.33). The motion continued for about 11s, which consists of 323 light field images. Figure 7A shows the whole 3D motion trajectory estimated by the proposed tracking algorithm. Video 6 demonstrates the dynamic tracking results. Figure 7B shows the coordinate positions of the microrobot during the motion. The motion ranges along each coordinate axes are about −375 to 175 µm (x), −200 to 500 µm (y), and −170 to 20 µm (z), respectively. The range covers a large proportion of the imaging volume calculated in Table 2, and the microrobot at each position during the motion can be clearly localized. Thus, the 3D tracking capability of the method in this paper is verified.
Discussion
This work proposed a high-resolution and high-speed 3D tracking method for microrobots using a FLFM. It provided the design of the system parameters, the achieved performances, and the 3D tracking algorithm using digital refocusing. We verified the accuracy of the method by simulations and built the FLFM system to perform the tracking of microrobots with representative size. The 3D tracking method achieves a 30 fps data acquisition rate, 10 µm lateral resolution and approximately 40 µm axial resolution over a volume of 1,200×1,200×326 µm3. The accuracy of the method can reach about 9 µm.
Compared with the existing 3D tracking methods for microrobots, the proposed FLFM in this work has the following advantages:
- Compared with FI by a conventional microscope, the DOF of the proposed method is extended without any reduction of FOV, so that the capacity of 3D imaging is improved;
- Compared with through-focus scanning or binocular microscope, the FLFM enables 3D imaging from a single-shot image using a simple experimental setup;
- Compared to other methods, such as MRI, US and CT, the method has advantages of good imaging sensitivity and good lateral resolution.
However, the current method still has some limitations. First, the 3D tracking algorithm in this work is based on a global sharpness evaluation measurement which requires a clean background to eliminate the tracking errors caused by other objects, such as cells or tissues. Second, although the imaging volume of the system is extended compared with FI by a conventional microscope, it is still insufficient for clinical application of in vivo tracking.
Our method could be further improved in the following ways in future work. First, the 3D tracking algorithm could be optimized to track multiple microrobots and even a swarm of microrobots simultaneously. Second, the FLFM could be integrated into the catheterization system or endoscopy, allowing in vivo 3D tracking for microrobots. And third, the FLFM could be re-built using sensors with high acquisition speed, so that the temporal resolution could be improved to record the ultrafast motion of microrobots.
Acknowledgments
Funding: This work is funded by the Shenzhen Institute of Artificial Intelligence and Robotics for Society (Nos. AC01202101002, AC01202101106, and 2020-ICP002).
Footnote
Conflicts of Interest: All authors have completed the ICMJE uniform disclosure form (available at https://qims.amegroups.com/article/view/10.21037/qims-22-430/coif). The authors have no conflicts of interest to declare.
Ethical Statement: The authors are accountable for all aspects of the work in ensuring that questions related to the accuracy or integrity of any part of the work are appropriately investigated and resolved. No ethical issue is involved in this paper.
Open Access Statement: This is an Open Access article distributed in accordance with the Creative Commons Attribution-NonCommercial-NoDerivs 4.0 International License (CC BY-NC-ND 4.0), which permits the non-commercial replication and distribution of the article with the strict proviso that no changes or edits are made and the original work is properly cited (including links to both the formal publication through the relevant DOI and the license). See: https://creativecommons.org/licenses/by-nc-nd/4.0/.
References
- Nelson BJ, Kaliakatsos IK, Abbott JJ. Microrobots for minimally invasive medicine. Annu Rev Biomed Eng 2010;12:55-85. [Crossref] [PubMed]
- Peyer KE, Zhang L, Nelson BJ. Bio-inspired magnetic swimming microrobots for biomedical applications. Nanoscale 2013;5:1259-72. [Crossref] [PubMed]
- Yu J, Wang B, Du X, Wang Q, Zhang L. Ultra-extensible ribbon-like magnetic microswarm. Nat Commun 2018;9:3260. [Crossref] [PubMed]
- Yu JF, Xu TT, Lu ZY, Vong CI, Zhang L. On-Demand Disassembly of Paramagnetic Nanoparticle Chains for Microrobotic Cargo Delivery. IEEE Transactions on Robotics 2017;33:1213-25. [Crossref]
- Wang B, Zhang Y, Zhang L. Recent progress on micro- and nano-robots: towards in vivo tracking and localization. Quant Imaging Med Surg 2018;8:461-79. [Crossref] [PubMed]
- Faivre D, Schüler D. Magnetotactic bacteria and magnetosomes. Chem Rev 2008;108:4875-98. [Crossref] [PubMed]
- Felfoul O, Martel S. Assessment of navigation control strategy for magnetotactic bacteria in microchannel: toward targeting solid tumors. Biomed Microdevices 2013;15:1015-24. [Crossref] [PubMed]
- Sanchez A, Magdanz V, Schmidt OG, Misra S, IEEE, editors. Magnetic control of self-propelled microjets under ultrasound image guidance. 5th IEEE RAS/EMBS International Conference on Biomedical Robotics and Biomechatronics (BioRob); 2014 Aug 12-15; Sao Paulo, BRAZIL 2014.
- Kesner SB, Howe RD. Robotic catheter cardiac ablation combining ultrasound guidance and force control. International Journal of Robotics Research. 2014;33:631-44. [Crossref]
- Olson ES, Orozco J, Wu Z, Malone CD, Yi B, Gao W, Eghtedari M, Wang J, Mattrey RF. Toward in vivo detection of hydrogen peroxide with ultrasound molecular imaging. Biomaterials 2013;34:8918-24. [Crossref] [PubMed]
- Scheggi S, Chandrasekar KKT, Yoon C, Sawaryn B, van de Steeg G, Gracias DH, Misra S. Magnetic motion control and planning of untethered soft grippers using ultrasound image feedback. 2017 IEEE International Conference on Robotics and Automation (ICRA), 2017:6156-61.
- Wen S, Zhao L, Zhao Q, Li D, Liu C, Yu Z, Shen M, Majoral JP, Mignani S, Zhao J, Shi X. A promising dual mode SPECT/CT imaging platform based on 99mTc-labeled multifunctional dendrimer-entrapped gold nanoparticles. J Mater Chem B 2017;5:3810-5. [Crossref] [PubMed]
- Vilela D, Cossío U, Parmar J, Martínez-Villacorta AM, Gómez-Vallejo V, Llop J, Sánchez S. Medical Imaging for the Tracking of Micromotors. ACS Nano 2018;12:1220-7. [Crossref] [PubMed]
- Zhao Y, Pang B, Luehmann H, Detering L, Yang X, Sultan D, Harpstrite S, Sharma V, Cutler CS, Xia Y, Liu Y. Gold Nanoparticles Doped with (199) Au Atoms and Their Use for Targeted Cancer Imaging by SPECT. Adv Healthc Mater 2016;5:928-35. [Crossref] [PubMed]
- Yan X, Zhou Q, Vincent M, Deng Y, Yu J, Xu J, Xu T, Tang T, Bian L, Wang YJ, Kostarelos K, Zhang L. Multifunctional biohybrid magnetite microrobots for imaging-guided therapy. Sci Robot 2017;2:eaaq1155. [Crossref] [PubMed]
- Hedhli J, Czerwinski A, Schuelke M, Płoska A, Sowinski P, Hood L, Mamer SB, Cole JA, Czaplewska P, Banach M, Dobrucki IT, Kalinowski L, Imoukhuede P, Dobrucki LW. Synthesis, Chemical Characterization and Multiscale Biological Evaluation of a Dimeric-cRGD Peptide for Targeted Imaging of α V β 3 Integrin Activity. Sci Rep 2017;7:3185. [Crossref] [PubMed]
- Medina-Sánchez M, Schmidt OG. Medical microbots need better imaging and control. Nature 2017;545:406-8. [Crossref] [PubMed]
- Cunha L, Horvath I, Ferreira S, Lemos J, Costa P, Vieira D, Veres DS, Szigeti K, Summavielle T, Máthé D, Metello LF. Preclinical imaging: an essential ally in modern biosciences. Mol Diagn Ther 2014;18:153-73. [Crossref] [PubMed]
- Singh AV, Ansari MHD, Mahajan M, Srivastava S, Kashyap S, Dwivedi P, Pandit V, Katha U. Sperm Cell Driven Microrobots-Emerging Opportunities and Challenges for Biologically Inspired Robotic Design. Micromachines (Basel) 2020;11:448. [Crossref] [PubMed]
- Wu Z, Li L, Yang Y, Hu P, Li Y, Yang SY, Wang LV, Gao W. A microrobotic system guided by photoacoustic computed tomography for targeted navigation in intestines in vivo. Sci Robot 2019;4:eaax0613. [Crossref] [PubMed]
- Yan Y, Jing W, Mehrmohammadi M. Photoacoustic Imaging to Track Magnetic-manipulated Micro-Robots in Deep Tissue. Sensors (Basel) 2020;20:2816. [Crossref] [PubMed]
- Hsiang JC, Jablonski AE, Dickson RM. Optically modulated fluorescence bioimaging: visualizing obscured fluorophores in high background. Acc Chem Res 2014;47:1545-54. [Crossref] [PubMed]
- Steager EB, Sakar MS, Magee C, Kennedy M, Cowley A, Kumar V. Automated biomanipulation of single cells using magnetic microrobots. International Journal of Robotics Research 2013;32:346-59. [Crossref]
- Yang Y, Zhao Q, Feng W, Li F. Luminescent chemodosimeters for bioimaging. Chem Rev 2013;113:192-270. [Crossref] [PubMed]
- Ma Y, Su H, Kuang X, Li X, Zhang T, Tang B. Heterogeneous nano metal-organic framework fluorescence probe for highly selective and sensitive detection of hydrogen sulfide in living cells. Anal Chem 2014;86:11459-63. [Crossref] [PubMed]
- Kim D, Kim J, Park YI, Lee N, Hyeon T. Recent Development of Inorganic Nanoparticles for Biomedical Imaging. ACS Cent Sci 2018;4:324-36. [Crossref] [PubMed]
- Azhdarinia A, Ghosh P, Ghosh S, Wilganowski N, Sevick-Muraca EM. Dual-labeling strategies for nuclear and fluorescence molecular imaging: a review and analysis. Mol Imaging Biol 2012;14:261-76. [Crossref] [PubMed]
- Shao J, Xuan M, Zhang H, Lin X, Wu Z, He Q. Chemotaxis-Guided Hybrid Neutrophil Micromotors for Targeted Drug Transport. Angew Chem Int Ed Engl 2017;56:12935-9. [Crossref] [PubMed]
- Su M, Liu M, Liu L, Sun Y, Li M, Wang D, Zhang H, Dong B. Shape-Controlled Fabrication of the Polymer-Based Micromotor Based on the Polydimethylsiloxane Template. Langmuir 2015;31:11914-20. [Crossref] [PubMed]
- Zheng G. editor. Innovations in Imaging System Design: Gigapixel, Chip-Scale and MultiFunctional Microscopy 2013. doi:
10.7907/SF6E-S775 . - Levoy M, Ng R, Adams A, Footer M, Horowitz M. Light field microscopy. Acm Transactions on Graphics 2006;25:924-34. [Crossref]
- Trifonov B, Bradley D, Heidrich W. Tomographic Reconstruction of Transparent Objects 2006:51-60.
- Hong A, Zeydan B, Charreyron S, Ergeneman O, Pane S, Toy MF, Petruska AJ, Nelson BJ. Real-Time Holographic Tracking and Control of Microrobots. Ieee Robotics and Automation Letters 2017;2:143-8. [Crossref]
- Khalil ISM, Magdanz V, Sanchez S, Schmidt OG, Misra S. Three-dimensional closed-loop control of self-propelled microjets. Appl Phys Lett 2013;103.
- Marino H, Bergeles C, Nelson BJ. Robust Electromagnetic Control of Microrobots Under Force and Localization Uncertainties. IEEE Transactions on Automation Science and Engineering 2014;11:310-6. [Crossref]
- Levoy M, Zhang Z, McDowall I. Recording and controlling the 4D light field in a microscope using microlens arrays. J Microsc 2009;235:144-62. [Crossref] [PubMed]
- Broxton M, Grosenick L, Yang S, Cohen N, Andalman A, Deisseroth K, Levoy M. Wave optics theory and 3-D deconvolution for the light field microscope. Opt Express 2013;21:25418-39. [Crossref] [PubMed]
- Guo C, Liu W, Hua X, Li H, Jia S. Fourier light-field microscopy. Opt Express 2019;27:25573-94. [Crossref] [PubMed]
- Wang D, Zhu Z, Xu Z, Zhang D. Neuroimaging with light field microscopy: a mini review of imaging systems. European Physical Journal-Special Topics 2022; [Crossref]
- Johannsen O, Honauer K, Goldluecke B, Alperovich A, Battisti F, Bok Y, et al. editors. A Taxonomy and Evaluation of Dense Light Field Depth Estimation Algorithms. 2017 IEEE Conference on Computer Vision and Pattern Recognition Workshops (CVPRW). doi:
10.1109/CVPRW.2017.226 .10.1109/CVPRW.2017.226 - Skocek O, Nöbauer T, Weilguny L, Martínez Traub F, Xia CN, Molodtsov MI, Grama A, Yamagata M, Aharoni D, Cox DD, Golshani P, Vaziri A. High-speed volumetric imaging of neuronal activity in freely moving rodents. Nat Methods 2018;15:429-32. [Crossref] [PubMed]
- Linda Liu F, Kuo G, Antipa N, Yanny K, Waller L. Fourier DiffuserScope: single-shot 3D Fourier light field microscopy with a diffuser. Opt Express 2020;28:28969-86. [Crossref] [PubMed]
- Sims RR, Rehman SA, Lenz MO, Benaissa SI, Bruggeman E, Clark A, et al. Single molecule light field microscopy. Optica 2020;7:1065-72. [Crossref]
- Schedl DC, Bimber O. Volumetric Light-Field Excitation. Sci Rep 2016;6:29193. [Crossref] [PubMed]
- Schedl DC, Bimber O. Compressive Volumetric Light-Field Excitation. Sci Rep 2017;7:13981. [Crossref] [PubMed]
- Pegard NC, Liu HY, Antipa N, Gerlock M, Adesnik H, Waller L. Compressive light-field microscopy for 3D neural activity recording. Optica 2016;3:517-24. [Crossref]
- Yang W, Yuste R. In vivo imaging of neural activity. Nat Methods 2017;14:349-59. [Crossref] [PubMed]
- Taylor MA, Nobauer T, Pernia-Andrade A, Schlumm F, Vaziri A. Brain-wide 3D light-field imaging of neuronal activity with speckle-enhanced resolution. Optica 2018;5:345-53. [Crossref]
- Hanrahan P, Ng R. editors. Digital light field photography 2006.
- Born M, Wolf E. Principles of optics: electromagnetic theory of propagation, interference and diffraction of light: Elsevier, 2013.
- Nayar SK, Nakagawa Y. Shape from focus. IEEE Transactions on Pattern Analysis and Machine Intelligence 1994;16:824-31. [Crossref]
- Ng R, Levoy M, Br M, Duval G, Horowitz M, Hanrahan P, et al. editors. Light Field Photography with a Hand-held Plenoptic Camera 2005.
- Liu J, Claus D, Xu T, Keßner T, Herkommer A, Osten W. Light field endoscopy and its parametric description. Opt Lett 2017;42:1804-7. [Crossref] [PubMed]
- Singh AV, Alapan Y, Jahnke T, Laux P, Luch A, Aghakhani A, Kharratian S, Onbasli MC, Bill J, Sitti M. Seed-mediated synthesis of plasmonic gold nanoribbons using cancer cells for hyperthermia applications. J Mater Chem B 2018;6:7573-81. [Crossref] [PubMed]
- Singh AV, Kishore V, Santomauro G, Yasa O, Bill J, Sitti M. Mechanical Coupling of Puller and Pusher Active Microswimmers Influences Motility. Langmuir 2020;36:5435-43. [Crossref] [PubMed]
- Wang X, Chen XZ, Alcântara CCJ, Sevim S, Hoop M, Terzopoulou A, de Marco C, Hu C, de Mello AJ, Falcaro P, Furukawa S, Nelson BJ, Puigmartí-Luis J, Pané S. MOFBOTS: Metal-Organic-Framework-Based Biomedical Microrobots. Adv Mater 2019;31:e1901592. [Crossref] [PubMed]


