
Group theoretic particle swarm optimization for multi-level threshold lung cancer image segmentation
Introduction
Image segmentation involves partitioning an image into multiple objects with meaningful structures in the homogeneous regions according to specific quantitative criteria (1-3). For medical image analysis, in order to help clinicians to make the diagnosis more accurately, the segmentation is a necessary step in advancing on which the quality of the diagnosis and analysis system depends (4,5).
There are numerous types of medical image modalities (6), for example ultrasound (US), X-ray, positron emission tomography (PET), computed tomography (CT), magnetic resonance imaging (MRI), etc. The characteristics of medical images consist of several factors, such as contrast, blur, noise, artifacts, distortion, etc. They represent main features of an image and determine its quality (7). As for lung cancers, about 30–40% of them are adenocarcinoma, which is a typical category of non-small cell lung cancer (NSCLC). The characteristic appearances of lung cancer images are the slow growth of a localized ground glass opacity and the rapid increment of a solid mass (8). And many promising technologies have been developed for detecting those appearance changes of medical image in segmentation tasks with remarkable performance, they range from traditional approaches, like thresholding, edge-based extraction, histogram-based bundling and watershed, region-based growing, to more superior methods, like active contour models, sparse representations, conditional and Markov random fields, graph cuts, deep learning-based algorithms (9-12). Although there exist many excellent methods like deep learning approaches, they still have some inevitable issues, for example, the results heavily depend on complex model structure and parameter configuration. The generalization of trained models is limited because of the huge cost of computational resources and reconstruction of deep models when dealing with heterogeneous data and objective functions during segmentation. Besides, a class of metaheuristic methods treat and reformulate the segmentation problems intrinsically as the global optimization, focusing on complicated objective functions with characteristics of noisy, non-continuous, non-convex and multi-modal information from a medical image (13). Metaheuristic is still one of the mainstreams of medical image segmentation since it has the ability to incorporate multiple criteria in objective function terms, the capacity to measure the qualities of different solutions and offer the trade-off between them by examining the quantitative metrics that a solution satisfies the specific criterion, and the availability to provide self-adaptive parameter configuration without too much background knowledge (14).
For multi-level threshold technologies in medical image segmentation, a method where the non-parametric multi-level variance that is maximized between classes during segmentation procedure is developed by Otsu (15), and after that, Kapur et al. (16) improve branch of method by introducing entropy and probability distribution of the image histogram into it. The Ant Colony Optimization (ACO) can boost the performance of optimal solution compared to the traditional one with Otsu-based multi-level image thresholding (17). Objective functions such as Otsu, Kapur and Tsallis entropy are fed into the efficient Krill Herd Algorithm (KHA) to search for the best values of threshold and it can prevent the drawbacks of single target function (18). Similar to this, an efficient Cuckoo Search Algorithm (CSA) is proposed for segmentation problem with multiple objectives functions (19). Partitioned-Cooperative Quantum-behaved Particle Swarm Optimization (SCQPSO) for auxiliary swarm and the search space is designed to achieve rapid convergence by shifting the mode of particle update (20). Chaotic Salp Swarm Algorithm (CSSA) is embedded into the combined model as the core to optimize the feature matrix obtained from two-dimensional (2D) curvelet transformation for segmentation (21). Multi-Leader Whale Optimization Algorithm (MLWOA) aims to overcome the drawbacks of traditional WOA during the segmentation process (22).
Despite good amount of works achieved by those researchers, we are still facing some critical shortcomings other than stagnation at local optimum or slow convergence. One of them is that most of the improvements enhance either the diversification (exploration) or intensification (exploitation) during the search, which will influence the performance of search algorithms and the qualities of optimal solutions. This also motivates us to propose a new method based on new mathematical foundation, aiming to enhance the balance between them and facilitate the overall efficiency of search.
The purpose of this article is to introduce a novel metaheuristic approach named Group Theoretic Particle Swarm Optimization (GT-PSO) (23), for multi-level threshold optimization in medical image segmentation. With the basic concepts of symmetric group, the search space would be decomposed exhaustively and exclusively, and the process can continue under the guidance of function composition-based operators and equilibrium evolution of both local and global search. Finally, it will reach the goal of finding the optimal combination of multi-level threshold. The main contributions of this article are summarized as follows: the search paradigm is rebuilt on the solid foundation of group theory, and hierarchical decomposition is carried out to generate corresponding operators and evolution strategies for guiding the search procedure. The rest of this article is organized as follows: the “Methods” section describes the details about GT-PSO methodology; the “Results” section presents the experimental results; the “Discussion” section analyzes the performances and discusses the properties of the proposed method; the “Conclusions” section concludes the paper. We present the following article in accordance with the TRIPOD reporting checklist (available at https://qims.amegroups.com/article/view/10.21037/qims-22-295/rc).
Methods
Particle encoding
The mapping function is designed for encoding the particles in the form of permutation with cycles of symmetric group of degree n, which is also the dimension of the objective function:
The encoded vector in each particle is regarded as a potential candidate of the solution.
Solution landscape
In terms of symmetric group theory, four-layered hierarchical method is applied to decompose the solution space into various partitions at different levels, which are conjugacy class, cyclic form, orbital plane and orbit, respectively (Figure 1).
Conjugacy class is the first order partition of hierarchy with the structure of numerous cyclic factors denoted by the factor form:
Cyclic form is the second order partition of hierarchy based on the permutation of cyclic factors denoted by the cyclic form:
Orbital plane is the third order partition of hierarchy where the elements in partition set X are same under two group actions of g1 and g2:
Orbit is the fourth order partition of hierarchy as the collection of all elements by group action g from a given group G:
Notice that four-layered hierarchy is the complete partitioning of the solution landscape, every partition is unique and exclusive to each other.
Neighborhood movement
The movement of a particle happens when the specific group action is used on the incumbent solution to change the permutation of original particle. Four types of operators are created based on four-layered hierarchical partitions. Movement details are illustrated in Figure 2 following the corresponding explanation below.
Conjugator operator shifts the particle to another conjugacy class, as shown with blue arrow (Figure 2). It is an inter conjugacy class operator of exploration.
Cycler operator moves the particle across different cyclic forms, as shown with red arrows (Figure 2). It is an intra conjugacy class and inter cyclic form operator of exploration.
Planer operator changes the particle from one orbital plane to another, as shown with green arrows (Figure 2). It is an intra cyclic form and inter orbital plane operator of exploitation.
Orbiter operator searches the particle along the orbit one by one, as shown with yellow arrows (Figure 2). It is an intra orbital plane and inter orbit operator of exploitation.
Four operators cooperate with each other to move neighborhoods heuristically in the hierarchical partitioned solution space (Figure 2).
Swarm topology
Let denote the operator based on various group actions by group multiplication , then the swarm evolutionary process is formulated as:
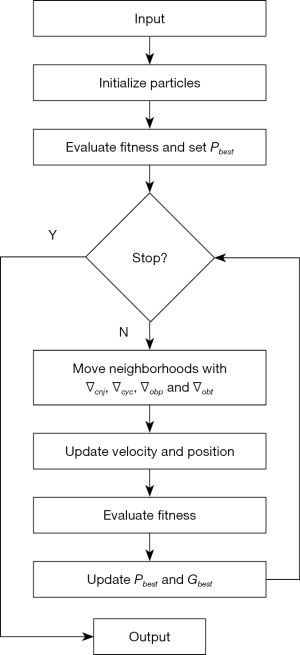
where r is the random number, i is the particle index, k is the iteration count, is the local best fitness of ith particle after k iterations and is the global best fitness of the entire swarm after k iterations. GT-PSO would initialize the entire swarm randomly with a particular number of particles whose representations are variable length encoding, and it will assess the fitness score by setting those best values of all particles. And then it can decompose the solution space hierarchically and generate the corresponding operators. They run concurrently to move the neighborhoods of particles in the solution space, and the self-adaptive evolutionary strategy is guaranteed by parameter configuration to make the updates of velocity and position. The whole search would be stopped when stopping conditions are satisfied, which can be configured to for example, when the maximum iteration number is reached, or the minimum error rate is achieved. The detailed flowchart of GT-PSO is demonstrated in (Figure 3).
Objective function
The popular measurement of Kapur’s entropy is evaluated as the objective function of medical image segmentation formulated as:
where:
j is the grayscale index, L is the upper bound of grayscale, hj is the number of pixels and pj is the probability distribution of jth grayscale. i is the segmentation class index, θi is the iththreshold, wi is the cumulative probability and Hi is the entropy of ith segmentation class. The optimization task of segmentation is to maximize . The notations of GT-PSO components are listed in (Table 1).
Table 1
| Notation | Remark |
|---|---|
| p | Particle encoding |
| X | Permutation set |
| g | Group action |
| Group multiplication | |
| cnj | Conjugacy class |
| cyc | Cyclic form |
| obp | Orbital plane |
| obt | Orbit |
| Operator |
GT-PSO, Group Theoretic Particle Swarm Optimization.
Parameter configuration
The proposed GT-PSO is compared to Tabu Search (TS), Genetic Algorithm (GA), Particle Swarm Optimization (PSO) and Differential Evolution (DE). The parameter configuration for every method is presented in (Table 2).
Table 2
| Method | Parameter | Value |
|---|---|---|
| TS | Tabu list | 20, 30 |
| GA | Mut rate | 0.3, 0.4 |
| Tour rate | 0.1, 0.2 | |
| DE | Cross prob | 0.2, 0.4 |
| Low bound | 0.2, 0.3 | |
| High bound | 0.7, 0.8 | |
| PSO | Inertial weight | 0.8, 1.2 |
| Acc coeff | 1.2, 1.5 | |
| GT-PSO | Random 1&2 | 0.5, 0.8 |
| Random 3&4 | 0.2, 0.5 | |
| Acc coeff | 1.2, 1.5 | |
| Pop size | 20, 30 |
DE, Differential Evolution; GT-PSO, Group Theoretic Particle Swarm Optimization; GA, Genetic Algorithm; TS, Tabu Search; Mut, mutation; prob, probability; Acc coeff, acceleration coefficients; Pop, population.
The study was conducted in accordance with the Declaration of Helsinki (as revised in 2013). This study was approved by our institutional review board. Informed consent was waived.
Results
As a case study of the effect of the proposed GT-PSO, the dataset of lung cancer MRI has been considered as the tested images. The illustrated result is based on the image #311 (Figure 4A) extracted from the dataset archive of Iraq-Oncology Teaching Hospital/National Center for Cancer Diseases (IQ-OTH/NCCD), which contains 110 cases of 1,190 images. The detail description of data archive is shown in (Table 3).
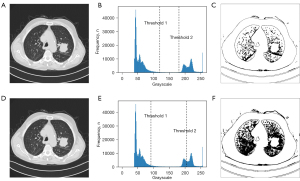
Table 3
| Image | Number |
|---|---|
| Train | 800 |
| Validate | 200 |
| Test | 190 |
| Cross-validation | 10-fold |
IQ-OTH, Iraq-Oncology Teaching Hospital; NCCD, National Center for Cancer Diseases.
During the segmentation process, the GT-PSO has identified three distinct classes of image with two levels of thresholds that just reside in the trough between two crests of grayscale distribution, and the illustration of final histogram of segmentation is shown in (Figure 4B), The optimized thresholds θ1 and θ2 obtained by GT-PSO in grayscale distribution are 118 and 182 respectively. The contour of sick region is detected and segmented from the background tissues in the right part of (Figure 4C). PSO is chosen as the baseline model compared to GT-PSO on the same image #311 (Figure 4D) because GT-PSO is the enhanced version of PSO based on group theory foundation. The optimized thresholds θ1 and θ2 obtained by PSO in grayscale distribution are 87 and 206 respectively (Figure 4E), and in contrast to the visualization of GT-PSO, the contour of sick region extracted by PSO has more noises and dark dots from the background (Figure 4F), causing the blurred quality of segmentation result. After 1,000 iterations of the search of multi-level threshold with variable numbers of feasible threshold combinations in each particle (Figure 5).
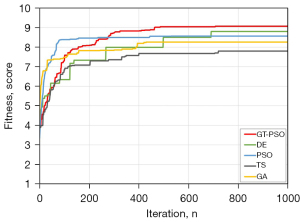
The numerical metrics of experimental results generated by those compared methods (TS, GA, DE, PSO and GT-PSO) are tabulate in (Table 4). The Kapur’s entropy is the same as pixel accuracy for segmentation evaluation.
Table 4
| Method | Kapur’s entropy | Kappa | Precision | Recall | F1-measure | IoU | AUC | Time (s) |
|---|---|---|---|---|---|---|---|---|
| TS | 7.799 | 0.651 | 0.855 | 0.848 | 0.847 | 0.718 | 0.834 | 90.120 |
| GA | 8.257 | 0.778 | 0.864 | 0.859 | 0.859 | 0.794 | 0.877 | 158.250 |
| DE | 8.801 | 0.860 | 0.917 | 0.917 | 0.917 | 0.866 | 0.940 | 151.920 |
| PSO | 8.568 | 0.821 | 0.893 | 0.892 | 0.892 | 0.832 | 0.916 | 142.830 |
| GT-PSO | 9.069 | 0.898 | 0.945 | 0.945 | 0.945 | 0.902 | 0.957 | 173.730 |
DE, Differential Evolution; GT-PSO, Group Theoretic Particle Swarm Optimization; GA, Genetic Algorithm; TS, Tabu Search; IoU, intersection over union; AUC, area under the curve.
As shown in (Figure 5), GT-PSO outperforms all the other compared methods on the tested image archives. The behavior of GT-PSO increases gradually in the early and middle of the search and gets converged in the last one third of the iterations around 700. Although its raising speed is not as fast as PSO and GA before the number of iterations about 300, GT-PSO still performs the best during the rest of the search process. And it is followed by the outcome of DE, which has the second-best performance of all compared methods. PSO and GA come to the next two rankings where TS shows the worst output among them.
The result of comparison of fitness values with Kapur’s entropy and time consumptions of all compared methods are displayed in (Table 4). It also proves the illustrated results (Figure 5) simultaneously, where GT-PSO generates the superior Kapur’s entropy of 9.07 at the acceptable time cost of 173.730 seconds. Without the consideration of running time, its achievement is 3% higher than DE and 16% higher than TS almost. As the time cost is concerned, GT-PSO still has balanced performance between fitness value and time consumption compared to others. Its average level of other evaluation metrics of Kappa, Precision, Recall, F1-measure, intersection over union (IoU) and area under the curve (AUC) is over 90%.
As shown in (Figure 6), the ablation study of GT-PSO is implemented via removing two categories of components gradually from the entire algorithm. GT-PSO is an enhanced method of conventional PSO rebuilt on group theory foundation, and there are four kinds of operators: cnj, cyc, obp and obt, where the previous two belong to the category of diversification and the latter two are intensified operators. GT-PSO outperforms the other three without any one module or both, its Kapur’s entropy is 9.07 while the value for worst case is only 7.51, and the gap between them is more than 20%. For detailed results of evaluation metrics please refer to (Table 5).
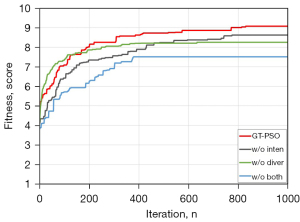
Table 5
| Method | Kapur’s entropy | Kappa | Precision | Recall | F1-measure | IoU | AUC | Time (s) |
|---|---|---|---|---|---|---|---|---|
| GT-PSO | 9.073 | 0.796 | 0.916 | 0.907 | 0.907 | 0.870 | 0.976 | 184.560 |
| w/o diver | 8.253 | 0.614 | 0.837 | 0.825 | 0.820 | 0.757 | 0.914 | 136.950 |
| w/o inten | 8.621 | 0.738 | 0.866 | 0.861 | 0.859 | 0.821 | 0.919 | 150.770 |
| w/o both | 7.509 | 0.541 | 0.800 | 0.751 | 0.713 | 0.692 | 0.822 | 103.520 |
AUC, area under the curve; GT-PSO, Group Theoretic Particle Swarm Optimization; diver, diversification; inten, intensification; IoU, intersection over union; w/o, without.
Discussion
As we know, the multi-level threshold image segmentation can be regarded as the problem of combinatorial optimization of various thresholds within the range of grayscale boundary to some certain extent. Meanwhile GT-PSO is originally designed for combinatorial optimization based on symmetric group definitions and concepts, thus it is also suitable for similar type of image segmentation tasks. This is the main reason why GT-PSO outperforms all the other comparison methods in our experiment (Table 4). Another reason of this superior achievement of GT-PSO is that the comparison methods are practical for solving continuous optimization problems with appropriate real number encoding, while the multi-level thresholding is actually considered as discrete optimization problem. GT-PSO can provide more suitable encoding and updating approaches with the mathematical foundation of symmetric group. During the early procedure of GT-PSO, since the conjugacy class and cyclic form operators dominate the search according to the parameter setting in (Table 2), it gets a relatively slow slope when iteration number increases, which indicates that the search is in the exploration stage and the solution diversities are maintained in order to reach more regions in the solution landscape. Furthermore, the orbital plane and orbit operators act as the major components of particle movements and intensify the search to converge in the exploitation stage. Meanwhile, the intermedia results displayed in (Figure 6) has the best numerical evidence for that, and both modules of diversification and intensification are necessary to the efforts of GT-PSO. The shape of GT-PSO curve in (Figure 5) demonstrates the self-adaptive strategy of swarm evolution of balanced optimization between exploration and exploitation.
For the rest of the comparison methods, DE and GA belong to the same class due to their evolutionary essences of selection, crossover, mutation, etc. Same for PSO and GT-PSO which both belongs to swarm intelligence optimization algorithm, and as result their curves share similar shapes and trends. In addition, TS is the single and non-population-based metaheuristic algorithm belonging to an independent branch besides the two classes previously mentioned, and its performance heavily relies on the local search ability controlled by tabu list memory, so it would suffer the stagnation at local optimum and the premature convergence during the search process.
Compared to GA, PSO seems to have better outcome because of its easier update mechanism and less parameter configuration. And DE shows a slower converging rate in the early phase compared to GA, probably caused by the mutant information of differential vectors of parents of DE, whereas the mutation of GA is directly based on fitness values of parents. So, in the beginning of the search, the vast majority of search information is focused on diversification and the differential values are relatively high, and it leads to the slower converging rate of DE. There is also a fatal problem for DE: it is very sensitive to the noisy raw data, and it would affect the behavior to some degrees. Despite the slower converging rate and random nature of search, DE would eventually outperform GA during the progressively growing iteration process.
The analysis of time complexity of GT-PSO is conducted as follows. Assuming that the dimension of objective function is n and its evaluating cost is cof, the swarm population is p and the maximum iteration number is k. In the initialization phase the time complexity of GT-PSO (Figure 3) is , and time complexity of each operator is since each of them is the linear rearrangement of threshold combination. Then in a single iteration phase the time complexity of GT-PSO should be , therefore the total time complexity would be . In image segmentation, the objective function is to assess the Kapur’s entropy with the polynomial time complexity of O (n2) at least, which is directly proportional to the size of the input image. Finally, the time complexity of GT-PSO for image segmentation is .
We would like to discuss and analyze the superiorities of our proposed method along with its shortcomings and challenges to come in the following list.
Contributions
- Proposed method partitions the space completely and approach global optimum accordingly;
- Proposed method statistically guarantees to find an optimal solution through mathematical proof;
- Proposed method is flexible to restrictive properties of the model and parameters, and versatile for practical discrete optimizations.
Challenges
- Proposed method does not yet guarantee completely to find the real global optimum solution during the search;
- Proposed method could possibly cost over-acceptable computational time when the objective function is extremely complex.
Optimization is one of the fundamental technologies for computer vision and machine learning tasks in general, and for these techniques in medical use. As a new search paradigm, we believe GT-PSO has decent potential and practical value for various medical applications. For example, in organ segmentation task, it can be applied for the process of feature selection, feature fusion, attenuation correction and intensity normalization in data pre-processing step. And in data augmentation step, it would reduce over-fitting and increase samples by optimizing distortion, elastic deformation and noise contamination. The optimizer of back-propagation in deep learning can be replaced by GT-PSO, as well as model structure optimization. The nature of hierarchy of GT-PSO would lead to the parallel search for multi-objective detection in organ segmentation.
Conclusions
A novel multi-level threshold image segmentation method using symmetric group theory-based metaheuristic is proposed to solve the combinatorial optimization problem of multiple grayscale thresholds of medical images. GT-PSO would generate a new search paradigm and improve the efficiency from four designable aspects: particle encoding, solution landscape, neighborhood movement and swarm topology. A case study of lung cancer CT image archive is conducted to demonstrate the performance of our proposed GT-PSO comparing to other metaheuristics algorithms. The ablation study is fulfilled to check the intermedia efforts of two major components of GT-PSO. Overall, the experimental results show that GT-PSO achieves the best performance and keep the equilibrium between exploitation and exploration, therefore we believe it has decent potential for interdisciplinary applications of clinical medicine and artificial intelligence.
Acknowledgments
Funding: This study is partially supported by National Natural Science Foundations of China under Grant 62101206 and 51806122, Zhejiang Provincial Natural Science Foundation of China under Grant LZY21E050003 and Joint Funds of Zhejiang Provincial Natural Science Foundation of China under Grant LZY22D010001.
Footnote
Reporting Checklist: The authors have completed the TRIPOD reporting checklist. Available at https://qims.amegroups.com/article/view/10.21037/qims-22-295/rc
Conflicts of Interest: All authors have completed the ICMJE uniform disclosure form (available at https://qims.amegroups.com/article/view/10.21037/qims-22-295/coif). The authors have no conflicts of interest to declare.
Ethical Statement: The authors are accountable for all aspects of the work in ensuring that questions related to the accuracy or integrity of any part of the work are appropriately investigated and resolved. The study was conducted in accordance with the Declaration of Helsinki (as revised in 2013). This study was approved by our institutional review board. Informed consent was waived.
Open Access Statement: This is an Open Access article distributed in accordance with the Creative Commons Attribution-NonCommercial-NoDerivs 4.0 International License (CC BY-NC-ND 4.0), which permits the non-commercial replication and distribution of the article with the strict proviso that no changes or edits are made and the original work is properly cited (including links to both the formal publication through the relevant DOI and the license). See: https://creativecommons.org/licenses/by-nc-nd/4.0/.
References
- Ramesh KKD, Kumar GK, Swapna K, Datta D, Rajest SS. A review of medical im-age segmentation algorithms. EAI Endorsed Transactions on Pervasive Health and Technology 2021;7:e6.
- Ma J, Chen J, Ng M, Huang R, Li Y, Li C, Yang X, Martel AL. Loss odyssey in med-ical image segmentation. Med Image Anal 2021;71:102035. [Crossref] [PubMed]
- Minaee S, Boykov Y, Porikli F, Plaza A, Kehtarnavaz N, Terzopoulos D. Image Segmentation Using Deep Learning: A Survey. IEEE Trans Pattern Anal Mach Intell 2022;44:3523-42. [PubMed]
- Lan K, Wang DT, Fong S, Liu LS, Wong KKL, Dey N. A Survey of Data Mining and Deep Learning in Bioinformatics. J Med Syst 2018;42:139. [Crossref] [PubMed]
- Fong S, Lan K, Sun P, Mohammed S, Fiaidhi J, Mohammed S, editors. A time-series pre-processing methodology for biosignal classification using statistical feature ex-traction. Proceedings of the 10th IASTED International Conference on Biomedical Engineering (Biomed’13); 2013.
- Faragallah OS, El-Hoseny H, El-Shafai W, Abd El-Rahman W, El-Sayed HS, El-Rabaie E-SM, Abd El-Samie FE, Geweid GG. A comprehensive survey analysis for present solutions of medical image fusion and future directions. IEEE Access 2020;9:11358-71.
- Suetens P. Fundamentals of medical imaging. 3rd edition. Cambridge University Press, 2017.
- Ryan DP, Hong TS, Bardeesy N. Pancreatic adenocarcinoma. N Engl J Med 2014;371:1039-49. [Crossref] [PubMed]
- Cai S, Tian Y, Lui H, Zeng H, Wu Y, Chen G. Dense-UNet: a novel multiphoton in vivo cellular image segmentation model based on a convolutional neural network. Quant Imaging Med Surg 2020;10:1275-85. [Crossref] [PubMed]
- Yang Q, Zhang H, Xia J, Zhang X. Evaluation of magnetic resonance image seg-mentation in brain low-grade gliomas using support vector machine and convolu-tional neural network. Quant Imaging Med Surg 2021;11:300-16. [Crossref] [PubMed]
- Zhou T, Tan T, Pan X, Tang H, Li J. Fully automatic deep learning trained on limited data for carotid artery segmentation from large image volumes. Quant Imaging Med Surg 2021;11:67-83. [Crossref] [PubMed]
- Lan K, Liu L, Li T, Chen Y, Fong S, Marques JAL, Wong RK, Tang R. Multi-view convolutional neural network with leader and long-tail particle swarm optimizer for enhancing heart disease and breast cancer detection. Neural Comput Appl 2020;32:15469-88. [Crossref]
- Oliva D, Abd Elaziz M, Hinojosa S. Metaheuristic algorithms for image segmenta-tion: theory and applications. 1st edition. Springer, 2019.
- Mesejo P, Ibáñez Ó, Cordón Ó, Cagnoni S. A survey on image segmentation using metaheuristic-based deformable models: state of the art and critical analysis. Appl Soft Comput 2016;44:1-29. [Crossref]
- Otsu N. A threshold selection method from gray-level histograms. IEEE Trans Syst Man Cybern 1979;9:62-6. [Crossref]
- Kapur JN, Sahoo PK, Wong AKC. A new method for gray-level picture thresholding using the entropy of the histogram. Computer Vision, Graphics, and Image Pro-cessing 1985;29:273-85. [Crossref]
- Qin J, Shen X, Mei F, Fang Z. An Otsu multi-thresholds segmentation algorithm based on improved ACO. J Supercomput 2019;75:955-67. [Crossref]
- He L, Huang S. An efficient krill herd algorithm for color image multilevel thresh-olding segmentation problem. Appl Soft Comput 2020;89:106063. [Crossref]
- Suresh S, Lal S. An efficient cuckoo search algorithm based multilevel thresholding for segmentation of satellite images using different objective functions. Expert Syst Appl 2016;58:184-209. [Crossref]
- Li Y, Bai X, Jiao L, Xue Y. Partitioned-cooperative quantum-behaved particle swarm optimization based on multilevel thresholding applied to medical image segmenta-tion. Appl Soft Comput 2017;56:345-56. [Crossref]
- Altan A, Karasu S. Recognition of COVID-19 disease from X-ray images by hybrid model consisting of 2D curvelet transform, chaotic salp swarm algorithm and deep learning technique. Chaos Solitons Fractals 2020;140:110071. [Crossref] [PubMed]
- Abd Elaziz M, Lu S, He S. A multi-leader whale optimization algorithm for global optimization and image segmentation. Expert Syst Appl 2021;175:114841. [Crossref]
- Lan K, Li G, Jie Y, Tang R, Liu L, Fong S. Convolutional neural network with group theory and random selection particle swarm optimizer for enhancing cancer image classification. Math Biosci Eng 2021;18:5573-91. [Crossref] [PubMed]




