A miniature U-net for k-space-based parallel magnetic resonance imaging reconstruction with a mixed loss function

Introduction

Magnetic resonance imaging (MRI) has become one of the most important means for investigations in the clinical setting due to its excellent ability to visualize both anatomical structure and physiological function. Nevertheless, time-consuming scanning is the main drawback of MRI, which affects patient comfort and imaging quality, especially in dynamic imaging applications. Substantial advances have been made over the last few decades to accelerate MRI scanning. Interpolation, simple conjugate symmetry features of k-space or statistical image priors were utilized in earlier applications (1). Later, parallel imaging technologies using multi-channel phased array coils were used to speed up MRI scanning by undersampling k-space data uniformly (2). Currently, most MRI scanners have the capacity for the parallel imaging technique; nevertheless, the acceleration factor in practice is lower than four due to the noise and electromagnetic interference between coils (2).

Compressed sensing (CS) can recover a signal accurately from a few randomly sampled data in a sparse transformed domain (3,4). By extending the idea of CS to matrices, low-rank matrix completion can recover the missing or corrupted entries in a matrix when it has the property of low rank (5). Recently, the self-consistency of k-space data and the low-rankness of the weighted k-space data have been combined to exploit the correlation among inter- and intra-coils simultaneously (6). Moreover, the low dimensionality of the patch manifold of the MRI images is used within the CS framework (7). Usually, CS-MRI algorithms exploit the sparse nature of MRI in an iterative manner. As a consequence, such optimization-based methods do not meet the real-time requirements in clinical applications due to the numerous computational loads (8).

In the past a few years, the power of deep learning has been clearly demonstrated for numerous medical image processing problems (9-12). Recently, applying deep learning networks for solving fast MRI reconstruction has gained much attention. These methods can be roughly divided into k-space-based methods and image-based methods. The image-based methods take an inverse Fourier transform (IFT) on zero-filled k-space data to obtain an initial image (13-17). Then, various network models are introduced to derive mapping from the initial image to an output image without artifacts and noise, which includes vanilla convolutional neural networks (CNNs) (13), cascade CNN (14), and generative adversarial nets (GANs) (17). All these image-based deep learning MRI methods require a separate dataset with thousands of images for each anatomical site to train the network model. In fact, constructing such databases is intractable due to ethical issues.

The k-space-based deep learning reconstruct is an emerging strategy that uses small amounts of autocalibration signals (ACS) data to train a scan-specific feedforward neural network for autoregressive k-space interpolation. Scan-specific robust artificial-neural-networks for k-space interpolation (RAKI) reconstruction uses three layers of convolutional network to interpolate the missing k-space data (18). It was recently extended to arbitrary undersampling for accelerating coronary MRI in self-consistent (s)RAKI (19) and multiple slice k-space collaborative reconstructing (20), where a huge network scale is employed to obtain sufficient train samples with ACS data. Motivated by ideas from RAKI and auto-calibrated low-rank modeling of local k-space neighborhoods (AC-LORAKS) (21,22), LORAKI takes a recurrent neural network (RNN) to recover missing k-space data (23). Nevertheless, the network training requires approximately 1 hour on Google Colab (https://colab.research.google.com/) for LORAKI.

The k-space-based method is trained to be scan-specific based on a small amount of ACS data, which alleviates one of the main drawbacks of most other deep learning methods. Nevertheless, commonly used networks trained with a small amount of ACS data cannot reap the benefits of nonlinear representation of deep learning. Moreover, current k-space deep learning methods separate the real and imaginary parts of the k-space data and double the effective number of channels to handle the real-valued k-space data.

In this study, a miniature U-net for k-space-based parallel MRI reconstruction is proposed, abbreviated as MUKR. The U-net (24) is the most famous CNN architecture for medical image segmentation, which can maintain good performance even with extremely few training data. The original U-net is truncated to access a trade-off between the network performance and requirement of training samples. The proposed network is trained individually for each scan with a mixing loss function involving magnitude loss and phase loss. The performance of the proposed method was evaluated with various acceleration factors using the phantom and in vivo datasets. We present the following article in accordance with the MDAR checklist (available at https://qims.amegroups.com/article/view/10.21037/qims-21-1212/rc).

Methods

In this section, we first detail generalized autocalibrating partially parallel acquisitions (GRAPPA) (25), which is the most classical k-space-based parallel imaging reconstruction and RAKI, and then present the architecture of, and training in, MUKR used for reconstruction.

GRAPPA reconstruction and RAKI

GRAPPA reconstructs the missing k-space data with nearby acquired data over all coils. Mathematically, the GRAPPA reconstruction can be represented as follows:

sl(kx,ky+mΔky)=∑j=1L∑h=H1H2∑b=N1N2wl,m(j,h,b)sj(kx+hΔkx,ky+bRΔky)[1]

where (k_x,k_y) denotes the k-space coordinate, and the sampling intervals along frequency encoding (FE) and phase encoding (PE) directions are represented as Δkx and Δky, respectively; s denotes the k-space signal; j and l indicate the coil indexes; L is the channel total; m represents the distance between the missing data and the acquired data along PE direction, m=1, 2, ..., R-1; and R denotes the acceleration factor. The size of the interpolation kernel is defined by N1, N2, H1, and H2. Further, wl,m(j,h,b) denotes the combination weights on the h-th offset along FE and b-th offset along PE to reconstruct the m-th offset of coil l. Generally, the central k-space data are fully sampled to calibrate the combination weights. In fact, the interpolation process can be regarded as a conventional operation on the zero-filled k-space data, and then it can be represented as follows:

ρ^=S⊗ω[2]

where S denotes the zero-filled k-space data, and ω represents a conventional kernel, also known as the GRAPPA reconstruction weight.

The RAKI uses a three-layer CNN structure to replace the linear interpolation in GRAPPA reconstruction. Each layer, except the last, is a combination of linear convolutional kernels and a rectified linear unit (ReLU), namely, ReLU(x) = max(x,0), which has desirable convergence properties. The final layer of the network produces the desired reconstruction output by applying convolutional filters. The overall mapping can be denoted as:

F(s)=w3⊗ReLU(w2⊗ReLU(w1⊗s))[3]

where s denotes the sub-sampled zero-filled k-space, and F(s) represents the mapping from sub-sampled zero-filled k-space to the fully sampled k-space. w₁, w₂, and w₃ represent the convolutional filters in the 1^st, 2^nd, and 3^rd layers, respectively.

MUKR

The overall pipeline of the proposed method is shown in Figure 1. Unlike RAKI, which attempts to reconstruct the original k-space data directly, the proposed method utilizes a modified U-net to reconstruct a patch of k-space data each time, where the patch slides along the PE and FE directions within the entire k-space. In view of network performance and the requirement of training samples, the patch size is set empirically as 64×64. The complex-valued k-space data are converted to two-channel real value signals, and data received from all the coils are stacked along the channel direction. Thus, the network accepts 2×N_c patches with a size of 64×64 as input each time, where N_c denotes the total number of coils. As shown in Figure 1, the training data can be acquired by sliding the patch along both the PE and FE directions within the ACS region. In the reconstruction step, the network reconstructs a patch of missing data each time when the patch slides along both the PE and FE directions outside the ACS region. Then, a two-dimensional (2D) inverse fast Fourier transform (IFFT) on the individual coil k-space data is applied. Finally, all coil images are combined in a sum-of-squares (SOS) style.

Figure 1 Network architecture of the proposed method.

Network architecture

The miniature U-net designed in this work for k-space reconstruction consists of two main parts: a contracting path for the feature extraction and an expanding path for the image reconstruction.

The contracting path involves a series of one 3×3 convolutional kernel, followed by a ReLU layer, and then a 2×2 shuffle-pooling operation with stride two. At the center layer of the autoencoder, the number of feature maps is 256 and the size of the feature map is 8×8. The expanding path includes a continuous block of an up-sampling with bilinear interpolation from the front layer, a 2×2 convolutional kernel that halves the number of feature maps, and one 3×3 convolutional kernel, followed by a ReLU layer. Finally, the network outputs 2×N_c patches with a size of 64×64.

Mixed loss function in k-space

Previous research on k-space-based reconstruction has paid much attention to various network architectures rather than loss function. In most cases, real and imaginary of k-space data are concatenated into different channels and make no discrimination in the loss function. However, amplitude and phase of frequency data have more physical meanings. Consequently, following the Fourier image transformer method reported in the literature (26), the loss function in this study is computed with amplitude and phase of k-space data. The amplitude loss is defined as:

Lamp=(a⌢i,ai)=1+(a⌢i−ai)2[4]

where the a⌢ denotes the predicted amplitudes and a the target amplitudes. The phase loss is defined as:

Lpha=(φ^i,φi)=2−cos(φ^i−φi)[5]

The final loss function is the multiplicative combination of both individual losses, given by:

Ltol(K^,K)=1N∑i=0NLamp(a⌢i,ai)Lpha(φ^i,φi)[6]

Alternatively, a combination of both individual losses is summed:

Ltol(K^,K)=1N∑i=0N(Lamp(a⌢i,ai)+Lpha(φ^i,φi))[7]

Training

As performed in parallel imaging, the center region of k-space is fully sampled to obtain ample training data. The fully sampled data, named ACS, are then reduced uniformly by removing some data on the computer to mimic the real undersampling processing in the parallel MRI scanner. The network weights are updated by the combination of magnitude and phase error between the original full k-space and the reconstructed k-space.

With the aim of training MUKR, the learning rate size was set to 0.0001, and the training batch was set to 45. The network was trained for 300 epochs. The algorithm was developed using pyTorch1.1.0 (https://pytorch.org/) for the Python 3.8 environment (Python Software Foundation, Wilmington, DE, USA) on a NVIDIA GeForce GTX 2060 (Nvidia, Santa Clara, CA, USA) with 8GB GPU memory.

Evaluation

The proposed MUKR method was evaluated on one set of phantom data and two sets of in vivo data. The phantom dataset was acquired using a spin echo (SE) pulse sequence [echo time (TE)/repetition time (TR) =14/400 ms, 33.3 kHz bandwidth, 512×512 pixels, field of view (FOV) =240×240 mm²] on a 3.0 T scanner (Siemens Healthcare, Erlangen, Germany) with 32-channel head coils. A set of axial brain datasets was acquired from an SE pulse sequence (TE/TR =14/400 ms, 33.3 kHz bandwidth, 256×256 pixels, FOV =240×240 mm²) on a 1.5 T scanner (Siemens Healthcare, Erlangen, Germany) with eight-channel head coils. The knee k-space dataset was downloaded from http://mridata.org/, which was acquired from a TurboSpinEcho sequence (TE/TR =22/2,800 ms, 768×770 pixels, FOV =280 mm × 280.7 mm × 4.5 mm) using a 3.0T whole body MR system (Discovery MR 750, DV22.0; GE Healthcare, Milwaukee, WI, USA).

The study was conducted in accordance with the Declaration of Helsinki (as revised in 2013). The study was approved by the Institutional Ethics Board of Chengdu University of Information Technology (Chengdu, China), and informed consent was provided by a healthy adult human volunteer (male, age 31 years). The data were fully sampled and later decimated by multiplying the mask matrix S with various factors to mimic a parallel imaging acquisition procedure.

Peak signal-to-noise ratio (PSNR) and structural similarity index matrix (SSIM) (27) were chosen to quantitatively assess the reconstruction performance. The latter was based on the mean squared error and is closer to the human visual system than conventional metrics. The PSNR is defined as follows:

NMSE=∑i=1N∑j=1N|Ii,jrecon−Ii,jref|2/∑i=1N∑j=1N|Ii,jref|2[8]

PSNR＝10×log(255×255/NMSE)[9]

where NMSE denotes the normalized root mean square error, Ii,jref represents the reconstruction result without undersampling, and i and j indicate the pixel coordinates along PE and FE directions, respectively.

The SSIM between images I and J is computed as:

SSIM(I,J)=1N∑i∈I,j∈J(2μiμ^j+c1)(2σi,j+c2)(μi2+μ^j2+c1)(σi2+σj2+c2)[10]

where μi and μ^j are the respective local mean values, σi and σj the respective standard deviations, σi,j covariance value, and c₁ and c₂ two predefined constants. Generally, a preferable image has higher PSNR and SSIM.

The reconstruction quality of the proposed method was compared with that of GRAPPA and RAKI. A PyTorch version implementation of the RAKI on github (https://github.com/geopi1/DeepMRI) was adopted to reproduce the RAKI. The network was trained for 1,000 epochs with a learning rate of 0.01 and the batch size was set as 45.

Results

To investigate the effects of different loss functions in MUKR, we compared the MUKR reconstructions with a multiplicative combination of magnitude and phase loss, summing the combination of magnitude and phase loss and L2 loss function (Figure 2). The phantom images were reconstructed with a sampling factor of six and ACS lines of 84. Minimal differences can be observed between the images reconstructed with multiplicative and summing combinations of magnitude and phase loss, although the zoom-in images show that the dots in the summing combinations reconstructed image are blurrier than those in the multiplicative combinations reconstructed image. The images reconstructed with L2 loss function have higher noise level and more artifacts. Quantitatively, the multiplicative combination reconstruction has the highest PSNR. Hence, the multiplicative combination was selected in the following experiments.

Figure 2 Comparison of different loss function for MUKR reconstruction using a 32-channel phantom dataset with uniform undersampling along the PE direction for reduction factor R=4 and number of ACS lines NSL =6. First row: images reconstructed using MUKR with L2 loss function (A), MUKR with multiplicative combination of magnitude and phase loss (B), and MUKR with summing combination of magnitude and phase loss (C). The PSNRs of resulting images are listed in the upper left corner of each difference image. Second row: zoomed-in patch image of MUKR with L2 loss function reconstructed result (D), zoomed-in patch image of MUKR multiplicative combination of magnitude and phase loss reconstructed result (E) and zoomed-in patch image of MUKR summing combination of magnitude and phase loss reconstructed result (F). PSNR, peak signal-to-noise ratio; MUKR, the proposed method; PE, phase encoding; R, reduce factor; ACS, autocalibration signals; NSL, number of autocalibration signals lines.

Figure 3 compares the reconstructed phantom images between GRAPPA, RAKI, and MUKR with a sampling factor 4 and 64 phase encoding lines in the center of k-space. The zoomed-in patch image is shown below the reconstructed image. Aliasing artifacts and blur are serious in the image reconstructed using RAKI, while slighter aliasing artifacts can also be seen in the GRAPPA reconstructed image. Although the noise is obvious in the image reconstructed by MUKR, the aliasing artifacts are significantly alleviated.

Figure 3 Comparison of GRAPPA, RAKI, and MUKR using a phantom dataset with uniform undersampling along the PE direction for R=4, NSL =64. First row: reference image reconstructed with full k-space data and corresponding zoomed-in patch image. Second row: GRAPPA, RAKI, and MUKR reconstructed images. Third row: corresponding zoomed-in patch images. GRAPPA, generalized autocalibrating partially parallel acquisitions; RAKI, scan-specific robust artificial-neural-networks for k-space interpolation; MUKR, the proposed method; R, reduce factor; ACS, autocalibration signals; NSL, number of autocalibration signals lines.

Figure 4 demonstrates the axial brain images reconstructed using GRAPPA, RAKI, and MUKR with a sampling factor of six and ACS lines of 84. The GRAPPA reconstructed image has a high noise level, which is suppressed in the MUKR reconstructed image. In addition, aliasing artifacts can be observed in the RAKI reconstructed images, which is not obvious in the MUKR reconstructed image.

Figure 4 Comparison of GRAPPA, RAKI and MUKR using an 8-channel axial brain dataset with for R=6, NSL =84. First row: reference image reconstructed with full k-space data (left) and the region marked with the blue box is zoomed-in and shown (right). Second row: GRAPPA (left), RAKI (middle), and MUKR (right) reconstructed images. Third row: corresponding zoomed-in patch images of GRAPPA (left), RAKI (middle) and MUKR (right). GRAPPA, generalized autocalibrating partially parallel acquisitions; RAKI, scan-specific robust artificial-neural-networks for k-space interpolation; MUKR, the proposed method; R, reduce factor; NSL, number of auto-calibration signals lines.

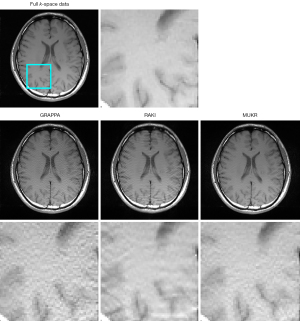
Figure 5 lists images reconstructed using GRAPPA, RAKI, and MUKR from the 15-channel knee dataset. The data are accelerated for sampling factor of four with 64 ACS lines and a sampling factor of six with 84 ACS lines. At the sampling factor of four, although no obvious difference exists between the images reconstructed by all methods, the zoomed-in patch images show that RAKI produces more oscillation artifacts than GRAPPA and MUKR. At the sampling factor of six, the GRAPPA reconstructed image is contaminated with serious noise, while noticeable aliasing artifacts can be observed in the image reconstructed by RAKI. By contrast, MUKR produces an image with less artifacts and noise.

Figure 5 Performance comparisons of GRAPPA, RAKI, and MUKR for a 15-channel knee dataset. First row: images reconstructed with full k-space data (A), GRAPPA (B), RAKI (C), and MUKR (D) for R=4, NSL =64. Second row: corresponding zoomed-in patch image of full k-space data (E), GRAPPA (F), RAKI (G) and MUKR (H). Third row: images reconstructed with GRAPPA (I), RAKI (J), and MUKR (K) for R=6, NSL =84. Fourth row: corresponding zoomed-in patch images of GRAPPA (L), RAKI (M) and MUKR (N). GRAPPA, generalized autocalibrating partially parallel acquisitions; RAKI, scan-specific robust artificial-neural-networks for k-space interpolation; MUKR, the proposed method; R, reduce factor; NSL, number of auto-calibration signal lines.

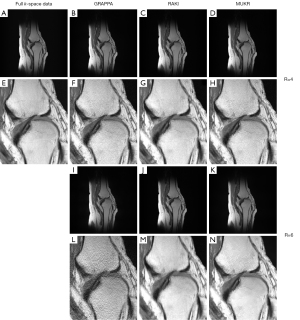
Table 1 quantitatively evaluates the images reconstructed with GRAPPA, RAKI, and MUKR. The highest PSNR and SSIM values are highlighted in each cell to facilitate the comparison. For phantom and brain imaging, MUKR has an improvement on SSIM with 0.05 and 0.02 over GRAPPA and RAKI, respectively. This is consistent with the findings displayed in Figure 5.

As shown, MUKR consistently yields higher PSNRs and SSIMs than GRAPPA and RAKI in all cases.

Discussion

The noise amplification is serious in the GRAPPA reconstructed images when the acceleration factor is larger than four. The distance between the interpolation target point and the source point in the GRAPPA interpolation increases with the undersampling factor. As a result, the linear interpolation in GRAPPA is insufficient to capture the data correlation in k-space when the acceleration factor is large. Owing to the power of nonlinear representation in deep learning, the noise levels of RAKI and MUKR reconstructed images are much lower than those of GRAPPA reconstructed images, but increased aliasing artifacts are introduced in the RAKI reconstruction.

The major problem in deep learning for MRI reconstruction is the availability of training datasets. To address this, RAKI directly reconstructs the full k-space data using a simple CNN network trained with individual ACS data. Thus, RAKI can be viewed as a deep learning version of the widely used nonlinear GRAPPA parallel imaging method, where the nonlinear ability is introduced by the ReLu in the CNN. As performed in GRAPPA, RAKI reconstructs each undersampled k-space data point with the nearby sampled data, which ignores many data consistency constraints (21,28). Furthermore, the simple CNN network could not reconstruct clear boundaries and high gradient components. In particular, the magnitude of k-space data fluctuates dramatically. As a result, the images reconstructed with RAKI give aliasing artifacts when the undersampling factor is large. Such artifacts can be alleviated with MUKR, in which the more complex network has stronger power of nonlinear representation. Previous work has also demonstrated that U-net has a better performance than simple CNN network for image segmentation and super resolution (24).

The depth of the original U-net is fixed to six, which means there are six downscale blocks and a corresponding six upscale blocks. There is considerable consent that the deeper network leads to a better performance with sufficient training samples (29). Nevertheless, the deeper network requires more training samples, which are intractable in the k-space-based reconstruction. In MUKR, the modified U-net has a depth of three. Meanwhile, the feature map is reduced by a factor of four. These clipping operations reduce the computational cost and the requirement of training samples. The size of input for the original U-net is generally larger than 256×256. Few training samples can be obtained in such a scenario, especially for the brain image where the k-space size is 256×256. The scaled-in U-net accepts a patch size of 64×64, which can slide along both PE and FE directions to obtain plentiful training samples. In the training step, the patch can slide with a step length of 1 to obtain more training samples; however, the step length for prediction can be set at 64 to reduce computational expense.

The k-space data are complex numbers, while most deep learning frameworks only support real number calculations. The complex data are split into two parts, that is real and imaginary, which are processed with different network channels. Nonetheless, such a real-imaginary split introduces phase error for MRI reconstruction (30). The magnitude loss and phase loss are measured in MUKR, and the final loss is a combination of both individual losses. The results show that the real-imaginary split with L2 loss function can yield more artifacts than a magnitude-phase split. Although the results show that multiplicative and summing combinations of magnitude and phase loss share similar results, a further study is needed to investigate the influence on the phase reconstruction application, such as quantitative susceptibility mapping.

Table 2 compares the time consumption of GRAPPA, RAKI, and MUKR in phantom and in vivo studies. The training time of GRAPPA denotes the time of computing interpolation weights with ACS data. The network training takes a considerable amount of time, and thus the calculation speed of RAKI and MUKR is five to eight times slower than that of GRAPPA. Since the proposed method reconstructs a patch of k-space data each time, while the RAKI reconstructs single k-space data points, the MUKR has less forward calculation times. For brain imaging, the forward reasoning in MUKR requires 12 times, explicitly, 3× for PE and 4× for FE; however, the forward calculation in RAKI needs 16,128 times, namely, 192× for PE and 256× for FE. As a result, RAKI consumes more time than MUKR. It should be noted that the implementation of MUKR was designed for simple proof-of-principle evaluation, and substantial acceleration may become possible with optimized hardware and more efficient programming language.

Conclusions

Overall, a miniature U-net has been introduced as a novel way to reconstruct the missing k-space data in MRI, which can provide an optimal trade-off between network performance and requirements of training samples. The network is trained individually for each scan using the scan-specific ACS data with a mixing loss function involving magnitude loss and phase loss. Experimental results demonstrate that the proposed MUKR method can offer improved k-space-based parallel MRI reconstruction with a miniature U-net.

Acknowledgments

Funding: This research work was supported by the Sichuan Science and Technology Program (No. 2021YFG0308, No. 2021YFG0133) and the Program of Henan Province (No. 2020GGJS123).

Footnote

Reporting Checklist: The authors have completed the MDAR checklist. Available at https://qims.amegroups.com/article/view/10.21037/qims-21-1212/rc

Conflicts of Interest: All authors have completed the ICMJE uniform disclosure form (available at https://qims.amegroups.com/article/view/10.21037/qims-21-1212/coif). The authors have no conflicts of interest to declare.

Ethical Statement: The authors are accountable for all aspects of the work in ensuring that questions related to the accuracy or integrity of any part of the work are appropriately investigated and resolved. The study was conducted in accordance with the Declaration of Helsinki (as revised in 2013). The study was approved by the Institutional Ethics Board of Chengdu University of Information Technology (Chengdu, China), and informed consent was provided by the participant.

Open Access Statement: This is an Open Access article distributed in accordance with the Creative Commons Attribution-NonCommercial-NoDerivs 4.0 International License (CC BY-NC-ND 4.0), which permits the non-commercial replication and distribution of the article with the strict proviso that no changes or edits are made and the original work is properly cited (including links to both the formal publication through the relevant DOI and the license). See: https://creativecommons.org/licenses/by-nc-nd/4.0/.

References

1. Ye X, Chen Y, Lin W, Huang F. Fast MR image reconstruction for partially parallel imaging with arbitrary k-space trajectories. IEEE Trans Med Imaging 2011;30:575-85. [Crossref] [PubMed]
2. Deshmane A, Gulani V, Griswold MA, Seiberlich N. Parallel MR imaging. J Magn Reson Imaging 2012;36:55-72. [Crossref] [PubMed]
3. Donoho DL. Compressed sensing. IEEE Transactions on Information Theory 2006;52:1289-306. [Crossref]
4. Lustig M, Donoho DL, Santos JM, Pauly JM. Compressed sensing MRI. IEEE Signal Processing Magazine 2008;25:72-82. [Crossref]
5. Shin PJ, Larson PE, Ohliger MA, Elad M, Pauly JM, Vigneron DB, Lustig M. Calibrationless parallel imaging reconstruction based on structured low-rank matrix completion. Magn Reson Med 2014;72:959-70. [Crossref] [PubMed]
6. Zhang X, Guo D, Huang Y, Chen Y, Wang L, Huang F, Xu Q, Qu X. Image reconstruction with low-rankness and self-consistency of k-space data in parallel MRI. Med Image Anal 2020;63:101687. [Crossref] [PubMed]
7. Abdullah S, Arif O, Bilal Arif M, Mahmood T. MRI reconstruction from sparse k-space data using low dimensional manifold model. IEEE Access 2019;7:88072-81.
8. Chung J, Ruthotto L. Computational methods for image reconstruction. NMR Biomed 2017; [Crossref] [PubMed]
9. Boublil D, Elad M, Shtok J, Zibulevsky M. Spatially-Adaptive Reconstruction in Computed Tomography Using Neural Networks. IEEE Trans Med Imaging 2015;34:1474-85. [Crossref] [PubMed]
10. Chen X, Wang X, Zhang K, et al. Recent advances and clinical applications of deep learning in medical image analysis. Med Image Anal 2022;79:102444. [Crossref] [PubMed]
11. Ronneberger O, Fischer P, Brox T. editors. U-Net: Convolutional Networks for Biomedical Image Segmentation. Cham: Springer International Publishing, 2015.
12. Bernard A, Comby PO, Lemogne B, Haioun K, Ricolfi F, Chevallier O, Loffroy R. Deep learning reconstruction versus iterative reconstruction for cardiac CT angiography in a stroke imaging protocol: reduced radiation dose and improved image quality. Quant Imaging Med Surg 2021;11:392-401. [Crossref] [PubMed]
13. Wang S, Su Z, Ying L, Peng X, Zhu S, Liang F, Feng D, Liang D. Accelerating magnetic resonance imaging via deep learning. Proc IEEE Int Symp Biomed Imaging 2016;2016:514-7. [Crossref] [PubMed]
14. Schlemper J, Caballero J, Hajnal JV, Price AN, Rueckert D. A Deep Cascade of Convolutional Neural Networks for Dynamic MR Image Reconstruction. IEEE Trans Med Imaging 2018;37:491-503. [Crossref] [PubMed]
15. Yang Y, Sun J, Li H, Xu Z. ADMM-CSNet: A deep Learning approach for image compressive sensing. IEEE Transactions on Pattern Analysis and Machine Intelligence 2020;521-38. [Crossref] [PubMed]
16. Zhou B, Zhou SK. DuDoRNet: Learning a dual-domain recurrent network for fast MRI reconstruction with deep T1 Prior. IEEE Computer Society Conference on Computer Vision and Pattern Recognition 2020:4273-82.
17. Yang G, Yu S, Dong H, Slabaugh G, Dragotti PL, Ye X, et al. DAGAN: Deep De-Aliasing Generative Adversarial Networks for Fast Compressed Sensing MRI Reconstruction. IEEE Trans Med Imaging 2018;37:1310-21. [Crossref] [PubMed]
18. Akçakaya M, Moeller S, Weingärtner S, Uğurbil K. Scan-specific robust artificial-neural-networks for k-space interpolation (RAKI) reconstruction: Database-free deep learning for fast imaging. Magn Reson Med 2019;81:439-53. [Crossref] [PubMed]
19. Hosseini SAH, Zhang C, Weingärtner S, Moeller S, Stuber M, Ugurbil K, Akçakaya M. Accelerated coronary MRI with sRAKI: A database-free self-consistent neural network k-space reconstruction for arbitrary undersampling. PLoS One 2020;15:e0229418. [Crossref] [PubMed]
20. Du T, Zhang Y, Shi X, Chen S. Multiple Slice k-space Deep Learning for Magnetic Resonance Imaging Reconstruction. Annu Int Conf IEEE Eng Med Biol Soc 2020;2020:1564-7. [Crossref] [PubMed]
21. Haldar JP. Low-rank modeling of local k-space neighborhoods (LORAKS) for constrained MRI. IEEE Trans Med Imaging 2014;33:668-81. [Crossref] [PubMed]
22. Lobos RA, Kim TH, Hoge WS, Haldar JP. Navigator-Free EPI Ghost Correction With Structured Low-Rank Matrix Models: New Theory and Methods. IEEE Trans Med Imaging 2018;37:2390-402. [Crossref] [PubMed]
23. Kim TH, Garg P, Haldar JP. LORAKI: autocalibrated recurrent neural networks for autoregressive MRI reconstruction in k-Space. arXiv preprint. arXiv:190409390 2019.
24. Ronneberger O, Fischer P, Brox T. U-Net: convolutional networks for biomedical image segmentation. Lect Notes Comput Sci 2015;9351:234-41. [Crossref]
25. Griswold MA, Jakob PM, Heidemann RM, Nittka M, Jellus V, Wang J, Kiefer B, Haase A. Generalized autocalibrating partially parallel acquisitions (GRAPPA). Magn Reson Med 2002;47:1202-10. [Crossref] [PubMed]
26. BuchholzTOJugF. Fourier image transformer. arXiv:210402555.
27. Wang Z, Bovik AC, Sheikh HR, Simoncelli EP. Image quality assessment: from error visibility to structural similarity. IEEE Trans Image Process 2004;13:600-12. [Crossref] [PubMed]
28. Xu L, Guo L, Liu X, Kang L, Chen W, Feng Y. GRAPPA reconstruction with spatially varying calibration of self-constraint. Magn Reson Med 2015;74:1057-69. [Crossref] [PubMed]
29. Subhas N, Li H, Yang M, Winalski CS, Polster J, Obuchowski N, Mamoto K, Liu R, Zhang C, Huang P, Gaire SK, Liang D, Shen B, Li X, Ying L. Diagnostic interchangeability of deep convolutional neural networks reconstructed knee MR images: preliminary experience. Quant Imaging Med Surg 2020;10:1748-62. [Crossref] [PubMed]
30. Wang S, Cheng H, Ying L, Xiao T, Ke Z, Zheng H, Liang D. DeepcomplexMRI: Exploiting deep residual network for fast parallel MR imaging with complex convolution. Magn Reson Imaging 2020;68:136-47. [Crossref] [PubMed]