
Validity and reliability of a computer-assisted system method to measure axial vertebral rotation
Introduction
Adolescent idiopathic scoliosis (AIS) is accepted as a 3-dimensional deformity involving axial, sagittal and frontal planes (1). AIS can progress over the years, especially during growth, and can cause musculoskeletal, lung, psychological problems and significant pain in adulthood (2). The Cobb angle measurement on the standing posteroanterior full-length spine X-ray is the gold standard for diagnosing and monitoring changes in the AIS (3). Axial vertebral rotation (AVR) is an essential parameter in the AIS study (4,5). Its measurement is necessary to assess the severity of scoliosis and to quantify the risk of progression (5-9), for the selection of treatment (3,6,10), and the analysis of orthopaedic and surgical procedures (3,5,8,11-13).
There are several methods for assessing AVR using conventional X-rays (by identifying the position of some vertebral anatomical structures and their relationships). The Perdriolle method is widely used and recommended by the Scoliosis Research Society (14,15). Another method employed for its simplicity and reliability is the Raimondi method that uses templates (Raimondi’s tables) to determine the degree of AVR on X-ray films (14,16,17). Both methods are quite similar and measure AVR in degrees, one of the main advantages of Raimondi’s method being that it measures in 2º intervals of rotation, while Perdriolle’s method measures in 5º intervals (14). We can obtain a three-dimensional reconstruction of the spine using computerised tomography (CT) scan and measure AVR with high accuracy (18). However, the CT-scan is not suitable for monitoring scoliotic progression because of the excessive and repeated radiation it involves [e.g., an estimated radiation dose of 5.2 mSv for each study (18)]. Radiographic medical imaging, especially standing posteroanterior full-length spine X-ray (19-21), continues to be the method of choice for diagnosing and monitoring scoliosis (22).
Advances in digital technology in radiology have allowed advantages such as reducing radiation exposure, more efficient image comparison, variable contrast scales or easy storage. These advantages have encouraged the development of computer tools to evaluate medical images. Raimondi’s tables were designed for X-rays films (physical format) and are therefore not directly compatible with digital images.
This study aimed to evaluate software’s validity and absolute reliability based on a new linear mathematical equation to determine the AVR on digital X-rays according to Raimondi’s method in evaluators with different degrees of experience. We have hypothesised that the measurements made with the software that allows using the mentioned equation are equally valid and present less variability among observers than those made with the conventional system. We present the following article in accordance with the MDAR checklist (available at https://dx.doi.org/10.21037/qims-21-575).
Methods
Software
We developed software that can calculate AVR on digital X-ray images, applying Raimondi’s method, without introducing the information of the scale of the X-ray performed study. The software was developed in C++ language under the Microsoft Visual Studio 2019 development environment and using the OpenCV 3.4.10 artificial vision libraries and the DCMTK libraries, from OFFIS - Institute for Information Technology, to operate with Digital Imaging and Communication On Medicine (DICOM) files.
The software incorporates additional tools, such as the ability to zoom in on regions of interest and to vary the contrast (fractional difference in optical density of the brightness between two regions of an image) of the digitalised X-ray image.
To perform the AVR calculation, the observer opens the X-ray image and selects the most rotated vertebra (in case of doubt among two vertebrae, the operator measured both). The observer zooms in on the vertebra and selects with a mouse click the two closest points of the vertebral body's lateral faces, and the two opposite sides of the shadow of the pedicle rotated towards the centre of the vertebra in the anteroposterior projection (Figure 1). Based on these points’ position, the software calculates the vertebral body’s width (D) and the distance from the centre of the pedicle to the side of the vertebral body (d). From their relationship, it applies Raimondi’s method according to the Eq. [1] (22):
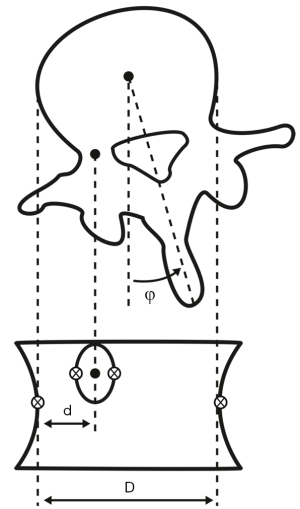
Study design and measurement protocol
We conducted a prospective and observational study of 33 scoliotic curves in 21 selected standing posteroanterior full-length spine X-ray of patients with AIS, with equivalent image quality and without defects. The radiographic images had been collected from an image repository in a retrospective manner during the routine medical care of patients with AIS. This study followed the World Medical Association Declaration of Helsinki's ethical standards (as revised in 2013). The study was granted exemption from requiring ethics approval and informed consent since the complete and irreversible anonymisation of the images did not involve data processing.
The X-ray images were obtained natively in digital format (in DICOM, with a resolution of 283.46 pixels/mm) and printed with a format of 350 mm ×430 mm. The selected X-rays showed, according to the angular classification proposed by the International Society on Scoliosis Orthopaedic and Rehabilitation Treatment (23), low scoliosis (with curves between 11º and 20º, 4 cases), moderate scoliosis (between 21º and 35º, 7 cases), moderate to severe scoliosis (between 36º and 40º, 4 cases), severe scoliosis (between 41º and 50º, 2 cases), severe to very severe scoliosis (between 51º and 55º, 1 case), and very severe scoliosis (56º or more, 3 cases). In each X-ray, each observer identified the most rotated major curve vertebra and the most rotated in the minor or main compensatory curve, if any, resulting in a total of 33 vertebrae in all 21 radiographs (T3, 2; T4, 1; T6, 1; T7, 8; T8, 2; T9, 4; T10, 1; T11, 1; T12, 1; L1, 4; L2, 7 and L3, 1).
We assessed absolute reliability according to the Hopkins criteria (minimum n of 30 cases, at least six blinded observers as assessors and at least three tests per observer, separated by at least 2 weeks) (24,25). The study was carried out with twelve independent evaluators with different experience levels in using Raimondi’s method. Three observers considered as “Experts” were an Orthopaedic Specialist and two Physical Therapy & Rehabilitation Specialists accustomed to measuring spinal misalignments in their daily practice. Two “Mid-level experienced observers” (a Physical Therapy & Rehabilitation Specialist and a Sports Medicine Specialist) occasionally measured spinal misalignment radiographs. Furthermore, seven “Novice” observers were professionals from different Health Sciences branches (not Orthopaedists) and who, although they knew the theory of how to make measurements on X-rays of the spine, had never measured with Raimondi’s method.
Each observer measured the 21 X-rays with the software on three occasions separated one month. The observers re-measured the same radiographic studies three months later, but in a conventional manual way on X-rays films (analogical radiographs). The manual measurement was also repeated on three occasions, one month apart. To avoid bias, the sequence in which the radiographs were presented was randomly assigned in each of the measurement rounds by the study coordinator, who kept the randomisation key confidential.
A 5-hour briefing was held before software measurements with comprehensive information on the study and training in the software using. Similarly, before the manual measurements, a briefing session was held with the correct AVR measurement’s relevant indications with Raimondi’s tables. For the manual measurements, the observers received the 21 X-ray film, Raimondi’s table, permanent black fine-point ink marker and transparent acetate sheets to mark the reference points and measure without altering the X-ray images.
Statistics
Statistical analysis was performed using the Statistical Package for the Social Sciences (SPSS), version 25 for Windows (SPSS, Inc., Chicago, IL, USA). Results were rounded to one decimal place in the measurements obtained with the software and to whole numbers in the measurements obtained manually due to each measuring instrument’s scale. We used the average of the 18 measurements (three measurements of six randomly selected observers) from the observers considered in Table S1 for each vertebra and measurement method to evaluate the software’s validity. The average of the measurements at each retest of two randomly selected observers of each group was employed for the agreement estimation within each experience group and between the different experience groups.
For the intra- and inter-group concordance analysis of the software and manually measurements, the validity or degree of agreement between the mean value obtained from a large set of results and the true value or the value accepted as a reference (MBE, mean bias error), the reliability (SD), the standard error of the sample (SEM), the minimum detectable change (MCD95) and the intra-class correlation coefficient of absolute concordance were calculated using a two-factor random-effects model [ICC (2,1) (26)].
We have assessed intra- and inter-observer reliability according to the criteria by Landis and Koch (<0 indicate no agreement, 0.00 to 0.20 indicate slight agreement, 0.21 to 0.40 indicate fair agreement, 0.41 to 0.60 indicate moderate agreement, 0.61 to 0.80 indicate substantial agreement, and 0.81 to 1.0 indicate almost perfect or perfect agreement) (27).
The Bland-Altmann graph was also obtained for the concordance between manual and software measurement methods analysis. The measurement error distributions’ norm was improved by identifying values lower than Q1 − (1.5 RIC) and higher than Q3 + (1.5 RIC). These values were considered outliers and were eliminated from each distribution.
We have removed outliers based on statistical methods because of their effect on the loss of normality in the data distributions. That these distributions are sufficiently normal is necessary to be able to apply statistical inference methods. Table S1 shows the outliers removed from each distribution.
The Shapiro-Wilk test was used to check that P values of the data were above the significance level of 0.05, with the null hypothesis that the data fit a normal distribution being accepted. All distributions met the normality criterion of this test.
Results
Tables S2,S3 of the supplementary material show the measurements made by the evaluators. We have obtained an almost perfect concordance, according to Landis and Koch (27), among the two measurement methods [ICC(2,1) = 0.957 with 95% confident interval (CI): 0.916–0.979 and MCD95 <1 degree]. The measurements with both methods (software and manual method) have shown good validity and reliability values, and the intraclass correlation coefficients were almost perfect (higher than 0.8). Measurements performed with the software have shown 1.72 times more valid and 1.9 times more reliable than those performed with the manual method (0.53 degrees ± 1.9 degrees compared to 0.91 degrees ± 3.61 degrees). These results are also reflected in the average ICC (2,1) of the measurements made with the software (ICC =0.913 with 95% CI: 0.87–0.949) and manually (ICC =0.814 with 95% CI: 0.734–0.886).
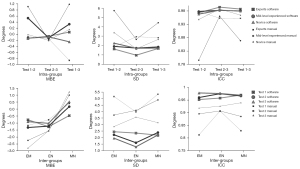
When measuring with the software, the differences between intra-group concordances are minimal in the three experience groups (the largest difference is between the 2–3 tests of the expert group and the 1–2 tests of the novice group, the ICC difference being 0.026), and when measuring manually, they are small (the largest difference is between the 1–2 tests of the semi-experts and the 2–3 tests of the novices, the ICC difference being 0.19). Table 1 shows the intra- and inter-groups validity and reliability analysis outcomes with the software and the manual measures.
Table 1
| Intragroup analysis | MBE | SD | gl | 1.96 SD | SEM | MDC95 | ICC (2,1) | 95% CI |
|---|---|---|---|---|---|---|---|---|
| Intragroup analysis with software | ||||||||
| E2E1 | −0.14 | 1.63 | 31 | 3.19 | 0.29 | 0.81 | 0.973 | 0.987–0.994 |
| E3E2 | −0.07 | 0.98 | 32 | 1.91 | 0.17 | 0.48 | 0.994 | 0.988–0.997 |
| E3E1 | 0.07 | 1.69 | 32 | 3.31 | 0.30 | 0.83 | 0.987 | 0.973–0.993 |
| M2M1 | 0.53 | 1.92 | 33 | 3.77 | 0.33 | 0.93 | 0.978 | 0.956–0.989 |
| M3M2 | −0.12 | 1.74 | 32 | 3.41 | 0.31 | 0.85 | 0.982 | 0.964–0.991 |
| M3M1 | 0.33 | 1.85 | 32 | 3.63 | 0.33 | 0.91 | 0.98 | 0.961–0.99 |
| N2N1 | −0.13 | 2.25 | 33 | 4.41 | 0.39 | 1.09 | 0.968 | 0.936–0.984 |
| N3N2 | −0.09 | 1.71 | 32 | 3.34 | 0.30 | 0.84 | 0.983 | 0.965–0.992 |
| N3N1 | −0.25 | 1.73 | 30 | 3.39 | 0.32 | 0.88 | 0.979 | 0.957–0.99 |
| Intragroup analysis with the manual method | ||||||||
| E2E1 | −0.08 | 1.88 | 31 | 3.68 | 0.34 | 0.93 | 0.978 | 0.954–0.989 |
| E3E2 | −0.15 | 2.94 | 33 | 5.77 | 0.51 | 1.42 | 0.953 | 0.907–0.976 |
| E3E1 | −0.86 | 2.83 | 32 | 5.56 | 0.50 | 1.39 | 0.952 | 0.903–0.976 |
| M2M1 | 0.91 | 5.74 | 33 | 11.25 | 1.00 | 2.77 | 0.796 | 0.628–0.893 |
| M3M2 | −0.20 | 2.67 | 32 | 5.23 | 0.47 | 1.31 | 0.96 | 0.92–0.98 |
| M3M1 | 0.98 | 4.44 | 33 | 8.71 | 0.77 | 2.14 | 0.869 | 0.753–0.933 |
| N2N1 | −0.02 | 3.39 | 32 | 6.65 | 0.60 | 1.66 | 0.948 | 0.897–0.974 |
| N3N2 | −0.20 | 1.65 | 27 | 3.24 | 0.32 | 0.88 | 0.987 | 0.972–0.994 |
| N3N1 | 0.15 | 2.66 | 33 | 5.22 | 0.46 | 1.28 | 0.964 | 0.928–0.982 |
| Intergroup analysis with software | ||||||||
| E1M1 | −0.77 | 2.44 | 31 | 4.79 | 0.44 | 1.22 | 0.964 | 0.926–0.983 |
| M1N1 | −0.47 | 2.18 | 32 | 4.27 | 0.39 | 1.07 | 0.97 | 0.939–0.985 |
| E1N1 | −1.27 | 2.35 | 31 | 4.60 | 0.42 | 1.17 | 0.958 | 0.889–0.982 |
| E2M2 | −1.33 | 2.21 | 31 | 4.33 | 0.40 | 1.10 | 0.96 | 0.881–0.982 |
| M2N2 | 0.17 | 2.39 | 32 | 4.69 | 0.42 | 1.17 | 0.966 | 0.932–0.983 |
| E2N2 | −1.23 | 1.60 | 30 | 3.14 | 0.29 | 0.81 | 0.975 | 0.888–0.991 |
| E3M3 | −0.90 | 1.96 | 31 | 3.84 | 0.35 | 0.97 | 0.978 | 0.947–0.99 |
| M3N3 | 0.53 | 2.21 | 30 | 4.32 | 0.40 | 1.12 | 0.969 | 0.936–0.985 |
| E3N3 | −1.03 | 1.29 | 27 | 2.53 | 0.25 | 0.69 | 0.976 | 0.884–0.992 |
| Intergroup analysis with the manual method | ||||||||
| E1M1 | −1.18 | 5.16 | 33 | 10.12 | 0.90 | 2.49 | 0.812 | 0.655–0.902 |
| M1N1 | 0.41 | 5.33 | 33 | 10.45 | 0.93 | 2.57 | 0.829 | 0.681–0.912 |
| E1N1 | −0.77 | 3.97 | 33 | 7.78 | 0.69 | 1.91 | 0.906 | 0.82–0.952 |
| E2M2 | −2.25 | 3.73 | 32 | 7.31 | 0.66 | 1.83 | 0.895 | 0.721–0.955 |
| M2N2 | 1.00 | 4.89 | 33 | 9.59 | 0.85 | 2.36 | 0.885 | 0.781–0.941 |
| E2N2 | −1.58 | 4.09 | 33 | 8.01 | 0.71 | 1.97 | 0.906 | 0.809–0.954 |
| E3M3 | −2.80 | 2.84 | 33 | 5.58 | 0.50 | 1.37 | 0.918 | 0.527–0.973 |
| M3N3 | 1.24 | 3.14 | 33 | 6.16 | 0.55 | 1.52 | 0.939 | 0.872–0.971 |
| E3N3 | −1.56 | 3.56 | 33 | 6.98 | 0.62 | 1.72 | 0.926 | 0.839–0.965 |
AXBY is the distribution of errors between the measurements of experience groups A and B in test × and Y. E: measurement obtained by the “Expert observer”; M: measurement from the “Mid-level experienced observer”. N: measurement from the “Novel observer”. MBE, mean bias error; SD, standard deviation; gl, the number of sample measurements (gl = 33 − outliers); SEM, standard error of the sample; MCD95, minimum detectable change (in degrees); ICC (2,1), intra-class correlation coefficient of absolute concordance; 95% CI, 95% confidence interval.
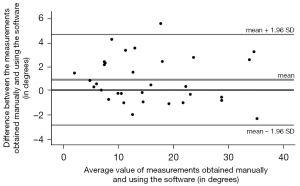
Figure 2 shows MBE, reliability, and ICC values of the error distributions of the measurements obtained with the software and manually in the three measuring sessions and the three experience groups. The evaluation of the agreement between both measurement methods has shown MBE of 0.85 degrees, SD of 1.92 degrees, SEM of 0.34 degrees, MCD95 of 0.94 degrees and an ICC (2,1) of 0.975 with 95% CI: 0.943–0.989. Figure 3 shows the absence of bias in both method agreement through the Bland-Altman graphical representation.
Discussion
The most important finding of the present study was that there is almost perfect agreement between the two methods. We have obtained an almost perfect concordance, according to Landis and Koch (24), among the two measurement methods [ICC (2,1) =0.975 with 95% CI: 0.943–0.989 and MCD95 <1 degree].
The software measurements are superior in validity and reliability to manual measurements, which indicates that the software and the built-in equation are suitable for determining AVR. To our knowledge, no software validation study or conventional measurements has been published for assessing AVR with X-ray images of real patients using Raimondi’s method, only with anatomical cadaver models (6,28). Similarly, we have not found publications on the validity and reliability of Raimondi’s method, according to the criteria of absolute reliability (neither for measurements with conventional methods nor using CAD systems), which requires a minimum of 30 cases, measured by at least six blinded observers and with at least three tests per observer, separated from each other by at least two weeks (24,25). Another novelty of the present study has been to use groups of observers with different grades of experience (6,12,28,29). From the standpoint of statistical inference, it has been necessary to treat the values obtained by the observers to reduce the error that exists in any statistical estimation. Thus, we examined the outliers and P values of each normal distribution. To avoid bias in the measurements, we established the procedure to follow employing training sessions for the observers, distinguishing their level of experience, using a sample of subjects sufficiently representative of the population, and considering the temporal stability of the measurements by repeating them at different times.
Our AVR measurement method discussed is based on Raimondi’s method, but it is not Raimondi’s method. Both have in common that they use the same anatomical references, but their results are not the same. Our software measures AVR using a linear mathematical equation that theoretically describes the empirical data from Raimondi’s table. The scale is linear (rather than AVR values in discrete 2º intervals), so the measurement accuracy can be increased. In addition, Raimondi acknowledges that the measurements obtained with his method involve systematic errors (30,31), which are not present in our equation. Part of the value of our study is that no previous studies are based on Raimondi’s method (6,9,29) or reported on the equation or algorithm used (28).
We may consider several aspects as the strengths of the study. First, when studying the inter-group concordances, it is observed that there is an improvement in the concordance attributable to practice when measuring manually, being more evident among mid-level experienced evaluators and novices [ICC equal to 0.829 (95% CI: 0.681–0.912) in the first evaluation, 0.885 (95% CI: 0.781–0.941) in the second evaluation and 0.939 (95% CI: 0.872–0.971) in the third evaluation]. In contrast, this improvement is not apparent in the measures obtained with software. Second, the reduced individual intervention required when operating the software helps less experienced observers measure AVR with accuracy and precision closer to more experienced professionals. Third, the mathematical equation developed for the software allows quantifying AVR using Raimondi’s method on digital X-rays with or without a scale (e.g., those from DICOM files without such information). Fourth, Raimondi’s tables measure the AVR in discrete two-degree steps, introducing a small systematic error in manual measurements, which does not occur with the mathematical equation used in the software. Fifthly, the set formed by the equation and the zoom installed in our software allows the most exact determination of the distances and explain part of our results.
There are some limitations to our study. Firstly, Raimondi’s method is not the most used method for assessing AVR. Secondly, we used the mean of the 18 measurements made by the observers considered in the study as the reference value. Thirdly, we have not considered each evaluator’s computer equipment (e.g., viewable image size, display resolution, luminance, contrast ratio or the characteristics of the mouse or touchpad) that may have influenced the accuracy of the measurements. Fourthly, there are outliers eliminated in some distribution used in the study due to imperfect measurement and errors in recording the value of the measurements in the database provided by each observer or incorrect selection of the most rotated vertebra. Finally, our measurement method allows us to quantify AVR but does not provide information about other variables such conjunct rotation, rotational instability, or kinematic asymmetries, in an identical manner as the Perdriolle or Nash-MOE methods. These limitations notwithstanding, the authors believe that the study’s outcomes are valuable because no published studies, to our knowledge, of the “absolute reliability” of software or conventional method, developed to assess AVR on digital X-rays according to Raimondi’s method.
Conclusions
According to our results, the software (registered under the name TraumaMeter v.873) with a built-in equation increases the validity and absolute reliability of AVR on digital X-rays according to Raimondi’s method, compared to the conventional manual measurement.
The improvement in the measurement quality is considerable for non-expert observers, so the software can be helpful. Besides, we add the value of the absolute reliability and validity of Raimondi’s method’s manual measurements, which did not exist until now.
Acknowledgments
We thank Rafael Leal Adán, Director of Centro Radiológico del Sureste for providing the copies of the X-rays used for this research.
Funding: None.
Footnote
Reporting Checklist: The authors have completed the MDAR checklist. Available at https://dx.doi.org/10.21037/qims-21-575
Conflicts of Interest: All authors have completed the ICMJE uniform disclosure form (available at https://dx.doi.org/10.21037/qims-21-575). The authors have no conflicts of interest to declare.
Ethical Statement: The authors are accountable for all aspects of the work in ensuring that questions related to the accuracy or integrity of any part of the work are appropriately investigated and resolved. This study followed the World Medical Association Declaration of Helsinki's ethical standards (as revised in 2013). The study was granted exemption from requiring ethics approval and informed consent since the complete and irreversible anonymisation of the images did not involve patient data processing.
Open Access Statement: This is an Open Access article distributed in accordance with the Creative Commons Attribution-NonCommercial-NoDerivs 4.0 International License (CC BY-NC-ND 4.0), which permits the non-commercial replication and distribution of the article with the strict proviso that no changes or edits are made and the original work is properly cited (including links to both the formal publication through the relevant DOI and the license). See: https://creativecommons.org/licenses/by-nc-nd/4.0/.
References
- Ma Q, Lin H, Wang L, Zhao L, Chen M, Wang S, Rao Z, Luo Y. Correlation between spinal coronal balance and static baropodometry in children with adolescent idiopathic scoliosis. Gait Posture 2020;75:93-7. [Crossref] [PubMed]
- Hefti F. Pathogenesis and biomechanics of adolescent idiopathic scoliosis (AIS). J Child Orthop 2013;7:17-24. [Crossref] [PubMed]
- Kuklo TR, Potter BK, Lenke LG. Vertebral rotation and thoracic torsion in adolescent idiopathic scoliosis: what is the best radiographic correlate? J Spinal Disord Tech 2005;18:139-47. [Crossref] [PubMed]
- Mangone M, Raimondi P, Paoloni M, Pellanera S, Di Michele A, Di Renzo S, Vanadia M, Dimaggio M, Murgia M, Santilli V. Vertebral rotation in adolescent idiopathic scoliosis calculated by radiograph and back surface analysis-based methods: correlation between the Raimondi method and rasterstereography. Eur Spine J 2013;22:367-71. [Crossref] [PubMed]
- Mohanty SP, Pai Kanhangad M, Gullia A. Curve severity and apical vertebral rotation and their association with curve flexibility in adolescent idiopathic scoliosis. Musculoskelet Surg 2021;105:303-8. [Crossref] [PubMed]
- Eijgenraam SM, Boselie TF, Sieben JM, Bastiaenen CH, Willems PC, Arts JJ, Lataster A. Development and assessment of a digital X-ray software tool to determine vertebral rotation in adolescent idiopathic scoliosis. Spine J 2017;17:260-5. [Crossref] [PubMed]
- Nault ML, Mac-Thiong JM, Roy-Beaudry M, Turgeon I, Deguise J, Labelle H, Parent S. Three-dimensional spinal morphology can differentiate between progressive and nonprogressive patients with adolescent idiopathic scoliosis at the initial presentation: a prospective study. Spine (Phila Pa 1976) 2014;39:E601-6. [Crossref] [PubMed]
- Carlson BB, Burton DC, Asher MA. Comparison of trunk and spine deformity in adolescent idiopathic scoliosis. Scoliosis 2013;8:2. [Crossref] [PubMed]
- Vrtovec T, Vengust R, Likar B, Pernus F. Analysis of four manual and a computerized method for measuring axial vertebral rotation in computed tomography images. Spine (Phila Pa 1976) 2010;35:E535-41. [Crossref] [PubMed]
- Tamura Y, Sugano N, Sasama T, Sato Y, Tamura S, Yonenobu K, Yoshikawa H, Ochi T. Surface-based registration accuracy of CT-based image-guided spine surgery. Eur Spine J 2005;14:291-7. [Crossref] [PubMed]
- Qiao J, Zhu F, Xu L, Zhu Z, Qian B, Liu Z, Qiu Y. Comparison of the aorta impingement risks between thoracolumbar/lumbar curves with different convexities in adolescent idiopathic scoliosis: a computed tomography study. Eur Spine J 2012;21:2043-9. [Crossref] [PubMed]
- Vrtovec T, Pernus F, Likar B. A review of methods for quantitative evaluation of axial vertebral rotation. Eur Spine J 2009;18:1079-90. [Crossref] [PubMed]
- Petit Y, Aubin CE, Labelle H. Spinal shape changes resulting from scoliotic spine surgical instrumentation expressed as intervertebral rotations and centers of rotation. J Biomech 2004;37:173-80. [Crossref] [PubMed]
- Weiss HR. Measurement of vertebral rotation: Perdriolle versus Raimondi. Eur Spine J 1995;4:34-8. [Crossref] [PubMed]
- Lam GC, Hill DL, Le LH, Raso JV, Lou EH. Vertebral rotation measurement: a summary and comparison of common radiographic and CT methods. Scoliosis 2008;3:16. [Crossref] [PubMed]
- Kadoury S, Cheriet F, Beauséjour M, Stokes IA, Parent S, Labelle H. A three-dimensional retrospective analysis of the evolution of spinal instrumentation for the correction of adolescent idiopathic scoliosis. Eur Spine J 2009;18:23-37. [Crossref] [PubMed]
- Defino HLA, Araújo PHM, de . Estudo comparativo da medida da rotação vertebral pelos métodos de Nash & Moe e método de Raimondi. Acta Ortopédica Bras 2004;12:167-73. [Crossref]
- Hattori T, Sakaura H, Iwasaki M, Nagamoto Y, Yoshikawa H, Sugamoto K. In vivo three-dimensional segmental analysis of adolescent idiopathic scoliosis. Eur Spine J 2011;20:1745-50. [Crossref] [PubMed]
- Fletcher ND, Bruce RW. Early onset scoliosis: current concepts and controversies. Curr Rev Musculoskelet Med 2012;5:102-10. [Crossref] [PubMed]
- Kuklo TR, Potter BK, Schroeder TM, O'Brien MF. Comparison of manual and digital measurements in adolescent idiopathic scoliosis. Spine (Phila Pa 1976) 2006;31:1240-6. [Crossref] [PubMed]
- Yazici M, Acaroglu ER, Alanay A, Deviren V, Cila A, Surat A. Measurement of vertebral rotation in standing versus supine position in adolescent idiopathic scoliosis. J Pediatr Orthop 2001;21:252-6. [Crossref] [PubMed]
- Colaboradores. Adolescent idiopathic scoliosis. Arch Argent Pediatr 2016;114:585-94. [PubMed]
- Negrini S, Donzelli S, Aulisa AG, Czaprowski D, Schreiber S, de Mauroy JC, et al. 2016 SOSORT guidelines: orthopaedic and rehabilitation treatment of idiopathic scoliosis during growth. Scoliosis Spinal Disord 2018;13:3. [Crossref] [PubMed]
- Atkinson G, Nevill AM. Selected issues in the design and analysis of sport performance research. J Sports Sci 2001;19:811-27. [Crossref] [PubMed]
- Hopkins WG. Measures of reliability in sports medicine and science. Sports Med 2000;30:1-15. [Crossref] [PubMed]
- Shrout PE, Fleiss JL. Intraclass correlations: uses in assessing rater reliability. Psychol Bull 1979;86:420-8. [Crossref] [PubMed]
- Landis JR, Koch GG. The measurement of observer agreement for categorical data. Biometrics 1977;33:159-74. [Crossref] [PubMed]
- Pinheiro AP, Tanure MC, Oliveira AS. Validity and reliability of a computer method to estimate vertebral axial rotation from digital radiographs. Eur Spine J 2010;19:415-20. [Crossref] [PubMed]
- Zhang J, Lou E, Hill DL, Raso JV, Wang Y, Le LH, Shi X. Computer-aided assessment of scoliosis on posteroanterior radiographs. Med Biol Eng Comput 2010;48:185-95. [Crossref] [PubMed]
- Prosperini V, Raimondi P, Martinelli E, Bizzarri F. Misurazione della rotazione vertebrale patologica su radiografie di piccolo e grande formato con il Metodo Raimondi. Chinesiologia 2010;1:23-7.
- Raimondi P, Prosperini V. La misurazione della rotazione vertebrale nelle scoliosi. Esperienze valutative e commento. Chinesiologia 2007;3:22-6.


