Volumetric analysis of pulmonary nodules: reducing the discrepancy between the diameter-based volume calculation and voxel-counting method
Introduction
Assessing pulmonary nodule size is crucial to deciding an appropriate management plan. Although an electronic caliper has been used to measure nodule diameter and growth (1,2), nodule volume assessment (volumetry) has been recently recognized as a more reliable method. Accordingly, several lung cancer screening trials have incorporated a volumetric analysis within their protocols (3-6). To facilitate a simple and accurate assessment of nodule volume, a wide range of volumetric software packages are commercially available. However, measuring an object’s length and volume in a digital radiological image is not simple.
In digital two-dimensional (2D) images, a pixel is the smallest addressable element. Although it occupies a certain area in the image, it is treated as a dot, which theoretically does not have an area. The Euclidean distance between two distant pixels in an image is calculated using the coordinates of the center of two pixels (Figure 1). To obtain the physical distance between two points, the Euclidean distance is multiplied by the pixel spacing (the physical distance between the centers of neighboring pixels). In a virtual three-dimensional (3D) space made of 2D radiological images, a voxel (a virtual volumetric unit which is a cuboid having a pixel as the floor) is the smallest addressable element. The physical volume of a voxel is a square with one pixel spacing as the floor and a height of the slice interval (interslice distance). The Euclidean distance between two voxels is calculated as in the 2D image, using the coordinates of the center of two voxels.

Assuming that pulmonary nodules are ellipsoid or spherical, the volume of a nodule can be measured using two methods: the voxel-counting method, which is the current standard in the segmentation-based volumetry (7-9), and a diameter-based volume calculation. Ideally, for a consistent management plan, the derived volume should be the same regardless of method; however, a slight difference is inevitable, as the curved surface of an ellipsoid object in digital 3D space is not perfectly smooth. Furthermore, the most important, but neglected, contributing factor is that at least one pixel spacing is lost in the assessment of the nodule diameter. As portions of voxels are excluded from the diameter measurement, the diameter-based calculation yields a smaller volume than that with the volume-counting method. For small nodules, this difference cannot be ignored. To ensure the consistent and accurate assessment of small nodules, the values based on the diameter-based volume calculation and the voxel-counting method cannot be treated as equal even in ellipsoid or spherical nodules. The result of voxel-counting method should be properly modified when it is compared to the result of diameter-based volume calculation.
Therefore, we evaluated the extent of the discrepancy between volumes derived from these methods using pulmonary phantom nodules, and the ability of a simple modification (adding one pixel spacing to the diameter in each axis to the diameter-based calculation) to reduce this discrepancy. Additionally, we determined a conversion equation to equate volumes derived from different methods. We present the following article in accordance with the Materials Design Analysis Reporting (MDAR) reporting checklist (available at https://dx.doi.org/10.21037/qims-21-485).
Methods
This study was exempt from Institutional Review Board approval of Seoul National University Bundang Hospital because only lung phantoms were used and no animal or human data were acquired.
Anthropomorphic phantom and synthetic nodules
Two commercially available anthropomorphic lung phantoms (LSCT001 and Lungman, Kyoto Kagaku, Japan) were used (Figure 2). LSCT001 is a lung cancer screening phantom; for which, the chest wall and mediastinum consist of a substance radiologically equivalent to water, and the vertebrae and ribs consist of a substance radiologically equivalent to bone. The targeted computed tomography (CT) value of the lung parenchyma is −900 HU. Five types of nodules (diameter: 4, 6, 8, 10, and 12 mm) with 270 HU contrast to the background were embedded in the right lung at three levels: apices, bifurcation, and base of the lungs. Another five types of nodules (diameter: 2, 4, 6, 8, and 10 mm) with 100 HU contrast to the background were embedded in the left lung at the same levels. We used a 10-mm nodule with a 270 HU contrast to the background as the target nodule. The Lungman is a multipurpose chest phantom that consists of simulated pulmonary vessels, heart, trachea, chest wall, diaphragm, and abdomen block. Simulated pulmonary nodules of various diameters and attenuations (diameter: 5, 8, 10, and 12 mm; attenuation: +100, −630, and −800 HU for each diameter) were manually placed within foam inserts to avoid any vessel attachment. We used nodules of 100 HU as the target.
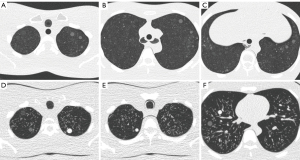
Image acquisition
The LSCT001 phantom was scanned using two 64-row multi-detector CT scanners: Brilliance 64 and IQon Spectral CT (Philips Healthcare, Eindhoven, The Netherlands). Images were acquired using two different radiation dose levels, with a collimated detector width of 64×0.625 mm, a tube voltage of 120 kVp, and a maximal tube current-time product of 30 or 15 mAs. In consideration of the interscan variability, each scan was repeated 30 times. The scans were reconstructed with a slice thickness of 1 mm and an increment of 1 mm, as recommended in lung cancer screening guidelines (10,11). Images from Brilliance 64 were reconstructed by two methods: filtered back projection (FBP) and iterative reconstruction (IR) (iDose4 level 5, Philips Healthcare, Eindhoven, The Netherlands). Images acquired by IQon Spectral CT were reconstructed with a dedicated spectral IR algorithm (Spectral Level 5, Philips Healthcare, Eindhoven, The Netherlands).
The Lungman phantom was scanned using a 256-channel multi-detector CT scanner (Philips Healthcare, Eindhoven, The Netherlands). Images from the iCT 256 were acquired with a collimated detector width of 128×0.625 mm, a tube voltage of 120 kVp, and a maximal tube current-time product of 30 mAs. The CT scan was repeated 19 times. The scans were reconstructed by FBP and iterative model reconstruction (IMR) (IMR level 2, Philips Healthcare, Eindhoven, The Netherlands) using a slice thickness of 1 mm with an increment of 1 mm.
Nodule segmentation and volume measurement
For nodule segmentation, a commercially available software program, LuCAS (Monitor Corporation, Seoul, Korea), was used. LuCAS is a deep learning-based computer-aided diagnosis (DL-CAD) solution that provides detection and segmentation applications for pulmonary nodules. After loading the DICOM images into the software, the software detected nodules and initiated the segmentation (Figure 3). Nodule volume and diameter were quantified in a fully automatic manner.
The volume of each nodule was calculated using three methods:
Voxel-counting method
Nodule volume (Vvc) was calculated using the total number of voxels within the segmented region and the pixel spacings:
Diameter-based volume calculation
Nodule volume (Vd) was calculated using the greatest transverse diameter in the x-y plane (a), the perpendicular diameter in the x-y plane (b), and the length in the z-axis (c):
Modified diameter-based volume calculation
Nodule volume (Vd+1) was calculated using the greatest transverse diameter in the x-y plane + the pixel spacing on the x-y plane (a’), the perpendicular diameter in the x-y plane + the pixel spacing on the x-y plane (b’), and the length in the z-axis + the pixel spacing along the z-axis (c’):
Statistical analysis
For each nodule, the Vd and Vd+1 were compared to Vvc by computing the absolute percentage error (APE) for all CT scans, as follows:
The APE of Vd (APEd) and Vd+1 (APEd+1) were calculated accordingly. As APEd, APEd+1, and APEd − APEd+1 were revealed to have non-normal distribution by the Shapiro-Wilks test, medians and non-parametric tests were used for further analysis. Comparisons between APEd and APEd+1 according to CT parameter setting were performed using the Wilcoxon signed-rank test. The Jonckheere-Terpstra test was used to evaluate trends across the four different nodule sizes. Data are presented as medians with interquartile range (IQR). P values <0.05 were considered to indicate statistical significance. Statistical calculations were performed using R 4.0.2 (R Foundation for Statistical Computing, Vienna, Austria).
Results
Nodule segmentation
Using the LSCT001 phantom, 120 scans were conducted and 180 images were generated. A total of 540 10-mm nodules were used for volume measurement. Using the Lungman phantom, 38 images were generated, and a total of 152 nodules of four different sizes (5, 8, 10, and 12 mm) were used for volume measurement. The DL-CAD successfully detected and segmented all nodules in a fully automatic manner. The program automatically calculated the nodule volume using the voxel-counting method. the greatest transverse diameter and the perpendicular diameter in the x-y plane and the length in the z-axis were also automatically measured.
Absolute percentage error reduction by the new method
In the LSCT001 series of scans, in which 10-mm nodules were scanned and measured under six different settings, the APE was significantly less with the modified diameter-based volume calculation than with the diameter-based volume calculation (Wilcoxon signed-rank test, P<0.05) under each scan setting (Figure 4 and Table 1). In the Lungman series of scans, in which 5-, 8-, 10-, and 12-mm nodules were scanned with different reconstruction algorithms, the APE was significantly less with the modified diameter-based calculation than with the diameter-based calculation for all nodule sizes (Wilcoxon signed-rank test, P<0.001) and each reconstruction algorithm (Figure 5 and Table 2). The APE median increased as the size of the nodule decreased. This trend was statistically significant (Jonckheere-Terpstra test, P<0.001), regardless of the reconstruction algorithm (FBP and IMR) and volume measurement method (diameter-based and modified diameter-based volume calculations).
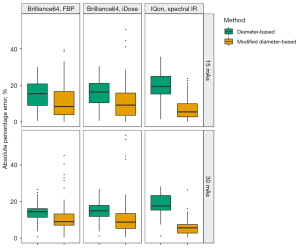
Table 1
| Machine | mAs | Reconstruction algorithm | Volume measurement method | Nodule volume (mm3)† | APE (%)† | P value* |
|---|---|---|---|---|---|---|
| Brilliance64 | 15 | FBP | Voxel-counting | 556.7 (547.6–568.9) | – | – |
| Diameter-based | 473.3 (441.5–513.2) | 15.4 (9.0–20.8) | – | |||
| Modified diameter-based | 604.9 (569.5–652.4) | 8.4 (3.9–16.6) | 0.012 | |||
| 15 | iDose | Voxel-counting | 554.0 (544.9–565.8) | – | – | |
| Diameter-based | 470.1 (440.4–503.0) | 16.3 (10.5–21.1) | – | |||
| Modified diameter-based | 602.5 (566.6–640.3) | 9.2 (3.6–15.8) | 0.004 | |||
| 30 | FBP | Voxel-counting | 561.3 (552.8–569.2) | – | – | |
| Diameter-based | 484.2 (467.5–504.2) | 14.5 (11.4–16.2) | – | |||
| Modified diameter-based | 616.9 (596.9–640.6) | 9.0 (7.1–13.3) | 0.002 | |||
| 30 | iDose | Voxel-counting | 560.8 (553.4–570.6) | – | – | |
| Diameter-based | 475.0 (468.1–496.6) | 14.9 (11.8–17.9) | – | |||
| Modified diameter-based | 605.8 (597.6–631.6) | 8.8 (5.3–13.4) | <0.001 | |||
| IQon | 15 | Spectral IR | Voxel-counting | 548.8 (534.1–561.7) | – | – |
| Diameter-based | 438.6 (408.1–469.5) | 19.3 (15.2–24.9) | – | |||
| Modified diameter-based | 559.4 (524.9–595.6) | 5.5 (2.8–9.9) | <0.001 | |||
| 30 | Spectral IR | Voxel-counting | 554.0 (545.5–565.7) | – | – | |
| Diameter-based | 465.5 (414.5–469.5) | 17.5 (15.3–23.3) | – | |||
| Modified diameter-based | 590.9 (532.2–595.6) | 5.6 (2.8–7.5) | <0.001 |
*, P value of the Wilcoxon signed-rank test for the comparison between APEs of two methods (diameter-based vs. modified diameter-based volume calculation). †, data are presented as median (first quartile–third quartile). APE, absolute percentage error; CT, computed tomography; FBP, filtered back-projection; IR, iterative reconstruction.
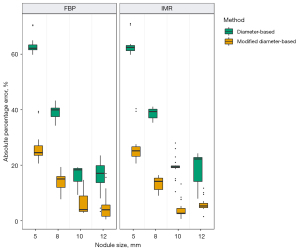
Table 2
| Nodule size (mm) | Reconstruction algorithm | Volume measurement method | Nodule volume (mm3)† | APE (%)† | P value* |
|---|---|---|---|---|---|
| 5 | FBP | Voxel-counting | 44.0 (43.3–44.4) | – | – |
| Diameter-based | 16.5 (16.5–16.8) | 62.1 (61.6–63.4) | – | ||
| Modified diameter-based | 32.9 (32.9–33.3) | 24.5 (23.6–27.0) | <0.001 | ||
| IMR | Voxel-counting | 44.7 (44.4–45.6) | – | – | |
| Diameter-based | 16.5 (16.5–17.7) | 62.5 (61.3–63.1) | – | ||
| Modified diameter-based | 32.9 (32.9–34.9) | 25.2 (23.2–26.6) | <0.001 | ||
| 8 | FBP | Voxel-counting | 219.6 (217.2–221.2) | – | – |
| Diameter-based | 131.5 (131.0–136.6) | 39.9 (37.5–40.6) | – | ||
| Modified diameter-based | 185.9 (185.3–192.6) | 15.1 (12.0–16.0) | <0.001 | ||
| IMR | Voxel-counting | 216.7 (213.7–217.8) | – | – | |
| Diameter-based | 131.5 (129.8–135.7) | 39.3 (37.1–40.2) | – | ||
| Modified diameter-based | 185.9 (183.7–191.4) | 14.2 (11.2–15.4) | <0.001 | ||
| 10 | FBP | Voxel-counting | 464.8 (463.4–465.9) | – | – |
| Diameter-based | 377.9 (376.9–399.6) | 18.3 (14.2–18.8) | – | ||
| Modified diameter-based | 481.0 (479.9–507.1) | 4.0 (3.3–8.9) | <0.001 | ||
| IMR | Voxel-counting | 467.8 (467.2–470.0) | – | – | |
| Diameter-based | 376.9 (376.9–378.3) | 19.4 (19.1–19.8) | – | ||
| Modified diameter-based | 479.9 (479.9–481.6) | 2.7 (2.5–4.5) | <0.001 | ||
| 12 | FBP | Voxel-counting | 825.2 (822.3–827.2) | – | – |
| Diameter-based | 684.2 (663.0–713.9) | 17.1 (13.7–19.8) | – | ||
| Modified diameter-based | 834.5 (809.9–868.9) | 4.0 (1.6–5.7) | <0.001 | ||
| IMR | Voxel-counting | 812.7 (810.0–814.0) | – | – | |
| Diameter-based | 635.4 (627.2–694.1) | 22.2 (14.1–22.8) | – | ||
| Modified diameter-based | 777.9 (768.3–846.0) | 5.3 (4.7–6.3) | <0.001 |
*, P value of Wilcoxon signed-rank test for comparison between APE of two methods (diameter-based vs. modified diameter-based volume calculation). †, data are presented as the median (first quartile–third quartile). APE, absolute percentage error; CT, computed tomography; FBP, filtered back-projection; IMR, iterative model reconstruction.
Discussion
The present study demonstrated a substantial difference between volumes derived from diameter-based and voxel-counting methods in synthetic spherical nodules; however, this difference was significantly reduced when one pixel spacing was added to the diameter in each axis as a modification to the diameter-based volume calculation.
To our knowledge, studies directly comparing volumes derived from these two methods in the same cohort of nodules are lacking. Additionally, the impact of manual measurements must be considered when nodule segmentation and voxel-counting are semi- or fully automated but the diameter is manually measured (using an electronic caliper). In a recent study, in which a semi-automated voxel-counting volume measurement was compared to diameter-based volume calculation using a lung phantom, the volumes were significantly larger with the semi-automated voxel-counting method than with the diameter-based calculation (12). The present study similarly compared these two methods; however, the same fully automated segmentation algorithm was used in both methods, without any human interference. We found that, even when using the same segmentation result, the volumes were consistently larger with the voxel-counting method than with the diameter-based calculation under various settings.
The inter-scan variability for the volume is as much as ±25% (13,14); accordingly, 25% has been used in some screening studies as the minimal percentage volume change signifying true growth (3,4,15). In our study, the APE of the diameter-based volume relative to the voxel-counting volume was substantial, and increased as the nodule size decreased, with medians exceeding 25% for 5- and 8-mm nodules. Our phantom study results may be applied to clinical settings. Unless consistent volume measurement method is used, follow-up images of small nodules can be prone to false interpretation: nodule growth or shrinkage. To minimize those confusing interpretations and avoid inconsistent nodule management, an adequate conversion should be applied when comparing diameter-based and voxel-based volumes of a pulmonary nodule. Among several factors that can cause disparity between two volume assessments, we focused on the loss of at least one pixel spacing when measuring the physical distance between two voxels, and added one extra pixel spacing to the diameter in each axis during the volume calculation. As a result, this simple new method significantly reduced the APE to a median of around 25% for 5- and 8-mm nodules, which would provide more consistent nodule management.
Assessment of pulmonary nodules by volumetry has benefits. Volumetry does not require the assumption that nodules are perfectly spherical and grow in a symmetrical fashion. Nodule growth can be evaluated three-dimensionally. Furthermore, semi-automatic volumetry results in less inconsistency among observers. In a previous study, repeated volume measurements of over 4,000 nodules showed identical results in 86% of nodules, with a relative volume difference of over 15% in only 4% of nodules (16). In contrast, the overall variation in manual diameter measurements is 20% or more (17,18), which equates to a 73% variation in the calculated volume, as the volume is proportional to the diameter cubed. Nevertheless, the volumetric analysis of pulmonary nodules has yet to become routine clinical practice because it requires additional software, and the measurement is time-consuming; thus, manual measurement of the nodule’s diameter is still more common, and volumetry is often used as an optional and enhanced approach. Considering the significant volume difference between the two methods, the volume derived from voxel-counting should be converted to its equivalent in diameter-based volume calculations. Based on the present results, we propose the following formula for a basic conversion between methods for ellipsoid nodules, where a, b, and c are the greatest transverse diameter and the perpendicular diameter in the x-y plane and the length of z-axis, respectively, and , , and are the respective greatest transverse diameters plus one pixel spacing.
The present study has some limitations. First, we used only spherical nodules in which “missing one pixel spacing” alone could signify volume difference with two methods. Volumetry of non-spherical nodules can be influenced by surficial appearance of nodules and they do not seem adequate for investigation of “missing one pixel problem”. In the clinical practice, however, suspicious nodules can vary in shape. Although we proposed a modified volume measurement method and a conversion method for synthetic ellipsoid nodules, they can be not practical in routine practice. Future studies could investigate the clinical impact of different volume measurement methods and usefulness of conversion between volume methods in true lung nodules. In the process, the unnecessary loss of length during distance measurement should also be considered for non-ellipsoid nodules. Second, the true volumes of the synthetic nodules were not compared to Vd and Vvc, because our study primarily focused on demonstrating discrepancy between volumes from voxel-counting and diameter-based methods. The ultimate goal of nodule volumetry is, however, accurate measurement of true volume. We did not intend to investigate variability in segmentation results and measured volumes across different settings. To achieve true volume measurement, further investigation is needed regarding the performance of different segmentation algorithms and their improvement. Third, we used a single DL-CAD software solution. As the Vvc is consistently larger than Vd within certain segmented voxels, we believed that this result was caused by the choice of the volume measurement method, not by the segmentation algorithm. Although segmentation results may differ slightly among various volumetric software packages, we expect Vvc to be larger than Vd within the same segmentation result. However, we used a single DL-CAD software solution and it remains unknown whether different segmentation algorithms would reproduce similar relationships between Vvc and Vd.
Conclusions
Adding one pixel spacing to the diameter in each axis reduced the discrepancy between the diameter-based volume calculation and the voxel-counting method across different settings. Our results also suggested that the loss of length during the diameter measurement should be considered when comparing diameter-based volumes and volumes derived from voxel-counting.
Acknowledgments
Funding: None.
Footnote
Reporting Checklist: The authors have completed the Materials Design Analysis Reporting (MDAR) reporting checklist. Available at https://dx.doi.org/10.21037/qims-21-485
Conflicts of Interest: All authors have completed the ICMJE uniform disclosure form (available at https://dx.doi.org/10.21037/qims-21-485). JK and KJL report that they hold stocks in Monitor Corporation. CMN worked for Monitor Corporation and held stocks in Monitor Corporation during the study. CMN works for a different company and does not hold stocks any more at the present time. The other authors have no conflicts of interest to declare.
Ethical Statement: The authors are accountable for all aspects of the work in ensuring that questions related to the accuracy or integrity of any part of the work are appropriately investigated and resolved. This study was exempt from Institutional Review Board approval of Seoul National University Bundang Hospital because no animal or human data were acquired.
Open Access Statement: This is an Open Access article distributed in accordance with the Creative Commons Attribution-NonCommercial-NoDerivs 4.0 International License (CC BY-NC-ND 4.0), which permits the non-commercial replication and distribution of the article with the strict proviso that no changes or edits are made and the original work is properly cited (including links to both the formal publication through the relevant DOI and the license). See: https://creativecommons.org/licenses/by-nc-nd/4.0/.
References
- Gould MK, Fletcher J, Iannettoni MD, et al. Evaluation of patients with pulmonary nodules: when is it lung cancer?: ACCP evidence-based clinical practice guidelines (2nd edition). Chest 2007;132:108S-30S.
- MacMahon H, Austin JH, Gamsu G, et al. Guidelines for management of small pulmonary nodules detected on CT scans: a statement from the Fleischner Society. Radiology 2005;237:395-400. [Crossref] [PubMed]
- Field JK, Duffy SW, Baldwin DR, et al. UK Lung Cancer RCT Pilot Screening Trial: baseline findings from the screening arm provide evidence for the potential implementation of lung cancer screening. Thorax 2016;71:161-70. [Crossref] [PubMed]
- Pastorino U, Rossi M, Rosato V, et al. Annual or biennial CT screening versus observation in heavy smokers: 5-year results of the MILD trial. Eur J Cancer Prev 2012;21:308-15. [Crossref] [PubMed]
- Saghir Z, Dirksen A, Ashraf H, et al. CT screening for lung cancer brings forward early disease. The randomised Danish Lung Cancer Screening Trial: status after five annual screening rounds with low-dose CT. Thorax 2012;67:296-301. [Crossref] [PubMed]
- Wilson DO, Ryan A, Fuhrman C, et al. Doubling times and CT screen–detected lung cancers in the Pittsburgh Lung Screening Study. Am J Respir Crit Care Med 2012;185:85-9. [Crossref] [PubMed]
- Goo JM. A computer-aided diagnosis for evaluating lung nodules on chest CT: the current status and perspective. Korean J Radiol 2011;12:145-55. [Crossref] [PubMed]
- Heckel F, Meine H, Moltz JH, et al. Segmentation-based partial volume correction for volume estimation of solid lesions in CT. IEEE Trans Med Imaging 2014;33:462-80. [Crossref] [PubMed]
- Hwang EJ, Goo JM, Kim J, et al. Development and validation of a prediction model for measurement variability of lung nodule volumetry in patients with pulmonary metastases. Eur Radiol 2017;27:3257-65. [Crossref] [PubMed]
- ACR. ACR-STR Practice Parameter for the Performance and Reporting of Lung Cancer Screening Thoracic Computed Tomography (CT). Available online: https://www.acr.org/Clinical-Resources/Lung-Cancer-Screening-Resources (accessed June 13 2020).
- Fischbach F, Knollmann F, Griesshaber V, et al. Detection of pulmonary nodules by multislice computed tomography: improved detection rate with reduced slice thickness. Eur Radiol 2003;13:2378-83. [Crossref] [PubMed]
- Xie X, Zhao Y, Snijder RA, et al. Sensitivity and accuracy of volumetry of pulmonary nodules on low-dose 16- and 64-row multi-detector CT: an anthropomorphic phantom study. Eur Radiol 2013;23:139-47. [Crossref] [PubMed]
- Wormanns D, Kohl G, Klotz E, et al. Volumetric measurements of pulmonary nodules at multi-row detector CT: in vivo reproducibility. Eur Radiol 2004;14:86-92. [Crossref] [PubMed]
- Gietema HA, Schaefer-Prokop CM, Mali WP, et al. Pulmonary nodules: Interscan variability of semiautomated volume measurements with multisection CT-- influence of inspiration level, nodule size, and segmentation performance. Radiology 2007;245:888-94. [Crossref] [PubMed]
- van Klaveren RJ, Oudkerk M, Prokop M, et al. Management of lung nodules detected by volume CT scanning. N Engl J Med 2009;361:2221-9. [Crossref] [PubMed]
- Wang Y, van Klaveren RJ, van der Zaag-Loonen HJ, et al. Effect of nodule characteristics on variability of semiautomated volume measurements in pulmonary nodules detected in a lung cancer screening program. Radiology 2008;248:625-31. [Crossref] [PubMed]
- Revel MP, Bissery A, Bienvenu M, et al. Are two-dimensional CT measurements of small noncalcified pulmonary nodules reliable? Radiology 2004;231:453-8. [Crossref] [PubMed]
- Oxnard GR, Zhao B, Sima CS, et al. Variability of lung tumor measurements on repeat computed tomography scans taken within 15 minutes. J Clin Oncol 2011;29:3114-9. [Crossref] [PubMed]