
Use of the volume-averaged Murray’s deviation method for the characterization of branching geometry in liver fibrosis: a preliminary study on vascular circulation
Introduction
Liver fibrosis refers to the reversible wound repair response to chronic liver injury characterized by excessive deposition of extracellular matrix (ECM) components, such as collagens. Recently, the role of collagen accumulation and vascular changes, such as the formation of new vessels (angiogenesis) and abnormal angio-architecture of the liver, has been increasingly implicated in liver fibrosis (1-3). Vascular changes can result in increased intrahepatic vascular resistance and impaired blood circulation, which hinders the reversibility of fibrosis and may eventually lead to portal hypertension, a major complication of cirrhosis and remains one of the leading causes of death in cirrhotic patients (4,5). Thus, selecting the appropriate imaging tool to visualize the vascular network in the whole liver and accurately assessing intrahepatic circulation during fibrogenesis are essential for diagnosing and treating liver fibrosis.
Currently, liver biopsy remains the gold standard for diagnosing liver fibrosis and can directly depict the subtle vascular architecture in the liver. However, the two-dimensional (2D) nature of histology renders it difficult to evaluate the intrahepatic circulation. Clinically, medical imaging techniques such as computed tomography angiography (CTA) and magnetic resonance angiography (MRA) can provide three-dimensional (3D) anatomical information on the vasculature in the liver (6). However, the resolution of these techniques (approximately hundreds of micrometers) is insufficient to detect small branches of the hepatic vessels with diameters of less than 200 µm (7). Micro-computed tomography (CT) or nano-CT overcomes these spatial resolution limitations. However, it fails to image soft tissues. X-ray phase-contrast computed tomography (PCCT), which utilizes the phase shift of X-rays passing through matter to generate tissue contrast, is one of the fastest-growing imaging technologies due to its unique ability to achieve high-spatial-resolution images of microstructures in soft tissues. Combined with synchrotron sources, PCCT can image the vascular network at micron- or even nanometer-scale resolution. With the aid of this technique, the main structures, such as the microvasculature (8,9), bile ducts (10), and hepatic sinusoid (11,12) in the liver, can be clearly distinguished on CT images at micrometer-scale resolution. In addition, the development of advanced vascular segmentation technology provides a solid foundation for 3D vascular reconstruction and analysis (13-17). Thus, PCCT can reveal the 3D network structure of hepatic vessels in the whole liver, providing novel insights for the accurate evaluation of intrahepatic circulation in liver fibrosis.
Murray’s law proposed by Murray in 1926 is a basic physical principle for transfer networks (18,19). Murray found that the basic condition necessary to achieve the maximum efficiency of blood circulation was as follows: the cube of the diameters of the parent vessel should be equal to the sum of the cube of the diameters of the daughter blood vessels. Several investigators have tested the validity of Murray’s law in the vascular circulatory systems of different species, including humans, rats, and chicken embryos (20-24). Recently, Rosenberg showed that Murray’s law outlines one of the necessary conditions for optimal circulation (lowest flow resistance) of the vascular system, and bifurcation yields a lower flow resistance than higher-order branches (25). Moreover, some researchers have reported that deviation from Murray’s law (hereafter, this deviation will be referred to as Murray’s deviation) for the vascular network in terms of geometry may be associated with coronary heart disease (26) and proliferative diabetic retinopathy (27), suggesting that Murray’s deviation may be a good indicator of the state of the circulation of the vascular system. In the field of liver diseases, Murray’s deviation has been used to determine portal pressure in fibrotic/cirrhotic rats. Murray’s deviation of rats with portal hypertension was significantly higher than that of normal rats, suggesting that the branching geometric characteristics of the microvasculature may be a promising marker for predicting the prognosis of portal hypertension in liver fibrosis/cirrhosis (9,23). In previous studies, Murray’s deviation has been assessed using the traditional method of measuring the diameter of the vessels (22,28,29). However, various abnormal features, such as vascular tortuosity, distortion, and deformation, exist in the hepatic vessels in liver fibrosis (30,31), making it difficult to measure the diameter of the vessels accurately. Thus, improved methods to accurately assess Murray’s deviation are urgently needed.
This study investigated the 3D vascular architecture in the liver during fibrosis and its subsequent regression using the PCCT technique. Based on the PCCT data, a novel approach using the vascular volume was proposed to calculate Murray’s deviation. Detailed comparative analysis of the volume-averaged Murray’s deviation and the traditional diameter-based method was performed to verify the accuracy of the volume-averaged method. Moreover, the efficacy of the volume-averaged method in assessing vascular circulation at different stages of liver fibrosis was investigated.
Methods
Sample preparation
This study was approved by the Research Ethics Committee of Beijing Friendship Hospital, Capital Medical University, in compliance with the guidelines for the care and use of animals. A total of 24 adult male Sprague-Dawley rats, weighing 180–220 g, were used in this study. Liver lesions and fibrosis were induced by subcutaneous injection of carbon tetrachloride (CCl4; 56-23-5, Damao Chemical Reagent Factory, Tianjin, China) dissolved in olive oil (8001-25-0, Solarbio, China) (4:6 v/v ratio) at 2 mL/kg body weight, twice a week for 10 weeks. The rats were randomized into 4 groups of 6 animals and euthanized at different time intervals, namely, at 0 weeks (normal group), 6 weeks (moderate fibrosis group), 10 weeks (severe fibrosis group), and after spontaneous recovery at 30 weeks (regressive group). For PCCT experiments, livers were collected after euthanasia and fixed in 10% neutral-buffered formalin.
PCCT experiments
The livers were scanned using BL13W1 Beamline at the Shanghai Synchrotron Radiation Facility (SSRF), Shanghai, China. The X-rays were derived from a 3.5 GeV electron storage ring and subsequently monochromatized by a double-crystal monochromator with Si(111) crystals. The energy of the X-ray beam in the experiments was set at 24 keV, and the detector employed an X-ray CCD camera system, allowing for an effective pixel size of 9 µm. During the CT scans, 600 raw projections were obtained with a 0.3° angular step over 180°. The exposure time of each projection was 12 ms, and the sample-to-detector distance (SDD) was 1.2 m. Additionally, 20 flat field images (with no sample in the beam) and 10 dark field images (with no photons hitting the detector) were collected before and after each scan to correct for a dark current offset of the detector. The detailed components and parameters of the PCCT setup are provided in Table S1.
Image processing
The raw projections from the CT scans were normalized using flat and dark images. The phase-attenuation duality Born-type approximation phase retrieval algorithm (PAD-BA) extracted phase information from the projections (32). The projection was then reconstructed using the filtered back-projection (FBP) algorithm to produce a set of CT images. The above image processing procedures were conducted with PITRE software, which was developed at SSRF (33). Finally, the CT datasets were imported into Avizo 8.0 software (FEI Visualization Sciences Group) for 2D and 3D visualization, segmentation, reconstruction, and measurements. Additional details of the software are available at https://www.thermofisher.cn/cn/zh/home/industrial/electron-microscopy/electron-microscopy-instruments-workflow-solutions/3d-visualization-analysis-software/avizo-materials-science.html.
Murray’s deviation
Murray’s law summarizes the relationship between mother and daughter vessel diameters (13) using the following Eq.:
where D0 is the diameter of the parent vessel and D1 and D2 are the diameters of the daughter branches. To measure Murray’s deviation (deviation from Murray’s law), the ratio of the cube of the mother vessel diameter to the sum of the cubes of the daughter vessel diameters is calculated according to the following formula (34):
While the traditional Murray’s deviation is calculated using the vascular diameter (22), this study proposed a volume-averaged method using the vascular volume to calculate Murray’s deviation (Figure 1). In this latter method, the vascular structures are assumed to be an ideal cylinder, and thus the following can be assumed:
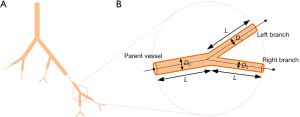
where V, L, D, and r represent the volume, length, diameter, and radius of the vessel, respectively. Thus, when the length of the parent and daughter vessels are represented by L, substituting Eq. [3] and Eq. [4] into Eq. [2], would result in the following:
where V0 denotes the volume of the parent vessel, V1 and V2 are the volumes of the daughter branches, and a Murray’s deviation of 1 indicates that Murray’s law is obeyed. To assess the accuracy of the volume-averaged method, a comparative analysis of this method and the diameter-based method was performed. In the diameter-based method, 3 radiologists (with more than 3 years of experience in vascular analysis) who were blinded to the sample information, measured the inside diameters of the vessels at different measurement positions (positions 5, 10, 15, 20, and 25) spaced out evenly on vascular segments with a length of 100 µm (L =100 µm, the selection criteria for the value of L is detailed in the Supplementary Materials) near the branching points. The average diameter was calculated and used to compute Murray’s deviation regarding previous studies (22,35). In the volume-averaged method, the same vascular segments as those in the diameter-based method were selected. The volume of the segments was directly acquired using the Avizo software. After the vasculature was extracted from the liver parenchyma using the iterative gray level threshold, the volume of the selected vascular segment could be automatically quantified using the “material statistics” function in the “measure and analyze” module of the Avizo software, and Murray’s deviation was obtained by substituting the volume values into Eq. [5]. To evaluate the vascular circulation in liver fibrosis, 20 measurements of Murray’s deviation in the main vessels (diameter ≥200 µm) and 20 measurements in the small branches (<200 µm) in each group were obtained via the volume-averaged method. The schematic diagram of the distribution of large and small vessels in the vascular system is shown in Figure S1. The measurement parameters and times of the diameter-based method and the volume-averaged method are shown in Table S2 of the Supplementary Materials.
Histological evaluation
After PCCT scanning, all livers were decalcified, dehydrated, and embedded in paraffin for histological analysis. Serial sections with a slice thickness of 4 µm were stained with Sirius Red. Pathological images were digitized with a dedicated camera, and image analysis was performed using Image Pro Plus 6.0 software (Media Cybernetics, Bethesda, Maryland, USA). Collagen proportionate area (CPA), expressed as a relative percentage between the area of collagen and the total area, has been proposed as an accurate and objective histological variable for subclassifying liver fibrosis (36). The area of collagen was identified on the pathological images at ×100 magnification, and the CPA was assessed by computer-assisted digital image analysis as previously described (9). A total of 20 measurements of CPA in each group were acquired in the histological process.
Statistical analysis
Statistical analysis was performed using SPSS 19.0 software (IBM, Chicago, IL, USA). Numerical results are presented as the means ± standard deviations. The Bonferroni test was applied for multiple comparison corrections. Repeated measures analysis of variance (ANOVA) were used to statistically analyze the diameter-based Murray’s deviation values obtained at different measurement points. A P value <0.05 was considered statistically significant.
Results
Imaging vascular changes via phase-contract computed tomography (PCCT)
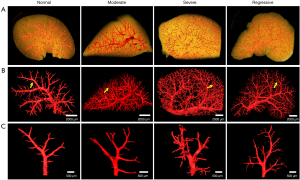
The morphology and branching of hepatic vessels at different stages of liver fibrosis were clearly visualized via PCCT, which revealed the angio-architecture over a wider length scale, from “macro” down to “micro” (Figure 2). The smallest distinguishable vessel was approximately 30 µm in diameter. In normal livers, the hepatic vessels were arranged in a tree-like branching pattern with equal distribution. During the progression of fibrosis, the vessels presented a high degree of branching with increasingly irregular and tortuous anatomy. During fibrosis regression, the aberrant vascular density decreased significantly, and the abnormal vascular morphology gradually normalized, but the final structure failed to completely revert to the normal state.
Comparative analysis of Murray’s deviation between the diameter-based and the volume-averaged method
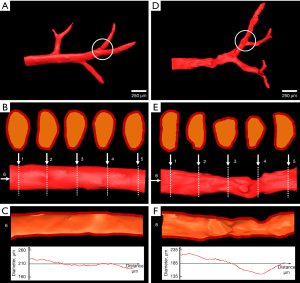
The 3D visualization and analysis of 2 representative vascular branches in the normal and severe fibrosis group are clearly presented in Figure 3. In the normal group, the vessel exhibited a smooth surface (Figure 3A) with round or oval vascular lumens (Figure 3B), and the vascular diameters gradually decreased along the axial direction of the vessel (Figure 3C). Unlike the vessel in the normal liver, the vessel in severe fibrosis presented a deformed shape (Figure 3D) with various irregular lumens (Figure 3E), and the diameters fluctuated up and down along the axial direction of the vessel (Figure 3F). A comparative analysis of the diameter properties and Murray’s deviation between diameter-based and volume-averaged methods was performed (Figure 4). In the diameter-based method, when less than 20 measurements were taken, the diameters and Murray’s deviation varied enormously among the radiologists, especially within the severe fibrosis group. As the number of measurements increased, the diameter and Murray’s deviation of each vessel tended to stabilize towards the same value, and the final stable values of all vessels in the diameter-based method were very close to those measured by the volume-averaged method. Bland-Altman analysis was performed on 12 pairs of Murray’s deviation values based on the diameter method (>20 repeat measurements) and the volume method in the normal and severe fibrosis groups. The results showed good agreement between the 2 methods (Figure S2). Moreover, in the severe fibrosis group, there was a significant negative correlation between the difference in Murray’s deviation based on the diameter and volume methods and the number of measurements collected for the diameter method (Pearson’s r=−0.678; P<0.01). However, no such correlation was observed in the normal group (Pearson’s r=−0.506; P=0.054). This suggested that increasing the number of measurements could improve the accuracy of the diameter method for patients with severe vascular deformation.
Assessment of intrahepatic vascular circulation using the volume-averaged Murray’s deviation
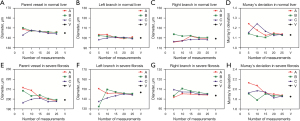
The results of the geometric parameters of the vascular bifurcations during progression and regression of liver fibrosis are shown in Figure 5. In the normal group, the value of Murray’s deviation (1.05±0.17 in the main branches and 1.05±0.09 in the small branches) was very close to the theoretical value of unity given by Murray’s law (Murray’s deviation =1). Moreover, the branch diameter ratio of the daughter vessels D2≈D1 (1.07±0.33 in the main branches and 1.02±0.24 in the small branches), indicating that the global bifurcation system in normal livers was symmetric (D2≈D1). Other geometrical parameters, such as D1/D0 and D2/D0 also had values similar to the symmetric bifurcation (D1/D0=D2/D0≈2−1/3≈0.794).

However, Murray’s deviation and other geometrical parameters deviated from the theoretical values during fibrosis progression. Murray’s deviation showed a relatively consistent trend with fibrosis progression, while the other geometrical parameters did not show any obvious relationships with the degree of fibrosis. Murray’s deviation in the small branches increased with the progression of fibrosis from 1.42±0.48 in the moderate group to 1.79±0.57 in the severe group, and the value rapidly decreased to 1.18±0.28 in the regressive group, but did not return to the normal condition (1.05±0.09). Compared to the Murray’s deviation in the small branches, the value in the main branches (1.17±0.21 in the moderate group, 1.34±0.18 in the severe group, and 1.17±0.19 in the regressive group) was significantly less than that in the small branches.
Histological analysis of the livers at different stages of fibrosis
The progression of liver fibrosis was analyzed by Sirius Red staining (Figure 6A-6D). In normal livers, collagen was only found in low amounts around the hepatic vessels (Figure 6A). After CCl4 treatment, deposition of thin collagen fibers along the central vein and formation of incomplete fibrous septa were observed in the moderate group (Figure 6B). In severe fibrosis, a complete fibrous septa was formed, and the liver parenchyma separated into small nodules (Figure 6C). During fibrosis regression, part of the fibrous septa was reabsorbed, and the nodules became enlarged (Figure 6D).
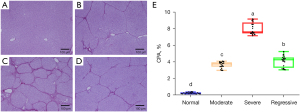
Additionally, the extent of fibrosis was quantitatively evaluated using the CPA (Figure 6E). During fibrogenesis, the CPA increased from 3.63%±0.36% in the moderate group to 8.01%±0.7% in the severe group, both of which were significantly higher than the CPA in the normal group (0.23%±0.08%). After regression, the CPA decreased to 4.08%±0.67% and was close to the value of the moderate group. Moreover, the changes in the CPA were correlated with the Murray’s deviation at different stages of fibrosis in the main branches (Pearson’s r=0.500; P<0.001) and the small branches (Pearson’s r=0.481; P<0.001). It is noteworthy that during the regression, the decrease in the CPA was significantly slower than that of Murray’s deviation, which returned close to normalcy.
Discussion
The present study demonstrated that PCCT could clearly reveal the 3D structure of the vascular network in the liver, and the smallest visible vessels were approximately 30 µm in diameter. The vascular geometry parameters, including diameter, length, and volume, could be obtained via the PCCT data. Based on the 3D data, we proposed a novel approach to calculating Murray’s deviation, in which the vascular volume was used instead of the vessel diameter. Moreover, a comparative analysis between these two methods was performed to verify the accuracy of the volume-averaged method. Subsequently, the volume-averaged Murray’s deviation was utilized to evaluate the circulation of the vascular system in the liver during fibrosis and subsequent regression. This revealed that the value of Murray’s deviation was closely related to the stages of fibrosis. Moreover, pathological experiments were performed to assess collagen accumulation, and the findings were compared with the vascular changes. The results demonstrated that changes in collagen deposition were correlated with vascular circulation at different stages of liver fibrosis.
Since Murray’s law was proposed in 1926, it has been widely applied in medical analysis (20). Murray’s deviation is used to characterize the circulatory state of the vascular system, and its efficacy has been demonstrated in our previous studies (9,23). According to Murray’s law, Murray’s deviation is calculated based on the vascular diameter. Early measurements of the diameter were mainly obtained from 2D images, which may superimpose the structural information onto one image (22), making it difficult to distinguish an integrated vascular branch for effective measurements, particularly when the vessels were enriched. In this study, the 3D structures of the hepatic vessels were clearly acquired by PCCT, which allowed the diameter to be directly measured on cross-sections of the vessels, avoiding the superimposition of the vascular structures in 2D images.
Interestingly, the vessels on the cross-sections were not regular circles. This was especially the case in severe fibrosis, where the vascular morphology was seriously damaged, making it difficult to obtain accurate diameter values using the cross-sections. Moreover, the use of different measurement positions on the vascular segments would also produce different diameter values. In this current study, 3 radiologists measured the diameters at different measurement positions (5, 10, 15, 20, and 25 positions on the vascular segments). When less than 20 measurements were collated, the diameter values varied greatly among different radiologists. However, when more than 20 measurements were collated, the variations decreased, and the values tended to be more consistent among the radiologists in both the normal and severe stages of fibrosis. This suggested that measurement errors could be reduced by increasing the sampling frequency (i.e., more measurements). Thus, the diameter-based method with high sampling frequency is suitable for small-scale analysis of Murray’s deviation. However, for big data analysis, applying this approach will obviously be a tedious and time-consuming process. In this current investigation, we proposed a volume-averaged method in which the vascular volumes replaced the diameters for calculating Murray’s deviation. The vascular volume can be directly obtained using the corresponding software, thereby decreasing the workload and human measurement errors. Moreover, a comparison of the diameter-based method with the volume-averaged method in the extreme stages of fibrosis (i.e., normal and severe fibrosis) revealed that the value of Murray’s deviation using the volume-averaged method was very close to that obtained with the diameter-based method (when more than 20 measurements were collated), indicating that the volume-averaged method had high sensitivity and accuracy in evaluating Murray’s deviation.
Liver fibrosis is a dynamic process characterized by increased collagen content and altered vascular structures. In recent years, vascular alterations have attracted much attention (37,38). PCCT, which has undergone rapid progress over the last 20 years, provides high spatial resolution and excellent soft-tissue contrast in imaging biological samples, making it possible to perform both 3D visualization and quantitative analysis of the vascular alterations in liver fibrosis (9,39). In these experiments, the 3D anatomy of the vascular networks at different stages of liver fibrosis was clearly presented by PCCT. During fibrogenesis, the vessels appeared in a tortuous and disordered form which might disturb the normal blood circulation, and this gradually recovered during fibrosis regression.
Moreover, the volume-averaged method was utilized to evaluate the intrahepatic circulation during the fibrosis and regression stages. For the bifurcation system of normal livers, the measured values showed reasonable agreement with the calculated optimal values, indicating that the normal hepatic vessels complied well with Murray’s law, confirming previous studies of the normal liver (29). However, with fibrotic livers, Murray’s deviation increased with the development of fibrosis and reached its maximum at the severe fibrotic phase, and subsequently decreased rapidly during regression, which showed a significant correlation with the vascular morphological alterations. Furthermore, Murray’s deviation did, in fact decrease but failed to completely return to normalcy, corroborating with previous histopathological findings that fibrosis is not fully reversible, especially with regards to the changes in liver microvasculature (40,41). As shown in the present study and others (22,28,29), the value of Murray’s deviation in normal livers is very close to the theoretical value of unity given by Murray’s law (Murray’s deviation =1), and the trend of Murray’s deviation during fibrogenesis in this study were in good agreement with our previous reports on liver fibrosis (9) and cirrhosis (23). Notably, the assessment methods used in this study were significantly superior compared to those used in previous studies. In our previous studies, the diameters were manually measured on the integrated parent and daughter vessels; however, only vascular segments with a length of 100 µm near the branching points were selected to evaluate Murray’s deviation in this study. As some researchers reported, the local hemodynamic condition (especially, the shape of velocity profile or wall shear stress) at the branching point will be temporarily altered (42); thus, the value of Murray’s deviation obtained near the bifurcation point in this study will be closer to the actual blood circulation state. We also compared Murray’s deviation of the main vessels and the small branches. We found that fibrosis mainly affected the microcirculation in the liver and had little effect on the main blood vessels, indicating that improvement of the microvascular circulation may be a potential target for the treatment of liver fibrosis.
Additionally, our results showed that the vascular circulation was consistent with the progression of fibrosis. Of note is that collagen degradation was significantly slower than circulation during regression. Thus, whether improvements in vascular circulation facilitate the degradation of collagen should be further investigated.
Although the volume-averaged method is appropriate for evaluating intrahepatic circulation, there were several limitations to this study. First, for vascular diseases such as vascular stenosis or embolism, the volume-averaged method averages the diameter of the entire vascular segment and cannot identify the stenotic lesions, so it is not suitable for the evaluation of such diseases. Second, the study mainly focuses on calculating Murray’s deviation of the microvasculature by using excised samples by PCCT. While some in vivo studies based on PCCT projections have been reported in the field of vascular research (43,44), more studies are needed to achieve 3D imaging of vascular structures. Our future work will involve in vivo studies to further investigate the value of PCCT in the study of the vascular system.
In conclusion, this study verified the validity of the volume-averaged method and demonstrated that this method could accurately evaluate the blood circulation state of the liver during fibrosis and its subsequent regression. Thus, the volume-averaged Murray’s deviation may be an objective and valuable staging criterion to evaluate intrahepatic circulation during liver fibrosis.
Acknowledgments
The authors thank the staff from Beamline (BL13W1) of SSRF, China, for their kind assistance in our experiments.
Funding: This study received funding from the National Natural Science Foundation of China (82071922, 82001813, 81671683, 81670545); the Natural Science Foundation of Tianjin City (16JCYBJC28600); and the Tianjin Municipal Education Commission (2020KJ208).
Footnote
Conflicts of Interest: All authors have completed the ICMJE uniform disclosure form (available at https://dx.doi.org/10.21037/qims-21-47). The authors have no conflicts of interest to declare.
Ethical Statement: The authors are accountable for all aspects of the work in ensuring that questions related to the accuracy or integrity of any part of the work are appropriately investigated and resolved. This study was approved by the Research Ethics Committee of Beijing Friendship Hospital, Capital Medical University, in compliance with the guidelines for the care and use of animals approved by the Research Ethics Committee of Beijing Friendship Hospital, Capital Medical University.
Open Access Statement: This is an Open Access article distributed in accordance with the Creative Commons Attribution-NonCommercial-NoDerivs 4.0 International License (CC BY-NC-ND 4.0), which permits the non-commercial replication and distribution of the article with the strict proviso that no changes or edits are made and the original work is properly cited (including links to both the formal publication through the relevant DOI and the license). See: https://creativecommons.org/licenses/by-nc-nd/4.0/.
References
- Valfrè di Bonzo L, Novo E, Cannito S, Busletta C, Paternostro C, Povero D, Parola M. Angiogenesis and liver fibrogenesis. Histol Histopathol 2009;24:1323-41. [PubMed]
- Coulon S, Heindryckx F, Geerts A, Van Steenkiste C, Colle I, Van Vlierberghe H. Angiogenesis in chronic liver disease and its complications. Liver Int 2011;31:146-62. [Crossref] [PubMed]
- Fernández M, Semela D, Bruix J, Colle I, Pinzani M, Bosch J. Angiogenesis in liver disease. J Hepatol 2009;50:604-20. [Crossref] [PubMed]
- Iwakiri Y. Endothelial dysfunction in the regulation of cirrhosis and portal hypertension. Liver Int 2012;32:199-213. [Crossref] [PubMed]
- Thabut D, Shah V. Intrahepatic angiogenesis and sinusoidal remodeling in chronic liver disease: new targets for the treatment of portal hypertension? J Hepatol 2010;53:976-80. [Crossref] [PubMed]
- Jhaveri K, Guo L, Guimarães L, Menezes R, McGilvray I, Cattral M, Grant D. Mapping of hepatic vasculature in potential living liver donors: comparison of gadoxetic acid-enhanced MR imaging using CAIPIRINHA technique with CT angiography. Abdom Radiol (NY) 2018;43:1682-92. [Crossref] [PubMed]
- Zhang X, Liu XS, Yang XR, Chen SL, Zhu PP, Yuan QX. Mouse blood vessel imaging by in-line x-ray phase-contrast imaging. Phys Med Biol 2008;53:5735-43. [Crossref] [PubMed]
- Jian J, Yang H, Zhao X, Xuan R, Zhang Y, Li D, Hu C. Visualization of microvasculature and thrombi by X-ray phase-contrast computed tomography in hepatocellular carcinoma. J Synchrotron Radiat 2016;23:600-5. [Crossref] [PubMed]
- Xuan R, Zhao X, Jian J, Hu D, Qin L, Lv W, Hu C. Phase-contrast computed tomography: A correlation study between portal pressure and three dimensional microvasculature of ex vivo liver samples from carbon tetrachloride-induced liver fibrosis in rats. Microvasc Res 2019;125:103884. [Crossref] [PubMed]
- Qin L, Zhao X, Jian J, Zhao Y, Sun M, Hu C. High-resolution 3D visualization of ductular proliferation of bile duct ligation-induced liver fibrosis in rats using x-ray phase contrast computed tomography. Sci Rep 2017;7:4215. [Crossref] [PubMed]
- Jian J, Zhang W, Yang H, Zhao X, Xuan R, Li D, Hu C. Phase-contrast CT: Qualitative and Quantitative Evaluation of Capillarized Sinusoids and Trabecular Structure in Human Hepatocellular Carcinoma Tissues. Acad Radiol 2017;24:67-75. [Crossref] [PubMed]
- Duan J, Hu C, Chen H. High-resolution micro-CT for morphologic and quantitative assessment of the sinusoid in human cavernous hemangioma of the liver. PLoS One 2013;8:e53507. [Crossref] [PubMed]
- Moccia S, De Momi E, El Hadji S, Mattos LS. Blood vessel segmentation algorithms - Review of methods, datasets and evaluation metrics. Comput Methods Programs Biomed 2018;158:71-91. [Crossref] [PubMed]
- Ciecholewski M, Kassjański M. Computational Methods for Liver Vessel Segmentation in Medical Imaging: A Review. Sensors (Basel) 2021;21:2027. [Crossref] [PubMed]
- Lamy J, Merveille O, Kerautret B, Passat N, Vacavant A. Vesselness filters: A survey with benchmarks applied to liver imaging. International Conference on Pattern Recognition (ICPR), 2020.
- Nazir A, Cheema MN, Sheng B, Li P, Kim J, Lee TY. Living Donor-Recipient Pair Matching for Liver Transplant via Ternary Tree Representation With Cascade Incremental Learning. IEEE Trans Biomed Eng 2021;68:2540-51. [Crossref] [PubMed]
- Yan Q, Wang B, Zhang W, Luo C, Xu W, Xu Z, Zhang Y, Shi Q, Zhang L, You Z. Attention-Guided Deep Neural Network With Multi-Scale Feature Fusion for Liver Vessel Segmentation. IEEE J Biomed Health Inform 2021;25:2629-42. [Crossref] [PubMed]
- Sherman TF. On connecting large vessels to small. The meaning of Murray's law. J Gen Physiol 1981;78:431-53. [Crossref] [PubMed]
- McCulloh KA, Sperry JS, Adler FR. Water transport in plants obeys Murray's law. Nature 2003;421:939-42. [Crossref] [PubMed]
- Kishi S, Giannopoulos AA, Tang A, Kato N, Chatzizisis YS, Dennie C, Horiuchi Y, Tanabe K, Lima JAC, Rybicki FJ, Mitsouras D. Fractional Flow Reserve Estimated at Coronary CT Angiography in Intermediate Lesions: Comparison of Diagnostic Accuracy of Different Methods to Determine Coronary Flow Distribution. Radiology 2018;287:76-84. [Crossref] [PubMed]
- Hahn JY, Gwon HC, Kwon SU, Choi SH, Choi JH, Lee SH, Hong KP, Park JE, Kim DK. Comparison of vessel geometry in bifurcation between normal and diseased segments: intravascular ultrasound analysis. Atherosclerosis 2008;201:326-31. [Crossref] [PubMed]
- Lee JY, Lee SJ. Murray's law and the bifurcation angle in the arterial micro-circulation system and their application to the design of microfluidics. Microfluid Nanofluid 2010;8:85-95. [Crossref]
- Sun M, Lv W, Zhao X, Qin L, Zhao Y, Xin X, Jian J, Chen X, Hu C. Vascular branching geometry relating to portal hypertension: a study of liver microvasculature in cirrhotic rats by X-ray phase-contrast computed tomography. Quant Imaging Med Surg 2020;10:116-27. [Crossref] [PubMed]
- Beare RJ, Das G, Ren M, Chong W, Sinnott MD, Hilton JE, Srikanth V, Phan TG. Does the principle of minimum work apply at the carotid bifurcation: a retrospective cohort study. BMC Med Imaging 2011;11:17. [Crossref] [PubMed]
- Rosenberg E. On deriving Murray's law from constrained minimization of flow resistance. J Theor Biol 2021;512:110563. [Crossref] [PubMed]
- Witt N, Wong TY, Hughes AD, Chaturvedi N, Klein BE, Evans R, McNamara M, Thom SA, Klein R. Abnormalities of retinal microvascular structure and risk of mortality from ischemic heart disease and stroke. Hypertension 2006;47:975-81. [Crossref] [PubMed]
- Crosby-Nwaobi R, Heng LZ, Sivaprasad S. Retinal vascular calibre, geometry and progression of diabetic retinopathy in type 2 diabetes mellitus. Ophthalmologica 2012;228:84-92. [Crossref] [PubMed]
- Sather BA, Hageman D, Wagenseil JE. Murray's Law in elastin haploinsufficient (Eln+/-) and wild-type (WT) mice. J Biomech Eng 2012;134:124504. [Crossref] [PubMed]
- Kline TL, Zamir M, Ritman EL. Relating function to branching geometry: a micro-CT study of the hepatic artery, portal vein, and biliary tree. Cells Tissues Organs 2011;194:431-42. [Crossref] [PubMed]
- Duan J, Hu C, Luo S, Zhao X, Wang T. Microcomputed tomography with diffraction-enhanced imaging for morphologic characterization and quantitative evaluation of microvessel of hepatic fibrosis in rats. PLoS One 2013;8:e78176. [Crossref] [PubMed]
- Peeters G, Debbaut C, Friebel A, Cornillie P, De Vos WH, Favere K, Vander Elst I, Vandecasteele T, Johann T, Van Hoorebeke L, Monbaliu D, Drasdo D, Hoehme S, Laleman W, Segers P. Quantitative analysis of hepatic macro- and microvascular alterations during cirrhogenesis in the rat. J Anat 2018;232:485-96. [Crossref] [PubMed]
- Peeters G, Debbaut C, Friebel A, Cornillie P, De Vos WH, Favere K, Vander Elst I, Vandecasteele T, Johann T, Van Hoorebeke L, Monbaliu D, Drasdo D, Hoehme S, Laleman W, Segers P. Quantitative analysis of hepatic macro- and microvascular alterations during cirrhogenesis in the rat. J Anat 2018;232:485-96. [Crossref] [PubMed]
- Chen RC, Dreossi D, Mancini L, Menk R, Rigon L, Xiao TQ, Longo R. PITRE: software for phase-sensitive X-ray image processing and tomography reconstruction. J Synchrotron Radiat 2012;19:836-45. [Crossref] [PubMed]
- Schoenenberger AW, Urbanek N, Toggweiler S, Seelos R, Jamshidi P, Resink TJ, Erne P. Deviation from Murray's law is associated with a higher degree of calcification in coronary bifurcations. Atherosclerosis 2012;221:124-30. [Crossref] [PubMed]
- Taber LA, Ng S, Quesnel AM, Whatman J, Carmen CJ. Investigating Murray's law in the chick embryo. J Biomech 2001;34:121-4. [Crossref] [PubMed]
- Calvaruso V, Burroughs AK, Standish R, Manousou P, Grillo F, Leandro G, Maimone S, Pleguezuelo M, Xirouchakis I, Guerrini GP, Patch D, Yu D, O'Beirne J, Dhillon AP. Computer-assisted image analysis of liver collagen: relationship to Ishak scoring and hepatic venous pressure gradient. Hepatology 2009;49:1236-44. [Crossref] [PubMed]
- Ehling J, Bartneck M, Wei X, Gremse F, Fech V, Möckel D, Baeck C, Hittatiya K, Eulberg D, Luedde T, Kiessling F, Trautwein C, Lammers T, Tacke F. CCL2-dependent infiltrating macrophages promote angiogenesis in progressive liver fibrosis. Gut 2014;63:1960-71. [Crossref] [PubMed]
- Wagner WL, Föhst S, Hock J, Kim YO, Popov Y, Schuppan D, Schladitz K, Redenbach C, Ackermann M. 3D analysis of microvasculature in murine liver fibrosis models using synchrotron radiation-based microtomography. Angiogenesis 2021;24:57-65. [Crossref] [PubMed]
- Lv WJ, Zhao XY, Hu DD, Xin XH, Qin LL, Hu CH. Insight into Bile Duct Reaction to Obstruction from a Three-dimensional Perspective Using ex Vivo Phase-Contrast CT. Radiology 2021;299:597-610. [Crossref] [PubMed]
- Desmet VJ, Roskams T. Cirrhosis reversal: a duel between dogma and myth. J Hepatol 2004;40:860-7. [Crossref] [PubMed]
- Di Vinicius I, Baptista AP, Barbosa AA, Andrade ZA. Morphological signs of cirrhosis regression. Experimental observations on carbon tetrachloride-induced liver cirrhosis of rats. Pathol Res Pract 2005;201:449-56. [Crossref] [PubMed]
- LaBarbera M. Principles of design of fluid transport systems in zoology. Science 1990;249:992-1000. [Crossref] [PubMed]
- Wang L, Zhou P, Mu Z, Lin X, Jiang L, Cheng Z, Luo L, Xu Z, Geng J, Wang Y, Zhang Z, Yang GY. Dynamic Detection of Thrombolysis in Embolic Stroke Rats by Synchrotron Radiation Angiography. Transl Stroke Res 2019;10:695-704. [Crossref] [PubMed]
- Wang F, Zhou P, Li K, Mamtilahun M, Tang Y, Du G, Deng B, Xie H, Yang G, Xiao T. Sensitive imaging of intact microvessels in vivo with synchrotron radiation. IUCrJ 2020;7:793-802. [Crossref] [PubMed]


