
Longitudinal clustering analysis and prediction of Parkinson’s disease progression using radiomics and hybrid machine learning
Introduction
Parkinson’s disease (PD) as a progressive (1-3) and heterogeneous disease (4-7) is the second-most common neurodegenerative disorder after Alzheimer’s disease (8,9). PD is characterized by motor (10,11) and non-motor symptoms (12-15). Even though there is currently no proven permanent therapies for PD, but symptomatic treatments with levodopa (16) and dopaminergic agonists (17) are considered in order to temporally control symptoms (18,19). A multicenter study (20) showed different progression rate in PD for 10 years follow-up. Identification of PD progression could enhance comprehension of PD mechanisms as well as improve design of clinical trials (21). While studies focused on identification of PD subtypes (6,22-29), identification of longitudinal progression in the course of several years can led to better understanding of underlying mechanisms (30-32).
Studies for prediction of individual outcomes in PD patients have recently been emerging (33-43). Discovery of new biomarkers of PD may enable improved treatment planning (24). Although motor dysfunctionalities were first proven as primary indicators of disease progression at screening (44), non-motor symptoms were shown to be significant considerations (45). Our past efforts (27-29,42,46) focusing on identifications of PD subtypes as well as prediction of motor and subtype outcome in PD showed that radiomics features, beyond conventional imaging measures, enable improvement in both tasks. Moreover, using HMLSs enabled significant improvements in both clustering and prediction tasks (38,42,43). In some studies, no significant correlations between conventional imaging features and clinical features (46) and no improvement in prediction when employing their mixture (42) were observed.
A recent study (30) focused on specifying progression rate of PD using some relevant features. The authors first clustered PD patients by global composite outcome score, and then compared the progression of this score among different subtypes in 4.5-year follow-up. Another effort (31) focused on specifying the heterogeneity of PD (subtypes) and then investigated the progression of some motor and non-motor features among sub-clusters in 6-year follow-up. Patient subtyping can be defined as a clustering problem (47), where the subjects within a cluster are similar to each other. Another longitudinal study (48) investigated the annual progression rate in activity and participation measures in 5-year follow-up. A study (49) also focused on clinical progression of postural instability gait disorders compared to tremor dominant using longitudinal clinical data in 4-year follow-up. This study employed the linear mixed-effects models to specify differences in progression rate between the two groups. Furthermore, a study explored the main clinical variables of PD progression in a selected population of subjects, identified by a long-term preserved response to dopaminergic treatment in 30-year follow up. They assessed the clinical and neuropsychological progression of 19 patients, treated with subthalamic nucleus deep brain stimulation.
Han et al. (50) applied unsupervised medical anomaly detection generative adversarial network (deep learning technique) on multi-sequence structural MRI to detect brain anomalies (Alzheimer disease) at a very early stage. In another study, Nakao et al. (51) employed an unsupervised anomaly detection method based on the variational autoencoder- generative adversarial network (VAE-GAN, as a deep learning technique) to detect various lesions using a large chest radiograph dataset. Rundo et al. (52) employed a fully automatic method for necrosis extraction, after the whole gross tumor volume (GTV) segmentation, using the Fuzzy C-Means (FCM) algorithm to detect the necrotic regions within the planned GTV for neuro-radiosurgery therapy. In another study (53), particle swarm optimization algorithm was employed to improve FCM algorithm via selecting the initial cluster centers optimally.
To the best of our knowledge, there has been very limited work focused on longitudinal clustering to stratify PD progression trajectories. Since patients in the same cross-sectional subtype can have similar properties but with different progression rates, clustering longitudinal trajectories constructed using PD subtypes can improve interpretation of disease progression instead of following specific features among PD subtypes over time (32). Our present effort includes derivation of distinct trajectories of PD progression during 4-year follow-up (unsupervised task) via longitudinal clustering, as well as prediction of these trajectories (supervised task) from early year data using HMLSs. Our methods and materials are described next, followed by results, discussion, and conclusion.
We present the following article in accordance with the MDAR checklist (available at https://dx.doi.org/10.21037/qims-21-425).
Methods
The study was conducted in accordance with the Declaration of Helsinki (as revised in 2013). We extracted patient data from the PPMI database (www.ppmi-info.org/data) including clinical information and DAT SPECT and MRI, for years 0 (baseline), 1, 2 and 4. As detailed next, image processing pipeline was implemented to perform MRI segmentation, then DAT SPECT/MRI fusion, and feature extraction from each segmented ROI were done. We then employed HMLSs, consisting of DRAs combined with clustering/classification algorithms, in order to identify the most optimal progression trajectories in PD and to predict these trajectories using data in years 0 and 1.
Image segmentation, fusion, and feature extraction
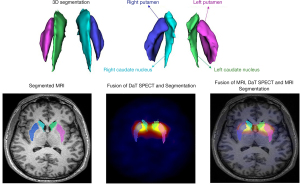
As shown in Figure S1 and elaborated in Appendix 1, we employed multiple steps towards extraction of radiomics feature from ROIs in dorsal striatum (DS) (left and right caudate and putamen). The FreeSurfer package was first utilized to directly segment T1 MRI (29), and then register DAT SPECT images to MRI. Example images are shown in Figure 1. We provided the ROIs to our standardized SERA software package (54) to extract radiomics features.
Patient features
We first select 885 patients (original dataset) who had 981 features: the features included motor, non-motor features and radiomics features extracted for each ROI using our standardized SERA software (these are further elaborated in Appendix 1 and the features were publicly shared as linked in “Data and Code Availability”). Since some information of some patients were missing in some years, for longitudinal clustering task, we arrived at dataset of 143 patients (years 0, 1, 2 and 4). For the prediction task based on year 0 and/or 1, we created 3 datasets: (I) CSD0 with 143 subjects: the use of cross-sectional dataset in year 0 as input and the related trajectories as outcome; (II) TD01 with 286 subjects: the use of datasets in year 0 and 1 as timeless approach as input and the related trajectories as outcome (i.e., effectively doubling the number of our cases; hypothesized to improve task due to added statistics); (III) CSD01 with 143 subjects: the use of cross-sectional datasets in year 0, 1 (putting cross-sectional datasets longitudinally next to each other) as input and related trajectories as outcome. We constructed the timeless dataset (TD01) by appending cross sectional datasets within a single set of data. This approach enables us to gather data with larger (double) number of patients.
Machine learning methods
We utilized HMLSs, utilizing 3 groups of algorithms including: (I) feature extraction algorithms, (II) clustering algorithms, and (III) classification algorithms. These are elaborated next.
Feature extraction algorithms (FEAs)
We employed FEAs to reduce high-dimensional data into fewer dimensions (i.e., as DRAs), in order to tackle overfitting issues in both unsupervised and supervised tasks. Unsupervised FEAs use no label for attribute extraction, and rely on patterns emerged between input features (55-57). In this study, 16 FEAs (only unsupervised) were employed (as elaborated in Appendix 1): (I) principle component analysis (PCA) (58); (II) Kernel PCA (59); (III) t-SNE (60); (IV) factor analysis (FA) (61); (V) Sammon Mapping algorithm (SMA) (62,63); (IV) Isomap algorithm (IsoA) (64); (VII) LandMark Isomap algorithm (LMIsoA) (65); (VIII) laplacian eigenmaps algorithm (LEA) (66,67); (IX) LLEA (68); (X) multidimensional scaling algorithm (MDSA) (69); (XI) diffusion map algorithm (DMA) (70,71); (XII) stochastic proximity embedding algorithm (SPEA) (72); (XIII) gaussian process latent variable model (GPLVM) (73,74); (XIV) SNEA (75); (XV) symmetric stochastic neighbor embedding algorithm (Sym_SNEA) (76); and (XVI) autoencoders algorithms (AA) (77). These methods were implemented in R 2020 respectively.
Clustering algorithms
For the unsupervised longitudinal clustering tasks, we employ clustering algorithm to group multidimensional data based on similarity measures (78-80). In our recent study involving cross-sectional and timeless data (27,28) (but not performing longitudinal clustering, which the present work pursues), the KMA (as elaborated in Appendix 1) outperformed various clustering algorithms. In the present work, we also study KMA as applied to longitudinal clustering. KMA was implemented in MATLAB R 2020 b platform.
Clustering evaluation methods (CEM): To evaluate clustering trajectories, the so-called EC (81), CHC (82) and BIC (83) were utilized (Appendix 1), selecting optimal number of clusters from a range of cluster numbers spanning 2 to 9.
Classification algorithms (CAs)
For the supervised prediction task, we utilize a range of optimal CAs selected between various families of learner algorithms. These are all listed in Appendix 1). Specifically, we selected 9 CAs: (I) decision tree classification (DTC) (84-86); (II) Lib_SVM (87-89); (III) K nearest neighborhood classifier (KNNC) (90,91); (IV) ensemble leaner classifier (ELC) (92,93); (V) linear discriminant analysis classifier (LDAC) (94,95); (VI) NPNNC (96,97); (VII) error-correcting output codes model classifier (ECOCMC) (98,99); (VIII) multilayer perceptron_back propagation classifier (MLP_BPC) (100,101); (IX) random forest classifier (RFC) (102,103); and (X) recurrent neural network classifier (RNNC) (20,104). We performed 5-fold cross validation for all CAs and automatically adjusted intrinsic hyperparameters through automated machine learning hyperparameter tuning (as elaborated in Appendix 1) (38). We implemented all CAs in MATLAB R 2020b.
Analysis procedure
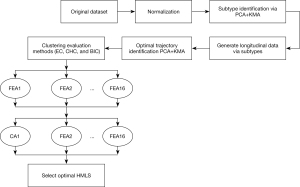
As shown in Figure 2, our work includes two main stages: (I) optimal identification of progression trajectories in PD (unsupervised task); and (II) usage of HMLSs to improve prediction performance (supervised task). For the first stage (unsupervised clustering), we first utilized a normalized original dataset (every feature was normalized based on minimum and maximum values for that feature) in order to cluster PD subjects in each year (“original subtypes”). We reproduced 3 sub-clusters as elaborated in our prior work (29), namely (I) mild, (II) intermediate, and (III) severe. Our prior work (29) showed that these clusters were consistent year to year (i.e., while patients of course may move from cluster to cluster in different years, the 3 clusters identified in each year are consistent with one another. Subsequently, a HMLS including PCA and KMA was applied to the longitudinal data as clustered in each year to a particular subtype. We then generated 4 components, and we used the first 2 components for 2-dimension visualization while we used all components to identify progression of trajectories. To optimize the number of longitudinal trajectories (clusters), we applied BIC and CHC to our results (for a range of 2–9 longitudinal clusters/trajectories) as generated by HMLS. Our optimized number of trajectories were further confirmed by EC as applied on clustering results provided by PCA + KMA. We also applied a statistical test, HTST, described in Appendix 1 (105) to measure similarities between sub-clusters. Subsequently, in stage two of our efforts (supervised task), prediction of the identified trajectories based on early years (data in year 0 and 1) was performed using multiple HMLSs, including 16 FEAs coupled to 10 CAs, as enlisted previously.
Data and code availability
All code (included prediction algorithms and feature extraction algorithms etc.) and all datasets are publicly shared at: https://github.com/MohammadRSalmanpour/Longitudinal-task
Results
First stage analysis for optimal identification of trajectories in PD
In a previous study of ours (29), involving analysis of cross-sectional data (not longitudinal clustering), HMLS including PCA + KMA enabled us to find 3 distinct subtypes consisting of: (I) mild, (II) intermediate and (III) severe. Figure 3 shows these distinct subtypes identified. We utilize these subtypes in our longitudinal data, to first cluster data from each year, followed by analysis of progression and prediction.
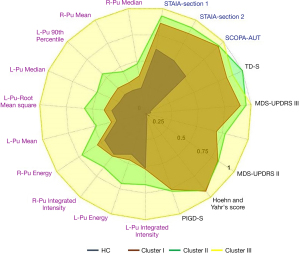
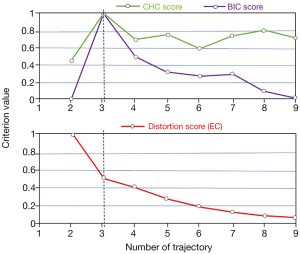
In this effort, we studied progression trajectories via following PD subtypes during year 0, 1, 2, and 4. In fact, the features define the subtypes and these subtypes change over time as features change. In fact, we used all imaging and non-imaging features as well as biologically defining PD subtypes in previous paper (29). Our important discovery was, by looking at timeless data as well as cross-sectional data, that disease in any year could be clustered to 1 of 3 distinct clusters; i.e., these clusters were significantly the same from year to year; in other words, while a patient can surely move between different clusters in different years, the 3 specific clusters themselves from year to year are very consistent. Thus, subtypes are means of representing the collective features, and changes of these subtypes over time display changes of these features over time. Next, employing 3 CEMs linked with PCA + KMA enabled us to find optimal number of trajectories. As shown in Figure 4 (top), the highest scores provided by CHC and BIC both belong to 3 optimal longitudinal trajectories, and results (bottom) provided by EC method confirms the finding.
As shown in Table 1, P values calculated by HTST show significant difference between sub-clusters. The 3 P values were adjusted via Bonferroni correction test. In short, this table demonstrates that our sub-clusters are quite distinct.
Table 1
| Subgroup (SG) | SG1 | SG2 | SG3 |
|---|---|---|---|
| SG1 | 1 | <0.001 | <0.001 |
| SG2 | <0.001 | 1 | <0.001 |
| SG3 | <0.001 | <0.001 | 1 |
After specifying optimal number of trajectories, we applied the dataset with PD subtypes to an HMLS including PCA + KMA. Figure 5 shows 3 distinct trajectory sub-clusters. The Y and X axes denote the first 2 principal components obtained by PCA, and each sub-cluster is shown using different colors. There are clear separations between the sub-clusters. In fact, we employed this plot as an independent visualization test in our effort to derive PD progression subtypes.
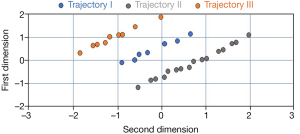
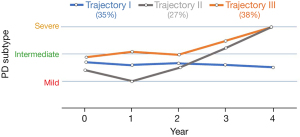
Figure 6 shows three distinct trajectories. Each point on the trajectories was calculated via averaging patient subtype values in specific year. PD patients in trajectory I (age range in year 69.4±9.5, female: 19, male: 31) showed slower progression in 4-year follow-up compared to other trajectories. In trajectory II (age range in year 67±10, female: 10, male: 28), patients show an improvement of the disease in the first 2 years and then enhanced progression in during years 2–4. Trajectory III (age range in year 68.2±11.5, female: 19, male: 36) illustrated significantly enhanced progression of PD in 4-year follow-up.
Second stage analysis including prediction of trajectories using data in year 0 and 1
After generating new dataset using data in year 0 and 1 as input and utilizing the identified trajectories as outcome (as elaborated in section II, part B), we applied the dataset to multiple HMLSs. The HMLSs consisted of FEAs and CAs (as elaborated in section II, part D). The performances are shown in Figure 7.
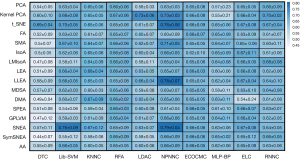
As shown in Figure 7, the hybrid HMLSs resulted in different performances for the TD01 dataset. The performances were averaged among 5 folds cross-validations tests and reported. Furthermore, their standard deviations were also calculated and reported. The best results were observed when SNEA as well as LLEA, were followed with NPNNC, resulting in accuracies of 78.4%±6.9% and 79.2%±3.6% respectively. Some other HMLSs such as SNEA linked with Lib_SVM and t_SNE linked with NPNNC resulted in 76.5%±8.9% and 76.1%±6.1% respectively. Other HMLSs such as Kernel PCA followed by RNNC, t-SNE followed by Lib-SVM, and SMA followed by NPNNC also resulted in accuracies over 70%. Meanwhile, most HMLSs including PCA + RNNC, FA + Lib-SVM, Kernel PCA + ECOCMC, DMA + KNNC, SNEA + RFA, AA + MLP-BP, etc. resulted in accuracies over 60%. Meanwhile, no improvement was observed when we used CSD0 nor CSD01 as input and the related trajectories as outcome. We achieved the maximum performance 53.6%±6.3% and 66.4%±7.6% obtained by CSD0 and CSD01 respectively (P<0.05; t-test). Moreover, we reached a maximum performance around 51%±3.3% (P<0.05; t-test) when we used sole classifiers. Employing classifiers followed by DRAs (HMLSs) has often proven to increase performance (38,43,106). In our previous study (42,106), we aimed to predict cross-sectional PD subtypes in year 4 by employing 3 kinds of dataset (such as CSD0, CSD01 and TD01) linked with different HMLSs. We also showed that the usage of TD01 only enabled us to achieve high accuracies while the usage of the other datasets such as CSD0 or CSD01 resulted poorer performances.
Discussion
Identification of PD subtypes can be defined as a clustering task so that patients within the same cluster would have more similar properties than the patients within other clusters (47), but these patients may have different progression speeds in the future (21). Longitudinal clustering enables us to identify progression of the disease in several-year follow-up (32). Clustering longitudinal trajectories constructing from the subtypes can improve the interpretation of the disease progression instead of following some specific features during several years (32) because these subtypes depict an outline of all features (29). A recent study (20) showed that different patients had different progression rates in 10-year follow-up despite the employment of various targeted treatment strategies so that 9 of 126 patients were diagnosed to confine to bed or a wheelchair unless aided, whereas 13 patients showed no significant functional restrictions. In short, PD is defined as a heterogeneous disease (4,5,7) and longitudinal clustering can help provide an easier way for the interpretation of the disease progression.
Even though prediction of PD progression was recently expressed as an important and challenging problem (107), a number of benefits are obtained by accurate prediction of the outcome in PD (108), including the improvement of the treatment methods, better comprehension of the disease progression, and the improvement in clinical interpretation for symptomatic therapy. This is particularly relevant as PD progression is heterogeneous; such variability encounters us with the challenge of predicting progression in PD patients (108). Since, large input dimensionality and small sample sizes are often common problems in research studies, dimensionality reduction algorithms have been used to deal with these problems (109). In this work, we aimed to identify optimal patterns (trajectories) of PD progression as well as predict these trajectories using data in years 0 and 1. In the first part, 3 optimal trajectories were identified by three CEMs. In the second part, we were able to accurately predict the trajectories in 4-year follow-up by HMLS that included LLEA and SNEA linked with NPNNC.
In the first effort, we analyzed the original dataset using HMLS including PCA + KMA to identify optimal PD subtypes, as described in our previous work (29). Subsequently, we utilized longitudinal datasets, where patients for each given year were associated with a subtype; the resulting longitudinal tracks were then provided to HMLSs including EC, CHC and BIC linked with KMA + PCA, for optimal longitudinal clustering. As depicted in Figure 4, the analysis of data resulted in 3 optimal trajectories. Table 1 showed that there is no similarity between the cluster, and they are quite distinct. Figure 5 shows these 3 distinct clusters; we employed this plot as an independent visualization test of our study to specify optimal PD trajectories. The plots show clear distinctions among the clusters. Figure 6 obviously depicts progression of 3 distinct trajectories in 4-year follow-up. Trajectory I showed a relatively smooth line during the 4-year follow-up. Thus, the patients in this trajectory experienced a slower progression compared to other patients. Trajectory II first showed a decrease during the first 2 years and then showed an increase to year 4. The patients in this trajectory first experienced an improvement and then a progression to the worse level (severe). The patients in trajectory III illustrated progression of PD to the worse level (severe) at the 4-year follow-up.
A challenge, and dichotomy, in data-driven discoveries is that subsequent studies may be needed to ascertain biological and clinical plausibility and value of these findings. This is also an issue in related fields. For instance, in the field of radiomics, there is significant evidence on the value of using advanced, and sometimes computationally-intense imaging features as biomarkers of disease; however, that is only one step, and subsequent or parallel analyses including biological plausibility and meaning are needed (110). Thus, there is a need for follow-up studies to further interpret and study data-driven identification of PD progression pathways.
Fereshtehnejad et al. (30) utilized the global composite outcome score from clinical data such as some motor and non-motor features to identify progression rate in PD. They first clustered PD patients using these scores and then compared progression of the scores between different subtypes in 4.5-year follow-up. Zhang et al. (31) attempted to specify the heterogeneity of PD (subtypes) using clinical data and conventional imaging features, as well as their progression rates using Long-Short Term Memory (a deep learning algorithm) applied to longitudinal clinical dataset. As proven in our previous paper (29), subtypes identified from the dataset without radiomics features are not robust to the variations in features and samples, and these subtypes may depend on the size of the features and samples. Thus, we do not compare the previous studied to this study. Meanwhile, unlike this study, to the best of our knowledge, previously published studies did not cluster the trajectory of the PD progression (30,31,38,39,43,46,111).
In the second part of this study, we employed HMLSs including multiple DRAs and CAs to predict these trajectories using TD01. As shown in Figure 7, HMLSs such as SNEA + NPNNC and LLEA + NPNNC generated accuracies of 78.4% and 79.2%, respectively. Meanwhile, Some HMLSs such as SNEA + Lib_SVM and t_SNE+ NPNNC also had appropriate results, although they were less consistent than the best HMLSs. In a recent study of ours to improve prediction (46) and diagnosis tasks (111), radiomics features extracted from DAT SPECT images, going beyond conventional imaging features, were observed to obtain significant performances. We later observed that utilizing HMLSs, predictive algorithms linked with feature subset algorithms enables very good predictions of motor (43) and cognitive (38) outcomes. In addition, employing deep learning methods enables us to significantly improve prediction of motor outcome (39). The usage of the other datasets such as CSD0 and CSD01 did not improve prediction of the trajectories. Furthermore, in our past effort (42), we employed HMLSs including feature selection algorithms linked with CAs to predict cross-sectional PD subtypes in year 4. In that study, we saw limited predictive performance when employed CSD0 and CSD01 while we reached accuracies over 90% using TD01. As a result, constructing datasets as timeless, resulting in an increase in the sample size, can enhance prediction performance.
In this study, there is a restricting factory in the size of patients for outcome prediction. To tackle the restriction, we employed a timeless approach and it led to improved prediction performance. In this work, we utilized FEAs for dimensionality reduction to avoid over-fitting, although employing feature selection algorithms such as GA and least absolute shrinkage and selection operator (LASSO) were also possible.
Our study has several strengths. Importantly, we combined different categories of databases including motor, non-imaging, conventional imaging features, and radiomics features to generate a very comprehensive set of features. In addition, we focused on added value of radiomic features which was provided by standardized manner as well as based on guidelines from the image biomarker standardization initiative, aiming towards identifying robust progression trajectories in PD, and then predicting these trajectories using data in years 0 and 1.
Conclusions
We aimed to identify robust PD progression trajectories in 4-year follow-up, incorporating clinical and imaging data. We also aimed to predict these trajectories using data in years 0 and 1. Based on three CEMs linked with PCA + KMA, we were able to identify three progression trajectories in 4-year follow-up. The identified trajectories were distinct. Trajectory I showed no enhanced progression for the period, while trajectories II and III showed enhanced progression. We also investigated a range of HMLSs including CAs linked with FEAs in order to predict these trajectories from early year data. SNEA + NPNNC and LLEA + NPNNC provided highest accuracies among all HMLSs. Overall, we conclude that combining clinical information with SPECT-based radiomics features, coupled with optimal utilization of HMLSs, can identify distinct trajectories and predict outcome in PD. In the future, we aim to predict non-motor outcome in year 4 by applying machine learning methods on datasets including clinical as well as radiomics features. Moreover, we aim to identify and predict different categories of response to treatment in PD patients, utilizing clustering of on/off-drug data as well as predicting these categories. Furthermore, we aim to predict start-date of taking drug and the administered dose. We also aim to predict rate of increase in the dose in subsequent years.
Acknowledgments
Funding: The project was supported in part by the Michael J. Fox Foundation, including use of data available from the PPMI—a public-private partnership—funded by the Michael J. Fox Foundation for Parkinson’s Research and funding partners (listed at www.ppmi-info.org/fundingpartners). This work was also supported in part by the Natural Sciences and Engineering Research Council of Canada.
Footnote
Reporting Checklist: The authors have completed the MDAR checklist. Available at https://dx.doi.org/10.21037/qims-21-425
Conflicts of Interest: The authors have completed the ICMJE uniform disclosure form (available at https://dx.doi.org/10.21037/qims-21-425). AR reports that he received grant from Natural Sciences and Engineering Research Council of Canada (NSERC) Discovery Grant RGPIN-2019-06467. The other authors have no conflicts of interest to declare.
Ethical Statement: The authors are accountable for all aspects of the work in ensuring that questions related to the accuracy or integrity of any part of the work are appropriately investigated and resolved. The study was conducted in accordance with the Declaration of Helsinki (as revised in 2013).
Open Access Statement: This is an Open Access article distributed in accordance with the Creative Commons Attribution-NonCommercial-NoDerivs 4.0 International License (CC BY-NC-ND 4.0), which permits the non-commercial replication and distribution of the article with the strict proviso that no changes or edits are made and the original work is properly cited (including links to both the formal publication through the relevant DOI and the license). See: https://creativecommons.org/licenses/by-nc-nd/4.0/.
References
- Simuni T, Sethi K. Nonmotor manifestations of Parkinson's disease. Ann Neurol 2008;64:S65-80. [Crossref] [PubMed]
- Wolter E. Non-motor extranigral signs and symptoms in Parkinson’s disease. Parkinsonism Relat Disord 2009;3:6-12. [Crossref]
- Bayulkem K, Lopez G. Non-motor fluctuations in Parkinson’s disease: clinical spectrum and classification. J Neurol Sci 2010;289:89-92. [Crossref] [PubMed]
- Foltynie T, Brayne C, Barker RA. The heterogeneity of idiopathic Parkinson's disease. J Neurol 2002;249:138-45. [Crossref] [PubMed]
- Berg D, Postuma RB, Bloem B, Chan P, Dubois B, Gasser T, Goetz CG, Halliday GM, Hardy J, Lang AE, Litvan I, Marek K, Obeso J, Oertel W, Olanow CW, Poewe W, Stern M, Deuschl G. Time to redefine PD? Introductory statement of the MDS Task Force on the definition of Parkinson's disease. Mov Disord 2014;29:454-62. [Crossref] [PubMed]
- Lewis SJ, Foltynie T, Blackwell AD, Robbins TW, Owen AM, Barker RA. Heterogeneity of Parkinson's disease in the early clinical stages using a data driven approach. J Neurol Neurosurg Psychiatry 2005;76:343-8. [Crossref] [PubMed]
- Eggers C, Pedrosa DJ, Kahraman D, Maier F, Lewis CJ, Fink GR, Schmidt M, Timmermann L. Parkinson subtypes progress differently in clinical course and imaging pattern. PLoS One 2012;7:e46813. [Crossref] [PubMed]
- Dai D, Wang Y, Wang L, Li J, Ma Q, Tao J, Zhou X, Zhou H, Jiang Y, Pan G, Xu L, Ru P, Lin D, Pan J, Xu L, Ye M, Duan S. Polymorphisms of DRD2 and DRD3 genes and Parkinson's disease: A meta-analysis. Biomed Rep 2014;2:275-81. [Crossref] [PubMed]
- Lebouvier T, Chaumette T, Paillusson S, Duyckaerts C, Bruley des Varannes S, Neunlist M, Derkinderen P. The second brain and Parkinson's disease. Eur J Neurosci 2009;30:735-41. [Crossref] [PubMed]
- McNamara P, Stavitsky K, Harris E, Szent-Imrey O, Durso R. Mood, side of motor symptom onset and pain complaints in Parkinson's disease. Int J Geriatr Psychiatry 2010;25:519-24. [Crossref] [PubMed]
- Bell PT, Gilat M, O'Callaghan C, Copland DA, Frank MJ, Lewis SJ, Shine JM. Dopaminergic basis for impairments in functional connectivity across subdivisions of the striatum in Parkinson's disease. Hum Brain Mapp 2015;36:1278-91. [Crossref] [PubMed]
- Bohnen NI, Albin RL. The cholinergic system and Parkinson disease. Behav Brain Res 2011;221:564-73. [Crossref] [PubMed]
- Maril S, Hassin-Baer S, Cohen OS, Tomer R. Effects of asymmetric dopamine depletion on sensitivity to rewarding and aversive stimuli in Parkinson's disease. Neuropsychologia 2013;51:818-24. [Crossref] [PubMed]
- Ventura MI, Baynes K, Sigvardt KA, Unruh AM, Acklin SS, Kirsch HE, Disbrow EA. Hemispheric asymmetries and prosodic emotion recognition deficits in Parkinson's disease. Neuropsychologia 2012;50:1936-45. [Crossref] [PubMed]
- Cubo E, Martín PM, Martin-Gonzalez JA, Rodríguez-Blázquez C, Kulisevsky JELEP Group Members. Motor laterality asymmetry and nonmotor symptoms in Parkinson's disease. Mov Disord 2010;25:70-5. [Crossref] [PubMed]
- Antonini A, Isaias IU, Canesi M, Zibetti M, Mancini F, Manfredi L, Dal Fante M, Lopiano L, Pezzoli G. Duodenal levodopa infusion for advanced Parkinson's disease: 12-month treatment outcome. Mov Disord 2007;22:1145-9. [Crossref] [PubMed]
- Tippmann-Peikert M, Park JG, Boeve BF, Shepard JW, Silber MH. Pathologic gambling in patients with restless legs syndrome treated with dopaminergic agonists. Neurology 2007;68:301-3. [Crossref] [PubMed]
- Lang AE, Lozano AM. Parkinson's disease. Second of two parts. N Engl J Med 1998;339:1130-43. [Crossref] [PubMed]
- Savitt JM, Dawson VL, Dawson TM. Diagnosis and treatment of Parkinson disease: molecules to medicine. J Clin Invest 2006;116:1744-54. [Crossref] [PubMed]
- Hely MA, Morris JG, Traficante R, Reid WG, O'Sullivan DJ, Williamson PM. The sydney multicentre study of Parkinson's disease: progression and mortality at 10 years. J Neurol Neurosurg Psychiatry 1999;67:300-7. [Crossref] [PubMed]
- Fereshtehnejad SM, Zeighami Y, Dagher A, Postuma RB. Clinical criteria for subtyping Parkinson's disease: biomarkers and longitudinal progression. Brain 2017;140:1959-76. [Crossref] [PubMed]
- Graham JM, Sagar HJ. A data-driven approach to the study of heterogeneity in idiopathic Parkinson's disease: identification of three distinct subtypes. Mov Disord 1999;14:10-20. [Crossref] [PubMed]
- Erro R, Vitale C, Amboni M, Picillo M, Moccia M, Longo K, Santangelo G, De Rosa A, Allocca R, Giordano F, Orefice G, De Michele G, Santoro L, Pellecchia MT, Barone P. The heterogeneity of early Parkinson's disease: a cluster analysis on newly diagnosed untreated patients. PLoS One 2013;8:e70244. [Crossref] [PubMed]
- Post B, Speelman JD, de Haan RJCARPA-study group. Clinical heterogeneity in newly diagnosed Parkinson's disease. J Neurol 2008;255:716-22. [Crossref] [PubMed]
- Gasparoli E, Delibori D, Polesello G, Santelli L, Ermani M, Battistin L, Bracco F. Clinical predictors in Parkinson's disease. Neurol Sci 2002;23:S77-8. [Crossref] [PubMed]
- Poletti M, Frosini D, Pagni C, Lucetti C, Del Dotto P, Tognoni G, Ceravolo R, Bonuccelli U. The association between motor subtypes and alexithymia in de novo Parkinson's disease. J Neurol 2011;258:1042-5. [Crossref] [PubMed]
- Salmanpour M, Shamsaei M, Saberi A, Hajianfar G, Ashrafinia S, Davoodi-Bojd E, Soltanian-Zadeh H, Rahmim A. Hybrid Machine Learning Methods for Robust Identification of Parkinson’s Disease Subtypes. J Nucl Med 2020;61:1429.
- Salmanpour M, Shamsaei M, Saberi A, Hajianfar G, Soltanian-Zadeh H, Rahmim A. Radiomic features combined with hybrid machine learning robustly identify Parkinson’s disease subtypes. Annual AAPM Meeting, 2020.
- Salmanpour MR, Shamsaei M, Saberi A, Hajianfar G, Soltanian-Zadeh H, Rahmim A. Robust identification of Parkinson's disease subtypes using radiomics and hybrid machine learning. Comput Biol Med 2021;129:104142. [Crossref] [PubMed]
- Fereshtehnejad SM, Romenets SR, Anang JB, Latreille V, Gagnon JF, Postuma RB. New Clinical Subtypes of Parkinson Disease and Their Longitudinal Progression: A Prospective Cohort Comparison With Other Phenotypes. JAMA Neurol 2015;72:863-73. [Crossref] [PubMed]
- Zhang X, Chou J, Liang J, Xiao C, Zhao Y, Sarva H, Henchcliffe C, Wang F. Data-Driven Subtyping of Parkinson's Disease Using Longitudinal Clinical Records: A Cohort Study. Sci Rep 2019;9:797. [Crossref] [PubMed]
- Salmanpour M, Saberi A, Hajianfar G, Shamsaei M, Soltanian-Zadeh H, Rahmim A. Cluster analysis on longitudinal data of Parkinson’s disease subjects. Proc Annual AAPM Meeting, 2020.
- Nieuwboer A, De Weerdt W, Dom R, Bogaerts K. Prediction of outcome of physiotherapy in advanced Parkinson's disease. Clin Rehabil 2002;16:886-93. [Crossref] [PubMed]
- Grill S, Weuve J, Weisskopf MG. Predicting outcomes in Parkinson's disease: comparison of simple motor performance measures and The Unified Parkinson's Disease Rating Scale-III. J Parkinsons Dis 2011;1:287-98. [Crossref] [PubMed]
- Arnaldi D, De Carli F, Famà F, Brugnolo A, Girtler N, Picco A, Pardini M, Accardo J, Proietti L, Massa F, Bauckneht M, Morbelli S, Sambuceti G, Nobili F. Prediction of cognitive worsening in de novo Parkinson's disease: Clinical use of biomarkers. Mov Disord 2017;32:1738-47. [Crossref] [PubMed]
- Fyfe I. Prediction of cognitive decline in PD. Nat Rev Neurol 2018;14:316-7. [Crossref] [PubMed]
- Gao C, Sun H, Wang T, Tang M, Bohnen NI, Müller MLTM, Herman T, Giladi N, Kalinin A, Spino C, Dauer W, Hausdorff JM, Dinov ID. Model-based and Model-free Machine Learning Techniques for Diagnostic Prediction and Classification of Clinical Outcomes in Parkinson's Disease. Sci Rep 2018;8:7129. [Crossref] [PubMed]
- Salmanpour MR, Shamsaei M, Saberi A, Setayeshi S, Klyuzhin IS, Sossi V, Rahmim A. Optimized machine learning methods for prediction of cognitive outcome in Parkinson's disease. Comput Biol Med 2019;111:103347. [Crossref] [PubMed]
- Leung K, Salmanpour MR, Saberi A, Klyuzhin I, Sossi V, Rahmim A. Using deep-learning to predict outcome of patients with Parkinson’s disease. Sydney, Australia: 2018 IEEE Nuclear Science Symposium and Medical Imaging Conference, NSS/MIC 2018.
- Emrani S, McGuirk A, Xiao W. Prognosis and Diagnosis of Parkinson’s Disease Using Multi-Task Learning. New York, NY, USA: Proceedings of the 23rd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining (KDD '17). Association for Computing Machinery, 1457-66.
- Salmanpour MR, Shamsaei M, Saberi A, Setayeshi S, Taherinezhad E, Klyuzhin IS, Tang J, Sossi V, Rahmim A. Machine Learning Methods for Optimal Prediction of Outcome in Parkinson’s Disease. Available online: https://rahmimlab.files.wordpress.com/2019/03/salmanpour_mic18_pd_prediction_machine_learning.pdf
- Salmanpour M, Saberi A, Shamsaei M, Rahmim A. Optimal Feature Selection and Machine Learning for Prediction of Outcome in Parkinson’s Disease. J Nucl Med 2020;61:524.
- Salmanpour MR, Shamsaei M, Saberi A, Klyuzhin IS, Tang J, Sossi V, Rahmim A. Machine learning methods for optimal prediction of motor outcome in Parkinson's disease. Phys Med 2020;69:233-40. [Crossref] [PubMed]
- Parashos SA, Luo S, Biglan KM, Bodis-Wollner I, He B, Liang GS, Ross GW, Tilley BC, Shulman LM. NET-PD Investigators. Measuring disease progression in early Parkinson disease: the National Institutes of Health Exploratory Trials in Parkinson Disease (NET-PD) experience. JAMA Neurol 2014;71:710-6. [Crossref] [PubMed]
- Chaudhuri KR, Naidu Y. Early Parkinson's disease and non-motor issues. J Neurol 2008;255:33-8. [Crossref] [PubMed]
- Rahmim A, Huang P, Shenkov N, Fotouhi S, Davoodi-Bojd E, Lu L, Mari Z, Soltanian-Zadeh H, Sossi V. Improved prediction of outcome in Parkinson's disease using radiomics analysis of longitudinal DAT SPECT images. Neuroimage Clin 2017;16:539-44. [Crossref] [PubMed]
- Parkinson Progression Marker Initiative. The Parkinson Progression Marker Initiative (PPMI). Prog Neurobiol 2011;95:629-35. [Crossref] [PubMed]
- Miller SA, Mayol M, Moore ES, Heron A, Nicholos V, Ragano B. Rate of Progression in Activity and Participation Outcomes in Exercisers with Parkinson's Disease: A Five-Year Prospective Longitudinal Study. Parkinsons Dis 2019;2019:5679187. [Crossref] [PubMed]
- Aleksovski D, Miljkovic D, Bravi D, Antonini A. Disease progression in Parkinson subtypes: the PPMI dataset. Neurol Sci 2018;39:1971-6. [Crossref] [PubMed]
- Han C, Rundo L, Murao K, Noguchi T, Shimahara Y, Milacski ZÁ, Koshino S, Sala E, Nakayama H, Satoh S. MADGAN: unsupervised medical anomaly detection GAN using multiple adjacent brain MRI slice reconstruction. BMC Bioinformatics 2021;22:31. [Crossref] [PubMed]
- Nakao T, Hanaoka S, Nomura Y, Murata M, Takenaga T, Miki S, Watadani T, Yoshikawa T, Hayashi N, Abe O. Unsupervised Deep Anomaly Detection in Chest Radiographs. J Digit Imaging 2021;34:418-27. [Crossref] [PubMed]
- Rundo L, Militello C, Tangherloni A, Russo G, Vitabile S, Gilardi MC, Mauri G. NeXt for neuro-radiosurgery: A fully automatic approach for necrosis extraction in brain tumor MRI using an unsupervised machine learning technique. Int J Imaging Syst Technol 2017;28:21-37. [Crossref]
- Mekhmoukh A, Mokrani K. Improved Fuzzy C-Means based Particle Swarm Optimization (PSO) initialization and outlier rejection with level set methods for MR brain image segmentation. Comput Methods Programs Biomed 2015;122:266-81. [Crossref] [PubMed]
- Ashrafinia S. Quantitative Nuclear Medicine Imaging using Advanced Image Reconstruction and Radiomics. USA: Johns Hopkins University, 2019.
- Mwangi B, Tian TS, Soares JC. A review of feature reduction techniques in neuroimaging. Neuroinformatics 2014;12:229-44. [Crossref] [PubMed]
- Reif M, Shafait F. Efficient feature size reduction via predictive forward selection. Pattern Recognition 2014;47:1664-73. [Crossref]
- Patel MJ, Khalaf A, Aizenstein HJ. Studying depression using imaging and machine learning methods. Neuroimage Clin 2016;10:115-23. [Crossref] [PubMed]
- Wold S, Esbensen K, Geladi P. Principal component analysis. Chemometr Intell Lab Syst 1987;2:37-52. [Crossref]
- Wenming Z, Cairong Z, Li Z. An Improved Algorithm for Kernel Principal Component Analysis. Neural Process Lett 2005;22:49-56. [Crossref]
- Maaten L, Hinton G. Visualizing Data Using t-SNE. J Mach Learn Res 2008;9:2579-605.
- Tinsley H, Tinsley D. Uses of factor analysis in counseling psychology research. J Couns Psychol 1987;34:414-24. [Crossref]
- Sammon JW. A Nonlinear Mapping for Data Structure Analysis. IEEE Transactions on Computers 1969;5:401-9. [Crossref]
- Sun J, Crowe M, Fyfe C. Extending Sammon mapping with Bregman divergences. Information Sciences 2012;187:72-92. [Crossref]
- Tenenbaum JB, de Silva V, Langford JC. A global geometric framework for nonlinear dimensionality reduction. Science 2000;290:2319-23. [Crossref] [PubMed]
- Shi H, Yin B. Robust L-Isomap with a Novel Landmark Selection Method. Available online: https://www.hindawi.com/journals/mpe/2017/3930957/
- Belkin M, Niyogi P. Laplacian Eigenmaps and Spectral Techniques for Embedding and Clustering. Available online: https://papers.nips.cc/paper/2001/file/f106b7f99d2cb30c3db1c3cc0fde9ccb-Paper.pdf
- Lewandowski M, Rincon JMd, Makris D, Nebel J. Temporal extension of laplacian eigenmaps for unsupervised dimensionality reduction of time series. Istanbul, Turkey: 20th International Conference on Pattern Recognition, 2010.
- Roweis ST, Saul LK. Nonlinear dimensionality reduction by locally linear embedding. Science 2000;290:2323-6. [Crossref] [PubMed]
- Mead A. Review of the Development of Multidimensional Scaling Methods. J R Stat Soc Ser C Appl Stat 1992;41:27-39.
- Coifman RR, Lafon S, Lee AB, Maggioni M, Nadler B, Warner F, Zucker SW. Geometric diffusions as a tool for harmonic analysis and structure definition of data: diffusion maps. Proc Natl Acad Sci U S A 2005;102:7426-31. [Crossref] [PubMed]
- Coifman R, Lafon S. Diffusion maps. Appl Comput Harmon Anal 2006;21:5-30. [Crossref]
- Agrafiotis DK. Stochastic proximity embedding. J Comput Chem 2003;24:1215-21. [Crossref] [PubMed]
- Li P, Chen S. A review on Gaussian Process Latent Variable Models. CAAI Trans Intell Technol 2016;1:366-76. [Crossref]
- Lawrence N. Learning for Larger Datasets with the Gaussian Process Latent Variable Model. J Mach Learn Res 2007;2:243-50.
- Hinton G, Roweis S. Stochastic Neighbor Embedding. Adv Neural Inf Process Syst 2003;15:857-64.
- Nam K, Je H, Choi S. Fast stochastic neighbor embedding: a trust-region algorithm. Budapest: IEEE International Joint Conference on Neural Networks, 2004.
- Hinton GE, Salakhutdinov RR. Reducing the dimensionality of data with neural networks. Science 2006;313:504-7. [Crossref] [PubMed]
- Jain A, Duin R, Mao J. Statistical Pattern Recognition: A Review. Available online: https://ieeexplore.ieee.org/document/824819
- Jain M, Murty M, Flynn P. Data Clustering: A Review. ACM Comput Surv 1999;31:264-323. [Crossref]
- Rodriguez MZ, Comin CH, Casanova D, Bruno OM, Amancio DR, Costa LDF, Rodrigues FA. Clustering algorithms: A comparative approach. PLoS One 2019;14:e0210236. [Crossref] [PubMed]
- Bholowalia P, Kumar A. Kmeans: A clustering technique based on elbow method and k-means in WSN. Int J Comput Appl 2014;105:17-24.
- Caliński T, Harabasz J. A dendrite method for cluster analysis. Commun Stat Theory Methods 1974;3:1-27. [Crossref]
- Schwarz G. Estimating the dimension of a model. Ann Stat 1987;6:461-4.
- Goodman RM, Smyth P. Decision tree design using information theory. Available online: https://www.sciencedirect.com/science/article/abs/pii/S1042814305800202
- Chourasia S. Survey paper on improved methods of ID3 decision tree. Available online: http://citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.402.7503
- Denison, D, Holmes C, Mallick B, Smith A. Bayesian Methods for Nonlinear Classification and Regression. New York: John Wiley and Sons, 2002.
- Chang CC, Lin CJ. LIBSVM: A library for support vector machines. ACM Trans Intell Syst Technol 2011;2:1-27. [Crossref]
- Cortes C, Vapnik V. Support-Vector Networks. Mach Learn 1995;20:273-97. [Crossref]
- Crammer K, Singer Y. On the algorithmic implementation of multiclass kernel-based vector machines. J Mach Learn 2001;2:265-92.
- Altman N. An introduction to kernel and nearest-neighbor nonparametric regression. Am Stat 1992;46:175-85.
- Suguna N, Thanushkodi K. An Improved k-Nearest Neighbor Classification Using Genetic Algorithm. Available online: https://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.404.1475&rep=rep1&type=pdf
- Talbot J, Lee B, Kapoor A, Tan D. EnsembleMatrix: interactive visualization to support machine learning with multiple classifiers. Boston, MA: CHI ‘09: CHI Conference on Human Factors in Computing Systems, 2009.
- Shan J, Zhang H, Liu W, Liu Q. Online Active Learning Ensemble Framework for Drifted Data Streams. IEEE Trans Neural Netw Learn Syst 2019;30:486-98. [Crossref] [PubMed]
- Lu Q, Qiao X. Sparse Fisher’s linear discriminant analysis for partially labeled data. Stat Anal Data Min 2018;11:17-31. [Crossref]
- McLachlan G. Discriminant Analysis and Statistical Pattern Recognition. New Jersey: John Wiley & Sons, 1992.
- Kusy M, Zajdel R. Probabilistic neural network training procedure based on Q(0)-learning algorithm in medical data classification. Appl Intell 2014;41:837-54. [Crossref]
- Specht DF. Probabilistic neural networks and the polynomial Adaline as complementary techniques for classification. IEEE Trans Neural Netw 1990;1:111-21. [Crossref] [PubMed]
- Joutsijoki H, Haponen M, Rasku J, Aalto-Setälä K, Juhola M. Error-Correcting Output Codes in Classification of Human Induced Pluripotent Stem Cell Colony Images. Biomed Res Int 2016;2016:3025057. [Crossref] [PubMed]
- Hamming R. Error Detecting and Error Correcting Codes. Bell System Technical Journal 1950;29:147-60. [Crossref]
- Alsmadi M, Omar K, Noah S. Back Propagation Algorithm: The Best Algorithm. Available online: http://paper.ijcsns.org/07_book/200904/20090451.pdf
- Rumelhart D, Geoffrey E. Leaner Representations By back-Propagating errors. Nature 1986;323:533-6. [Crossref]
- Breiman L. Random Forests. Mach Learn 2001;45:5-32. [Crossref]
- Jehad A, Khan R, Ahmad N. Random Forests and Decision Trees. Available online: https://www.uetpeshawar.edu.pk/TRP-G/Dr.Nasir-Ahmad-TRP/Journals/2012/Random%20Forests%20and%20Decision%20Trees.pdf
- Nijole M, Aleksan. Investigation of financial market prediction by recurrent neural network. Available online: http://journal.kolegija.lt/iitsbe/2011/Maknickiene-investigation-IITSBE-2011-2(11)-3-8.pdf
- Hu Z, Tong T, Genton MG. Diagonal likelihood ratio test for equality of mean vectors in high-dimensional data. Biometrics 2019;75:256-67. [Crossref] [PubMed]
- Salmanpour MR, Shamsaei M, Rahmim A. Feature selection and machine learning methods for optimal identification and prediction of subtypes in Parkinson's disease. Comput Methods Programs Biomed 2021;206:106131. [Crossref] [PubMed]
- Tiwari K, Jamal S, Grover S, Goyal S, Singh A, Grover A. Cheminformatics Based Machine Learning Approaches for Assessing Glycolytic Pathway Antagonists of Mycobacterium tuberculosis. Comb Chem High Throughput Screen 2016;19:667-75. [Crossref] [PubMed]
- Marras C, Rochon P, Lang AE. Predicting motor decline and disability in Parkinson disease: a systematic review. Arch Neurol 2002;59:1724-8. [Crossref] [PubMed]
- Saeys Y, Inza I, Larrañaga P. A review of feature selection techniques in bioinformatics. Bioinformatics 2007;23:2507-17. [Crossref] [PubMed]
- Tomaszewski MR, Gillies RJ. The Biological Meaning of Radiomic Features. Radiology 2021;298:505-16. [Crossref] [PubMed]
- Cheng Z, Zhang J, He N, Li Y, Wen Y, Xu H, Tang R, Jin Z, Haacke EM, Yan F, Qian D. Radiomic Features of the Nigrosome-1 Region of the Substantia Nigra: Using Quantitative Susceptibility Mapping to Assist the Diagnosis of Idiopathic Parkinson's Disease. Front Aging Neurosci 2019;11:167. [Crossref] [PubMed]


