
A data-driven approach to optimal beam/arc angle selection for liver stereotactic body radiation therapy treatment planning
Introduction
Liver tumor has relatively high occurrence among cancer patients: Primary liver cancer has been shown to be one of the most frequently occurred cancer and leading causes of death worldwide; and liver is a frequent metastasize site for many high occurrence cancers such as breast and lung (1). In the last decade it has been shown that stereotactic body radiation therapy (SBRT) is an effective treatment modality for liver tumors that are relatively small in size (2-5), particularly for patient with unresectable liver metastases (6).
The technical aspect of delivering liver SBRT extends beyond regular positional and dosimetric accuracies that are commonly emphasized for other SBRT treatment such as lung. Most often for a typical radiation therapy clinic, intensity modulated radiation therapy (IMRT) or volumetric modulated arc therapy (VMAT) are mostly widely available delivery techniques for SBRT treatment (7). Due to the high demand of dose conformity and normal liver sparing, careful choice of beam angle is critical at the beginning of treatment planning process. A suboptimal choice of beam angles cannot be compensated by intensity or volumetric modulation (8), and is often difficult to correct at later planning stage as no adjustment to beam directions can be made within the optimization process.
Although several studies have shown that non-coplanar IMRT could result in improved dosimetry (8-10), it is not directly applicable to VMAT-based treatment that are often preferred due to better conformity and efficiency. In addition, increasing number of institutions have adopted Halcyon™ ring-gantry linac system or Ethos™ online adaptive treatment system that are only capable of delivery coplanar treatment. Therefore, exploring optimal beam angle selection for coplanar IMRT and VMAT is still a meaningful clinical pursuit.
In practice the selection of beam or arc angles by human planners is often achieved relying on experience, which could potentially lead to variability in plan quality due to non-uniform experience levels of the planners (11). To address this issue, many researchers have proposed automated beam angle choice solutions for IMRT. Some of the proposed methods were based on exhaustive or random search that typically takes 1–20 hours to finish (12-27), while others employed shape-driven methods based mostly on patient anatomy and beam’s eye view as well as dose-volume histogram (DVH) features that required iterative dose calculation (28-36). No prior study was found to provide automatic VMAT arc geometry selection. Through observations of expert planner’s beam angle selection decision process, we noticed that the choice of optimal beam angles for liver SBRT is neither equidistant nor purely anatomy driven—rather the planner’s beam placement is guided by intentionally placing beams to drive key isodose lines (e.g., 20 Gy) away from normal liver. This represents an active trade-off decision process that allows for heterogeneous dose fall-off outside planning target volume (PTV) in exchange for better liver sparing, which is somewhat unique to liver SBRT.
In the subsequent sections we describe and evaluate a model that captures the abovementioned unique human planner decision process during liver SBRT planning and provides a unified decision support tool for beam and arc angle selection. The algorithm models human planner’s decision process by analyzing relationship between important isodose lines, key structure contours, and planner’s choice of beam angles. This model is applicable to both IMRT and VMAT techniques and can rapidly adapt to the preference of individual physician or institution.
Methods
Materials
In this study, a total of 27 liver SBRT or hypo-fractionated image-guided radiation therapy (HIGRT) patients treated at Duke University Medical Center were retrospectively included with Internal Review Board (IRB) approval. All plans were generated in Eclipse® treatment planning system (TPS) version 15.6 or earlier (Varian Medical Systems, Palo Alto, CA) for a TrueBeam® linear accelerator (Linac). Plan parameter details were listed in Table 1. Total prescription was dependent on the patient liver volume, prior liver radiation therapy history etc. The most common prescription for SBRT liver treatment is 5,000 cGy in 5 fractions while for liver HIGRT the dose was reduced to 5,000 cGy in 10 fractions. Key organs-at-risk (OARs) included liver, chest wall, skin and gastro-intestine (GI) luminal structures such as bowel and duodenum. Treatment technique was determined by the planner. The choice of the technique is largely dependent on several factors, including PTV volume, healthy liver volume, PTV shape, PTV location and treatment planning constraints etc. The final treatment technique and corresponding gantry setting is reflection of patient specific geometry and associated planning constraints after several iterations of trial-and-error optimization.
Table 1
| Category | Variation | Number of cases (N) |
|---|---|---|
| Technique | IMRT | 11 |
| VMAT | 14 | |
| DCA | 2 | |
| Energy | 6XFFF | 2 |
| 10X | 7 | |
| 10XFFF | 17 | |
| 15X | 1 | |
| Fractions | 3 | 3 |
| 5 | 8 | |
| 8 | 1 | |
| 10 | 12 | |
| 15 | 1 | |
| 25 | 2 |
IMRT, intensity modulated radiation therapy; VMAT, volumetric modulated arc therapy; DCA, dynamic conformal arc.
Modeling approach
In this study, we tried to model the decision process of beam setting by the planner. In addition, we attempted to create a unified formulism that is generalizable between IMRT and VMAT (or dynamic conformal arc, DCA). We introduced the concept of “dosimetric budget index” which is used to describe the dose penetration feature of each IMRT beam/VMAT beamlet. As human planners try to place a beam, they often try to avoid long penetration depth through the body as well as the liver tissue while balancing the beam angle span for IMRT and arc span for VMAT. Therefore, a cost function combining the dosimetric budget index and the beam/arc span function was generated to model the human planner’s decision process. It was written as follows:
where Bbody and Bliver are body and liver dosimetric budget index, respectively. tbody and tliver, a and b are weighting coefficients. fbeam is the beam/arc span penalty function defined separately for IMRT and VMAT. The first two terms are combined body and liver dosimetric budget index, respectively. Coefficient tbody and tliver were used as the offset cutoff threshold for body and liver dosimetric budget index. Weighting coefficient a and b were used for tuning the relative weighting between three terms. The dosimetric budget was calculated as the radiological depth (in mm) within the respective organ prior to reaching the surface of the PTV, averaged across all beams (for IMRT) or beamlets/control points (for VMAT).
The beam/arc span penalty function was written as:
for IMRT. Nb is the number of total beams. The threshold gantry angle of 20 degrees for adjacent beams and 5 degrees diversion for opposing beams were decided based on routine clinical practice. The formulism was written to balance the IMRT beam angle span while maximizing the freedom of optimization.
For VMAT, the function was written as:
where Gstart and Gterminal are the first and last control point gantry angle. The threshold arc span was chosen as 180 degrees as VMAT plans often avoid less than 180-degree arc as the freedom of optimization is substantially reduced when arc span is less than 180-degree.
Solving the optimal beam/arc setting B for IMRT/VMAT could then be expressed as the minimization problem for the cost function Ω.
and
All weighting coefficients were tuned with training dataset using grid search. For coefficient a and b, the search grid was (0, 10) with step size of 0.2. For tbody and tliver, the grid range was (0, 150) with step size of 5. Tuned parameters were then applied in Eqs. [4] and [5] to optimize for the beam setting for the validation case. For IMRT prediction, candidate beam angles were sampled with 5-degree increment (a total of 72 candidates) and beams were sequentially added which minimizes the cost function. In this study, we aimed to predict 10-beam IMRT setting. For VMAT, start and terminal control point beam angle was also sampled at every 5-degree increment. The start-terminal arc setting that minimizes the overall cost function was chosen as the optimal arc setting for the VMAT plan.
Model validation
Due to the data scarcity of liver SBRT/HIGRT nature, all cases included in this study were used in leave-one-out validation process. All 27 cases were divided into two groups: (I) IMRT with 11 cases and (II) rotational arc therapy (VMAT and DCA) with 16 cases. All N-1 cases within each group were used to tune coefficients in nested cross validation fashion and the remained one case was used for testing (N=11 for IMRT group and N=16 for VMAT/DCA group). All predicted beam/arc setting was used to guide a manual replan, i.e., a model plan, to validate the efficacy and robustness of the knowledge model. For IMRT plans, a 10-beam IMRT beam setting was predicted. For VMAT plans, the replan shared the same number of arcs as the clinical plan to reduce confounding effect from the degree of modulation. The model plans were optimized with original optimization constraints and normalized to the same PTV coverage at prescription dose level. Same dose calculation algorithm and leaf sequencing algorithm were used as the original clinical plan to eliminate impact from dose calculation engines. The model plan was compared with the clinical plan to assess key dosimetric endpoints including PTV D98%, D2%, liver V20Gy and total monitor units (MU). Wilcoxon Signed-Rank test was performed with the null hypothes being that no difference exists between two groups. All patient data were anonymized and exported to Matlab® R2019b (Natick, MA) for processing. All model plans were generated in Eclipse® treatment planning system version 15.6.
Results
Knowledge guided beam setting prediction for all 27 cases included in this study is shown Figure 1. Overall the beam setting was comparable between prediction (left column) and clinically employed beam setting (right column). For IMRT plans, the beam clusters were generally similar between the manually set clinical beam angles and the model predicted beam angles, indicating the model’s capability to mimic planner’s decision process in tailoring the beam angles to maximize target coverage and OAR sparing. For VMAT plans, the arc span as well as the start/terminal beam angle were comparable for the majority of the cases.
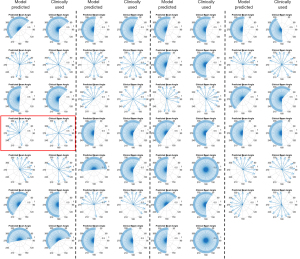
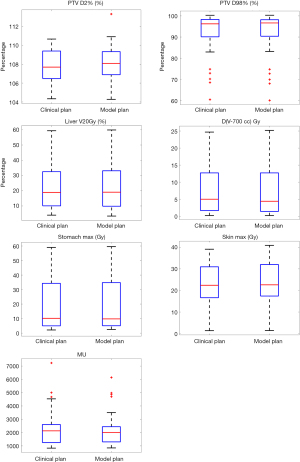
Table 2 summarizes the dosimetric comparison between the clinical plan with manually placed beams and the model plan with model predicted beam angles. With the identical plan normalization at V100% for the PTV for both plans, D2% (%) and D98% (%) was 107.9% and 91.3% for the clinical plan, compared to 108.1% and 91.3% for the model plan, with no statistical significance observed (P=0.164 and 0.566). For key dosimetric sparing of liver V20Gy, the mean value was 23.3% for clinical plan and 23.4% for the model plan (P=0.590). For 700 cc healthy liver tissue, the max dose was 7.5 Gy for both the clinical plan and model plan (P=0.972). Overall similar liver V20Gy and D(V-700cc) Gy indicated that the knowledge modeled beam setting was capable of generating clinically acceptable liver sparing without manual trial-and-error beam placement process. Max dose to the stomach was 20.5 Gy in the clinical plan and 20.6 Gy in the model plan (P=0.952). Max dose to the skin was 23.3 Gy in the clinical plan and 23.7 Gy in the model plan (P=0.883). MU between two plan groups were also similar: the mean MU was 2,389.6 and 2,319.6 for the clinical plan and the model plan, respectively. Similar MU indicates that the model’s predicted beam setting balanced the dosimetric budget while maintained sufficient beam/arc span to provide adequate degree of freedom for optimization, in other words the modulation complexity between corresponding clinical-plans and model-plans was similar.
Table 2
| PTV | Liver | Stomach | Skin | MU | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| D2% (%) | D98% (%) | V20Gy (%) | D(V-700cc) Gy | Max Dose (Gy) | Max Dose (Gy) | |||||
| Clinical Plan | ||||||||||
| Mean | 107.9 | 91.3 | 23.3 | 7.5 | 20.5 | 23.3 | 2,389.6 | |||
| SD | 1.6 | 11.4 | 17.2 | 7.1 | 17.7 | 9.6 | 1,472.8 | |||
| Model Plan | ||||||||||
| Mean | 108.1 | 91.3 | 23.4 | 7.5 | 20.6 | 23.7 | 2,319.6 | |||
| SD | 2.0 | 11.5 | 17.4 | 7.2 | 17.9 | 9.7 | 1,373.2 | |||
| P value | 0.164 | 0.566 | 0.590 | 0.972 | 0.952 | 0.883 | 0.256 | |||
Statistical significance was based on Wilcoxon Signed-Rank test and significance level was set to 0.05. SD, standard deviation.
Figure 2 shows the boxplot of dosimetric endpoint comparison between two plan groups. Not only was the mean and standard deviation similar between two groups as presented in Table 2, the overall distribution as indicated in the interquartile range and median (red bar in the box) were also similar as shown in Figure 2.
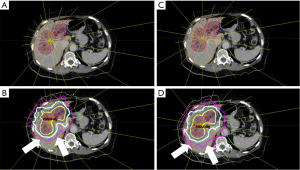
An example case (row 4 column 1 in Figure 1) of isodose distribution comparison between the clinical plan and the model plan is shown in Figure 3. The yellow lines indicated the IMRT beam central axis with the short end representing beam sources. It was observed that the model plan used more clustered beam bouquet from patient anterior-right direction while minimizing beams coming from patient posterior direction. This particular arrangement helped reduced the 20 Gy isodose line (pink) from expanding beyond the posterior of the PTV which was predominantly healthy liver tissue, while purposefully driving the dose spill to patient anterior-right surface which was primarily adipose tissue. The model plan showed improved liver V20Gy from clinical plan (48.1% vs. 51.5%) as shown in the DVH comparison in Figure 4. This observation clearly demonstrated that he evidence based model was capable of capturing the human planner’s decision making and reasoning of selecting and arranging beams, and actively making reasonable trade-off to achieve dosimetric constraints with higher clinical priorities.

Discussion
In this study, we proposed a knowledge modeling approach to assist beam angle/arc placement for liver SBRT/HIGRT treatment planning. The results were promising and showed encouraging capability of capturing and understanding the rationale of human planner to place beam after trial-and-error process. The overall beam angle and arc span were similar between the clinical plan and the model plan, in terms of the range that was covered in 2π space. Some exceptions were observed between half-arc versus full-arc, which was probably due to the small volume of the PTV for which beam selection would have less impact on shaping key dose gradient around the PTV. Model plans using the model predicted beam setting showed overall comparable plan quality as the clinical expert plans that were delivered to the patient. The beam angle prediction was instantaneous and could substantially improve the clinical workflow efficiency.
It is worth noting the difference between our knowledge modeling methods and previously reported beam angle automation methods that employed human knowledge. Yan et al. (36) proposed a fuzzy-logic-based method of beam angle optimization simultaneously with fluence optimization. The authors modeled human decision making process by using fuzzy inference system to follow a predefined set of rules and add beams iteratively. However, their method did not explicitly incorporate the end result of planner decision, which is the dose fall-off distribution largely determined by non-uniform beam arrangement. Pugachev et al. developed a method to incorporate prior knowledge into beam orientation optimization in IMRT (22). In their method the prior knowledge came from dosimetric impact of a single beam on the patient geometry in BEV. Although this was based on physical parameters, it could not reflect the human planner’s active decision making process during planning. Compared to these previous methods, our method focused on modeling the trade-off balance specifically to liver SBRT cases using established and clinically approved plans. It was substantially less computationally intensive and ensured the knowledge and preferences of a specific practice group is reflected in the beam angle recommendation process, and that the resulting plan conforms with the quality requirement specific to the training data cohort.
Another potential advantage of our approach is its simplicity and portability. Because the model formulism is relatively simple and physically meaningful, the size of the training dataset does not need to be very large. In contrast to previous knowledge-based systems utilizing PCA and DVH modeling that requires 50–100 cases per site as training dataset, and convolutional neural network methods that rely on large training data and implicit models, our approach is simpler to understand and faster to deploy. Therefore the initial cost of model building and ongoing cost for model maintenance is expected to be relatively low. Because of its portability, the model can also be tailored towards different physician’s preference in the same institution with only a small number of training cases.
There were several limitations in this study. First, the data sample size was relatively small due to the limited cases available for this particular site (liver) and procedure (SBRT). In future studies, we aim to include additional liver SBRT cases to further validate the model. Along this line, this study was carried out in retrospective manner. It would be more robust to prospectively validate cases in a clinical setting. Second, no prior radiation therapy treatment record was considered in this study. Patients under liver treatment often have prior treatments which would affect beam setting determination due to efforts to actively avoid dose overlapping with prior courses and spare critical healthy liver tissue. We plan to incorporate this factor in the next step to help customize the beam setting based patient-specific treatment history. Thirdly, in this prototype the data processing was performed offline in MATLAB, which requires manually exporting from and importing into treatment planning system. It is possible that with well-trained model, it can be incorporated into Eclipse Scripting API (ESAPI) in Varian Eclipse® treatment planning system to further enhance streamlined process with one-click prediction and beam placement.
Conclusions
In this study, we developed a knowledge modeling approach to provide beam angles prediction for liver stereotactic body radiation therapy treatment planning. The lightweight model is effective, portable, and generalizable without extensive training data, and requires very little computational power to generate clinical-quality beam placement without further trial-and-error manual editing process. The proposed tool could serve as a key component towards a comprehensive decision support system for radiation therapy treatment planning.
Acknowledgments
Funding: This work is partially supported by NIH R01CA201212 research grant and Varian master research grant.
Footnote
Provenance and Peer Review: With the arrangement by the Guest Editors and the editorial office, this article has been reviewed by external peers.
Conflicts of Interest: All authors have completed the ICMJE uniform disclosure form (available at https://dx.doi.org/10.21037/qims-21-169). The special issue “Artificial Intelligence for Image-guided Radiation Therapy” was commissioned by the editorial office without any funding or sponsorship. TL reports consulting fees, honoraria, and travel expenses from Varian Medical Systems unrelated to this work. YS, YG, WW and QJW reports funding support from NIH R01CA201212 research grant and Varian master research grant. YS, TL, YG and QJW reports that a patent titled “Systems and methods for automatic, customized radiation treatment plan generation for cancer” was filed. The authors have no other conflicts of interest to declare.
Ethical Statement: The authors are accountable for all aspects of the work in ensuring that questions related to the accuracy or integrity of any part of the work are appropriately investigated and resolved. The study was conducted in accordance with the Declaration of Helsinki (as revised in 2013). The study was approved by Duke University IRB Protocol Pro00102095. Informed consent was taken from all individual participants.
Open Access Statement: This is an Open Access article distributed in accordance with the Creative Commons Attribution-NonCommercial-NoDerivs 4.0 International License (CC BY-NC-ND 4.0), which permits the non-commercial replication and distribution of the article with the strict proviso that no changes or edits are made and the original work is properly cited (including links to both the formal publication through the relevant DOI and the license). See: https://creativecommons.org/licenses/by-nc-nd/4.0/.
References
- American Cancer Society. Cancer Facts & Figures 2018. Am Cancer Soc. 2018
- Goodman KA, Wiegner EA, Maturen KE, Zhang Z, Mo Q, Yang G, Gibbs IC, Fisher GA, Koong AC. Dose-escalation study of single-fraction stereotactic body radiotherapy for liver malignancies. Int J Radiat Oncol Biol Phys 2010;78:486-93. [Crossref] [PubMed]
- Rusthoven KE, Kavanagh BD, Cardenes H, Stieber VW, Burri SH, Feigenberg SJ, Chidel MA, Pugh TJ, Franklin W, Kane M, Gaspar LE, Schefter TE. Multi-institutional phase I/II trial of stereotactic body radiation therapy for liver metastases. J Clin Oncol 2009;27:1572-8. [Crossref] [PubMed]
- Schefter TE, Kavanagh BD, Timmerman RD, Cardenes HR, Baron A, Gaspar LE. A phase I trial of stereotactic body radiation therapy (SBRT) for liver metastases. Int J Radiat Oncol Biol Phys 2005;62:1371-8. [Crossref] [PubMed]
- Herfarth KK, Debus J, Wannenmacher M. Stereotactic radiation therapy of liver metastases: update of the initial phase-I/II trial. Front Radiat Ther Oncol 2004;38:100-5. [Crossref] [PubMed]
- Scaggion A, Fusella M, Bacco S, Pivato N, Roggio A, Rossato M, Zandonà R, Paiusco M. Quantifying the operator variability reduction driven by knowledge-based planning in VMAT treatments. Radiother Oncol 2017;123:S816-7. [Crossref]
- Lagerwaard FJ, Meijer OW, van der Hoorn EA, Verbakel WF, Slotman BJ, Senan S. Volumetric modulated arc radiotherapy for vestibular schwannomas. Int J Radiat Oncol Biol Phys 2009;74:610-5. [Crossref] [PubMed]
- de Pooter JA, Méndez Romero A, Wunderink W, Storchi PR, Heijmen BJ. Automated non-coplanar beam direction optimization improves IMRT in SBRT of liver metastasis. Radiother Oncol 2008;88:376-81. [Crossref] [PubMed]
- Dong P, Long T, Ruan D, Lee P, Romeijn D, Low D, Kupelian P, Sheng K. 4Pi Radiation therapy for Liver SBRT. Int J Radiat Oncol Biol Phys 2012;84:S202. [Crossref]
- Sharfo AW, Dirkx ML, Breedveld S, Méndez Romero A, Heijmen BJ. VMAT plus a few computer-optimized non-coplanar IMRT beams (VMAT+) tested for liver SBRT. Radiother Oncol 2017;123:49-56. [Crossref] [PubMed]
- Nelms BE, Robinson G, Markham J, Velasco K, Boyd S, Narayan S, Wheeler J, Sobczak ML. Variation in external beam treatment plan quality: An inter-institutional study of planners and planning systems. Pract Radiat Oncol 2012;2:296-305. [Crossref] [PubMed]
- Wang X, Zhang X, Dong L, Liu H, Wu Q, Mohan R. Development of methods for beam angle optimization for IMRT using an accelerated exhaustive search strategy. Int J Radiat Oncol Biol Phys 2004;60:1325-37. [Crossref] [PubMed]
- Li Y, Yao J, Yao D. Automatic beam angle selection in IMRT planning using genetic algorithm. Phys Med Biol 2004;49:1915-32. [Crossref] [PubMed]
- Das SK, Marks LB. Selection of coplanar or noncoplanar beams using three-dimensional optimization based on maximum beam separation and minimized nontarget irradiation. Int J Radiat Oncol Biol Phys 1997;38:643-55. [Crossref] [PubMed]
- Breedveld S, Storchi PR, Voet PW, Heijmen BJ. iCycle: Integrated, multicriterial beam angle, and profile optimization for generation of coplanar and noncoplanar IMRT plans. Med Phys 2012;39:951-63. [Crossref] [PubMed]
- Rocha H, Dias JM, Ferreira BC, Lopes MC. Beam angle optimization for intensity-modulated radiation therapy using a guided pattern search method. Phys Med Biol 2013;58:2939-53. [Crossref] [PubMed]
- Bertsimas D, Cacchiani V, Craft D, Nohadani O. A hybrid approach to beam angle optimization in intensity-modulated radiation therapy. Comput Oper Res 2013;40:2187-97. [Crossref]
- Zhang HH, Gao S, Chen W, Shi L, D'Souza WD, Meyer RR. A surrogate-based metaheuristic global search method for beam angle selection in radiation treatment planning. Phys Med Biol 2013;58:1933-46. [Crossref] [PubMed]
- Jia X, Men C, Lou Y, Jiang SB. Beam orientation optimization for intensity modulated radiation therapy using adaptive l(2,1)-minimization. Phys Med Biol 2011;56:6205-22. [Crossref] [PubMed]
- Nazareth DP, Brunner S, Jones M, Malhotra H, Bakhtiari M. Optimization of beam angles for intensity modulated radiation therapy treatment planning using genetic algorithm on a distributed computing platform. J Med Phys 2009;34:129-32. [Crossref] [PubMed]
- Li Y, Yao D, Yao J, Chen W. A particle swarm optimization algorithm for beam angle selection in intensity-modulated radiotherapy planning. Phys Med Biol 2005;50:3491-514. [Crossref] [PubMed]
- Pugachev A, Xing L. Incorporating prior knowledge into beam orientation optimization in IMRT. Int J Radiat Oncol Biol Phys 2002;54:1565-74. [Crossref] [PubMed]
- D'Souza WD, Zhang HH, Nazareth DP, Shi L, Meyer RR. A nested partitions framework for beam angle optimization in intensity-modulated radiation therapy. Phys Med Biol 2008;53:3293-307. [Crossref] [PubMed]
- Djajaputra D, Wu Q, Wu Y, Mohan R. Algorithm and performance of a clinical IMRT beam-angle optimization system. Phys Med Biol 2003;48:3191-212. [Crossref] [PubMed]
- Bedford JL, Webb S. Direct-aperture optimization applied to selection of beam orientations in intensity-modulated radiation therapy. Phys Med Biol 2007;52:479-98. [Crossref] [PubMed]
- Liu HH, Jauregui M, Zhang X, Wang X, Dong L, Mohan R. Beam angle optimization and reduction for intensity-modulated radiation therapy of non-small-cell lung cancers. Int J Radiat Oncol Biol Phys 2006;65:561-72. [Crossref] [PubMed]
- Stein J, Mohan R, Wang XH, Bortfeld T, Wu Q, Preiser K, Ling CC, Schlegel W. Number and orientations of beams in intensity-modulated radiation treatments. Med Phys 1997;24:149-60. [Crossref] [PubMed]
- Ramella S, Trodella L, Mineo TC, Pompeo E, Gambacorta MA, Cellini F, Ciresa M, Fiore M, Greco C, Gaudino D, Stimato G, Piermattei A, Cesario A, D'Angelillo RM. Beams arrangement in non-small cell lung cancer (NSCLC) according to PTV and dosimetric parameters predictive of pneumonitis. Med Dosim 2010;35:169-78. [Crossref] [PubMed]
- Rowbottom CG, Webb S, Oldham M. Beam-orientation customization using an artificial neural network. Phys Med Biol 1999;44:2251-62. [Crossref] [PubMed]
- Potrebko PS, McCurdy BM, Butler JB, El-Gubtan AS, Nugent Z. A simple geometric algorithm to predict optimal starting gantry angles using equiangular-spaced beams for intensity modulated radiation therapy of prostate cancer. Med Phys 2007;34:3951-61. [Crossref] [PubMed]
- Potrebko PS, McCurdy BM, Butler JB, El-Gubtan AS. Improving intensity-modulated radiation therapy using the anatomic beam orientation optimization algorithm. Med Phys 2008;35:2170-9. [Crossref] [PubMed]
- Meyer J, Hummel SM, Cho PS, Austin-Seymour MM, Phillips MH. Automatic selection of non-coplanar beam directions for three-dimensional conformal radiotherapy. Br J Radiol 2005;78:316-27. [Crossref] [PubMed]
- Schreibmann E, Xing L. Dose-volume based ranking of incident beam direction and its utility in facilitating IMRT beam placement. Int J Radiat Oncol Biol Phys 2005;63:584-93. [Crossref] [PubMed]
- Bangert M, Oelfke U. Spherical cluster analysis for beam angle optimization in intensity-modulated radiation therapy treatment planning. Phys Med Biol 2010;55:6023-37. [Crossref] [PubMed]
- Pugachev A, Xing L. Computer-assisted selection of coplanar beam orientations in intensity-modulated radiation therapy. Phys Med Biol 2001;46:2467-76. [Crossref] [PubMed]
- Yan H, Dai JR. Intelligence-guided beam angle optimization in treatment planning of intensity-modulated radiation therapy. Phys Med 2016;32:1292-301. [Crossref] [PubMed]


