
Utilizing pre-determined beam orientation information in dose prediction by 3D fully-connected network for intensity modulated radiotherapy
Introduction
The goal of treatment planning in radiotherapy is to maximize uniform dose delivered to planning target volumes (PTVs) while minimizing the dose irradiated to surrounding normal tissues (1,2). However, this manual process is time-consuming and the quality of the resulting plan is inconsistent between treatment planners. To overcome this issue, automatic treatment planning has been proposed which aims to promote efficiency and quality of treatment planning with advanced computer and automation techniques (3-5). As an important component, dose prediction, is especially crucial in automatic treatment planning as the ideal parameters could be obtained from its (6). With the advancement in deep learning, there has been a remarkable progress in dose prediction in recent years following the debut of three-dimensional (3D) convolution neural network. The application of dose prediction is wide spreading, covering parameter optimization and quality assurance in intensity modulated radiotherapy (IMRT) (7-11).
The origin of dose prediction work can be traced back to the study on revealing geometrical relationship between tumors and critical organs (12,13). The earlier prediction model was developed based on the assumption that the dose distribution is highly correlated with the geometric relationship between PTV and organs at risk (OARs). Distance-to-target histogram (DTH) was thus introduced to characterize the geometric relationship between PTV and OARs, which has become an important one-dimensional (1D) feature in predicting dose-volume histogram (DVH) curves (14). Subsequently, different types of geometric features were introduced to correlate with DVH parameters and their effectiveness was systematically analyzed (15). Conventionally, principal component analysis (PCA) and support vector regression (SVR) were used to model the correlation between DTH and DVH (16). Although these methods succeeded in dose prediction, considerable loss of geometric information existed during feature extraction or dimensionality reduction, potentially incurring larger deviations in prediction accuracy.
With the emergence of deep learning, there has been a rapidly growing interest in implementing this high-end technique in dose prediction. The recent prediction models are mostly based on U-Net (17,18), an encoder-decoder network with skip connections used for two-dimensional (2D)/3D image prediction. Efforts have been made to optimize the integration of network architecture to improve the performance of prediction model (19-22). The residual learning and dense connectivity were introduced to enhance feature representation ability in deep learning models (23,24). Fan et al. employed two independent encoders for PTVs and OARs separately to distinguish different structures in their models (25). Kearney et al. extended 2D U-Net to 3D U-Net with residual blocks to obtain an elevated amount of spatial information (26). There were also studies that focused on improving model inputs by constructing knowledge-based features (27), extracting contours of interested organs (28), and stacking a series of neighboring PTV slices (29).
Despite these recent advancements, it is still challenging to predict dose at border or overlapping regions of PTV. Apart from this, IMRT plans often contain multiple statistic fields, posing difficulties in incorporating information of beam orientations into a prediction model. To address these issues, in this study, the direction map representing the beam orientation information was proposed and jointly used with distance map in characterizing geometric relationship between PTV and OARs. In addition, pyramid blocks were employed in our proposed model to compensate for the deficiency of a widely used U-Net framework in capturing multi-scale information. The rest of this paper is organized as follows. In section “Methods”, the direction and distance maps are introduced, and the network framework and performance evaluation measures are described. In section “Results”, the effectiveness of the new features, direction map, distance map, and pyramid blocks to the prediction accuracy are examined. Results of comparative analysis between our proposed prediction model and three other published models, including 3D U-Net, U-ResNet-D, and ResNet-anti-ResNet, are demonstrated. Finally, the strengths and weaknesses of our proposed method are discussed, and future work is prospected in section “Discussion”.
Methods
The proposed dose prediction framework is illustrated in Figure 1. The computed tomography (CT) image, anatomical structure contours, beam orientation information and dose map were first retrieved from treatment planning system. The mask images of PTV and OARs were generated by labeling voxels of different structures with given numbers. The distance map was calculated based on the distance between voxels of OARs and surface of PTV. The direction map was produced based on the paths passing through PTV and OAR along the beam orientation. The feature images together with CT images were then used as input of a deep learning network, 3D-UNet with pyramid decoder (3D-UNet-PD), to train a regression model. After the training session, the 3D-UNet-PD can predict 3D dose distribution from CT and radiotherapy structures. It is worth noting that the 3D dose distribution was also employed as target of network for training purpose. In Figure 1, the workflow of the training process and prediction process is indicated by dot line and solid line, respectively.
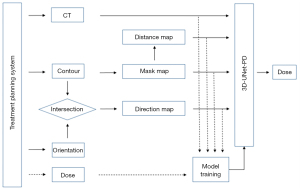
Feature maps
The direction maps provide detailed per-voxel beam orientation effect of PTV and OARs. Given the masks of PTV and OARs, beam path, and voxel coordinate (x, y, z) in 3D, the direction map (mapping R3 to R) is defined as:
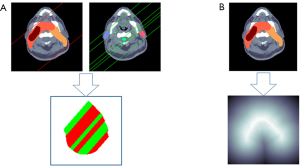
where ΩPTV and ΩOAR denote the regions (masks) of PTV and OAR, respectively. BPPTV (or BPOAR) denote radiation paths passing through PTV (or OAR). In this study, the IMRT treatment plans of head-and-neck cancer patients consists of 9 beams and thus 9 direction maps were generated correspondingly. Figure 2A demonstrates one direction map at beam angle of 40°. The radiation paths passing through the PTV and OARs are represented by red color (+1) and green color (−1), respectively. The green area of the direction map indicates regions of normal tissue which could be less affected by radiation.
The distance map provides detailed per-voxel distance information of regions of interest, which was introduced in our previous publication (30). Given the PTV mask and voxel coordinate (x, y, z) in 3D, the distance map (mapping R3 to R) is defined as:
where S represents the surface of PTV and p is any point at surface S, Ωin and Ωout denote the region inside and outside the PTV, respectively. As shown in Figure 2B, the distance map is generated based on the PTV mask. Its value represents the shortest distance from the voxel to the surface of PTV. Its sign indicates either inside or outside the PTVs. The light area of the distance map displays the regions of normal tissue closet to the PTV, which is more affected by higher radiation.
Deep learning model
As shown in Figure 3, the proposed prediction model is based on a 3D-UNet with pyramid decoder (3D-UNet-PD), which is a variant of 3D fully-connected network (FCN) (31). 3D-UNet-PD is composed of a down-sampling encoder and an up-sampling pyramid decoder, along with skip connections to bring lower layers features from encoder to decoder for preserving more feature details. As shown in Figure 1, the 3D-UNet-PD model is represented by a box and handles input from four types of images. The proposed model contained 19 separate input channels (1 CT image, 1 PTV mask, 7 OAR masks, 1 distance map, and 9 direction maps) and the model resulted in an output of a 3D dose map. All the layers in FCN were able to handle volumetric data.
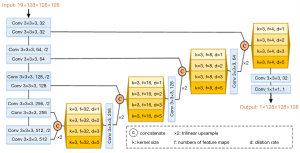
Five stage width-reduced 3D VGG10 (32) was used as a backbone structure, considering that the 3D FCN often suffers from a large memory footprint. Each stage consists of similar modules: 3×3×3 convolutions layers followed by a normalization layer and a rectified linear unit (ReLU). The instance normalization (33), instead of batch normalization (34), was adopted based on the observation that the instance normalization performed better with small batch size. 3×3×3 convolutions layers with stride 2. Taking into account the memory footprint and sample size (194 patients), the number of feature maps was set to 32 and it was doubled after each down-sampling operation.
It has been shown that incorporating additional information can significantly improve dense prediction tasks (35,36). Pyramid blocks were employed to exploit multi-scale features from the encoder part and gradually recover the spatial resolution using bi-linear up-sampling. Since features in the lower layer preserve accurate location information, the output of each stage of the encoder was passed to the decoder module by skip connection. In this work, atrous convolution was applied, which allowed us to effectively enlarge the receptive fields to incorporate long-range context without additional parameters in pyramid blocks. As illustrated in Figure 3, the proposed module consists of 4 atrous convolutions with various rates. The dilation rates of 3×3×3 convolutions in pyramid blocks are {1,2,3,5}, and their corresponding receptive field could vary in the range of {3×3×3, 5×5×5, 7×7×7, 11×11×11}.
L1 loss was applied as the loss function in this study. Adam (37) was used as an optimizer with a batch size of 2. The initial learning rate was set to 0.0003 and weight decay was set to 0.0001. Whenever the training loss did not improve within the last 5,000 iterations, the learning rate was dropped by a factor of 0.1. The training procedure ultimately stopped at 80,000 iterations. All the experiments were conducted with Pytorch (version 1.2.0) using two NVIDIA GTX 1080 TI Graphics Processing Units (GPUs).
Experiments
The official OpenKBP dataset at https://github.com/ababier/open-kbp was used in this study, which was structured in a way to facilitate the development and validation of dose prediction models. IMRT treatment plans delivered at 6 mega-voltage (MV) for a total of 194 head-and-neck cancer patients were retrospectively analyzed. All IMRT plans consist of 9 static fields with beam angles equally spaced at 0°, 40°, 80°, 120°, 160°, 200°, 240°, 280°, and 320°. CT images, mask images, feature maps, and dose maps were all resized to 128×128×128 with a resolution of 4 mm × 4 mm × 2.5 mm. PTVs include PTV70, PTV63, and PTV56. Primary OARs include the brainstem, spinal cord, right parotid, left parotid, esophagus, larynx, and mandible.
The prediction accuracy of 3D dose distribution was evaluated by using the mean absolute error (MAE), which is the averaged error across all voxels of a structure (PTV or OARs) (30). It is defined as follows:
Where Nk is the number of total voxels belonging to the k-th structure. DP and DT are the predicted and ground-truth (or calculated) doses of the i-th voxel. The voxel doses were normalized by the value of prescription dose. It is worth noting that MAE is a measurement of difference between two images (such as dose distributions), it doesn’t reflect the dosimetric effect on a structure or partial volume of a structure. For clinical use, the performance of prediction models was also evaluated based on dose-volume metrics (D0.1cc, Dmean for OARs and D1, D95, D99 for PTVs) and DVH.
Our experiments were conducted in two parts. First, ablation experiments were performed to evaluate the effect of feature maps, distance map, and pyramid decoder on prediction accuracy. In the context of machine learning, an ablation study has been widely adopted to investigate the impact of removing specific “feature” or component of the model on the network performance. In this study, specific feature maps (distant map, direction map) were eliminated from the input and the pyramid decoder was excluded from the learning network to examine their impacts on network performance in aspects of prediction accuracy. Second, the proposed model was compared with three state-of-the-art dose prediction models, including: (I) 3D U-Net (17), which is a 3D encoder-decoder network that takes the full labeled PTVs and OARs as input; (II) ResNet-anti-ResNet (25), which is a dual encoder model that takes labeled PTVs and OARs from a single slice as input; (III) U-ResNet-D (29), which is a residual U-Net that takes labeled PTVs and OARs from adjacent five slices as input.
A five-fold cross-validation procedure was employed for model training and evaluation. Each fold contained approximately 40 patient cases. Among the five folds, one was selected as the test data, and the remaining four folds were deployed as training data. Taking average on the prediction accuracy across the five folds yielded the overall accuracy estimate of our proposed method. In each fold of cross-validation, the selected networks were trained on the same 4/5 of patients and tested on the remaining 1/5 of patients. After completing the five-fold cross-validation, different models were inter-compared by using the average score over the 194 patient cases.
Results
Ablation experiment
Table 1 summarizes the effect of each new feature on prediction accuracy by using the MAE scores. In accordance with a previous work (38), we developed the baseline model (BL) and adjusted the model parameters for fitting data dimension. The features of direction map, distance map, and pyramid decoder are represented by their acronyms DRCTN, DIST, and PD, respectively in Table 1. With these feature maps included in the BL model, the prediction accuracy was improved especially for spinal cord, esophagus, and larynx, which has long extension in length. In comparison to the BL model, the prediction errors of BL + DRCTN model and BL + DIST model were decreased by 0.43 and 0.38, respectively. If both types of feature maps were applied, the prediction error of BL + DRCTN + DIST model was decreased by 0.44. If all the three new features were applied, the prediction error of BL + DRCTN + DIST + PD model was further decreased by 0.56.
Table 1
| Structures | BL | BL + DRCTN | BL + DIST | BL + DRCTN + DIST | BL + DRCTN + DIST + PD |
|---|---|---|---|---|---|
| All | 4.53±1.72 | 4.10±1.40 | 4.15±1.26 | 4.09±1.45 | 3.97±1.42 |
| Tumor | 3.33±1.37 | 2.58±0.69 | 2.47±0.74 | 2.62±0.63 | 2.47±0.69 |
| Brainstem | 2.25±1.59 | 2.24±1.43 | 1.85±1.14 | 1.97±1.20 | 1.82±1.03 |
| Spinal Cord | 3.25±1.81 | 3.16±1.31 | 2.64±1.27 | 2.71±1.16 | 2.40±1.12 |
| Right Parotid | 4.50±1.19 | 4.62±1.27 | 5.01±1.28 | 4.53±1.33 | 4.43±1.11 |
| Left Parotid | 5.13±2.36 | 4.72±1.09 | 4.48±1.13 | 4.82±1.21 | 4.31±1.04 |
| Esophagus | 3.35±1.67 | 3.03±1.17 | 3.20±1.35 | 2.74±1.13 | 2.64±1.18 |
| Larynx | 5.99±6.13 | 5.28±4.73 | 5.58±5.41 | 5.38±4.39 | 4.90±4.25 |
| Mandible | 5.98±1.78 | 5.86±1.73 | 5.81±1.62 | 5.71±1.45 | 5.60±1.71 |
BL represents the 3D UNet baseline model; DRCTN represents the direction map; DIST represents the distance map; PD represents pyramid decoder. All represents the total region including PTV and OARs. PTV, planning target volume; OARs, organs at risk.
Model comparison
Table 2 summarizes the results of prediction accuracy of four types of prediction models in terms of MAE scores. Our proposed 3D-UNet-PD achieved the least MAE (3.97±1.42) comparing with the three comparing models: 3D-Unet (4.53±1.72), ResNet-anti-ResNet (5.37±1.51), and U-ResNet-D (4.45±1.52). For OARs, the prediction error of 3D-UNet-PD was decreased by 0.37 for brainstem, 0.51 for spinal cord, 0.07 for right parotid, 0.75 for left parotid, 0.69 for esophagus, 0.59 for larynx, and 0.38 for mandible, in comparison to the comparing model that had the least prediction error. For PTV, ResNet-anti-ResNet achieved the least MAE (2.25±0.81) while 3D-UNet-PD yielded comparable prediction error (2.47±0.69). However, for several OARs, the prediction errors of 3D-UNet-PD were more than 3%. They are right parotid (4.43±1.11), left parotid (4.31±1.04), larynx (4.90±4.25), and mandible (5.60±1.71).
Table 2
| Structures | 3D-Unet | ResNet-anti-ResNet | U-ResNet-D | 3D-UNet-PD |
|---|---|---|---|---|
| All | 4.53±1.72 | 5.37±1.51 | 4.45±1.52 | 3.97±1.42 |
| Tumor | 3.33±1.37 | 2.25±0.81 | 3.39±0.68 | 2.47±0.69 |
| Brainstem | 2.25±1.59 | 4.01±2.54 | 2.19±1.72 | 1.82±1.03 |
| Spinal Cord | 3.25±1.81 | 3.35±1.25 | 2.91±1.06 | 2.40±1.12 |
| Right Parotid | 4.50±1.19 | 5.98±1 .57 | 4.79±1.37 | 4.43±1.11 |
| Left Parotid | 5.13±2.36 | 5.37±1.84 | 5.06±1.97 | 4.31±1.04 |
| Esophagus | 3.35±1.67 | 6.34±3.06 | 3.82±1.69 | 2.64±1.18 |
| Larynx | 5.99±6.13 | 6.34±5.58 | 5.45±4.42 | 4.90±4.25 |
| Mandible | 5.98±1.78 | 6.16±1.65 | 6.15±1.95 | 5.60±1.71 |
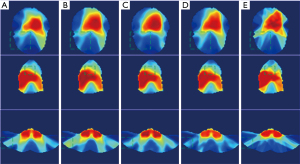
The dose distributions predicted by the four prediction models and the ground-truth dose distribution of one representative patient case are illuminated in Figure 4. The doses on three typical slices are illustrated and the area with large dose discrepancy is indicated by dashed box. Results demonstrated that the dose distribution predicted by our proposed 3D-UNet-PD was the closest one to the ground-truth dose distribution, particularly in regions indicated in the dashed box on each slice. The predicted accuracy of dose distribution generated by 3D UNet and U-ResNet-D ranked the second and third, respectively, among the all the four models. The prediction accuracy by Resnet-anti-Resnet was the worst as reflected by the larger dose discrepancy of PTV and low dose areas. This could partly be explained by the characteristics of 2D convolution neural network in Resnet-anti-Resnet, which is deficient in learning 3D spatial correlation.
Dosimetric metrics
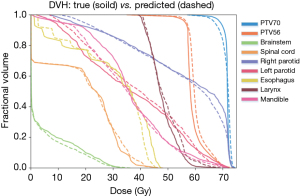
The comparison between DVHs generated from our proposed 3D-UNet-PD and that from the ground-truth dose distribution of one representative patient is shown in Figure 5. Minor dose difference for high-dose region of small volume in right parotid, esophagus, and larynx was observed. Besides, apparent dose difference for low-dose region of large volume in esophagus and mandible was observed. For PTV, the prediction errors of three dosimetric metrics (D1, D95, and D99) were 1.51±1.27, 1.81±1.56, and 2.16±1.67 for PTV70, 1.31±1.02, 1.62±1.28, and 1.55±1.38 for PTV63, and 1.47±1.15, 1.17±1.2, and 1.37±1.2 for PTV56. The largest dose discrepancies for D1, D95, and D99 were 1.51%, 1.81%, and 2.16% at PTV70. For OARs, the prediction errors of two dosimetry metrics (D0.1cc and Dmean) were 2.16±1.62 and 0.68±0.55 for brainstem, 1.98±2.03 and 0.74±0.73 for spinal cord, 1.72±1.41 and 1.48±1.15 for right parotid, 1.33±1.11 and 1.47±1.13 for left parotid, 2.05±1.69 and 0.89±0.8 for esophagus, 1.71±2.0 and 1.94±3.36 for larynx, 1.23±0.85 and 1.76±1.23 for mandible. The largest dose discrepancies for D0.1cc and Dmean were 2.16% for brainstem and 1.94% for larynx.
Discussion
In this study, a novel deep learning model called 3D-UNet-PD for 3D dose distribution prediction was developed and its performance was evaluated. The proposed model demonstrated superior prediction accuracy, compared with the other three state-of-the-art prediction models. In the border of PTV and low dose region of OARs, the predicted dose from our proposed 3D-UNet-PD was closer to the ground truth, compared to other studied models. The incorporation of direction map into the prediction model was demonstrated to be crucial in improving model prediction accuracy, as shown in Table 1. When additional feature maps were included, such as distance map, the prediction accuracy was further strengthened. Notably, although the proposed model achieved the least MAE among the four studied prediction models, there was more than 3% prediction error for several OARs. This could be partially ascribed to the large variation in these regions and inadequate training samples, which will be improved in the future work. On the other hand, the current work can be easily extended to other treatment sites, treatment techniques [such as volumetric modulated arc radiotherapy (VMAT)], and prediction tasks (such as position of multi-leaf collimator and segment of radiation beam).
The effect of the feature maps on the accuracy of prediction model is critical. The importance of distance map has been investigated in previous studies and demonstrated to be effective in reducing dose prediction error (30). The effect of beam orientation is crucial for dose distribution, but less investigated in predictive modeling. The main reason lies to the difficulty in characterizing this information in digital form, for example image or matrix. In this study, we proposed a way to characterize it by incorporating direction map, of which the effectiveness was tested on the predicted dose. Our results showed that it was effective and comparable to other features, such as distance map. However, the expression of the direction map in Eq. [1] is relatively simple. In Figure 2A, the radiation path is represented by a parallel-shape beam from a line source. While, in reality, it was a cone-shaped beam originating from a point source. This simplification could have certain impacts on the predicted dose accuracy. The beam shape will be taken into account to mimic the real setting of on-board imager geometry in our future work.
Although capability of the 3D-UNet in dose prediction has been extensively reported in the body of literature, there still exist deficiencies in numerous aspects, such as the arrangement of convolution layers in decoder. The stacking of multiple convolution layers in decoder would increasingly enlarge receptive field, while it also restricted capability of the network in capturing features in multi-scale resolution. As the dose at a given voxel is not only dependent on the neighboring voxels, but also influenced by the spatial relationship between the PTV and OARs. Therefore, the incorporation of the pyramid blocks was necessary in this study for the sake of extracting multi-scale features from image simultaneously. We also performed experiments on arranging the modules in cascade or in a parallel manner. It was found that stacking them in a cascade way would be better in dose prediction task. The effectiveness of pyramid decoder on prediction accuracy was demonstrated, as shown in Table 1. It implied that it would be necessary to optimize 3D-UNet structure for each specific task.
There are several limitations in this study. First, the introduction of pyramid decoder increased the complexity of the prediction model, GPU memory consumption and the time required for model training. Nevertheless, this only affected the training process, its influence on prediction process during testing and clinical application should be minimal. As tested, the time required on dose prediction (excluding pre-processing and post-processing) was within 1.6 s for each patient on a workstation equipped with two NVIDIA GeForce 1080Ti GPUs. Second, the effectiveness of direction map might be compromised by improper selection of IMRT plans. Since the beam orientations in this study were equally spaced, the advantage of direction map might not be fully manifested. The beam orientation with irregular spacing would be more suitable for this new feature map. In the future, we will test our proposed model on more complex IMRT plans with non-equally-spaced beams.
Conclusions
The proposed 3D-UNet-PD model improved the accuracy of dose prediction for both the PTVs and OARs, compared to the three UNet-based models. The introduction of direction maps and distance map effectively reduced the prediction error near the border of the PTV and low-dose regions. The application of pyramid decoder resulted in less prediction error, compared to the baseline model. In general, our 3D-UNet-PD model was more accurate in predicting dose distribution of IMRT treatment plans in comparison with the three studied state-of-the-art prediction models, providing. It provides an effective dose prediction alternative as a supplementary tool to assist in current quality assurance and automated treatment planning tasks in radiotherapy.
Acknowledgments
Funding: This work is supported by the Natural Science Foundation (NSF) of China (No. 11975312, No. 61702001), Beijing Municipal Natural Science Foundation (7202170), Anhui Provincial Natural Science Foundation of China (No. 1908085J25, No. 1808085MF209), and Key Support Program of University Outstanding Youth Talent of Anhui Province (No. gxyqZD2018007), and Open Research Foundation of Key Laboratory of Polarization Imaging Detection Technology of Anhui Province (No. 2019KJS030009).
Footnote
Provenance and Peer Review: With the arrangement by the Guest Editors and the editorial office, this article has been reviewed by external peers.
Conflicts of Interest: All authors have completed the ICMJE uniform disclosure form (available at http://dx.doi.org/10.21037/qims-20-1076). The special issue “Artificial Intelligence for Image-guided Radiation Therapy” was commissioned by the editorial office without any funding or sponsorship. The authors have no other conflicts of interest to declare.
Ethical Statement: The authors are accountable for all aspects of the work in ensuring that questions related to the accuracy or integrity of any part of the work are appropriately investigated and resolved. The study was conducted in accordance with the Declaration of Helsinki (as revised in 2013). The study was approved by institutional Ethics Committee of the Cancer Hospital Chinese Academy of Medical Sciences and Peking Union Medical College. Informed consent was waived in this retrospective study.
Open Access Statement: This is an Open Access article distributed in accordance with the Creative Commons Attribution-NonCommercial-NoDerivs 4.0 International License (CC BY-NC-ND 4.0), which permits the non-commercial replication and distribution of the article with the strict proviso that no changes or edits are made and the original work is properly cited (including links to both the formal publication through the relevant DOI and the license). See: https://creativecommons.org/licenses/by-nc-nd/4.0/.
References
- Webb S. The physical basis of IMRT and inverse planning. Br J Radiol 2003;76:678-89. [Crossref] [PubMed]
- Cho B. Intensity-modulated radiation therapy: a review with a physics perspective. Radiat Oncol J 2018;36:1-10. [Crossref] [PubMed]
- Yan H, Yin FF, Guan HQ, Kim JH. AI-guided parameter optimization in inverse treatment planning. Phys Med Biol 2003;48:3565-80. [Crossref] [PubMed]
- Yang Y, Xing L. Clinical knowledge-based inverse treatment planning. Phys Med Biol 2004;49:5101-17. [Crossref] [PubMed]
- Stieler F, Yan H, Lohr F, Wenz F, Yin FF. Development of a neuro-fuzzy technique for automated parameter optimization of inverse treatment planning. Radiat Oncol 2009;4:39. [Crossref] [PubMed]
- Appenzoller LM, Michalski JM, Thorstad WL, Mutic S, Moore KL. Predicting dose-volume histograms for organs-at-risk in IMRT planning. Med Phys 2012;39:7446-61. [Crossref] [PubMed]
- Fogliata A, Nicolini G, Clivio A, Vanetti E, Laksar S, Tozzi A, Scorsetti M, Cozzi L. A broad scope knowledge based model for optimization of VMAT in esophageal cancer: validation and assessment of plan quality among different treatment centers. Radiat Oncol 2015;10:220. [Crossref] [PubMed]
- Yu G, Li Y, Feng Z, Tao C, Yu Z, Li B, Li D. Knowledge-based IMRT planning for individual liver cancer patients using a novel specific model. Radiat Oncol 2018;13:52. [Crossref] [PubMed]
- Zhang J, Wu QJ, Xie T, Sheng Y, Yin FF, Ge Y. An Ensemble Approach to Knowledge-Based Intensity-Modulated Radiation Therapy Planning. Front Oncol 2018;8:57. [Crossref] [PubMed]
- Wang J, Jin X, Zhao K, Peng J, Xie J, Chen J, Zhang Z, Studenski M, Hu W. Patient feature based dosimetric Pareto front prediction in esophageal cancer radiotherapy. Med Phys 2015;42:1005-11. [Crossref] [PubMed]
- Shiraishi S, Moore KL. Knowledge-based prediction of three-dimensional dose distributions for external beam radiotherapy. Med Phys 2016;43:378. [Crossref] [PubMed]
- Lian J, Yuan L, Ge Y, Chera BS, Yoo DP, Chang S, Yin F, Wu QJ. Modeling the dosimetry of organ-at-risk in head and neck IMRT planning: an intertechnique and interinstitutional study. Med Phys 2013;40:121704 [Crossref] [PubMed]
- Yuan L, Wu QJ, Yin FF, Jiang Y, Yoo D, Ge Y. Incorporating single-side sparing in models for predicting parotid dose sparing in head and neck IMRT. Med Phys 2014;41:021728 [Crossref] [PubMed]
- Wu B, Ricchetti F, Sanguineti G, Kazhdan M, Simari P, Chuang M, Taylor R, Jacques R, McNutt T. Patient geometry-driven information retrieval for IMRT treatment plan quality control. Med Phys 2009;36:5497-505. [Crossref] [PubMed]
- Yuan L, Ge Y, Lee WR, Yin FF, Kirkpatrick JP, Wu QJ. Quantitative analysis of the factors which affect the interpatient organ-at-risk dose sparing variation in IMRT plans. Med Phys 2012;39:6868-78. [Crossref] [PubMed]
- Zhu X, Ge Y, Li T, Thongphiew D, Yin FF, Wu QJ. A planning quality evaluation tool for prostate adaptive IMRT based on machine learning. Med Phys 2011;38:719-26. [Crossref] [PubMed]
- Ronneberger O, Fischer P, Brox T. U-Net: Convolutional Networks for Biomedical Image Segmentation. Medical Image Computing and Computer-Assisted Intervention (MICCAI), Springer, LNCS, 2015;9351:234-41. available at arXiv:1505.04597 [cs.CV].
- Çiçek Ö, Abdulkadir A, Lienkamp S, Brox T, Ronneberger O. 3D U-Net: Learning Dense Volumetric Segmentation from Sparse Annotation. Medical Image Computing and Computer-Assisted Intervention (MICCAI), Springer, LNCS, Oct 2016;9901:424-32.
- Nguyen D, Jia X, Sher D, Lin MH, Iqbal Z, Liu H, Jiang S. 3D radiotherapy dose prediction on head and neck cancer patients with a hierarchically densely connected U-net deep learning architecture. Phys Med Biol 2019;64:065020 [Crossref] [PubMed]
- Chen X, Men K, Li Y, Yi J, Dai J. A feasibility study on an automated method to generate patient-specific dose distributions for radiotherapy using deep learning. Med Phys 2019;46:56-64. [Crossref] [PubMed]
- Barragán-Montero AM, Nguyen D, Lu W, Lin MH, Norouzi-Kandalan R, Geets X, Sterpin E, Jiang S. Three-dimensional dose prediction for lung IMRT patients with deep neural networks: robust learning from heterogeneous beam configurations. Med Phys 2019;46:3679-91. [Crossref] [PubMed]
- Babier A, Mahmood R, McNiven AL, Diamant A, Chan TCY. Knowledge-based automated planning with three-dimensional generative adversarial networks. Med Phys 2020;47:297-306. [Crossref] [PubMed]
- He K, Zhang X, Ren S, Sun J. Deep Residual Learning for Image Recognition. 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR). 27-30 June 2016; Las Vegas, NV, USA. IEEE, 2016:770-8.
- Huang G, Liu Z, van der Maaten L, Weinberger KQ. Densely Connected Convolutional Networks. 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR). 21-26 July 2017; Honolulu, HI, USA. IEEE, 2017:2261-9.
- Fan J, Wang J, Chen Z, Hu C, Zhang Z, Hu W. Automatic treatment planning based on three-dimensional dose distribution predicted from deep learning technique. Med Phys 2019;46:370-81. [Crossref] [PubMed]
- Kearney V, Chan JW, Haaf S, Descovich M, Solberg TD. DoseNet: a volumetric dose prediction algorithm using 3D fully-convolutional neural networks. Phys Med Biol 2018;63:235022 [Crossref] [PubMed]
- Liu J, Wu QJ, Kirkpatrick JP, Yin FF, Yuan L, Ge Y. From active shape model to active optical flow model: a shape-based approach to predicting voxel-level dose distributions in spine SBRT. Phys Med Biol 2015;60:N83-92.
- Nguyen D, Long T, Jia X, Lu W, Gu X, Iqbal Z, Jiang S. A feasibility study for predicting optimal radiation therapy dose distributions of prostate cancer patients from patient anatomy using deep learning. Sci Rep 2019;9:1076. [Crossref] [PubMed]
- Liu Z, Fan J, Li M, Yan H, Hu Z, Huang P, Tian Y, Miao J, Dai J. A deep learning method for prediction of three-dimensional dose distribution of helical tomotherapy. Med Phys 2019;46:1972-83. [Crossref] [PubMed]
- Zhang J, Liu S, Yan H, Li T, Mao R, Liu J. Predicting voxel-level dose distributions for esophageal radiotherapy using densely connected network with dilated convolutions. Phys Med Biol 2020;65:205013 [Crossref] [PubMed]
- Shelhamer E, Long J, Darrell T. Fully Convolutional Networks for Semantic Segmentation. IEEE Trans Pattern Anal Mach Intell 2017;39:640-51. [Crossref] [PubMed]
-
Simonyan K Zisserman A. Very Deep Convolutional Networks for Large-Scale Image Recognition. arXiv:1409.1556 [cs.CV],2014 . -
Ulyanov D Vedaldi A Lempitsky V. Instance Normalization: The Missing Ingredient for Fast Stylization. arXiv:1607.08022 [cs.CV],2017 . -
Ioffe S Szegedy C. Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift. arXiv:1502.03167 [cs.LG],2015 . - Chen LC, Papandreou G, Kokkinos I, Murphy K, Yuille AL. DeepLab: Semantic Image Segmentation with Deep Convolutional Nets, Atrous Convolution, and Fully Connected CRFs. IEEE Trans Pattern Anal Mach Intell 2018;40:834-48. [Crossref] [PubMed]
- Yang M, Yu K, Zhang C, Li Z, Yang K. DenseASPP for Semantic Segmentation in Street Scenes. 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition. 18-23 June 2018; Salt Lake City, UT, USA. IEEE, 2018:3684-92.
-
Kingma DP Ba J Adam: A Method for Stochastic Optimization. arXiv:1412.6980 [cs.LG],2017 . -
Isensee F Petersen J Klein A Zimmerer D Jaeger PF Kohl S Wasserthal J Koehler G Norajitra T Wirkert S Maier-Hein KH nnU-Net: Self-adapting Framework for U-Net-Based Medical Image Segmentation. arXiv:1809.10486 [cs.CV],2018 .


