
Speed of sound and shear wave speed for calf soft tissue composition and nonlinearity assessment
Introduction
In the last decades, the analysis of muscle composition has gained increased importance due to the unprecedented size of the older adult population worldwide. The aging process is associated with sarcopenia, a disease characterized by the progressive loss of skeletal muscle mass and function. This condition dramatically worsens the quality of life of older adults by increasing the risk for functional disabilities, falls and fractures, hospitalizations, and mortality (1-3). Current reference standards for quantifying tissue composition include computed tomography and magnetic resonance imaging (MRI) (4,5), which are capable of providing high-resolution cross-sectional body images. However, both are costly systems, involve either exposure to ionizing radiation or potential patient complications, and are therefore difficult to perform in everyday clinical practice. Ultrasound (US) may offer a fast, non-invasive, and affordable bedside alternative.
Shear-wave elastography is a well-established quantitative US modality that has recently been introduced into clinical units. It quantifies tissue stiffness by measuring the velocities of shear waves generated by an acoustic radiation force. US elastography has been recognized as an excellent diagnostic method for chronic liver disease assessment (6). Applications to musculoskeletal soft tissues are becoming increasingly popular (7-9). In a recent paper, Alfuraih et al. (10) showed that muscle stiffness decreases with age and correlates significantly with muscle mass and strength. However, SWS measurements are highly sensitive to confounders (11-13), which may limit their reliability and reproducibility. For example, SWS measurements in muscle show large variability when the operator applies different tissue compression with the US probe (13). These variations are attributed to nonlinear tissue elasticity effects arising under finite tissue deformations (13). Several studies suggested quantifying tissue nonlinearity to reduce its confounding effect and, by doing so, extract a potential novel biomarker (14,15). This can be achieved by analyzing acoustoelastic tissue effects, namely changes in the speed when tissue is subjected to stress (16). Tissue nonlinearity is then determined from the relationship between SWS and stress. Its clinical utility is still under investigation (17,18).
Speed-of-sound (SoS) quantification in tissue is an emerging US modality. SoS measures the speed of longitudinal waves, which are conventionally used for B-mode image formation. Nominal SoS values for muscle and fatty tissue are 1,585 and 1,440 m/s, respectively (19). SoS ultrasound (SoS-US) has recently been suggested as a promising candidate for tissue composition analysis. In particular, strong correlations have been reported between SoS and MRI proton density fat fraction measurements in calf muscles and liver (20,21). As a consequence, SoS-US in calf muscles has proven useful in differentiating sarcopenic and healthy populations (22).
Studies comparing SWS and SoS in soft tissue are still very scarce, though they could provide useful information about their complementary roles in tissue composition assessment. In a study with ex-vivo tissues, Glozman et al. (23) showed that SWS is strongly affected by the tissue mechanical state and that SoS might outperform SWS in tissue differentiation. Their results suggest that SoS measurements might be less confounded by tissue nonlinearity. This has two main benefits compared to SWS. SoS could provide both more reliable information about tissue composition and robust characterizations of tissue nonlinearity. Thus, analyzing acoustoelastic effects on in-vivo SoS and SWS can provide relevant information about their differences and potential clinical use.
This study had three main objectives. First, we investigated the correlations of SWS and SoS in the gastrocnemius muscle of a healthy population. Second, we used reproducible tissue compression to characterize tissue nonlinear elasticity effects on SWS and SoS. Finally, we compared the potential of SoS and SWS for tissue composition assessment in terms of measurements variability between both calves and correlations with body fat percentage (BF%).
Methods
Study design
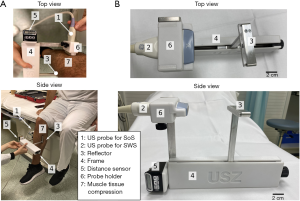
The study was conducted in accordance with the Declaration of Helsinki (as revised in 2013). This prospective single-institution study was approved by the institutional review board and the local ethics committee (Kantonale Ethikkomission Zürich; KEK-ZH-Nr. 2015-0323) and written informed consent was obtained from all subjects. Ten healthy volunteers (two females and eight males) were prospectively assessed with both SoS and SWS US. The data has not been published in previous studies. Examinations were performed between August and September 2019. In the first step, gastrocnemius muscles were examined using SoS-US. The volunteers were placed in a sitting position with the calf muscles in a relaxed state and slight ankle plantarflexion (Figure 1). The muscle compression was applied using a Plexiglas® plate positioned opposite to the US probe at the largest calf circumference level, with the superficial posterior compartment of the calf longitudinally in between (Figure 1). The probe-reflector distance, which was adjusted with a measurement frame, was used to apply reproducible compression. Starting from the lightest compression, the probe-reflector distance was reduced in 5 mm steps, acquiring SoS measurements in each step. Next, the SoS probe was replaced by the SWS probe in the measurement frame. Then, the gastrocnemius muscles were examined using SWS at the same muscle position and with the same muscle compression sequence as before. Muscles from both legs were examined in each subject.
Volunteers
All subjects were selected after personal recruitment, and signed informed consent was provided prior to participation. Inclusion criteria were: 20–35 years of age, ability to withstand compression on the calf musculature, no mobility problems (Tegner score >1), absence of acute fracture, myopathies, or extensive leg edema in either or both calves, and no recent surgery or fracture in the legs within the last 5 years. The leg circumference and the Tegner activity level (24) were assessed for all volunteers. Tegner activity level is scored from 0 for no activity to 10 for competitive activity level. The dominant leg was determined as the leg used to kick a ball. Body fat percentage and mass were assessed with a bioelectrical impedance analysis device (BF 300, Omron Healthcare Europe, Hoofddorp, The Netherlands). The measurements were acquired twice, and their average value was taken for further analysis. The examinations were performed by two radiology residents with 2 years of US experience.
Shear-wave elastography
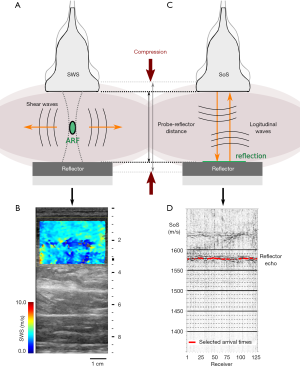
Shear-wave elastography examinations were performed using a 9 L-D linear probe (GE Healthcare, Chicago, IL, USA), which has 192 elements, a bandwidth of 2 to 9 MHz, and an aperture of 44 mm. SWS reconstructions were performed with a LOGIQ E9 system (Software Version R6 XDclear 2.0, GE Healthcare). Figure 2A illustrates the experimental setup and the generation of shear waves in tissue. The system combines the time aligned sequential tracking method for shear wave tracking and the comb-push US elastography technique to improve signal-to-noise ratio (25). Following the recommendations of the manufacturer, the preset mode was chosen to “penetration” to access deeper regions. The device computes local tissue SWS (in meters/second) values within a rectangular region of interest (Figure 2B). The elastogram with local SWS values was processed to extract the average SWS value within the region of interest. The top edge of this region of interest was located at the top edge of the gastrocnemius muscle, immediately below the skin and subcutaneous adipose tissue layers. The maximum region-of-interest size provided by the LOGIQ E9 was used for every subject, with size 44 mm (width) × 30 mm (height). Each measurement was repeated three times, and the mean value was used for further statistical analysis.
SoS-US
We collected US radiofrequency data for SoS using a UF-760AG system (Fukuda Denshi Co., Tokyo, Japan) with a linear US probe operating at frequencies of 5–12 MHz (FUT-LA385-12P, Fukuda Denshi). The probe consisted of 128 elements with an elevation of 7 mm and an inter-element pitch of 0.3 mm. The total aperture was 38 mm. The Plexiglas® plate acted as a reflector and was used as a timing reference for US signals. Figure 2C illustrates the acquisition setup and the fundamentals of longitudinal-wave propagation in tissue. To accurately control the probe-reflector distance d (in millimeters), both elements were attached to an adjustable frame that incorporates a distance sensor (Figure 1). The transducers emitted US pulses sequentially. For each emitter, the same transducer element was used to receive the echoes. The reflector generates strong echoes that are registered by the US probe and visible in radiofrequency signals (Figure 2D). By identifying these echoes, we measured the reflector echo time t (in seconds) for each transducer. This is the time that US signals need to propagate through the gastrocnemius muscle a distance equal to 2d. From here, we calculated SoS (in m/s) as SoS =2*d/t. An automatic algorithm was used to compute average SoS values across the transducer array (26). Each measurement was repeated three times, and the mean value was used for further statistical analysis.
Muscle compression
The Plexiglas® reflector was also used to compress the muscle in a controlled manner. This is illustrated in Figures 2A,C. We measured the muscle compression in terms of the distance between the US probe and the reflector. Thus, no direct measurements of the compression force were made. Instead, we measured the strain of tissue through the probe-reflector distance. This was adjusted to a resolution of 5 mm with the measurement frame (Figure 1B). Customized 3D printed transducer holders were used to alternately attach the SWS and SoS probes to the measurement frame. They ensured the same compression position and footprint in both measurements. We acquired the first SoS measurements by applying the minimum compression that ensures adequate acoustic coupling between the probe, skin, and reflector. We performed the subsequent measurements by decreasing the probe-reflector distance, i.e., increasing the compression, in steps of 5 mm. The maximum compression was given by the smallest probe-reflector distance that was comfortably tolerated by the subjects. To ensure that both SoS and SWS were measured in the same region of the gastrocnemius muscle, we marked the positions of both reflector and probe on the leg with a skin pen.
Acoustoelastic model for tissue nonlinearity quantification
Soft tissues exhibit hyperelastic properties. This means that the stress-strain relationship in soft tissue is nonlinear and, thus, acoustoelastic effects arise under large tissue compression (16,27). Values of SWS and SoS become stress dependent and vary with applied tissue compression. The acoustoelastic model predicts a linear relationship between squared wave velocities and the applied stress (16,28,29). The slope of this relationship, which we refer to as the acoustoelastic parameter, is related to the third-order elastic constants that quantify tissue nonlinearity (27). Thus, the experimental quantification of this slope provides access to novel tissue characterization properties (see Appendix A). In this study, we did not have direct measurements of stress. Instead, we measured probe-reflector distances from which strain values can be computed. To represent the acoustoelastic model, we transformed strain values to stress using the Ogden hyperelastic model (30), which describes the nonlinear stress-strain relationship in rubber-like solids, including biological tissue (31,32). For uniaxial compression, the model states that
where N, µ, and α are tissue-dependent parameters, σ is the applied uniaxial stress, and λ is the stretch ratio (30). The latter is related to the compressive strain, which is directly measured in our experiments as the ratio between the probe-reflector distance reduction and the probe-reflector distance without compression. The Ogden model is essentially empirical and requires experimental observations to find suitable values of N, µ, and α for the tissue under consideration. We define these parameters following the experimental observations of Zhai et al. (31) in porcine muscle tissue, with N =1 and α =8. The compressive stress is therefore proportional to the Ogden stretch parameter λ7 − λ−5. This parameter provides a proxy for estimating applied compressive stress in our examinations. We performed a linear regression for squared velocities as a function of the Ogden stretch parameter and defined its slope as the new empirical tissue characterization parameter. As shown in Appendix A, this acoustoelastic parameter is related to parameters describing tissue nonlinearity.
Statistical analysis
Statistical analysis and visualization were performed using Python (version 3.7.6) with SciPy (1.5.0), Pandas (1.0.5), Seaborn (0.10.1), and Pingouin (0.3.8) libraries. The coefficient of variation (CoV) was computed to measure the variability of the measurements. D’Agostino’s K-squared test was used to verify a Gaussian distribution of the data. Pearson correlation coefficient was used to analyze correlations, and we considered values from 0 to 0.19 as very weak, 0.20 to 0.39 as weak, 0.40 to 0.59 as moderate, 0.60 to 0.79 as strong, and 0.80 to 1.00 as very strong (33). Differences between dependent correlation coefficients were assessed using the Steiger method (34). P values less than 0.05 were considered statistically significant. Average correlation coefficients were computed by applying Fisher’s z-transformation. Statistical differences between both calves and different compression levels were analyzed with paired sample t-test (mean) and F-test (variance). In case the variances were significantly different, we used Welch’s t-test to analyze differences in mean. Variability of different tissue characterization metrics was assessed using the intraclass correlation coefficient (ICC). We compared both legs and applied the two-way mixed-effects model based on averaged three measurements. ICC values were assessed following Koo et al. (35).
Results
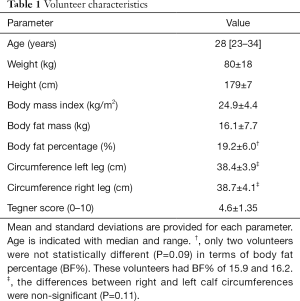
Overall, 381 out of 381 (100%) SWS measurements and 366 out of 381 (96%) SoS measurements were successful. Unsuccessful SoS measurements identified the wrong echo arrival time. There were no serious comfort issues and no drop-offs in volunteers. Volunteer characteristics are listed in Table 1.
Full table
Comparison between SWS and SoS measurements
The values of SWS for all compression steps ranged from 2.09 to 6.18 m/s with a median of 3.68 m/s and a CoV of 22.04%. For SoS, the values for all compression values ranged from 1,430 to 1,579 m/s with a median of 1,537 m/s and a CoV of 2.18%. Both SWS and SoS measurements were normally distributed (P<0.01).
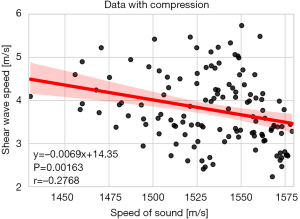
A non-significant correlation was observed between SWS and SoS when measurements with no tissue compression were considered (r=−0.08, P=0.73). For all tissue compression values, SWS and SoS showed a weak negative correlation [r=−0.28, 95% confidence interval (CI): −0.43 to −0.11, P=0.002] (Figure 3).
Tissue-compression effects on SWS and SoS measurements
Figure 4 shows the mean variations in SWS and SoS of both gastrocnemius muscles of different volunteers with respect to tissue compression, which is indicated in terms of the probe-reflector distance. SWS values, though highly variable, tend to increase with increasing compression, while SoS values decay nonlinearly.
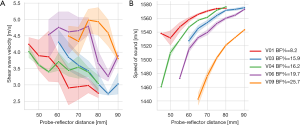
When considering measurements without tissue compression, the mean and standard deviation of SWS and SoS were 3.53±0.85 m/s (CoV: 24.1%) and 1,558±18 m/s (CoV: 1.18%), respectively. For measurements with tissue compression, the mean SWS and SoS became 3.85±0.83 m/s (CoV: 21.56%) and 1,527±34 m/s (CoV: 2.19%), respectively. Differences in the mean and variance between measurements with and without compression were non-significant for SWS (t-test: P=0.10, F-test: P=0.65) and significant for SoS (t-test: P<0 .001; F-test: P=0.002).
We observed a non-significant correlation between SWS and probe-reflector distance (r=−0.024, P=0.64). By comparing relative values, which means that we compare the differences in SWS with respect to the baseline without compression (hereinafter referred to as changes in SWS) and the compressive strain, we found a moderate negative correlation (r=−0.42, 95% CI: −0.50 to −0.33, P<0.001).
The SoS correlated moderately with probe-reflector distance (r=0.46, 95% CI: 0.31–0.58, P<0.001). Strong correlations were found between changes in SoS and strain (r=0.79, 95% CI: 0.72–0.85, P<0.001).
Fitting the acoustoelastic model for tissue nonlinearity quantification
Figure 5A represents changes in squared SoS with respect to the Ogden stretch parameter, which is proportional to the estimated compressive stress. When considering all subjects together, we found a strong correlation (r=0.78, 95% CI: 0.70–0.84, P<0.001) between these two quantities. By considering each of the subjects separately, the mean of the individual correlations became very strong (r=0.86, 95% CI: 0.81–0.90, P<0.001). We defined the slope of their linear regression model (i.e., the acoustoelastic model) as the SoS acoustoelastic parameter. It correlated negatively and strongly with SoS of tissue without compression (r=−0.73, 95% CI: −0.88 to −0.44, P<0.001). Figure 5B shows that the acoustoelastic model describes well the nonlinear decay of SoS values with respect to the probe-reflector distance.

For SWS, we found a weak negative correlation between the changes in squared SWS and the Ogden stretch parameter (r=−0.36, 95% CI: −0.44 to −0.27, P<0.001). When considering all subjects separately, the mean of individual correlations remained weak (r=−0.36, 95% CI: −0.49 to −0.33, P<0.001), which, contrary to SoS, did not allow us to extract metrics related to tissue nonlinearity.
Variability of SWS and SoS measurements
Mean differences between dominant and non-dominant legs were not significant for SWS (t-test: P=0.15; F-test: P=0.29) and SoS (t-test: P=0.92; F-test: P=0.76). By comparing measurements in both legs, we found a weak correlation (r=0.37, 95% CI: 0.13–0.057, P=0.003) for SWS and a very strong correlation (r=0.90, 95% CI: 0.84–0.94, P<0.001) for SoS. The mean difference and standard deviation between both legs was −0.16±0.89 m/s for SWS and 0.17±14.21 m/s for SoS.
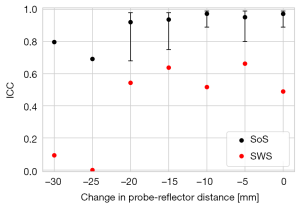
By analyzing variability between both legs, SoS showed an excellent reliability (ICC =0.91, 95% CI: 0.65–0.98, P<0.001) whereas the reliability of SWS was not significant (ICC =0.62, P=0.08) (Figure 6). These results considered measurements with all compression levels. For fixed compressions, the reliability of SWS remained non-significant. The reliability of SoS was maximum (ICC =0.97, 95% CI: 0.89–0.99, P<0.001) when no compression was applied (Figure 6). The reliability of the SoS acoustoelastic parameter was good (ICC =0.88, 95% CI: 0.52–0.97, P=0.002).
Comparison of SWS and SoS measurements with body fat percentages
SWS correlated strongly with BF% (r=0.60, 95% CI: 0.42–0.74, P<0.001) when no compression was applied and moderately (r=0.44, 95% CI: 0.35–0.51, P<0.001) when all compression values were considered together. For SoS, the correlation was moderate and negative with BF% (r=−0.43, 95% CI: −0.73 to −0.01, P=0.05) for data without compression. For data with all compression values, we found a weak negative correlation between SoS and BF% (r=−0.30, 95% CI: −0.45 to −0.14, P<0.001). These correlations were significantly different from the ones obtained for SWS (P<0.01). The SoS acoustoelastic parameter correlated moderately with BF% (r=0.48, 95% CI: 0.05–0.76, P=0.03).
Discussion
The results of this study indicate that SoS and SWS in the gastrocnemius muscle correlate weakly with each other, meaning that they provide fundamentally different information about tissue composition and mechanical properties. With increasing tissue compression, SoS values decayed nonlinearly, whereas the values of SWS showed an increasing trend. The decay in SoS was monotonic and consistent between both calves. SWS showed more oscillatory trends, with high variability between both calves. SoS measurements were therefore more reliable than SWS and better suited to extract novel parameters quantifying tissue nonlinear elasticity. SWS showed stronger correlations than SoS with global adipose content (BF%).
Various clinical studies have shown the potential of SoS and SWS for tissue characterization and diagnostics. Yet, little attention has been devoted to comparing both parameters. Glozman et al. (23) measured SoS and SWS values in different ex-vivo phantoms, and although correlations were not directly analyzed, their results show no apparent relationship between the two velocities [see Figure 7 in Glozman et al. (23)]. This is consistent with our results, which showed a weak correlation between SoS and SWS (r=−0.28).
Strong empirical correlations between longitudinal and shear wave velocities, however, have been observed in other materials in nature. For instance, in earth sciences, it is well known that a broad range of crustal lithologies exhibit quasi-linear relations between both velocities (36). In industrial US testing, it is generally assumed that SWS is approximately half the value of SoS, an approximation that holds well for most metals, plastics, and ceramics (37).
In soft tissue, these velocities are approximately uncorrelated, which we attribute to the differences in the order of magnitude of typical SWS and SoS values. In muscle, we observed a median of 3.68 m/s for SWS and 1,537 m/s for SoS, which means that SWS is about three orders of magnitude smaller than SoS. This is a consequence of the quasi-incompressibility of soft tissues (38). In such cases, shear and longitudinal velocities are decoupled and provide independent information about different elastic moduli describing elastic tissue properties. If we consider, for simplicity, tissue as isotropic, given the tissue density ρ, SoS fully determines tissue compressibility (bulk modulus K ≈ ρ*SoS2), whereas SWS provides stiffness information (shear modulus G ≈ ρ*SWS2) (23). In this case, tissue elastic properties are entirely described by both SoS and SWS. Muscle tissue, however, is often approximated as transversely isotropic with the symmetry axis parallel to the fiber direction (39). While the relationship between wave speeds and elastic moduli is more complex, SoS and SWS still appear decoupled and provide information about 2 out of 5 independent elastic constants (39). In this case, a full description of tissue elastic properties would require SoS and SWS measurements in different directions relative to muscle fibers.
Variations in ultrasonic wave velocities in stressed materials have been well described by several authors since the 1940s (40). Hughes and Kelly (27) first introduced the use of controlled stress to determine third-order elastic parameters characterizing nonlinear elasticity of solids, known as the acoustoelasticity experiment. Acoustoelastic theory predicts a linear relationship between squared velocities and the applied stress. The slope of this relationship depends on third-order elastic parameters describing nonlinear elasticity. Its clinical use for determining tissue nonlinearity has focused on studying changes in SWS (15-17). For instance, this information has been shown to be promising for the classification of breast tumors (41). In a study with ex-vivo liver samples, Otesteanu et al. (15) measured an increase of SWS values with increasing compressive strain, reporting changes of approximately 25% for a maximum strain of 14%. For the same order of magnitude in strain, we observed relatively lower increase in SWS of the gastrocnemius muscle that ranged from 7% to 20%. Similar increasing trends in SWS have also been reported in ex-vivo porcine kidneys (18) and in-vivo human breast (17).
Acoustoelastic analysis using longitudinal waves has been extensively applied for material characterization in non-destructive testing (42) and material sciences (43,44). To the best of our knowledge, our work constitutes the first clinical study for in-vivo tissue of this class. Following the acoustoelastic theory, we transformed strain measurements to stress values and represented squared SoS with respect to the stress. We found a very strong correlation between these two quantities (r=0.86), suggesting that our observations agree with theoretically predicted linear relationships (see Appendix A). This allowed us to define a new tissue characterization parameter (SoS acoustoelastic parameter) related to tissue nonlinearity that could potentially be used as a novel biomarker. A similar acoustoelastic analysis for SWS found a weak correlation (r=−0.36), indicating that the trends are strongly affected by other confounding variables and cannot be reliably used for quantifying nonlinearity with the current clinical setup.
The acoustoelastic parameter is related to a set of linear and nonlinear elastic constants (see Appendix A). However, a complete description of tissue nonlinear elasticity is obtained by estimating individual nonlinear elastic moduli. For isotropic tissue, there are three independent nonlinear moduli. Assuming incompressible tissue, changes in SWS are directly related to one particular modulus (16). This is why clinical applications of acoustoelasticity have been only focused on SWS so far. Our work empirically demonstrates that acoustoelastic effects on SoS are meaningful. By relaxing the incompressibility assumption, these effects can help to estimate different nonlinear moduli and ultimately fully characterize tissue nonlinearity. The latter requires future studies that measure waves propagating in three different directions relative to the applied stress (27). The extension of acoustoelasticity to transversely isotropic tissues, such as muscles, was recently suggested (45). Such tissues have nine independent nonlinear moduli and would require additional wave speed measurements.
Our study did not directly measure the applied compressive stress. To estimate the stress from strain measurements, we needed the stress-strain constitutive relationship in the gastrocnemius muscle. We approximated this using the Ogden hyperelastic model suggested by Zhai et al. (31) from empirical observations in porcine muscle tissue. While being beyond the scope of this study, direct stress measurements would allow us to characterize better the elastic tissue model describing the observed effects. Stress measurements would also be beneficial to (I) understand whether we have exceeded the range of validity of the acoustoelasticity theory, and (II) investigate other plausible explanations for observed speed changes, for instance, related to the stress-induced microstructural changes.
SWS measurements are known to be very sensitive to confounders, especially in muscles (12,46). Overall, we found larger variability in measurements of SWS than SoS when comparing both calves of the same subject. SoS provided higher reliability (ICC =0.91) than SWS (ICC =0.62, P=0.08). The reliability of SoS decayed for compressions larger than 10 mm and affected the variability of the SoS acoustoelastic parameter (ICC =0.88). Finer compression steps and a smaller maximum compression could therefore improve the estimations of the acoustoelastic parameter. Excellent reliability for SoS was also reported by other studies in calf muscle (ICC =0.98) (20) and breast tissue (ICC =0.990) (26). These values are slightly higher than ours. The reliability measured in our study is limited for two reasons. First, our approach is based on the comparison of both legs. This is not strictly rigorous, although it is justified due to the non-significant differences in speed (P=0.92) and calf circumferences (P=0.11) between the legs. Second, we compute ICC based on averaged three measurements in each leg. Larger datasets that include more repeated measurements are necessary to provide accurate reliability estimations.
We studied the clinical use of the three metrics considered in this work for muscle composition. Possible applications include sarcopenia assessment in older adults or sports medicine in active young populations. SWS correlated stronger with BF% (r=0.60, P<0.001) than SoS (r=−0.43, P=0.05) and SoS acoustoelastic parameter (r=0.48, P=0.03). These results are unexpected since the evidence in the literature points to SoS as a better metric for body fat quantification. For instance, Ruby et al. (20) found a strong correlation between SoS in the calf muscle and BF%, whereas Alfuraih et al. (10) observed moderate, negative correlations between SWS in hamstring muscles and fat mass. The disagreement with our results may be caused by the low heterogeneity of our examined population, which was composed by healthy young individuals with a moderate range of BF% values. Furthermore, to better understand the utility of these metrics for muscle composition assessment, comparisons to regional analysis of fat quantification with MRI are desirable. This is supported by the very strong correlations between SoS and MRI fat fraction measurements found in calf tissue (r=−0.83) (20) and liver (r=0.85) (21). On the contrary, very weak correlations with MRI fat fraction have been reported for SWS in liver (r=0.06) (47). In a similar regional analysis, therefore, we expect superior correlations with tissue fat content for both SoS and SoS acoustoelastic parameter.
This study was limited to a low number of healthy young participants. This allowed us to analyze correlations and nonlinear effects on SoS and SWE minimizing the impact of other disease-related factors on our results. To better understand the utility of these metrics for tissue composition assessment, future studies with larger and more heterogeneous populations are required. The limited number of female/male participants was not suitable to analyze sex-related differences in our measurements.
In conclusion, SWS and SoS provided uncorrelated and independent information about tissue elastic properties. SWS showed stronger correlations with BF%, but SoS measurements were more reliable than SWS. SoS enabled the extraction of new metrics related to tissue nonlinearity, potentially offering complementary tissue information.
Acknowledgments
Funding: This project has been generously supported by a donation from Hans-Peter-Wild to the University Hospital Zurich Foundation. Sergio J. Sanabria was supported by the mobility grant 0141/2019 from Gottfried and Julia Bangerter-Rhyner foundation.
Footnote
Conflicts of Interest: All authors have completed the ICMJE uniform disclosure form (available at http://dx.doi.org/10.21037/qims-20-1321). The authors have no conflicts of interest to declare.
Ethical Statement: The authors are accountable for all aspects of the work in ensuring that questions related to the accuracy or integrity of any part of the work are appropriately investigated and resolved. The study was conducted in accordance with the Declaration of Helsinki (as revised in 2013). This study was approved by institutional review board and the local ethics committee (Kantonale Ethikkomission Zürich; KEK-ZH-Nr. 2015-0323), and written informed consent was obtained from all subjects.
Open Access Statement: This is an Open Access article distributed in accordance with the Creative Commons Attribution-NonCommercial-NoDerivs 4.0 International License (CC BY-NC-ND 4.0), which permits the non-commercial replication and distribution of the article with the strict proviso that no changes or edits are made and the original work is properly cited (including links to both the formal publication through the relevant DOI and the license). See: https://creativecommons.org/licenses/by-nc-nd/4.0/.
References
- Cawthon PM, Fox KM, Gandra SR, Delmonico MJ, Chiou CF, Anthony MS, Sewall A, Goodpaster B, Satterfield S, Cummings SR, Harris TB. Health, Aging and Body Composition Study. Do muscle mass, muscle density, strength, and physical function similarly influence risk of hospitalization in older adults? J Am Geriatr Soc 2009;57:1411-9. [Crossref] [PubMed]
- Landi F, Russo A, Liperoti R, Pahor M, Tosato M, Capoluongo E, Bernabei R, Onder G. Midarm muscle circumference, physical performance and mortality: re-sults from the aging and longevity study in the Sirente geographic area (ilSI-RENTE study). Clin Nutr 2010;29:441-7. [Crossref] [PubMed]
- Janssen I, Heymsfield SB, Ross R. Low relative skeletal muscle mass (sarcopenia) in older persons is associated with functional impairment and physical disability. J Am Geriatr Soc 2002;50:889-96. [Crossref] [PubMed]
- Buckinx F, Landi F, Cesari M, Fielding RA, Visser M, Engelke K, et al. Pitfalls in the measurement of muscle mass: a need for a reference standard. J Cachexia Sarcopenia Muscle 2018;9:269-78. [Crossref] [PubMed]
- Cruz-Jentoft AJ, Bahat G, Bauer J, Boirie Y, Bruyère O, Cederholm T, Cooper C, Landi F, Rolland Y, Sayer AA, Schneider SM, Sieber CC, Topinkova E, Vande-woude M, Visser M, Zamboni M. Writing Group for the European Working Group on Sarcopenia in Older People 2 (EWGSOP2), and the Extended Group for EWGSOP2. Sarcopenia: revised European consensus on definition and diag-nosis. Age Ageing 2019;48:16-31. Erratum in: Age Ageing 2019 Jul 1;48(4):601. [Crossref] [PubMed]
- Sigrist RMS, Liau J, Kaffas A, El , Chammas MC, Willmann JK. Ultrasound elas-tography: Review of techniques and clinical applications. Theranostics 2017;7:1303-29. [Crossref] [PubMed]
- Taljanovic MS, Gimber LH, Becker GW, Latt LD, Klauser AS, Melville DM, Gao L, Witte RS. Shear-Wave Elastography: Basic Physics and Musculoskeletal Applications. Radiographics 2017;37:855-70. [Crossref] [PubMed]
- Chiu YH, Chang KV, Chen IJ, Wu WT, Özçakar L. Utility of sonoelastography for the evaluation of rotator cuff tendon and pertinent disorders: a systematic re-view and meta-analysis. Eur Radiol 2020;30:6663-72. [Crossref] [PubMed]
- Lin CP, Chen IJ, Chang KV, Wu WT, Özçakar L. Utility of Ultrasound Elas-tography in Evaluation of Carpal Tunnel Syndrome: A Systematic Review and Meta-analysis. Ultrasound Med Biol 2019;45:2855-65. [Crossref] [PubMed]
- Alfuraih AM, Tan AL, O’Connor P, Emery P, Wakefield RJ. The effect of ageing on shear wave elastography muscle stiffness in adults. Aging Clin Exp Res 2019;31:1755-63. [Crossref] [PubMed]
- Šarabon N, Kozinc Ž, Podrekar N. Using shear-wave elastography in skeletal muscle: A repeatability and reproducibility study on biceps femoris muscle. Ae-gerter CM, editor. PLoS One 2019;14:e0222008.
- Ruby L, Mutschler T, Martini K, Klingmüller V, Frauenfelder T, Rominger MB, Sanabria SJ. Which Confounders Have the Largest Impact in Shear Wave Elas-tography of Muscle and How Can They be Minimized? An Elasticity Phantom, Ex Vivo Porcine Muscle and Volunteer Study Using a Commercially Available System. Ultrasound Med Biol 2019;45:2591-611. [Crossref] [PubMed]
- Rominger MB, Kälin P, Mastalerz M, Martini K, Klingmüller V, Sanabria S, Frauenfelder T. Influencing Factors of 2D Shear Wave Elastography of the Mus-cle - An Ex Vivo Animal Study. Ultrasound Int Open 2018;4:E54-60. [Crossref] [PubMed]
- Oberai AA, Gokhale NH, Goenezen S, Barbone PE, Hall TJ, Sommer AM, Jiang J. Linear and nonlinear elasticity imaging of soft tissue in vivo: demonstration of feasibility. Phys Med Biol 2009;54:1191-207. [Crossref] [PubMed]
- Otesteanu CF, Chintada BR, Rominger MB, Sanabria SJ, Goksel O. Spectral Quantification of Nonlinear Elasticity Using Acoustoelasticity and Shear-Wave Dispersion. IEEE Trans Ultrason Ferroelectr Freq Control 2019;66:1845-55. [Crossref] [PubMed]
- Gennisson JL, Rénier M, Catheline S, Barrière C, Bercoff J, Tanter M, Fink M. Acoustoelasticity in soft solids: assessment of the nonlinear shear modulus with the acoustic radiation force. J Acoust Soc Am 2007;122:3211-9. [Crossref] [PubMed]
- Bernal M, Chammings F, Couade M, Bercoff J, Tanter M, Gennisson JL. In vivo quantification of the nonlinear shear modulus in breast lesions: Feasibility study. IEEE Trans Ultrason Ferroelectr Freq Control 2016;63:101-9. [Crossref] [PubMed]
- Aristizabal S, Amador Carrascal C, Nenadic IZ, Greenleaf JF, Urban MW. Appli-cation of Acoustoelasticity to Evaluate Nonlinear Modulus in Ex Vivo Kidneys. IEEE Trans Ultrason Ferroelectr Freq Control 2018;65:188-200. [Crossref] [PubMed]
- Szabo TL. Diagnostic Ultrasound Imaging: Inside Out. Elsevier Academic Press, 2004.
- Ruby L, Kunut A, Nakhostin DN, Huber FA, Finkenstaedt T, Frauenfelder T, Sanabria SJ, Rominger MB. Speed of sound ultrasound: comparison with proton density fat fraction assessed with Dixon MRI for fat content quantification of the lower extremity. Eur Radiol 2020;30:5272-80. [Crossref] [PubMed]
- Imbault M, Dioguardi Burgio M, Faccinetto A, Ronot M, Bendjador H, Deffieux T, Triquet EO, Rautou PE, Castera L, Gennisson JL, Vilgrain V, Tanter M. Ultra-sonic fat fraction quantification using in vivo adaptive sound speed estimation. Phys Med Biol 2018;63:215013 [Crossref] [PubMed]
- Sanabria SJ, Martini K, Freystätter G, Ruby L, Goksel O, Frauenfelder T, Rominger MB. Speed of sound ultrasound: a pilot study on a novel technique to identify sarcopenia in seniors. Eur Radiol 2019;29:3-12. [Crossref] [PubMed]
- Glozman T, Azhari H. A method for characterization of tissue elastic properties combining ultrasonic computed tomography with elastography. J Ultrasound Med 2010;29:387-98. [Crossref] [PubMed]
- Tegner Y, Lysholm J. Rating systems in the evaluation of knee ligament injuries. Clin Orthop Relat Res 1985;43-9. [Crossref] [PubMed]
- Song P, Macdonald M, Behler R, Lanning J, Wang M, Urban M, Manduca A, Zhao H, Callstrom M, Alizad A, Greenleaf J, Chen S. Two-dimensional shear-wave elastography on conventional ultrasound scanners with time-aligned sequen-tial tracking (TAST) and comb-push ultrasound shear elastography (CUSE). IEEE Trans Ultrason Ferroelectr Freq Control 2015;62:290-302. [Crossref] [PubMed]
- Ruby L, Sanabria SJ, Obrist AS, Martini K, Forte S, Goksel O, Frauenfelder T, Kubik-Huch RA, Rominger MB. Breast Density Assessment in Young Women with Ultrasound based on Speed of Sound: Influence of the Menstrual Cycle. Medicine (Baltimore) 2019;98:e16123 [Crossref] [PubMed]
- Hughes DS, Kelly JL. Second-Order elastic deformation of solids. Phys Rev 1953;92:1145-9. [Crossref]
- Destrade M, Gilchrist MD, Saccomandi G. Third- and fourth-order constants of incompressible soft solids and the acousto-elastic effect. J Acoust Soc Am 2010;127:2759-63. [Crossref] [PubMed]
- Zhu Q, Burtin C, Binetruy C. Acoustoelastic effect in polyamide 6: Linear and nonlinear behaviour. Polym Test 2014;40:178-86. [Crossref]
- Ogden RW, Hill R. Large deformation isotropic elasticity - on the correlation of theory and experiment for incompressible rubberlike solids. Proc R Soc London A Math Phys Sci 1972;326:565-84. [Crossref]
- Zhai X, Chen WW. Compressive Mechanical Response of Porcine Muscle at In-termediate (100/s-102/s) Strain Rates. Exp Mech 2019;59:1299-305. [Crossref]
- Mihai LA, Chin LK, Janmey PA, Goriely A. A comparison of hyperelastic consti-tutive models applicable to brain and fat tissues. J R Soc Interface 2015;12:0486.
- Stewart A. Basic statistics and epidemiology: a practical guide. 3rd edition. Ab-ingdon, VA, USA: Radcliffe Pub, 2010.
- Howell DC. Statistical methods for psychology. 7th edition. Belmont, CA, USA: Wadsworth, Cengage Learning, 2010.
- Koo TK, Li MY. A Guideline of Selecting and Reporting Intraclass Correlation Coefficients for Reliability Research. J Chiropr Med 2016;15:155-63. [Crossref] [PubMed]
- Brocher TM. Empirical relations between elastic wavespeeds and density in the Earth’s crust. Bulletin of the Seismological Society of America 2005;95:2081-92. [Crossref]
- Krautkrämer J, Krautkrämer H. Ultrasonic testing of materials. 4th edition. Springer Verlag Berlin Heldelberg, 1990.
- Fung Y. Biomechanics: mechanical properties of living tissues. Springer Science & Business Media, 2013.
- Mol CR, Breddels PA. Ultrasound velocity in muscle. J Acoust Soc Am 1982;71:455-61. [Crossref] [PubMed]
- Biot MA. The influence of initial stress on elastic waves. J Appl Phys 1940;11:522-30. [Crossref]
- Sayed A, Layne G, Abraham J, Mukdadi OM. 3-D visualization and non-linear tissue classification of breast tumors using ultrasound elastography in vivo. Ultrasound Med Biol 2014;40:1490-502. [Crossref] [PubMed]
- Egle DM, Bray DE. Measurement of acoustoelastic and third-order elastic con-stants for rail steel. J Acoust Soc Am 1976;60:741-4. [Crossref]
- Crecraft DI. Ultrasonic Wave Velocities in Stressed Nickel Steel. Nature 1962;195:1193-4. [Crossref]
- Smith RT. Stress-induced anisotropy in solids—the acousto-elastic effect. Ultra-sonics 1963;1:135-47. [Crossref]
- Bied M, Jourdain L, Gennisson JL. Acoustoelasticity in transverse isotropic soft tissues: quantification of muscles’ nonlinear elasticity. 2020 IEEE International Ultrasonics Symposium (IUS), 2020:1-4.
- Creze M, Nordez A, Soubeyrand M, Rocher L, Maître X, Bellin MF. Shear wave sonoelastography of skeletal muscle: basic principles, biomechanical concepts, clinical applications, and future perspectives. Skeletal Radiol 2018;47:457-71. [Crossref] [PubMed]
- Kramer H, Pickhardt PJ, Kliewer MA, Hernando D, Chen GH, Zagzebski JA, Reeder SB. Accuracy of Liver Fat Quantification With Advanced CT, MRI, and Ultrasound Techniques: Prospective Comparison With MR Spectroscopy. AJR Am J Roentgenol 2017;208:92-100. [Crossref] [PubMed]


