Stress distribution in the walls of major arteries: implications for atherogenesis

Introduction

Atherosclerosis may be a generalised affliction of the arterial system predisposed by genetic factors and accelerated or induced by the external influence of other risk factors such as high cholesterol diet, chronic hypertension, smoking and the degenerative effects of aging (1). Sometimes however, there may be isolated plaques of atheroma without generalised atherosclerosis and these plaques may pose critical target organ ischaemia because of their location and rapid growth where there is no collateral circulation, for example the origin of the left main coronary artery, or where the growth of the lesion outstrips the growth of potential collaterals, such as the superior mesenteric or internal carotid arteries.

Predicting the vulnerable zones for developing clinically important critical atheroma plaques and pre-emptive intervention is the basis of modern arterial vascular surgery. As with epidemiology, observation and correlation of clusters leads to rational management of the disease entity. The relevant observation for stenosing lesions of atherosclerosis and plaque development is that they correspond with the geographical location of stress in the arterial tree (2,3). Vessel bifurcations, and branch origins are noticeable sites. Genetic predispositions and environmental risk factors may vary, but pulsatile blood pressure is a unique constant property. Elevations of blood pressure and increases in the pulse pressure are commonly observed in ageing patients with atherosclerosis.

Wall stress is exponentially related to the blood pressure and particularly to the pulse pressure (2). Generally, the stresses imposed by blood pressure on the arterial wall are longitudinal stress, radial stress or normal stress (acting perpendicular to the axis of the vessel) and tangential stress or hoop stress (Figure 1). Shear stress acts parallel to the surface of the intima, media and adventitia layers and may cause one layer to slide over another. Stress is related to strain (amount of deformation per initial length of material). Shear stress may damage the wall of a vessel by injuring the intima (the inner layer of the vessel) as blood flows over the surface and this is currently considered the portal for imbibition of plasma lipid into the wall leading to atherogenesis (3,4). However, the effect of shear stress does not end at the intima. Shear stress may affect the inner layers of a multi-layer blood vessel and cause one layer to shift in relation to another depending on the blood pressure and the different properties of each layer (5).

Figure 1 The layers of the arterial vessel are anisotropic i.e., unlike isotropic materials like steel, which have same material properties in X, Y and Z directions, anisotropic materials have different mechanical properties in different directions. The stresses acting on the vascular vessel are generally caused by internal fluid/blood pressure. The three principle stresses acting on the vessel segment are longitudinal stress (σ_l), radial stress or normal stress (σ_r) and tangential stress or hoop stress (σ_h). Longitudinal stress: the axial force puts the vascular vessel in either tension or compression. Radial stress: normal stress, perpendicular to symmetry axis. Hoop stress or circumferential stress: this is stress as a result of vessel’s resistance to bursting effect of the applied internal pressure. Shear stress (not apparent on the figure): it may cause one layer to slide over another. It may cause deformation, or delamination.

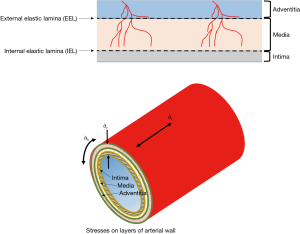
This study uses Computational Fluid Dynamics (CFD), Finite Element Analysis (FEA) and ANSYS Composite PrepPost (ACP) software to model the shear stresses in the layers of the arterial wall of a patient-specific but typical carotid bifurcation. CFD is used to investigate fluid flow behaviours and analyse stresses at the fluid-solid interface, FEA is applied for structural mechanical analysis and ACP to model arterial layers, stress and failure analysis of the vascular vessel. Consequently, three models were developed and subsequently combined for this study. The complex movement of the carotid artery during the cardiac cycle can be simplified by using a short segment of anatomy (here just 7.5 cm; only 3 cm of which is the internal and external length and 4.5 cm the common carotid length).

The CFD model was used to analyse variable volume of blood flow under pulsatile blood pressure and extract the drag forces of the blood flow on the inner surface of the artery. The drag forces were then exported from CFD into the FEA model, where the shear stress in the arterial structure was calculated. Previous studies have considered vascular vessels as isotropic, i.e., as a single layer with the same identical material properties in all directions. When a load is applied at any point in the X, Y or Z-axis, the vessel will exhibit the same stress and strain in the three different directions. In reality however, the vascular vessel is a laminate consisting of adventitial, medial and intimal layers. These individual layers exhibit different mechanical properties. Therefore, the vascular vessel is not isotropic, but rather orthotropic. Each of the arterial wall layers have different mechanical properties in X, Y and Z directions. To analyse the mechanical response of the vessel, the behaviour of each individual layer must be predicted. We used the theory of laminate analysis, also referred to as Classical Laminate Plate Theory, to analyse the stress distribution on the carotid artery wall. Therefore, the ACP model was used to analyse and provide shear stress distributions in each of the arterial layers. Shear stresses in vessel walls can be calculated as a result of the pulsatile effect that the flowing blood imparts on the walls, in terms of circumferential (‘hoop’ stresses in engineering) as well as normal and longitudinal stress. Using these combined modelling methods, we calculate the stress gradient within and across the layers of the arterial wall, and identify the most vulnerable location within the wall for mechanical injury.

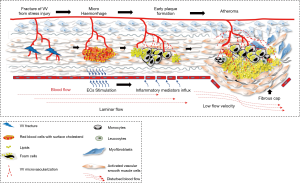
The underlying hypothesis that this modelling would support is that there are shear stresses within the layers of arterial wall that cause injury to the penetrating branches of the vasa vasora and the tissues of the media, causing micro-haemorrhages and interstitial injury which would stimulate inflammation and form a lipid nidus in the injured media from extravasated plasma cholesterol and erythrocyte membranes (Figure 2). This may be an explanation for the initiation of atherosclerosis in this region separately from the established evidence for haemorrhage into a plaque from neoangiogenesis that is part of the response to plaque hypoxia and inflammation and also a consequence of ongoing pulsatile stress with further lipid deposition from microhaemorrhage. Once started, such a lesion would become prone to an injury/healing cycle (6-10). This paper investigates whether there is a relationship between (shear) stress variation within the arterial wall and the location of plaque in the carotid bifurcation.

Figure 2 Stress injury to the penetrating branches of the vasa vasora in the media results in microhaemorrhage. Cholesterol from red blood cell membranes forms a nidus for inflammation. Repeated stress injury forms a healing/injury cycle resulting in atherosclerotic plaque. Meanwhile, intimal injury from shear stress contributes to plaque development according to current theory.

Methods

In order to study the distribution of shear stress variation within the layers of a carotid artery, a de-identified patient-specific geometry was used after Sir Charles Gairdner and Osborne Park Hospitals Human Research Ethics Committee approval and patient informed consent. The geometry of a left sided in-vivo carotid artery of a healthy 70-year-old volunteer with 90% stenosis of the right carotid and 10% of the left was used for the geometry of the vessel and the wall modelled without the plaque. The patient had no risk factors for vascular disease or evidence of plaque elsewhere, and was chosen as a typical anatomy. Imaging was obtained in DICOM format from CT-scan images, and converted into a 3D-image. The 3D-image of the lumen (blood flow domain) of the carotid bifurcation was read by a 3D-Slicer (11) visualization tool and segmented, reconstructed and smoothed to obtain a real sized 3D-model. The process of relating pulsatile blood pressure to the inter-layer blood vessel model was performed in four steps:

• The first step was to create a 3D-model from CT-scan images and convert them into a 3D-CAD model which represented the blood flow domain in the carotid artery. The 3D-CAD model was used to create the blood flow volume for CFD simulation (12). A mean element (mesh) size of 0.3 mm was used and all the blood flow boundaries reconstructed.
• A pulsatile non-Newtonian (Carreau viscous model) blood inlet was used as the inlet boundary condition. The flow rate was derived from literature for at rest (360 mL/min at 60 beats/min) and exertion (1,300 mL/min at 120 beats/min) as the input conditions to most accurately represent the human physiology. The output boundary condition was defined using typical human physiological blood pressures at rest (120/80 mmHg) and exertion (200/100 mmHg). A stationary and no slip wall was defined as a wall boundary condition of the CFD model. ACP was used to construct and define the arterial layers. Structural analysis on the arterial layup was done using ANSYS FEA. ANSYS FLUENT was used to analyse the flow regime and calculate the shear stress magnitude on and between the layers of the arterial wall.
• In order to represent the arterial wall, a layer of 1-mm thickness was added to the blood flow domain’s outer boundary. The common carotid artery (CCA) end of the arterial wall was defined as the fixed-end and the external carotid artery (ECA) and internal carotid artery (ICA) ends of the arterial wall had one degree of freedom (DOF) in the direction of the blood fluid flow. A 3D-geometry of the blood vessel was established to simulate the arterial wall and a computational mesh of size 0.2 mm was generated (mesh sensitivity analysis is discussed later).
• Thirdly, a multi-layer finite element model of 1 mm average thickness layer (accepting that thickness changes) was created in the arterial wall to represent the different layers of a carotid artery (intima, media and adventitia) and elastic interlaminar layers using the ACP application. ACP is commonly used in engineering to model and analyse layered composites. HyperSizer^TM, computer-based software developed by NASA, is similar to ACP and is used to design, analyse and optimize laminate composite aerospace structural systems (13). Arterial vessels are layered composites consisting of adventitia, media and intima plies or laminates. Each of the laminates are orthotropic and have different mechanical properties in X, Y and Z directions. From constitutive equations of a laminate, as indicated in Eq. [1] below, the stress in the X-direction, Y-direction and shear stress in each of the vascular layers can be deduced.

  $$\begin{array}{l}{N}_x={\displaystyle {\int }_{-h/2}^{h/2}{\sigma }_{x}dz}\\ N_y={\displaystyle {\int }_{-h/2}^{h/2}{\sigma }_{y}dz}\\ N_{xy}={\displaystyle {\int }_{-h/2}^{h/2}{\sigma }_{xy}dz}\end{array}$$[1]

• As shown in Figure 3, the 1 mm thickness of the arterial wall was divided into five layers—three main arterial wall layers and two elastic laminae interlayers. The medial layer is of similar constituency throughout being composed of smooth muscle cells embedded in a matrix of elastin, collagen and proteoglycan matrix (14,15). We therefore, divided it into five arbitrary equal sublayers in order to investigate which part of the media was under most stress.
  

  Figure 3 Multi-layer carotid artery depicting thickness of layers.
• Finally, the arterial wall was assumed to be an elastic, anisotropic and inhomogeneous material (16,17) while the blood flow was assumed to be the standard K-epsilon (two equations) viscous model, with enhanced wall treatment, non-Newtonian Carreau viscosity modelling {18,19). The five arbitrary layers in the media were provided with the same material properties (shown in Table 1), as is the conventional engineering approach (14).
  

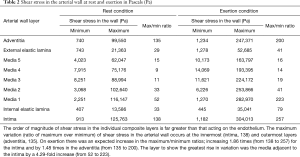  Table 1 Anisotropic mechanical properties of the layers of arterial wall in kilopascals (kPa)
  Full table

  $${\mu }_c={\mu }_{\infty }+\left({\mu }_0-{\mu }_{\infty }\right){\left[1+{\left(\lambda \dot{\gamma }\right)}^2\right]}^{\left(n-1\right)/2}$$[2]

The parameters of the Carreau viscosity which have the best fit to the blood flow shear rate (γ˙) and fluid characteristics (18) are given below:

• Viscosity at zero shear rate (

  ${\mu }_0$): 0.056 (Pa.s);

• Viscosity at infinite shear rate (

  ${\mu }_{\infty }$): 0.00345 (Pa.s);

• Time of viscosity changes from Newtonian to Power-law (λ): 3.313 (s);
• The slope of the Power-law (n): 0.3568.

ANSYS was employed to solve the fluid (CFD) and solid mechanic (FEA) packages with pulsatile blood flow using the carotid bifurcation’s geometry described above. The pressure distributions on the arterial wall were stored at systole and diastole; the effects on shear stress through different composite layers of the arterial wall were computed as a difference in ratio between these two states. Mesh size sensitivity analysis was performed using both CFD and FEA to validate mesh size independent of the solutions.

The CFD model was run to compute the shear stress values and pressures in order to then input these force and pressure data into the FEA model, to allow the structural analysis to take place.

Results

The major parameters which can influence stress/strain magnitude in a multilayer carotid artery model and consequently relative interlayer movement, are blood vessel geometry (21,22), the mechanical characteristics of the arterial wall (6) and blood pulse pressure (23). The ACP application can determine the magnitude of shear stress in all five separate layers.

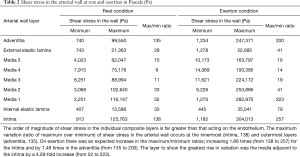
In Table 2, the order of magnitude of shear stress in the individual composite layers is far greater than that acting on the endothelium. The maximum variation (ratio of maximum over minimum) of shear stress in the arterial wall during rest conditions occurs at the innermost (intima, 138) and outermost layers (adventitia, 135). On exertion there was an expected increase in the maximum/minimum ratios; an increase by 1.86 times (from 138 to 257) for the intima and by 1.48 times in the adventitia (from 135 to 200). The layer to show the greatest rise in variation was the media adjacent to the intima by a 4.29-fold increase (from 52 to 223).

Table 2 Shear stress in the arterial wall at rest and exertion in Pascals (Pa)
Full table

It is clear in Table 2 that shear stress in the individual composite layers is far greater than conventional wall shear stresses (less than 5 Pa) acting on the endothelium (24).

On exertion there was an expected increase in the maximum/minimum ratios increasing 1.86 times (from 138 to 257) for the intima and by 1.48 times in the adventitia (from 135 to 200). The layer to show the greatest rise in variation was the media adjacent to the intima by a 4.29-fold increase (from 52 to 223).

In Table 1 (reproduced with permission from author), the ultimate stress magnitude represents the stress at which the complete failure (i.e., a break or rupture occurrence as the strain rate continues beyond yield stress) will occur. It can be observed from anisotropic mechanical properties of arterial wall layers (Table 1), that during rest, the maximum shear stress in the media (116 kPa) was less than the minimum ultimate stress across the arterial wall.

During simulated exertion, for the pressure parameters we used, the maximum shear stress magnitude in the intimal layer (304 kPa) and the adjacent medial layer (283 kPa) seen in Table 2 is within the range of the ultimate stress levels in Table 1. Hence, the stress and strain magnitude may go beyond the ultimate point in the stress-strain graph and reach the potential tissue failure zone at this tissue interface where there is the possibility of tissue failure with injury.

Discussion

Table 2 illustrates that not only does the maximum shear stress value occur in the range of ultimate stress (as shown in Table 1) of the artery wall, but also that those layers would be experiencing the highest ratios of maximum to minimum artery shear stresses (with each layer being separately calculated as discussed earlier). Therefore, the arterial wall would be prone to damage during exertion with 200/100 mmHg blood pressure. This means that the fluctuation of stress and consequently mechanical fatigue will be most evident in the intima and adjacent media. The magnitude of ratio changes in the media adjacent to the intima, compared to the intima and adventitia layers, makes this layer the most susceptible to injury, because the fluctuation causes the greatest fatigue motion.

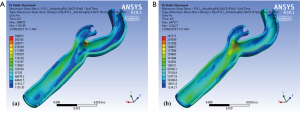
The shear stress contours in our carotid model (Figure 4) illustrate that the maximum magnitude of shear stress under normal physiological conditions occurs at the tip of the flow divider in the intimal layer while the maximum shear stress in the adventitia is located at the bifurcation segment of the carotid artery. It should be noted that the differences in mapping colour schemes is to adequately demonstrate the differences in local stress values along the layers, and the scale is also different as a demonstration of how the values of stress have changed between the intima and adventitia (having the same colour scheme for stress values would not enhance the appearance for interpretation purposes of the areas of local stress differences).

Figure 4 Maximum shear stress variations of a carotid bifurcation at rest for (A) intima and (B) adventitia layers.

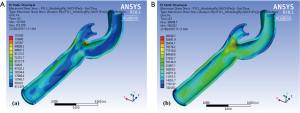
Figure 5 illustrates the maximum shear stress variations of a carotid bifurcation under exertion for (Figure 5A) intima and (Figure 5B) adventitia layers. An increase in pulse pressure from 120/80 to 200/100 mmHg causes an increase in the maximum shear stress level in all layers of the arterial wall. These maps show that the maximum shear stress contours are very similar under resting and exertional conditions around the bifurcation point.

Figure 5 Maximum shear stress variations of a carotid bifurcation under exertion for (A) intima and (B) adventitia layers.

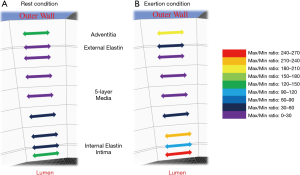
A schematic variation of the maximum/minimum shear stress ratios, during both rest and during exertion, is shown in Figure 6. The figure illustrates in different colours the nine layers of the arterial wall during (Figure 6A) rest and (Figure 6B) exertion, and shows that the highest ratio during exertion occurs in the inner layers of the arterial wall. The stress direction here suggests this is dominantly circumferential stress (in engineering parlance referred to as ‘hoop stress’). This is expected, as the hoop stress is due to the vessel’s resistance of the bursting effect of blood pulse pressure.

Figure 6 A schematic variation of maximum shear stress in different layers of the arterial wall (A) at rest, (B) under exertion.

The major parameters which can influence stress/strain magnitude in a multilayer carotid artery model and consequently relative interlayer movement, are blood vessel geometry, the mechanical characteristics of the arterial wall and blood pulse pressure (19,20,25-27). In our paper, an angio CT based model of a multicomponent Fluid-Solid Interaction (FSI) computational model of a human carotid artery was used to perform shear stress analysis in the arterial wall, and to identify critical stress variations which may cause injury within the wall of the vessel. This injury would most likely affect the fragile branches of the vasa vasora, particularly where they cross the boundaries between layers which have differential movement relative to each other throughout the cardiac cycle, as their material properties are different, and they respond differently to pulsatile pressure.

In order to obtain a more accurate location of shear stress, we used a multidisciplinary stress analysis process to transfer the pressure distribution from the blood flow onto the luminal surface of the blood vessel using an FSI system to simulate the coupling between the blood flow and the artery wall using ANSYS software. Hence, actual blood pressure loads were able to be used for shear stress analysis in the layers of the arterial wall, increasing accuracy.

Accuracy of CFD simulation is heavily reliant on realistic geometry. We endeavoured to account for all the relevant parameters by using a patient specific model, typical anatomy (free from the confounders of tortuosity and kinking etc. that occur not infrequently), physiological values and pulsatile. Haemodynamics and the mechanical properties of the arterial wall at the carotid bifurcation must have an important role in the development of atherosclerosis as they do in vessels elsewhere because plaques form at predictable sites in the arterial tree (5). Arterial haemodynamics are affected by blood viscosity, mean and pulse pressure, and, in the case of the carotid bifurcation, by the geometry of the bifurcation (26). Thus, the torsional effects of the two different pulsatile blood outflows, one blood flow to the face and the other blood flow to the brain, are of minimal relevance here. The greatest shear stress magnitude in the carotid artery is observed at the bifurcation, and this corresponds with the typical site for atheroma. We note here that this study used arterial mechanical properties for simulation modelling. These mechanical properties which include Young’s moduli (E_X, E_Y, E_Z), Poisson’s ratio (Ʋ_YZ, Ʋ_ZX, Ʋ_XY) and Shear moduli (G_YZ, G_ZX G_XY), will vary from one patient to another. This variation in the model input parameters may, accordingly, lead to variation in the reported magnitude of stress levels in the arterial wall layers. However, the stress profile, and hence, the location of highest stress level in the arterial wall, is expected to follow a similar trend found in this study, and corroborated by surgical observations.

The anisotropic mechanical behaviour of blood vessels presents a challenge to understanding the properties in this area and therefore to modelling, as the collagen fibres are arranged both longitudinally and circumferentially in different layers, and though these provide mechanical strength, they respond differently to longitudinal and circumferential stretch (28). The details of the comprehensive anisotropic mechanical properties of the arterial wall have been reported elsewhere (14,26-31).

Even though we chose significant hypertension, it is of concern that the shear stress measured approaches the ultimate limit of the mechanical properties of the blood vessel. The range of the maximal to minimal ratios indicate the potential movement of the individual arterial wall layers which may lead to fatigue and ultimately to mechanical failure of some components of the artery wall. At rest, the shear stress ratio is high in both the adventitial and the intimal layers of the artery. During exertion with 60 mmHg increase in pulse pressure, the shear stress ratio increases by less than 2-fold in the same layers, but increases in the innermost medial layer more than 4-fold indicating that the media is more vulnerable than the intima when the absolute and pulse pressures rise.

We have shown that the highest stress variations occur in the medial layer which is directly adjacent to the intima. If this layer fails due to fatigue, and the intima remains intact, then the highest shear stress level would transfer to the next closest layer (second medial layer) and so on, progressing through the layers until mechanical strength cancels out the imposed shear stress. This process is called first ply failure (FPF) in anisotropic material engineering using composite material failure criteria. This scenario could induce fractures of the vasa vasora which extend to the 3^rd medial layer potentially resulting in a micro-haemorrhage. This blood would contain lipid from both the plasma and walls of the red cells and could then become an initiation point for atherosclerosis (Figure 2). The geography of typical atheroma sites corresponds with both the zones of most stress in the arterial walls and concentration of vasa vasora, suggesting a link between these observations. Thubrikar and Robicsek used FEA analysis to demonstrate 4–6-fold increases in wall stress at arterial branch points in 1995 (2). They were proponents of the links between atherosclerosis, and pressure and wall stress, and modelled the carotid bifurcation, the aortic bifurcation, the intraosseous vertebral artery, the descending thoracic aorta and the intramyocardial coronary vessels, providing supporting evidence that increased wall stress was highly relevant to the location of plaque. However, the FEA methodology would have been less sophisticated in the mid-1990s.

Salzar et al., obtained six carotid bifurcations from cadavers and imposed internal pressure (120 and 80 mmHg) into the arteries and precisely recorded the geometry changes. The measured geometry of the bifurcation specimens placed into the FEA analyser to demonstrate 4–6-fold increases in wall stress at arterial branch points in 1995 (23). They were proponents of the links between atherosclerosis, and pressure and wall stress, and modelled the carotid bifurcation, the aortic bifurcation, the intraosseous vertebral artery, the descending thoracic aorta and the intramyocardial coronary vessels, providing supporting evidence that increased wall stress was highly relevant to the location of plaque.

There has been little other work in this area other than that by Cinthio et al. (25), who utilized a high-resolution ultrasonic method to measure longitudinal movement (forward and backward) of different layers of the arterial wall in the carotid bifurcation. The inner layers (intima and media) of the arterial wall demonstrated a larger magnitude of longitudinal movement than the adventitia layer. However, this study only estimated magnitude of movement of intima and media with respect to adventitia, but neither measured the shear stress and strain rate between different layers nor individual intra-layer of the arterial wall. CFD modelling of non-Newtonian and pulsatile blood flow; and the corresponding multi-layer FEA simulation approach can provide an accurate measurement of longitudinal shear stress fluctuations in an arterial wall.

We have used changes in blood pressure and pulse pressure that occur in older people and those with atherosclerosis to determine the stress levels within the different layers in the vessel. Such rises in pulse pressure are not seen in the young and healthy individuals where exercise tolerance is greater. There are two reasons for this—the first reason is related to the amount of elastin in the great vessels and its progressive loss during senescence. The capacitance of the great vessels and the energy storage during systole in the young is greater and distributed more efficiently to working muscles, including cardiac muscles that can only accept blood flow during the relaxation phase; and the peripheral working muscles fed by dilated arteries during exercise to accommodate the increase in cardiac output. When the major vessels stiffen or the run-off via the muscular arteries decreases due to arterial wall thickening with chronic hypertension, or because the volume of muscle diminishes from disuse, age, injury or disease, then increasing cardiac output, or even maintaining the same level, demands that the systolic pressure must rise and the pulse pressure widen.

The role of risk factors in humans for atherogenesis is supported by a large volume of evidence, but there remains some doubt about the initiating mechanism, because in most of the animal studies showing trans-intimal movement of lipid is in small animals and maybe these equate more to the size of the vasa vasorum and not the larger vessels. There are many animal experiments to show that lipid may traverse the intima and especially if it be damaged or affected by inflammation with increased porosity. This would be true for small vessels; for major vessels there maybe doubt because intimal injury during intervention leads to restenosis from intimal hyperplasia.

The question of the effect of exercise requires discussion in the context of the known benefits of exercise and the encouragement from healthcare providers that exercise will improve cardiovascular health and reduce cardiovascular risk. Rather than countering this sage advice, it may be more realistic to appreciate that there may be bespoke individual exercise limits which may be dependent on the degree of vessel stiffening with age, and a blanket one size fits all approach may not be appropriate.

Whilst this means that exercise is beneficial in attuning the muscular-skeletal system to optimise run-off and improve or maintain vascular health, exercise beyond a certain level could overstress vulnerable, often critical, zones predisposed to higher wall stress and lead to immediate or progressive “wear and tear” damage which might lead to plaque formation in those without other risk factors for vascular disease as they age, or indeed exacerbate the shear moment between established plaque and less diseased vessel wall. This latter could compound the risk of cardiovascular events from intraplaque haemorrhage as a sudden and potentially critical impact on end organ function by compromising lumen and end organ flow such as myocardial infarction or stroke.

With this reasoning, regular exercise is better than sudden or infrequent exertion. Exercise within the comfort zone, such as regular walking rather than brief irregular exertional gym workouts has been shown to have more benefit (32). Training and high-performance activities must balance benefit and harm, although there will be individual differences depending on age, fitness, risk factors and extent of pre-existing disease which call for a tailored or bespoke approach to exercise.

This study showed that the magnitude of exertion-induced shear stress approaches the ultimate stress limit in the intima and the immediate adjacent medial layer. The variation in stress is maximal in the inner layer of the media. These findings correlate the site of atheroma development with the most vulnerable site for injury in the media and emphasise the impact of pulse pressure. Further biological studies are required to ascertain whether this leads to injury that initiates atheroma that then precipitates an injury/healing cycle.

Acknowledgments

Funding: This research was supported by the Vascular and Radiology Research Fund of the WA Health Department and Curtin University.

Footnote

Conflicts of Interest: All authors have completed the ICMJE uniform disclosure form (available at http://dx.doi.org/10.21037/qims-20-614). The authors have no conflicts of interest to declare.

Ethical Statement: The authors are accountable for all aspects of the work in ensuring that questions related to the accuracy or integrity of any part of the work are appropriately investigated and resolved. The study was conducted in accordance with the Declaration of Helsinki (as revised in 2013). Sir Charles Gairdner and Osborne Park Hospitals Human Research Ethics Committee approval and patient informed consent.

Open Access Statement: This is an Open Access article distributed in accordance with the Creative Commons Attribution-NonCommercial-NoDerivs 4.0 International License (CC BY-NC-ND 4.0), which permits the non-commercial replication and distribution of the article with the strict proviso that no changes or edits are made and the original work is properly cited (including links to both the formal publication through the relevant DOI and the license). See: https://creativecommons.org/licenses/by-nc-nd/4.0/.

References

1. Wang JC, Bennett M. Aging and atherosclerosis: mechanisms, functional consequences, and potential therapeutics for cellular senescence. Circ Res 2012;111:245-59. [Crossref] [PubMed]
2. Thubrikar MJ, Robicsek F. Pressure induced arterial wall stress and atherosclerosis. Ann Thorac Surg 1995;59:1594-603. [Crossref] [PubMed]
3. Dhawan SS, Avati Nanjundappa RP, Branch JR, Taylor WR, Quyyumi AA, Jo H, McDaniel MC, Suo J, Giddens D, Samady H. Shear stress and plaque development. Expert Rev Cardiovasc Ther 2010;8:545-56. [Crossref] [PubMed]
4. Zarins CK, Giddens DP, Bharadvaj BK, Sottiurai VS, Mabon RF, Glagov S. Carotid bifurcation atherosclerosis. Quantitative correlation of plaque localization with flow velocity profiles and wall shear stress. Circ Res 1983;53:502-14. [Crossref] [PubMed]
5. Ahlgren AR, Cinthio M, Persson HW, Lindström K. Different patterns of longitudinal displacement of the common carotid artery wall in healthy humans are stable over a four-month period. Ultrasound Med Biol 2012;38:916-25. [Crossref] [PubMed]
6. Lawrence-Brown M, Stanley BM, Sun Z, Semmens JB, Liffman K. Stress and strain behaviour modelling of the carotid bifurcation. ANZ J Surg 2011;81:810-6. [Crossref] [PubMed]
7. Bentzon JF, Otsuka F, Virmani R, Falk E. Mechanisms of plaque formation and rupture. Circ Res 2014;114:1852-66. [Crossref] [PubMed]
8. Parma L, Baganha F, Quax PHA, de Vries MR. Plaque angiogenesis and intraplaque hemorrhage in atherosclerosis. Eur J Pharmacol 2017;816:107-15. [Crossref] [PubMed]
9. Moreno PR, Purushothaman KR, Sirol M, Levy AP, Fuster V. Neovascularization in human atherosclerosis. Circulation 2006;113:2245-52. [Crossref] [PubMed]
10. Kolodgie FD, Gold HK, Burke AP, Fowler DR, Kruth HS, Weber DK, Farb A, Guerrero LJ, Hayase M, Kutys R, Narula J, Finn AV, Virmani R. Intraplaque hemorrhage and progression of coronary atheroma. N Engl J Med 2003;349:2316-25. [Crossref] [PubMed]
11. Fedorov A, Beichel R, Kalpathy-Cramer J, Finet J, Fillion-Robin JC, Pujol S, Bauer C, Jennings D, Fennessy F, Sonka M, Buatti J, Aylward S, Miller JV, Pieper S, Kikinis R. 3D Slicer as an image computing platform for the Quantitative Imaging Network. Magn Reson Imaging 2012;30:1323-41. [Crossref] [PubMed]
12. Long Q, Xu XY, Ariff B, Thom SA, Hughes AD, Stanton AV. Reconstruction of blood flow patterns in a human carotid bifurcation: a combined CFD and MRI study. J Magn Reson Imaging 2000;11:299-311. [Crossref] [PubMed]
13. Hrinda GA. Automating Structural Analysis of Spacecraft Vehicles. In: Vancouver: 55th International Astronautical Congress, 2004. doi: 10.2514/6.IAC-04-U.3.A.07.10.2514/6.IAC-04-U.3.A.07
14. Wang Y, Zeinali-Davarani S, Zhang Y. Arterial mechanics considering the structural and mechanical contributions of ECM constituents. J Biomech 2016;49:2358-65. [Crossref] [PubMed]
15. Sommer G. Mechanical properties of healthy and diseased human arteries. TU Graz. 2008.
16. Matsumoto T, Sugita S, Yaguchi T. Biomechanics of blood vessels: structure, mechanics, and adaptation. In: Niinomi M, Narushima T, Nakai M. editors. Advances in metallic biomaterials. Heidelberg: Springer, 2015:71-98.
17. Jia Y, Qiao Y, Ricardo Argueta-Morales I, Maung A, Norfleet J, Bai Y, Divo E, Kassab AJ, DeCampli WM. Experimental study of anisotropic stress/strain relationships of aortic and pulmonary artery homografts and synthetic vascular grafts. J Biomech Eng 2017; [Crossref] [PubMed]
18. Cho YI, Kensey KR. Effects of the non-Newtonian viscosity of blood on flows in a diseased arterial vessel. Part 1: Steady flows. Biorheology 1991;28:241-62. [Crossref] [PubMed]
19. Moradicheghamahi J, Sadeghiseraji J, Jahangiri M. Numerical solution of the Pulsatile, non-Newtonian and turbulent blood flow in a patient specific elastic carotid artery. Int J Mech Sci 2019;150:393-403. [Crossref]
20. Holzapfel GA, Sommer G, Gasser CT, Regitnig P. Determination of layer-specific mechanical properties of human coronary arteries with nonatherosclerotic intimal thickening and related constitutive modeling. Am J Physiol Heart Circ Physiol 2005;289:H2048-58. [Crossref] [PubMed]
21. Steinman DA. Image-based computational fluid dynamics modeling in realistic arterial geometries. Ann Biomed Eng 2002;30:483-97. [Crossref] [PubMed]
22. Wells DR, Archie JP Jr, Kleinstreuer C. Effect of carotid artery geometry on the magnitude and distribution of wall shear stress gradients. J Vasc Surg 1996;23:667-78. [Crossref] [PubMed]
23. Salzar RS, Thubrikar MJ, Eppink RT. Pressure-induced mechanical stress in the carotid artery bifurcation: a possible correlation to atherosclerosis. J Biomech 1995;28:1333-40. [Crossref] [PubMed]
24. Ballermann BJ, Dardik A, Eng E, Liu A. Shear stress and the endothelium. Kidney Int Suppl 1998;67:S100-8. [Crossref] [PubMed]
25. Cinthio M, Ahlgren AR, Bergkvist J, Jansson T, Persson HW, Lindström K. Longitudinal movements and resulting shear strain of the arterial wall. Am J Physiol Heart Circ Physiol 2006;291:H394-402. [Crossref] [PubMed]
26. Morbiducci U, Gallo D, Ponzini R, Massai D, Antiga L, Montevecchi FM, Redaelli A. Quantitative analysis of bulk flow in image-based hemodynamic models of the carotid bifurcation: the influence of outflow conditions as test case. Ann Biomed Eng 2010;38:3688-705. [Crossref] [PubMed]
27. Conti M, Long C, Marconi M, Berchiolli R, Bazilevs Y, Reali A. Carotid artery hemodynamics before and after stenting: a patient specific CFD study. Computers & Fluids 2016;141:62-74. [Crossref]
28. Schriefl AJ, Zeindlinger G, Pierce DM, Regitnig P, Holzapfel GA. Determination of the layer-specific distributed collagen fibre orientations in human thoracic and abdominal aortas and common iliac arteries. J R Soc Interface 2012;9:1275-86. [Crossref] [PubMed]
29. Teng Z, Tang D, Zheng J, Woodard PK, Hoffman AH. An experimental study on the ultimate strength of the adventitia and media of human atherosclerotic carotid arteries in circumferential and axial directions. J Biomech 2009;42:2535-9. [Crossref] [PubMed]
30. Teng Z, Zhang Y, Huang Y, Feng J, Yuan J, Lu Q, Sutcliffe MPF, Brown AJ, Jing Z, Gillard JH. Material properties of components in human carotid atherosclerotic plaques: a uniaxial extension study. Acta Biomater 2014;10:5055-63. [Crossref] [PubMed]
31. Sommer G, Regitnig P, Költringer L, Holzapfel GA. Biaxial mechanical properties of intact and layer-dissected human carotid arteries at physiological and supraphysiological loadings. Am J Physiol Heart Circ Physiol 2010;298:H898-912. [Crossref] [PubMed]
32. O'Mara S. In praise of walking: The new science of how we walk and why it’s good for us. New York: Penguin Random House, 2019.