Continuous diffusion spectrum computation for diffusion-weighted magnetic resonance imaging of the kidney tubule system

Introduction

Kidney diseases are a major health issue, with increasing incidence and an estimated two million deaths per year worldwide due to acute kidney injury (AKI) (1-7). While several biomarkers are currently being investigated for diagnosis of AKI, to date clinical point-of-care biomarkers for AKI are still lacking (8-11). To address this urgent unmet clinical need, MRI may provide quantitative imaging markers to inform on the different stages of pathophysiology, improve prediction and interception of disease progression and evaluate treatment of AKI (6,12-20).

The renal tubules are a unique anatomical compartment of the kidney, comprising a large fraction of the renal volume. The tubular volume fraction can change due to (I) changes in the glomerular filtration rate, (II) alterations in tubular outflow towards and beyond the renal pelvis, (III) modulation of the transmural pressure gradient and (IV) changes in tubular fluid resorption (21). The tubular volume fraction may develop into a novel marker for clinical diagnostics of kidney diseases, for two reasons. First, MR-based assessment of the tubular volume fraction could serve as a diagnostic tool, for instance to detect glomerular hyperfiltration—a hallmark of early-stage diabetic nephropathy (22). It may also help in the distinction between AKI that is caused by obstructions of the urinary tract and AKI of other origins (23). Tubular atrophy and interstitial fibrosis play a major role in the microstructural changes occurring during kidney pathology e.g., renal allograft injury (24). Being able to assess renal fibrosis and alterations in the tubular volume fraction with non-invasive MRI would be clinically valuable (3,7,22,23,25-28). Second, as the renal capsule is comparatively rigid, changes in the tubular volume fraction will result in opposite changes in the renal blood volume fraction, thereby confounding the relationship between renal blood oxygenation level-dependent (BOLD) T₂*, oxygen saturation of hemoglobin, and tissue partial pressure of oxygen (21,29). Concomitant assessment of the tubular volume fraction will thus help to accurately interpret quantitative renal T₂* data.

Diffusion-weighted MRI (DWI) probes self-diffusion of water in tissue on a microscopic level and reflects micro-morphological and (patho)physiological changes in renal tissue and renal diseases (30,31). When performing DWI of the kidney, the incoherent blood flow in the renal microvasculature contributes to pseudo-diffusion (32-38) resulting in a fast signal decay component. The displacement of water molecules in the renal tissue contributes a slow water diffusion component, according to the two-compartment model (32-38). Acknowledging the morphological and physiological importance of renal tubules, recent studies have shown that the intra-tubular fluid compartment introduces a third component in the renal DWI signal decay. To account for this tubular water diffusion component, a rigid tri-exponential model was proposed to better decipher diffusion MRI signals from the kidney (39,40).

The performance of rigid multi-exponential models is often highly dependent on initial values, and on the upper and lower boundaries of the optimization parameters (41). Fixing some coefficients of the rigid model is common practice to increase fit stability and to improve the sensitivity to physiological changes. This applies particularly to tri-exponential models (with six variables to fit) but runs the risk of introducing a bias (40). To address this limitation, an unbiased data-driven analysis of the diffusion signal decay is required. Non-negative least squares (NNLS) continuum modelling provides an alternative to rigid model fitting techniques, which does not require a priori assumptions of the number of components of the signal decay nor starting values (42-44). A predefined basis set of more than 500 exponential components spanning the entire range of feasible diffusion coefficients can be used as input to the NNLS algorithm. As output, the NNLS continuum modelling yields a spectrum of the contributions of all exponential basis vectors to the signal decay. NNLS continuum modelling can be a useful tool to determine the number of major diffusion compartments actually present in the tissue, and offers a means for their quantification during (patho)physiological changes (43). It has been successfully employed for multicomponent diffusion analysis of microstructural alterations in multicellular tumor spheroids, bone marrow, the central nervous system, and liver as well as in the parenchyma of healthy organs of the upper abdomen (32,45-52).

Notwithstanding this pioneering work, the literature does not include reports on a systematic examination of the performance of NNLS-based multicomponent diffusion analysis of microstructural alterations in the kidney. Recognizing the opportunity and challenges of this task, this work presents a simulation study focusing on NNLS computation for DWI of the kidney tubule system. Such simulations are a crucial precursor to in vivo studies, in order to establish the optimal selection of experimental parameters, and to estimate effect sizes for power analysis to ensure appropriate sample sizes of experimental animals. Our numerical simulations center on three metrics including (I) the signal-to-noise ratio (SNR), (II) the number of data points needed for the characterization of the diffusion signal decay, and (III) the range of diffusion sensitization (b-value range), which are essential for renal DWI applications. To meet this objective, detailed numerical simulations were conducted with the goal to optimize renal DWI parameters in order for the NNLS continuum modelling to provide an error of less than 5% and 10%, for the assessment of tubular fluid, intrarenal blood, and renal tissue volume fractions. As ground truth, a tri-exponential and a four-exponential function using defined volume fractions and diffusion coefficients for each renal compartment were applied for baseline renal tissue conditions. To approach a pathophysiological scenario, NNLS continuum modelling was evaluated for conditions that mimic an increase in tubular volume fraction and different degrees of renal fibrosis.

Methods

Multi-compartment model

Two-compartment (bi-exponential) models generally used for representing DWI data of organs other than the kidney were recently shown to be unsuitable for fully representing renal DWI data, as they neglect the impact of the tubular volume fraction (39,40). Therefore, a three-compartment model of the kidney was used, implementing a tri-exponential decay function with defined parameters according to the following equation:

SI=ftissuee−bDtissue+ftubulese−bDtubules+fbloode−bDblood[1]

where SI is the normalized signal intensity as a function of b (b-value), f_tissue the signal fraction of the tissue component, D_tissue the diffusion coefficient of restricted water diffusion in renal tissue, f_tubules the signal fraction of the tubular component, D_tubules the pseudo-diffusion coefficient of the tubular fluid component, f_blood the signal fraction of the blood component, and D_blood the pseudo-diffusion coefficient of the blood component.

Since the number of compartments might change in pathophysiological conditions of the kidney including the development of fibrosis, a fourth compartment was applied.

SI=ffibrosise−bDfibrosis+ftissuee−bDtissue+ftubulese−bDtubules+fbloode−bDblood[2]

where f_fibrosis is the signal fraction of the fibrotic component, D_fibrosis the diffusion coefficient of restricted water diffusion in fibrotic tissue.

The sum of the fractions equals 1 in all multi-compartment models used.

NNLS continuum modelling

A multi-exponential analysis based on the NNLS algorithm of Lawson and Hanson (53) was used. The NNLS MATLAB (The Mathworks Inc., Natick, USA) implementation was adapted from the open-source software AnalyzeNNLS from Bjarnason and Mitchell (43).

The diffusion signal decay y_i can be expressed as a sum of exponential functions:

yi=∑j=1Msje−biDj,i=1,2,⋯,N[3]

where s_j is the relative amplitude for each partitioned D-value D_j, b_i is the b-value that governs the diffusion sensitization for each data point in the signal decay, M is the number of logarithmically spaced D values (300 values were used), and N represents the total number of data points.

The NNLS algorithm is used to minimize:

χr2=min[∑i=1N|∑j=1Msje−biDj−yi|2+μ∑j=2M−1|sj+1−2sj+sj−1|2][4]

Eq. [4] includes a regularization term with a weighting factor µ, found using generalized cross validation (54). The regularization term acts as a smoothing constraint that minimizes the curvature of the NNLS spectrum to provide a robust fit in the presence of noise. Another equally valid regularization paradigm used in the literature is L1-norm or sparsity regularization. The curvature regularization approach was chosen because of its analytic solvability, its justifiable assumption on the resulting spectrum and its successful use in the literature (32,45-52).

The output of NNLS is a diffusion coefficient distribution with distinct log-normal-like peaks. Each peak corresponds to a major (pseudo-)diffusion compartment. These peaks can be characterized by (I) area under the spectral curve fraction on the predefined logarithmic scale, and (II) geometric mean D coefficient. The number of peaks was not constrained a priori.

Numerical simulations

All numerical simulations were implemented in MATLAB using the open-source tool AnalyzeNNLS (43). The ground truth signal was created assuming a three-compartment or a four-compartment model {Eq. [1] and Eq. [2]} using three sets of parameters:

• The first parameter set was used to represent baseline conditions;
• The second parameter set was used to represent pathophysiological conditions of increased tubular volume fraction (ITV) (f_tubules);
• The third parameter set was used to represent pathophysiological conditions of two degrees of renal fibrosis (f_fibrosis).

Figure 1 describes the workflow from simulation of these parameters to visualization and mean absolute percentage error (MAPE) assessment. All parameters used for (I) baseline, (II) increased f_tubules and (III) fibrosis (55-57) conditions are presented in Table 1. These parameters were obtained from the literature (39) and provide a fair approximation. The volume fractions f_fibrosis of 10% and 30% represent grade I (mild) and a low grade II (moderate) of renal fibrosis, respectively, according to grading schemes used in human patients (grade I <25%, grade II >25–50%, grade III >50% area) (56). Effects of experimental parameters such as the echo time and the diffusion time were not considered explicitly, but rather implicitly through varying SNR and the b-value range.

Figure 1 Workflow used for LS and NNLS computation for DWI of the kidney tubule. Numerical simulations were performed and analysed using NNLS continuum modelling. For the ground truth a tri-exponential function using defined volume fractions and diffusion coefficients for each renal compartment were applied. For NNLS and LS computations (patho)physiological conditions (baseline and ITV), range of b-values (from small b-value range: b=0–800 s/mm² to large value range: b=0–2,180 s/mm²) and parameter fixation (D_blood and D_tissue fixed vs. D_blood and D_tissue not-fixed) were applied. MAPE was calculated (average n=500) using the ground truth as a reference. The results were displayed using a MAPE heat map showing the difference between the ground truth and the data obtained from NNLS or LS for each condition. From the MAPE heat map the percentage of combinations (SNR/number of b-values) with a difference between the ground truth and the NNLS data or the LS data of less than 5% or less than 10% were quantified and plotted in an error proportion plot. LS, least squares; NNLS, non-negative least squares; DWI, diffusion-weighted MRI; MAPE, mean absolute percentage error; SNR, signal-to-noise ratio; f_blood, volume fraction of blood; f_tubules, volume fraction of tubules; f_tissue, volume fraction of tissue; f_fibrosis, volume fraction of fibrosis; D_blood, diffusion coefficient of blood; D_tubules, diffusion coefficient of tubules; D_tissue, diffusion coefficient of tissue; D_fibrosis, diffusion coefficient of fibrosis; b-value, diffusion weighting.

Table 1 Summary of multi-exponential parameters used for the generation of the synthetic diffusion decay data
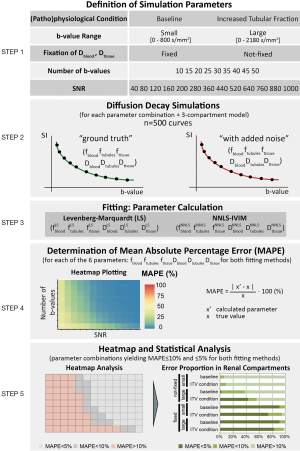
Full table

For each b-value, Rician noise was added to the signal. The signal SI was then fitted using the NNLS implementation and the common non-linear least squares (LS) fitting routine using a trust region growing algorithm [fastnnls routine, N-way toolbox for MATLAB (58)]. This procedure was repeated n=500 times for each (patho)physiological condition (baseline, increased f_tubules, two fibrotic conditions). Five hundred repetitions lead to error estimates with an uncertainty below 5% of the error magnitude. By using the same 500 realizations of noise for all cases we were able to reduce the impact of random fluctuation on our comparisons even further resulting in robust and interpretable results.

Non-linear least square fitting

The created tri-exponential function was also fitted with the common LS method using a trust region growing algorithm. For this purpose, starting values and parameter ranges were established (40) as summarized in Table 2 with the starting values for each fraction being balanced between the conditions at baseline and ITV.

Table 2 Summary of LS fitting parameters
Full table

SNR

Diffusion decays were simulated at different SNR conditions to explore the impact of the noise for the NNLS and LS approach. For this purpose, Rician noise was added to the synthetic multi-exponential signal decay. SNR was defined as the signal intensity of the first b-value (b=0 s/mm²), divided by the standard deviation of the noise added. The first b-value was used as an SNR reference, since acquiring b=0 s/mm² scans is standard procedure in DWI studies and therefore facilitates comparisons with other studies (30). In order to keep the comparison between different SNR-levels and simulated scenarios free from statistical fluctuations, the same set of noise realizations (n=500) was used for all SNR-levels and scenarios. An SNR range from 40 to 1,000 (SNR =40, 80, 120, 160, 200, 280, 360, 440, 520, 640, 760, 880, 1,000) was chosen to cover the SNR of typical raw images as well as the SNR derived from restoration of DWI data using noise filtering (59-61). The SNR range also covers SNRs obtained from averaging over regions of interest (ROI) where the averaged SNR_ROI is proportional to the square root of the number of the pixels included.

Diffusion sensitization

To study the impact of the number of b-values, this parameter was varied from 10 to 50 b-values in increments of 5. We hypothesized that a larger number of b-values would result in a lower error for both fitting methods. However, increasing the number of b-values prolongs examination times and imaging protocols, which is not always feasible for in vivo experiments.

To investigate the impact of the range of b-values, 10 sets of diffusion sensitization ranges were examined. For the first set, a b-value range of b=0 to 800 s/mm² (small b-value range) was obtained from consensus-based technical recommendations for clinical translation of renal DWI (30). Figure 2A describes the decomposition of the 1^st derivative of the diffusion decay together with the 1^st derivative of the decay of individual components of a tri-exponential model including intrarenal blood, tubules and renal tissue. For the tubule system the full width half maximum (FWHM) of the 1^st derivative encompasses a b-value range of b=40 to 460 s/mm². The 1^st derivative of the tissue signal component is dominant for b≥250 s/mm². For quantification of D_tissue and f_tissue sampling of this b-range is important to obtain SI(b) and the 1^st derivative of SI(b). However, if D_tissue is known a priori the focus remains on b≤800 s/mm² where most of the tubular signal component is decayed. For comparison diffusion sensitization was extended to b=0–1,110 s/mm² (10 b-values), b=0–1,380 s/mm² (15 b-values, designated as medium b-value range), b=0–1,570 s/mm² (20 b-values), b=0–1,710 s/mm² (25 b-values), b=0–1,840 s/mm² (30 b-values), b=0–1,940 (35 b-values), b=0–2,030 s/mm² (40 b-values), b=0–2,110 s/mm² (45 b-values) and b=0–2,180 s/mm² (50 b-values, designated as large b-value range). For each b-value range the largest b-value was set so that the expected relative signal intensity is equal to (1/number b-values) for the largest b-value (Figure 2B). In order to create an unbiased b-scale that does not favor any one component at the expense of any other, each b-value was distributed over the b-value range to yield a constant signal intensity decrement (1/number of b-values) from one b-value to another as outlined in Figure 2B, assuming the ground truth values outlined in Table 1. Maintaining the signal intensity decay constant from one b-value to the next ensures independence of the individual measurements of the signal decay, and is therefore a reasonable approach for quantification of the individual exponential contributions. The equidistant intensity drop from one b-value to the next was computed by interpolating on a fine evaluation of the tri-exponential decay with exponential weights in between the baseline and the increased tubular fraction case (f_blood =0.075; f_tubules =0.4; f_tissue =0.525).

Figure 2 Diffusion sensitization considerations. (A) The 1^st derivative of the diffusion decay (purple) together with the 1^st derivative of the individual components of a tri-exponential model: blood (red), tubules (orange) and tissue (green). For the tubules system the FWHM of the 1^st derivative encompasses a b-value range of b=40–460 s/mm². The cyan line marks b=800 s/mm². (B) Diffusion decay using a logarithmic scale. The number of b-values (n=20) was set so that the relative signal intensity is equal to (1/number of b-values) for the largest b-value. This approach yields a constant signal intensity decrement (1/number of b-values) from one b-value to the next, to ensure that individual measurements are independent of the signal decay. FWHM, full width half maximum; b-value, diffusion weighting.

Under physiological conditions and upon changes in the tubular volume fraction, the physicochemical properties of renal tissue and intrarenal blood are recognized to be essentially invariable (62). It is therefore reasonable to study the effect of fixing the diffusion coefficients D_tissue and D_blood for these compartments. Fixing fitting parameters to improve the robustness of the fit is common practice (40), especially when dealing with multi-exponential functions, where at least six parameters are needed. We tested the effect of fixing diffusion coefficients on NNLS continuum modelling by setting the diffusion parameter to a predefined value for the slowest and fastest components. A similar simplification was applied for the NNLS continuum modelling by restricting the diffusion-coefficient-basis to the range of the intermediate component between 3×10^–3 and 33×10^–3 mm²/s, and two single exponentials with known diffusion coefficients for the fast and slow components. The two fixed NNLS-basis-vectors were excluded from curvature regularization. Areas under the continuous diffusion spectrum were determined using the MATLAB function SUM between two adjacent minima in the spectra. Relative areas were obtained by dividing each peak by the total area obtained for all peaks.

MATLAB Code Availability Statement: The MATLAB code will be made openly available in GitHub at https://github.com/JoaoPeriquito/NNLS_computation_of_renal_DWI.

Statistics

For the simulations the MAPE was used to show the percentage difference between the calculated value and the true value, for the 9×13 matrix of b-values and SNR values (Figure 1). MAPE is defined as:

MAPE=|x′−x|x⋅100[5]

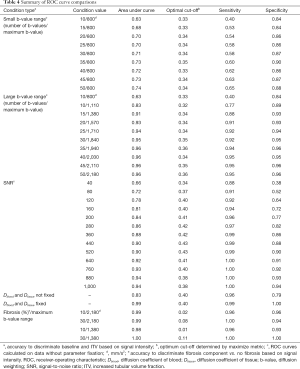
where x’ is the calculated parameter and x the true-value. The Shapiro-Wilk test was used to assess for Gaussian distribution. MAPE values did not conform to a Gaussian distribution, thus non-parametric statistical tests were used including the paired Wilcoxon signed-rank test, the Kruskal-Wallis test and Dunn’s post-hoc procedure. Differences in MAPE obtained for fixing vs. not-fixing the D_blood and D_tissue diffusion parameters, for the b-value ranges used (b_{range_small} =0–800 mm²/s up to b_{range_large} =0–2,180 mm²/s), and for the physiological state (baseline vs. ITV) were tested independently using the paired Wilcoxon signed-rank test. Differences in MAPE among the 2³ permutations of the independent variables volume fraction, b-value and fixation state—with each variable having two levels—were assessed with the Kruskal-Wallis non-parametric ANOVA test. To determine which specific pair-wise comparisons were different, Dunn’s post-hoc test was performed for selected pairwise comparisons with Holm’s correction for multiple comparisons. The accuracy to discriminate between baseline and the pathophysiological conditions of an ITV or renal fibrosis was evaluated using signal intensity-based receiver-operating characteristic (ROC) curves. The area under the curve (AUC) was calculated and compared with DeLong’s test (63), using the R packages pROC (64), plotROC (65) and cutpointr (66). The Kruskal-Wallis test was used to compare the AUC of the fibrotic compartment between the simulated conditions of 30%, 10% and no fibrosis. Data analysis was done using the statistical computing environment R (v.3.3.4) (https://www.R-project.org).

Results

NNLS continuum modelling

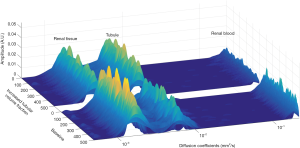
Analysis of the simulated data with the NNLS continuum modelling resulted in a distribution of diffusion coefficients covering the full range expected for the three components. Figure 3 demonstrates that it is possible to ascribe each of the three peaks along the diffusion coefficient spectrum to a diffusion decay component. The left peak can be attributed to the slow-decay component of tissue (D_tissue: ~1.50×10^–3 mm²/s), the middle peak to the intermediate-decay component from tubules (D_tubules: ~5.80×10^–3 mm²/s) and the right peak to the fast-decaying component associated with blood (D_blood: ~180.00×10^–3 mm²/s). The graph shows 1,000 NNLS spectra produced from simulations of baseline conditions (n=500) and of ITV conditions (n=500). The change of the intensity ratio of the two slower component peaks is clearly visible when transitioning from baseline conditions to ITV conditions. Similar datasets were acquired for all combinations of SNR, b-value number and b-value range. To process this large amount of data, peak areas and geometric mean positions were first extracted from the spectra and then compared to the ground truth by using the MAPE.

Figure 3 Example of an NNLS spectrum for baseline and for the (patho)physiological condition of an ITV. The spectra were obtained for a signal intensity decay covering 25 b-values using a SNR =360 for b=0 s/mm². The three peaks along the diffusion coefficient direction represent three diffusion decay components: a slow-decay component for renal tissue (left peak), an intermediate-decay component for tubules (middle peak) and a fast-decay component for intrarenal blood (right peak). The (patho)physiological condition of ITV decreased the areas under the left and right peaks and increased the area under the middle peak. NNLS, non-negative least squares; ITV, increased tubular volume fraction; SNR, signal-to-noise ratio; b-value, diffusion weighting.

MAPE of tubular volume fraction, blood and renal tissue

MAPE was used as a metric to assess which combination of SNR/number of b-values provides less than 5% or 10% error from the true value. Figure 4A shows heat maps of the individual MAPE of the tubular volume fraction. As expected, the error decreases with increasing SNR. Increasing the number of b-values is also beneficial for tubular volume fraction quantification. Correspondingly, using 10 b-values at SNR =80 provides similar MAPE as using 40 b-values at SNR =40 (Figure 4A). Furthermore, the benefit of additional b-values diminishes with each subsequent addition. From 25 b-values onwards, the benefit becomes less apparent. A pronounced increase in the precision is also discernible when the range of b-values is increased (small range, b=0–800 s/mm²vs. large range, b=0–2,180 s/mm²). In all cases MAPE is substantially improved when reducing the number of determined parameters from 6 to 4 by fixing the (pseudo-)diffusion coefficients of blood and tissue.

Figure 4 MAPE heat maps for tubular volume fraction for all simulations. (A) MAPE heat maps related to the tubular fraction for all continuum modelling NNLS simulations. Left column: no fixation of D_blood and D_tissue, right column: fixation of D_blood and D_tissue. (B) Highlight of the MAPE heat maps related to the tubular fraction for all NNLS continuum modelling simulations with MAPE <5%, <10% and >10%. Left column: no fixation of D_blood and D_tissue, right column: fixation of D_blood and D_tissue. MAPE, mean absolute percentage error; NNLS, non-negative least squares; SNR, signal-to-noise ratio; D_blood, diffusion coefficient of blood; D_tissue, diffusion coefficient of tissue; b-value, diffusion weighting.

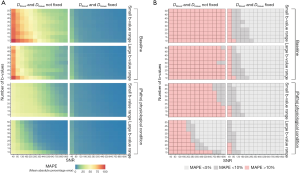
Figure 4B highlights the combinations of SNR/number of b-values that provide a MAPE below 5% (light gray) or 10% (dark gray) for the tubular volume fraction. The percentage of these successful combinations was extracted from each of the MAPE heat maps as the quantitative description of the method’s precision for further consideration. The number of combinations with an error below 10% with no fixation used was 0% for baseline-small b-value range, 3% for baseline-large b-value range, 10% for increased tubular fraction-small b-value range, and 58% for increased tubular fraction-large b-value range. In non-fixed cases, an error below 5% was only found for increased tubular fraction-large b-value range (44% of combinations). The fraction of combinations below 10% error when fixation of D_blood and D_tissue was used was 91% for baseline and 97% for increased tubular fraction (for both small and large range). An error below 5% was observed in 68% of baseline-small b-value range, 75% of baseline-large b-value range, 81% of ITV-small b-value range, and 86% of ITV-large b-value range combinations.

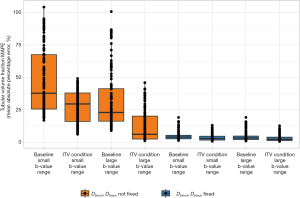
Figure 5 shows the percentages of excellent (MAPE <5%), good (MAPE <10%) and unsuitable (MAPE >10%) simulation results for each of the eight combination of parameters for the renal blood, tubules and tissue compartments. Here we compare LS with NNLS continuum modelling with respect to different MAPE stratifications for each simulated permutation. By fixing the value of blood diffusion coefficient D_blood and tissue diffusion coefficient D_tissue, more than 60% of all combinations yielded an error below 10% for all parameters and more than 40% provided an error below 5% for all parameters using NNLS continuum modelling. For LS the use of fixation yielded for more than 70% of all combinations an error below 10% for all parameters. More than 50% of the combinations showed an error below 5% for all parameters.

Figure 5 Survey of the results obtained from error analysis. The error proportion plots show the percentage of combinations with the MAPE below 5% or below 10% using non-linear LS fitting (left column) and NNLS continuum modelling (right column) for all kidney fractions: intrarenal blood, tubule and renal tissue. MAPE, mean absolute percentage error; LS, least squares; NNLS, non-negative least squares; ITV, increased tubular volume fraction; D_blood, diffusion coefficient of blood; D_tissue, diffusion coefficient of tissue; b-value, diffusion weighting.

In addition to improving the proportion of combinations with good and excellent error levels, fixing the blood (D_blood) and tissue diffusion (D_tissue) coefficients significantly reduced the absolute value of the MAPE of the tubular volume fraction (P=2.13×10^–78 fixed vs. not-fixed, Wilcoxon signed-rank test). Similarly, using a large range of b-values significantly reduced the MAPE in the tubular volume fraction (P=2.78×10^–77 smallest vs. largest b-value range, Wilcoxon signed-rank test).

Pathophysiological condition of ITV

For the first pathophysiological condition, we studied the impact of an increase in the tubular volume fraction. This condition does not alter the number of compartments. Increasing tubular volume fraction significantly reduced the MAPE in this compartment, compared to baseline (P=2.15×10^–78, Wilcoxon signed-rank test). When considering differences among all permutations of the three simulation conditions (i.e., baseline vs. ITV, smallest vs. largest b-value range, fixation of D_blood and D_tissue vs. no fixation—three conditions with two levels each, 2³=8), the error values differed significantly (Kruskal-Wallis statistic =621.1, eta² effect size =0.662, which was independent of the number of simulations, P=7.07×10^–130) (Figure 6). Pairwise post-hoc comparisons corrected for selected multiple comparisons are shown in Table 3.

Figure 6 Statistical comparison of the effects of (I) fixation of D_blood and D_tissue (not-fixed vs. fixed), (II) of the (patho)physiological condition (baseline vs. increased tubular volume) and (III) of the b-value range (small vs. large b-value range). MAPE analysis of the tubular volume fraction from NNLS continuum modelling was compared between all permutations of the simulation conditions: fixation of D_blood and D_tissue (fixed or not-fixed), (patho)physiological condition (baseline vs. increase in tubular volume) and range of b-values (small b-value range over large b-value range). Each of these three factors had significant effects on the error values when considered independently. Comparing among the permutations showed significant differences in MAPE (P=7.07×10^–130, Kruskal-Wallis non-parametric ANOVA, followed by Dunn’s procedure with Holm’s correction for multiple comparisons). Selected pairwise comparisons are summarized in Table 3. MAPE, mean absolute percentage error; NNLS, non-negative least squares; ITV, increased tubular volume fraction; D_blood, diffusion coefficient of blood; D_tissue, diffusion coefficient of tissue; b-value, diffusion weighting.

Table 3 Pairwise post-hoc comparisons of the MAPE
Full table

We then proceeded to evaluate the accuracy to discriminate between baseline and increased tubular volume conditions based on the signal intensity. When diffusion coefficients were not fixed, and the b-value range was kept constant at a small value (b=0–800 s/mm²) increasing the number of b-values significantly improved discrimination accuracy, with the AUC increasing from 0.63 to 0.74 (10 vs. 50 b-values, P<2.2×10^–16, DeLong’s test, Figure 7A). The optimal cut-off values, sensitivity and specificity for all ROC curves are listed in Table 4. Increasing to a larger range of b-values had a greater impact on discrimination accuracy. Maintaining 10 b-values while increasing the range to b=0–1,100 s/mm² improved the AUC to 0.83. Using a medium b-value range of b=0–1,380 s/mm² (with 15 b-values) improved the AUC to >0.90, and further increases beyond this range yielded diminishing improvements, although these were statistically significant (AUC =0.91 vs. 0.96, medium b-value range 0–1,380 vs. maximum b-value range 0–2,180 s/mm², P<2.2×10^–16, DeLong’s test, Figure 7B, Table 4). Based on our empirical testing illustrated in Figure 7A,B and Figure 4A, we conclude that a minimum number of 10 b-values is right at the limit of yielding an appropriate description of the tri-exponential decay. When D_blood and D_tissue were not fixed, SNR had a more profound impact on discrimination accuracy. At SNR =40, the discrimination between baseline and ITV was rather poor, with an AUC of 0.66 for the ROC curve. This performance increased steadily with increasing SNR, achieving a maximum discrimination accuracy of 0.94 at a maximum SNR of 1,000. However, the magnitude of this improvement diminished at higher SNR values. While the increase in discrimination accuracy from SNR 880 to SNR 1,000 was significant, the improvement was nevertheless marginal (AUC =0.93 vs. 0.94, P=1.1×10^–5, DeLong’s test, Figure 7C, Table 4). Fixing the diffusion coefficients for blood and renal tissue had a profound effect on discrimination accuracy. Considering all numbers of b-values, b-value ranges and SNR levels, the AUC was 0.83. When D_blood and D_tissue were fixed, the discrimination accuracy was near perfect, with AUC of 0.99 (not fixed vs. fixed, P<2.2×10^–16, DeLong’s test, Figure 7D, Table 4).

Figure 7 Effects of number of b-values, range of b-values, SNR and fixation of D_blood and D_tissue (fixed vs. not-fixed) on accuracy to discriminate baseline and ITV. ROC curves show the accuracy of discriminating between baseline renal tubular volume conditions and pathophysiological conditions that mimic an ITV, based on signal intensity. (A) When diffusion coefficients were not fixed, and the b-value range was kept constant at a small value (b=0–800 s/mm²) increasing the number of b-values significantly improved discrimination accuracy, with the AUC increasing from 0.63 to 0.74 (10 vs. 50 b-values, P<2.2×10^–16, DeLong’s test). (B) Increasing to a larger range of b-values had a greater impact on discrimination accuracy. Maintaining 10 b-values while increasing the range to b=0–1,100 s/mm² improved the AUC to 0.83. Using a medium b-value range of b=0–1,380 s/mm² improved the AUC to >0.90, and further increases beyond this range yielded diminishing improvements (AUC =0.91 vs. 0.96, maximum b-value range 1,380 vs. 2,180 s/mm², P<2.2×10^–16, DeLong’s test). (C) When D_blood and D_tissue were not fixed, SNR had a pronounced impact of discrimination accuracy: At low SNR of 40 the AUC was 0.664, increasing to 0.942 at the highest SNR of 1,000 (P<2.2×10^–16, DeLong’s test). (D) Fixing the diffusion coefficients for blood and renal tissue had a profound effect on discrimination accuracy. Considering all numbers of b-values, b-value ranges and SNR levels, the AUC was 0.83. When D_blood and D_tissue were fixed, the discrimination accuracy was near perfect, with AUC of 0.99 (not fixed vs. fixed, P<2.2×10^–16, DeLong’s test). All values for AUC, optimal cut-off, sensitivity and specificity are listed in Table 4. SNR, signal-to-noise ratio; ITV, increased tubular volume fraction; ROC, receiver-operating characteristic; AUC, area under the curve; b-value: diffusion weighting.

Table 4 Summary of ROC curve comparisons
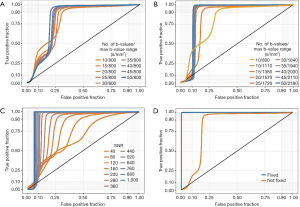
Full table

Pathophysiological condition of fibrosis

Next, we simulated pathophysiological conditions that mimic grade I (mild, 10%) and low grade II (moderate, 30%) interstitial renal fibrosis, thereby adding another component that may be considered as an additional renal compartment (f_fibrosis). Using data with the maximum b-value range of 0–2,180 s/mm² (50 b-values), NNLS continuum modelling was able to detect the diffusion component of the fibrotic compartment, to differentiate it from the other three diffusion components, and to distinguish 10% from 30% fibrosis (Figure 8A). Furthermore, this was also the case when the medium b-value range of 0–1,380 s/mm² (15 b-values) was used (Figure 8B). For both the large and the medium b-value ranges, the AUC (signal intensity) of the fibrotic compartment was significantly greater under both the simulated conditions of grade I and grade II fibrosis (affecting 10% and 30% of the renal area, respectively) compared to the fibrosis-free condition. The signal intensities obtained for grade II were significantly higher than for grade I. This distinction improved with increasing SNR (Figure 8A,B, P<2.2×10^–16, Kruskal-Wallis non-parametric ANOVA, followed by Dunn’s procedure with Holm’s correction for multiple comparisons). Discrimination between either 30% or 10% fibrosis or non-fibrosis based on the signal intensity of the fibrotic compartment was near perfect. The ROC curves show AUC =0.98, 1.00 (medium b-value range), and 0.99, 0.99 (large b-value range), for 30% and 10% fibrosis, respectively (Table 4).

Figure 8 NNLS detection of simulated fibrosis component. The simulations included baseline (no fibrosis) and a pathophysiological condition to mimic fibrosis, thus adding a fourth renal compartment. (A) NNLS could readily detect this additional compartment, when using a large b-value range of 0–2,180 s/mm². (B) This result was also true when a medium b-value range of 0–1,380 s/mm² was used. For both the large and medium b-value ranges, the AUC (signal intensity) of the fibrotic compartment was significantly greater under both the simulated conditions of grade I (mild) and grade II (moderate) fibrosis (affecting 10% and 30% of the renal area, respectively) compared to the non-fibrosis condition. The signal intensities obtained for grade II were significantly higher than for grade I. This distinction improved with increasing SNR (P<2.2×10^–16, Kruskal-Wallis non-parametric ANOVA, followed by Dunn’s procedure with Holm’s correction for multiple comparisons; whiskers denote ±1.5× interquartile range). NNLS, non-negative least squares; AUC, area under the curve; AUC, area under the curve; SNR, signal-to-noise ratio.

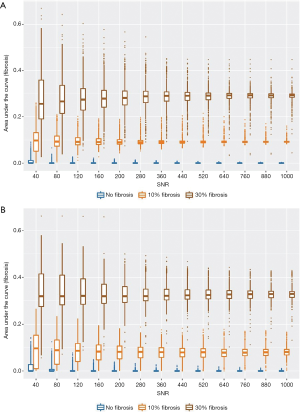
Discussion

This study is the first report on a systematic examination of NNLS computation for DWI of the kidney tubule system. Our results demonstrate the feasibility of NNLS continuum modelling for renal DWI as a less constrained, data-driven alternative for monitoring changes in the tubular volume fraction and the degree of tissue fibrosis. Our numerical simulations demonstrate the impact of SNR, the number of b-values needed for characterization of the diffusion signal decay and the range of diffusion sensitization on NNLS continuum modelling-based renal DWI applications. We show that while the error inherent to the NNLS continuum modelling is not superior to conventional fitting approaches using rigid multi-exponential models per se, it strongly depends on the specific parameter combinations applied during renal DWI. Our simulations present DWI-MRI parameters that ensure an error of less than 10% and 5%, respectively, for NNLS continuum modelling of the tubular volume fraction when compared to the ground truth given by the tri-exponential model.

Most renal DWI studies report two compartments: pseudo-diffusion related to incoherent water motion in the microvasculature, and true diffusion attributed to restricted diffusion in the tissue. Analysis of DWI using this approach, along with tracking of pathological changes, requires a priori assumptions in conjunction with rigid bi-exponential models. The fitting routine forces the data to conform to a bi-exponential behavior, and consequently, linear segmentation is frequently performed based on a given b-value threshold, assuming a bi-exponential behavior. Alternatively, parameters used for data acquisition may be customized by designing the diffusion sensitization with a specific number and magnitude of b-values (32-38).

Recently it was shown that a three-compartment model is more appropriate for representation of the diffusion properties of the kidney assuming that incoherent renal water motion is linked to three sources: (I) tissue water diffusion, (II) incoherent blood motion, and (III) incoherent tubular fluid motion (39,40). The rigid bi-exponential and tri-exponential models share a common limitation: they may not accurately reflect the complex nature of renal water diffusion, because the data are forced to conform to simplified models. This limitation could introduce a bias that runs the risk of obscuring (patho)physiological changes inherent to incoherent water motion probed with renal DWI. NNLS continuum modelling does not suffer from this limitation. Because NNLS continuum modelling does not presume that only three compartments or sources are associated with renal incoherent water motion, it allows for the detection of additional sources such as lesions, tumors, or fibrosis. This advantage is particularly relevant for DWI-MRI of the kidney, as the number of compartments or sources cannot necessarily be known in advance, and might change during the progression, interception or therapeutic treatment of renal disease. An alternative framework for determining co-existing diffusion compartments without prior assumptions on their number has been recently demonstrated for DWI of the brain and is conceptually appealing for renal DWI (67).

Our data indicate that increasing the b-value range alone is not sufficient to ensure reliable measurements of the tubular volume fraction. However, even modest increases above the lowest b-value range of 0–800 s/mm² resulted in substantial improvements in discrimination accuracy. While we simulated a series of b-value ranges extending up to 0–2,180 s/mm², we observed that a medium b-value range of 0–1,380 s/mm² yielded the majority of the benefits, and that further increases in b-value range had diminishing returns. Using the large b-value range resulted in a clear distinction between mild and moderate fibrosis. Furthermore, the medium b-value range was also sufficient to discriminate between mild and moderate fibrosis with a high degree of accuracy. This medium b-value range is achievable on clinical grade MRI systems, where the progress in gradient coil technology has triggered the implementation of high performance whole body gradients offering G_{max_combined} =100 mT/m (68) or G_max =113 mT/m (69). In addition, the SNR had a pronounced effect. At low SNR, the accuracy to discriminate between baseline and ITV was poor but improved steadily with increasing SNR. Our data suggest that a minimum number of 10 b-values is at the limit for reliable and robust diffusion coefficient fitting with NNLS under baseline conditions and with pathological changes. The use of 15 b-values significantly improved the fitting results and can be considered as an appropriate minimum number of b-values for reliable and robust diffusion coefficient fitting with NNLS. Increasing the number of b-values further would prolong the scan time, with diminishing benefits. Arguably, this extra scan time burden can be compensated by using acceleration techniques such as parallel imaging or compressed sensing approaches (70,71). Our simulations used an SNR range of 40–1,000 for b=0 s/mm² which meets the minimum SNR levels suggested for advanced renal DWI (30). Using the SNR obtained for higher b-values or for the largest b-value presents a viable alternative.

Beyond the effects of SNR and b-value numbers and ranges, we investigated the effects of fixing the blood diffusion coefficient D_blood and the tissue diffusion coefficient D_tissue. With this approach we obtained superior results, compared to the non-fixed value approach. Acceptable errors levels (<10%) were achieved in the majority of the combinations studied (>89%). Data superiority (errors levels <5%) was achieved in more than 60% of the SNR/number of b-values combinations, in both (patho)physiological conditions and when using small and large b-value ranges. The fixation of the two diffusion coefficients did not prevent the appearance of multiple peaks in the continuous region, where the curvature regularization was kept active. Fixing these coefficients led to near perfect sensitivity and specificity to discriminate between the baseline and increased tubular volume conditions based on signal intensity. The approach to fix the diffusion coefficients of blood and tissue is advisable in situations where one can presume that (patho)physiological conditions or interventions do not dramatically change the physicochemical properties of blood and tissue.

The common non-linear LS fitting method using the trust region growing algorithm is considered the gold standard for fitting the DWI decay. After fixing D_blood and D_tissue, NNLS continuum modelling showed a similar degree of reliability as the non-linear LS with some slight differences in the case of tubules and tissue. 89% of combinations had acceptable error levels <10%, and more than 50% of SNR/b-values had errors below 5% for all parameters, compared to 40% on NNLS continuum modelling. While both approaches showed a similar degree of error, rigid models like LS can introduce a bias in the analysis, since the number of compartments (number of exponential decays), must be specified a priori. Furthermore, starting values are crucial, and each additional exponential (additional compartment) included in the model requires two additional variables. Multi-exponential models with too many variables suffer from poor fit stability (40). NNLS continuum modelling is less constrained than LS. NNLS can delineate the complex nature of water diffusion and possible (patho)physiological changes with far fewer a priori assumptions. NNLS continuum modelling yields a distribution of diffusion coefficients rather than a unique value, which has the potential to better reflect the complex characteristics of biological tissues. This potential is underscored by the demonstration that the NNLS approach could detect simulated renal fibrosis. By not constraining the number of renal compartments in advance, NNLS could detect a fourth fibrosis compartment when this was introduced. Moreover, NNLS proved capable to distinguish between simulated 10% vs. 30% fibrosis.

This work lays the foundation for preclinical studies aimed at further elucidating the pathophysiology of various kidney diseases, as well as studies that aim to establish MR markers for diagnostics of those disorders. Renal tissue hypoxia is generally regarded as an early pivotal element in the pathophysiology of AKI, the possible progression of AKI to chronic kidney disease (CKD), and diabetic nephropathy. In virtually all of these disorders, the tubular volume fraction is altered, either due to changes in glomerular filtration rate, the tubular outflow towards the renal pelvis and beyond, in the transmural pressure gradient, or in tubular fluid resorption (3,7,22,23,25).

Because changes in the tubular volume fraction likely change the blood volume fraction, they result in changes in renal T₂* independent of changes in blood oxygenation. Indeed, the tubular volume fraction is a confounding factor influencing the relationship between renal T₂* mapping, oxygen saturation of hemoglobin, and tissue oxygen tension (21,29). Hence, DWI-based assessments of changes in the tubular volume fraction are highly relevant for elucidating the mechanisms of renal pathophysiology. Concomitant DWI-based measurements of the tubular volume fraction will help to accurately determine the pathophysiological role of changes in renal oxygenation as assessed by renal T₂*.

This work also provides potential insights for translational research into MR-based diagnostic tools, as changes in the tubular volume fraction are present in a multitude of kidney disorders. Such changes are prominent in AKI as induced by disturbed systemic hemodynamics, by intravascular administration of X-ray contrast media, and by obstructions of the urinary tract and diabetic nephropathy (3,7,22,23). CKD of most origins is marked by fibrosis in addition to reduced glomerular filtration, which contributes to a decrease in the tubular volume fraction (46). In addition to pathological changes in the tubular volume, our simulations revealed that NNLS continuum modelling for renal DWI may also be useful for detection and treatment monitoring of renal fibrosis, which is an important biomarker of CKD and a powerful predictor of renal outcome (26,28). These same considerations likely apply to pathologies such as kidney lesions, polycystic kidney disease, or tumors.

A relevant caveat of this study is that the effect of kurtosis at high b-values (b>1,000 s/mm²) was not considered. At high b-values, the probability distribution of the diffusion displacement deviates from a Gaussian distribution. This is considered to be a consequence of the restrictions on water molecule displacement imposed by microstructures (72). However, the main focus of this work was to assess the kidney tubule system, where the absence of organelles and cell boundaries that might hinder diffusion renders the kurtosis effect less relevant (73,74).

The use of deep learning neural networks could potentially achieve the same or even better accuracy in disentangling the different DWI decay components at low SNR regimes with a low number of b-values. Neural networks could be trained to extract the water diffusion-related components of the tubules from the DWI decay directly, without complex pre- and post-processing methods. However, neural networks depend heavily on having a large body of ground truth training data, covering the entire range of biological variability and potential pathophysiological conditions.

The present study relies on numerical simulations, as a prelude to the acquisition of in vivo data. In the interests of time, resources, and adherence to the 3Rs principles to minimize the use of experimental animals, we consider that such in silico studies are a necessary precursor before proceeding to in vivo experiments, and that the results of these simulations must be disseminated to the community. The insights gained from the current study regarding the appropriate selection of experimental parameters will enhance the robustness and reproducibility of subsequent in vivo studies, which are the logical next step for future investigations of renal diffusion properties.

Conclusions

In conclusion, our results demonstrate the implications of using NNLS continuum modelling with specific DWI acquisition and data processing protocols to provide assessment of the kidney tubule volume fraction with less than 5% or 10% error, and to offer the potential to detect diffusion compartments associated with renal pathology.

Acknowledgments

Funding: This work was funded in part (Thoralf Niendorf, Andreas Pohlmann, Thomas Gladytz, Erdmann Seeliger, Sonia Waiczies, Kathleen Cantow) by the German Research Foundation [Gefoerdert durch die Deutsche Forschungsgemeinschaft (DFG), Projektnummer 394046635, SFB 1365, RENOPROTECTION. Funded by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation), Project number 394046635, SFB 1365, RENOPROTECTION].

Footnote

Conflicts of Interest: All authors have completed the ICMJE uniform disclosure form (available at http://dx.doi.org/10.21037/qims-20-1360). TN, AP, TG, ES, SW, KC report funding provided by the German Research Foundation [Gefoerdert durch die Deutsche Forschungsgemeinschaft (DFG), Projektnummer 394046635, SFB 1365, RENOPROTECTION. Funded by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation), Project number 394046635, SFB 1365, RENOPROTECTION]. The other authors have no conflicts of interest to declare.

Ethical Statement: Ethical approval and written informed consent are not applicable to this manuscript, because it does not include any human or animal data.

Open Access Statement: This is an Open Access article distributed in accordance with the Creative Commons Attribution-NonCommercial-NoDerivs 4.0 International License (CC BY-NC-ND 4.0), which permits the non-commercial replication and distribution of the article with the strict proviso that no changes or edits are made and the original work is properly cited (including links to both the formal publication through the relevant DOI and the license). See: https://creativecommons.org/licenses/by-nc-nd/4.0/.

References

1. Hoste EAJ, Kellum JA, Selby NM, Zarbock A, Palevsky PM, Bagshaw SM, Goldstein SL, Cerda J, Chawla LS. Global epidemiology and outcomes of acute kidney injury. Nat Rev Nephrol 2018;14:607-25. [Crossref] [PubMed]
2. Selby NM, Taal MW. Long-term outcomes after AKI-a major unmet clinical need. Kidney Int 2019;95:21-3. [Crossref] [PubMed]
3. Zuk A, Bonventre JV. Recent advances in acute kidney injury and its consequences and impact on chronic kidney disease. Curr Opin Nephrol Hypertens 2019;28:397-405. [Crossref] [PubMed]
4. Glassock RJ, Warnock DG, Delanaye P. The global burden of chronic kidney disease: estimates, variability and pitfalls. Nat Rev Nephrol 2017;13:104-14. [Crossref] [PubMed]
5. Fortrie G, de Geus HRH, Betjes MGH. The aftermath of acute kidney injury: a narrative review of long-term mortality and renal function. Crit Care 2019;23:24. [Crossref] [PubMed]
6. Levin A, Tonelli M, Bonventre J, Coresh J, Donner JA, Fogo AB, et al. Global kidney health 2017 and beyond: a roadmap for closing gaps in care, research, and policy. Lancet 2017;390:1888-917. [Crossref] [PubMed]
7. Fähling M, Seeliger E, Patzak A, Persson PB. Understanding and preventing contrast-induced acute kidney injury. Nat Rev Nephrol 2017;13:169-80. [Crossref] [PubMed]
8. van Duijl TT, Ruhaak LR, de Fijter JW, Cobbaert CM. Kidney injury biomarkers in an academic hospital setting: where are we now? Clin Biochem Rev 2019;40:79-97. [Crossref] [PubMed]
9. Luft FC. Biomarkers and predicting acute kidney injury. Acta Physiol (Oxf) 2021;231:e13479 [Crossref] [PubMed]
10. Schrezenmeier EV, Barasch J, Budde K, Westhoff T, Schmidt-Ott KM. Biomarkers in acute kidney injury - pathophysiological basis and clinical performance. Acta Physiol (Oxf) 2017;219:554-72. [Crossref] [PubMed]
11. Molitoris BA. Urinary biomarkers: alone are they enough? J Am Soc Nephrol 2015;26:1485-8. [Crossref] [PubMed]
12. Simms R, Sourbron S. Recent findings on the clinical utility of renal magnetic resonance imaging biomarkers. Nephrol Dial Transplant 2020;35:915-9. [Crossref] [PubMed]
13. Pickkers P, Ostermann M, Joannidis M, Zarbock A, Hoste E, Bellomo R, Prowle J, Darmon M, Bonventre JV, Forni L, Bagshaw SM, Schetz M. The intensive care medicine agenda on acute kidney injury. Intensive Care Med 2017;43:1198-209. [Crossref] [PubMed]
14. Matejovic M, Ince C, Chawla LS, Blantz R, Molitoris BA, Rosner MH, Okusa MD, Kellum JA, Ronco C. Renal hemodynamics in AKI: in search of new treatment targets. J Am Soc Nephrol 2016;27:49-58. [Crossref] [PubMed]
15. Khwaja A. KDIGO clinical practice guidelines for acute kidney injury. Nephron Clin Pract 2012;120:c179-84. [PubMed]
16. Grenier N, Merville P, Combe C. Radiologic imaging of the renal parenchyma structure and function. Nat Rev Nephrol 2016;12:348-59. [Crossref] [PubMed]
17. Zarjou A, Sanders PW, Mehta RL, Agarwal A. Enabling innovative translational research in acute kidney injury. Clin Transl Sci 2012;5:93-101. [Crossref] [PubMed]
18. Evans RG, O'Connor PM. Initiation and progression of chronic kidney disease: can we definitively test the chronic hypoxia hypothesis? Hypertension 2013;62:827-8. [Crossref] [PubMed]
19. Cantow K, Hummel L, Flemming B, Waiczies S, Niendorf T, Seeliger E. Imagine physiology without imaging. Acta Physiol (Oxf) 2020;230:e13549 [Crossref] [PubMed]
20. Niendorf T, Frydman L, Neeman M, Seeliger E. Google maps for tissues: Multiscale imaging of biological systems and disease. Acta Physiol (Oxf) 2020;228:e13392 [Crossref] [PubMed]
21. Niendorf T, Pohlmann A, Arakelyan K, Flemming B, Cantow K, Hentschel J, Grosenick D, Ladwig M, Reimann H, Klix S, Waiczies S, Seeliger E. How bold is blood oxygenation level-dependent (BOLD) magnetic resonance imaging of the kidney? Opportunities, challenges and future directions. Acta Physiol (Oxf) 2015;213:19-38. [Crossref] [PubMed]
22. Premaratne E, Verma S, Ekinci EI, Theverkalam G, Jerums G, MacIsaac RJ. The impact of hyperfiltration on the diabetic kidney. Diabetes Metab 2015;41:5-17. [Crossref] [PubMed]
23. Barasch J, Zager R, Bonventre JV. Acute kidney injury: a problem of definition. Lancet 2017;389:779-81. [Crossref] [PubMed]
24. Mengel M. Deconstructing interstitial fibrosis and tubular atrophy: a step toward precision medicine in renal transplantation. Kidney Int 2017;92:553-5. [Crossref] [PubMed]
25. He L, Wei Q, Liu J, Yi M, Liu Y, Liu H, Sun L, Peng Y, Liu F, Venkatachalam MA, Dong Z. AKI on CKD: heightened injury, suppressed repair, and the underlying mechanisms. Kidney Int 2017;92:1071-83. [Crossref] [PubMed]
26. Ferguson CM, Eirin A, Abumoawad A, Saad A, Jiang K, Hedayat AF, Misra S, Glockner J, Textor SC, Lerman LO. Renal fibrosis detected by diffusion-weighted magnetic resonance imaging remains unchanged despite treatment in subjects with renovascular disease. Sci Rep 2020;10:16300. [Crossref] [PubMed]
27. Zhao J, Wang ZJ, Liu M, Zhu J, Zhang X, Zhang T, Li S, Li Y. Assessment of renal fibrosis in chronic kidney disease using diffusion-weighted MRI. Clin Radiol 2014;69:1117-22. [Crossref] [PubMed]
28. Hysi E, Yuen DA. Imaging of renal fibrosis. Curr Opin Nephrol Hypertens 2020;29:599-607. [Crossref] [PubMed]
29. Pohlmann A, Arakelyan K, Hentschel J, Cantow K, Flemming B, Ladwig M, Waiczies S, Seeliger E, Niendorf T. Detailing the relation between renal T2* and renal tissue pO2 using an integrated approach of parametric magnetic resonance imaging and invasive physiological measurements. Invest Radiol 2014;49:547-60. [Crossref] [PubMed]
30. Ljimani A, Caroli A, Laustsen C, Francis S, Mendichovszky IA, Bane O, et al. Consensus-based technical recommendations for clinical translation of renal diffusion-weighted MRI. MAGMA 2020;33:177-95. [Crossref] [PubMed]
31. Caroli A, Schneider M, Friedli I, Ljimani A, De Seigneux S, Boor P, Gullapudi L, Kazmi I, Mendichovszky IA, Notohamiprodjo M, Selby NM, Thoeny HC, Grenier N, Vallee JP. Diffusion-weighted magnetic resonance imaging to assess diffuse renal pathology: a systematic review and statement paper. Nephrol Dial Transplant 2018;33:ii29-40. [Crossref] [PubMed]
32. Wurnig MC, Germann M, Boss A. Is there evidence for more than two diffusion components in abdominal organs? - A magnetic resonance imaging study in healthy volunteers. NMR Biomed 2018; [Crossref] [PubMed]
33. Fan M, Xing Z, Du Y, Pan L, Sun Y, He X. Quantitative assessment of renal allograft pathologic changes: comparisons of mono-exponential and bi-exponential models using diffusion-weighted imaging. Quant Imaging Med Surg 2020;10:1286-97. [Crossref] [PubMed]
34. Sułkowska K, Palczewski P, Furmańczyk-Zawiska A, Perkowska-Ptasińska A, Wójcik D, Szeszkowski W, Durlik M, Gołębiowski M, Małkowski P. Diffusion weighted magnetic resonance imaging in the assessment of renal function and parenchymal changes in chronic kidney disease: a preliminary study. Ann Transplant 2020;25:e920232 [Crossref] [PubMed]
35. Kuai ZX, Liu WY, Zhu YM. Effect of multiple perfusion components on pseudo-diffusion coefficient in intravoxel incoherent motion imaging. Phys Med Biol 2017;62:8197-209. [Crossref] [PubMed]
36. Schneider MJ, Dietrich O, Ingrisch M, Helck A, Winter KS, Reiser MF, Staehler M, Casuscelli J, Notohamiprodjo M. Intravoxel incoherent motion magnetic resonance imaging in partially nephrectomized kidneys. Invest Radiol 2016;51:323-30. [Crossref] [PubMed]
37. Barbieri S, Donati OF, Froehlich JM, Thoeny HC. Impact of the calculation algorithm on biexponential fitting of diffusion-weighted MRI in upper abdominal organs. Magn Reson Med 2016;75:2175-84. [Crossref] [PubMed]
38. Le Bihan D, Breton E, Lallemand D, Aubin ML, Vignaud J, Laval-Jeantet M. Separation of diffusion and perfusion in intravoxel incoherent motion MR imaging. Radiology 1988;168:497-505. [Crossref] [PubMed]
39. van Baalen S, Leemans A, Dik P, Lilien MR, Ten Haken B, Froeling M. Intravoxel incoherent motion modeling in the kidneys: comparison of mono-, bi-, and triexponential fit. J Magn Reson Imaging 2017;46:228-39. [Crossref] [PubMed]
40. van der Bel R, Gurney-Champion OJ, Froeling M, Stroes ESG, Nederveen AJ, Krediet CTP. A tri-exponential model for intravoxel incoherent motion analysis of the human kidney: in silico and during pharmacological renal perfusion modulation. Eur J Radiol 2017;91:168-74. [Crossref] [PubMed]
41. Niendorf T, Dijkhuizen RM, Norris DG, van Lookeren Campagne M, Nicolay K. Biexponential diffusion attenuation in various states of brain tissue: implications for diffusion-weighted imaging. Magn Reson Med 1996;36:847-57. [Crossref] [PubMed]
42. Whittall KP, MacKay AL. Quantitative interpretation of NMR relaxation data. J Magn Reson (1969) 1989;84:134-52.
43. Bjarnason TA, Mitchell JR. AnalyzeNNLS: magnetic resonance multiexponential decay image analysis. J Magn Reson 2010;206:200-4. [Crossref] [PubMed]
44. Wiggermann V, Vavasour IM, Kolind SH, MacKay AL, Helms G, Rauscher A. Non-negative least squares computation for in vivo myelin mapping using simulated multi-echo spin-echo T2 decay data. NMR Biomed 2020;33:e4277 [Crossref] [PubMed]
45. Smouha E, Neeman M. Compartmentation of intracellular water in multicellular tumor spheroids: diffusion and relaxation NMR. Magn Reson Med 2001;46:68-77. [Crossref] [PubMed]
46. Nezamzadeh M. Diffusion time dependence of magnetic resonance diffusion signal decays: an investigation of water exchange in human brain in vivo. MAGMA 2012;25:285-96. [Crossref] [PubMed]
47. Marchand AJ, Hitti E, Monge F, Saint-Jalmes H, Guillin R, Duvauferrier R, Gambarota G. MRI quantification of diffusion and perfusion in bone marrow by intravoxel incoherent motion (IVIM) and non-negative least square (NNLS) analysis. Magn Reson Imaging 2014;32:1091-6. [Crossref] [PubMed]
48. Gao J, Jiang M, Magin RL, Gatto RG, Morfini G, Larson AC, Li W. Multicomponent diffusion analysis reveals microstructural alterations in spinal cord of a mouse model of amyotrophic lateral sclerosis ex vivo. PLoS One 2020;15:e0231598 [Crossref] [PubMed]
49. Gambarota G, Hitti E, Leporq B, Saint-Jalmes H, Beuf O. Eliminating the blood-flow confounding effect in intravoxel incoherent motion (IVIM) using the non-negative least square analysis in liver. Magn Reson Med 2017;77:310-7. [Crossref] [PubMed]
50. Wong SM, Backes WH, Drenthen GS, Zhang CE, Voorter PHM, Staals J, van Oostenbrugge RJ, Jansen JFA. Spectral diffusion analysis of intravoxel incoherent motion MRI in cerebral small vessel disease. J Magn Reson Imaging 2020;51:1170-80. [Crossref] [PubMed]
51. Liu J, Gambarota G, Shu H, Jiang L, Leporq B, Beuf O, Karfoul A. On the identification of the blood vessel confounding effect in intravoxel incoherent motion (IVIM) Diffusion-Weighted (DW)-MRI in liver: an efficient sparsity based algorithm. Med Image Anal 2020;61:101637 [Crossref] [PubMed]
52. Keil VC, Madler B, Gielen GH, Pintea B, Hiththetiya K, Gaspranova AR, Gieseke J, Simon M, Schild HH, Hadizadeh DR. Intravoxel incoherent motion MRI in the brain: Impact of the fitting model on perfusion fraction and lesion differentiability. J Magn Reson Imaging 2017;46:1187-99. [Crossref] [PubMed]
53. Lawson CL, Hanson RJ. Solving least squares problems. Englewood Cliffs: Prentice-Hall, 1974.
54. Golub GH, Heath M, Wahba G. Generalized cross-validation as a method for choosing a good ridge parameter. Technometrics 1979;21:9. [Crossref]
55. Friedli I, Crowe LA, Berchtold L, Moll S, Hadaya K, de Perrot T, Vesin C, Martin PY, de Seigneux S, Vallee JP. New magnetic resonance imaging index for renal fibrosis assessment: a comparison between diffusion-weighted imaging and T1 mapping with histological validation. Sci Rep 2016;6:30088. [Crossref] [PubMed]
56. Chen PS, Li YP, Ni HF. Morphology and evaluation of renal fibrosis. Adv Exp Med Biol 2019;1165:17-36. [Crossref] [PubMed]
57. Hauge A, Wegner CS, Gaustad JV, Simonsen TG, Andersen LMK, Rofstad EK. Diffusion-weighted MRI-derived ADC values reflect collagen I content in PDX models of uterine cervical cancer. Oncotarget 2017;8:105682-91. [Crossref] [PubMed]
58. Andersson CA, Bro R. The N-way Toolbox for MATLAB. Chemom Intell Lab Syst 2000;52:5. [Crossref]
59. Aja-Fernandez S, Niethammer M, Kubicki M, Shenton ME, Westin CF. Restoration of DWI data using a Rician LMMSE estimator. IEEE Trans Med Imaging 2008;27:1389-403. [Crossref] [PubMed]
60. Veraart J, Novikov DS, Christiaens D, Ades-Aron B, Sijbers J, Fieremans E. Denoising of diffusion MRI using random matrix theory. Neuroimage 2016;142:394-406. [Crossref] [PubMed]
61. Wang H, Zheng R, Dai F, Wang Q, Wang C. High-field mr diffusion-weighted image denoising using a joint denoising convolutional neural network. J Magn Reson Imaging 2019;50:1937-47. [Crossref] [PubMed]
62. De Wardener HE. The kidney: an outline of normal and abnormal structure and function. 4th ed. Edinburgh & New York: Churchill Livingstone, 1973.
63. DeLong ER, DeLong DM, Clarke-Pearson DL. Comparing the areas under two or more correlated receiver operating characteristic curves: a nonparametric approach. Biometrics 1988;44:837-45. [Crossref] [PubMed]
64. Robin X, Turck N, Hainard A, Tiberti N, Lisacek F, Sanchez JC, Muller M. pROC: an open-source package for R and S+ to analyze and compare ROC curves. BMC Bioinformatics 2011;12:77. [Crossref] [PubMed]
65. Sachs MC. plotROC: a tool for plotting ROC curves. J Stat Softw 2017;79:2. [Crossref] [PubMed]
66. Lopez-Raton M, Rodriguez-Alavarz MX, Cadarso Suarez C, Gude-Sampedro F. OptimalCutpoints: An R Package for Selecting Optimal Cutpoints in Diagnostic Tests. J Stat Softw 2014;61:1-36. [Crossref]
67. De Luca A, Leemans A, Bertoldo A, Arrigoni F, Froeling M. A robust deconvolution method to disentangle multiple water pools in diffusion MRI. NMR Biomed 2018;31:e3965 [Crossref] [PubMed]
68. Siemens-Healthineers. Embrace human nature at 3T MAGNETOM Vida with BioMatrix. 2020. Available online: https://static.healthcare.siemens.com/siemens_hwem-hwem_ssxa_websites-context-root/wcm/idc/groups/public/@global/@imaging/@mri/documents/download/mda5/nzgw/~edisp/siemens_healthineers_mr_magnetom_vida-07268000.pdf (Accessed November 14th 2020).
69. U.S. Food & Drug Administration. 2020. Available online: https://www.accessdata.fda.gov/cdrh_docs/pdf20/K201615.pdf (Accessed November 22th 2020).
70. Wu Y, Zhu YJ, Tang QY, Zou C, Liu W, Dai RB, Liu X, Wu EX, Ying L, Liang D. Accelerated MR diffusion tensor imaging using distributed compressed sensing. Magn Reson Med 2014;71:763-72. [Crossref] [PubMed]
71. Zhang C, Arefin TM, Nakarmi U, Lee CH, Li H, Liang D, Zhang J, Ying L. Acceleration of three-dimensional diffusion magnetic resonance imaging using a kernel low-rank compressed sensing method. Neuroimage 2020;210:116584 [Crossref] [PubMed]
72. Jensen JH, Helpern JA, Ramani A, Lu H, Kaczynski K. Diffusional kurtosis imaging: the quantification of non-gaussian water diffusion by means of magnetic resonance imaging. Magn Reson Med 2005;53:1432-40. [Crossref] [PubMed]
73. Pentang G, Lanzman RS, Heusch P, Müller-Lutz A, Blondin D, Antoch G, Wittsack HJ. Diffusion kurtosis imaging of the human kidney: a feasibility study. Magn Reson Imaging 2014;32:413-20. [Crossref] [PubMed]
74. Huang Y, Chen X, Zhang Z, Yan L, Pan D, Liang C, Liu Z. MRI quantification of non-Gaussian water diffusion in normal human kidney: a diffusional kurtosis imaging study. NMR Biomed 2015;28:154-61. [Crossref] [PubMed]