Multi-detector computed tomography (MDCT) imaging: association of bone texture parameters with finite element analysis (FEA)-based failure load of single vertebrae and functional spinal units

Introduction

Osteoporosis is a systemic skeletal disease that shows exceedingly high prevalence worldwide (1-3). It is characterized by low bone mass in combination with the microarchitectural deterioration of bone tissue, increasing the risk for fragility fractures (3-5). Sustained fragility fractures reduce the health-related quality of life of affected subjects and can result in premature mortality (6-10). One of the most common anatomical sites of osteoporotic fragility fractures is the spine, with affected subjects presenting a 12.6-fold increase in the risk of future additional vertebral fractures (3-5,11,12). However, vertebral fractures often stay silent without causing physical symptoms, delaying the initiation of treatment (13,14). The valid prediction of individual fracture risk in osteoporosis is key to start timely pharmacological interventions and improve clinical outcome.

The measurement of areal bone mineral density (BMD) in dual-energy X-ray absorptiometry (DXA) of the spine and/or hip is the current reference standard for diagnosing osteoporosis and for assessing fracture risk (4,15-17). However, DXA-derived areal BMD values of subjects with and without osteoporosis can overlap, thus hampering reliable identification of osteoporotic subjects at risk of suffering fractures (17-19). Attempts to overcome mere DXA-based areal BMD values as the only metric to assess fracture risk are manifold, including the Fracture Risk Assessment Tool (FRAX) that allows calculating the 10-year fracture probability by including several known risk factors besides areal BMD, which is an optional entry (20,21). Furthermore, the application of computed tomography (CT)—mostly used opportunistically when acquired for other clinically indicated purposes than a dedicated assessment of BMD—shows high potential to overcome limitations of DXA for osteoporosis screening by measuring BMD and by analyzing other parameters related to bone quality (17,22,23).

Finite element analysis (FEA) applied to CT data of the spine seems a promising approach to assess vertebral bone strength and to predict incident vertebral fractures in osteoporosis (24-26). Specifically, lower vertebral strength using FEA was associated with an increased risk of new or worsening vertebral fractures, and vertebral strength better predicted incident vertebral fractures when compared to CT-based areal BMD [area under the curve (AUC) =0.804 vs. 0.715] (24). Importantly, FEA does not require increased radiation exposure during CT acquisition, as a dose reduction of at least 75% compared to standard-dose imaging is still workable for an adequate prediction of vertebral failure load based on FEA in-vivo (25). Correspondingly, in an ex-vivo setup using thoracic mid-vertebrae specimens for CT scanning with different exposures, dose reduction in the range of 80 to 500 mAs had no significant impact on FEA-predicted vertebral fracture loads (26).

While most studies have considered single vertebral bodies in an isolated fashion, recent FEA-based work stressed the importance of the functional spinal unit [FSU; i.e., two adjacent vertebrae with the intervertebral disc (IVD) and adjoining ligaments between them], because IVDs also considerably influence the total load on the spine (27,28). In detail, one study found that only stiffness, but not FEA-derived failure load was significantly correlated to experimentally measured failure load (27). Another study revealed that the FEA-predicted vertebral failure load showed no significant correlations with experimentally measured failure loads, whereas FEA-predicted failure loads of FSUs best predicted experimentally measured failure loads (28). Thus, while FEA of vertebral bodies alone may probably only provide limited information on vertebral bone strength, models considering the FSUs could come closer to an adequate evaluation of strength and impending osteoporotic fractures at the spine.

Although the FEA-based assessment of vertebral failure load is considered the gold standard (29-31), FEA is a sophisticated and methodologically demanding approach, which requires the input of assumptions for force direction and spread as well as for modeling of IVDs. Furthermore, sufficient computational power is needed, entailing a rather long duration for FEA computation that would hamper seamless application in the direct clinical setting. Another valuable approach besides FEA is texture analysis (TA), which has shown feasibility for assessment of the spine with high discriminatory power to identify patients with vertebral fractures and to accurately predict fracture risk (32,33). The approach of TA is an objective and quantitative method to analyze the distribution and relationship of pixel or voxel gray levels in an image or volume, which is applicable to CT data (34). Specifically, TA combined with machine learning algorithms for evaluation of standard CT enabled identifying subjects who will suffer from vertebral insufficiency fractures with high accuracy and an AUC of 0.97 (32). In a study assessing the performance of global volumetric BMD with a random forest classifier based on regional values and TA to separate patients with and without osteoporotic fractures, the random forest classifier showed a better discriminatory power (AUC =0.88) than that of volumetric global BMD alone (AUC =0.64) (33). Notably, opportunistic osteoporosis screening at the spine using specific texture parameters could even be performed in contrast-enhanced CT scans, thus probably further increasing seamless application of TA (35). Normative values of TA features for CT scans of the spine have been provided and showed age-, gender-, and region-specific differences beyond information provided by conventionally used DXA (36).

Yet, it is unclear whether FEA as the gold-standard method for vertebral failure load evaluation correlates well with parameters from TA when considering single vertebrae and, more importantly, FSUs. Thus, the aim of this study is to systematically compare the FEA-based vertebral failure load with parameters of TA derived from CT data of the spine.

Methods

Setup and cohort

This retrospective study was approved by the local institutional review board and was conducted in accordance with the Declaration of Helsinki. The requirement for written informed consent was waived due to the study’s retrospective character.

Eligible subjects underwent multi-detector CT (MDCT) scans covering the thoraco-lumbar spine and were retrospectively identified in our institution’s digital Picture Archiving and Communication System (PACS). Patients with pathological bone changes like bone metastases, hematological or metabolic bone disorders aside from osteoporosis, and vertebral fractures were excluded. A cohort of seven subjects (two females and five males; mean age: 71.9±7.4 years) was included for FEA and TA. The same sample has been investigated in a previous study with different purposes (35).

Figure 1 shows the four-step analysis methodology followed in the current study. In the first step, the contrast-enhanced MDCT images were acquired for the thoracolumbar spine. In the second step, vertebral bodies were segmented, the three-dimensional (3D) models were generated, the models were meshed, and material mapping was applied to the elements. In the third step, the meshed models were simulated under loading and boundary conditions. Finally, in the fourth step, evaluation of the data from FEA and TA were performed.

Figure 1 The four-step analysis methodology followed in the current computational study. Step 1: multi-detector computed tomography (MDCT) image acquisition; step 2: model segmentation; step 3: finite element analysis (FEA); step 4: data analysis. (A) Analysis steps shown for a single vertebral body; (B) analysis steps shown for the functional spinal unit (FSU).

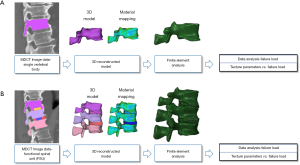
Image acquisition

Imaging was performed during clinical routine using a 64-row MDCT scanner (Somatom Sensation Cardiac 64; Siemens Medical Solutions, Erlangen, Germany). Routine contrast-enhanced MDCT images were obtained after administration of an intravenous contrast medium (Imeron 400; Bracco, Konstanz, Germany), which was delivered using a high-pressure injector (Fresenius Pilot C; Fresenius Kabi, Bad Homburg, Germany). The injection was performed with a delay of 70 s, a flow rate of 3 mL/s, and a body weight-dependent dose (80 mL for body weight up to 80 kg, 90 mL for body weight up to 100 kg, and 100 mL for body weight over 100 kg). Scanning parameters were 120 kVp tube voltage with an adapted tube load of averaged 200 mAs. Sagittal reformations of the spine were reconstructed using a bone kernel (B70f) with a standard slice thickness of 3 mm.

Image segmentation

Manual segmentations of the vertebral bodies T11, T12, L1, and L2 and the IVDs T11/12, T12/L1, L1/2, and L2/3 were performed by a board-certified radiologist with 10 years of experience, considering the sagittal reformations of the spine and using the open-source software Medical Imaging Interaction Toolkit (MITK; developed by the Division of Medical and Biological Informatics, German Cancer Research Center, Heidelberg, Germany; www.mitk.org). The segmentations were achieved without assistance by (semi)automatic tools, and the contours of the four vertebral bodies and IVDs were carefully followed during segmentations using all available slices covering the vertebrae in bone windowing. Adjacent soft tissue or other surrounding structures were spared. Two distinct FSUs were defined based on the segmented structures: FSU-1 (T11-IVD-T12-IVD-L1) and FSU-2 (T12-IVD-L1-IVD-L2).

Simulation and modeling

Finite element modeling and analysis

The contrast-enhanced MDCT images and segmentation masks were imported to image processing software MIMICS (Materialise NV; Leuven, Belgium), and the 3D models were developed. These 3D models were imported to a 3-Matic software program (Materialise NV; Leuven, Belgium) for generating the finite element mesh. For capturing the vertebral geometry, tetrahedral elements (C3D4 in the Abaqus element library) were used for meshing.

After meshing, patient-specific material properties were applied to the vertebrae based on image intensity [in Hounsfield units (HU)] and its relationship to material density (ρ) and elasticity (E; Table 1). For maintaining the accuracy of the computational models, a mesh sensitivity study was performed by varying the maximum element edge length from 1.0 to 3.0 mm with an interval of 0.5 mm. The sensitivity study showed that 2-mm size produced mesh-independent results and, thus, the same size was used for all models. The meshed and material-mapped models were imported to commercial FEA software (Abaqus, version 6.10; Hibbitt, Karlsson, and Sorensen, Inc., Pawtucket, RI, USA) for downstream analysis, including the application of loading and boundary conditions application and analysis.

Table 1 Vertebrae and intervertebral disc (IVD) material mapping (density-intensity-modulus) relations used in the current finite element analysis (FEA)
Full table

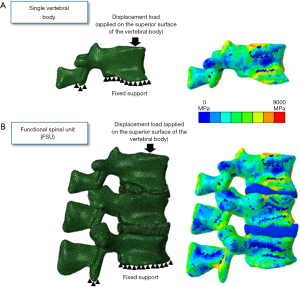
For FSU models, tie constraint contact condition was applied between the vertebrae and IVDs and in-between nucleus and annulus to prevent any relative motion between the structures (37). For avoiding penetration in the posterior elements, no penetration contact conditions were applied. The individual vertebrae and FSU models were simulated under compression loading conditions. The nodes on the inferior surface of the vertebrae were fixed and the displacement loading was applied on the superior surface of the vertebrae (Figure 2). The FEA methodology followed in the current work has been experimentally validated in previous studies (26,28,30,36). Figure 2 shows the axial modulus distribution for the vertebrae and FSU models.

Figure 2 Loading and boundary conditions and axial modulus distribution. (A) For the individual vertebra, the model is fixed at the bottom, and displacement load is applied on the superior surface. (B) For FSU models, the model is fixed at the bottom, and displacement load is applied on the superior surface of the top vertebra.

Texture analysis

The gray level quantization was performed on each segmented vertebra using the normalized gray levels (scale 0 to 1) of the region of interest. Cubic interpolation was used to generate the isotropic volume of the image dataset for TA. The extracted textural features included the first-order statistical moments of skewness, variance, and kurtosis of gray level histograms, second-order gray level co-occurrence matrix (GLCM), and higher-order gray level run-length matrix (GLRLM). These features mentioned above quantify textural patterns (fine, coarse, smooth, or irregular) in an image.

A total of 8 features from GLCM (energy, contrast, correlation, homogeneity, dissimilarity, entropy, variance, and sum average) and 13 features from GLRLM [short-run emphasis (SRE), long-run emphasis (LRE), gray level non-uniformity (GLN), run-length non-uniformity (RLN), run percentage (RP), low gray level run emphasis (LGLRE), high gray level run emphasis (HGLRE), short-run low gray level emphasis (SRLGLE), short-run high gray level emphasis (SRHGLE), long-run low gray level emphasis (LRLGLE), long-run high gray level emphasis (LRHGLE), gray level variance (GLV), and run-length variance (RLV)] were derived.

Each entry in GLCM was based on the probability of gray level co-occurrence between pixel pairs at a given vector direction and fixed length 1 between the voxel pair. Each entry in GLRLM was the probability of voxel occurrences of a specific gray level for a possible run-length along a given vector. There are 13 direction vectors with a displacement of (dx, dy, dz). The matrices of all 13 directions were added together, averaged, and normalized before the calculation of the second-order GLCM and higher-order GLRLM indices. GLCM is an (n × n) matrix where n is the number of gray levels in each image. GLRLM is an (n × m) matrix, where n is the number of gray levels in the scan, and m is the run length. Depending on the dimensions of the scan, the number of columns equals the largest value from either the height, length, or breadth. The bone material has high compressive strength, but low tensile strength, and most fibers are located along the vertical direction. Therefore, the orientations of the y- and z-axis were fixed, where positive dy is in the anterior direction, and positive dz is in the superior direction.

Statistical analysis

GraphPad Prism (version 6.0; GraphPad Software Inc., San Diego, CA, USA) and SPSS (version 26.0; IBM SPSS Statistics for Windows, IBM Corp., Armonk, NY, USA) were used for statistical data analyses. The level of statistical significance was set at P<0.05.

FEA-derived failure loads and parameters derived from TA were averaged for all subjects regarding the four segmented vertebrae. Furthermore, these measures were averaged to obtain an average value for the FSU-1 and FSU-2, respectively. Descriptive statistics including mean ± standard deviation (SD) and ranges are reported for vertebrae and the two FSUs. Furthermore, Spearman’s rho was calculated to explore associations between FEA-derived failure loads and each texture parameter, again considering the vertebrae only as well as the two FSUs. Adjustment for multiple testing was performed using the Benjamini-Hochberg procedure with a false discovery rate of 10%. Furthermore, statistical significance between correlation coefficients was evaluated using the Fisher z-transformation.

Multivariate regression models were computed to identify the texture parameter that predicts the FEA-derived failure load best. Again, this was done separately for the vertebrae as well as the two FSUs. Texture parameters were considered as independent variables and included in a stepwise approach in the models (if the level of significance was P<0.05). Adjusted regression coefficients (R²_adj) were calculated and extracted for each model.

Results

Calculation of the failure load by means of FEA, as well as computation of texture parameters, was possible in all enrolled subjects and for all investigated vertebral bodies and the FSUs. Table 2 provides an overview of values obtained by FEA and TA.

Table 2 Results of texture analysis (TA) and finite element analysis (FEA)
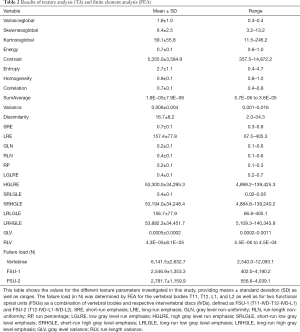
Full table

Furthermore, there were statistically significant correlations between most of the extracted texture parameters as well as the FEA-derived failure load (Table 3). When investigating single vertebrae, the strongest correlations were observed for skewnessglobal (rho =−0.767, P<0.001), kurtosisglobal (rho =−0.766, P<0.001), and GLV (rho =−0.736, P<0.001; Table 3, Figure 3). For the FSUs, SumAverage (FSU-1: rho =0.654, P=0.0182; FSU-2: rho =0.841, P=0.0006), LRE (FSU-1: rho =−0.637, P=0.0221), LRLGLE (FSU-1: rho =−0.637, P=0.0221), homogeneity (FSU-2: rho =−0.819, P=0.0011), and energy (FSU-2: rho =−0.819, P=0.0011) were among the texture parameters showing the strongest correlations (Table 3, Figure 3). When comparing the obtained correlation results, the correlation coefficients were indicative of stronger associations for a majority of parameters compared to single vertebrae (particularly FSU-2; Table 3). Yet, there were no statistically significant differences detected between the correlation coefficients of the vertebrae and FSUs according to the Fisher z-transformation.

Table 3 Correlations between texture parameters and failure load
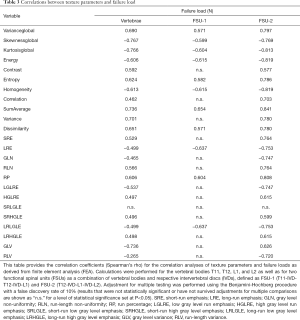
Full table

Figure 3 Correlations between texture parameters and failure load. This figure plots the correlations of texture parameters and failure loads as derived from finite element analysis (FEA). Single graphs are shown for the three strongest correlations (Spearman’s rho) considering the vertebral bodies T11, T12, L1, and L2 as well as two functional spinal units (FSUs) as a combination of vertebral bodies and respective intervertebral discs (IVDs), defined as FSU-1 (T11-IVD-T12-IVD-L1) and FSU-2 (T12-IVD-L1-IVD-L2).

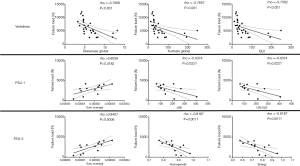
Multivariate regression models did not include more than one statistically significant texture parameter. For single vertebrae, SumAverage best predicted the FEA-based failure load with R²_adj =0.523 (P<0.001). For the two FSUs, kurtosisglobal (FSU-1: R²_adj =0.611, P=0.001) and skewnessglobal (FSU-2: R²_adj =0.579, P=0.002) predicted the FEA-based failure loads best. In this context, skewness measures the (lack of) symmetry in the image intensity distribution, with positive skewness indicating most of the distribution at the left side of the curve (around the mean), suggesting that most pixels are skewed toward lower CT attenuation values. Kurtosis represents the peakedness of the distribution, and a distribution with high kurtosis has a sharp peak near the mean and rapidly declining long tails, which indicates a lower variation of pixel intensities in the image. Curves leaning toward lower CT attenuation values are suggestive of bone loss and depletion, predisposing to vertebral fractures.

Discussion

This study correlated FEA-based vertebral failure load with parameters of TA, which were derived from clinical routine MDCT. Overall, significant associations were observed for almost all texture parameters and the FEA-based failure load, with stronger correlations being obtained particularly for FSU-2 compared to the analyses using single vertebrae. Kurtosisglobal and skewnessglobal best predicted failure loads for FSUs. In this context, kurtosis and skewness represent the frequency of distribution of the image intensities in the form of distortion and the disparity deviation of a histogram with respect to a normal distribution. Skewness is a measure of (lack of) symmetry in the image intensity distribution, kurtosis represents the peakedness of the distribution. Positive skewness indicates that most pixels are skewed toward lower CT attenuation, while a distribution with high kurtosis indicates a lower variation of pixel intensities in the image. Lower and concentrated CT attenuation affects the material property mappings in the modeling protocol and, in turn, results in a lower failure load.

The approach of FEA can be applied to investigate how morphological variation and properties relate to functional characteristics (38-40). It enables to reduce a complex geometry into a finite number of elements with simple geometries, and allows the strain to be modeled across the entire surface and throughout the internal architecture of a structure like the vertebral body (38-40). To date, several studies have demonstrated that FEA-based measurements of vertebral strength are strongly correlated with actual failure loads as derived from in-vitro mechanical testing using cadaveric vertebrae (41-44); thus, validation of the approach has been achieved, and FEA-based assessment of vertebral failure loads is considered gold standard. Recently, also the FSU has been incorporated in FEA approaches, revealing that the FEA-predicted failure load of FSUs best predicted the experimentally measured failure loads (28). Thus, FEA of FSUs may be considered a more realistic approach to predict actual failure load. We observed partly stronger correlations for the texture parameters versus failure load of FSUs (particularly FSU-2) as compared to the analyses based on single vertebrae. Thus, our findings indicate a good performance of texture parameters in predicting failure load not only for single vertebrae but also for FSUs as the more realistic in-vivo scenario.

However, the FEA-based assessment of vertebral failure load is time-consuming, particularly for FSUs. Using TA, though, may be a more feasible and faster approach, which has previously shown potential to identify patients with vertebral fractures and to predict fracture risk (32,33). TA has furthermore shown to be robust also for low-dose or contrast-enhanced CT as well as specifically for opportunistic osteoporosis screening (35,45). Results of this study indicate that there is a good correlation between FEA-based failure loads and texture parameters, particularly considering kurtosisglobal and skewnessglobal, which predicted failure loads best for FSUs. While it has been largely unknown whether FEA correlates with parameters derived from TA, the results of the present study suggest that TA may be sufficient to predict vertebral failure loads specifically when considering FSUs. Thus, TA could serve as a viable option to be applied to existing MDCT data acquired for clinical purposes.

When interpreting the results of this study we have to acknowledge some limitations. First, the cohort size was relatively small. This is related to the rather long computational time that is needed per patient. However, per patient, four vertebral bodies and adjacent IVDs were segmented and incorporated in the analyses, thus investigating 28 vertebrae and their IVDs. A future study including patients with and without osteoporotic vertebral fractures has to confirm the results of the present study. Second, although correlation coefficients for FSUs were indicative of stronger associations with FEA-based failure loads, there were no statistically significant differences compared to the correlation coefficients of single vertebrae. This may be due to the small cohort size, with future studies in larger samples being mandatory to achieve higher statistical power. Third, we used MDCT data that was acquired after administration of an intravenous contrast agent. In this regard, previous work has shown that for TA, significant correlations between texture parameters derived from the same MDCT system with and without contrast agents exist (35). Yet, a study using non-contrast-enhanced MDCT for FEA and TA should follow the results of the present study. Fourth, in the current study the FEA-based failure loads for FSUs are lower compared to individual vertebrae; thus, further studies are needed to analyze and quantify the effect of IVDs on the FEA-predicted failure load value of the FSU models.

Conclusions

This study provides evidence for the utility of TA in MDCT data of the spine for the assessment of FEA-derived failure loads of FSUs. Texture parameters predicted failure loads of FSUs as a more realistic in-vivo scenario equally well as compared to single vertebrae analyses.

Acknowledgments

Funding: This work was supported by the German Research Foundation (Deutsche Forschungsgemeinschaft, DFG; project 432290010, JSK & TB), the German Society of Musculoskeletal Radiology (Deutsche Gesellschaft für Muskuloskelettale Radiologie, DGMSR; NS & MD), the SGP Healthcare Fund, PIE-SGP-HC-2019-01 (Thrust 3-2; KS), and the B. Braun Foundation (project BBST-D-19-00106, NS).

Footnote

Conflicts of Interest: All authors have completed the ICMJE uniform disclosure form (available at http://dx.doi.org/10.21037/qims-20-1156). Dr. JSK reports grants from European Research Council (ERC, grant agreement No 637164), grants from Deutsche Forschungsgemeinschaft, project 432290010, during the conduct of the study; personal fees from Philips Healthcare, outside the submitted work. The other authors have no conflicts of interest to declare.

Ethical Statement: This retrospective study was approved by the local institutional review board and was conducted in accordance with the Declaration of Helsinki. The requirement for written informed consent was waived due to the study’s retrospective character.

Open Access Statement: This is an Open Access article distributed in accordance with the Creative Commons Attribution-NonCommercial-NoDerivs 4.0 International License (CC BY-NC-ND 4.0), which permits the non-commercial replication and distribution of the article with the strict proviso that no changes or edits are made and the original work is properly cited (including links to both the formal publication through the relevant DOI and the license). See: https://creativecommons.org/licenses/by-nc-nd/4.0/.

References

1. Cooper C, Campion G, Melton LJ 3rd. Hip fractures in the elderly: a world-wide projection. Osteoporos Int 1992;2:285-9. [Crossref] [PubMed]
2. Reginster JY, Burlet N. Osteoporosis: a still increasing prevalence. Bone 2006;38:S4-9. [Crossref] [PubMed]
3. Compston JE, McClung MR, Leslie WD. Osteoporosis. Lancet 2019;393:364-76. [Crossref] [PubMed]
4. NIH Consensus Development Panel on Osteoporosis Prevention Diagnosis and Therapy. Osteoporosis prevention, diagnosis, and therapy. JAMA 2001;285:785-95. [Crossref] [PubMed]
5. Consensus development conference. diagnosis, prophylaxis, and treatment of osteoporosis. Am J Med 1993;94:646-50. [Crossref] [PubMed]
6. Hallberg I, Bachrach-Lindstrom M, Hammerby S, Toss G, Ek AC. Health-related quality of life after vertebral or hip fracture: a seven-year follow-up study. BMC Musculoskelet Disord 2009;10:135. [Crossref] [PubMed]
7. Tarride JE, Burke N, Leslie WD, Morin SN, Adachi JD, Papaioannou A, Bessette L, Brown JP, Pericleous L, Muratov S, Hopkins RB. Loss of health related quality of life following low-trauma fractures in the elderly. BMC Geriatr 2016;16:84. [Crossref] [PubMed]
8. Bliuc D, Nguyen ND, Milch VE, Nguyen TV, Eisman JA, Center JR. Mortality risk associated with low-trauma osteoporotic fracture and subsequent fracture in men and women. JAMA 2009;301:513-21. [Crossref] [PubMed]
9. Bliuc D, Nguyen ND, Nguyen TV, Eisman JA, Center JR. Compound risk of high mortality following osteoporotic fracture and refracture in elderly women and men. J Bone Miner Res 2013;28:2317-24. [Crossref] [PubMed]
10. Center JR, Nguyen TV, Schneider D, Sambrook PN, Eisman JA. Mortality after all major types of osteoporotic fracture in men and women: an observational study. Lancet 1999;353:878-82. [Crossref] [PubMed]
11. Kanis JA, Johnell O, De Laet C, Johansson H, Oden A, Delmas P, Eisman J, Fujiwara S, Garnero P, Kroger H, McCloskey EV, Mellstrom D, Melton LJ, Pols H, Reeve J, Silman A, Tenenhouse A. A meta-analysis of previous fracture and subsequent fracture risk. Bone 2004;35:375-82. [Crossref] [PubMed]
12. Melton LJ 3rd, Atkinson EJ, Cooper C, O'Fallon WM, Riggs BL. Vertebral fractures predict subsequent fractures. Osteoporos Int 1999;10:214-21. [Crossref] [PubMed]
13. Cooper C, Atkinson EJ, O'Fallon WM, Melton LJ 3rd. Incidence of clinically diagnosed vertebral fractures: a population-based study in Rochester, Minnesota, 1985-1989. J Bone Miner Res 1992;7:221-7. [Crossref] [PubMed]
14. Haczynski J, Jakimiuk A. Vertebral fractures: a hidden problem of osteoporosis. Med Sci Monit 2001;7:1108-17. [PubMed]
15. Kanis JA. Diagnosis of osteoporosis and assessment of fracture risk. Lancet 2002;359:1929-36. [Crossref] [PubMed]
16. Kanis JA. Diagnosis of osteoporosis. Osteoporos Int 1997;7:S108-16. [Crossref] [PubMed]
17. Löffler MT, Sollmann N, Mei K, Valentinitsch A, Noël PB, Kirschke JS, Baum T. X-ray-based quantitative osteoporosis imaging at the spine. Osteoporos Int 2020;31:233-50. [Crossref] [PubMed]
18. Ammann P, Rizzoli R. Bone strength and its determinants. Osteoporos Int 2003;14:S13-8. [Crossref] [PubMed]
19. Schuit SC, van der Klift M, Weel AE, de Laet CE, Burger H, Seeman E, Hofman A, Uitterlinden AG, van Leeuwen JP, Pols HA. Fracture incidence and association with bone mineral density in elderly men and women: the Rotterdam Study. Bone 2004;34:195-202. [Crossref] [PubMed]
20. Kanis JA, Hans D, Cooper C, Baim S, Bilezikian JP, Binkley N, et al. Interpretation and use of FRAX in clinical practice. Osteoporos Int 2011;22:2395-411. [Crossref] [PubMed]
21. Kanis JA, Johnell O, Oden A, Johansson H, McCloskey E. FRAX and the assessment of fracture probability in men and women from the UK. Osteoporos Int 2008;19:385-97. [Crossref] [PubMed]
22. Brett AD, Brown JK. Quantitative computed tomography and opportunistic bone density screening by dual use of computed tomography scans. J Orthop Translat 2015;3:178-84. [Crossref] [PubMed]
23. Engelke K. Quantitative Computed Tomography-Current Status and New Developments. J Clin Densitom 2017;20:309-21. [Crossref] [PubMed]
24. Allaire BT, Lu D, Johannesdottir F, Kopperdahl D, Keaveny TM, Jarraya M, Guermazi A, Bredella MA, Samelson EJ, Kiel DP, Anderson DE, Demissie S, Bouxsein ML. Prediction of incident vertebral fracture using CT-based finite element analysis. Osteoporos Int 2019;30:323-31. [Crossref] [PubMed]
25. Anitha D, Mei K, Dieckmeyer M, Kopp FK, Sollmann N, Zimmer C, Kirschke JS, Noel PB, Baum T, Subburaj K. MDCT-based Finite Element Analysis of Vertebral Fracture Risk: What Dose is Needed? Clin Neuroradiol 2019;29:645-51. [Crossref] [PubMed]
26. Anitha D, Subburaj K, Mei K, Kopp FK, Foehr P, Noel PB, Kirschke JS, Baum T. Effects of dose reduction on bone strength prediction using finite element analysis. Sci Rep 2016;6:38441. [Crossref] [PubMed]
27. Groenen KHJ, Bitter T, van Veluwen TCG, van der Linden YM, Verdonschot N, Tanck E, Janssen D. Case-specific non-linear finite element models to predict failure behavior in two functional spinal units. J Orthop Res 2018;36:3208-18. [Crossref] [PubMed]
28. Anitha DP, Baum T, Kirschke JS, Subburaj K. Effect of the intervertebral disc on vertebral bone strength prediction: a finite-element study. Spine J 2020;20:665-71. [Crossref] [PubMed]
29. Bevill G, Keaveny TM. Trabecular bone strength predictions using finite element analysis of micro-scale images at limited spatial resolution. Bone 2009;44:579-84. [Crossref] [PubMed]
30. Dall'Ara E, Pahr D, Varga P, Kainberger F, Zysset P. QCT-based finite element models predict human vertebral strength in vitro significantly better than simulated DEXA. Osteoporos Int 2012;23:563-72. [Crossref] [PubMed]
31. Stadelmann MA, Schenk DE, Maquer G, Lenherr C, Buck FM, Bosshardt DD, Hoppe S, Theumann N, Alkalay RN, Zysset PK. Conventional finite element models estimate the strength of metastatic human vertebrae despite alterations of the bone's tissue and structure. Bone 2020;141:115598 [Crossref] [PubMed]
32. Muehlematter UJ, Mannil M, Becker AS, Vokinger KN, Finkenstaedt T, Osterhoff G, Fischer MA, Guggenberger R. Vertebral body insufficiency fractures: detection of vertebrae at risk on standard CT images using texture analysis and machine learning. Eur Radiol 2019;29:2207-17. [Crossref] [PubMed]
33. Valentinitsch A, Trebeschi S, Kaesmacher J, Lorenz C, Loffler MT, Zimmer C, Baum T, Kirschke JS. Opportunistic osteoporosis screening in multi-detector CT images via local classification of textures. Osteoporos Int 2019;30:1275-85. [Crossref] [PubMed]
34. Lubner MG, Smith AD, Sandrasegaran K, Sahani DV, Pickhardt PJ. CT Texture Analysis: Definitions, Applications, Biologic Correlates, and Challenges. Radiographics 2017;37:1483-503. [Crossref] [PubMed]
35. Mookiah MRK, Rohrmeier A, Dieckmeyer M, Mei K, Kopp FK, Noel PB, Kirschke JS, Baum T, Subburaj K. Feasibility of opportunistic osteoporosis screening in routine contrast-enhanced multi detector computed tomography (MDCT) using texture analysis. Osteoporos Int 2018;29:825-35. [Crossref] [PubMed]
36. Mannil M, Eberhard M, Becker AS, Schonenberg D, Osterhoff G, Frey DP, Konukoglu E, Alkadhi H, Guggenberger R. Normative values for CT-based texture analysis of vertebral bodies in dual X-ray absorptiometry-confirmed, normally mineralized subjects. Skeletal Radiol 2017;46:1541-51. [Crossref] [PubMed]
37. Xiao Z, Wang L, Gong H, Zhu D, Zhang X. A non-linear finite element model of human L4-L5 lumbar spinal segment with three-dimensional solid element ligaments. Theoretical and Applied Mechanics Letters 2011;1:064001 [Crossref]
38. Panagiotopoulou O. Finite element analysis (FEA): applying an engineering method to functional morphology in anthropology and human biology. Ann Hum Biol 2009;36:609-23. [Crossref] [PubMed]
39. Engelke K, Libanati C, Fuerst T, Zysset P, Genant HK. Advanced CT based in vivo methods for the assessment of bone density, structure, and strength. Curr Osteoporos Rep 2013;11:246-55. [Crossref] [PubMed]
40. Carpenter RD. Finite element analysis of the hip and spine based on quantitative computed tomography. Curr Osteoporos Rep 2013;11:156-62. [Crossref] [PubMed]
41. Crawford RP, Cann CE, Keaveny TM. Finite element models predict in vitro vertebral body compressive strength better than quantitative computed tomography. Bone 2003;33:744-50. [Crossref] [PubMed]
42. Imai K, Ohnishi I, Bessho M, Nakamura K. Nonlinear finite element model predicts vertebral bone strength and fracture site. Spine (Phila Pa 1976) 2006;31:1789-94. [Crossref] [PubMed]
43. Zysset PK, Dall'ara E, Varga P, Pahr DH. Finite element analysis for prediction of bone strength. Bonekey Rep 2013;2:386. [Crossref] [PubMed]
44. Wang X, Sanyal A, Cawthon PM, Palermo L, Jekir M, Christensen J, Ensrud KE, Cummings SR, Orwoll E, Black DM. Osteoporotic Fractures in Men Research G, Keaveny TM. Prediction of new clinical vertebral fractures in elderly men using finite element analysis of CT scans. J Bone Miner Res 2012;27:808-16. [Crossref] [PubMed]
45. Mookiah MRK, Baum T, Mei K, Kopp FK, Kaissis G, Foehr P, Noel PB, Kirschke JS, Subburaj K. Effect of radiation dose reduction on texture measures of trabecular bone microstructure: an in vitro study. J Bone Miner Metab 2018;36:323-35. [Crossref] [PubMed]