A denoising and enhancing method framework for 4D ultrasound images of human fetal heart

Introduction

Ultrasound examination has long been widely used in clinical diagnosis, and is the top choice in prenatal examination due to its non-radiating property. Prenatal evaluation of the fetal heart is a standard procedure in a pregnancy, and is necessary to detect congenital heart malformations such as the hypoplastic left heart syndrome and the Tetralogy of Fallot. Congenital heart malformations occur to 0.6–1.9% of the population, and detection can enable decision making and disease management. Because the fetal heart is very small and the interrogating ultrasound need to pass through much body tissues (both maternal and fetal), fetal ultrasound images tended to have higher noise and lower contrast, making evaluation and diagnosis a challenge even for experienced physicians. Advancements in image processing methods for fetal ultrasound images is thus important.

Denoising and enhancing are two main ways of image processing fetal ultrasound images. The process of denoising aims to remove speckle noise and smooth artifact differences as much as possible. The aims of enhancing can vary with different applications. For example, it could aim to distinguish regions of different tissue types, or to highlight regions of specific organs or tissues, etc. In computer assisted fetal heart assessment based on 3D geometrical model, enhancing is useful for distinguishing the myocardium from other tissues such as blood.

Among current ultrasound image processing methods, denoising methods related to the non-local means (NLM) approach and enhancing methods related to the contrast limited adaptive histogram equalization (CLAHE) method are commonly used. In NLM, a small image patch around a pixel is used to search for similarity information in a large search window, and this information is used to heighten the image quality in the pixel. As for CLAHE, it can limit noise amplification effectively. However, in our current study, we found these methods can still be improved. Here, we proposed a new denoising and enhancing method framework inspired by the NLM and CLAHE methods, and demonstrate these improvements.

Related works

Medical image denoising

For image denoising, there are several classical filter methods, such as median filter (1), Wiener filter (2,3), mean filter (4), Gaussian filter (5), and Fourier transform (6). A widely used method is the Non-Local Means (NLM) (7), which improves image quality via searching for useful information within the same image. Several variants of NLM have been developed (8-11). In addition, several state-of-the-art methods have been proposed, each having a different denoising effect. For example, Dabov et al. proposed an image restoration technique exploiting regularized inversion and the recent block-matching and 3D filtering (BM3D) denoising filter (12); Zoran et al. proposed a concept of Expected Patch Log Likelihood (EPLL) to improve image quality (13); Gu et al. studied the weighted nuclear norm minimization (WNNM) problem and applied this algorithm to image denoising by exploiting the image nonlocal self-similarity (14); Dong et al. introduced the concept of sparse coding noise and proposed a nonlocally centralized sparse representation (NCSR) model to implement image denoising (15); Yang et al. improved Non-Local Means with local statistics(NLMLS) for ultrasound images (16); Ai et al. proposed an adaptive non-local means (ANLM) method for speckle reduction in ultrasound images (17); Yu et al. proposed an ultrasound image denoising method based on fuzzy logic (FL) (18). Further, recently, an increasing number of deep learning based denoising methods have been proposed, such as Kokil's deep residual learning method (19), Liao’s features combination migration method (20) and Cao’s method for nonalcoholic fatty liver disease (21).

Medical image enhancing

Progress has also been made in image enhancing methods. In the early stage, several classical methods were proposed, such as histogram equalization (HE) (22), log transformation (LT) (23), and gamma transformation (GT) (24). Later, contrast limited adaptive histogram equalization (CLAHE) (25) was proposed and has since been widely used, but the need to reduce noise amplification has limited this method’s contrast amplification. In recent years, several state-of-the-art methods were reported. For example, Shan et al. proposed a globally optimized linear windowed tone mapping (GOLWT) method to enhance image and preserve image structures (26); Deng proposed a generalized unsharp masking (GUM) algorithm using the exploratory data model as a unified framework (27); Researchers also proposed several low-light image oriented enhancing methods (28,29); Demirel et al. proposed an image contrast enhancement technique based on singular value decomposition and discrete wavelet transform (SVD-DWT) (30). However, although deep learning is increasingly widely used, there are few ultrasound image enhancement methods based on deep learning. One such method is Mishra's structure oriented adversarial network (31).

Methods

From above methods we can see that researchers have made much valuable contribution to ultrasound image denoising and enhancing. However, it is unclear if they are suitable for fetal heart ultrasound images, such as that from 4D imaging mode (Spatial Temporal Image Correlation or STIC mode) (32). In this paper, we test a wide range of denoising and enhancing techniques of clinical ultrasound images of fetal hearts to investigate their effectiveness. We further propose novel strategies to improve results, via a special method framework containing both denoising and enhancing. Clinical ultrasound images of human fetal hearts were obtained from the National University Hospital, Singapore, under the approved Domain Specific Review Board (DSRB) protocol number 2014/00056. Informed consent was sought from all participants. Fetal ultrasound images were obtained in the STIC mode, which provided 4D images, and details of theses scans are described previously. Images for 3 fetal subjects were obtained and analyzed.

In our experiment, 4D ultrasound images of human fetal heart are utilized as experimental data. 4D Ultrasound images were acquired using the Voluson 730 ultrasound machine with the RAB 4-8L transducer (GE Healthcare, Chicago, IL, USA), under the Spatio-Temporal image Correlation (STIC) mode. STIC imaging were acquired with the four chamber view on screen, and STIC sweep occurred over 10–15 seconds, with an image capture rate of 70–90 frames per second, thus giving 29–37 volumes for 1 cardiac cycle. The images were extracted by the 4DView software (GE Healthcare, Chicago, IL, USA), and a stack of 30–40 image slices parallel to the four-chamber view was exported from the volumetric images at each time pint, spaced at 0.5mm apart. The images are 21+ weeks gestation.

Image denoising for 4D ultrasound image of human fetal heart

For general image denoising research, the noise models are always additive, and can be modelled as

v=u+n[1]

where v is observed image; n is clean image and n is additive noise. Such models are often used in denoising research of medical images such as those from the CT. however, this is not suitable for ultrasound images, which has not only additive noise but also speckle noise in the image. Speckle noise is multiplicative noise, and can be modelled as

v=m×u+n[2]

where m is the multiplicative component of noise.

4D ultrasound images have both time sequence (dimension) and space sequence (dimension). most images has two spatially neighboring images (blue frames in Figure 1) and two temporally neighboring images (green frames in Figure 1). Our denoising method takes full advantage of this characteristic, by utilizing these four neighbor images as reference images.

Figure 1 Adjacent relationship about reference images in 4D ultrasound image sequence.

Our denoising method was inspired by the NLM method (7). We adopted this approach as NLM has superior edge-preserving filtering algorithm which fully considers self-similar property of image and makes full use of the redundant information of the image. It can also retain detailed characteristic in the image when denoising. In NLM, a small image patch around a pixel is used to search for similarity information in a large search window to calculate the noise-free intensity in the pixel.

When we apply NLM to denoise fetal heart ultrasound image without consideration of images in neighboring time points and slices, we find that the denoising effect is not sufficiently strong. As shown in Figure 2, after denoising by NLM method with different filter coefficients, h, there is still laminar artifact noise (such as in the purple rectangle in Figure 2 even after denoising). This may be because there is not sufficient self-similar information within the image.

Figure 2 Denoised ultrasound image by NLM method.

However, we can see that the target image is similar to the two temporally neighboring images and the two spatially neighboring images. There is much mutual-similar information in these neighboring images. Therefore, we propose a 4D-NLM denoising method that will take advantage of the contextual information in these neighboring sequences of images. Let the search window have dimensions of n × n and the kernel window have dimensions of n × n (Figure 3A). In our method, for each pixel in the target image, there will be 4 search windows with m × m pixels at the corresponding pixel position in the temporally and spatially neighboring images (as shown in Figure 3B).

Figure 3 Search window and neighborhood window. (A) In the search window, the orange point is the target pixel; the blue box is the neighborhood window; the green point is the center pixel of neighborhood window. (B) 4 search windows at the corresponding positions of 4 neighbor images.

In our method, we need to calculate 4 different weights in 4 neighboring images. To calculate the weight in one of these images, we need to obtain the Euclidean distance, which we model as follows,

E=‖v(Ni)−v(Nj)‖2,a2[3]

where N_K denotes a square neighborhood of fixed size and centered at a pixel K, and a is the standard deviation of the Gaussian kernel. We use neighborhood variance to represent the Euclidean distance.

Consider the K-th neighbor image, where there is a pixel P in the search window whose grayscale value is S. All the pixel grayscale values in the neighborhood window, whose center is at P, can be expressed as ti,i∈[1,n2]. So, the cumulative variance for P will be:

ek=∑i=1n2(s−ti)2[4]

For all the 4 search windows, the cumulative variances for pixels with the same position coordinates can be calculated as the average cumulative variance

e=∑k=14ek/4[5]

Traversing the entire search window domain, the average cumulative variance of each pixel with same position coordinates can be obtained.

Next, we can calculate the similarity between the central pixel and each neighborhood window in a search window. In our method, this similarity is expressed by a weight represented by the Euclidean distance. We calculate the neighborhood variance for each pixel in each search window. For a pixel _P in a search window, its neighborhood variance is

eP=en2[6]

Considering that we use the neighborhood variance to represent the Euclidean distance, we will obtain

eP=‖v(Ni)−v(Nj)‖2,a2[7]

and the Gaussian weight can be denoted as

WG=e−‖u(Ni)−u(Nj)‖2,a2h2[8]

where u is the hypothetical noise-free image. We do not have clean images, but the application of the Euclidean distance to the noisy neighborhoods raises the following equality,

‖v(Ni)−v(Nj)‖2,a2=‖u(Ni)−u(Nj)‖2,a2+2σ2[9]

By combining equations (9) and (10), we can obtain the Gaussian weight

WG=exp(2σ2−ePh2)[10]

where $\sigma$ is the Gaussian standard deviation and h is the filter coefficient. We can use h and $\sigma$ to control the decay of the exponential function so that we can obtain the most suitable Gaussian weight. For the j-th pixel in a search window, we can use Eq. [10] to calculate its Gaussian weight WGj,j∈[1,m2]. We can then obtain the normalization coefficient N=∑j=1m2WGj, which is the sum of all Gaussian weights, and obtain the similarity between the central pixel and the j-th pixel in a search window as

$$W_j=\frac{W_{Gj}}{N}$$[11]

For the k-th adjacent image, its corresponding central ^{pixel value is}sk=∑j=1m2Wjsj^{, whereS_j is thej-th pixel value in} search window. The final grayscale value of the central pixel can be calculated from all the 4 adjacent images

$$s^{\prime }=\sum _{k=1}^4{s}_k/4$$[12]

Image enhancing for 4D ultrasound image of human fetal heart

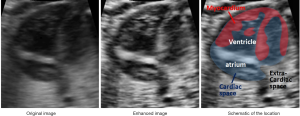
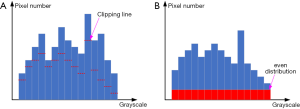
Our enhancing method was inspired by the CLAHE method (25), and we call it the Adaptive Clipping for Each Histogram Pillar (ACEHP) method. We developed this because we found that in our enhancing experiment of human fetal heart ultrasound images, there is room for improving the CLAHE method in terms of distinguishing between the cardiac region (inclusive of the myocardium and luminal spaces) and the other (extra-cardiac) regions. As shown in Figure 4, the boundary between the pericardial boundaries are noisy and pocketed with black spaces, while extra-cardiac regions have very similar appearances to myocardial spaces. CLAHE cannot achieve sufficient distinction the cardiac and non-cardiac regions.

Figure 4 Enhanced ultrasound image by CLAHE method and indicative schematic of the location of the cardiac space and features in it.

In ACEHP, the grayscale histogram H of the whole image is first constructed. Then the histogram will be clipped by Otsu threshold strategy (33). For an image with a size of M × N, the number of pixels whose grayscale values are smaller than threshold T is denoted as N₀ and whose grayscale values are larger than T is denoted as N₁. So, the corresponding probabilities of two pixel category are

ω0=N0M×N[13]

ω1=N1M×N[14]

where ω0+ω1=1 and N0+N1=M×N. Let μ0 be the average grayscale value of the pixels corresponding to ω0 and μ1 be the average grayscale value of the pixels corresponding to ω1. The interclass variance will then be

g=ω0ω1(μ0μ1)2[15]

We can obtain the Otsu threshold T when g is the maximal value. The clipping length for the i-th histogram pillar based on T will be

CLi=HiiT[16]

where i is the grayscale value and H_i is the corresponding grayscale histogram height. The residual length of this histogram pillar will then be

Hir=Hi−CLi[17]

When H_i is less than CL_i, Hir is set to be 0 to avoid the problem of it becoming negative. That means that the histogram will lose some pillar, especially in the higher levels of grayscale. However, this is advantageous to image enhancement because it can highlight the regions of interest (ROI). Enhanced results were shown in section “Human fetal heart ultrasound image enhancing”. However, if these clipped histogram pillars are eliminated, the image will integrally become darker. To solve this problem, our method evenly distributes all the clipped histogram pillars to all gray levels (as shown in Figure 5). Then we can obtain the final histogram

Figure 5 Adaptive histogram clipping. (A) histogram pillars higher than the red line are clipped. (B) final histogram with the evenly distributed clipped grayscale components.

$${H^{\prime }}_i=H_i{}^r+{\displaystyle \sum _{i=0}^{255}C{L}_i}/r$$[18]

where r is number of gray levels (for gray level ultrasound image, r=256).

Based on the new histogram $H_i{}^{\prime }$, we can obtain the cumulative frequency for each gray level. Assume that n_i is the number of pixels corresponding to the i-th gray level and n is the total number of pixels of the entire image. The grayscale cumulative frequency for each gray level is

$$\{\begin{array}{l}{P}_i=\frac{n_i}{n},i=0\hfill \\ P_i=P_{i-1}+\frac{n_i}{n},0<i<r\hfill \end{array}$$[19]

Therefore, we can define a grayscale mapping function

si=L×Pi[20]

where a is the maximum value of the gray level in the grayscale histogram. Finally, each gray level can be mapped to a new gray level and an enhanced ultrasound image can be obtained.

Results

Because we did not have training data, we could not implement deep learning methods for comparison with other methods, and as such, we kept to non-machine learning methods.

Human fetal heart ultrasound image denoising

To verify our method’s effectiveness, we compared it to several classical and state-of-the-art methods [NLM (7), median filter (1), Wiener filter (2,3), mean filter (4), Gaussian filter (5), Fourier transform (6), BM3D (12), EPLL (13), NCSR (14), WNNM (15), NLMLS (16), ANLM (17) and FL (18)]. In general, the denoising result will be better if the search window is larger, however the time efficiency will be reduced. For NLM, NLMLS, ANLM and our method (4D-NLM), we adopt the search window size of 21×21 pixels and the neighborhood window size of 7×7 pixels as a balance between denoising strength and time efficiency (7). The window size of mean filter, median filter and Gaussian filter were 7×7. The window size of Wiener filter was 5×5. The search window size of BM3D was 21×21. The number of iterations of NCSR and WNNM were both 5. The a in FL was −0.7, and the Gaussian standard deviation and filter coefficient of NLM, NLMLS and our method (4D-NLM) were 0.8 and 20. These parameters were all set to the original papers' recommended values. Under these parameter values, better result can be achieved.

Results are shown in Figure 6. Visually, we can observe that the original ultrasound image of human fetal heart has much noise, and that after being blurred by the median filter, the image is smoother but still has much noise. Using mean filter and Gaussian filter appear to eliminate most of the noise, but the feature edges also becomes blurred, indicating that useful information in the image is removed. Fourier transform and Wiener filter are better than other classical methods, but results are still not smooth enough. We can see that classical denoising methods are not very effective to the human fetal heart ultrasound images. The state-of-the-art methods generally performed better at denoising than classical methods. Compared with our proposed method, EPLL method and WNNM method have the similar denoising effect, but both of them have blurred edge; while NLM method, BM3D method and NCSR method have more noise. We tested two improved NLM algorithm, ANLM and NLMLS, but they also resulted in more noise than our method. FL can make image smoother in the regions of interest (ROI), but the contrast has changed. Our proposed method can effectively utilize the information of neighborhood images, so it has less noise and clearer edges.

Figure 6 Denoising results by different methods.

To validate these visual observations and formally evaluate denoising effects, we adopted the “method noise” strategy to quantify improvements (34). Method noise is an established evaluation technique that is particularly useful where there is no reference image for calculating noise parameters. Method noise is defined as the difference between original image and denoised image

n^i=xi−yi+M[21]

where i is the index of pixel; x_i and y_i denote the pixel value of original and denoised image; M is a constant to promote result image of method noise easier to observe.

Method noise has two main functions. Firstly, it can evaluate how much noise has been removed, as the resulting image contains all noise removed by denoising. If the resulting image is uniform, less noise has been removed and if the result image is noisy, more noise has been removed. Secondly, it can also be used to evaluate whether the denoising process removed structural information, by observing whether the resulting image contains the structures of the original image. A good denoising method should not remove such structures from the image. If method noise result contains these structures (such as edges and outlines), these details of original image are lost after denoising and the denoising method is not desirable.

Figure 7 shows the method noise result images of different approaches. We can see that different methods resulted in different residual pixel method noise intensities. EPLL method, WNNM method, NLM method and our proposed 4D-NLM method can generate better method noise result images (residual pixels intensity level can be ranked as: 4D-NLM>NLM>WNNM>EPLL>other methods). From the global perspective, the result image by 4D-NLM method contains more uniform residual pixels than all other methods, suggesting more uniform denoising. Improved NLM algorithm, ANLM and NLMLS, resulted in less edges and outlines, however these two methods have lower residual pixels intensities. Furthermore, the result image of NLM and FL methods contain obvious edge and outline, which means a lot of original image information is lost after denoising. On the other hand, the result image of our 4D-NLM method contains hardly any edge and outline, demonstrating that it retains more structural information than NLM.

Figure 7 Method noise result images by different approaches.

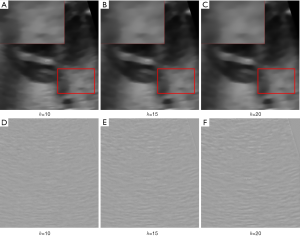
For 4D-NLM, filter coefficient (h) has a great effect on the smoothness of the image. The denoising results with different filter coefficients are shown in Figure 8. Form Figure 8A,B,C we can see that when the filter coefficient is 20, the image is the smoothest. And according to Figure 8D,E,F, method noise analysis show that when filter coefficient is 20, the most noise is removed and the edge information are preserved well. However, when filter coefficient increases, the run time of 4D-NLM will increase significantly. To balance the run time and denoising effect, we recommend a filter coefficient of 20.

Figure 8 Denoising results (A,B,C) of 4D-NLM with different filter coefficients and corresponding method noise results (D,E,F).

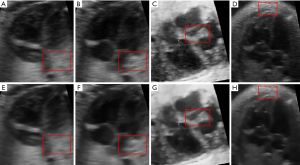
In order to prove the versatility of our method, we also used 4 different images for comparison (as shown in Figure 9). Figure 9A,B,C,D are original images before denoising (Figure 9B is from another imaging plane but at the same time point as Figure 9A, while Figure 9C and Figure 9D are selected from two further different datasets.). We can see there is much speckle noise in these original images. In particular, Figure 9C has more speckle noises than others in ventricle. The overall intensity of Figure 9D is very low, making it more difficult to process its noise. After denoising by 4D-NLM method, we can obtain clearer result image (Figure 9E,F,G,H). This experiment show that our method is effective for different ultrasound images of human fetal hearts. For easy observation, we selected a brighter part of the image as the test region.

Figure 9 Original images and result images denoised by 4D-NLM. (A,B,C,D) are original images and (E,F,G,H) are denoising results. The red box is focused region.

We use CNR to evaluate image quality, computed as

CNR=x¯ROI−x¯bgσbg[22]

where x¯ROI is the average pixel value inside the regions of interest (ROI); x¯bg is the average pixel value inside the background and σbg is the standard deviation in the surrounding background. The standard deviation of image can be computed as

σ=1M×N∑i=1M∑j=1N(P(i,j)−μ)2[23]

where M and N are the width and height of image; P(i,j) is corresponding pixel value and µ is the average pixel value ^{of image. When calculating}σbg^{, we only need to remove} ROI from the image.

To quantify which method is better able to retain structure information during denoising, we introduced the sharpness metric based on histogram of strong edge width (HSEW) (35). This method is based on edge information. It has low computational complexity, fast calculation speed and good independence from image content. The main computing procedure is as follows.

For image f, the horizontal and vertical gradient map can be expressed as G_x and G_y respectively.

Gx=Sx∗f[24]

Gy=Sy∗f[25]

where S_x is the horizontal gradient Sobel operator and S_y is the vertical gradient Sobel operator. Then we can obtain the horizontal binary image B_x and vertical binary image B_y with strong edge.

{Bx(i,j)={1,Gx2(i,j)>ξx0,Gx2(i,j)≤ξxBy(i,j)={1,Gy2(i,j)>ξy0,Gy2(i,j)≤ξy[26]

{ξx=4MN∑i=1M∑j=1NGx2(i,j)ξy=4MN∑i=1M∑j=1NGy2(i,j) [27]

where (i,j) denotes the pixel coordinates; ξx and ξy are horizontal and vertical thresholds; _M and _N are width and height of image. Then, we calculate the widths of strong edges by locating them from the binary image, and obtaining the maximum distance across the edges. Let ℵ be the total number of strong edges and ℵi is the number of strong edges with the width of w_i, the probability of strong edge with width w_i is thus

p(wi)=ℵiℵ[28]

We can then calculate the distance factor of strong edge width, d(w_i) as

d(wi)={(wiwm)2,wi<wm1,wi=wm(we−wiwe−wm)2,wi>wm[29]

where w_m denotes edge width with the maximum probability; w_e denotes the largest edge width. Finally, the sharpness metric is

Metric=∑wowed(wi)p(wi)wi[30]

where w_o is the minimum edge width. This method expresses that if Metric is smaller, the image is clearer.

Table 1 shows the CNR values and HSEW values of denoising result images by different methods. Image-1 is Figure 9A and Image-2 is Figure 9C. From Table 1 we can see that 4D-NLM has better CNR and HSEW than not only traditional methods (BM3D, EPLL, NCSR and Wiener filter), but methods based on NLM (NLM, ANLM, NLMLS). We can also see that the Gaussian filter has higher CNR, but it also has higher HSEW. This means Gaussian filter destroys edge information in the image during noise removal. Similarly, although FL has higher CNR (for Image-1 and Image-2) and lower HSEW (for Image-2) than 4D-NLM, the visual denoising effect of this method is not satisfactory (as shown in Figure 6, the noisy region is enhanced). Therefore, combining Table 1 and Figure 6, 4D-NLM can generate better denoising effect than the other methods mentioned. We also tested the average CNR and HSEW values for two large image sets (each set has 100 ordinary fetal heart ultrasound images), the similar parameter performance can be seen.

Table 1 Comparison of image quality measures after denoising
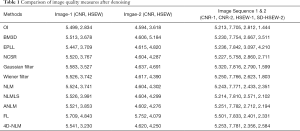
Full table

Human fetal heart ultrasound image enhancing

In this experiment, original image (OI) and the image denoised by 4D-NLM are used as the input images to test various enhancing approaches. Several classical and state-of-the-art enhancing methods were compared to our proposed method. These methods include histogram equalization (HE) (22), contrast limited adaptive histogram equalization (CLAHE) (25), log transformation (LT) (23), gamma transformation (GT) (24), GOLWT (26), GUM (27), BIMEF (28), CETLLI (29), LLIE (36) and SVDDWT (30). In the gamma transformation, the gamma value was 0.4. All other methods use the default parameters in their respective publications.

As shown in Figure 10, for four experimental groups with different input images, HE and CLAHE methods improve the contrast, but amplify the noise, such that the cardiac regions appear very similar to extra-cardiac regions. With log transformation, the whole image becomes brighter but the edge becomes blurred. The result of grayscale stretching is high contrast effect but serious amplification of noise. The same goes for BIMEF and CETLLI methods. SVDDWT method also amplifies noise. Gamma transformation, LLIE, GUM and GOLWTM methods generate obvious less contrast enhancing effect than other methods. Our enhancing method (ACEHP) is found to keep low-noise level while creating cleaner pericardial boundaries. It also enhances the distinction between the fetal heart regions and extra-cardiac regions by homogenizing extra-cardiac regions. We can see the left part of image enhanced by HE, it has artefact. But image enhanced by ACEHP does not have these problems. On the other hand, the HE has artefacts and noise in the bottom right corner of the image. That means that when we use these images to implement 3D volume rendering, the results will not be good enough.

Figure 10 Enhancing results by different method combinations.

To validate visual observations, we used entropy to gauge the enhancement. Entropy is a measurement of information uncertainty and is calculated by

E=−∑i=0255HiMlog2HiM[31]

where M denotes the pixel number of image and H_i is the corresponding grayscale histogram height of the i-th grayscale. A large entropy indicates more random and disordered information in the image, while a smaller entropy indicates clearer classification of information in the image. A small entropy value will also imply clearer distinguishing of various regions in the image. Table 2 shows the entropy values of different methods' enhancing result images. We can see that the entropy value of our method (ACEHP) performed better than other methods examined.

Table 2 Entropy values of result images after enhancing
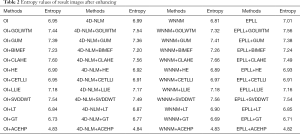
Full table

Volume rendering for human fetal heart ultrasound image

Our aim is distinguishing the human fetal cardiac region and non-cardiac regions via denoising and enhancing process, so that other important image processing steps like image registration, tissue movement tracking, etc. can be better implemented. Based on the image sets of several different human fetus, we utilized 3D volume rendering (under a same transfer function) to evaluate the processing effect of different means (denoising + enhancing). In this experiment, we selected several method combinations with well denoising and enhancing effect as the comparing methods.

As shown in Figure 11, in the volume rendering for original image set, it is difficult to find out the cardiac region and obvious boundary. In the volume rendering for processed image sets via “BM3D+GOLWTM” method combination and “median filter+GOLWTM” method combination, the cardiac lumen region is very unclear. For the images processed via "EPLL+GUM" and "NCSR+GUM" combinations, we can see relatively complete cardiac lumen region by volume rendering, however, the boundaries are not very neat. “Gaussian filter+CLAHE” and “Wiener filter+CLAHE” method combinations can also generate relatively clear cardiac lumen, however, noise level remained high. “WNNM+CETLLI” and “Gaussian filter+CETLLI” method combinations has similar problems as “BM3D+GOLWTM” and “median filter+GOLWTM” in being unable to generate the cardiac lumen region. But on top of this, the boundary generated are less sharp. In the volume rendering for processed image sets via our method combination "4D-NLM+ACEHP", the cardiac region and non-cardiac regions can be obviously distinguished. In addition, the cardiac lumen is clear and the boundary is neat. Even the ventricular walls can be well rendered.

Figure 11 Volume rendering for heart ultrasound image sets of different human fetus.

Discussion

In the current study, we propose a new denoising and enhancing method framework to improve 4D clinical fetal heart ultrasound images, the 4D-NLM denoising and ACEHP enhancing methods. 4D-NLM utilize additional information available from both spatial and temporal neighboring images to improve denoising, while ACEHP adopts an adaptive clipping technique that can ensure enhancing without amplification of noise.

For image denoising, we implemented a wide range of methods to compare to our proposed 4D-NLM method. Via visual observation, we can see that some methods (e.g., median filter, BM3D and NCSR) can smooth the image to a certain extent, but not sufficiently so, some methods (e.g., mean filter, Gaussian filter, EPLL, WNNM) can eliminate most of the noise but also blurred the edge, while some methods (e.g., Fourier transform) can keep the edge clear but resulted in very uneven boundaries. NLM and its improved algorithm (e.g., ANLM and NLM) can remove most of the noise but NLM blurred the edge of images, and ANLM and NLM has deficiencies in evaluating indicators (CNR and HSEW). Some methods (e.g., FL) has no denoising effect. our proposed 4D-NLM method can effectively utilize the information from neighboring images, so it has lesser noise and clearer feature edges. Evaluations using “method noise” strategy demonstrated that 4D-NLM method denoise more uniformly in the field of view, and does not remove structural information from the image. In particular, we can see that it improves upon the traditional NLM method by removing much less structural information. We thus believe that 4D-NLM method can be effective for human fetal heart ultrasound image denoising.

For image enhancing, similar experiments comparing a range of classical and state-of-the-art approaches were performed to compare to our proposed ACEHP method. ACEHP could give superior entropy and HSEW outcomes, indicating a strong ability to generate distinguishing features between different regions, and yet retain boundary clarity.

With both 4D-NLM and ACEHP, volume rendering enabled better visualization of the cardiac luminal space, and also ventricular walls, although signal losses in the walls is still common, due to low quality original images. Our approach can be a good way to improve 3D/4D rendering of fetal hearts from scans, to better enable obstetricians and cardiologists to detect malformations and dysfunction of the heart. However, it should be noted that this study has examined only on 4D human fetal heart ultrasound images. Our proposed denoising method (4D-NLM) requires images with both spatial and temporal neighbors, and can thus be used only in 4D images. In addition, our ultrasound image enhancing method has only been tested on fetal cardiac images, and may not be generalizable to other body structures. Our proposed enhancing method (ACEHP) should be tested before being applied for other applications.

Conclusion

In this paper, we proposed a special method framework of denoising and enhancing for ultrasound image of human fetal heart. For denoising, we designed a 4D-NLM method to smooth target image utilizing contextual information from spatially and temporally neighboring images. It can more effectively reduce the laminar artifact noise that is common in ultrasound images. For enhancing, we designed the ACEHP method to distinguish (enhance) the cardiac region and non-cardiac regions via adaptive clipping for each histogram pillar. These two methods form a holistic method framework, which we believe can be useful for medical applications. Our method is tested and validated using clinical fetal heart ultrasound images.

Acknowledgments

Funding: This study was supported by the National Natural Science Foundation of China (Nos. 61972440, 61572101 and 61300085), the Fundamental Research Funds for the Central Universities of China (Nos. DUT20YG108 and DUT20TD107), the Scientific Research Project of Educational Department of Liaoning Province of China (No. LZ2020031) and by the Singapore Ministry of Education AcRF Tier 2 Grant (No. MOE2018-T2-1-003, PI: Yap).

Footnote

Conflicts of Interest: All authors have completed the ICMJE uniform disclosure form (available at http://dx.doi.org/10.21037/qims-20-818). The authors have no conflicts of interest to declare.

Ethical Statement: The study was approved by Domain Specific Review Board (DSRB) of the National University Hospital, Singapore (NO.: 2014/00056) and informed consent was taken from all the patients.

Open Access Statement: This is an Open Access article distributed in accordance with the Creative Commons Attribution-NonCommercial-NoDerivs 4.0 International License (CC BY-NC-ND 4.0), which permits the non-commercial replication and distribution of the article with the strict proviso that no changes or edits are made and the original work is properly cited (including links to both the formal publication through the relevant DOI and the license). See: https://creativecommons.org/licenses/by-nc-nd/4.0/.

References

1. Huang T, Yang G, Tang G. A fast two-dimensional median filtering algorithm. IEEE Trans Acoust 1979;27:13-8. [Crossref]
2. Extrapolation WN. Interpolation and Smoothing of Stationary Time Ser‐ies. New York: Wiely 1949.
3. Brown RG, Hwang PY. Introduction to random signals and applied Kalman filtering: with MATLAB exercises. John Wiley & Sons New York, NY, USA; 2012.
4. Boyle RD, Thomas RC. Computer vision: A first course. Blackwell Scientific Publications, Ltd.; 1988.
5. Blinchikoff HJ, Zverev AI. Filtering in the time and frequency domains. 1976.
6. Averbuch A, Coifman R, Donoho D, Israeli M, Waldén J. Polar FFT, rectopolar FFT, and applications. Stanford Univ., Stanford, CA, Tech. Rep; 2000.
7. Buades A, Coll B, Morel JM, editors. A non-local algorithm for image denoising. 2005 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR'05); 2005: IEEE.
8. Mingliang X, Pei L, Mingyuan L, Hao F, Hongling Z, Bing Z, Yusong L, Liwei Z. Medical image denoising by parallel non-local means. Neurocomputing 2016;195:117-22. [Crossref]
9. Ho-Chiang C, Huang H, Huang C-C. High-frequency ultrasound deformation imaging for adult zebrafish during heart regeneration. Quant Imaging Med Surg 2020;10:66. [Crossref] [PubMed]
10. Sudeep P, Palanisamy P, Rajan J, Baradaran H, Saba L, Gupta A, Suri JS. Speckle reduction in medical ultrasound images using an unbiased non-local means method. Biomed Signal Process Control 2016;28:1-8. [Crossref]
11. Almahdi R, Hardie RC, editors. Recursive non-local means filter for video denoising with Poisson-Gaussian noise. 2016 IEEE National Aerospace and Electronics Conference (NAECON) and Ohio Innovation Summit (OIS); 2016: IEEE.
12. Dabov K, Foi A, Katkovnik V, Egiazarian K, editors. Image restoration by sparse 3D transform-domain collaborative filtering. Image Processing: Algorithms and Systems VI; 2008: International Society for Optics and Photonics.
13. Zoran D, Weiss Y, editors. From learning models of natural image patches to whole image restoration. 2011 International Conference on Computer Vision; 2011: IEEE.
14. Gu S, Zhang L, Zuo W, Feng X, editors. Weighted nuclear norm minimization with application to image denoising. Proceedings of the IEEE conference on computer vision and pattern recognition; 2014.
15. Dong W, Zhang L, Shi G, Li X. Nonlocally centralized sparse representation for image restoration. IEEE Trans Image Process 2013;22:1620-30. [Crossref] [PubMed]
16. Yang J, Fan J, Ai D, Wang X, Zheng Y, Tang S, Wang Y. Local statistics and non-local mean filter for speckle noise reduction in medical ultrasound image. Neurocomputing 2016;195:88-95. [Crossref]
17. Ai L, Ding M, Zhang X, editors. Adaptive non-local means method for speckle reduction in ultrasound images. Medical Imaging 2016: Image Processing; 2016: International Society for Optics and Photonics.
18. Yu J, Chen L, Li H, Zhou S, Wang L, Zhang Z, editors. Ultrasound Image Denoising Based on Fuzzy Logic. 2019 International Conference on Communications, Information System and Computer Engineering (CISCE); 2019: IEEE.
19. Kokil P, Sudharson S. Despeckling of clinical ultrasound images using deep residual learning. Comput Methods Programs Biomed 2020;194:105477. [Crossref] [PubMed]
20. Liao WX, He P, Hao J, Wang XY, Yang RL, An D, Cui LG. Automatic Identification of Breast Ultrasound Image Based on Supervised Block-Based Region Segmentation Algorithm and Features Combination Migration Deep Learning Model. IEEE J Biomed Health Inform 2020;24:984-93. [Crossref] [PubMed]
21. Cao W, An X, Cong L, Lyu C, Zhou Q, Guo R. Application of Deep Learning in Quantitative Analysis of 2‐Dimensional Ultrasound Imaging of Nonalcoholic Fatty Liver Disease. J Ultrasound Med 2020;39:51-9. [Crossref] [PubMed]
22. Pizer SM, Amburn EP, Austin JD, Cromartie R, Geselowitz A, Greer T, ter Haar Romeny B, Zimmerman JB, Zuiderveld K. Adaptive histogram equalization and its variations. Computer Vision, Graphics, and Image Processing 1987;39:355-68. [Crossref]
23. Maini R, Aggarwal H. A comprehensive review of image enhancement techniques. arXiv preprint arXiv:10034053 2010.
24. Bedi SS, Khandelwal R. Various image enhancement techniques-a critical review. International Journal of Advanced Research in Computer and Communication Engineering 2013;2:1605-9.
25. Zuiderveld K. Contrast limited adaptive histogram equalization. Graphics Gems 1994:474-85.
26. Shan Q, Jia J, Brown MS. Globally optimized linear windowed tone mapping. IEEE Trans Vis Comput Graph 2020;16:663-75. [Crossref] [PubMed]
27. Deng G. A generalized unsharp masking algorithm. IEEE Trans Image Process 2011;20:1249-61. [Crossref] [PubMed]
28. Ying Z, Li G, Gao W. A bio-inspired multi-exposure fusion framework for low-light image enhancement. arXiv preprint arXiv:171100591 2017.
29. Singh A, Gupta K, editors. A contrast enhancement technique for low light images. AIP Conference Proceedings; 2016: AIP Publishing LLC.
30. Demirel H, Ozcinar C, Anbarjafari G. Satellite image contrast enhancement using discrete wavelet transform and singular value decomposition. IEEE Geosci Remote Sens Lett 2009;7:333-7. [Crossref]
31. Mishra D, Chaudhury S, Sarkar M, Soin AS. Ultrasound image enhancement using structure oriented adversarial network. IEEE Signal Process Lett 2018;25:1349-53. [Crossref]
32. Ahmed BI. The new 3D/4D based spatio-temporal imaging correlation (STIC) in fetal echocardiography: a promising tool for the future. J Matern Fetal Neonatal Med 2014;27:1163-8. [Crossref] [PubMed]
33. Otsu N. A threshold selection method from gray-level histograms. IEEE Trans Syst Man Cybern Syst 1979;9:62-6. [Crossref]
34. Buades A, Coll B, Morel JM. On image denoising methods. CMLA 2004.5. Preprint.
35. Zhang TY, Feng HJ, Xu ZH, Li Q, Chen YT. Sharpness metric based on histogram of strong edge width. Journal of ZheJiang University (Engineering Science) 2014;48:312-20.
36. Li M, Liu J, Yang W, Sun X, Guo Z. Structure-revealing low-light image enhancement via robust retinex model. IEEE Trans Image Process 2018;27:2828-41. [Crossref] [PubMed]