A theory of fine structure image models with an application to detection and classification of dementia

Introduction

When viewing a complete, as opposed to a region of interest, medical image such as an axial MRI brain scan, the diagnostician typically makes an overall image assessment and then studies from region to region seeking elements of normal structure and pathology. The eye cannot readily assess the thousands of small image regions for comparison. Thus, image fine structure information at the individual pixel level, of necessity, has been visually ignored. Whether such fine structure of closely spaced pixels, of any size image, will be useful for medical purposes is an open question since it has been difficult to obtain such data. Further, in the problem of diagnosing neurological diseases, our bioengineering application addresses a long recognized clinical need of dementia diagnosis: MR image quantification has been, and still is, an arduous task, currently requiring considerable processing time and operator attention (1). In Alzheimer’s disease (AD), for example, it is difficult to distinguish normal aging changes of increased ventricular and sulcus size from AD degeneration.

The definitive diagnosis of dementia is by autopsy but of the ten recognized cognitive tests, the most popular in use is the Mini Mental State Examination (MMSE) which has the best correlation with autopsy outcomes and is the most useful in following diagnosed dementia over time (2). Therefore we use subject MMSE scores to categorize normal or demented subjects. To support this definition of subject cognitive state, we seek a brain scan image model whose parameters not only capture discriminating image information but also indicate which parameters of the image carry the most discriminating information as measured by their inferred confidence intervals (3).

Materials and methods

Our original computational method is based on ordinary least squares (OLS) regression because we discovered a simple matrix transformation that enables images to be represented as linear combinations of row and column spatial lags of the original image. These row and column lagged images give rise to the “fine structure” description of the images we model because the row and column spatially lagged images are visually indistinct from the original. The key step in our analysis is to transform any two dimensional (2D) image pixel array to a one dimensional (1D) pixel array. Next we show that transformed images can be modeled by traditional OLS methods. Therefore, under verified distributional conditions, the OLS model parameters can be tested for statistical significance. This is an important model property as it means recognized neurological conditions can be tested for causality by parameter significance. In addition, the most significant parameters carry the most discrimination information in implementing image classifications.

Image model development

To reduce a 2D pixel array (an image) to a 1D pixel array (a column) a transformation called vectorization is applied by stacking the left-most column of image pixels onto its neighbor pixel column and these two columns onto the third and so on, until all pixel columns are stacked (4). For example, an image A of 208 rows and 176 columns of pixels becomes a single column of [208] × [176]=36,608 pixels. We call this column the vectorized form of A and write it as vec(A). The next step is to recognize that any image y(i,j), whose intensity y at pixel location (i,j), can be hypothesized to be a solution of the linear autoregressive (AR) model (5).

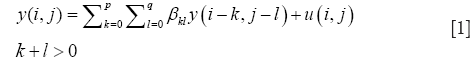
In Eq. [1], u(i,j) is a random process error term and we note Eq. [1] is a discrete approximation to a general, linear, causal, partial differential equation in two space dimensions.

The final step is to show, see Appendix A₁, that if c_t and A_t are real constants and matrices then:

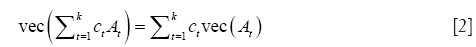
Define y_o = vec[y(i,j)], x₁ = vec[y(i,j-1)], x₂ = vec[y(i-1,j)], .., x_p+q+qp = vec[y(i-p,j-q)], and u_o = vec[u(i,j)]. By Eq. [2], the model in Eq. [1], with β as a column vector with p+q+qp elements β_kl, has the familiar OLS regression form.

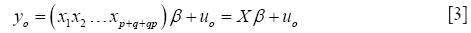
In Eq. [3], Xβ is called a minimum variance representation (MVR) of the vectorized image y_o if a β can be found such that u_o^T u_o is minimized. A necessary and sufficient condition that such a β exists is:

MVR existence theorem: [Th1].

An image of pixel intensity y(i,j) has a MVR in the form of

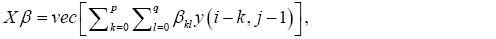
if and only if k+l>0, the image column vectors x₁x₂ .. x_{p +q +pq} are linearly independent.

When this condition is met the minimizing β satisfies:

and the image MVR is:

The finite sample form of Eq. [3] employed to estimate β is

where b is the OLS estimate of the population (true) value β and the vector e_o estimates the random residual vector uo. Using the format of Eq. [6], each image of the Alzheimer’s Disease Neuroimaging Initiative (ADNI) and Open Access Series of Imaging Studies (OASIS) data sets had an estimated MVR, denoted as Xb, minimizing e_o^Te_o and computed as:

The integer p, q orders are determined by increasing p and q so that (X^TX)⁻¹ exists for all image data. For both the ADNI and OASIS data this was for p=q=2. Larger p or q made (X^TX) ill-conditioned. If the image to be modeled is m by n pixels then the minimum variance realization Xb of the image is a column vector of (m-p) × (n-q) by 1 pixels. To realize the 2D picture of Xb it must be unstacked into 2D image model starting at the top of Xb.

Only in the rarest of cases will the residual vector e_o in Eq. [6] test to be white Gaussian noise which would permit Student’s t-tests of parameter statistical significance. So we have developed, see Appendix A₂, a nonparametric significance statistic, w_kl, based on the Chebychev inequality (6). |w_kl| measures the width, normalized by b_kl, of a 1-α confidence interval of the true β_kl. The smaller |w_kl| is for a given b_kl, the more significant is the estimated parameter b_kl multiplying lagged image vec[y(i-k,j-l)]. For the diagnostician the confidence interval of β_kl is the most important property derived from its estimate b_kl since it tells him the probability with which the true parameter he seeks, β_kl, is estimated by what he estimates, b_kl.

The X matrix in Eq. [6] has eight column vectors, eight spatially lagged, vectorized images of y(i-k,j-l) for k =0,1,2, l =0,1,2, k + l >0. However, we found that adding a column of ones to X to account for image sample means slightly increases the likelihood of correct classification as developed in the following section. Relative to the theoretical model in Eq. [1], this amounts to adding a constant to the right-hand side. The column of ones is crucial because it assures the residual vector e_o in Eq. [6] and is estimated without bias, a bias which would also induce a bias in the estimated vector b.

Optimal image classification

In this section we derive a discriminator by which a given subject’s MMSE score identifies the subject as normal or demented and also gives a ranking statistic to compare with other subjects in the same class. A range of MMSE scores is chosen and subjects with scores in that range are categorized as members of the demented class. Another unique MMSE range is chosen for those subjects categorized as normal subjects. Let N_d and N_n be the respective number of subjects in each class. For each subject Eq. [7] estimates a b vector of size p+q+pq+1=9. These are arranged in parameter matrices B_d, 9 by N_d and B_n, 9 by N_n and the pooled parameter matrix B_p which is 9 by N_d + N_n. Let 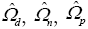be estimates of the covariance matrices of B_d, B_n, and B_p. The projections onto the scalar z axis of z_n = B_nv, z_d = B_dv, and z_p = B_pv are maximally separated in sample means if the projection vector v satisfies the Fisher linear discriminant eigenvector identity (7),

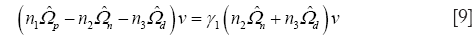
for the only nonzero eigenvalue γ₁. In Eq. [9], n₁ = N_d + N_n –1, n₂ = N_n –1, n₃ = N_d –1. For even modest sample sizes, N_d and N_n ≥10, a Kolmogorov-Smirnov test (K-S test) confirms the hypothesis the z projections are normally distributed (8).

Since z_n and z_d are normally distributed with estimated densities f_n(z) and f_d(z), the Kullback-Leibler discrimination (KLD) statistic for a zero threshold, L_o(z), is a convenient means of comparing projections for “strength of class membership” since |L_o(z)| is monotonic with membership probability (9).

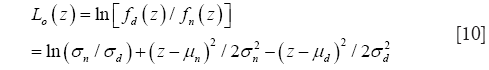
In Eq. [10], means and variances are estimated from the sample z projections. L_o(z) >0 classifies a z-projection as demented and L_o(z) <0 as a normal.

The KLD statistics provide a graphical display of TP, TN, FP, and FN measures of the classification algorithm.

Large-sample ADNI dataset

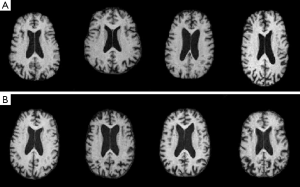
Our large sample study employed ADNI archive axial MR image slices. The images were 1.5 T, T1 weighted using the MP Rage sequence, calibration scans for B₁ correction, dual fast spin echo and were 256 by 170 gray scale pixels. All ADNI images were selected from one slice axially above the anterior commissure brain structure. ADNI subject inclusion criteria varied over four classes: (I) normal subjects had no subjective memory complaints; (II) normal memory function stratified by educational attainment; (III) MMSE scores between 24 and 30; and (IV) a Clinical Dementia Rating (CDR) of 0. EMCI subjects had subjective memory complaints, abnormal memory function stratified by age, MMSE 24 to 30, a CDR of 0.5, and AD could not be diagnosed at time of screening visit. LMCI subjects had the same criteria as the EMCI subjects but educational attainment was lower. AD subjects had memory complaints, abnormal memory function, MMSE scores 20 to 27, CDR of 0.5 to 1.0, and satisfied a NINCDS criteria for probable AD. The 50 subjects we took as normal were screened as males, ages 65 to 84 years with MMSE scores of 29 to 30. The 47 subjects we took as demented were of ages 65 to 84 years with MMSE scores of 17 to 27. Therefore the 97 subjects were identified as normal or demented according to the range of their MMSE scores. The 97 subjects so identified exhausted the four classes cited above for the constraints we specified. It is likely that about 70% of the categorized demented subjects suffered from AD (10). The chosen MMSE score ranges are typical for normal/demented studies with 20 year age spans (2). All ADNI axial images had cranium and dura artifacts manually cropped. Figure 1 displays typical ADNI images.

Figure 1 (A) Typical MMSE-designated normal MR axial images from a sample of size 50 from the ADNI national archive; (B) typical MMSE-designated demented MR axial images from a sample of 47 from the ADNI national archive. Subjects matched for age and gender. MMSE, Mini Mental State Examination; ADNI, Alzheimer’s Disease Neuroimaging Initiative.

Small-sample OASIS data set

Our small sample study employed OASIS axial MR image slices screened as right-handed males of ages 65 to 75 years with MMSE scores of 29 to 30. The database produced 14 such images we refer to as the normal class. Screening for right-handed males of ages 67 to 84 years with MMSE scores of 17 to 27 produced 12 images we refer to as the demented class. These images came from a set of 416 subjects aged 18 to 96. For each subject, 3 or 4 individual T1-weighted MRI scans obtained in single scan sessions were averaged to get the images, 208 by 176 pixels, for our study. A total of 100 of the included subjects over the age of 60 had been clinically diagnosed with very mild to moderate AD, in addition, a reliability data set of 20 non-demented subjects imaged on a subsequent visit within 90 days of their initial session were available as normal subjects. OASIS images had dura and cranium artifacts manually cropped. All axial images from the OASIS archive were at a fixed, unspecified number of 1.5 mm slices from the anterior commissure brain structure. Figure 2 are typical OASIS images.

Figure 2 (A) Typical MMSE-designated normal MR axial images from a sample of size 14 from the OASIS archive; (B) typical MMSE-designated demented MR axial images from a sample of size 12 from the OASIS archive. Subjects are matched for age and gender. MMSE, Mini Mental State Examination; OASIS, Open Access Series of Imaging Studies.

Results

Typical image OLS models, parameters, and statistics

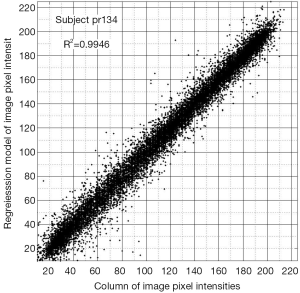
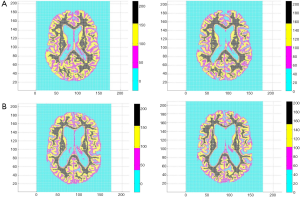
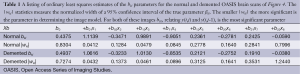
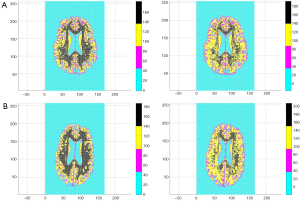
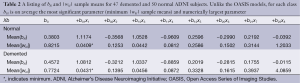
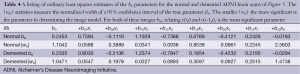
All 123 images were modeled using the OLS Eqs. [7] and [8] and the |w_kl| significance statistics (for a 95% confidence interval) computed for all b_kl parameters. Figure 3 is a typical OLS scatter diagram, this for a demented subject from the OASIS dataset. The regression R² for this model is typical of image regressions for both datasets as they all exceeded 99%. Figure 4 illustrates typical estimation results for two OASIS subjects and Table 1 lists the OLS b_kl parameters and |w_kl| statistics for the images in Figure 4. Typical normal and demented images and models of ADNI subjects are shown in Figure 5; b_kl parameters and |w_kl| statistics for these two ADNI subjects are in Table 4.

Figure 3 A scatter diagram of a typical regression determining a MVR of a demented subject from the OASIS archive. Horizontal axis is the scale for the pixel intensities of the vectorized image y_o. The vertical axis is the scale for the vectorized image model pixel intensities Xb estimated by the regression formula Eq. [8]. Regression models of all 123 subjects from both archives had R² exceeding 99%. MVR, minimum variance representation; OASIS, Open Access Series of Imaging Studies.

Figure 4 (A) A MMSE-designated normal image from the OASIS archive and a 9 MVR of that image; (B) a MMSE-designated demented image from the OASIS archive and a 9 MVR of that image. The b_kl parameters and their |w_kl| parameter significance statistics for the models of Figure 4 are listed in Table 1. With |w₀₁| =0.0412 for the normal subject, b₀₁ is the most significant parameter for the normal image model and |w₀₁| =0.0432 for b₀₁ of the demented subject makes this parameter the most significant for the demented subject. MMSE, Mini Mental State Examination; OASIS, Open Access Series of Imaging Studies; MVR, minimum variance representation.

Table 1 A listing of ordinary least squares estimates of the b_kl parameters for the normal and demented OASIS brain scans of Figure 4. The |w_kl| statistics measure the normalized width of a 95% confidence interval of the true parameter β_kl. The smaller |w_kl| the more significant is the parameter in determining the image model. For both of these images b₀₁, relating y(i,j) and y(i,j-1), is the most significant parameter
Full table

Figure 5 (A) Typical MMSE-designated normal MR axial images from a sample of size 50 from the ADNI archive; (B) typical MMSE-designated demented MR axial images from a sample of size 47 from the ADNI archive. Subjects are matched for age and gender. For these images b₀₁ is the most significant parameter (see Table 2), while for the OASIS images (see Figure 4), b₁₀ is the most significant (see Table 3). MMSE, Mini Mental State Examination; ADNI, Alzheimer’s Disease Neuroimaging Initiative; OASIS, Open Access Series of Imaging Studies.

Table 2 A listing of b_kl and |w_kl| sample means for 47 demented and 50 normal ADNI subjects. Unlike the OASIS models, for each class b₀₁ is on average the most significant parameter (minimum |w_kl| sample means) and numerically largest parameter
Full table

Table 3 A listing of b_kl and |w_kl| sample means for 12 demented and 14 normal OASIS subjects. For each class b₁₀ is on average the most significant parameter (minimum |w_kl| sample means) and numerically largest parameter
Full table

Table 4 A listing of ordinary least squares estimates of the b_kl parameters for the normal and demented ADNI brain scans of Figure 5. The |w_kl| statistics measure the normalized width of a 95% confidence interval of the true parameter β_kl. The smaller |w_kl| the more significant is the parameter in determining the image model. For both of these images b₁₀, relating y(i,j) and y(i-1,j), is the most significant parameter
Full table

Sample means of model parameters and their significance statistics

Table 3 tabulates sample means of estimated parameters and sample means of their |w_kl| statistics for the OASIS dataset and Table 2 tabulates these sample means for the ADNI dataset. With sample sizes of 50 and 47, the entrees in Table 2 are highly significant. For example, an interpretation of the mean(|w_kl|) value of b₀₁ is: with a probability of 0.95 the average true demented parameter β₀₁ is in the interval 1.0812±0.0232; for normal subject b₀₁ the 95% interval of β₀₁ is 1.1174±0.0228.

Table 3 entrees for the OASIS (26 samples) dataset do not differ dramatically from the ADNI Table 2 entrees but there is a subtle shift of the most significant b_kl parameter from b₁₀ for the OASIS data to b₀₁ for the ADNI data. This shift is interpreted later.

Optimal image classification

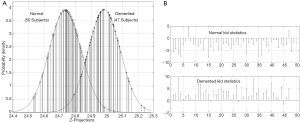
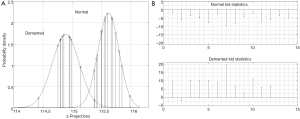
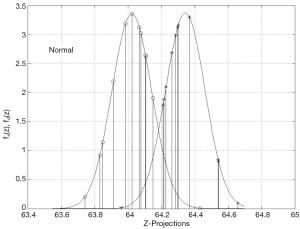
Figure 6 shows the inferred probability density functions of the ADNI z-projections resulting from projecting the b_kl parameters with the eigenvector solution of Eq. [9]. These probability densities passed K-S tests for normality at level 10⁻⁵ which decisively supports the classification probability inference of the KLD statistics, computed from Eq. [10] and also shown in Figure 6. Figure 7 shows the inferred z-projection probability density functions for the OASIS subjects. These densities passed K-S tests for normality at level 10⁻³. An interpretation of the KLD statistics for the demented (normal) projections is that the larger (smaller) the KLD statistic is, then the more likely the sample is correctly classified. For example, in Figure 7 the leftmost z-projection (near 114.4) corresponds to demented sample number 7 with KLD of 20. On the other hand, the demented projection near 115.4 corresponds to sample number 2 which has a negative KLD and this sample is misclassified.

Figure 6 (A) Estimated z-projection probability densities resulting from the Fisher linear discriminant projections of the normal and demented b_kl parameter matrices B_n and B_d for all of the ADNI image models; (B) the KLD statistics calculated from Eq. [10]. KLD statistics measure the likelihood a given subject is correctly classified; more negative normal and more positive demented KLD statistics imply higher likelihood of correct classification. For example, the largest demented KLD statistic is 9 for subject number 3, the right-most sample in Figure 6A. This demented subject is clearly the most likely to be correctly classified. ADNI, Alzheimer’s Disease Neuroimaging Initiative; KLD, Kullback-Leibler discrimination.

Figure 7 (A) Estimated z-projection probability densities resulting from the Fisher linear discriminant projections of the normal and demented b_kl parameter matrices B_n and B_d of the OASIS image models; (B) the KLD statistics are computed as described in the Figure 6 caption. Demented subject number 7 has a KLD of 20 and a z-projection in Figure 7A of 114.4. OASIS, Open Access Series of Imaging Studies; KLD, Kullback-Leibler discrimination.

We also performed a cross validation test for the ADNI images by randomly selecting 12 normal and 12 demented subjects to be test subjects for a training classifier based on 38 normal and 35 demented subjects. The results of that test are shown in Figure 8. In that figure the accuracy of the training classifier (inferred z-projection densities shown) was 69/73=94.5%, while the test subjects were classified with an accuracy of 22/24=91.7%.

Figure 8 Z-projection probability density functions estimated from 38 normal and 35 demented ADNI subject images. Density functions represent a classification accuracy of 94.5%. Accuracy for the 24 test images is 91.7%. ADNI, Alzheimer’s Disease Neuroimaging Initiative.

Comparison with other medical image classifiers

The first comparison study is selected because it is comprehensive in feature extractions (gray level histogram, gray level co-occurrence matrix, shape invariant moment, and FFT frequency), uses an average of 408 CT and MR images (102 testing for a 25% testing-to-training ratio) and tests 4 popular classification methods (C4.5, SVM, naive Bayes, KNN) (11). The averages over feature extractions shown in Table 5 are to be compared to our OLS method’s 91.7% accuracy using a 24.2% testing-to-training ratio. The authors give no computational time or computer specification results.

Table 5 Average accuracy of 12 categories of medical X-ray images (average sample size 306 training, 102 testing). Feature types are gray-level histogram, gray level co-occurrence matrix, shape invariant moment, FFT frequency (11)
Full table

The second comparison study is selected because it tests an advanced form of the random forest (RF) classifier, uses a test–to-training ratio of 33% on 300 region of interest MR images of 256×216 pixels each (12). They report a computation time of 304 seconds average with 86.4% accuracy using a 2.66 GHz machine of unspecified RAM.

The final comparison study is selected because it tests three forms of the RF classifier, uses 10 fold cross-validation, and gives comprehensive computation times using a 3.4 GHz, 12 GB RAM computer (13). Images are 3 color of 174 colon biopsies. The grid size modeled is a rather crude 49 blocks. The original feature set produced an accuracy of 91.3% averaged over the three classifiers. Increasing features from 20 to 50 boosted the average accuracy to 93.0% with run times of 104 seconds averaged over the three RF classifiers. The authors quote five other comparable colon studies whose average accuracy is 85.43%.

The dramatic difference between our OLS method and those cited above is computation time. Using a 3.00 GHz computer with 3.72 RAM our all-training result, Figure 6, required 0.9014 seconds, Figure 7 took 0.2516 seconds while Figure 8 required 0.6466 seconds. The RF classifier of ROI images (of a comparable number of pixels) cited above required 224 seconds on a machine 13% slower than ours. Derating 224 seconds by 13% and increasing our run time by 300/73 to compensate for sample sizes implies our runtime is 195/2.66=73.3 times faster than the cited classification of ROI images.

The colon biopsy classifiers must classify red, green and blue images so we must triple our runtimes and compensate for sample sizes by 174/73. This gives our estimated comparable runtime of 0.6466×3×2.38=4.62 seconds which is 104/4.62=22.5 times faster than the RF image classifiers. Individually, the red, green and blue images required 34, 48, and 22 seconds respectively. OLS equivalent time is 2.38×0.6466=1.54 seconds for each color.

Summary

Including the 5 colon studies cited in (13), we have compared our OLS classifier to 13 classifiers from the literature and our training-test accuracy of 91.7% is better than all but one average.

In the runtime domain, none of the cited classifiers is competitive with the OLS classifier. The lowest runtime cited for the reviewed classifiers is a minimum of 14 times slower than the OLS classifier.

The implied superiority of the OLS method over the comparison image classification methods in accuracy and computation times results from two properties of the OLS method: (I) the OLS image models are rigorously defined in terms of statistical estimation of partial difference equation solutions; (II) the vec(.) transformation and its theoretical preservation of the OLS format for the partial difference equation model and [Th1], is complemented by a runtime-optimized vec(.) function on Matlab.

Discussion

The innovation of OLS image modeling

Modeling of discrete time series, representing native discrete time systems or discretized ordinary differential equations, has advanced to the stage that transfer function theory and ubiquitous software to model data are commonplace (14-16). OLS is the estimation method of choice for such linear system models (also called 1D system because they employ one independent variable). In our past work we have found the estimated parameters of such models are capable of classifying the subject data they model and can provide insight into physical system interpretations (17-21).

The AR model hypothesis in Eq. [1], the vector transformation in Eq. [2], and the MVR theorem [Th1] make available to 2D modeling all of the methods cited above for 1D systems. Further, images are a special case of 2D systems which include image modalities of X-ray, US, MRI, PET, and SPECT.

Interpretation of image model parameters for large brain scans

While OLS models of medical image parameters are capable of robust image classification, an equally important utility lies in their diagnostic potential.

Diagnosis is taken to be at two image sizes: (I) entire brain scans, for example the axial brain scans of this study; (II) and ROI size images which are not investigated in this study. An interpretation of average image parameters we found in image height to width ratios. This ratio calculated for all ADNI and OASIS images averages 24.9% greater for the ADNI images. Thus, the subtle shift, noted above, in the most significant parameters b₁₀ in Table 3 to b₀₁ in Table 2 is due to the ADNI images having more informative pixel columns than rows, thereby favoring correlations between y(i,j) and y(i,j-1) as measured by b₀₁. Analogously, b₁₀, relating y(i,j) and y(i-1,j), is more significant for the OASIS images whose pixel rows are more informative than their columns.

Image parameter medical interpretation addresses the difficulty in distinguishing which of seven possible dementia types a given subject is suffering. Having nine parameter image models and statistics to measure individual parameter significance presents the opportunity to design a study in which cognitive test scores and post mortem dementia identification outcomes can be used to identify parameters or groups of parameters specific to dementia types.

Figures 1,2 and 4,5 indicate a large within-sample variation in ventricle size as a percent of total brain scan. To determine the possible classifying effect this variation might have on z-projections, a 20% image random sample from both datasets was used to cross-correlate ventricle area with z-projection size. The correlations were not significant at the 10% level. Further, even within-class correlation was not evident, two OASIS demented subjects differed 67% in ventricle area and only 2.2×10⁻⁴ percent in z-projection size. The reason for this outcome lies in the observation that ventricles are interpreted by OLS as zero pixel intensity background similar to that which fills the rectangle surrounding the brain scan.

Interpretation of image model parameters for region of interest scans

ROI scan models can have more diagnostic potential than those of entire image scans. This derives from the fact that ROI regions can be modeled by generalized least squares (GLS). A smaller number of pixels make GLS computationally tractable and estimated parameters normally distributed. Consequently, one-way classification of regression models becomes a powerful diagnostic tool (22). In a preliminary study we showed that a 40×40 pixel ROI of an OASIS slice and a similar sized ROI one 1.5 mm slice above the first were significantly different at level 0.029 by a Snedecor F test. Clearly, such analysis also is applicable to therapy progress.

Three color RGB images, such as prostate biopsies, require three OLS models which combine for the color model. Such models present no additional estimation problems but we still must work out how to compare images represented by three mutually exclusive groups of nine parameters each.

Acknowledgements

Authors’ contributions: W O’Neill wrote the manuscript with R Penn who also provided neurological interpretations of modeling results. M Werner and J Thomas gathered, categorized, and prepared data for analysis. They also ran the regression and subject classification programs.

Disclosure: The authors declare no conflicts of interest.

Appendix

A₁—Derivation of the vec(A_t) transformation

We need to show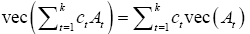

or equivalently (I) vec(cA) = cvec(A) and (II) vec(A+B) = vec(A) + vec(B). (I) is trivial since a matrix can be scaled by rows or columns. If A and B are m by n then A = [a₁a₂ ..a_n] and B = [b₁b₂ .. b_n] so vec(A+B) = [a₁^T+b₁^T a₂^T+b₂^T.. a_n^T+b_n^T]^T = [a₁^T a₂^T .. a_n^T]^T + [b₁^T b₂^T .. b_n^T]^T = vec(A) + vec(B).

A₂—Derivation of the w_kl statistic

The well-known result using Eq. [3] in Eq. [7] is E(b) = β. Then for every k,l, and defining 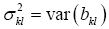, the Chebyshev inequality is:

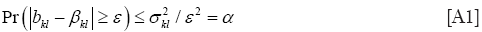
Therefore a 1–α confidence interval for the true β_kl satisfies:

b and β have the same scale so it is clearly better to have a large estimated b_kl and a small confidence interval for β_kl than conversely.

Thus, we normalize the confidence interval width 2ε by b_kl, and define w_kl = 2ε/b_kl. The coefficient of variation of the estimate bkl is c_kl = σ_kl / b_kl and 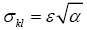, so:

Calculating w_kl for a given model requires an estimate of 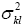, the k,l diagonal element of the covariance matrix cov(b). From Eq. [3] in Eq. [7]:

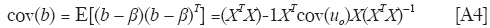
and cov(u_o) is readily estimated from the residual vector e_o in Eq. [6].

References

1. Neuroimaging Work Group of the Alzheimer’s Association, The Use of MRI and PET for Clinical Diagnosis of Dementia and Cognitive Impairment: A Consensus Report, 2005.
2. Lin JS, O’Connor E, Rossom RC, Perdue LA, Eckstrom E. Screening for cognitive impairment in older adults: A systematic review for the U.S. Preventive Services Task Force. Ann Intern Med 2013;159:601-12. [PubMed]
3. Azimi-Sadjadi MR. Estimation and identification for 2-D block Kalman filtering. Signal Processing IEEE Trans 1991;39:1885-89.
4. Magnus JR. eds. Linear Structures. New York: Oxford U. Press, 1988.
5. Jain AK. Partial differential equations and finite-difference methods in image processing, part 1: Image representation. J Optim Theory Appl 1977;23:65-91.
6. Wilks SS. eds. Mathematical Statistics. New York: Wiley, 1963:75.
7. Wilks SS. eds. Mathematical Statistics. New York: Wiley, 1963:573.
8. Wilks SS. eds. Mathematical Statistics. New York: Wiley, 1963:454.
9. Kullback S. eds. Information Theory and Statistics. Mineola, NY: Dover Publications, 1997:6.
10. Plassman BL, Langa KM, Fisher GG, Heeringa SG, Weir DR, Ofstedal MB, Burke JR, Hurd MD, Potter GG, Rodgers WL, Steffens DC, Willis RJ, Wallace RB. Prevalence of dementia in the United States: the aging, demographics, and memory study. Neuroepidemiology 2007;29:125-32. [PubMed]
11. Li B, Li W, Zhao D. Multi-scale feature based medical image classification. IEEE 3rd International Conference on Computer Science and Network Technology. Chengdu, China, 2013:1182-6.
12. Mahapatra D. Analyzing training information from random forests for improved image segmentation. IEEE Trans Image Process 2014;23:1504-12. [PubMed]
13. Rathore S, Iftikhar MA, Hussain M, Jalil A. Classification of colon biopsy images based on novel structural features. IEEE Int Conf on Emerging Technologies. Islamabad, Pakistan, 2013:1-6.
14. Box G, Jenkins G, Reinsel G. eds. Time Series Analysis, 3rd ed. Upper Saddle River NJ: Prentice Hall, 1994.
15. Fuller W. eds. Introduction to Statistical Time Series. New York: Wiley & Son, 1996.
16. Ljung L. eds. System Identification: Theory for the User. Upper Saddle River, NJ: Prentice Hall, 1999.
17. O’Neill WD, Oroujeh AM, Merritt SL. Pupil noise is a discriminator between narcoleptics and controls. IEEE Trans Biomed Eng 1998;45:314-22. [PubMed]
18. O'Neill WD, Zimmerman S. Neurologial interpretations and the information in the cognitive pupillary response. Methods Inf Med 2000;39:122-4. [PubMed]
19. O'Neill WD, Trick KP. The narcoleptic cognitive pupillary response. IEEE Trans Biomed Eng 2001;48:963-8. [PubMed]
20. O'Neill W, Mercer P, Sheldon S, Kotsos T. Detection of juvenile sleep deprivation by stochastic optimization of pupillographic records. Methods Inf Med 2003;42:282-6. [PubMed]
21. Shuhaiber J, O’Neill W. The Diagnostic Efficacy of Left Ventricle Hemodynamic Parameters: Classifying Normal Mitral Valves Against Prosthetic Disease Proxies. Cardiovasc Eng and Tech 2012;3:112-22.
22. Kullback S. eds. Information Theory and Statistics. Mineola, NY: Dover, 1997:219-22.