3D acoustic resolution-based photoacoustic endoscopy with dynamic focusing

Introduction

Acoustic resolution-based photoacoustic endoscopy (ARPAE) is a fast developing and promising tool for the non-invasive imaging of gastrointestinal and urogenital tracts (1-5). ARPAE typically adopts a reflection mirror-based side-view design, in which a single focused transducer is employed for focused photoacoustic detection. This simple design reduces the catheter size, and allows employing a large-sized transducer with high numerical aperture (NA) and high sensitivity to improve the image quality. Because ultrasound scattering is 2–3 orders smaller than the optical scattering in the biologic tissue, tight acoustic focusing is guaranteed beyond the optical diffusion limit’s depth. Therefore, although the lateral resolution of ARPAE (on order of sub-millimeter) is relatively lower than that of the optical resolution-based photoacoustic endoscopy (6,7), its penetration depth is greatly increased.

However, conventional ARPAE only provides 2D sectorial B-mode images. With the fixed-focused transducer, tradeoff exists between the optimal lateral resolution at the transducer focus and depth of focus (DOF), one of the biggest problems in current ARPAE. Employing annular transducer array can achieve dynamic focusing, which has already been demonstrated in photoacoustic endoscopy and microscopy (8-11). The sensitivity of a single element in annular array is quite low due to the small element size, and the fabrication of the annular array is complicated and expensive; therefore, the annular array-based method is not popular in ARPAE. While attention is focused on reducing the ARPAE catheter size, increasing its central frequency, and extending its biomedical application fields, the problem of the enlarged lateral resolution in the out-of-focus region in ARPAE, which leads to a limited DOF, is left unresolved.

Efforts have been made to improve the lateral resolution in acoustic resolution-based photoacoustic microscopy (ARPAM), which is mainly focused on synthetic aperture focusing technique (SAFT)-based methods (12-21). The SAFT was first applied to improve the later resolution in ARPAM with a 200-µm needle hydrophone as the point detector (12). SAFT-based methods, with the focus of a large NA transducer as the virtual detector in ARPAM, were demonstrated by different groups in both phantom and in-vivo experiments, and significant improvement of the degraded lateral resolution, along with the improved signal-to-noise ratio (SNR) in the out-of-focus region, was observed (13-20). In most of these studies, a coherent factor is often introduced to further improve the imaging quality (21); however, this is a non-linear factor and sensitive to data noise (16). A spatial impulse response function is also needed in these SAFT-based methods so that SAFT can be applied to the transducer focus region (16,17), yet the SAFT-based results near the focus are still not as good as those of conventional B-mode images. SAFT was recently applied in ARPAE, in which an optical fiber was used to as a point detector to receive the photoacoustic pressure. However, its catheter design was significantly different from the conventional single focused transducer and reflection mirror-based ARPAE systems (22). Therefore, there is need for new reconstruction algorithms in ARPAE to improve the lateral resolution in the out-of-focus regions.

In our previous studies, we proposed, for the first time, a modified back-projection algorithm to improve the lateral resolution in ARPAE by considering the detecting surface geometry of the focused transducer (23). We studied the final lateral resolution changes with the transducer central frequency, aperture size, and working distance using this method. However, in our previous work, image reconstruction was only performed in 2D on the x-y plane (the sectorial scanning plane). In the present study, the method was extended to 3D, so that not only the lateral resolution in the x-y plane and the lateral resolution in the x-z plane (in the z direction) were improved. Here, we provide a new algorithm and lateral resolution changes of the target locations by simulation. The new reconstruction method was tested with 2 phantom experiments; 1 phantom contained several metal wires, and the other was with a short piece of pig small intestine buried. The results showed that our new method can greatly improve image quality.

Methods

Algorithms

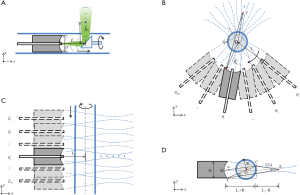
The schematic of conventional ARPAE catheter is shown in Figure 1A. The single element focused transducer is usually hollow structured with a multi-mode fiber in the center for optical illumination. A 45° titled optical/acoustic reflection mirror rotates at the catheter's distal end for the 2D circular side-view scan. If the distance between the reflection mirror and the focused transducer is L1, its equivalent focused detector is placed at its mirrored position and follows a circular scanning path with a diameter of L1 in the x-y plane illustrated in Figure 1B. Here, the distance between the reflection mirror and the transducer focus is L2, so that the transducer focal length is L1+L2. To perform the scan along the z direction, both the focused transducer and the reflection mirror as a whole are moved along the catheter axis, which is equivalent to the scanning in Figure 1C. In cylindrical coordinates, the voxel value given by the conventional ARPAE reconstruction method for an arbitrary point (r, θ, z) in the 2D sectorial B-mode images is:

Figure 1 Schematic of the acoustic resolution photoacoustic endoscopy (ARPAE) scanning. (A) Structure of the conventional ARPAE catheter. (B) Equivalent view of the ARPAE scanning in the x–y plane. (C) Equivalent view of the ARPAE scanning in the x–z plane. (D) Schematic for determining the judge angle and number of point detectors.

I (r, θ, z) = S (θ, z, (L1+ r) / v),[1]

where S (θ, z, t) is the collected photoacoustic signal when the transducer is positioned at (θ, z). The angle is defined concerning the positive x-axis, as illustrated in Figure 1B; v is the acoustic velocity in the media. However, with this kind of reconstruction method, high acoustic resolution is only achieved within the transducer focus. The lateral resolution in the out-of-focus regions is poorly reduced.

In our new method, the focused transducer’s detection surface is modeled to be spherical, which has an aperture size D, the same as the focused transducer, and its radius of curvature is equal to the focal length. Next, this spherical surface is evenly divided into the number of point detector (Np) small elements, and each element can be treated as point detectors. In the forward model, the transducer signal from a photoacoustic source at $\overrightarrow{r}$ can be calculated as the Rayleigh integral of the signals from these point detectors (23,24), as with Eq. [2]:

$$\begin{array}{c}S(\theta ,z,\overrightarrow{r},t)={\displaystyle \underset{-\infty }{\overset{\infty }{\int }}({\displaystyle {\int }_{S}h(t_0)\frac{\delta (t-t_0-\left|{\overrightarrow{R}}_{\theta ,z}-\overrightarrow{r}\right|/v)}{2\pi \left|{\overrightarrow{R}}_{\theta ,z}-\overrightarrow{r}\right|}dS})d{t}_0}\\ ={\displaystyle {\int }_S\frac{h(t-\left|{\overrightarrow{R}}_{\theta ,z}-\overrightarrow{r}\right|/v)}{2\pi \left|{\overrightarrow{R}}_{\theta ,z}-\overrightarrow{r}\right|}dS}\\ \approx {\displaystyle \sum _{k=1}^{Np}\frac{h(t-\left|{\overrightarrow{R}}_{\theta ,z}^k-\overrightarrow{r}\right|/v)}{2\pi \left|{\overrightarrow{R}}_{\theta ,z}^k-\overrightarrow{r}\right|}}\end{array}$$[2]

Here, h(t) is the system impulse response function for unit transducer surface, ${\overrightarrow{R}}_{\theta ,z}^k$ is the position of the transducer at ${\overrightarrow{R}}_{\theta ,z}^k$, and ${\overrightarrow{R}}_{\theta ,z}^k$ is the position of the k-th point detector.

In the image reconstruction, the value of the voxel at $\overrightarrow{r}$ with the coordinates (r, θ, z) is given by:

$$I(r,\theta ,z)={\displaystyle \sum _{i=1}^{Nd}{\displaystyle \sum _{j=1}^{Nz}(A\times {\displaystyle \sum _{k=1}^{Np}S({\theta }_i,z_j,(\left|{\overrightarrow{R}}_{{\theta }_i,z_j}^k-\overrightarrow{r}\right|/v)}}})$$,[3]

where θ₁, θ₂, .., θ_Nd and z₁, z₂, .., z_Nz are the angular and z positions of the transducer in the 3D scan. Here, A is the weighting of the contributions of signals collected at different transducer positions to the voxel. For simplicity, the coefficient A was defined to be 1 or 0 to indicate whether the signal at that transducer position will be used or not. It was set to 1 if the voxel’s directional angle concerning the transducer axis (the angle α) was lower than a judge angle ϕ, as illustrated in Figure 1D. Here, point A is the transducer focus, point B is the center of the transducer detection surface, and O is the center of the catheter, so that line AB or AO is the transducer axis, and R is the radius of the catheter.

In the calculations, only the voxels that are within the detectable range of the focused transducer need to be considered; the blue acoustic field lines outline these. For a point C that is outside of the catheter, but in this region, it can be easily seen that angle α has a upper limit of D/(2(L1+R)), which can be set as the minimum value of the judge angle ϕ. We have previously shown that reconstruction results have no significant change when the judge angle is greater than this value (23).

The Np needs to be sufficiently large to ensure the point detector interval Δl = λ/sin β, where Δl = D/Np, β is the acoustic beam’s incident angle on the transducer detection surface, and λ is the acoustic wavelength. As illustrated in Figure 1D, angle β reaches its maximum when the photoacoustic source is close to the catheter at the edge of detectable range, and the corresponding point detector is at the edge of the transducer on the opposite side, such as ∠AEC, which has a upper limit of D/(2(L1+R)). According to the Shannon’s theorem, the upper limit of sin βΔl / λ is 0.5 (25), which means the Np needs to be larger than D² = (L1+R) / λ. Although a larger Np helps improve the calculation accuracy, it becomes less significant to the reconstruction results when sufficiently large. In the present study, this parameter was set significantly larger than the Shannon theorem’s lower limit to give enough accuracy, but with an acceptable image reconstruction time.

Numerical simulations

The simulation aimed to demonstrate the dynamic focusing ability of our method. In the simulation, the forward data were generated using equation 2. The aperture of the focused transducer was 3 mm in diameter, which consisted of 7,845 evenly distributed point detectors. The central frequency of the transducer was 40 MHz, and the band width was about 70%. The distance between the reflection mirror and the transducer L1 was fixed to 2 mm, and the transducer focal length was 7.5 mm, so the working distance L2 was 7.5–2 mm=5.5 mm. This set of parameters was similar to some existing small ARPAE catheters (1-3). A sufficient large judge angle of 50° was set through the paper, compared with D/(2(L1+R)), which was about 9.5° here. The sectorial scan in the x–y plane was performed from –60° to 60° relative to the x-axis in 480 steps, and the scan along the z direction was from –2 to 2 mm in 161 steps. 7-point targets were evenly distributed between 2.5, 0, 0 and 8.5, 0, 0, with an interval of 1 mm in the x direction, which were later reconstructed with the conventional method and our proposed method. For the noise assessment, Gaussian white noise was added to the simulated data using the Box-Muller method, with a standard deviation (SD) of 2% of the peak signal. The full widths at half-maxima (FWHM) of the target lateral profiles (created with the maximum projection of the targets) in both the y and z directions were obtained as lateral resolutions in these 2 directions. The SNR of the targets were also calculated to compare the 2 methods using the following equation:

SNR = 20log10 (MaxT/SDb),[4]

MaxT is the amplitude of the reconstructed targets, and SDb is the SD of a selected background region in the reconstructed images. This region was selected as a 0.5-mm size cube between the first and second point targets in this simulation.

Phantom experiments

Two phantoms were imaged. The first phantom were inserted with 34 metal wires (0.15 mm thick) as point targets in the background to verify the improvement of lateral resolution with our proposed method. The second phantom was with a piece of fresh harvested pig intestine buried to explore our method’s capability for imaging biologic samples. The phantom (made of agar, intralipid, and ink) had a scattering coefficient of 1 mm^–1 and an absorption coefficient of 0.07 mm^–1 for the background. Its inner diameter was about 15 mm and its outer diameter was about 40 mm.

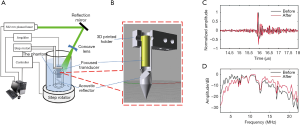
Figure 2A shows the schematic of the 3D ARPAE scanning system. Pulsed 532 nm laser from a Neodymium-doped yttrium aluminum garnet (Nd:YAG) laser (Nimma-600; Beamtech Optronics, Beijing, China) was delivered to the top surface of the hollow structured phantom by a reflection mirror and a concave lens. The illumination area on the phantom was about 2 cm², with an almost homogeneous intensity of 3 mJ/cm². A focused transducer (V324-SM; Olympus NDT; 25 MHz central frequency, 6 mm element size, about 15 mm focal length) was mounted on a 3D printed photopolymer holder inserted into the center hole of the phantom for the endoscopic scan. The 3D printed transducer holder had a 45° tilted acoustic reflector structure below the transducer to reflect the generated photoacoustic signals (Figure 2B), and the working distance was about 10 mm. The signal from the transducer was successively amplified with a home-built radiofrequency amplifier (30 dB) and a pulser/receiver (5073PR; Olympus NDT; 20 dB gain), and then digitalized with a DAQ card (LDI400SE; DIYANG; 100 MHz sampling frequency). The final acquired signal was averaged 4 times. The phantom was mounted at the bottom of the water tank and rotated by a step rotator for the 360° circular scan in the x-y plane, with a step number of 360. Following each circular scan in the x-y plane, the focused transducer and its holder was driven by a line step motor along the z direction with a step size of 0.25 mm for the 3D volume scan. The step numbers in the z direction for the first and second phantoms were 50 and 32, respectively. Whole scanning was synchronized with the pulsed laser.

Figure 2 Schematic of the 3D acoustic resolution photoacoustic endoscopy (ARPAE) phantom experiments and data preprocessing. (A) Imaging system. (B) 3D printed holder for the focused transducer. (C) Representative signal from a metal wire before and after preprocessing. (D) Frequency charts for the representative metal wire signal before and after preprocessing.

Data processing

Before the 3D reconstruction, the collected experimental data were differentiated to filter out the low-frequency noise to which our method is quite sensitive, so that the strong background artifacts in the tangential direction in our previous work could be avoided. Hilbert transform was then applied. Data differentiation results of a representative data from a metal wire in the first phantom experiment are shown in Figure 2C and D. Although the focused transducer’s central frequency was 25 MHz, the obtained original signal was about 4–13.5 MHz in –6 dB bandwidth, whose envelope after Hilbert transform was about 0.095 µs in FWHM, which coincided with the thickness of the metal wire (0.15 mm). After the differential, the signal’s lower-frequency component was well reduced, the main frequencies of the signal were shifted 3 MHz higher, and the signal envelope was improved to 0.075 µs. Therefore, the image resolution was slightly improved due to data preprocessing.

The image reconstruction with our proposed method was accelerated by a Graphics Processing Unit (GPU) parallel technique running on a Tesla P100 PCI-E 16 GB card, which was about 700 times faster than running on a PC with an Intel Core i7-4700MQ CPU and 8 GB memory. In the reconstruction with our phantom experimental data method, the detector aperture was divided into 31,417 point detectors. The signal summing for different detector position-voxel pairs was performed in different grids, and the signal summing for different point detectors at the same transducer position was calculated with the threads in the same grid. Pined memories were created for the collected data and the reconstructed 3D images to accelerate the calculation, and 100 voxels were calculated each time in the kernel due to the time limit of the GPU card. 3D images with the conventional ARPAE reconstruction method were also obtained for comparison. For 3D image display, the complex voxel value amplitude was obtained, and the maximum value of each 3D set of images was normalized to 1. Amira (Visage Imaging) was used to render the 3D images.

Results

Simulation results

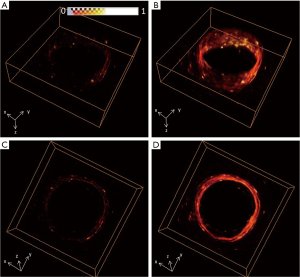
Figure 3A shows the reconstructed image with the conventional method in the x-y plane through the targets, compared with the corresponding results with our proposed method in Figure 3B. Figure 3C and D shown the reconstruction results with the conventional method and our proposed method in the x-z plane, respectively. Figure 3E shows the obtained lateral resolutions from Figure 3A, B, C, and D. Figure 3F shows the calculated SNRs of the targets with the 2 methods.

Figure 3 Reconstruction results with the conventional acoustic resolution photoacoustic endoscopy (ARPAE) method and our proposed method. Results with the conventional method (A) and our proposed method (B) in the x-y plane. (C,D) Results for the x-z plane. (E) Extracted lateral resolutions along the y-axis and z-axis. (F) Obtained signal-to-noise ratios for the targets.

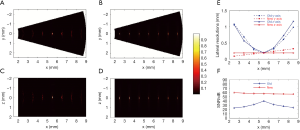
It can be seen that our proposed method not only gave a lateral resolution close to the conventional method near the transducer focus, but also effectively improved the lateral resolution for targets out of the transducer focal zone (Figure 3E). Our proposed method’s lateral resolution improved more than 11 times in the y-direction for the target at 2.5 mm. The lateral resolution with our proposed method in the x–y plane increased as the targets moved away from the rotation center (Figure 3E). When the target was closer than the transducer focal region, our proposed method demonstrated a lateral resolution superior to that of the focused transducer’s focal waist in the x–y plane. The lateral resolution in the z-direction was almost identical along the x direction, which was close to the lateral resolution obtained with the conventional method at the transducer focus. As shown in Figure 3F, the SNRs of the out-of-focus regions’ targets were significantly low with the conventional method, which was up to 17 dB lower than the target at the transducer focus. In comparison, our proposed method demonstrated that the SNRs for these targets were greatly improved, so that the depth of SNRs of all the targets were similar. Our proposed method also improved the SNR of the target in the transducer focal zone (up to 20 dB), which was due to the averaging of the photoacoustic signals so that the background noise was low.

Phantom experiment results

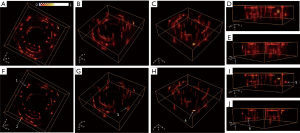
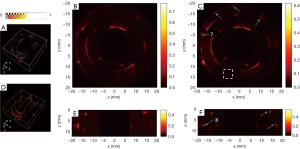
The reconstructed images of the first phantom with the conventional method from different views are shown in Figure 4A,B,C,D,E, and the corresponding results with our proposed method are shown in Figure 4F,G,H,I,J. The image quality with our proposed method was clearly improved compared with Figure 4A,B,C,D,E. The reconstruction domain was 40×40×12.5 mm, with a voxel size of 0.1×0.1×0.125 mm. Representative targets were selected and marked with white arrows for demonstration. As seen in Figure 4F and G, the lateral profiles in the x–y plane for targets 1–3 were notably improved compared with those in Figure 4A and B; the lateral profiles in the z direction for targets 4–6 in Figure 4H,I,J were clearly thinner than the corresponding results in Figure 4C,D,E.

Figure 4 Reconstructed 3D results of the metal wire phantom in different views with the conventional method (A-E) and our proposed method (F-J).

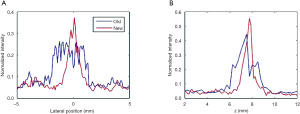
The 2D reconstruction results of the first phantom with the conventional method and our proposed method in the x–y and x-z planes are shown in Figure 5. The lateral profiles of the targets marked with white arrows in Figure 5C and F are thinner, with corresponding results in Figure 5B and E. We extracted the lateral profile of target 7 in the x–y plane, and the lateral profile of target 8 in the z direction, as shown in Figure 6A and B, respectively, and obtained their FWHM. For the SNR calculation, a small 4×4 mm rectangular region was selected in the phantom background, as indicated in Figure 5C. The obtained FWHM and SNRs of these 2 targets are summarized in Table 1. It can be seen that, using our method, the SNR of target 7 increased about 6.5 dB, and the FWHM of its lateral profile in the x–y plane improved from 3.34 to 1.08 mm; the SNR of target 8 also increased 5.2 dB, and the FWHM of its lateral profile in the z direction improved from 2.42 to 0.77 mm.

Figure 5 Comparison of the 2D reconstruction results of the metal wire phantom with the conventional acoustic resolution photoacoustic endoscopy method and our proposed method. (A) The picked x-y plane as indicated in the 3D image. (B,C) Reconstruction results of the x–y plane with the conventional method and our proposed method, respectively. (D) The picked x-z plane. (E, F) Corresponding results for the x–z plane.

Figure 6 Comparison of the target lateral profiles with the conventional acoustic resolution photoacoustic endoscopy method (blue lines) and our proposed method (red lines). (A) Reconstruction lateral profiles in the x–y plane with the 2 methods for target 7. (B) Corresponding results of the lateral profiles along the z direction for target 8.

Table 1 Comparison of SNR and FWHM between the conventional method and our proposed method
Full table

Figure 7 shows the reconstruction results of the second phantom with the conventional method (Figure 7A,C) and our proposed method (Figure 7B,D) from different views. The reconstruction domain was 30×30×8 mm, and the voxel size was also 0.1×0.1×0.125 mm. Figure 8 shows the 2D reconstruction results of the x–y plane and the results of the 2D x-z plane. With the conventional method, the pig intestine was hardly seen due to the low SNR. However, with our proposed method, the overall image quality was greatly improved, and the walls of the sample which were hardly seen in Figure 8B and E were clearly imaged in Figure 8C and F, as indicated by the white arrows.

Figure 7 Reconstruction results of the pig intestine phantom in different views with the conventional method (A, C) and the proposed method (B, D).

Figure 8 Comparison of the 2D reconstruction results of the pig intestine phantom with the conventional acoustic resolution photoacoustic endoscopy method and our proposed method. (A) The picked x-y plane as indicated in the 3D image. (B, D) Reconstruction results of the x–y plane with the conventional method and our proposed method, respectively. (D) The picked x-z plane. (E, F) Corresponding results for the x–z plane.

Discussion

There have been a variety of designs for ARPAE catheters. Some ARPAE catheters are front view based and employ a fiber bundle, such as the Fabry-Pérot-based ultrasound detection array (26); some employ a large-size ring-shaped multiple element transducer array (27); and some employ an annular transducer array for in-depth dynamic focusing (8). However, these designs all have disadvantages in functionality, size, cost, resolution, and sensitivity. Current ARPAE catheters are based on a single focused transducer for tight acoustic focusing deep in the tissue and a rotation mirror to perform the 3D helical side-view scan. This simple and compact design has the merits of easy miniaturization, deep penetration, high lateral resolution, and high sensitivity. However, most current reconstruction algorithms for this kind of ARPAE catheter design only give 2D sectorial B-mode images, in which the collected photoacoustic data are directly back-projected along the transducer axis based on the signal’s acoustic flight time to obtain the tissue’s local optical absorption (1-4). These algorithms simply assume that the ultrasound beam travels along a straight thin line, which is only valid in the transducer focal zone, so that the lateral resolution and SNR in the out-of-focus region are significantly low due to the model mismatch. To overcome this problem, we proposed a new reconstruction algorithm for the prototype ARPAE catheter design. This new method inherently considers the 3D acoustic field of the focused transducer by the finite discretion of its detecting surface, improving the photoacoustic wave propagation during the signal collection. Therefore, high lateral resolution is not only achieved with the transducer’s focus, but also in the out-of-focus region. This method can also greatly improve the SNRs for targets in the out-of-focus regions so as to provide homogenous SNRs. In addition, compared with our previously proposed 2D algorithm, the new algorithm extends the dynamic focusing of ARPAE to 3D, which is critical to promote the biomedical application of ARPAE, as ARPAE is essentially 3D. This new method can be readily applied for most current ARPAE systems of this prototype catheter design.

With the dynamic imaging using our proposed method, both the lateral resolutions and the SNRs in the out-of-focus regions are improved to the same level as the transducer focal region. This means that the sensitivity of the system in these regions is greatly improved. As a consequence, some detailed information in these out-of-focus regions may not be revealed by the conventional method, but they can now be reliably detected with our proposed new method. Our proposed method also helps to lower the background noise. The lateral resolution along the depth direction is different in the x-y plane from that in the x-z plane, as shown in the simulation results. The lateral resolution in the x-y plane increases as the target moves far from the rotation center, while the lateral resolution in the x-z plane is almost spatially invariant. The anisotropy of lateral resolution is due to the difference in the scanning mode in these 2 planes. Based on the ex-vivo experiment results, our proposed method provides clearer boundaries and finer details of the pig intestine, supporting the potential of our proposed method over the conventional method in future biomedical applications. Furthermore, the proposed method can be easily modified, so that dynamic focusing can be realized for simultaneous photoacoustic and ultrasound endoscopic imaging.

However, the present study has some limitations. We only carried out a simple phantom experiment to demonstrate our proposed method. The system is based on a focused transducer with a relatively large diameter, and the central frequency of the collected signal was low due to the size of the sample. For example, the thickness of the metal wire was 0.15 mm, leading to a low-signal central frequency. Our previous study already showed that the proposed method was more effective for transducers with high central frequency and shorter working distance. A compact ARPAE catheter with higher spatial resolution and scanning speed for in-vivo experiments would be beneficial. Another major limitation in our proposed method was the long computational time. In this work, the typical reconstruction time for a single 451×301 pixel image (Figure 3B) was about 3.4 min (compared with Figure 3A, which was <1 s), which may be reduced by optimizing the scanning and reconstruction parameters. Therefore, future studies should include building smaller catheters with higher central frequencies and scanning speeds for real in-vivo experiments, developing new algorithms, and developing simultaneous photoacoustic and ultrasound endoscopic imaging.

In conclusion, we proposed, for the first time, a modified back-projection method for 3D ARPAE. By considering the geometry of the detecting surface of the focused transducer in the image reconstruction, this method can achieve dynamic focusing in ARPAE, and significantly improve the lateral resolution and SNR in out-of-focus regions. The pig intestine phantom experiment also demonstrated that our proposed method can improve image quality over the conventional ARPAE method. These promising results suggest that our proposed method is a suitable alternative to the conventional ARPAE method.

Acknowledgments

Funding: The present study was funded by the National Natural Science Foundation of China (No. 81501517, 61401520) and the Fundamental Research Funds for the Central Universities of Central South University (No. 2018zzts826).

Footnote

Conflicts of Interest: All authors have completed the ICMJE uniform disclosure form (available at http://dx.doi.org/10.21037/qims-20-625). The authors have no conflicts of interest to declare.

Ethical Statement: Ethical approval/informed consent was not applicable, because the in-vitro pig intestine in the phantom experiment was obtained from a local market.

Open Access Statement: This is an Open Access article distributed in accordance with the Creative Commons Attribution-NonCommercial-NoDerivs 4.0 International License (CC BY-NC-ND 4.0), which permits the non-commercial replication and distribution of the article with the strict proviso that no changes or edits are made and the original work is properly cited (including links to both the formal publication through the relevant DOI and the license). See: https://creativecommons.org/licenses/by-nc-nd/4.0/.

References

1. Yang JM, Li C, Chen R, Zhou Q, Shung KK, Wang LV. Catheter-based photoacoustic endoscope. J Biomed Opt 2014;19:066001. [Crossref] [PubMed]
2. Yang JM, Favazza C, Yao J, Chen R, Zhou Q, Shung KK, Wang LV. Three-dimensional photoacoustic endoscopic imaging of the rabbit esophagus. PLoS One 2015;10:e0120269. [Crossref] [PubMed]
3. Yang JM, Chen R, Favazza C, Yao J, Li C, Hu Z, Zhou Q, Shuang KK, Wang LV. A. 2.5-mm diameter probe for photoacoustic and ultrasonic endoscopy. Opt Express 2012;20:23944-53. [Crossref] [PubMed]
4. Li C, Yang JM, Chen R, Yeh CH, Zhu L, Maslov K, Zhou QF, Shuang KK, Wang LV. Urogenital photoacoustic endoscope. Opt Lett 2014;39:1473-6. [Crossref] [PubMed]
5. Li H, Jiang LJ, Liu Q, Fu L. Advanced endoscopic methods in gastrointestinal diseases: a systematic review. Quant Imaging Med Surg 2019;9:905-20. [Crossref] [PubMed]
6. Cao Y, Hui J, Kole A, Wang P, Yu Q, Chen W, Sturek M, Cheng J. High-sensitivity intravascular photoacoustic imaging of lipid–laden plaque with a collinear catheter design. Sci Rep 2016;6:25236. [Crossref] [PubMed]
7. Li Y, Lin R, Liu C, Chen J, Liu H, Zheng R, Gong X, Song L. In vivo photoacoustic/ultrasonic dual-modality endoscopy with a miniaturized full field-of-view catheter. J Biophotonics 2018;11:e201800034. [Crossref] [PubMed]
8. Xiao J, Wang T, Peng K, Zhang X, Wang B. Lithography of Aluminum coated PVDF annular array for photoacoustic endoscopy. Commun Comput Phys 2018;23:561-71. [Crossref]
9. Wang H, Xing D, Xiang L. Photoacoustic imaging using an ultrasonic fresnel zone plate transducer. J Phys D: Appl Phys 2008;41:095111. [Crossref]
10. Yin G, Xing D, Yang S. Dynamic monitoring of blood oxygen saturation in vivo using double-ring photoacoustic sensor. J Appl Phys 2009;106:013109. [Crossref]
11. Passler K, Nuster R, Gratt S, Burgholzer P, Paltauf G. Piezoelectric annular array for large depth of field photoacoustic imaging. Biomed Opt Express 2011;2:2655-64. [Crossref] [PubMed]
12. Liao CK, Li ML, Li PC. Optoacoustic imaging with synthetic aperture focusing and coherence weighting. Opt Lett 2004;29:2506-8. [Crossref] [PubMed]
13. Li ML, Zhang HF, Maslov K, Stoica G, Wang LV. Improved in vivo photoacoustic microscopy based on a virtual-detector concept. Opt Lett 2006;31:474-6. [Crossref] [PubMed]
14. Deng Z, Yang X, Gong H, Luo Q. Two-dimensional synthetic-aperture focusing technique in photoacoustic microscopy. J Appl Phys 2011;109:104701. [Crossref]
15. Zhang W, Ma H, Cheng Z, Wang Z, Yang S. Miniaturized photoacoustic probe for in vivo imaging of subcutaneous microvessels within human skin. Quant Imaging Med Surg 2019;9:807-14. [Crossref] [PubMed]
16. Turner J, Estrada H, Kneipp M, Razansky D. Improved optoacoustic microscopy through three-dimensional spatial impulse response synthetic aperture focusing technique. Opt Lett 2014;39:3390-3. [Crossref] [PubMed]
17. Cai D, Li Z, Li Y, Guo Z, Chen SL. Photoacoustic microscopy in vivo using synthetic-aperture focusing technique combined with three-dimensional deconvolution. Opt Express 2017;25:1421-34. [Crossref] [PubMed]
18. Park J, Jeon S, Meng J, Song L, Lee JS, Kim C. Delay-multiply-and-sum-based synthetic aperture focusing in photoacoustic microscopy. J Biomed Opt 2016;21:36010. [Crossref] [PubMed]
19. Cai D, Li Z, Chen SL. Photoacoustic microscopy by scanning mirror-based synthetic aperture focusing technique. Chin Opt Lett 2015;13:101101. [Crossref]
20. Jeon S, Park J, Managuli R, Kim C. A novel 2-D synthetic aperture focusing technique for acoustic-resolution photoacoustic microscopy. IEEE trans Med Imag 2018;38:250-60.
21. Jeon S, Park EY, Choi W, Managuli R, Lee K, Kim C. Real-time delay-multiply-and-sum beamforming with coherence factor for in vivo clinical photoacoustic imaging of humans. Photoacoustics 2019;15:100136. [Crossref] [PubMed]
22. Cai D, Li G, Xia D, Li Z, Guo Z, Chen SL. Synthetic aperture focusing technique for photoacoustic endoscopy. Opt Express 2017;25:20162-71. [Crossref] [PubMed]
23. Wang B, Wei N, Peng K, Xiao J. Modified back-projection method in acoustic resolution-based photoacoustic endoscopy for improved lateral resolution. Med Phys 2018;45:4430-8. [Crossref] [PubMed]
24. Lingvall F. User Manual for the DREAM Toolbox Version 2.1.3 an ultrasound simulation software for use with Matlab and GNU Octave. 2009. Available online: http://www.signal.uu.se/Toolbox/dream/userman-2.1.3.pdf
25. Piwakowski B, Sbai K. A new approach to calculate the field radiated from arbitrarily structured transducer arrays. IEEE Trans Ultrason Ferroelectr Freq Control 1999;46:422-40. [Crossref] [PubMed]
26. Ansari R, Zhang E, Mathews S, Desjardins AE, Beard PC. Photoacoustic endoscopy probe using a coherent fibre-optic bundle. Eur Conf Biomed Opt 2015;142:3399-404.
27. Yuan Y, Yang S, Xing D. Three-dimensional endoscopic photoacoustic imaging based on multielement linear transducer array. J Appl Phys 2011;110:1. [Crossref]