Quantitative assessment of inter-individual variability in fMRI-based human brain atlas

Introduction

Human brain atlases, which represent the spatial and functional parcellation of the brain, are critical for visualizing the brain’s functional organization (1,2). A major challenge for neuroscience research is to delineate the hundreds of different brain regions based on functional and anatomical criteria. In the last few decades, features extracted by structural and functional magnetic resonance imaging (MRI) of different brain regions have been used to accurately segment the human brain (3-5), producing databases of reliable brain parcellations (6). Parcellations based on structural MRI which is acquired on a none-ultra-high field scanner (3T and below) are clinically useful as they demarcate physical regions of individual brains, but have low resolution; on the other hand, those based on functional (f)MRI which is acquired on a none-ultra-high field scanner (3T and below) are more precise but are difficult to apply to individual assessments (7-11). Therefore, many studies have employed group-average brain atlases such the Anatomical Automatic Labeling atlas to analyze the brain at the group level (11). However, inter-individual variability in fMRI-based parcellations limit their clinical utility—for example, for pre-surgical functional localization (12).

The temporal signal-to-noise ratio (SNR) for the blood oxygenation level-dependent (BOLD) signals is relatively low, so features extracted from fMRI that are obtained in a short time interval (<30 min) cannot be used to accurately segment individual human brains (13,14). To overcome this problem, individual data have been used to verify group-level centralized trends that include individual information (15). Although a large number of datasets are used to reduce inter-individual variability, unique features in each brain are overlooked in group-level analyses (16,17).

Many studies have investigated methods for accurate parcellation of individual brains (15,18,19). For instance, one study segmented a single brain based on resting-state functional connectivity (RSFC) fMRI data collected over 14 h (12). The study demonstrated that accurate individual brain parcellations can be obtained with a large amount of data, in greater detail than by group-level data analysis. However, the data collection period was long (1 year), which can be useful in cases of rare neurologic disease but is too long for those requiring an immediate diagnosis (20), for which accurate group-level brain parcellations are more appropriate. However, although many parcellations are available online, there are no methods for identifying the one that is most suited to a particular study or clinical application (6). Furthermore, there have been no quantitative assessments of inter-individual variability in resting-state fMRI-based human brain atlases, which is required to ensure the accuracy of data interpretation.

To this end, the aim of the present study was to quantify the inter-individual variability in different brain atlases using tasked-based fMRI data from hand and foot motor regions and temporal lobe language regions in both hemispheres of healthy young subjects. Briefly, we compared the sites of maximal activation of six brain areas in Montreal Neurological Institute (MNI) space to the coordinates of corresponding regions in nine brain atlases. The Euclidean distance (ED) between tasked-based fMRI hotspots and functional areas in the brain atlases was calculated as a feature of inter-individual variability. We also compared the inter-individual variability in six motor regions and evaluated the influence of different brain atlases on the extraction of tasked-based fMRI general linear model (GLM) parameters. Based on previous findings, we hypothesized that (I) inter-individual variability significantly differed across different brain atlases for the same fMRI dataset, and (II) inter-individual variability significantly differed across different brain regions for the same fMRI dataset. Our findings provide insights that can guide the application of brain atlases in clinical and research settings.

Methods

Participants and data acquisition

We analyzed complete motor task-based fMRI and T1 data of 1,080 subjects from the Human Connectome Project (HCP) database (21) in the present study. The data were acquired on a 3T Skyra scanner (Siemens, Erlangen, Germany) using a 32-channel head coil. BOLD changes were examined in gradient-echo echo-planar imaging sequence with the following parameters: repetition time (TR) =720 ms; echo time (TE) =33.1 ms; flip angle =52°; field of view (FOV) =208×180 mm [readout (RO) × phase-encoding (PE)]; matrix =104×90 (RO × PE); slice thickness =2.0 mm; 72 slices; 2.0 mm isotropic voxels; multiband factor =8; echo spacing =0.58 ms; and bandwidth (BW) =2,290 Hz/pixel. T1 data were obtained in a magnetization prepared rapid gradient echo sequence with the following parameters: TR =2,400 ms; TE =2.14 ms; TI =1,000 ms; flip angle =8°; FOV =224×224; voxel size =0.7 mm isotropic; BW =210 (Hz/pixel); integrated parallel acquisition technique =2; and acquisition time =7:40 (min:s).

Details of the motor task-based fMRI data from the HCP database have been previously reported (22). Briefly, subjects were shown 3-s text cues instructing them to tap their fingers, squeeze their toes, or move their tongue to activate different motor brain regions. Ten movements for each motor task were executed for 12 s. Each subject participated in two runs of 13 motor tasks (two tasks each for tongue, right hand (RH), left hand (LH), right foot (RF), and left foot (LF); and three 15-s fixation tasks performed to obtain baseline measurements). Details of the language task-based fMRI data from the HCP database have been previously reported (23). Briefly, the task consists of two runs that each interleave 4 blocks of a story task and 4 blocks of a math task. Each task were executed for approximately 30 seconds, however, each task was designed in order that the math task blocks match the length of the story task blocks, with some additional math trials at the end of each task. The Story–Math protocol provides a reliable method for activation of the temporal lobe language regions of the left (LL) and right (RL) hemispheres. Two runs of each sequence were performed (Figure 1); the activation sequences from left to right hemisphere and from right to left hemisphere were defined as LtoR and RtoL, respectively. The study were approved by the Joint Ethics Committee of the Chinese Academy of Medical Sciences and Peking Union College.

Figure 1 Block diagram of experimental procedures and data analysis.

FMRI preprocessing

Statistical Parametric Mapping (SPM)12 (London, UK) software package in Matlab v.2013b (MathWorks, Natick, MA, USA) was used to process T1 and task-based fMRI data. Task-based fMRI volumes of LtoR and RtoL motor and language task fMRI runs were realigned to the mean volume of each run. T1 volumes were coregistered with realigned task-based fMRI volumes, and all volumes were normalized to MNI space using the standard segmentation method for group-level analysis. Task-based fMRI volumes were smoothed using an isotropic Gaussian kernel with 4 mm full width at half-maximum (FWHM). A larger FWHM improves SNR but reduces spatial resolution. The voxel size of our data was 2 mm × 2 mm × 2 mm; setting the FWHM to 2 to 3 times the voxel size is considered acceptable (24,25). As high spatial resolution was critical for our analyses, we changed the FWHM of the isotropic Gaussian kernel to 4 mm in SPM12. A flow diagram of tasked-based fMRI data preprocessing is shown in Figure 1.

Feature extraction and fMRI statistics

For single participant first-level modeling, a GLM design matrix was constructed based on the experimental design (26). Signal drift periods longer than 128 s were removed with a 1/128-Hz high-pass filter. Realignment parameters based on head movement were introduced as multiple regressors, and GLM parameters were estimated using classic approaches. Four t-contrast vectors were defined to generate statistical parametric maps of the LF, LH, RF, and RH against the fixation baseline. Two t-contrast vectors were defined to generate statistical parametric maps of the story against the math baseline. The blocked tongue movement task was not included in analysis due to the complexity of head muscles.

Subjects 1 to 50 were selected for second-level modeling. A one-sample t test was used to analyze group-level activation of six separate brain regions with a random-effects model (voxel-level family-wise error correction method, P<0.05) (27). The largest activation cluster was selected from primitive SPM {T} mapping; the selected LF, RF, LH, RH, LL and RL activation regions are shown in Figure 2. Six binary masks were extracted from these clusters to negate the impact of the remaining brain data on the results. For each subject, the peak-level activation point in a mask was identified from the corresponding SPM {T} map. The coordinates in MNI space were recorded as a feature parameter of each activated region. The above processing steps yielded twelve feature coordinates for each subject representing the activated points in brain regions representing the LF, LH, RF, RH, LL and RL. Each brain region had two feature coordinates from two runs. It should be noted that not all twelve regions in each subject could be activated; data for a subject were excluded if there was one region that was not activated. Ultimately, data for 893 subjects were used for further analysis. Additionally, mean values of parameters that were estimated by the GLM in first-level modeling for each subject were also calculated using masks selected from nine brain atlases and second-level modeling analysis.

Figure 2 Definition of mask with region of interests (ROIs) from task-based functional MRI (fMRI) LtoR runs. (A) Left foot (LF); (B) left hand (LH); (C) right foot (RF); (D) right hand (RH); (E) left language (LL) and right language (RL).

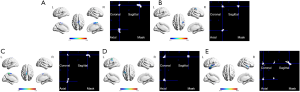
Atlas selection

Brain atlases can be divided into three categories according to the type of raw data (i.e., structural images, resting-state (rs-)fMRI, and multi-modal images) used in their construction. The parcel numbers of an atlas based on macro-anatomical information extracted from structural images were 60 to 150. The primary motor cortex is in the precentral gyrus. Brain atlases were screened based on the following criteria: (I) the precentral gyrus and paracentral lobule were segmented; and (II) central or maximum probabilistic coordinates of each region were reported in the publication or were retrievable online. Based on these criteria, nine brain atlases from six studies were selected for analysis (Table S1). Five studies involved rs-fMRI, and one utilized probabilistic diffusion tractography calculated from structural MRI, rs-fMRI, and diffusion MRI. The parcel numbers of the selected atlases were 184 to 400.

It should be noted that not all brain atlases described the functionality of each brain region in detail. For instance, one study reported hand regions in the precentral gyrus of the left and right hemispheres at (−26, −25, 63) and (34, −19, 59) in MNI space, foot regions in the paracentral lobule of the left and right hemispheres at (−8, −38, 58), (−4, −23, 61) and (10, −34, 54), (5, −21, 61), and temporal lobe language regions of the left and right hemispheres at (−55, −3, −10) and (56, −12, −5), respectively, in MNI space (28). Thus, for the other eight atlases, regions that were closest to the above coordinates in precentral gyrus, paracentral lobule and anterior temporal lobe were selected as corresponding functional regions; their coordinates are presented in Table S1.

Statistical tests

Inter-individual variability in each brain atlas was assessed by calculating the ED between brain atlas coordinates and a subject’s maximum activation point for each region in MNI space according to the following equation:

$$D=\sqrt{（x_{(i,rg)}-x_{(j,rg)}{）}^2+（y_{(i,rg)}-y_{(j,rg)}{）}^2+（z_{(i,rg)}-z_{(j,rg)}{）}^2}(i=1\mathrm{...}893,j=1\mathrm{...}9,rg=1\mathrm{...}6)$$[1]

where x (i,rg), y (i,rg), and z (i,rg) are the coordinates of each subject’s maximum activation point; i is the subject number; x (j,rg), y (j,rg), and z (j,rg) are the atlas coordinates; j is the atlas number, and rg is the region. Data from two runs were calculated separately, yielding eight characteristic EDs for each subject.

The mean value of GLM parameters was also calculated with the equation below to assess the inter-individual variability of each brain atlas:

$$\overline{\beta }=\frac{{\displaystyle \sum _{(x,y,z)\in mask}{\beta }_{(x,y,z)}}}{N}$$[2]

where β is the estimated GLM parameter in each mask and N is the number of voxels in the calculation.

We used the paired t test for data validation; two-way analysis of variance (ANOVA) to evaluate significant differences in EDs and extracted GLM parameters; and linear regression to assess the linear interdependence of parcel number and EDs and of GLM parameters and ED. One-way ANOVA was used to evaluate differences between EDs of different regions. All statistical analyses were performed using Prism 6 software (GraphPad Inc., La Jolla, CA, USA).

Results

Data validation

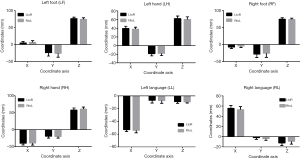
All subjects participated in two runs of the motor and language task-based fMRI test; data for 893 subjects with all six regions activated in the two runs were available for analysis. That is, for each region in each subject, two feature coordinates were obtained. Given the low SNR of the BOLD signals, no significant differences were found in the group-level analysis of the two runs of data. The means and standard deviations of maximum activation coordinates of the six brain regions are shown in Figure 3. A two-tailed paired t test showed no significant difference between the two runs for each of the six regions (LF, P=0.6252; LH, P=0.3633; RF, P=0.3731; RH, P=0.4828; LL, P=0.092 and RL, P=0.8119).

Figure 3 Coordinates of subjects’ maximum activation points in the LF, LH, RF, RH, LL and RL. The symbols and error bars represent mean values and standard deviations, respectively, of 893 subjects.

Inter-individual variability of ED in brain atlases

The mean EDs between brain atlas coordinates and subjects’ maximum activation points in four motor regions were calculated as the inter-individual variability of each atlas, and their significance was evaluated by two-way ANOVA (Figure 4A). The factors in the analysis were two runs of task-based fMRI (LtoR and RtoL) and nine brain atlases. The 893 subjects showed a significant interaction effect [SS =772.7, DF =8, MS =96.59, F(8, 16056) =13.79, P<0.0001]; inter-individual variability differed across the nine brain atlases [SS =108,631, DF =8, MS =13,579, F(8, 16056) =1,939, P<0.0001], with no significant differences between the two runs of each scan [SS =9.213, DF =1, MS =9.213, F(1, 16056) =1.316, P=0.2514]. The mean EDs between brain atlas coordinates and subjects’ maximum activation points in two language regions were calculated as the inter-individual variability of each atlas, and their significance was evaluated by two-way ANOVA (Figure 4B). The factors in the analysis were two runs of task-based fMRI (LtoR and RtoL) and nine brain atlases. The 893 subjects showed a significant interaction effect [SS =1,545, DF =8, MS =193.1, F(8, 16056) =6.444, P<0.0001]; inter-individual variability differed across the nine brain atlases [SS =95,882, DF =8, MS =11,985, F(8, 16056) =399.9, P<0.0001], with significant differences between the two runs of each scan [SS =5,094, DF =1, MS =5,094, F(1, 16056) =170, P<0.0001]. The minimum mean EDs in four motor regions was gotten at Schaefer’s brain Atlas consisted of 200 parcels (12.66±2.69 mm for LtoR, 12.85±2.79 mm for RtoL). The minimum mean EDs in two language regions was gotten at Schaefer’s brain Atlas consisted of 200 parcels (7.99±3.77 mm for LtoR, 7.57±3.78 mm for RtoL).

Figure 4 Inter-individual variability in euclidean distance (ED) in different brain atlases. (A) ED between brain atlas coordinates and subjects’ maximum activation point of four motor regions. (B) ED between brain atlas coordinates and subjects’ maximum activation point of two language regions. (C) Interdependence of mean ED in four motor brain regions on parcel number in the brain atlas. (D) Interdependence of mean ED in two language brain regions on parcel number in the brain atlas. Symbols and error bars represent mean values and standard deviations, respectively, of four motor regions in the 893 subjects. Linear regression lines are also shown.

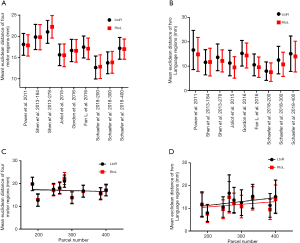
The interdependence between parcel number and inter-individual variability was evaluated by linear regression analysis (Figure 4C for motor regions and Figure 4D for language regions). There was no correlation between parcel number and inter-individual variability of LtoR (r=0.01021, F=0.07221, P=0.7959) and RtoL (r=0.01357, F=0.09629, P=0.7654) ED for motor regions. There was no correlation between parcel number and inter-individual variability of LtoR (r=0.2222, F=2, P=0.2002) and RtoL (r=0.1232, F=0.9832, P=0.3544) ED for language regions.

Inter-individual variability of ED in different brain regions

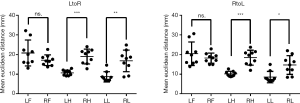
We next examined the inter-individual variability in different brain regions (Figure 5). The mean LtoR EDs and standard deviations of the LF (20.84±6.56), RF (17.16±2.75), LH (10.72±1.39), RH (19.02±3.8), LL (8.7±2.63) and RL (16.81±5.49) and mean RtoL EDs and standard deviations of the LF (20.44±5.97), RF (18.22±2.58), LH (10.16±1.35), RH (18.4±3.83), LL (8.56±2.9) and RL (14.7±4.78) were calculated. One-way ANOVA and Tukey’s multiple post-hoc comparisons test were used to analyze the inter-individual variability of ED in different brain regions. The results showed significant differences for LtoR [F=11.88, sum of squares (SS) =1,862, degrees of freedom (DF) =53, P≤0.0001] and RtoL (F=13.98, SS =1,768, DF =53, P≤0.0001) in different brain regions. Tukey’s test results indicated that LtoR (P=0.0008) and RtoL (P=0.0004) EDs were higher for the RH than for the LH, LtoR (P=0.0019) and RtoL (P=0.0179) EDs were higher for the RL than for the LL, whereas no difference was observed between the RF and LF (LtoR, P=0.2469 and RtoL, P=0.6140).

Figure 5 Inter-individual variability of euclidean distance (ED) in different brain regions. EDs between brain atlas coordinates and subjects’ maximum activation points. Symbols and error bars represent mean values and standard deviations, respectively, of EDs in each region for 893 subjects in the nine brain atlases. *P<0.05; **P<0.01; ***P<0.001.

Interdependence of inter-individual variability of EDs in different brain regions

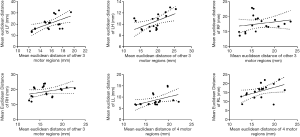
The interdependence between mean ED in one motor region and the other three motor regions was evaluated by linear regression analysis; the interdependence between mean ED in language region and four motor regions was also evaluated by linear regression analysis; data from the two runs were calculated and are presented in Figure 6. A positive correlation was observed between the LH and the other three motor regions (slope =0.23±0.085, r=0.3196, F=7.515, P=0.0145), between the LF and the other three motor regions (slope =1.80±0.62, r=0.3459, F=8.461, P=0.0103) and between the LL and the four motor regions (slope =0.48±0.22, r=0.2334, F=4.873, P=0.0422). There was also a non-significant positive correlation between the RH and the other three motor regions (slope =0.47±0.29, r=0.1362, F=2.522, P=0.1318), between the RF and the other three motor regions (slope =0.18±0.20, r=0.04878, F=0.8206, P=0.3785) and between the RL and the four motor regions (slope =0.69±0.33, r=0.217, F=4.434, P=0.0514).

Figure 6 Interdependence of euclidean distance (ED) in one motor region and mean EDs in the other three motor regions, and interdependence of ED in language region and mean EDs in the four motor regions. Data from two runs are presented along with their linear regression lines.

Inter-individual variability of GLM parameter extraction in brain atlases

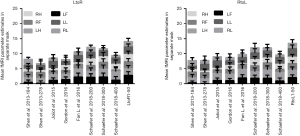
One way to use the brain atlas is to extract GLM parameters from tasked-based fMRI statistical parametric maps with a region of interest (ROI) as a mask. The mean GLM parameters extracted from the relevant mask (LF, LH, RF, RH, LL and RL) of eight brain atlases and second-level modeling analysis are shown in Figure 7. In a previous study, the ROI that was applied to functional areas of the model was spheroid (Powell, 2011). As we were unable to obtain the true shapes of functional regions, the data from this earlier work were not used here. Two-way ANOVA was used to investigate the influence of different brain atlases on parameter extraction; the factors were the nine different brain atlases and six relevant masks. The results revealed a significant interaction effect of the 893 subjects for LtoR [SS =10,088, DF =40, MS =252.2, F(40, 48,168) =216.5, P<0.0001] and RtoL [SS =8,365, DF =40, MS =209.1, F(40, 48,168) =180.7, P<0.0001]. Signal extraction differed for LtoR [SS =6,642, DF =8, MS =830.3, F(8, 48,168) =712.7, P<0.0001] and RtoL (SS =4,911, DF =8, MS =613.8, F(8, 48,168) =530.4, P<0.0001) across the nine brain atlases, and differed between the four different masks for LtoR [SS =5,655, DF =5, MS =1,131, F(5, 48,168) =970.9, P<0.0001] and RtoL [SS =9,007, DF =5, MS =1,801, F(5, 48,168) =1,557, P<0.0001]. The maximum mean GLM parameters extracted from the four motor region masks was gotten at Schaefer’s brain Atlas consisted of 200 parcels (2.078±0.15 for LtoR, 2±0.14 for RtoL). The maximum mean GLM parameters extracted from the two language region masks was gotten at Schaefer’s brain Atlas consisted of 200 parcels (1.91±0.4 for LtoR, 2.01±0.3 for RtoL).

Figure 7 Inter-individual variability of general linear model (GLM) parameter extraction in different brain regions. Symbols and error bars represent mean values and standard deviations, respectively, in four motor regions and two language regions in 893 subjects. RH, right hand; RF, right foot; LH, left hand; LF, left foot; LL, left language; RL, right language.

Interdependence of extracted GLM parameters and ED

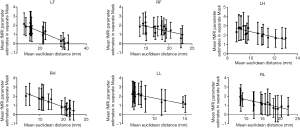
The interdependence of mean ED and extracted mean GLM parameters of each region are shown in Figure 8. Data were collected from two runs in eight brain atlases. The interdependence of extracted GLM parameters and EDs was evaluated by linear regression analysis. A negative correlation was found between extracted GLM parameters and EDs for LF (slope =−0.1048±0.01367, r=0.8076, F=58.76, P<0.0001), RF (slope =−0.1127±0.03348, r=0.4474, F=11.34, P=0.0046), LH (slope =−0.2893±0.04670, r=0.7327, F=38.37, P<0.0001), RH (slope =−0.1843±0.01496, r=0.9156, F=151.8, P<0.0001), LL (slope =−0.1364±0.01657, r=0.8288, F=67.78, P<0.0001)and RL (slope =−0.08767±0.01201, r=0.7919, F=53.27, P<0.0001).

Figure 8 Interdependence of euclidean distance (ED) on extracted general linear model (GLM) parameters. Symbols and error bars represent mean values and standard deviations, respectively, for 893 subjects. Linear regression lines are also shown. LF, left foot; RF, right foot; LH, left hand; RH, right hand; LL, left language; RL, right language.

Discussion

The present study evaluated the inter-individual variability in nine brain atlases using motor regions and temporal lobe language regions mapped by task-based fMRI. Our findings were as follows: (I) inter-individual variability in signal extraction and ED differed across nine brain atlases; (II) compared to the RH, ED was lower for the LH, compared to the RL, ED was lower for the LL whereas no difference was observed between the LF and RF; (III) mean EDs in one motor region were positively correlated with those in the other three motor regions, mean EDs in language region were positively correlated with those in the four motor regions, although only those of LH, LF and LL were significant; and (IV) extracted GLM parameters were negatively correlated with EDs in all six regions.

Brain atlases describe distinct functional regions and large-scale connectivity networks (1, 2, and 4). All image-based atlases generated to date have been established based on imaging labels that depict brain tissue characteristics (6). The images are collected from dozens or even hundreds of subjects; a brain atlas that is generated from this dataset only reflects group-level results of these subjects whereas individual variability could exist for others. Therefore, it is important to use a brain atlas with minimal variability for research or pre-surgical planning.

The two main techniques that have been used to map the human motor cortex are tasked-based fMRI and neuronavigated transcranial magnetic stimulation (29-31). Some studies have demonstrated that the former is more useful than the latter for mapping the hand, foot, and other body parts (29). However, despite being broadly applicable, non-invasive, and able to localize neural activity associated with a specific task on a millimeter scale, tasked-based fMRI is limited by low SNR and time resolution (32). System noise, head movements, and cardiac cycles also affect the quality of acquired signals (33). In the present study, we analyzed motor task-based fMRI data from the HCP. All of the data were collected using standard and rigorous experimental procedures and the data quality has been verified by numerous studies. Additionally, head movement parameters were introduced in multiple regressors to reduce their impact while data from subjects with non-activated brain regions were excluded.

Rs-fMRI is the main source of data for constructing image-based brain atlases (6). Many studies have demonstrated that the organization of rs-fMRI and activation mode of task-based fMRI have group-level consistency (16,17,20), and rs-fMRI data tracking task-based fMRI activation at the individual level have also been reported (34). Recent studies have shown that some task-based fMRI activation corresponds to data in rs-fMRI-based brain atlases, especially for movement tasks (20,22,35). Mapping motor regions for quantitative assessment of inter-individual variability in rs-fMRI-based atlases takes into account the correlation between task-based fMRI and rs-fMRI and has the advantages of simplicity in terms of experimental procedure and data processing.

Inter-individual variability is a major problem for the application of brain atlases. Although detailed brain atlases have been developed for individual subjects based on cumulative rs-fMRI data collected over a long term (12), in many instances, patients cannot tolerate such long periods. Thus, group-level brain atlases are still very useful and quantification of their inter-individual variability is important. For example, brain atlas was frequently applied in segmenting fMRI data using regions of interest, and then obtaining respective time series of each region of interest by averaging the fMRI time series across all voxels in the region of interest. Generally, these time series were used to calculate the effective brain connectivity between different regions of interest (36,37). Our results revealed significant inter-individual variability in signal extraction and EDs in nine brain atlases. Therefore, applying same region from different brain atlas to segment fMRI data may affect the next-step calculation results because of different inter-individual variability in different brain atlases. As there was no correlation between ED and parcel number the latter cannot be used as a sole criterion for selecting a brain atlas. All subjects included in our analysis were right-handed, which could account for the greater inter-individual variability of the RH compared to the LH. Thus, for a given functional area in the left or right hemisphere, higher activation is associated with increased inter-individual variability. Most importantly, we found a positive correlation between the inter-individual variability in one region and that in the other three regions, although the biological basis of this observation is unclear. We used motor and language task-based fMRI data to estimate inter-individual variability in different brain regions and applied GLMs to the data analysis. A design matrix depicting the nature of the experiment was used to estimate the GLM parameters, which reflected the correlations between voxel BOLD signals and the experimental design; the more relevant the brain area, the larger the estimated GLM parameters (17) and the farther away from the relevant brain area, the smaller the estimated GLM parameters (20). This explains why the extracted GLM parameters were negatively correlated with the ED.

This study had several limitations. Firstly, only motor and language task-based fMRI data were analyzed. Correlation analyses of inter-individual variability between motor and other brain regions such as visual areas or Broca’s area would be more convincing. Secondly, the data were collected from young, healthy subjects and it remains to be seen whether the same trends are present in elderly or impaired individuals such as stroke patients who are unable to complete the assigned task.

Conclusions

The results presented here demonstrate that inter-individual variability exists in different brain atlases constructed from the same dataset as well as in different brain regions. Determining the inter-individual variability of a brain atlas—for instance, by task-based fMRI mapping of motor regions—is essential before it can be considered as reliable and used in clinical and research settings. Along the same lines, brain atlas with less inter-individual variability which was quantitative assessed by present method should be applied in future study. Finally, the Schaefer’s brain Atlas which is consisted of 200 parcels was recommended for motor task and temporal lobe language task as studied.

Acknowledgments

MRI Data were provided by the Human Connectome Project, WUMinn Consortium (Principal Investigators: David Van Essen, and Kamil Ugurbil; 1U54MH091657) funded by the 16 NIH Institutes and Centers that support the NIH Blueprint for Neuroscience Research. We acknowledge the researches provide the Atlas which were included in present study. Extensive editing of both the content and the language was performed by the Charlesworth Author Services Team.

Funding: Funding to pay the Open Access publication charges for this article was provided by the Natural Science Foundation of China (Grant No. 81801798 and No. 81772003). TY acknowledges grant support from CAMS Initiative for Innovative Medicine (CAMS-I2M-2016-I2M-1004).

Footnote

Conflicts of Interest: All authors have completed the ICMJE uniform disclosure form (available at http://dx.doi.org/10.21037/qims-20-404). The authors have no conflicts of interest to declare.

Ethical Statement: The study was approved by the Joint Ethics Committee of the Chinese Academy of Medical Sciences and Peking Union College.

Open Access Statement: This is an Open Access article distributed in accordance with the Creative Commons Attribution-NonCommercial-NoDerivs 4.0 International License (CC BY-NC-ND 4.0), which permits the non-commercial replication and distribution of the article with the strict proviso that no changes or edits are made and the original work is properly cited (including links to both the formal publication through the relevant DOI and the license). See: https://creativecommons.org/licenses/by-nc-nd/4.0/.

References

1. Bullmore E, Sporns O. Complex brain networks: graph theoretical analysis of structural and functional systems. Nat Rev Neurosci 2009;10:186-98. [Crossref] [PubMed]
2. Tononi G, Sporns O, Edelman GM. A measure for brain complexity: relating functional segregation and integration in the nervous system. Proc Natl Acad Sci U S A 1994;91:5033-7. [Crossref] [PubMed]
3. Kong R, Li J, Orban C, Sabuncu MR, Liu H, Schaefer A, Sun N, Zuo XN, Holmes AJ, Eickhoff SB, Yeo BTT. Spatial Topography of Individual-Specific Cortical Networks Predicts Human Cognition, Personality, and Emotion. Cereb Cortex 2019;29:2533-51. [Crossref] [PubMed]
4. Rubinov M, Sporns O. Complex network measures of brain connectivity: uses and interpretations. Neuroimage 2010;52:1059-69. [Crossref] [PubMed]
5. Sporns O. The human connectome: a complex network. Ann N Y Acad Sci 2011;1224:109-25. [Crossref] [PubMed]
6. Eickhoff SB, Yeo BTT, Genon S. Imaging-based parcellations of the human brain. Nat Rev Neurosci 2018;19:672-86. [Crossref] [PubMed]
7. Desikan RS, Ségonne F, Fischl B, Quinn BT, Dickerson BC, Blacker D, Buckner RL, Dale AM, Maguire RP, Hyman BT, Albert MS, Killiany RJ. An automated labeling system for subdividing the human cerebral cortex on MRI scans into gyral based regions of interest. Neuroimage 2006;31:968-80. [Crossref] [PubMed]
8. Destrieux C, Fischl B, Dale A, Halgren E. Automatic parcellation of human cortical gyri and sulci using standard anatomical nomenclature. Neuroimage 2010;53:1-15. [Crossref] [PubMed]
9. Huth AG, de Heer WA, Griffiths TL, Theunissen FE, Gallant JL. Natural speech reveals the semantic maps that tile human cerebral cortex. Nature 2016;532:453-8. [Crossref] [PubMed]
10. Schaefer A, Kong R, Gordon EM, Laumann TO, Zuo XN, Holmes AJ, Eickhoff SB, Yeo BTT. Local-Global Parcellation of the Human Cerebral Cortex from Intrinsic Functional Connectivity MRI. Cereb Cortex 2018;28:3095-3114. [Crossref] [PubMed]
11. Tzourio-Mazoyer N, Landeau B, Papathanassiou D, Crivello F, Etard O, Delcroix N, Mazoyer B, Joliot M. Automated anatomical labeling of activations in SPM using a macroscopic anatomical parcellation of the MNI MRI single-subject brain. Neuroimage 2002;15:273-89. [Crossref] [PubMed]
12. Laumann TO, Gordon EM, Adeyemo B, Snyder AZ, Joo SJ, Chen MY, Gilmore AW, McDermott KB, Nelson SM, Dosenbach NU, Schlaggar BL, Mumford JA, Poldrack RA, Petersen SE. Functional System and Areal Organization of a Highly Sampled Individual Human Brain. Neuron 2015;87:657-70. [Crossref] [PubMed]
13. Biswal B, Yetkin FZ, Haughton VM, Hyde JS. Functional connectivity in the motor cortex of resting human brain using echo-planar MRI. Magn Reson Med 1995;34:537-41. [Crossref] [PubMed]
14. Choi EY, Yeo BT, Buckner RL. The organization of the human striatum estimated by intrinsic functional connectivity. J Neurophysiol 2012;108:2242-63. [Crossref] [PubMed]
15. Cohen AL, Fair DA, Dosenbach NU, Miezin FM, Dierker D, Van Essen DC, Schlaggar BL, Petersen SE. Defining functional areas in individual human brains using resting functional connectivity MRI. Neuroimage 2008;41:45-57. [Crossref] [PubMed]
16. Power JD, Cohen AL, Nelson SM, Wig GS, Barnes KA, Church JA, Vogel AC, Laumann TO, Miezin FM, Schlaggar BL, Petersen SE. Functional network organization of the human brain. Neuron 2011;72:665-78. [Crossref] [PubMed]
17. Smith SM, Fox PT, Miller KL, Glahn DC, Fox PM, Mackay CE, Filippini N, Watkins KE, Toro R, Laird AR, Beckmann CF. Correspondence of the brain's functional architecture during activation and rest. Proc Natl Acad Sci U S A 2009;106:13040-5. [Crossref] [PubMed]
18. Hacker CD, Laumann TO, Szrama NP, Baldassarre A, Snyder AZ, Leuthardt EC, Corbetta M. Resting state network estimation in individual subjects. Neuroimage 2013;82:616-33. [Crossref] [PubMed]
19. Mueller S, Wang D, Fox MD, Yeo BT, Sepulcre J, Sabuncu MR, Shafee R, Lu J, Liu H. Individual variability in functional connectivity architecture of the human brain. Neuron 2013;77:586-95. [Crossref] [PubMed]
20. Wig GS, Laumann TO, Cohen AL, Power JD, Nelson SM, Glasser MF, Miezin FM, Snyder AZ, Schlaggar BL, Petersen SE. Parcellating an individual subject's cortical and subcortical brain structures using snowball sampling of resting-state correlations. Cereb Cortex 2014;24:2036-54. [Crossref] [PubMed]
21. Van Essen DC, Smith SM, Barch DM, Behrens TE, Yacoub E, Ugurbil K. WU-Minn HCP Consortium. The WU-Minn Human Connectome Project: an overview. Neuroimage 2013;80:62-79. [Crossref] [PubMed]
22. Buckner RL, Krienen FM, Castellanos A, Diaz JC, Yeo BT. The organization of the human cerebellum estimated by intrinsic functional connectivity. J Neurophysiol 2011;106:2322-45. [Crossref] [PubMed]
23. Binder JR, Gross WL, Allendorfer JB, Bonilha L, Chapin J, Edwards JC, Grabowski TJ, Langfitt JT, Loring DW, Lowe MJ, Koenig K, Morgan PS, Ojemann JG, Rorden C, Szaflarski JP, Tivarus ME, Weaver KE. Mapping anterior temporal lobe language areas with fMRI: a multicenter normative study. Neuroimage 2011;54:1465-75. [Crossref] [PubMed]
24. Turner R, Howseman A, Rees GE, Josephs O, Friston K. Functional magnetic resonance imaging of the human brain: data acquisition and analysis. Exp Brain Res 1998;123:5-12. [Crossref] [PubMed]
25. Weibull A, Gustavsson H, Mattsson S, Svensson J. Investigation of spatial resolution, partial volume effects and smoothing in functional MRI using artificial 3D time series. Neuroimage 2008;41:346-53. [Crossref] [PubMed]
26. Penny W, Flandin G, Trujillo-Barreto N. Bayesian comparison of spatially regularised general linear models. Hum Brain Mapp 2007;28:275-93. [Crossref] [PubMed]
27. Friston KJ, Holmes AP, Price CJ, Büchel C, Worsley KJ. Multisubject fMRI studies and conjunction analyses. Neuroimage 1999;10:385-96. [Crossref] [PubMed]
28. Fan L, Li H, Zhuo J, Zhang Y, Wang J, Chen L, Yang Z, Chu C, Xie S, Laird AR, Fox PT, Eickhoff SB, Yu C, Jiang T. The Human Brainnetome Atlas: A New Brain Atlas Based on Connectional Architecture. Cereb Cortex 2016;26:3508-26. [Crossref] [PubMed]
29. Weiss C, Nettekoven C, Rehme AK, Neuschmelting V, Eisenbeis A, Goldbrunner R, Grefkes C. Mapping the hand, foot and face representations in the primary motor cortex - retest reliability of neuronavigated TMS versus functional MRI. Neuroimage 2013;66:531-42. [Crossref] [PubMed]
30. Simões EL, Bramati I, Rodrigues E, Franzoi A, Moll J, Lent R, Tovar-Moll F. Functional expansion of sensorimotor representation and structural reorganization of callosal connections in lower limb amputees. J Neurosci 2012;32:3211-20. [Crossref] [PubMed]
31. Muellbacher W, Boroojerdi B, Ziemann U, Hallett M. Analogous corticocortical inhibition and facilitation in ipsilateral and contralateral human motor cortex representations of the tongue. J Clin Neurophysiol 2001;18:550-8. [Crossref] [PubMed]
32. Kim DS, Duong TQ, Kim SG. Reply to "Can current fMRI techniques reveal the micro-architecture of cortex?". Nat Neurosci 2000;3:414. [Crossref] [PubMed]
33. Krüger G, Glover GH. Physiological noise in oxygenation-sensitive magnetic resonance imaging. Magn Reson Med 2001;46:631-7. [Crossref] [PubMed]
34. Blumensath T, Jbabdi S, Glasser MF, Van Essen DC, Ugurbil K, Behrens TE, Smith SM. Spatially constrained hierarchical parcellation of the brain with resting-state fMRI. Neuroimage 2013;76:313-24. [Crossref] [PubMed]
35. Gordon EM, Laumann TO, Adeyemo B, Huckins JF, Kelley WM, Petersen SE. Generation and Evaluation of a Cortical Area Parcellation from Resting-State Correlations. Cereb Cortex 2016;26:288-303. [Crossref] [PubMed]
36. Wu GR, Liao W, Stramaglia S, Ding JR, Chen H, Marinazzo D. A blind deconvolution approach to recover effective connectivity brain networks from resting state fMRI data. Med Image Anal 2013;17:365-74. [Crossref] [PubMed]
37. Shen X, Tokoglu F, Papademetris X, Constable RT. Groupwise whole-brain parcellation from resting-state fMRI data for network node identification. Neuroimage 2013;82:403-15. [Crossref] [PubMed]