Deep learning based fully automatic segmentation of the left ventricular endocardium and epicardium from cardiac cine MRI

Introduction

Cardiovascular disease (CVD) is the leading cause of global mortality and morbidity. According to the Center for Disease Control, 610,000 people in the United States die of heart disease each year (1). Different imaging modalities, including magnetic resonance (MR), echocardiography (ECHO), computed tomography (CT), and nuclear medicine, are used in the diagnosis, monitoring, and treatment of cardiac disease. Cardiac cine MR imaging has become the standard for the measurement of cardiac function. Conventionally, 2D cardiac cine MR imaging is applied during a series of breath-holds. This provides high blood to myocardium contrast that is good for image post-processing, and the breath holding minimizes artifacts from respiratory motion.

On the other hand, 3D cardiac cine imaging provides contiguous volumetric coverage and thinner slices compared to 2D imaging without the patient’s need to hold their breath. This allows for more flexible post-processing and more accurate cardiac metrics measurement by avoiding the slice misregistration errors seen with 2D imaging (2-4). Free-breathing imaging methods also improve patient comfort during the scan and enable image acquisition unconstrained by breath-hold length, permitting more advantageous MRI parameter settings (5-7). In this study, both conventional 2D cardiac cine images and free-breathing 3D cardiac cine images were used for evaluating the proposed segmentation method.

Manual delineation remains the reference standard for left ventricle (LV) segmentation from cardiac MR images. However, 2D slice-wise manual segmentation of the LV is time-consuming, tedious, and prone to fatigue errors (8-12). The development of an efficient, repeatable, reproducible, computer-aided method for cardiac segmentation to replace manual contouring is highly sought. Previous techniques have been reported for the segmentation of the LV on cardiac cine MR images, including the clustering method, level-set or deformable method (13-20), atlas model (16), registration model (21), and deep learning method (22-25). Most of the methods above that use shape priors can achieve a good performance; however, their robustness is highly dependent on the initial contour. Deep-learning based methods also usually require a large number of training data to achieve automatic LV segmentation. In this study, we aimed to develop a combined prior information-based level-set and deep learning method for accurate and automatic segmentation of the LV, which could be efficiently and generally utilized for clinical practice without the use of large amounts of training data.

Previous studies

Many deep learning methods have been applied to cardiac segmentation. Xue et al. (26) and Dangi et al. (27) proposed deep multitask learning methods to segment and quantify the LV. Nasr-Esfahani et al. (28) and Romaguera et al. (29) used a fully convolutional neural network (CNN) to assess the LV endocardium. Oktay et al. introduced an anatomically constrained neural network and applied it to cardiac image enhancement and segmentation (30). Zotti et al. performed an algorithm using CNN with the shape before segmenting cardiac images (31). Duan et al. proposed a shape refined multitask deep learning approach to segment the LV and right ventricle (RV) (32). Chen et al. used CNN with a loss function incorporated with an active contour model to segment the LV and RV (33). Bai et al. used a deep neural network to analyze cardiac MR images (34). Tao et al. performed a multi-vendor, multi-center study using CNN for LV quantification (35). However, these methods usually require large training datasets (500–1,000 cases) to build a general model to obtain accurate LV segmentation with a Dice value bigger than 0.9. On the other hand, small datasets (~100 cases) may result in a large bias that limits the accuracy of those methods with a Dice value smaller than 0.9, especially when the shape of the heart is different from the training set such as seen in post-infarct remodeling and congenital heart disease.

To reduce the size of the training dataset required, some studies have explored the idea of combining machine learning and level-set methods for cardiac MRI segmentation. Avendi et al. proposed using the traditional level set method with initial contours provided by CNN to segment the LV endocardium (23) and the RV (24). Ngo et al. first segmented the LV endocardium using a combined machine learning and level set method (25) and then used LV endocardial contours as the initial contours in LV epicardium segmentation.

Contributions

We propose a novel, fully automatic segmentation method to address the limitations of current approaches. Specifically, we make the following contributions:

• We propose a novel method by combining the multitask deep learning network and the level-set method, which will allow the use of a limited training dataset;
• We apply an annular shape-constrained before the level set method to simultaneously capture the LV endocardium and epicardium;
• To test the robustness and adaptability of the proposed method, we show that the proposed method can be successfully applied to highly accelerated 3D cine MR images, which have a relatively lower image contrast between LV blood and myocardium than conventional 2D cine images.

The proposed LsUnet method provides higher accuracy compared with state-of-the-art methods using the same online dataset. Our method compares favorably with other deep learning or/and level-set methods based on standard segmentation evaluation metrics.

Methods

MRI data acquisition

We developed a combined deep-learning and level-set method and validated it on both conventional breath-hold 2D cardiac cine MR images and advanced free-breathing 3D cine cardiac images. Two open-source datasets were used; 2D cine MR images from MICCAI 2009 LV (36) and 2012 RV (37) segmentation challenges, and a dataset with a highly accelerated free-breathing 3D imaging method (38), which was acquired under the approval of the Institutional Review Board (IRB) at University of California San Francisco (UCSF).

The MICCAI 2009 LV challenge dataset (36) consists of 45 cardiac studies with different diseases (12 cases have heart failure without myocardial scar; 12 cases have heart failure with a myocardial scar, 12 hypertrophy cases, and 9 healthy cases). Subjects in this dataset underwent an MRI cardiac scan on a 1.5T scanner (GE Medical Systems, Milwaukee, WI). The scan parameters for breath-hold 2D cine images were as follows: FOV =320×320 mm², thickness =8 mm, matrix =256×256, 6–12 short-axis slices, and 20 cardiac phases. The 2012 RV challenge dataset (37) includes data from 16 patients obtained using a 1.5T scanner (Siemens Medical System, Germany). The scan parameters were: FOV =360×420 mm², slice thickness =7 mm, matrix size =216×256, 10–14 short-axis slices, and 20 cardiac phases.

The highly accelerated free-breathing 3D image dataset was acquired from 17 subjects (9 males and 8 females, age 37.6±15.1 years, and heart rate of 64.3±8.8 bpm) using a 3.0T MR scanner (GE Medical Systems, Milwaukee, WI) with an 8-channel cardiac coil (38). The 3D imaging acquisition parameters were chosen as follows: image matrix =256×144, FOV =34.0×25.5 cm², slices number =28–32, slice thickness =4.0–5.0 mm, scan time =2.5±0.3 minutes, and temporal resolution =40 ms (37).

Ethical statement

The University of California San Francisco institutional review board approved the study, and all participants gave informed consent.

Manual segmentation

Manual delineation has been used as the reference standard to evaluate automatic segmentation (38-40). The dice coefficient is the commonly used parameter for assessing segmentation accuracy. This was calculated by measuring the overlap between manual and automatic segmentation. An in-house tool developed under a medical image-processing platform, MeVisLab (version 2.7.1, Bremen, DE), was used by our readers to draw the manual contours.

Experienced cardiologists manually segmented LV endocardial and epicardial contours at end-diastole for the MICCAI LV challenge dataset following the convention of including papillary muscles and endocardial trabeculations in the ventricular cavity. An experienced radiologist drew the LV endo- and epicardial contours at end-diastole for the MICCAI RV challenge dataset. The LV endo-and epicardial contours at both end-diastole and end-systole were also drawn for the highly accelerated free-breathing 3D dataset. A total of 95, 3D volumes that included 1,076 2D slices were used for both deep learning algorithms and as a reference standard for evaluation, with each slice including LV endo and epicardium segmentation.

Overview of the segmentation scheme

The segmentation scheme and automatic representative segmentation of the proposed LsUnet method are shown in Figure 1. The U-net based multi-channel fully convolutional neural network (MFCN) is first applied to segment the LV endocardial and epicardial contours simultaneously based on the training dataset. An epicardial region is a diffuse object with low contrast relative to neighboring tissues, as opposed to the endocardial contour, which separates the high signal intensities of blood from the myocardium’s low signal intensities. The segmented contours from MFCN are then used as an MFCN-based appearance term in the level-set algorithm to refine the segmentation results. The annular-like shaped endocardial and epicardial contours can be approximated by two elliptical contours and added to the level-set model for improving the final segmentation. This yields an efficient and reliable delineation of the borders. Myocardial thickness is then calculated based on the LV endocardium and epicardium segmentation. Detailed information about the algorithm is described in the following sections.

Figure 1 Schematic diagram of segmenting left ventricle endocardial and epicardial contours using the proposed LsUnet method. LsUnet, level set and Unet.

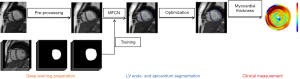
Image pre-processing

We implemented a fully automated pre-processing step, including cropping images to the region of interest and enhancing the image contrast, to improve segmentation’s efficiency and reliability.

All input images for the proposed MFCN network have the same size (256×256). For larger image size cases, we generated a cropped field of view (FOV) before segmentation, centered on and including the heart. For cardiac cine images, most signal changes through the cardiac cycle occur in a region located on the heart. An image is generated from the maximum time-derivative (MTD) over the cardiac cycle, which is calculated for each pixel where I is the image intensity and n is the number of measured time points (41).

$$M=\underset{i}{\max }\left\{{\frac{\partial i}{\partial t}|}_{t=t_i}\right\},i\in \left[\text{1,}\dots \text{,}n\right]$$[1]

The time derivative of I is calculated as a forward difference. For cases with an image size smaller than 256x256, we pad the images with zeros. Linear image enhancement (39) was applied to enhance the contrast of images within the cropped FOV.

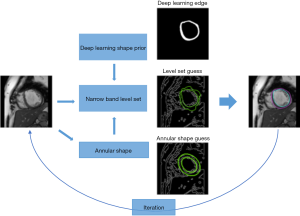
Combined level set and Unet (LsUnet)

The proposed LsUnet algorithm consists of three parts: (I) deep learning edge from the MFCN network; (II) level set guess from the narrow band level-set equation; (III) annular shape guess from the annular shape equation (Figure 2). The energy function for the proposed optimization algorithm was set to:

Figure 2 Model of the LV endocardium and epicardium segmentation using the proposed LsUnet algorithm. LV, left ventricle.

$$E=E_{Levelset}+\alpha \times E_{learning}+\beta \times E_{annual}$$[2]

where the weight α and β correspond to a positive hyperparameter that balances the influence between these three terms. We used fixed numbers, α = 0.3 and β = 0.2, in the present study.

Multi-channel fully convolutional neural (MFCN) network

The neural network was implemented with Tensorflow (https://www.tensorflow.org/) on a Windows 7 system with an Intel Core i7-6700 3.4GHz CPU and a Quadro M2000 GPU (4GB VRAM). A total of 902 slices were processed (463 from 2D cine imaging and 439 from 3D cine imaging). Approximately 80% of the slices were randomly selected as the training set and the remainder for the testing set, resulting in 373/90 and 355/84 training/testing slices for 2D and 3D cine, respectively. Raw MRI images were pre-processed before entering into the neural networks.

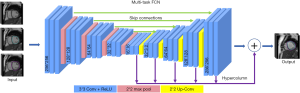
The MFCN was created based on a single-channel FCN and U-net structure (42). Figure 3 shows the scheme of the model. The MFCN contains by-pass paths for lower layers that reconstruct spatial information lost due to spatial pooling in the lower layers. The kernel size of each convolutional/de-convolutional layer was 3×3. The MFCN contains three levels. Six convolutional layers are used on the first and second levels, and one pooling layer and one de-convolutional layer are used on the third level. The number of features for each convolutional layer is 32. The maximum pooling with a stride size of 2×2 is used on each level. The 5-fold cross-validation with the training data is used in the proposed MFCN network, and each of the 5-fold models was used to make predictions on the testing data. All the predictions were averaged to obtain results for evaluating the proposed method. The ReLU activation function was used inside the MFCN, while the sigmoid activation function was used in the output layer as a softmax function to obtain the pixel-wise 2 class probabilities. For the network’s training, a pixel-wise weighted loss function and an ADAM optimizer with a learning rate of 1e-4 were used.

Figure 3 Illustration of the multi-channel FCN network based on single-channel FCN and U-net structure to account for the proposed network’s 3-channel input patch. FCN, fully convolutional neural.

MFCN term

The MFCN term controlling the final result should be similar to that obtained from deep learning. This is a fixed shape before each slice obtained from the MFCN network. This prior shape term can be described as follows:

$$E_{learning}={\displaystyle \int {\left(\Phi (x)-{\Phi }_{MFCN}(x)\right)}^2}H\left(\Phi (x)\right)dx$$[3]

where Φ is a Lipschitz-continuous function {more detailed definition in Eq. [6]}, Φ_MFCN is the distance function of point to the deep learning segmentation result, and H is the Heaviside function,

$$H(n)={\displaystyle {\int }_{-\infty }^n\delta (s)ds}$$[4]

where δ is the dirac function, defined as:

$$\delta (s)=\{\begin{array}{l}+\infty s\text{=0}\\ \text{0 }s\ne \text{0}\end{array}$$[5]

Both the level set and annular shape guess are generated based on image features, including image intensity, gradient, and initial contour. These guesses are updated at each iteration, where the edge from the MFCN deep learning is used as the initial contour in the LsUnet algorithm.

Level-set term

Geodesic active contour (GAC) is a deformable object detection model that has been widely used in medical image segmentation. The active contour is defined as an energy-minimizing spline associated with internal and external constraint forces (43). The following formula applies. Let I be a given image domain Ω→R, the GAC is denoted as C(x,t)→R² and represented as the zero level-set Φ(x,t)→R. The distance function is used for level-set function with the negative inside the zero level-set and positive outside. The mathematical equation is given as,

$$\Phi (x,t)=\{\begin{array}{l}-dx\in {\Omega }^{-}\\ +dx\in {\Omega }^{+}\\ 0x\in C\end{array}$$[6]

where C is the Euclidian distance of evolving curve C to the initial curve C₀. Li et al. (44) added a distance regularization term to solve the reinitialization problem, as described by

$$E_{levelset}(\Phi )=\mu R_p(\Phi )+E_{ext}(\Phi )$$[7]

in which μ is a positive constant. The expression of the level-set regularization term R_p(Φ) is defined as follows

$$R_p(\Phi )={\displaystyle {\int }_{}^{}p(\nabla \Phi )dx=\frac{1}{2}}{\displaystyle {\int }_{}^{}{(\left|\nabla \Phi \right|-\text{1})}^{\text{2}}dx}$$[8]

This penalty term forces the gradient magnitude of the level-set function | ΦÑ| Therefore, close to 1 effectively reduces the deviation of level-set function from Eq. [8] and ensures stable contour evolution. The external constraint E_ext(Φ) is associated with an edge indicator,

$$g=\frac{1}{1+{\left|\nabla G_{\sigma }\ast I\right|}^2}$$[9]

where Gσ is a Gaussian filter of standard deviation δ. The prefiltering operation is necessary to smooth the image and reduce noise. Ideally, the gradient magnitude |ÑI| is maximum at the object boundaries (edge detection) and gives function g a minimum value,

$$E_{ext}(\Phi )=\lambda {\displaystyle {\int }_{\Omega }^{}g\delta (\Phi )\left|\nabla \Phi \right|}dx+\alpha {\displaystyle {\int }_{\Omega }^{}gH(-\Phi )dx}$$[10]

where λ and α are both positive constants, and δ and H are the Dirac Delta and Heaviside functions, respectively. The external energy term is designed to slow down the curve evolution at the location of interest.

To find optimal curve C, the objective function must be minimized by solving the associated Euler-Lagrange equation. According to the gradient descent concept, the zero level-set contours evolves most efficiently in the opposite direction of the maximum gradient, N = −ΦÑ/|ΦÑ|, the steady-state solution can be then solved by

$$\frac{\partial \Phi }{\partial t}=-\frac{\partial E_{levelset}}{\partial \Phi }$$[11]

The Gateaux derivative of energy function gives,

$$\frac{\partial \Phi }{\partial t}=-\left(\mu \frac{\partial Rp}{\partial \Phi }\text{+}\frac{\partial E_{ext}}{\partial \Phi }\right)=\mu \left[{\nabla }^2\Phi -div\left(\frac{\nabla \Phi }{\left|\nabla \Phi \right|}\right)\right]+\lambda \delta (\Phi )div\left(g\frac{\nabla \Phi }{\left|\nabla \Phi \right|}\right)+\alpha g\delta (\Phi )$$[12]

Annular shape term

Assuming that the LV endo- and epicardium follows an annual shape, the above-mentioned level-set model is further refined with a shape constraint. The new energy term’s basic idea is to measure the area difference between an evolving shape and desired elliptical shape. The proposed energy function is given as,

$$E_{shape}(\Phi ,\lambda )={\displaystyle \int {\Phi }_a(x,\lambda )}\Vert \nabla \Phi (x)\Vert \delta (\Phi (x))dx$$[13]

where Φ_a(x,λ) is the distance function of a point x to the annular shape. Eq. [13] measures the distance between the level-set curve and the annular shape. The parametric expression for Φ is given as follows:

$${\Phi }_a(x,\lambda )=\max \left\{\epsilon (x,{\lambda }_{out})-\epsilon (x,{\lambda }_{in})\right\}$$[14]

where λ=[λ_in,λ_out] and λ_in, λ_out are the parameters of ellipses. The function ε is the algebraic distance of a point x=(x₁, x₂) to an ellipse:

$$\epsilon (x,{\lambda }_i)={\lambda }_{i1}{x}_1^2+{\lambda }_{i2}{x}_1{x}_2+{\lambda }_{i3}{x}_2^2+{\lambda }_{i4}{x}_1+{\lambda }_{i5}{x}_2+{\lambda }_{i6},\text{ with }{\lambda }_{i2}^{\text{2}}<4{\lambda }_{i1}{\lambda }_{i3}$$[15]

Thickness measurement

Myocardial wall thickness is typically measured on end-diastolic images in the sagittal view. The 17-segment model of the American Heart Association is typically used to analyze wall thickness (45). However, advances in fully automated segmentation have allowed us to provide more information than the traditional 17-segment model. Two contours were extracted for each image slice, representing the endocardial and epicardial contours based on the proposed fully automatic segmentation. Thickness was calculated at 360 locations (per degree) per image slice, where rays radiating from the center of the LV intersected those contours (41).

Evaluation criteria

The segmentation results were evaluated by comparing the results with the reference standard from manual delineation using the Dice coefficient. The definition of the Dice coefficient (46) is given as follows:

$$Dice\%=\frac{2\left|R_A\cap R_M\right|}{\left|R_A\right|+\left|R_M\right|}\times 100$$[16]

where |^·| are the pixels numbers in the corresponding region, R_A is the automatic segmentation result, and R_M is the reference standard from manual delineation. Dice value measures the overlap between manual and automatic segmentation, and the greater the Dice value, the better the agreement between manual and automatic segmentation.

Results

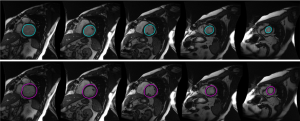
In Figure 4, the LV endocardium and epicardium segmentation using the proposed LsUnet method (the first and second rows) are displayed. Most of the segmentation results have a reasonable appearance. Figure 5 shows the proposed LsUnet algorithm and manual segmentation results for one case on seven representative slices. The green lines and red dot lines correspond to the proposed method and manual segmentation results, respectively. Both contours were successfully segmented using the proposed LsUnet algorithm with results comparable to the manual delineations, as clearly shown in Figure 5.

Figure 4 The LV endocardium (the first row, contours highlighted in cyan) and epicardium (the second row, contours highlighted in magenta) segmentation results using the proposed LsUnet method.

Figure 5 LV endocardium and epicardium segmentation. Green lines were generated by the proposed optimization method, and red dot lines were the manual delineation.

Quantitative comparisons between the automatic (MFCN and LsUnet methods) and manual delineations are shown in Table 1. The average Dice coefficient and CV for endocardium and epicardium segmentation were 92.15%±7.94% and 95.42%±3.75%, which is comparable to the manual segmentation on those three datasets.

Table 1 Quantitative LV endocardium and epicardium segmentation comparison between manual and the proposed automatic segmentations (MFCN method and optimization method) using the three datasets
Full table

As previously stated, three datasets were used to evaluate the proposed methods. The LV endocardium and epicardium segmentation accuracy (Dice coefficient and CV) for each dataset are listed in Table 1. The Bland-Altman plots of LV volume and the mass obtained with manual and the proposed LsUnet for each case are seen in Figure 6. This was used to evaluate the association and difference between manual and automatic segmentation. The mean bias and confidence intervals for LV endocardium and epicardium segmentation were calculated and are shown in Figure 6, demonstrating that good segmentation was achieved.

Figure 6 Agreement of automatic and manual cardiac functional measurements. Bland-Altman plots of the LV volume and mass obtained with manual and the proposed LsUnet.

Although manual segmentation was used as the reference for evaluating the proposed automatic segmentation algorithm, we compared the MFCN method and LsUnet method with several state-of-the-art methods: (I) level-set method; (II) deep learning method; (III) combined level-set and deep learning method; (IV) other methods. Table 2 shows the Dice value for these methods, which were performed on the MICCAI 2009 LV challenge dataset for comparison.

Table 2 Quantitative comparison between state-of-the-art methods and manual delineation
Full table

Based on these Dice coefficients, the MFCN method attained the average LV endocardium and high LV epicardium segmentation accuracy. Moreover, the proposed LsUnet method reached the highest LV epicardium segmentation accuracy. Although LV endocardium accuracy from the optimization method was 1% lower than the method developed by Avendi et al. (23), the optimization method can segment both the LV endo- and epicardium simultaneously. Overall, the proposed methods work well on LV endo- and epicardium segmentation.

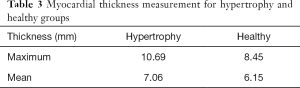
Following LV endo- and epicardium segmentation, we calculated the chamber volume, ejection fraction, and myocardial wall thickness. This study validated the myocardial wall thickness measurement using the proposed segmentation method by comparing it with manual delineation as the reference standard. Myocardial wall thickness was determined to be 6.85±1.99 mm and 6.81±1.27 mm by manual and LsUnet evaluation, respectively. LsUnet had high accuracy (86.9%) for LV wall thickness measurements. Two myocardial thickness cases from a hypertrophic patient and a healthy individual are shown in Figure 7. The 1^st to 3^rd columns shows three slices from the top, middle, and bottom for each patient. The 4^th column shows the wall thickness for all the slices. LV wall thickness for the hypertrophic group and the healthy group from the MICCAI 2009 dataset are shown in Table 3.

Figure 7 LV thickness maps (mm) for a hypertrophy patient and a healthy case. Three slices were chosen from each case (top, middle, and bottom). On the right are radial thickness maps that provide more detailed information than the standard AHA bullseye plot. Thickness values are provided for each axial image slice. AHA, American Heart Association.

Table 3 Myocardial thickness measurement for hypertrophy and healthy groups
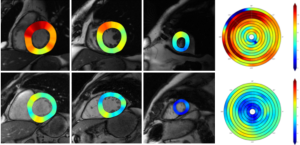
Full table

Discussion

Deep learning methods have been proposed for image segmentation to derive complex shapes using training data (51-53). However, to obtain robust and accurate results, training data must be comprehensive, leading to large training set requirements. The level-set method does not require training, but the shape model may be too simple to account for all physiological shape variations. This study combined the deep learning and level-set methods to get accurate segmentation using a small training dataset.

Image intensity variation in cardiac MRI is the major challenge for image segmentation. One effective way to overcome this is to exploit the image’s structured dependency by assigning the same class labels to spatial and structural adjacent pixels. This can be implemented through deep CNN. In particular, the hierarchical feature representation of CNN is robust against significant appearance variations. However, CNN can cause spatial blurring due to spatial pooling in the feedforward structure. The FCN can effectively eliminate this issue. In this study, the combined use of MFCN and annular shape level-set significantly improved structural detection accuracy in the cardiac ventricle, complementing the existing local structure-based segmentation methods.

Our proposed method is efficient, with comparable segmentation performance to that obtained with manual segmentation and achieving high accuracy with an average Dice coefficient of 92.15% and 95.42% for LV endocardial and epicardial boundaries, respectively. The results also show that the proposed method provides higher accuracy than other state-of-the-art segmentation methods, including deep learning, level-set, and other methods.

The segmented contours of MFCN are used as the initial contour and an appearance term in the Level Set method’s energy function. For all the cases processed in this study, LsUnet was able to further improve segmentation from the segmented contours of MFCN, which were not necessary to be perfect but located the LV well with close contours.

An epicardial region is a diffuse object with low contrast relative to neighboring tissues. This makes segmentation difficult for traditional signal intensity-based segmentation methods; however, it may be less problematic for methods that use prior information or are deep learning-based. The endocardial region usually has a higher image contrast; however, the accuracy of its segmentation depends more on the accurate tracing of the papillary muscles and endocardial trabeculations that are irregular in shape. This study achieved a higher Dice value for segmentation of the epicardium than the endocardium using the proposed segmentation method.

To test the minimum training dataset required for the proposed LsUnet, we evaluated it on only 45 cases from the MICCAI LV challenge dataset (37) with ~80% cases as the training set and the remaining ~20% as the testing set. The Dice value reached 0.93 and 0.92 to the LV endocardium segment and epicardium, respectively, demonstrating good segmentation. Although the proposed LsUnet method provided accurate segmentation using only 36 cases as the training set, it would still be challenging to use a training set of fewer than 36 cases. This is because, in an experiment with 45 cases with 80% as the training set, the 5-fold cross-validation test already reaches the limit of having only 1–2 cases for each type of disease (or healthy) in each fold.

The MFCN was implemented with Tensorflow (https://www.tensorflow.org/) on a Windows 10 system with an Intel Core i7-6700 3.4GHz CPU and a Quadro M2000 GPU (4GB VRAM). It took approximately 8 hours for the entire MFCN process (76 training cases, 19 testing cases). The second step was using LsUnet to refine the segmentation result, which was performed on an OS X system with an Intel Core i7 CPU and 8 GB RAM using MATLAB-based software developed in-house. Although this step was not applied on a high-performance computer, it only took 2–3 s for one slice and about 9 minutes for the entire testing set.

The measurement of LV myocardial wall thickness is vital for diagnosing and assessing progress in patients with common cardiac diseases such as hypertrophic cardiomyopathy, dilated cardiomyopathy, hypertensive heart disease, and myocardial infarction (54). Myocardial wall thickness measurement is vital for assessing disease progression. This study validated the myocardial wall thickness measurement using the proposed segmentation method by comparing it with manual delineation as the reference standard. LsUnet had high accuracy (86.9%) for LV wall thickness measurements.

The present study has limitations. The heart moves along the longitudinal axis during the cardiac cycle, so the number of the slices that cover the heart could vary in different cardiac phases, which would need to be manually determined. In the future, we plan to improve the current study by using a 3D neural network and 3D level-set method to determine the slices automatically.

Acknowledgments

Funding: This work was supported in part by a grant from the NIH R01HL114118 (DS), R56HL133663 (JL), and AHA 19POST34450257 (YW).

Footnote

Conflicts of Interest: All authors have completed the ICMJE uniform disclosure form (available at http://dx.doi.org/10.21037/qims-20-169). The authors have no conflicts of interest to declare.

Ethical Statement: The University of California San Francisco institutional review board approved the study, and informed consent was taken from all the patients.

Open Access Statement: This is an Open Access article distributed in accordance with the Creative Commons Attribution-NonCommercial-NoDerivs 4.0 International License (CC BY-NC-ND 4.0), which permits the non-commercial replication and distribution of the article with the strict proviso that no changes or edits are made and the original work is properly cited (including links to both the formal publication through the relevant DOI and the license). See: https://creativecommons.org/licenses/by-nc-nd/4.0/.

References

1. Multiple cause of death 1999–2013 on CDC WONDER online database, released 2015. Data are from the multiple cause of death files, 1999–2013, as compiled from data provided by the 57 vital statistics jurisdictions through the vital statistics cooperative program. Available online: https://wonder.cdc.gov/mcd-icd10.html
2. Jeong D, Schiebler ML, Lai P, Wang K, Vigen KK, François CJ. Single breath hold 3D cardiac cine MRI using kat-ARC: preliminary results at 1.5T. Int J Cardiovasc Imaging 2015;31:851-7. [Crossref] [PubMed]
3. Satriano A, Heydari B, Narous M, Exner DV, Mikami Y, Attwood MM, Tyberg JV, Lydell CP, Howarth AG, Fine NM, White JA. Clinical feasibility and validation of 3D principal strain analysis from cine MRI: comparison to 2D strain by MRI and 3D speckle tracking echocardiography. Int J Cardiovasc Imaging 2017;33:1979-92. [Crossref] [PubMed]
4. Earls JP, Ho VB, Foo TK, Castillo E, Flamm SD. Cardiac MRI: recent progress and continued challenges. J Magn Reson Imaging 2002;16:111-27. [Crossref] [PubMed]
5. Finn JP, Nael K, Deshpande V, Ratib O, Laub G. Cardiac MR imaging: state of the technology. Radiology 2006;241:338-54. [Crossref] [PubMed]
6. Liu J, Spincemaille P, Codella NC, Nguyen TD, Prince MR, Wang Y. Respiratory and cardiac self-gated free-breathing cardiac CINE imaging with multiecho 3D hybrid radial SSFP acquisition. Magn Reson Med 2010;63:1230-7. [Crossref] [PubMed]
7. Nijveldt R, Hofman MB, Hirsch A, Beek AM, Umans VA, Algra PR, Piek JJ, van Rossum AC. Assessment of microvascular obstruction and prediction of short-term remodeling after acute myocardial infarction: cardiac MR imaging study. Radiology 2009;250:363-70. [Crossref] [PubMed]
8. Lötjönen JM, Järvinen VM, Cheong B, Wu E, Kivistö S, Koikkalainen JR, Mattila JJ, Kervinen HM, Muthupillai R, Sheehan FH, Lauerma K. Evaluation of cardiac biventricular segmentation from multiaxis MRI data: a multicenter study. J Magn Reson Imaging 2008;28:626-36. [Crossref] [PubMed]
9. Xuan Y, Wang Z, Liu R, Haraldsson H, Hope MD, Saloner DA, Guccione JM, Ge L, Tseng E. Wall stress on ascending thoracic aortic aneurysms with bicuspid compared with tricuspid aortic valve. J Thorac Cardiovasc Surg 2018;156:492-500. [Crossref] [PubMed]
10. van Rikxoort EM, Isgum I, Arzhaeva Y, Staring M, Klein S, Viergever MA, Pluim JP, van Ginneken B. Adaptive local multi-atlas segmentation: application to the heart and the caudate nucleus. Med Image Anal 2010;14:39-49. [Crossref] [PubMed]
11. Wang Z, Wood NB, Xu XY. A viscoelastic fluid–structure interaction model for carotid arteries under pulsatile flow. Int J Numer Method Biomed Eng 2015;31:e02709. [Crossref] [PubMed]
12. Wang Z, Flores N, Lum M, Wisneski AD, Xuan Y, Inman J, Hope MD, Saloner DA, Guccione JM, Ge L, Tseng EE. Wall stress analyses in patients with ≥5 cm versus <5 cm ascending thoracic aortic aneurysm. J Thorac Cardiovasc Surg 2020. [Crossref] [PubMed]
13. Gao Y, Kikinis R, Bouix S, Shenton M, Tannenbaum A. A 3D interactive multi-object segmentation tool using local robust statistics driven active contours. Med Image Anal 2012;16:1216-27. [Crossref] [PubMed]
14. Schaerer J, Casta C, Pousin J, Clarysse P. A dynamic elastic model for segmentation and tracking of the heart in MR image sequences. Med Image Anal 2010;14:738-49. [Crossref] [PubMed]
15. Mitchell SC, Bosch JG, Lelieveldt BP, van der Geest RJ, Reiber JH, Sonka M. 3-D active appearance models: segmentation of cardiac MR and ultrasound images. IEEE Trans Med Imaging 2002;21:1167-78. [Crossref] [PubMed]
16. Zhu Y, Papademetris X, Sinusas AJ, Duncan JS. Segmentation of the left ventricle from cardiac MR images using a subject-specific dynamical model. IEEE Trans Med Imaging 2010;29:669-87. [Crossref] [PubMed]
17. Andreopoulos A, Tsotsos JK. Efficient and generalizable statistical models of shape and appearance for analysis of cardiac MRI. Med Image Anal 2008;12:335-57. [Crossref] [PubMed]
18. Zhuang X, Rhode KS, Razavi RS, Hawkes DJ, Ourselin S. A registration-based propagation framework for automatic whole heart segmentation of cardiac MRI. IEEE Trans Med Imaging 2010;29:1612-25. [Crossref] [PubMed]
19. Zhang S, Zhan Y, Dewan M, Huang J, Metaxas DN, Zhou XS. Towards robust and effective shape modeling: sparse shape composition. Med Image Anal 2012;16:265-77. [Crossref] [PubMed]
20. Zhang S, Zhan Y, Metaxas DN. Deformable segmentation via sparse representation and dictionary learning. Med Image Anal 2012;16:1385-96. [Crossref] [PubMed]
21. Zhuang X, Bai W, Song J, Zhan S, Qian X, Shi W, Lian Y, Rueckert D. Multiatlas whole heart segmentation of CT data using conditional entropy for atlas ranking and selection. Med Phys 2015;42:3822-33. [Crossref] [PubMed]
22. Tran PV. A fully convolutional neural network for cardiac segmentation in short-axis MRI. arXiv preprint arXiv:160400494, 2016.
23. Avendi MR, Kheradvar A, Jafarkhani H. A combined deep-learning and deformable-model approach to fully automatic segmentation of the left ventricle in cardiac MRI. Med Image Anal 2016;30:108-19. [Crossref] [PubMed]
24. Avendi MR, Kheradvar A, Jafarkhani H. Automatic segmentation of the right ventricle from cardiac MRI using a learning‐based approach. Magn Reson Med 2017;78:2439-48. [Crossref] [PubMed]
25. Ngo TA, Lu Z, Carneiro G. Combining deep learning and level set for the automated segmentation of the left ventricle of the heart from cardiac cine magnetic resonance. Med Image Anal 2017;35:159-71. [Crossref] [PubMed]
26. Xue W, Brahm G, Pandey S, Leung S, Li S. Full left ventricle quantification via deep multitask relationships learning. Med Image Anal 2018;43:54-65. [Crossref] [PubMed]
27. Dangi S, Yaniv Z, Linte CA. Left Ventricle Segmentation and Quantification from Cardiac Cine MR Images via Multi-task Learning. Stat Atlases Comput Models Heart 2019;11395:21-31. [Crossref] [PubMed]
28. Nasr-Esfahani M, Mohrekesh M, Akbari M, Soroushmehr SMR, Nasr-Esfahani E, Karimi N, Samavi S, Najarian K. Left Ventricle Segmentation in Cardiac MR Images Using Fully Convolutional Network. Annu Int Conf IEEE Eng Med Biol Soc 2018;2018:1275-8. [Crossref] [PubMed]
29. Romaguera LV, Costa MGF, Romero FP, Costa Filho CFF (editors). Left ventricle segmentation in cardiac MRI images using fully convolutional neural networks. Medical Imaging 2017: Computer-Aided Diagnosis, 2017: International Society for Optics and Photonics.
30. Oktay O, Ferrante E, Kamnitsas K, Heinrich M, Bai W, Caballero J, Cook SA, de Marvao A, Dawes T, O'Regan DP, Kainz B, Glocker B, Rueckert D. Anatomically constrained neural networks (ACNNs): application to cardiac image enhancement and segmentation. IEEE Trans Med Imaging 2018;37:384-95. [Crossref] [PubMed]
31. Zotti C, Luo Z, Lalande A, Jodoin PM. Convolutional Neural Network With Shape Prior Applied to Cardiac MRI Segmentation. IEEE J Biomed Health Inform 2019;23:1119-28. [Crossref] [PubMed]
32. Duan J, Bello G, Schlemper J, Bai W, Dawes TJW, Biffi C, de Marvao A, Doumoud G, O'Regan DP, Rueckert D. Automatic 3D Bi-Ventricular Segmentation of Cardiac Images by a Shape-Refined Multi- Task Deep Learning Approach. IEEE Trans Med Imaging 2019;38:2151-64. [Crossref] [PubMed]
33. Chen X, Williams BM, Vallabhaneni SR, Czanner G, Williams R, Zheng Y (editors). Learning active contour models for medical image segmentation. Proceedings of the IEEE conference on computer vision and pattern recognition, 2019.
34. Bai W, Sinclair M, Tarroni G, Oktay O, Rajchl M, Vaillant G, Lee AM, Aung N, Lukaschuk E, Sanghvi MM, Zemrak F, Fung K, Paiva JM, Carapella V, Kim YJ, Suzuki H, Kainz B, Matthews PM, Petersen SE, Piechnik SK, Neubauer S, Glocker B, Rueckert D. Automated cardiovascular magnetic resonance image analysis with fully convolutional networks. J Cardiovasc Magn Reson 2018;20:65. [Crossref] [PubMed]
35. Tao Q, Yan W, Wang Y, Paiman EHM, Shamonin DP, Garg P, Plein S, Huang L, Xia L, Sramko M, Tintera J, de Roos A, Lamb HJ, van der Geest RJ. Deep Learning-based Method for Fully Automatic Quantification of Left Ventricle Function from Cine MR Images: A Multivendor, Multicenter Study. Radiology 2019;290:81-8. [Crossref] [PubMed]
36. Radau P, Lu Y, Connelly K, Paul G, Dick A, Wright G. Evaluation framework for algorithms segmenting short axis cardiac MRI. The MIDAS Journal-Cardiac MR Left Ventricle Segmentation Challenge, 2009.
37. Petitjean C, Zuluaga MA, Bai W, Dacher JN, Grosgeorge D, Caudron J, Ruan S, Ayed IB, Cardoso MJ, Chen HC, Jimenez-Carretero D, Ledesma-Carbayo MJ, Davatzikos C, Doshi J, Erus G, Maier OM, Nambakhsh CM, Ou Y, Ourselin S, Peng CW, Peters NS, Peters TM, Rajchl M, Rueckert D, Santos A, Shi W, Wang CW, Wang H, Yuan J. Right ventricle segmentation from cardiac MRI: a collation study. Med Image Anal 2015;19:187-202. [Crossref] [PubMed]
38. Liu J, Feng L, Shen HW, Zhu C, Wang Y, Mukai K, Brooks GC, Ordovas K, Saloner D. Highly-accelerated self-gated free-breathing 3D cardiac cine MRI: validation in assessment of left ventricular function. MAGMA 2017;30:337-46. [Crossref] [PubMed]
39. Chen Y, Navarro L, Wang Y, Courbebaisse G. Segmentation of the thrombus of giant intracranial aneurysms from CT angiography scans with lattice Boltzmann method. Med Image Anal 2014;18:1-8. [Crossref] [PubMed]
40. Wang Y, Zhang Y, Navarro L, Eker OF, Corredor Jerez RA, Chen Y, Zhu Y, Courbebaisse G. Multilevel segmentation of intracranial aneurysms in CT angiography images. Med Phys 2016;43:1777. [Crossref] [PubMed]
41. Wang Y, Zhang Y, Xuan W, Kao E, Cao P, Tian B, Ordovas K, Saloner D, Liu J. Fully automatic segmentation of 4D MRI for cardiac functional measurements. Med Phys 2019;46:180-9. [Crossref] [PubMed]
42. Ronneberger O, Fischer P, Brox T (editors). U-net: Convolutional networks for biomedical image segmentation. International Conference on Medical Image Computing and Computer-Assisted Intervention. Springer: 2015.
43. Caselles V, Kimmel R, Sapiro G. Geodesic active contours. Int J Comput Vis 1997;22:61-79. [Crossref]
44. Li C, Xu C, Gui C, Fox MD. Distance regularized level set evolution and its application to image segmentation. IEEE Trans Image Process 2010;19:3243-54. [Crossref] [PubMed]
45. Cerqueira MD, Weissman NJ, Dilsizian V, Jacobs AK, Kaul S, Laskey WK, Pennell DJ, Rumberger JA, Ryan T, Verani MS. American Heart Association Writing Group on Myocardial Segmentation and Registration for Cardiac Imaging. Standardized myocardial segmentation and nomenclature for tomographic imaging of the heart: a statement for healthcare professionals from the Cardiac Imaging Committee of the Council on Clinical Cardiology of the American Heart Association. Circulation 2002;105:539-42. [Crossref] [PubMed]
46. Dice LR. Measures of the amount of ecologic association between species. Ecology 1945;26:297-302. [Crossref]
47. Zheng S, Jayasumana S, Romera-Paredes B, Vineet V, Su Z, Du D, Huang C, Torr PHS, editors. Conditional random fields as recurrent neural networks. Proceedings of the IEEE international conference on computer vision, 2015. Available online: https://arxiv.org/abs/1502.03240
48. Constantinides C, Chenoune Y, Kachenoura N, Roullot E, Mousseaux E, Herment A, Frouin F. Semi-automated cardiac segmentation on cine magnetic resonance images using GVF-Snake deformable models. The MIDAS Journal-Cardiac MR Left Ventricle Segmentation Challenge 2009;77. Available online: https://www.midasjournal.org/browse/publication/678
49. Queirós S, Barbosa D, Heyde B, Morais P, Vilaça JL, Friboulet D, Bernard O, D'hooge J. Fast automatic myocardial segmentation in 4D cine CMR datasets. Med Image Anal 2014;18:1115-31. [Crossref] [PubMed]
50. Poudel RP, Lamata P, Montana G. Recurrent fully convolutional neural networks for multi-slice MRI cardiac segmentation. Reconstruction, segmentation, and analysis of medical images. Springer, 2016:83-94.
51. Ghodrati V, Shao J, Bydder M, Zhou Z, Yin W, Nguyen KL, Yang Y, Hu P. MR image reconstruction using deep learning: evaluation of network structure and loss functions. Quant Imaging Med Surg 2019;9:1516-27. [Crossref] [PubMed]
52. Li W, Li Y, Qin W, Liang X, Xu J, Xiong J, Xie Y. Magnetic resonance image (MRI) synthesis from brain computed tomography (CT) images based on deep learning methods for magnetic resonance (MR)-guided radiotherapy. Quant Imaging Med Surg 2020;10:1223-36. [Crossref] [PubMed]
53. Cai S, Tian Y, Lui H, Zeng H, Wu Y, Chen G. Dense-UNet: a novel multiphoton in vivo cellular image segmentation model based on a convolutional neural network. Quant Imaging Med Surg 2020;10:1275-85. [Crossref] [PubMed]
54. Kawel N, Turkbey EB, Carr JJ, Eng J, Gomes AS, Hundley WG, Johnson C, Masri SC, Prince MR, van der Geest RJ, Lima JA, Bluemke DA. Normal left ventricular myocardial thickness for middle-aged and older subjects with steady-state free precession cardiac magnetic resonance: the multi-ethnic study of atherosclerosis. Circulation 2012;5:500-8. [PubMed]