Multi-energy CT reconstruction using tensor nonlocal similarity and spatial sparsity regularization

Introduction

Multi-energy computed tomography (MECT) has received increasing focus in the field of tomographic imaging for medical diagnosis due to its discriminating capabilities across different materials (1,2). MECT utilizes measurement projections at different energy spectra to jointly reconstruct the multi-channel of CT images. Two types of data acquisition technologies can be applied to realize MECT imaging. Dual-energy CT (DECT) is a simple realization of MECT that requires two sets of measurement data at two distinct X-ray spectra (3,4). Several techniques have been developed to perform DECT, including dual-source dual-energy CT (5), fast kVp switching CT (6), and dual-layer sandwich detector CT (7). Although DECT has been applied to X-ray imaging, the energy separation capability of DECT is limited due to the utilization of energy-integrating detectors. Another technology that performs MECT is based on a photon-counting detector (8), capable of photon energy discrimination (9,10). Multi-energy measurement projections can be obtained by individually quantifying the photons in a narrow energy window (11). However, given the limited number of X-ray photons in each energy bin, multi-energy projections obtained from a photon-counting detector usually leads to the increase of background noise (12,13). This induces a more ill-posed inversion process, rendering subsequent image reconstruction and material decomposition extremely difficult. Therefore, the development of advanced algorithms has become a research focus for optimizing imaging quality, generated by photon-counting detectors.

Conventional denoising methods were applied either in the projection domain or image domain (14,15). However, such methods usually cannot deliver satisfactory performance due to difficulties associated with determining the statistical properties of noise observed in MECT. The advent of the compressed sensing theory (16,17) has led to the development of many sparse regularization-based iterative reconstruction algorithms, such as total variation (TV) (18), wavelet transform (19), and dictionary learning (20), which incorporate data consistency into the process of noise suppression. TV regularization utilizes the basis of sparsity or compressibility of gradient image and has been the most widely used regularization method for imaging inverse problems (21-23). In MECT, sparse regularization can be imposed in each energy bin to reduce image noise. Xu et al. applied TV penalties to each channel of the CT to reconstruct the interior region of interest (ROI) from spectral images (24). Zhao et al. demonstrated that the tight-frame based iterative reconstruction method for MECT generated higher image quality than its counterparts (25). Zeng et al. incorporated the concept of structure tensor TV regularization into a penalized weighted least-squares scheme and obtained superior results to conventional methods (26). These procedures separately reconstructed each channel of CT image, leading to a powerful capability in noise reduction for MECT images. However, they do not address the correlations of interchannel for multi-energy images, resulting in the degradation of image textures and edges.

Comparatively advanced methods exploit the inherent tensorial nature problems associated with MECT. Low-rank regularization is utilized to explore the interchannel correlations. Chu et al. combined the low rank and sparsity of MECT images to improve multi-channel CT images (27). Gao et al. proposed the Prior Rank, Intensity, and Sparsity Model (PRISM) by modeling a MECT image as a superposition of a low-rank and sparsity matrix (28). Li et al. improved the PRISM by tensor knowledge (29,30). Based on tensor singular value decomposition (31), Semerci et al. designed the generalized tensor nuclear norm as regularizers of image reconstruction (32). Rigie and La Rivière proposed a constrained total nuclear variation minimization algorithm for MECT; the algorithm renders the gradient vectors of CT images at each energy to point to a prevailing direction (33). Utilizing high-quality full-spectra image as pilot signals, Yu et al. proposed a spectral prior image-constrained compressed sensing method (34), and Zhang et al. proposed a TV spectral mean method for MECT (35). Tensor dictionary learning methods were also applied to MECT reconstruction. Zhao et al. proposed a dual-dictionary learning method for breast MECT systems (36), while Wu et al. proposed a tensor dictionary learning method with a constraint of image gradient L0-norm for spectral CT reconstruction (37). Recently, similarities among various small patches in the multi-channel of medical images were exploited by researchers (38). Kim et al. utilized the self-similarity of patches in multi-channel images and applied low-rank regularization to the three-dimensional patches for sparse-view spectral CT reconstruction (39). Xu et al. combined the dictionary-based sparse representation method and the patch-based low-rank constraint to improve the reconstruction (40). Niu et al. proposed an iterative reconstruction method that utilized the nonlocal low-rank and sparse matrix decomposition (41). More recently, Xie et al. proposed a novel nonlocal tensor sparsity measurement technique called intrinsic tensor sparsity regularization to denoise a multispectral image, verifying its powerful performance in exploring the intrinsic sparsity of image tensors (42,43). This method was further developed by Zeng et al., who designed a novel dynamic cerebral perfusion CT method (44). Also, Wu et al. proposed a nonlocal low-rank cube-based tensor factorization method to reconstruct MECT images (45,46). Xia et al. stacked similar patches among multi-channel images into a tensor unit and decomposed such patches into a low-rank and a sparse component to improve the MECT reconstruction quality (47).

The abovementioned reconstruction methods exhibit the success and value in exploiting the similarity of interchannel images and outperform conventional methods. This paper aims to further improve reconstruction quality by synthesizing the nonlocal similarity and spatial sparsity in both interchannel and single-channel images to suppress image noise while maintaining image quality. This concept has led to the application of a MECT reconstruction model, based on tensor nonlocal similarity and spatial sparsity regularization in the present study. The nonlocal tensor similarity of interchannel images is exploited by the intrinsic tensor sparsity regularization that combines the Tucker (48) and canonical polyadic (CP) (49) low-rank tensor decomposition techniques. The spatial sparsity is depicted by TV regularization that imposes the sparsity on the gradient map of a single-channel image. The alternating direction method is applied to solve the new reconstruction model by deriving a concise iteration form.

Methods

MECT reconstruction model

In a fan-beam CT system, the forward projection model was considered to be the following discretized linear system:

$$\text{A}\overrightarrow{x}+\overrightarrow{e}\text{= }\overrightarrow{y},$$[1]

where $\overrightarrow{x}\in {ℝ}^{N_W\times N_H}$ denoted a discrete image in a vector form, and $N_W$ and $N_H$ represented the width and height of the reconstructed image, respectively. Measurement projections were denoted by a vector $\overrightarrow{y}\in {ℝ}^{U\times N_{views}}$ where $U$ and $N_{views}$ represented the number of detectors and projection views. $\overrightarrow{e}\in {ℝ}^{U\times N_{views}}$ denoted the inconsistency in projection data. $A\in {ℝ}^{\left(U\times N_{views}\right)\times \left(N_W\times N_H\right)}$ represented the system matrix, which was a forward-projection operator calculated through the intersection length between the X-rays and pixels.

In MECT, the emitted X-ray photons were divided into different energy bins, and the photon counting detector collected multi-energy measurement data for the same scanned object. The discretized linear system of MECT was formulated as follows:

$$\text{A}{\overrightarrow{x}}_s+{\overrightarrow{e}}_s\text{= }{\overrightarrow{y}}_s,$$[2]

where $s\left(s=1,2,3,\mathrm{..},S\right)$ represented the index of energy bins, and ${\overrightarrow{x}}_s$ and ${\overrightarrow{y}}_s$ represented the $s$th channels of vectorized energy-independent CT images and projections, respectively. Eq. [2] was solved by optimizing the following minimization problem:

$$\underset{{\overrightarrow{x}}_s}{\text{min}}{\displaystyle \sum _{s=1}^S{\Vert \text{A}{\overrightarrow{x}}_s-{\overrightarrow{y}}_s\Vert }_2^2},$$[3]

where ${\Vert \Vert }_2^{}$ represented the L2-norm. In theory, the simultaneous algebraic reconstruction technique (SART) (50) accurately solved Eq. [3] with sufficient accurate measurement data. However, photon crosstalk, energy overlap, and scanning noises led to different equations, resulting in the non-uniqueness of solution for the abovementioned optimization problem. For the improvement of reconstruction quality, the regularization term was introduced by exploiting the prior knowledge of the image itself, formulated as follows:

$$\underset{X}{\text{min}}R\left(X\right)\text{,}\text{s}\text{.t}\text{.}{\displaystyle \sum _{s=1}^S{\Vert \text{A}{\overrightarrow{x}}_s-{\overrightarrow{y}}_s\Vert }_2^2}\le \epsilon ,$$[4]

where $X\in {ℝ}^{N_W\times N_H\times N_S}$ was a three-order tensor stacked by the MECT images ${\left\{{\overrightarrow{x}}_s\right\}}_{s=1}^S$, where $N_S$ represented the number of energy channels. $R\left(X\right)$ represented the regularization term $X$. $\epsilon$ represented the tolerance parameter for noises and inconsistencies in the observed data and was used in controlling a feasible region. Hence, the design of the regularization term was an essential issue in MECT reconstruction.

Multi-energy nonlocal tensor formulation and similarity measurement

Methods that explored the correlations of interchannel images imposed a low-rank on the three-order tensor of MECT images to improve reconstruction quality. In our work, through the exploitation of similar image patches in spatial and spectral domains, a novel multi-energy nonlocal tensor was formulated for MECT images. Figure 1 shows the diagram of generating this new tensor.

Figure 1 Diagram of the formulation of the multi-energy nonlocal tensor. (A) The MECT image tensor; (B) the process of matching similar patches in the spatial and spectral domain; (C) the generated nonlocal tensor composed of vectorized similar patches of MECT images.

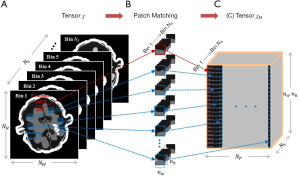
For a single channel of a CT image, it was divided into a group of 2D image patches ${\left\{P_{i,j}\right\}}_{1\le i\le N_{W-}{n}_w,1\le j\le N_{H-}{n}_h}\subset {ℝ}^{n_w\times n_h}$, where $n_w$ and $n_h$ was the width and height of the image patch, respectively. For the reference patch $p_{i,j}$ (denoted by a red square in Figure 1A), similar $N_p$ patches (denoted by a blue square in Figure 1A in a nonlocal area was matched within a single channel CT image by measuring the Euclidean distances between the reference and searching patches. Meanwhile, counterpart patches in other channels were extracted in the same position (Figure 1B). By stacking all vectorized similar patches across channels, a nonlocal three-order tensor was formulated as $X_M\in {ℝ}^{I_1\times I_2\times I_3}$ for all similar patches (Figure 1C), where $I_1=n_w{n}_h;I_2=N_S;I_2=N_P$. $N_S$ represented the number of divided energy bins and $N_p$ denoted the number of similar patches in one single channel CT image. $M$ represented the position of the reference patch with the size of $N_M=\left(N_W-n_w+1\right)\times \left(N_H-n_h+1\right)$. The nonlocal tensor preserved nonlocal self-similarity along with its spectral and spatial modes. Let $T$ represent the formulation of the nonlocal tensor. We obtained

$$X_M=T\left(X\right),M=1,2,3,\mathrm{..},N_M.$$[5]

For the nonlocal tensor $X_M\in {ℝ}^{I_1\times I_2\times I_3}$, intrinsic tensor sparsity regularization (42) was used in exploiting the sparsity of similar patches and was expressed as

$$R\left(X_M\right)={\Vert S\Vert }_0+t{\displaystyle {\prod }_{i=1}^{I}rank\left(X_{{}_M}^{\left(i\right)}\right)},$$[6]

where $S$ was the core tensor of $X_M$ calculated by the Tucker decomposition. ${\Vert \Vert }_0$ indicates the L0 norm. $X_{{}_M}^{\left(i\right)}$ represented the unfolding matrix along with mode i, I denoted the tensor order, and equal to 3 in this work. t was a tradeoff parameter to balance two terms. The first term constrained the number of Kronecker bases, which was calculated by decomposing $X_M$ through CP low-rank techniques. Such term complied with the intrinsic mechanism of CP decomposition, delivering sparsity information underlying a tensor. The second term included the size of the core tensor in Tucker decomposition, which regularized the low-rank subspace of each tensor mode. Combining the two terms enabled the simultaneous measurement of the inner sparsity of the core tensor and the low-rank property of unfolding tensor at all modes. The utilization of this regularization term improved the ability of the reconstruction method in the preservation of image details and fine structures.

Proposed model and solution algorithm

To fully exploit the nonlocal similarity of interchannel images and the spatial sparsity in a single-channel image, the regularization term $R\left(X\right)$ in Eq. [4] was designed as a combination of intrinsic tensor sparsity and TV regularization. The MECT reconstruction model was formulated as follows:

$$\underset{X}{\text{min}}\left(\alpha R\left(T\left(X\right)\right)+{\displaystyle \sum _{s=1}^S{\Vert {\overrightarrow{x}}_s\Vert }_{TV}}\right)\text{,}\text{s}\text{.t}\text{.}{\displaystyle \sum _{s=1}^S{\Vert \text{A}{\overrightarrow{x}}_s-{\overrightarrow{y}}_s\Vert }_2^2}\le \epsilon ,$$[7]

where ${\Vert {\overrightarrow{x}}_s\Vert }_{TV}={\displaystyle \sum _i{\Vert D_i{\overrightarrow{x}}_s\Vert }_1}$ and $D_i$ denoted the discrete directional gradient operators in direction $i$. Horizontal and vertical directions were applied in the current work. α was the parameter to balance two regularization terms. For the solution of the abovementioned problem, an auxiliary tensor $Z\in {ℝ}^{N_W\times N_H\times N_S}$ was introduced and rewritten as follows:

$$\begin{array}{l}\underset{X,Z}{\text{min}}\left(\alpha R\left(T\left(Z\right)\right)+{\displaystyle \sum _{s=1}^S{\Vert {\overrightarrow{x}}_s\Vert }_{TV}}\right),\\ \text{s}\text{.t}\text{.}{\displaystyle \sum _{s=1}^S{\Vert \text{A}{\overrightarrow{x}}_s-{\overrightarrow{y}}_s\Vert }_2^2}\le \epsilon ,X=Z.\end{array}$$[8]

The equality constraint was substituted into the objective using the augmented Lagrange function. For the inequality constraints, we defined a convex set $\Omega \left(\epsilon \right):=\left\{{\overrightarrow{x}}_s|{\Vert \text{A}{\overrightarrow{x}}_s-{\overrightarrow{y}}_s\Vert }_2^2\le \epsilon ,{\overrightarrow{x}}_s\in {ℝ}^{N_W\times N_H}\right\},$ and the indicator function $\Upsilon$ on the convex set $\Omega$ as

$${\Upsilon }_{\Omega }\left({\overrightarrow{x}}_s\right):=\{\begin{array}{c}0,{\overrightarrow{x}}_s\in \Omega ,\\ \infty ,{\overrightarrow{x}}_s\notin \Omega .\end{array}$$[9]

Given the introduction of the indicator function, the optimization problem (Eq. [8]) was written as follows:

$$\underset{X,Z}{\text{min}}\left(\alpha R\left(T\left(Z\right)\right)+{\displaystyle \sum _{s=1}^S{\Vert {\overrightarrow{x}}_s\Vert }_{TV}+\frac{\beta }{2}{\Vert X-Z+\frac{\Lambda }{\beta }\Vert }_F^2+{\displaystyle \sum _{s=1}^S{\Upsilon }_{\Omega }\left({\overrightarrow{x}}_s\right)}}\right),$$[10]

where $\Lambda \in {ℝ}^{N_W\times N_H\times N_S}$ is the Lagrange multipliers in the tensor norm, and β is the penalty coefficient. ${\Vert \Vert }_F^{}$ is the Frobenius norm.

The iterative alternating minimization method was applied for the abovementioned problem. Given an intermediate point $\left(X^k,Z^k\right)$, Eq. [10] was divided into two subproblems. The $X$-subproblem was written as follows:

$$X^{k+1}=\arg \underset{X}{\min }{\displaystyle \sum _{s=1}^S{\Vert {\overrightarrow{x}}_s^k\Vert }_{TV}+\frac{\beta }{2}{\Vert X^k-Z^k+\frac{{\Lambda }^k}{\beta }\Vert }_F^2+{\displaystyle \sum _{s=1}^S{\Upsilon }_{\Omega }\left({\overrightarrow{x}}_s^k\right)}},$$[11]

where ${\Upsilon }_{\Omega }\left({\overrightarrow{x}}_s^k\right)$ is 0 or $+\infty$ based on the definition in Eq. [9]. To address the indicator function ${\Upsilon }_{\Omega }\left({\overrightarrow{x}}_s^k\right)$, this problem was solved in two steps. Based on the method in (51), we first solved the problem of Eq. [11] without the indicator function ${\Upsilon }_{\Omega }\left({\overrightarrow{x}}_s^k\right)$. Given that $X$ it was the tensor representation of the MECT images ${\left\{{\overrightarrow{x}}_s\right\}}_{s=1}^S$, it was considered a minimization problem with ${\overrightarrow{x}}_s$ the unknown variable. When the $s$th channel of CT image ${\overrightarrow{x}}_s^{k+1/2}$ was updated, the other channel images were fixed as constants. Hence, the problem of Eq. [11] excluding the indicator function of a convex set was written as:

$${\overrightarrow{x}}_s^{k+\frac{1}{2}}=\arg \underset{X}{\min }{\Vert {\overrightarrow{x}}_s^k\Vert }_{TV}+\frac{\beta }{2}{\Vert {\overrightarrow{x}}_s^k-{\overrightarrow{z}}_s^k+\frac{{\lambda }_s^k}{\beta }\Vert }_2^2,s=1,2,\mathrm{..},S,$$[12]

where ${\overrightarrow{z}}_s^k$ and ${\lambda }_s^k$ is the $s$th channel of vectorized image for tensor $Z^k$ and ${\Lambda }^k$, respectively. Eq. [12] was attributed to TV denoising, where the input image was ${\overrightarrow{z}}_s^k-{\lambda }^k/\beta$. By minimizing Eq. [12] using the TV minimization method in (52), we obtain the intermediate variable ${\overrightarrow{x}}_s^{k+1/2}$.

Subsequently, we determined if ${\overrightarrow{x}}_s^{k+1/2}$ was in the convex set $\Omega \left(\epsilon \right)$, indicated by the ${\Upsilon }_{\Omega }\left({\overrightarrow{x}}_s^{k+1/2}\right)$. If ${\overrightarrow{x}}_s^{k+1/2}\in \Omega \left(\epsilon \right)$, then ${\overrightarrow{x}}_s^{k+1}={\overrightarrow{x}}_s^{k+1/2}$. If ${\overrightarrow{x}}_s^{k+1/2}\notin \Omega \left(\epsilon \right)$, we project ${\overrightarrow{x}}_s^{k+1/2}$ onto the convex set $\Omega \left(\epsilon \right)$ as ${\overrightarrow{x}}_s^{k+1}={\text{Proj}}_{\Omega \left(\epsilon \right)}\left({\overrightarrow{x}}_s^{k+1/2}\right)$ to make the hard constraint ${\overrightarrow{x}}_s^{k+1}\in \Omega \left(\epsilon \right)$ to hold consistently. In summarizing, the two cases, ${\overrightarrow{x}}_s^{k+1}\in \Omega \left(\epsilon \right)$ was able to hold by applying the projection onto the convex set (POCS) as follows:

$${\overrightarrow{x}}_s^{k+1}={\text{Proj}}_{\Omega \left(\epsilon \right)}\left({\overrightarrow{x}}_s^{k+1/2}\right).$$[13]

For the POCS operation, SART was utilized to solve the abovementioned problem. Finally, we obtained the updated tensor $X^{k+1}$ by stacking all channels of ${\overrightarrow{x}}_s^{k+1}$.

The Z-subproblem was written as the following problem with fixed $X^{k+1}$ and ${\Lambda }^k$:

$$Z^{k+1}=\arg \underset{Z}{\min }\left({\Vert S_M^k\Vert }_0+t{\displaystyle {\prod }_{i=1}^{I}rank\left(Z_{{}_M}^{k,\left(i\right)}\right)}+\frac{\delta }{2}{\Vert X^{k+1}-Z^k+\frac{{\Lambda }^k}{\beta }\Vert }_F^2\right),$$[14]

where $S_M^k$ and $Z_{{}_M}^{k,\left(i\right)}$ was the core tensor and unfolding matrix along with the mode i of $Z_{{}_M}^k$, respectively. $\delta =\beta /\alpha$. In the procedure of program implementation, the L0 norm and rank terms took discrete values, resulting in a combinatorial optimization problem that wa hard to solve. The intrinsic tensor sparsity regularization was then relaxed as a log-sum form to simplify computation (53,54), and Eq. [14] was written as follows:

$$Z^{k+1}=\arg \underset{Z}{\min }\left(L\left(S_M^k\right)+t{\displaystyle {\prod }_{i=1}^I{L}^{*}\left(Z_{{}_M}^{k,\left(i\right)}\right)}+\frac{\delta }{2}{\Vert X^{k+1}-Z^k+\frac{{\Lambda }^k}{\beta }\Vert }_F^2\right),$$[15]

where $L\left(S_M^k\right)={\displaystyle \sum _{i_1,i_2,i_3}^{I_1,I_2,I_3}\log \left(\left|s_{i_1,i_2,i_3}^k\right|+\varsigma \right)}$ and $L^{*}\left(Z_{{}_M}^{k,\left(i\right)}\right)={\displaystyle {\sum }_j\log \left({\sigma }_j\left(Z_{{}_M}^{k,\left(i\right)}\right)+\varsigma \right)}$. $\varsigma$ was a small positive value and ${\sigma }_j\left(Z_{{}_M}^{k,\left(i\right)}\right)$ was the jth singular of $Z_{{}_M}^{k,\left(i\right)}$. The minimization problem of Eq. [15] was solved as described in Xie et al. (43). Alternating direction method of multipliers (ADMM) (55) was applied to solve this large scale optimization problem, where three auxiliary tensors and Lagrange multipliers were introduced in the solution to separate three unknown variables. In this way, Eq. [15] was divided into three subproblems, and each of them deduced the closed-form equations for updating each involved variables. We streamlined the derivation of the solution of Eq. [15] to avoid repeated content with previous works and the complete derivation procedure can be found in (43)].

Finally, the multipliers $\Lambda$ were updated as follows:

$${\Lambda }^{k+1}={\Lambda }^k+\beta \left(X^{k+1}-Z^{k+1}\right).$$[16]

Overall, the proposed algorithm for MECT reconstruction is summarized as follows:

Implementation of the proposed method

For the solution to the $X$-subproblem (line 3), the iteration number of TV denoising was set from 5 to 10 based on our experiences. The step of the TV method, which determines the strength of TV denoising, was set from 0.01 to 0.05 according to the noise level. More iterations and large TV steps led to a smooth result with the loss of detail information. A large β led to an enhanced effect of TV denoising, and a simple way to determine was to vary β from 1 to 2⁸ before reconstruction results were compared. Theoretically, the operation of ${\text{Proj}}_{\Omega \left(\epsilon \right)}$ (line 4) is required to be conducted iteratively for infinite times. In our work, we only performed the operation ${\text{Proj}}_{\Omega \left(\epsilon \right)}$ once in each iteration to reduce computation time.

For the solution of the Z-subproblem (line 6), pixel variances σ should be estimated in advance, which determines the strength of intrinsic sparsity regularization and becomes the most significant parameter in the proposed algorithm. Values ranging from 0.01 to 0.15 were suitable for most MECT reconstructions. We discussed the influence of parameter σ on the reconstruction results in the following contents. δ was the penalty coefficient dependent on σ, calculated by $\delta =c{\sigma }^{-1}$, where t was generally set as a constant 10⁻³. The other parameters showed a relatively small influence on the results, and their settings refer to parameters of (42). The compromise parameter t aiming to balance two sparsity terms was set as 0.5. The iteration of ADMM in the solution of Eq. [15] (line 6) was fixed as 25.

Evaluation

The performance of the proposed method was tested using digital phantom and real data. We compared the proposed method with the filtered-back projection (FBP) method (56), which is a classic analytic reconstruction algorithm. The results of the TV-based method (52) were provided to demonstrate the performance of TV in noise suppression on each channel of the CT image. A tensor sparsity regularization-based method was also implemented in this experiment, which imposed low-rank tensor approximation (LRTA) (57) on the MECT images and was combined with the TV regularization of single-channel image. Given the results of the LRTA-based method, we tested the performance of the proposed method in MECT reconstruction and compared it with the same type of tensor regularization-based reconstruction method. To further evaluate the algorithm performance, the results of material decomposition were also generated using a direct material decomposition method (58) based on reconstructed MECT images with different methods.

We first constructed a digital phantom comprised of 512 × 512 image pixels based on the walnut data in (59). As shown in Figure 2A, the digital phantom was composed of three materials, i.e., bone, tissue, and iodine. The concentration of the iodine contrast agent was 15 mg/mL. The mass attenuation coefficients of basis materials were obtained from the National Institute of Standards and Technology database (https://physics.nist.gov/PhysRefData/XrayMassCoef/tab4.html). Figure 2B shows the normalized X-ray spectrum with an energy sampling interval of 1 keV, generated using SpekCalc software. To perform MECT reconstruction, the X-ray spectrum was divided into six energy bins: [20, 25) keV, [25, 30) keV, [30, 35) keV, [35, 40) keV, [40, 45) keV, [45, 50) keV. The source-to-object and source-to-detector distances were 1,000 and 1,500 mm, respectively. The scanning angle covers 360° with an interval of 0.5°. Projections in each view were collected using a linear detector that consists of 1,024 bins with a size of 0.388 mm. Poisson noise was added on projections to simulate image noises as follows:

Figure 2 Simulated and real experimental data. (A) Digital phantom with different materials in colors, where bone, tissue, and iodine material is denoted by red, green, and yellow, respectively; (B) normalized X-ray spectrum with six divided energy bins; (C) real mouse data reconstructed from full energy spectra with display window [0, 0.08].

$$N_{\text{p\_noise}}=\text{Poisson}\left(N_0\exp \left(-{\overrightarrow{p}}_0\right)\right),$$[17]

where N₀ denoted the number of incident X-ray photons, and N₀ referred to the measured number of photons in the projection data. N₀ is set as 1×10⁴ in the current work. Reconstruction results of the SART method, based on noise-free projections, were taken as the reference of MECT for the following evaluation. An ROI, containing some complicated fine structures, was magnified for detailed comparison. The RMSE, peak-signal-to-noise ratio (PSNR), and structural similarity (SSIM) of the reconstruction results of different methods were calculated for quantitative evaluation. The line profiles of the reconstruction results were provided for a comparison of accuracy across the different methods. Three basis material images were generated, based on the reconstruction results of different methods before ROI magnification was performed for detailed comparison.

The proposed method was further evaluated on real mouse data. Figure 2C showed the real mouse CT image, reconstructed from full energy spectra using an iodine contrast agent. The experiments on real data were performed on a MECT system developed by the Institute of High Energy Physics, Chinese Academy of Sciences. The tube parameters were set as 60 kVp and 72 mAs. The energy thresholds were set at 12, 26, 34, and 42 keV. Four energy bins were utilized to perform MECT reconstruction. The distances between the source to the object and to the detector were 200.8 and 362.8 mm, respectively. The detector consisted of 512×15 bins at 0.4 mm × 0.4 mm. A total of 1,080 projections were collected from 360°. The central slice of each projection was extracted for two-dimensional MECT reconstruction. The channel size of each reconstructed image was 512×512 pixels. To clearly evaluate the mouse body, the reconstruction images of all methods were orientated horizontally and presented as 228×340 pixels. Four channels of reconstructed CT images are shown in this work. An ROI in the mouse trunk was magnified to assess and compare the efficacy of noise suppression and detail preservation across the different methods. Another ROI in a homogeneous area was selected for the quantitative comparison of the mean value of attenuation coefficients and standard deviation (STD), calculated as follows:

$$\text{STD}=\sqrt{\frac{1}{N_{Roi}}{\displaystyle \sum _{n_{Roi}=1}^{N_{Roi}}\left(x_{n_{Roi}}^{}-{\overline{x}}_{}^{}\right)}},$$[18]

where $x_{n_{Roi}}^{}$ represented the value of $n_{Roi}$th pixel. $\overline{x}$ was the mean value of all $N_{Roi}$ image pixels belonging to the selected ROI. Material decomposition was finally performed based on the reconstructed MECT images, where bone, tissue, and iodine materials served as basic materials. An ROI injected with iodine was selected for the detailed comparison of decomposition results.

Results

Simulation experiments

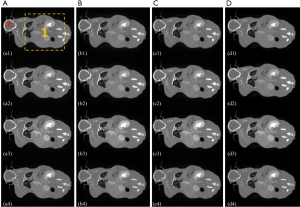
Figure 3 shows the reconstruction results of digital phantom walnut from different methods. Columns from left to right depict reference images and the results of FBP, TV-based, LRTA-based, and proposed methods, accordingly. Reconstructed CT images in the first to sixth energy bins are represented by rows 1 to 6, respectively. The ROI (denoted by a yellow square in Figure 3A1) was magnified for detailed comparisons across different methods in Figure 4. As shown in Figures 3 and 4, imaging via FBP yielded the lowest image quality due to interferences from reconstruction noise, leading to difficulties in distinguishing the inner structures. The TV-based method largely reduced reconstruction noise and generated clean CT images. However, this method displayed a limited capacity in preserving image details and fine structures. This is attributed to the assumption of the piecewise constant of TV minimization model. The LRTA-based method obtained better image quality at all energy bins compared to FBP and LRTA-based methods. However, the LRTA-based method still exhibited image noise distributed across the reconstructed image. In addition, as denoted by the black arrow in Figure 4, obvious degradation was observed in the reconstruction of fine structures. The LRTA-based method was not able to clearly reconstruct a specific region of the walnut containing one or two pixels. By contrast, the proposed method generated the same region of the walnut, preserving image clarity with a low level of noise, not achievable by the other compared methods.

Figure 3 Reconstructed images of the digital walnut phantom from different methods. Reference images (column A) and the reconstruction results are depicted from FBP (column B), TV-based (column C), LRTA-based (column D), and proposed methods (column E). First to the sixth channel of reconstructed images depicted in rows 1 to 6, respectively. The display window of the first (row 1) and second (row 2) channel of images is [0, 0.12] and [0, 0.10], respectively. The display windows of the third (row 3) to sixth (row 6) channel of images are [0, 0.08].

Figure 4 Reconstructed images of magnified ROIs (denoted by the yellow rectangle in Figure 3). Images of reference (column A) and reconstruction results of the FBP (column B), TV-based (column C), LRTA-based (column D), and proposed methods (column E). ROIs of the first to the sixth channel of reconstructed images are shown in rows 1 to 6, respectively. The display window of the first (row 1) and second (row 2) channel of images is [0, 0.12] and [0, 0.10], respectively. The display windows of the third (row 3) to sixth (row 6) channel of images are [0, 0.08].

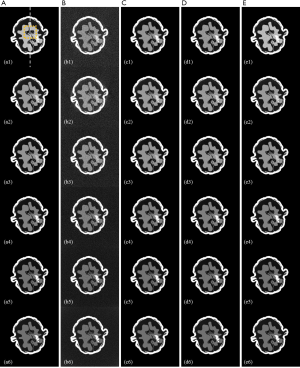
Table 1 lists the RMSEs, PSNRs, and SSIMs of reconstructed images generated by different methods. To measure the overall performance of different methods, the metrics for the results of the full energy bin were determined. The proposed method exhibited the lowest RMSE at each energy bin, as indicated in Table 1. By contrast, the FBP method displayed the largest RMSE, followed by the TV-based and LRTA-based methods. The RMSE of full energy bin is low to 0.0033 for the proposed method, which reduced RMSEs by 89.75%, 50.75%, and 36.54% compared with those for the FBP, TV-based, and LRTA-based methods, respectively. For the evaluation of PSNR and SSIM, the proposed method also achieved the highest values among all compared methods. The PSNR of the full energy bin was up to 49.5761 dB for the proposed method, which increased PSNRs by 19.7264, 6.0997, and 3.9466 dB compared with those for the FBP, TV-based, and LRTA-based methods, respectively. The SSIM of the full energy bin was up to 0.9914 for the proposed method, whereas the SSIMs of other methods were below 0.9900. The partial line profiles from the 155th pixel to 290th pixel along the gray dashed line in Figure 3A1 are plotted in Figure 5. The line profiles provided by the proposed method were closest to the ground truth. In addition, the proposed method exhibited more accurate lines than the other methods, particularly in the region with complicated structures (denoted by the black arrows).

Table 1 RMSEs, PSNRs, and SSIMs of reconstruction images with different methods
Full table

Figure 5 Line profiles of each channel of reconstruction from different methods. Results of the first to the sixth channel of reconstruction images are shown in A,B,C,D,E,F, respectively. Results of images from the reference (black), FBP (gray), blue (TV-based), green (LRTA-based), and proposed methods (red lines) are also shown.

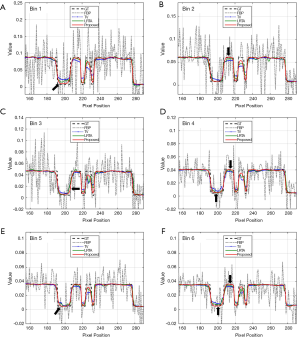
Figure 6 shows the decomposition results, based on the reconstructed images. Since reconstruction noise was magnified during material decomposition, the images revealed by the FBP method yielded substantial noise interference, rendering structures within the ROI indistinguishable. TV-based and LRTA-based methods obtained improved decomposition results compared to the FBP method. However, some noise was still present in the adjacent area, demonstrating a limited ability in the preservation of clarity within the inner structure (Figure 6, rows C and D). By contrast, the proposed method achieved decomposition results of the highest quality, closest to the image shown by the reference image, with near-invisible noise levels whilst preserving image details of the ROI. Thus, the decomposition results demonstrate that although the material decomposition is very sensitive to noise, the proposed method obtained superior decomposition results among all compared modalities, further validating the efficacy of the proposed method in MECT reconstruction.

Figure 6 Decomposition results based on the reconstruction images from different methods. Columns 1 to 3 represent the basis material image of tissue, bone, and iodine, respectively. Decomposition results based on the reference and the reconstructed images with the FBP, TV-based, LRTA-based, and proposed methods are depicted in rows (A) to (E), respectively. The red rectangle represents the magnified ROI on tissue material images. The display windows of all figures are [0.1, 1.0], respectively.

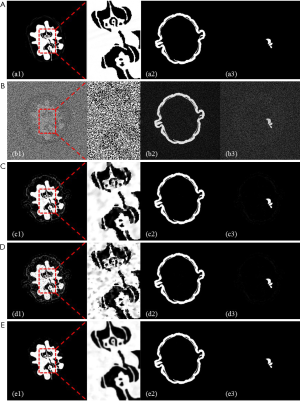
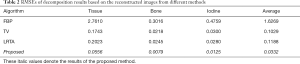
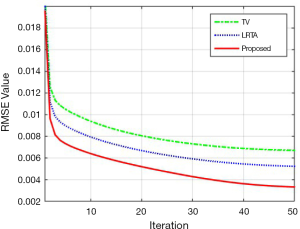
Table 2 lists the RMSEs of basis materials across different methods. Decomposition results, based on the reference MECT images served as the ground truth. The RMSEs of the FBP method was highest among all tested methods, whilst TV- and LRTA-based methods displayed reduced RMSEs to a limited extent for all basic materials. The proposed method achieved the smallest RMSEs, with an average of 0.0332 in the decomposition data, resulting in a reduction by 97.96%, 67.74%, and 72.05% compared to the FBP, TV-based, and LRTA-based methods, respectively. This method also achieved superior convergence properties (Figure 7). Overall, we conclude that the proposed method is capable of reconstructing MECT images of higher quality compared with other methods in this simulated data experiment.

Table 2 RMSEs of decomposition results based on the reconstructed images from different methods
Full table

Figure 7 Convergence lines of RMSEs from different iteration methods. Green, blue, and red line represents the results of the TV-based, LRTA-based, and proposed methods, respectively.

Real data experiments

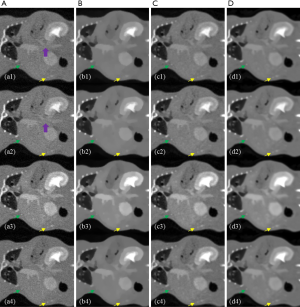
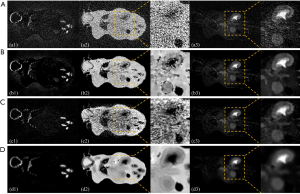
Figure 8 shows the MECT reconstruction images of mouse data, derived across the different methods. The reconstruction results of the FBP, TV-based, LRTA-based, and proposed methods are depicted in columns A-D, respectively. The first to the fourth channel of reconstruction images are shown in rows 1 to 4, respectively. Magnification of an ROI, denoted by a yellow rectangle in Figure 8A1 is shown in Figure 9. The FBP method displayed considerable noise, attributed to an artifact of scanning (Figures 8,9). The noise severely impaired the clarity of most details in the ROI, rendering them indistinguishable (as denoted by the purple arrow in Figure 9A1 and A2). The TV-based method largely reduced noise in the reconstruction images but failed to preserve the image details of the ROI. The LRTA-based method improved the reconstruction quality and preserved most of the detailed information, which exhibited improved results compared to the former two methods. However, some noise was observed in the reconstruction data, which affected the material decomposition. The proposed method achieved superior reconstruction results among all compared methods indicating the elimination of noise whilst achieving the preservation of detailed information. As denoted by the green and yellow arrows in Figure 9, the proposed method successfully reconstructed the dot object at each energy bin, unlike the FBP and TV-based methods where they were not visible in some energy bins. Furthermore, the noise was also evident in the LRTA-based method. We, therefore, conclude from Figures 8 and 9 that the proposed method provides better capability in MECT reconstruction for real data.

Figure 8 Reconstruction results of mouse data from different methods. The reconstruction results of the FBP, TV-based, LRTA-based, and proposed methods are depicted in columns A to D, respectively. First to the forth channel of reconstructed images depicted in rows 1 to 4, respectively. The display windows of the first (row 1) and second (row 2) channel of images are [0, 0.08]. The display window of the third (row 3) and fourth (row 4) channel of images are [0, 0.07] and [0, 0.06], respectively.

Figure 9 Reconstruction results of magnified ROIs in the mouse (denoted by the yellow rectangle in Figure 8A1) from FBP (column A), TV-based (column B), LRTA-based (column C), and proposed methods (column D). Rows 1 to 4 represent the ROIs of the first to the fourth channel of reconstructed images, respectively. The display windows of the first (row 1) and second (row 2) channel of images are [0, 0.08]. Arrows in different colors denote the image information for detailed comparison. The display window of the third (row 3) and fourth (row 4) channel of images are [0, 0.07] and [0, 0.06], respectively.

Another ROI denoted by the red circle in Figure 8A1 was selected for quantitative evaluation. As the ground truth of mouse data was unknown, the mean value was used to evaluate the accuracy of the reconstruction results, whilst the STD measured the performance of noise suppression for the different methods. These results are shown in Table 3. The proposed method reconstructed each channel of CT images with mean values similar to other methods, verifying its accuracy in MECT reconstruction. The FBP method displayed the largest STD compared to the other methods. The LRTA-based method exhibited a limited reduction in STD. The TV-based and proposed methods achieved the smallest STDs. Despite exhibiting the lowest noise level in certain energy bins, the TV-based method failed to retain detailed information. By evaluating the quantitative results of the mouse data, we also conclude that the proposed method has the capacity to reconstruct high-quality MECT images.

Table 3 Mean values and STDs of ROI 2 denoted by the red circle in Figure 8A1
Full table

The decomposition results of MECT images in the mouse are shown in Figure 10. Noise observed in the reconstructed image from the FBP method was significantly magnified. The TV-based method reduced noise to a large extent, but its decomposition results displayed evident artifacts in the inner region of the mouse body. Whilst the LRTA-based method achieved acceptable reconstruction results in Figures 8 and 9, the decomposition results showed substantial degradation (Figure 10), with images in the inner region of the mouse body of lower quality than that of the TV-based method. Compared with the former methods, the proposed method exhibited decomposition results of the highest quality. The noise was largely suppressed (Figure 10), with the image detail of the tissue fully retained. Therefore, the decomposition results of the mouse data also demonstrated the successful reconstruction of MECT images and basis images by the proposed method with high quality.

Figure 10 Decomposition results based on reconstructed mouse images with different methods. Basis material images of bone, tissue, and iodine are depicted in columns 1 to 3, respectively. Decomposition results based on the reconstructed images with the FBP, TV-based, LRTA-based, and proposed methods are depicted in rows (A) to (D), respectively. The display window of bone, tissue, and iodine material is [0, 0.8], [0.2, 1.2], and [0, 1.0], respectively.

Discussion

The synthesis of the two regularisation approach resulted in the superiority of the proposed method. Intrinsic tensor sparsity regularization aimed to exploit the nonlocal similarity of interchannel images and provides a promising approach to depict the correlations of MECT images at different energies. It plays an important role in the preservation of detail information for MECT reconstruction. For example, some detail information is displayed with poor quality at lower energy due to the noise interferences, but exhibit relatively high quality at high energy. In this case, the intrinsic tensor sparsity regularization enhanced the detailed reconstruction of the low energy CT image by utilizing the information of high energy CT image through the formulated nonlocal tensor. TV regularization further improved noise suppression in a single-channel image for the proposed method, which was proven effective in single energy CT reconstruction. The synthesis of intrinsic tensor sparsity and TV regularization enabled the proposed algorithm to simultaneously exploit the nonlocal similarity of interchannel image and spatial sparsity in single-channel images. The lack of either regularisation may lead to the decline of reconstruction performance.

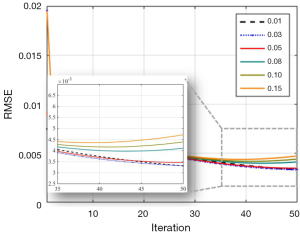
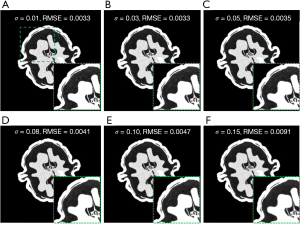
Like most regularization-based algorithms, potential parameter adjustments were necessary for the proposed method to generate reconstruction results of the highest quality. A guidance of parameter selection was provided in this study to address each subproblem. Among them, parameter σ that denoted the pixel variances was a critical and should be estimated in advance. In this work, the reconstructed image of the first channel of walnut data was utilized to compare the influences of parameters σ on the reconstruction results. The parameter σ was set at 0.01, 0.03, 0.05, 0.08, 0.10, and 0.15. Figure 11 shows the convergence lines of RMSEs of the proposed method at different σ values. The parameter σ with value 0.01, 0.03, and 0.05 achieved better convergence and obtained lower RMSE than other parameter values. Figure 12 shows the reconstruction results of the first channel of the walnut CT image at different σ values. The green square in Figure 12A represents the magnified ROI for detailed comparison. Large parameter σ values indicated improved noise suppression but yielded large RMSEs in the reconstruction results. The parameter σ of values 0.01 and 0.03 exhibited the lowest RMSE among all compared results. However, as shown in the magnified ROI, some dotted noise was evident in the air region and led to a decline of reconstruction quality. By contrast, the σ value of 0.05 achieved the best reconstruction results among all parameter values, consistent with the walnut data in this work. For different reconstruction tasks, varying parameter σ values and comparing the reconstruction results were necessary to obtain the best reconstruction performance for the proposed method. Nevertheless, in this work, since each subproblem was taken as an independent module and solved separately, the suitable parameters were relatively easy to be determined.

Figure 11 Convergence lines of RMSEs of the proposed method. The lines in different colors denote the results at different σ values.

Figure 12 Reconstruction results of the first channel of walnut CT image with different parameter σ values. (A) to (F) represents the results with parameter value 0.01, 0.03, 0.05, 0.08, 0.10, 0.15, respectively. The RMSEs of reconstruction results are denoted on the top of the reconstructed images. The green square represents the magnified ROI for detailed comparison. The display windows of (A,B,C,D,E,F) and their ROIs are [0, 0.10] and [0, 0.08], respectively.

The proposed method outperforms its counterparts in image reconstruction and material decomposition. However, we should note that the accuracy of the proposed method still holds the potential for improvement. For example, the shape of some details in Figure 4 is not accurate compared with the reference images, which subsequently influenced the decomposition results in Figure 6. The weighted TV minimization approach that incorporated the edge information could be applied to the proposed method to solve this problem in the future. Nevertheless, this work proposed a flexible framework for the solution of the MECT reconstruction model with two regularization terms. Based on this framework, the regularization term can be easily modified with minor changes for different tasks. In the derivation of the proposed method, the solution of Eq. [12] serves as a denoising problem, where the TV minimization method is applied to this problem. This operation can be substituted by a plug-and-play network (60,61), which utilizes deep priors to reduce noises. It is worth noting that re-training, based on a new MECT dataset, is required before it can be applied to the proposed framework. In the implementation of the proposed method, the introduction of intrinsic tensor sparsity regularization increases algorithm complexity. The solution of intrinsic tensor sparsity regularization took approximately 200 seconds in our work, and need to be accelerated to meet the requirement of fast imaging in medical diagnosis. The graphic processing unit can be applied in the future to speed up the algorithm implementation by utilizing its powerful ability in parallel computing.

Conclusions

We proposed a MECT reconstruction method, based on tensor nonlocal similarity and spatial sparsity regularization. Nonlocal similar patches of interchannel images in the spectral and spatial domain were extracted and stacked into a three-order tensor. Intrinsic tensor sparsity regularization was applied to impose the sparsity and low-rank property into the core tensor and the unfolding matrix of the formulated three-order tensor, respectively. TV regularization term exploited the sparsity on the gradient map of the single-channel image. A MECT reconstruction model was established by incorporating the two abovementioned regularization terms and solved by the iterative alternating minimization method. The experimental results on digital walnut phantom and real mouse data indicated that the proposed method outperforms its counterparts with regard to noise suppression and detail preservation in MECT reconstruction.

Acknowledgments

We thank Prof. Cunfeng Wei and Prof. Zhe Wang in the Institute of High Energy Physics, Chinese Academy of Sciences, who kindly provide the mouse data for this study. We also thank the reviewers for their effort and time to review this paper.

Funding: This work was supported by the National Natural Science Foundation of China (Grant No. 61601518) and the National Science Foundation for Post-doctoral Scientists of China (Grant No. 2019M663996).

Footnote

Conflicts of Interest: All authors have completed the ICMJE uniform disclosure form (available at http://dx.doi.org/10.21037/qims-20-594). The authors have no conflicts of interest to declare.

Ethical Statement: The study obtained ehtics approval from the Biomedical Ethics Committee, Institute of High Energy Physics, Chinese Academy of Sciences (IHEPLLSC202006).

Open Access Statement: This is an Open Access article distributed in accordance with the Creative Commons Attribution-NonCommercial-NoDerivs 4.0 International License (CC BY-NC-ND 4.0), which permits the non-commercial replication and distribution of the article with the strict proviso that no changes or edits are made and the original work is properly cited (including links to both the formal publication through the relevant DOI and the license). See: https://creativecommons.org/licenses/by-nc-nd/4.0/.

References

1. Sawatzky A, Xu Q, Schirra C, Anastasio M. Proximal ADMM for multi-channel image reconstruction in spectral X-ray CT. IEEE Trans Med Imaging 2014;33:1657-68. [Crossref] [PubMed]
2. Lu X, Lu Z, Yin J, Gao Y, Chen X, Guo Q. Effects of radiation dose levels and spectral iterative reconstruction levels on the accuracy of iodine quantification and virtual monochromatic CT numbers in dual-layer spectral detector CT: an iodine phantom study. Quant Imaging Med Surg 2019;9:188-200. [Crossref] [PubMed]
3. Sorin V, Sklair-Levy M. Dual-energy contrast-enhanced spectral mammography (CESM) for breast cancer screening. Quant Imaging Med Surg 2019;9:1914-7. [Crossref] [PubMed]
4. Mengfei Li, Yunsong Zhao, Peng Zhang. Accurate Iterative FBP Reconstruction Method for Material Decomposition of Dual Energy CT. IEEE Trans Med Imaging 2019;38:802-12. [Crossref] [PubMed]
5. Graser A, Johnson TR, Chandarana H, Macari M. Dual energy CT: preliminary observations and potential clinical applications in the abdomen. Eur Radiol 2009;19:13-23. [Crossref] [PubMed]
6. Li L, Zhao Y, Luo D, Yang L, Hu L, Zhao X, Wang Y, Liu W. Diagnostic value of single-source dual-energy spectral computed tomography in differentiating parotid gland tumors: initial results. Quant Imaging Med Surg 2018;8:588-96. [Crossref] [PubMed]
7. Gorecki A, Brambilla A, Moulin V, Gaborieau E, Radisson P, Verger L. Comparing performances of a CdTe X-ray spectroscopic detector and an X-ray dual-energy sandwich detector. J Instrum 2013;8:P11011. [Crossref]
8. Shikhaliev PM, Xu T, Molloi S. Photon counting computed tomography: Concept and initial results. Med Phys 2005;32:427-36. [Crossref] [PubMed]
9. Taguchi K, Iwanczyk JS. Vision 20/20: Single photon counting x-ray detectors in medical imaging. Med Phys 2013;40:100901. [Crossref] [PubMed]
10. Shikhaliev PM, Fritz SG. Photon counting spectral CT versus conventional CT: Comparative evaluation for breast imaging application. Phys Med Biol 2011;56:1905-30. [Crossref] [PubMed]
11. Iwanczyk JS, Nygard E, Meirav O, Arenson J, Barber WC, Hartsough NE, Malakhov N, Wessel JC. Photon counting energy dispersive detector arrays for X-ray imaging. IEEE Trans Nucl. Sci 2009;56:535-42. [Crossref] [PubMed]
12. Leng S, Yu L, Wang J, Fletcher JG, Mistretta CA, McCollough CH. Noise reduction in spectral CT: reducing dose and breaking the trade-off between image noise and energy bin selection. Med Phys 2011;38:4946-57. [Crossref] [PubMed]
13. Barber W, Nygard E, Iwanczyk J, Zhang M, Frey E, Tsui B, Wessel J, Malakhov N, Wawrzyniak G, Hartsough N, Gandhi T, Taguchi K. Characterization of a novel photon counting detector for clinical CT: Count rate, energy resolution, and noise performance. Medical Imaging 2009: Physics of Medical Imaging. International Society for Optics and Photonics 2009;7258:725824-1-9.
14. Borsdorf A, Raupach R, Flohr T, Hornegger J. Wavelet based noise reduction in CT-images using correlation analysis. IEEE Trans Med Imaging 2008;27:1685-703. [Crossref] [PubMed]
15. Tang S, Tang X. Statistical CT noise reduction with multiscale decomposition and penalized weighted least squares in the projection domain. Med Phys 2012;39:5498-512. [Crossref] [PubMed]
16. Candès EJ, Romberg J, Tao T. Robust uncertainty principles: Exact signal reconstruction from highly incomplete frequency information. IEEE Trans Inf Theory 2006;52:489-509. [Crossref]
17. Donoho DL. Compressed sensing. IEEE Trans Inf Theory 2006;52:1289-306. [Crossref]
18. Sidky EY, Pan X. Image reconstruction in circular cone-beam computed tomography by constrained, total-variation minimization. Phys Med Biol 2008;53:4777-807. [Crossref] [PubMed]
19. Dong B, Li J, Shen Z. X-ray CT image reconstruction via wavelet frame based regularization and radon domain. J Sci Comput 2013;54:333-49. [Crossref]
20. Xu Q, Yu H, Mou X, Zhang L, Jiang H, Wang G. Low-dose X-ray CT reconstruction via dictionary learning. IEEE Trans Med Imaging 2012;31:1682-97. [Crossref] [PubMed]
21. Sidky E, Kao C, Pan X. Accurate image reconstruction from few-views and limited-angle data in divergent-beam CT. J X-ray Sci Technol 2006;14:119-39.
22. Tang J, Nett B, Chen G. Performance comparison between total variation (TV)-based compressed sensing and statistical iterative reconstruction algorithms. Phys Med Biol 2009;54:5781-804. [Crossref] [PubMed]
23. Chen Z, Jin X, Li L, Wang G. A limited-angle CT reconstruction method based on anisotropic TV minimization. Phys Med Biol 2013;58:2119-41. [Crossref] [PubMed]
24. Xu Q, Yu H, Bennett J, He P, Zainon R, Doesburg R, Opie A, Walsh M, Shen H, Butler A, Mou X, Wang G. Image reconstruction for hybrid true-color micro-CT. IEEE Trans Biomed Eng 2012;59:1711-9. [Crossref] [PubMed]
25. Zhao B, Gao H, Ding H, Molloi S. Tight-frame based iterative image reconstruction for spectral breast CT. Med Phys 2013;40:031905. [Crossref] [PubMed]
26. Zeng D, Gao Y, Huang J, Bian Z, Zhang H, Lu L, Ma J. Penalized weighted least-squares approach for multienergy computed tomography image reconstruction via structure tensor total variation regularization. Comput Med Imaging Graph 2016;53:19-29. [Crossref] [PubMed]
27. Chu J, Li L, Chen Z, Wang G, Gao H. Multi-energy CT reconstruction based on Low Rank and Sparsity with the Split-Bregman Method (MLRSS). IEEE Nuclear Science Symposium and Medical Imaging Conference Record 2012;2411-2414.
28. Gao H, Yu H, Osher S, Wang G. Multi-energy CT based on a prior rank, intensity and sparsity model (PRISM). Inverse Probl 2011;27:115012. [Crossref] [PubMed]
29. Li L, Chen Z, Wang G, Chu J, Gao H. A tensor PRISM algorithm for multi-energy CT reconstruction and comparative studies. J Xray Sci Technol 2014;22:147-63. [Crossref] [PubMed]
30. Li L, Chen Z. Cong W, Wang G. Spectral CT modeling and reconstruction with hybrid detectors in dynamic-threshold-based counting and integrating modes. IEEE Trans Med Imaging 2015;34:716-28. [Crossref] [PubMed]
31. Kilmer ME, Martin CD. Factorization strategies for third-order tensors. Linear Algebra Appl 2011;435:641-58. [Crossref]
32. Semerci O, Hao N, Kilmer ME, Miller EL. Tensor-Based Formulation and Nuclear Norm Regularization for Multienergy Computed Tomography. IEEE Trans Image Process 2014;23:1678-93. [Crossref] [PubMed]
33. Rigie DS, La Rivière PJ. Joint Reconstruction of Multi-channel, Spectral CT Data via Constrained Total Nuclear Variation Minimization. Phys Med Biol 2015;60:1741-62. [Crossref] [PubMed]
34. Yu Z, Leng S, Li Z, McCollough CH. Spectral Prior Image Constrained Compressed Sensing (Spectral PICCS) for Photon-Counting Computed Tomography. Phys Med Biol 2016;61:6707-32. [Crossref] [PubMed]
35. Zhang Y, Xi Y, Yang Q, Cong W, Zhou J, Wang G., Spectral CT. Reconstruction With Image Sparsity and Spectral Mean. IEEE Trans Comput Imaging 2016;2:510-23. [Crossref] [PubMed]
36. Zhao B, Ding H, Lu Y, Wang G, Zhao J, Molloi S. Dual-dictionary learning-based iterative image reconstruction for spectral computed tomography application. Phys Med Biol 2012;57:8217. [Crossref] [PubMed]
37. Wu W, Zhang Y, Wang Q, Liu F, Chen P, Yu H. Low-dose spectral CT reconstruction using image gradient L0-norm and tensor dictionary. Appl Math Model 2018;63:538-57. [Crossref] [PubMed]
38. Dabov K, Foi A, Katkovnik V, Egiazarian K. Image denoising by sparse 3-D transform-domain collaborative ltering. IEEE Trans Image Process 2007;16:2080-95. [Crossref] [PubMed]
39. Kim K, Ye JC, Worstell W, Ouyang J, Rakvongthai Y, Fakhri GE, Li Q. Sparse-View Spectral CT Reconstruction Using Spectral Patch-Based Low-Rank Penalty. IEEE Trans Med Imaging 2015;34:748-60. [Crossref] [PubMed]
40. Xu Q, Liu H, Yu H, Wang G, Xing L. Dictionary learning based reconstruction with low-rank constraint for low-dose spectral CT. Med Phys 2016;43:3701. [Crossref]
41. Niu S, Yu G, Ma J, Wang J. Nonlocal low-rank and sparse matrix decomposition for spectral CT reconstruction. Inverse Probl 2018;34:024003. [Crossref] [PubMed]
42. Xie Q, Zhao Q, Meng D, Xu Z, Gu S, Zuo W, Zhang L. Multispectral images denoising by intrinsic tensor sparsity regularization. IEEE Conference on Computer Vision and Pattern Recognition 2016:1692-700.
43. Xie Q, Zhao Q, Meng D, Xu Z. Kronecker-Basis-Representation based tensor sparsity and its Applications to tensor recovery. IEEE Trans Pattern Anal Mach Intell 2018;40:1888-902. [Crossref] [PubMed]
44. Zeng D, Xie Q, Cao W, Lin J, Zhang H, Zhang S, Huang J, Bian Z, Meng D, Xu Z, Liang Z, Chen W, Ma J. Low-Dose Dynamic Cerebral Perfusion Computed Tomography Reconstruction via Kronecker-Basis-Representation Tensor Sparsity Regularization. IEEE Trans Med Imaging 2017;36:2546-56. [Crossref] [PubMed]
45. Wu W, Liu F, Zhang Y, Wang Q, Yu H. Non-local Low-rank Cube-based Tensor Factorization for Spectral CT Reconstruction. IEEE Trans Med Imaging 2019;38:1079-93. [Crossref] [PubMed]
46. Wu W, Zhang Y, Wang Q, Liu F, Luo F, Yu H. Spatial-spectral cube matching frame for spectral CT reconstruction. Inverse Probl 2018;34:104003. [Crossref] [PubMed]
47. Xia W, Wu W, Niu S, Liu F, Zhou J, Yu H, Wang G, Zhang Y., Spectral CT. Reconstruction—ASSIST: Aided by Self-Similarity in Image-Spectral Tensors. IEEE Trans Comput Imag 2019;5:420-36. [Crossref]
48. Tucker LR. Some mathematical notes on three-mode factor analysis. Psychometrika 1966;31:279-311. [Crossref] [PubMed]
49. Kolda TG, Bader BW. Tensor decompositions and applications. SIAM Review 2009;51:455-500. [Crossref]
50. Andersen AH, Kak AC. Simultaneous algebraic reconstruction technique (SART): a superior implementation of the ART algorithm. Ultrason Imaging 1984;6:81-94. [Crossref] [PubMed]
51. Cai A, Li L, Zheng Z, Wang L, Yan B. Block-matching sparsity regularization-based image reconstruction for low-dose computed tomography. Med Phys 2018;45:2439-52. [Crossref] [PubMed]
52. Yu H, Wang G. Compressed sensing based interior tomography. Phys Med Biol 2009;54:2791-805. [Crossref] [PubMed]
53. Candes EJ, Wakin MB, Boyd SP. Enhancing sparsity by reweighted L1 minimization. J Fourier Anal Appl 2008;14:877-905. [Crossref]
54. Lu C, Zhu C, Xu C, Yan S, Lin Z. Generalized singular value thresholding. Twenty-Ninth AAAI Conference on Artificial Intelligence 2015:1805-11.
55. Boyd S, Parikh N, Chu E, Peleato B, Eckstein J. Distributed optimization and statistical learning via the alternating direction method of multipliers. Found Trends Mach Learn 2011;3:1-122. [Crossref]
56. Turbell H. Cone-beam reconstruction using filtered backprojection. Ph.D. dissertation, Linköping Univ, Linköping, Sweden, 2001.
57. Renard N, Bourennane S, Blanc-Talon J. Denoising and dimensionality reduction using multilinear tools for hyperspectral images. IEEE Trans Geosci Remote Sens Lett 2008;5:138-42. [Crossref]
58. Mendonca PR, Lamb P, Sahani DV. A flexible method for multi-material decomposition of dual-energy CT images. IEEE Trans Med Imaging 2014;33:99-116. [Crossref] [PubMed]
59. Jørgensen JS, Sidky EY. How little data is enough? Phase-diagram analysis of sparsity-regularized X-ray computed tomography. Philos Trans A Math Phys Eng Sci 2015;373:20140387. [PubMed]
60. Ryu EK, Liu J, Wang S, Chen X, Wang Z, Yin W. Plug-and-Play Methods Provably Converge with Properly Trained Denoisers. arXiv preprint arXiv:1905.05406, 2019.
61. Guo S, Zhang Y, Zhang K, Zuo W, Zhang L. Toward convolutional blind denoising of real photographs. IEEE Conference on Computer Vision and Pattern Recognition 2019:1712-22.