Three-dimensional organ extraction method for color volume image based on the closed-form solution strategy
Introduction
The Virtual Human Project (VHP) was founded by the United States National Library of Medicine (NLM). As the first research stage, the visualization of virtual human data has extraordinary significance. It has broad application prospects in medical research and clinical education: surgical training, prosthetic modeling, and digitalized teaching of human body morphology. The foundation and application for this research rely on the acquisition of accurate three-dimensional (3D) models of VHP organs. Therefore, extracting the organs from the massive VHP 3D image database has become an urgent need. At present, the most commonly used approach is manually extracting regions of interest in serialized slice images. Obviously, the efficiency of this procedure (slice-by-slice processing) is very low. For computing, the most direct approach is segmenting the VHP images with the matting method. However, existing methods are also two-dimensional (2D)-image-oriented (slice-by-slice processing). In addition, it is common for sudden changes to occur between the extracted regions in adjacent slice images. Another potential method is machine learning-based strategy. However, because of its heavy reliance on the training model, the machine learning strategy is mainly suitable for large scale image data but not suitable for single image data (such as VHP image data). Therefore, it is essential to design an approach for the direct segmentation of the VHP 3D volume image.
Here, we propose a 3D organ extraction method for color volume image based on the closed-form solution strategy. In this method, to address the massive coefficient matrix processing, we designed an upper triangular storage strategy to store the considerable data and used the preconditioned conjugate-gradient (PCG) method to solve the linear equation. This method only needs to mark the target region and non-target region with manual markings to directly extract the 3D organs.
Literature review
Image matting is a classic research topic and mainly focuses on obtaining the region of interest (ROI) in the image. Several outstanding methods have been proposed to solve this issue. Levin et al. presented a closed-form solution to natural image matting (1). High-quality mattes for natural images may be obtained from a small quantity of user input. Yan et al. presented a correlation-based sampling method in which the image pixel correlation is employed in color sampling (2). Cai et al. proposed a cooperative coevolution differential evolution (DE) algorithm to improve the efficiency of searching for high-quality sample pairs (3), and other studies have used a similar method (4-7). Johnson et al. conceived the matting problem as a sparse coding of pixel features (8). Cho et al. presented an image matting algorithm to extract consistent alpha mattes across sub-images of a light field image (9). Several other similar methods (10-13) also achieved a satisfactory effect.
In addition to geometrical and mathematical means, some matting methods use learning to achieve their results. Chen et al. proposed a deep learning framework (called TOM-Net) to learn the refractive flow (14). He et al. proposed an approach with RGB-Depth (RGB-D) data based on iterative transductive learning (15). They also presented a new method to form the Laplacian matrix in transductive learning. Xu et al. proposed a deep image matting method (16) that could address 2 issues: (I) the use of only low-level features and (II) the lack of high-level context. Zou et al. introduced a method of video matting via sparse and low-rank representation (17). Other studies (18-20) have implemented similar research methods.
Matting methods have not yet been extensively applied in medical imaging. This may be due to the fact that because matting methods are more suitable for multi-channel color image segmentation rather than single-channel gray level image segmentation. There have been a few typical related studies in recent years. Cheng et al. worked on improving the matting algorithm by adding a weight extension and referred to this as adaptive weight matting (AWM) (21). Li et al. proposed a new end-to-end iterative network for tongue image matting, which directly learns the alpha matte from the input image by correcting any misunderstandings in intermediate steps (22). Fan et al. proposed a hierarchical image matting model, where a hierarchical strategy is integrated to extract blood vessels from fundus images (23). Several other methods have also been designed and tested for different medical image processing applications (24-27).
From a review of the existing methods, we can see that all strategies, including common matting methods, learning-based methods, medical image-oriented methods, are designed and suitable for 2D images. How to directly extract target organs from 3D volume images by matting strategy is thus an interesting and challenging issue.
Methods
From the above methods, we can see that all the published literature centers around 2D image matting. However, there has not been a matting method developed thus far for 3D volume images. Here, we propose a closed-form solution-based volume matting (CFSVM) method for the VHP 3D volume image dataset. The main flow chart of the 3D volume image data matting in this paper is shown in Figure 1.
Volume image construction of VHP slices
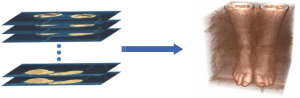
The VHP image dataset is composed of a large number of serialized slice images. Our goal is to directly extract the target 3D organ from an original 3D volume image dataset. Therefore, the first step in reconstructing the volume image by the serialized 2D slice images (as shown in Figure 2).
Markings for foreground and background
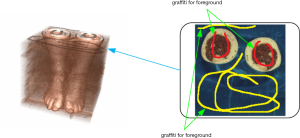
To obtain the 3D ROI from the constructed 3D volume image, it is necessary to mark the foreground (target) and the background (nontarget) in the 3D volume image. In our method, a brush is used to manually mark the foreground markings and background markings on a certain layer of the 3D volume image (as shown in Figure 3). Meanwhile, the coordinates of the markings path and its corresponding voxel values are recorded in different vectors.
3D ROI extraction from the 3D volume image
For image matting, we can consider an image as a linear combination of its foreground image and its background image. In our method, by referencing 2D image segmentation methods (28), this linear combination for a 3D volume image can be presented as the following:
|
| [1] |
where V is the 3D volume image, α is the transparency of the foreground image, F represents the foreground voxels, and B represents the background voxels. Then, the deformation of the formula can be obtained as follows:
|
| [2] |
A known 3D volume image V is the summation of the foreground F and background B. Thus, it α is obtained; the foreground (ROI) F can be calculated. Here, we utilize the value of local αl to estimate the value of αg for the whole volume image. Then, the 3D ROI in the volume image can be extracted. The specific steps are outlined below.
αg computation by closed-form solution strategy
Similar to the formula above [1], we can obtain the linear formula of the i-th voxel in a locally small window (3×3×3 voxels in our method):
|
| [3] |
where Vi is the i-th voxel, Fi and Bi are the i-th voxel’s foreground and background, and αi is the i-th voxel’s opacity of the foreground. Referencing the second formula [2], a formula transformation can be obtained from the third formula [3]:
|
| [4] |
where . To obtain the value of αg for the whole volume image, an energy function (1) is utilized. The αg value can be calculated by minimizing the energy function as follows:
|
| [5] |
where Wk is a small window around voxel k, and εak2 is a regular term to maintain the stability of the values in the window. According to the deformation and derivation of the energy function, we can obtain the following:
|
| [6] |
where L is an N×N matrix whose (i, j) -th element is
|
| [7] |
where μ is a covariance matrix, μk is the color mean vector in a small window Wk, V3 is an identity matrix, Vi and Vj represent values of the i-th and j-th voxels, and δij is the Kronecker delta.
To match the extracted αg with the handmade graffiti, we can solve the following formula:
|
| [8] |
where λ is a constant (100 in our method), d is a vector that is composed of the specified αg values for voxels in the graffiti and 0 for other voxels, D is a diagonal matrix whose diagonal elements are 1 for voxels in the markings and 0 for other voxels. To obtain the minimum value in the eighth formula [8], we need to set only its derivatives to 0. Thus, the following formula can be derived:
|
| [9] |
All variables are known in the final formula [9], so by solving sparse linear equations, we can obtain the value of αg.
Voxel traversal in the volume image
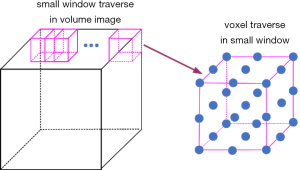
In the process of solving the energy function, we need to traverse all the voxels in the 3D volume image. This process contains two steps: (I) small windows (3×3×3 voxels) traversal in the entire 3D volume image and (II) all voxels traversal in each small window. This procedure is shown in Figure 4.
Storage and solution for computational matrix
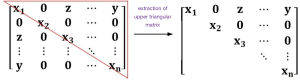
In the process of solving the energy function [5], we found that the obtained intermediate data were sparse, which means that the number of nonzero elements was relatively small. For a simpler and more convenient computation when the matrix is inverted in solving linear equations, a storage method of the sparse matrix was designed. In this design, the coordinates of nonzero elements and their values are mainly stored. For a large-scale 3D sparse matrix, there may be memory abnormalities in solving linear equations. Because the sparse matrix is symmetric, positive, and definite, we propose a space-saving strategy. In our method, the upper triangle storage format is utilized for matting storage. Meanwhile, the stored data are accessed many times until all of the data in the sparse matrix are traversed. After all the computational results are stored in the original storage format in the sparse matrix, we can obtain the solution of the linear equations. Assuming that the storage form of the matrix is shown in the left part of Figure 5 (the matrix has n rows and n columns, and y represent values of some nonzero elements), the right part is its form of an upper triangular matrix. This storage method ensures that memory abnormalities can be avoided.
In the process of solving equation [9], the processing speed is also very important. In mathematics, preconditioned conjugate gradient (PCG) is a fast and effective method for solving a large linear sparse equation Ax = B (where A is a N×N matrix, B is a N×1 vector, x is unknown). It has the advantage of a fast convergence rate and small storage. In the PCG method, residuals and margins are used to search the solution of linear equations. Using this method, we can obtain the following:
|
| [10] |
where B = M−1 A, c = Bx, M is the matrix preprocessed in the conjugate gradient method, rk+1 is the residue after k+1 times iteration, Zk+1 is the conjugate direction after k+1 times iteration, and xk+1 is the solution after k+1 times iteration. The iteration times should not be larger than matrix order N.
ROI extraction in the volume image
|
| [11] |
By the obtaining αg, we can construct a mask image in the following way:
where ⊙ is a dot product operation, αgT min is the minimum threshold of αg, αgT max is the maximum threshold of αg, (αg≥αgT min) represents that all the elements in αg that are not less than αgT min are set to 1 (and are otherwise set to 0), (αg<αgT max) means that all the elements in αg that are not greater than αgT max are set to 1 (and are otherwise set to 0). In our method, when the maximum and minimum thresholds are 0.2 and 0.9, the mask image is better. Under this condition, the ROI can be extracted by solving the formula representing the target 3D ROI: . VROI.
Experiments and results
In this paper, the VHP slices were utilized as 3D volume experimental images to test our method. The image data sets were collected by the United States National Library of Medicine and the Southern Medical University of China. There were 4 image data sets available (2 virtual human male and 2 virtual human female). Other image data set information was as follows: digit capacity, 24 bits color; interlayer spacing, 2 mm for U.S. Virtual Human and 0.2 mm for Chinese Virtual Human. Our method was implemented by the C++ language (Microsoft Visual Studio). The hardware parameters were the following: CPU, 1.90 GHz, memory, 4 GB. Several typical organ slices (including brain slices, eye slices, lung slices, heart slices, liver slices, kidney slices, spine slices, arm slices, vastus slices, and foot slices) were selected to extract the 3D volume organ models. The original slice images and the extracted 3D volume organs are shown in Figure 6. Our method could segment the ROI organs directly from the original 3D volume image. The 3D organs obtained were acceptable and satisfactory. Some local tiny organ details could also be accurately extracted, such as those of the central cerebral sulcus, leg vessels, pupil, and cardiac aorta. For the experimental result assessment, there is presently no common indicator or benchmark, but one commonly used means is visual assessment. In our experiment, we invited the professional anatomical physician of the Dalian Medical University of China to evaluate the experimental results, and the assessment feedback was positive.
Conclusions
In the traditional means for segmenting the organ regions in the VHP image dataset, we usually utilize software (e.g., Photoshop) to manually extract the ROIs slice by slice, which is a very tedious job. To promote other related research (e.g., computer-assisted surgery), there is an urgent need for direct organ extraction from the VHP original volume image data. However, no such method currently exists.
In this paper, a CFSVM method is proposed to extract the organs of interest in the VHP volume image data. This volume image matting method has the advantage of good interaction and limited input requirements from users. We only need to mark (manual markings) the ROI (foreground) and region of noninterest (background) in the volume image to obtain the target organs. In the experiment, the greatest difficulty was the volume of data processed. The colors of different human organs are very similar. Thus, completing massive coefficient matrix processing is a challenging issue. We designed an upper triangular storage strategy to store the considerable data and use the PCG method to solve the linear equation. Thus, the processing procedure was made more robust. The extraction results show the effectiveness of our CFSVM method. In the future, this method may have more applications in medical and other scientific research fields.
Acknowledgments
Funding: This work is supported by the National Natural Science Foundation of China (Nos. 61972440, 61572101 and 61300085).
Footnote
Conflicts of Interest: All authors have completed the ICMJE uniform disclosure form (available at http://dx.doi.org/10.21037/qims.2020.03.21). The authors have no conflicts of interest to declare.
Open Access Statement: This is an Open Access article distributed in accordance with the Creative Commons Attribution-NonCommercial-NoDerivs 4.0 International License (CC BY-NC-ND 4.0), which permits the non-commercial replication and distribution of the article with the strict proviso that no changes or edits are made and the original work is properly cited (including links to both the formal publication through the relevant DOI and the license). See: https://creativecommons.org/licenses/by-nc-nd/4.0/.
References
- Levin A, Lischinski D, Weiss Y. A closed-form solution to natural image matting. IEEE Trans Pattern Anal Mach Intell 2008;30:228-42. [Crossref] [PubMed]
- Yan X, Hao Z, Han H. Alpha matting with image pixel correlation. Int J Mach Learn Cybern 2016;9:621-7. [Crossref]
- Cai ZQ, Lv L, Huang H, Hu H, Liang YH. Improving sampling-based image matting with cooperative coevolution differential evolution algorithm. Soft Comput 2017;21:4417-30. [Crossref]
- Karacan L, Erdem A, Erdem E. Image matting with KL-divergence based sparse sampling. 2015 IEEE International Conference on Computer Vision (ICCV), Santiago, 2015, pp. 424-32.
- Feng X, Liang X, Zhang Z. A cluster sampling method for image matting via sparse coding In: Leibe B, Matas J, Sebe N, Welling M. (editors). Computer Vision – ECCV 2016. ECCV 2016. Lecture Notes in Computer Science, vol 9906. Springer, Cham, 2016:204-19.
- Jin M, Kim BK, Song WJ. Adaptive propagation-based color-sampling for alpha matting. IEEE Trans Circuits Syst Video Technol 2014;24:1101-10. [Crossref]
- Wu H, Li Y, Miao Z, Wang Y, Zhu R, Bie R, Lie R. A new sampling algorithm for high-quality image matting. J Vis Commun Image Represent 2016;38:573-81. [Crossref]
- Johnson J, Varnousfaderani ES, Cholakkal H, Rajan D. Sparse coding for alpha matting. IEEE Trans Image Process 2016;25:3032-43. [Crossref] [PubMed]
- Cho D, Kim S, Tai YW. Consistent Matting for Light Field Images. In: Fleet D, Pajdla T, Schiele B., Tuytelaars T. editors. Computer Vision – ECCV 2014. ECCV 2014. Lecture Notes in Computer Science, vol 8692. Springer, Cham, 2014:90-104.
- Fiss J, Curless B, Szeliski R. Light field layer matting. 2015 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Boston, MA, 2015, pp. 623-631.
- Wang L, Xia T, Guo Y, Liu L, Wang J. Confidence-driven image co-matting. Comput Graph 2014;38:131-9. [Crossref]
- Tan G, Chen H, Qi J. A novel image matting method using sparse manual clicks. Multimed Tools Appl 2016;75:10213-25. [Crossref]
- Zhu X, Wang P, Huang Z. Adaptive propagation matting based on transparency of image. Multimed Tools Appl 2018;77:19089-112. [Crossref]
- Chen G, Han K, Wong KYK. TOM-Net: Learning Transparent Object Matting from a Single Image. Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. 2018:9233-41.
- He B, Wang G, Zhang C. Iterative transductive learning for automatic image segmentation and matting with RGB-D data. J Vis Commun Image Represent 2014;25:1031-43. [Crossref]
- Xu N, Price B L, Cohen S, et al. Deep Image Matting. Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. 2017:2970-9.
- Zou D, Chen X, Cao G, et al. Video matting via sparse and low-rank representation. Proceedings of the IEEE International Conference on Computer Vision. 2015:1564-72.
- Cho D, Tai YW, Kweon I. Natural Image Matting Using Deep Convolutional Neural Networks. In: Leibe B, Matas J, Sebe N, Welling M. editors. Computer Vision – ECCV 2016. ECCV 2016. Lecture Notes in Computer Science, vol 9906. Springer, Cham, 2016:626-43.
- Shen X, Tao X, Gao H, Zhou C, Jia J. Deep automatic portrait matting. European Conference on Computer Vision. Springer, Cham, 2016:92-107.
- Hu H, Pang L, Shi Z. Image matting in the perception granular deep learning. Knowl Based Syst 2016;102:51-63. [Crossref]
- Cheng J, Zhao M, Lin M, Chiu B. WM. Adaptive Weight Matting for medical image segmentation. Medical Imaging 2017: Image Processing. International Society for Optics and Photonics 2017;10133:101332P.
- Li X, Yang T, Hu Y, Xu M, Zhang W, Li F. Automatic tongue image matting for remote medical diagnosis. 2017 IEEE International Conference on Bioinformatics and Biomedicine (BIBM), Kansas City, MO, 2017, pp. 561-4.
- Fan Z, Lu J, Wei C, Huang H, Cai X, Chen X. A hierarchical image matting model for blood vessel segmentation in fundus images. IEEE Trans Image Process 2018;28:2367-77. [Crossref] [PubMed]
- Amintoosi M. Enhancement of Learning Based Image Matting Method with Different Background/Foreground Weights. Signal and Data Processing 2019;16:75-90. [Crossref]
- Manonmani S, Rangaswamy S, Dhanush Kumar K, Ishan S, Akhilesh J, Joshua I. 2D to 3D Conversion of Images Using Defocus Method Along with Laplacian Matting for Improved Medical Diagnosis. J Appl Inf Sci 2018;6:6-13.
- Zhong Z, Kim Y, Buatti J, Wu X. 3d Alpha Matting Based Co-segmentation of Tumors on PET-CT Images. Molecular Imaging, Reconstruction and Analysis of Moving Body Organs, and Stroke Imaging and Treatment. Springer, Cham, 2017:31-42.
- Wong LM, Shi L, Xiao F, Griffith JF. Fully automated segmentation of wrist bones on T2-weighted fat-suppressed MR images in early rheumatoid arthritis. Quant Imaging Med Surg 2019;9:579-89. [Crossref] [PubMed]
- Smith AR, Blinn JF. Blue screen matting. Proceedings of the 23rd annual conference on Computer graphics and interactive techniques. 1996:259-68.