A hybrid double-density dual-tree discrete wavelet transformation and marginal Fisher analysis for scoring sleep stages from unprocessed single-channel electroencephalogram
Introduction
There is little doubt that sleep is one of the most essential aspects of an individual’s health. A number of illnesses, including hypersomnia, insomnia, sleep-oriented breathing difficulties, circadian rhythm sleep-wake disorder, sleep movement disorders, and parasomnia, are associated with sleep, with polysomnography (PSG) being the primarily approach for finding, suppressing, or curing these sleep-related illnesses. A gathering of numerous signals used for monitoring the sleep of a patient under watch is called a polysomnogram. A polysomnogram works by gathering and using derived physiological signals, like electroencephalograms (EEG) and electromyograms (EMG), and ambient signals, like microphones and accelerometers.
Sleep staging includes distributing data gathered form PSG into consecutive short periods of 20 or 30 s, and sorting these periods into a distinct sleep phase alongside a few other candidates chosen based on sorting rules (1,2). We are able to use this approach on a full polysomnogram or on subcategories of its channels with the help of an educated operator or computer-oriented algorithm. From time to time, algorithms can be used by operators for pre-recording.
A hypnogram is the continuous exhibition of night-long sleep levels and is useful for diagnosing or clarifying sleep disorders. Properly dividing sleep time into distinct phases is considered to be an arduous task, requiring specialists to spend substantial time and energy on its completion. Furthermore, the conditions of grading are highly dependent on the skills and fatigue of the grader, and the acceptance of the results between the graders does not often exceed 90% (3,4). For this reason, computer-aided automated algorithms are used to divide the sleep time into separate phases.
Although the main focus of our discussion here is concerned with the first steps of multichannel analyzing systems, sleep phasing with a single channel is a promising approach, as it provides a system that is light, portable, and unobtrusively applicable on mobile devices, meaning it can facilitate undisturbed sleep due being less bulky, having fewer parts, and using 2 to 3 electrodes. Most research done on automated sleep recording originates from single-channel EEG using a two-phase method. The first phase entails deriving attributes from the time waveform, and the second phase involves having a highly trained organizer forecast the sleep phases using the data derived from the waveforms. In terms of sorting, the usual approaches consist of decision trees and arbitrary forests (5), support vector machines (SVM) (6), and neural network (NN)-based methods (7). Alternatively, entropy with numerous scales, auto declining attributes, and linear separator analysis were used by the authors of (8). Zhu et al. (9) used attributes from a diversity visibility graph and sorted them via an SVM. Fraiwan et al. (5) focused on using time-frequency attributes, Renyi’s entropy attributes, and an arbitrary forest sorter. Meanwhile, Hassan and Bhuiyan (10) were able to acquire attributes from observational mode disintegration and sort them based on bootstrap aggregation with decision trees. They (11) also experimented with spectral attributes from an adjustable Q-factor wavelet change and an arbitrary forest categorizer. Sharma et al. (12) used frequentative refinement, a separated energy splitting algorithm, and different organizers, whereas Hsu et al. (13) used frequent neural organizers on attributes related to energy.
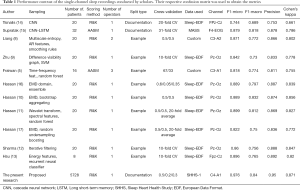
Recently, researchers have chosen to use end-to-end trained NN organizers, which can be used both as attribute extractors and organizers. Garcia-Molina et al. (7) performed research with a heap of infrequent auto-encoders and (14) the use of cascade neural networks (CNNs). In another study (15), CNN preprocessing was completed via coupling to a double-routed long interim momentary network (LSTM). The outcomes for this array of approaches reported in the literature above can be found in Table 1.
Full table
We here present a new methodology of sleep phasing achieved by a single-channel EEG utilizing a double-density dual-tree discrete wavelet transformation (DDDTDWT)-based decomposition of the image and a marginal Fisher analysis (MFA)-based reduction of the dimension on an unprocessed signal model. Related models include image recognition (18,19), innate language processing (20), advocate systems (21), and different monitored arrangement understanding functions. Here, we hope to demonstrate the importance of DDDTDWT and MFA as useful tools capable of aiding reliable sleep recording performance on a large sleep recording database comprising multiple centers. These systems may also be useful in other domains like in brain illnesses where repeated EEG documentation has seen growing interest. This end-to-end approach also has the advantage of not requiring an engineering phase for attributes. Our network, illustrated in “Methods” section, has the ability to learn attribute discoverers suitable to the task of categorizing, and thus have a higher likelihood of yielding accurate results than those attributes extracted by humans. As described in “Results” and “Discussion” sections, this approach can be very powerful if used on a large sleep recording database.
Methods
Data procurement
A group of 50 healthy and 43 ischemic cardiac illness (ICI) cases were evaluated, and a total of 279 ultrasound images were obtained which were based on the signs and assessments of left ventricular ejection fraction (LVEF), with LVEF rates lower than 45% implying significant results for ICI cases (22). The volunteers who came for periodic inspections were assumed to be healthy cases. The GE VIVID 7 health check and DICOM four-chamber left ventricular images were used. The images were converted into 800×600 JPG format. Three images were chosen from every case in total (the main image, along with the 20th preceding image and the 20th successive image to the main image).
Data preparation for processes
Preparation of the data is an essential step in the signal assessment, as it can enhance the total efficiency of the technique. In this preparation, all of the EEGs are improved contrast-wise using contrast-limited adaptive histogram equalization (CLAHE) (23). Next, the artifacts are omitted from the image by mathematical morphology (closing operator) with a circular shape where the element structure is 5 (24). In the next stage, a narrow box is created for limiting the region of interest (ROI) (4 chambers of the heart) using the modified element assessment.
DDDTDWT technique
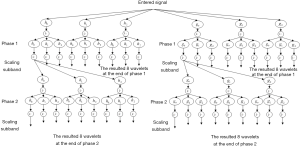
The DDDTDWT is a multi-resolution technique that is added to the discrete wavelet transform (DWT) (25,26). It is used to exploit the benefits of double-density DWT and dual-tree DWT at the same time (25). Another interpretation of dual-tree DWT is WT with complex magnitudes (25). In comparison to the critically-sampled DWT, the dual-tree DWT performs well in different processing of images (27,28). As shown in Figure 1, the DDDTDWT uses repeated filter groups that are oversampled and work in parallel. Four different wavelets and 2 different scale equations are used for its derivation. Eq. [1] can be used to state it.
|
| [1] |
In which wavelets Ψh,x(t) and Ψh,x+1(t) have a difference of 0.5, which also is the case for Ψg,x(t) and Ψg,x+1(t) . This is also shown in Eq. [2].
|
| [2] |
Also, Ψh,x(t) and Ψg,x(t) produce an estimated Hilbert transform pair. The resulting wavelets are flat with short distances.
The assessment and combination configuration are both shown in Figure 2. This figure shows that the different filter banks are generated (25) as follows: gi(n) and hi(n), i= 0, 1, 2. A total of 32 directional wavelet sub-bands are obtained using DDDTDWT (without scale sub-bands). In addition, the orientation of the wavelets is influenced by the wavelets being further exposed to the double-density transformation and dual-tree complex configuration. The attributes can be localized in various orientations by the DDDTDWT approach because of the higher quantity of sub-bands and the other previously mentioned characteristics. Having the high-frequency elements, the low-frequency ones can be obtained using the DDDTDWT.
Moreover, this technique can obtain constant brightness attributes and use other attributes to eliminate excess data. Hence, the double-density dual-tree discrete wavelet transformation yields better performance compared to others, and it is more advisable for EEGs.
Entropy attributes
Four different entropy attributes are obtained from the DDDTDWT factors, including Kapur, Shannon, Renyi, and Yager entropies. The Renyi and Shannon entropies determine the size of the signal. In addition, the Shannon entropy is the highest advisable one for assessing the dynamic sequence of the systems. In this entropy, the minimum and maximum numbers are calculated using the probability density graph width (29). The Renyi technique is recommended for assessing the spectrum complication of a given time-series signal (30). In addition, to obtain the entropy magnitude and entropy calculation, the Kapur technique uses the universal historical data and prior probability distribution, respectively (31). Finally, the Yager technique assesses the unknown system data (32).
These entropies are computed using the DDDTDWT factor.
Kapur technique:
|
| [3] |
Here, α is the order and β is the kind.
Shannon technique:
|
| [4] |
Here, hi denotes the i-th intensity occurrence.
Yager technique:
|
| [5] |
Renyi technique:
|
| [6] |
α is the order.
MFA technique
Various entropic attributes were derived from the DDDTDWT factor and reduced according to its dimensions. The major purpose of the dimensional decrease procedure is to have a smaller dimension attribute set and to simplify the subsequent categorization task. The principal component assessment (PCA) and independent component assessment (ICA) approaches are usually implanted on the assessment of patients’ imagery, which is an unmonitored training technique that has been previously reported (33,34). However, recently the graph embedding technique (GET) has been used to produce the dimension decrease technique. Our study used MFA, in which the curves are produced to describe the ability to be separated between the classes and be compacted inside the classes (35).
|
| [7] |
|
| [8] |
Here, Mk1 denotes the group of intra-class k1, the closest neighbors of candidates xi, and Qk2 denotes the group of the k2 pairs of data. This procedure enables unprecedented characterization of the input without the need for knowing its distribution. In addition, since MFA takes account of marginal areas, it efficiently provides distinguishing orientation (36,37). Therefore, 30 attributes remained from the many that were obtained.
Optimum feature selection
To achieve desirable efficiency without any repetitive features, the feature selection is mixed with pattern recognition. Also, the feature categorization techniques demonstrate higher efficiency because of the optimum feature selection. This combination leads to an approach that is faster and more practical from an economic point of view. A group of optimum feature selection techniques is highlighted in this paper, including Bhattacharyya distance (38), Student’s t-test (39), entropy criteria (40,41), Wilcoxon ranking experiment (42,43), and Bootstrapped receiver operating characteristic (ROC) curve (44). In order to find analogies of the average of the 2 groups, the Student’s t-test was conducted. The approach can provide the P and t values of the obtained attributes of the 2 sets. Sometimes a lower value for P (P≤0.05) and a higher value for t are selected to enhance the ranking. Moreover, to assess the test’s sensitivity and particularity, we can utilize the ROC curve. To acquire the ROC curve for multi-threshold points, the assessment is completed, and sensitivity in terms of 1 particularity is plotted. When the 2 types are distinguished, the yielded curve is acquired. Thus, the required information about the accuracy of the approach is obtained utilizing the zone found beneath the curve. The seen amount of the zone beneath the curve is between 0.5 and 1. The approach is as acceptable if the zone is close to 1. In order to rank the characteristics on the basis of the ability to distinguish the training information, the Bhattacharya approach is used (38). The examination based on the entropy shows that it has a lower amount for sorted information and a higher amount for unsorted points (40,41). The evaluation of divergence is performed by estimating the dimension among the probability density functions (PDF). The difference between 2 internally related samples on a single sample is acquired utilizing the Wilcoxon signed-rank test, which is a statistical theory examination. The mean ranks, is performed to test the mean population (42). It is also assumed that each data pair is randomly selected and does not rely on other data pairs (43,45).
Classifying the characteristic
At this phase, the tags of randomly selected samples were examined by utilizing a machine learning method. We examined a series of typical categorizers for the diagnosis of healthy and ICI groups.
We used linear discriminant analysis (46); quadratic discriminant analysis (46); probabilistic NN (47); k-nearest neighbor (48); an SVM categorizer with their various kernels including radial basis function; polynomial kernels of order 1, 2, and 3 (49); decision tree; and Naïve Bayes categorizer (50). The performance evaluation was carried out using accuracy, sensitivity, specificity, and positive predicted value (51).
Cardiac vessel illness probability
By utilizing 2 marginal Fisher analyses (MFA1 and MFA2) characteristics, the novel cardiac vessel illness probability can be proposed. Initially, Ghista et al. (52) suggested developing this probability index, and then it was tested (53-56) for various medical image process uses. With higher placed characteristics, we formulated a novel cardiac vessel illness probability, which is as follows.
This equation is experimentally formulated so that by using a single amount, it evidently divides 2 categories. Moreover, based on their average and normal deviations, the MFA characteristics are selected in an optimal way, which divides 2 categories of cases.
Results
Performance outputs
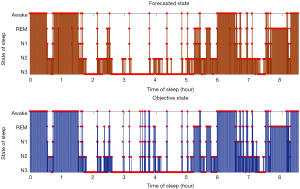
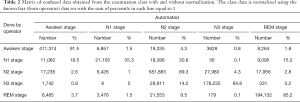
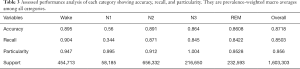
Table 2 exhibits the output confusion matrix in the test group. In Table 3, we can see multi-category and overall accuracy, recall, and particularity, with N1 being the most disorganized phase with 35% of precise organizations. The wake category showed the most proper organization reaching a size of 91%, followed by phase N2 with 89%, REM with 86%, and N3 with 85%. From the table we can also see that the total multi-category organization reaches 87%, and the total Cohen’s kappa is 0.81.
Full table
Full table
The proposed model can be summarized as follows:
- Phase N1 is very often confused with N2 (35%), REM (15%), and wake (19%) while the obtained results did not show any confusion with N3.
- Phase N2 can sometimes be confused with phase N3 (4%), but results did not show any major confusion with other phases.
- Phase N3 is very often confused with N2 (14%), and results generally showed no major confusion with other phases.
- Phase REM is very often confused with phases N2 and wake (9%, 4%).
- Phase wake can sometimes be confused with N2 (4%).
Accordingly, we present Figure 2, which is a hypnogram test set. Further descriptions and research can be found in “Discussion” section.
Visualizations
Figure 3 represents the artificial inputs that can boost the output quality of our 5 preceding neurons (preceding the softmax non-linearity). Here, it is important to note that the artificial signals we produced were exactly similar optically to an EEG series signal, but they were magnifiers of trends that our network uses for categorizing sleep phases. Also, signals were not going to be similar in every sleep phase that we worked on. Here, we have tried to showcase the archetypes. Useful codes for producing these examples can be found in Sors et al. (57). It is clear that the wake phase possesses the highest frequency signals. In more descriptions, we can see that phase N1 has θ waves reaching 6Hz frequency. Phase N2 exhibits some arrangements identical to sleep spindles (range of frequency is 11–16 Hz). In stage N3, we can also see some θ waves and sleep spindles as well as other higher frequency waves.
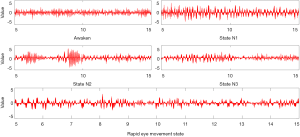
However, solely from this illustration, we cannot demonstrate a single arrangement that our algorithm can count as the most significant for distinguishing phase N3. The final description is about how phase REM shows kinds of arrangements with almost all of them being of higher frequency compared to other phases, excluding the wake phase. In some tests previously conducted on other databases via the Fpz-Pz channel, an illustration of REM included visible arrangements of eye movements; however, relying solely on C4-A1 eye movements will not appear on EEG results. We speculate that making use of 2 derivations can prove useful in this case.
Discussion
Core discoveries
Our research demonstrates the feasibility of categorizing sleep phases through using a single EEG channel and a DDDTDWT with MFA. This approach applied unprocessed signal models without any sort of attribute derivation stage and performed as well as other highly developed approaches. Our training contains all aspects of proposed method and does not require any technical knowledge for attribute choices or signal preprocessing. This, combined with its ability to learn the attributes that are most eligible to be utilized in categorization tasks, may provide a considerable advantage compared to other methods. Also, it is worth noting that we were unable to produce better results while using band-pass finite impulse response filters (FIR) due to convolutional rows already having the knowledge of choosing the best fitting filters. The other advantage to this approach is that it can be easily used on other applications or methodologies. Training large DDDTDWT with MFA places high demands on computers, but after the first training, adjustments can be performed easily on a personal computer or a portable device. Looking at the types of errors that can occur in process, we understand that the errors are mostly correlating phases that are connected to sleep cycles. One reason for this is perhaps that the largest identical aspect between REM and wake phases is eye movements that can appear in negligible amounts on C4-A1 derivation.
Cases of imbalance in the categories
Just like other sleep recording databases, this one can also have some unbalanced results in class division. In the outcomes presented above, all had ordinary expenses and modeling. To give further information on imbalances occurring in the class division, more studies should be conducted. Ensemble learning (58) and DDDTDWT with MFA-specific methods (59) have the potential to be improved.
Comparative analysis
Visible in Table 3 are some aspects and performance measures from research conducted on single-channel EEG sleep recording. Research done on sleep recording in studies might prove difficult due to a diversity in the datasets, the number of patients, the rules of recording, and differences in class division. For instance, the PhysioNet Sleep-European Data Format (EDF)x dataset (60) possesses a far greater quantity of periods of the wake phase than other phases due to the fact these periods are recorded not only before but also after sleep. In several other studies (5,9,16,19), all these wake periods were kept in their performance measures, but other researcher have attempted to readjust balancing. Thus, the outcomes are varied. Now, to equitably compare these types of research, we need to use known confusion matrices, and in a case where the wake phase is the most displayed category, we should re-adjust the balancing in order to make its size equal to the biggest category that comes after a wake in this method.
It is possible to achieve a categorization performance on par with other well-established and up-to-date approaches with a precision of 0.87 and Cohen’s kappa of 0.81. Table 1 shows a comparison of other aspects of these studies including the dataset, quantity of patients, quantity of graders for each record, and type of division. The division (for each second in each example) is based on if the training-test-verification sets were achieved via dividing over recordings or overall instances. It is noticeable that, excluding 2 of the studies (14,15), all use a model division. This type of progress is considered undesirable as this will mean that we can see models from identical records in the test group and the training set, thus making the algorithm learn aspects of each record. This event can restrict globalization performance when graded on unfamiliar and new patients. In this research, we used a division for each record. In the end, these recently conducted studies (9-14,16,17) used the sleep-EDF, although the longer and better dataset, sleep-EDFx, has been accessible for a considerable amount of time. This choice was noticeable; therefore, we graded a new, simplified clone of our DDDTDWT with MFA that was not as deep and was used on sleep-EDFx and sleep-EDF via a 10-fold cross verification. Unexpectedly, we achieved better outcomes on the smaller sleep-EDF database. This might have been due to human grader error and the lower quantity of operators involved in recording sleep-EDF compared to the more extensive sleep-EDFx: techniques assessed by EDF sleep standardization were merely simpler for teaching the categorization preferences of graders.
This trend is also bad for globalization. On the contrary, our technique is assessed by grading at the examination time on 1,698 records, which are scored by a large number of operators. This approach can ensure that the system does not have bias due to a small number of operator categorizing preferences.
Sleep recording and manual glossary
In general, this algorithm’s performance was highly constrained as a result of the quality of the accessible glossary. There were many graders working in recording data from the SHHS database. It can be concluded that there was some level of dispute between our operators for the period ratings. As an example, recorded Cohen’s Kappa of 0.46-0.89 while working with 2 human graders, while Svetnik et al. (4) recorded Cohen’s kappa of 0.72 and 0.85 (0.82–0.85 while working with graders showing good performance). In order to be approved, an operator was required to reach a concurrence of at least 90% with a master polysomnologist. Validation of this concurrence has not been not analyzed over time. Although these measures possess a fair degree of concurrence (0.87% and Cohen’s kappa of 0.81), proposed algorithm can perform on par with them, making the quality of these glossaries a constraint. The easiest method for boosting the performance of an organizer having an inexact ground truth is to collect the glossaries from diverse graders per record and to derive the ground truth from the plurality (and probably with the milder description or value for doubt). The proposed method has also been applied in other medical areas like skin cancer categorization (61) and diabetic retinopathy discovery (62), through the use of DDDTDWT with MFA categorizers. We can conclude that acquiring a database possessing numerous graders is the next step in automating sleep recording algorithm enhancement. It is notable that human specialists do not use a single-channel approach during sleep recording. As an example, at least 3 channels are recommended in the American Association of School Administrations instructions, and in most cases, markers are EOG, EMG, or movement that is most helpful for neuropsychologists to distinguish REM. In our research, although utilizing a single-channel approach yielded noteworthy outcomes for portable systems, it definitely limited our performance (63). Utilizing numerous channels might prove valuable in future research.
Conclusions
This article highlights the use of the proposed algorithm for an EEG sleep recording with one channel using unprocessed signal models. Furthermore, DDDTDWT was used for decomposing the image, and MFA was used for reducing the dimension. In this process, the MFA is considered in which the curves are produced to describe the ability to be separated between the classes and be compacted inside the classes. Our findings also demonstrate that, performance-wise, our approach is up to standard and that this network can learn realistic arrangement detection capable of visualization. The approach of sleep recording with one channel provides a less bulky, unobtrusive, completely portable system. The easiest method to boost the performance of the organizer having an inexact ground truth is collecting glossary from diverse grader per-record and making the ground truth with a choice of plurality. This method approach is working by DDDTDWT based on MFA categorizers, for skin cancer categorizing and diabetic retinopathy discovery. Finally, the development of EEG systems working on multiple but still a little number of channels has a promising outlook. There might be other approaches for future improvements like further one-sided processing of proposed wavelet transforms and MFA algorithms.
Acknowledgments
Funding: None.
Footnote
Conflicts of Interest: The authors have no conflicts of interest to declare.
Open Access Statement: This is an Open Access article distributed in accordance with the Creative Commons Attribution-NonCommercial-NoDerivs 4.0 International License (CC BY-NC-ND 4.0), which permits the non-commercial replication and distribution of the article with the strict proviso that no changes or edits are made and the original work is properly cited (including links to both the formal publication through the relevant DOI and the license). See: https://creativecommons.org/licenses/by-nc-nd/4.0/.
References
- Rechtschaffen A, Kales A. A Manual of Standardized Terminology, Techniques and Scoring System for Sleep Stages of Human Subjects (1968) Washington, DC. Public Health Service, US Government, Printing Office 2017.
- Berry RB, Budhiraja R, Gottlieb DJ, Gozal D, Iber C, Kapur VK, Marcus CL, Mehra R, Parthasarathy S, Quan SF. Rules for scoring respiratory events in sleep: update of the 2007 AASM manual for the scoring of sleep and associated events. J Clin Sleep Med 2012;8:597-619. [Crossref] [PubMed]
- Popovic D, Ayappa I, Hauri P, Levendowski D, Velimirovic V, Burschtin O, Rapoport DM, Westbrook P. Accuracy of automated sleep staging using signals from a single forehead site. Sleep 2008;31:1007.
- Svetnik V, Ma J, Soper KA, Doran S, Renger JJ, Deacon S, Koblan KS. Evaluation of automated and semi-automated scoring of polysomnographic recordings from a clinical trial using zolpidem in the treatment of insomnia. Sleep 2007;30:1562-74. [Crossref] [PubMed]
- Fraiwan L, Lweesy K, Khasawneh N, Wenz H, Dickhaus H. Automated sleep stage identification system based on time–frequency analysis of a single EEG channel and random forest classifier. Comput Methods Programs Biomed 2012;108:10-9. [Crossref] [PubMed]
- Geng D, Zhao J, Dong J, Jiang X. Comparison of support vector machines based on particle swarm optimization and genetic algorithm in sleep staging. Technol Health Care 2019;27:143-51. [Crossref] [PubMed]
- Garcia-Molina G, Baehr K, Steele B, Tsoneva T, Pfundtner S, Riedner B, White DP, Tononi G, editors. Automatic characterization of sleep need dissipation using a single hidden layer neural network. 2017 25th European Signal Processing Conference (EUSIPCO); 2017: IEEE.
- Liang SF, Kuo CE, Hu YH, Pan YH, Wang YH. Automatic stage scoring of single-channel sleep EEG by using multiscale entropy and autoregressive models. IEEE Trans Instrum Meas 2012;61:1649-57. [Crossref]
- Zhu G, Li Y, Wen PP. Analysis and classification of sleep stages based on difference visibility graphs from a single-channel EEG signal. IEEE J Biomed Health Inform 2014;18:1813-21. [Crossref] [PubMed]
- Hassan AR, Bhuiyan MIH. Computer-aided sleep staging using complete ensemble empirical mode decomposition with adaptive noise and bootstrap aggregating. Biomed Signal Process Control 2016;24:1-10. [Crossref]
- Hassan AR, Bhuiyan MIH. A decision support system for automatic sleep staging from EEG signals using tunable Q-factor wavelet transform and spectral features. J Neurosci Methods 2016;271:107-18. [Crossref] [PubMed]
- Sharma R, Pachori RB, Upadhyay A. Automatic sleep stages classification based on iterative filtering of electroencephalogram signals. Neural Comput Appl 2017;28:2959-78. [Crossref]
- Hsu YL, Yang YT, Wang JS, Hsu CY. Automatic sleep stage recurrent neural classifier using energy features of EEG signals. Neurocomputing 2013;104:105-14. [Crossref]
- Tsinalis O, Matthews PM, Guo Y, Zafeiriou S. Automatic sleep stage scoring with single-channel EEG using convolutional neural networks. arXiv preprint arXiv:161001683, 2016.
- Supratak A, Dong H, Wu C, Guo Y. DeepSleepNet: A model for automatic sleep stage scoring based on raw single-channel EEG. IEEE Trans Neural Syst Rehabil Eng 2017;25:1998-2008. [Crossref] [PubMed]
- Hassan AR, Bhuiyan MIH. Automatic sleep scoring using statistical features in the EMD domain and ensemble methods. Biocybern Biomed Eng 2016;36:248-55. [Crossref]
- Hassan AR, Bhuiyan MIH. Automated identification of sleep states from EEG signals by means of ensemble empirical mode decomposition and random under sampling boosting. Comput Methods Programs Biomed 2017;140:201-10. [Crossref] [PubMed]
- Liang M, Hu X. editors. Recurrent convolutional neural network for object recognition. Proceedings of the IEEE conference on computer vision and pattern recognition; 2015.
- Hijazi S, Kumar R, Rowen C. Using convolutional neural networks for image recognition. Cadence Design Systems Inc: San Jose, CA, USA, 2015.
- Conneau A, Schwenk H, Barrault L, Lecun Y. Very deep convolutional networks for natural language processing. arXiv preprint arXiv:160601781, 2016;2.
- Saga R, Duan Y. editors. Apparel Goods Recommender System Based on Image Shape Features Extracted by a CNN. 2018 IEEE International Conference on Systems, Man, and Cybernetics (SMC); 2018: IEEE.
- Solomon SD, Anavekar N, Skali H, McMurray JJ, Swedberg K, Yusuf S, Granger CB, Michelson EL, Wang D, Pocock S. Influence of ejection fraction on cardiovascular outcomes in a broad spectrum of heart failure patients. Circulation 2005;112:3738-44. [Crossref] [PubMed]
- Pizer SM, Amburn EP, Austin JD, Cromartie R, Geselowitz A, Greer T, ter Haar Romeny B, Zimmerman JB, Zuiderveld K. Adaptive histogram equalization and its variations. Computer vision, graphics, and image processing 1987;39:355-68. [Crossref]
- Hassanpour H, Samadiani N, Salehi SM. Using morphological transforms to enhance the contrast of medical images. Egypt J Radiol Nucl Med 2015;46:481-9. [Crossref]
- Selesnick IW. The double-density dual-tree DWT. IEEE Trans Signal Process 2004;52:1304-14. [Crossref]
- Baradarani A, Wu QJ, Ahmadi M. An efficient illumination invariant face recognition framework via illumination enhancement and DD-DTCWT filtering. Pattern Recognition 2013;46:57-72. [Crossref]
- Vimala C, Priya PA. Double density dual tree discrete wavelet transform implementation for degraded image enhancement. Journal of Physics: Conf Series 2018;1000:012120. [Crossref]
- Chen S, Qiu B, Zhao F, Li C, Du H. Fast Compressed Sensing MRI Based on Complex Double-Density Dual-Tree Discrete Wavelet Transform. Int J Biomed Imaging 2017;2017:9604178. [Crossref] [PubMed]
- Shannon CE. A mathematical theory of communication. Bell Syst Tech 1948;27:379-423. [Crossref]
- Rényi A. editor. On measures of entropy and information. Proceedings of the Fourth Berkeley Symposium on Mathematical Statistics and Probability, Volume 1: Contributions to the Theory of Statistics; 1961: The Regents of the University of California.
- Kapur JN, Sahoo PK, Wong AK. A new method for gray-level picture thresholding using the entropy of the histogram. Computer vision, graphics, and image processing 1985;29:273-85. [Crossref]
- Hu Q, Yu D. Entropies of fuzzy indiscernibility relation and its operations. International Journal of uncertainty, fuzziness and knowledge-based systems 2004;12:575-89. [Crossref]
- Duda RO, Hart PE, Stork DG. Pattern classification. John Wiley & Sons; 2012.
- Hyvärinen A, Oja E. Independent component analysis: algorithms and applications. Neural Netw 2000;13:411-30. [Crossref] [PubMed]
- Yan S, Xu D, Zhang B, Zhang H-J, Yang Q, Lin S. Graph embedding and extensions: A general framework for dimensionality reduction. IEEE Trans Pattern Anal Mach Intell 2007;29:40-51. [Crossref] [PubMed]
- Sharma K, Virmani J. A decision support system for classification of normal and medical renal disease using ultrasound images: A decision support system for medical renal diseases. International Journal of Ambient Computing and Intelligence 2017;8:52-69. (IJACI). [Crossref]
- Li Y, Dixit M, Vasconcelos N, editors. Deep scene image classification with the MFAFVNet. Proceedings of the IEEE International Conference on Computer Vision; 2017.
- Guorong X, Xiuming Z, Peiqi C, Zhenping Z, Yun QS, Dongdong F, editors. Feature Selection based on the Bhattacharyya Distance. 18th International Conference on Pattern Recognition (ICPR'06); 2006 20-24 Aug. 2006.
- Cleary TJ, Konopasky A, La Rochelle JS, Neubauer BE, Durning SJ, Artino AR Jr. First-year medical students’ calibration bias and accuracy across clinical reasoning activities. Adv Health Sci Educ Theory Pract 2019;24:767-81. [Crossref] [PubMed]
- Biesiada J, Duch W, Kachel A, Maczka K, Palucha S, editors. Feature ranking methods based on information entropy with parzen windows. International Conference on Research in Electrotechnology and Applied Informatics; 2005.
- Abe N, Kudo M, editors. Entropy criterion for classifier-independent feature selection. International Conference on Knowledge-Based and Intelligent Information and Engineering Systems; 2005: Springer.
- Lopes N. Comparing machine learning algorithms with the Wilcoxon Signed Rank Test. Information. Available online: (date accessed on 04/10/2015) 2015.http://www.uc.pt/fctuc/dei/statisticalHypothesis/noel
- Yuan Y, Van Allen EM, Omberg L, Wagle N, Amin-Mansour A, Sokolov A, Byers LA, Xu Y, Hess KR, Diao L. Assessing the clinical utility of cancer genomic and proteomic data across tumor types. Nat Biotechnol 2014;32:644. [Crossref] [PubMed]
- Xu P, Liu X, Hadley D, Huang S, Krischer J. Feature Selectio n using Bootstrapped ROC Curves. J Proteomics Bioinform S 2014;9:2.
- Hwang T, Sun CH, Yun T, Yi G-S. FiGS: a filter-based gene selection workbench for microarray data. BMC Bioinformatics 2010;11:50. [Crossref] [PubMed]
- Guo Y, Hastie T, Tibshirani R. Regularized linear discriminant analysis and its application in microarrays. Biostatistics 2007;8:86-100. [Crossref] [PubMed]
- Specht DF. Probabilistic neural networks and the polynomial Adaline as complementary techniques for classification. IEEE Trans Neural Netw 1990;1:111-21. [Crossref] [PubMed]
- Thearling K. An introduction to data mining. Direct Marketing Magazine 1999:28-31.
- Kecman V. Learning and soft computing: support vector machines, neural networks, and fuzzy logic models. MIT press; 2001.
- Rish I. editor. An empirical study of the naive Bayes classifier. IJCAI 2001 workshop on empirical methods in artificial intelligence; 2001.
- Kerlikowske K, Grady D, Barclay J, Sickles EA, Eaton A, Ernster V. Positive predictive value of screening mammography by age and family history of breast cancer. JAMA 1993;270:2444-50. [Crossref] [PubMed]
- Ghista DN. Nondimensional physiological indices for medical assessment. J Mech Med Biol 2009;9:643-69. [Crossref]
- Acharya UR, Fujita H, Sudarshan VK, Sree VS, Eugene LWJ, Ghista DN, San Tan R. An integrated index for detection of sudden cardiac death using discrete wavelet transform and nonlinear features. Knowledge-Based Systems 2015;83:149-58. [Crossref]
- Acharya UR, Ng EYK, Tan JH, Sree SV, Ng KH. An integrated index for the identification of diabetic retinopathy stages using texture parameters. J Med Syst 2012;36:2011-20. [Crossref] [PubMed]
- Sharma R, Pachori R, Acharya U. An integrated index for the identification of focal electroencephalogram signals using discrete wavelet transform and entropy measures. Entropy 2015;17:5218-40. [Crossref]
- Acharya UR, Fujita H, Sudarshan VK, Mookiah MRK, Koh JE, Tan JH, Hagiwara Y, Chua CK, Junnarkar SP, Vijayananthan A. An integrated index for identification of fatty liver disease using radon transform and discrete cosine transform features in ultrasound images. Information Fusion 2016;31:43-53. [Crossref]
- Sors A, Bonnet S, Mirek S, Vercueil L, Payen J-F. A convolutional neural network for sleep stage scoring from raw single-channel EEG. Biomed Signal Process Control 2018;42:107-14. [Crossref]
- Dietterich TG, editor. Ensemble methods in machine learning. International workshop on multiple classifier systems; 2000: Springer.
- Huang C, Li Y, Change Loy C, Tang X, editors. Learning deep representation for imbalanced classification. Proceedings of the IEEE conference on computer vision and pattern recognition; 2016.
- Goldberger AL, Amaral LA, Glass L, Hausdorff JM, Ivanov PC, Mark RG, Mietus JE, Moody GB, Peng C-K, Stanley HE. PhysioBank, PhysioToolkit, and PhysioNet: components of a new research resource for complex physiologic signals. Circulation 2000;101:e215-20. [Crossref] [PubMed]
- Esteva A, Kuprel B, Novoa RA, Ko J, Swetter SM, Blau HM, Thrun S. Dermatologist-level classification of skin cancer with deep neural networks. Nature 2017;542:115. [Crossref] [PubMed]
- Gulshan V, Peng L, Coram M, Stumpe MC, Wu D, Narayanaswamy A, Venugopalan S, Widner K, Madams T, Cuadros J. Development and validation of a deep learning algorithm for detection of diabetic retinopathy in retinal fundus photographs. JAMA 2016;316:2402-10. [Crossref] [PubMed]
- Chambon S, Galtier MN, Arnal PJ, Wainrib G, Gramfort A. A deep learning architecture for temporal sleep stage classification using multivariate and multimodal time series. IEEE Trans Neural Syst Rehabil Eng 2018;26:758-69. [Crossref] [PubMed]