Sparse parallel transmission on randomly perturbed spiral k-space trajectory
Introduction
Parallel transmission can reduce the excitation duration using the coil sensitivity pattern of a RF coil array (1-13). Recently, sparse undersampled k-space trajectory inspired by compressed sensing technique demonstrates the unique capability in shortening the excitation pulse width and thus accelerating the excitation (14-28). Unlike the parallel transmission technique, this method is simple and does not require specialized RF hardware. Studies show that the sparse parallel transmission, a technique combining parallel transmission and sparse undersampling, would be advantageous in fast excitation, providing augmented capability of reducing excitation time while maintaining the excitation fidelity (29,30). However, the conventional k-space trajectories take much time in traveling k-space samples. In implementing sparse parallel excitation, how to design an optimal k-space trajectory is an overarching issue needed to be addressed, which is technically challenging. Methods of designing a short k-trajectory to connect all the sparse excitation samples have been explored (30). In this study, we propose and investigate a randomly perturbed spiral k-space trajectory for sparse parallel transmission. The spiral trajectory is firstly designed using the k-space method (31,32) and then randomly perturbed by utilizing the variable density and Monto-Carlo sampling schemes (33) which are commonly used in compressed sensing MRI (34-49). Finally the gradient waveforms and parallel transmission pulses are designed. The feasibility of this method is evaluated by taking Bloch simulation of the sparse parallel transmission at different reduction rates. The accuracy of the excitation profile of each transmission is also investigated by calculating the maximum error of the passband.
Theory and methods
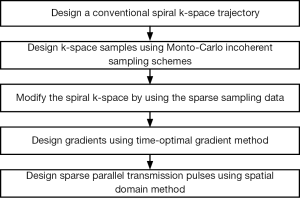
Figure 1 describes the design procedure of the proposed method. In this procedure, a conventional spiral k-space trajectory was designed firstly. Then, the Mote-Carlo incoherent sampling strategy was used to sample the k-space. These sparse sampling data were used to modify the path of the previous designed spiral k-space trajectory. The new trajectory was along the spiral trajectory. But if a sample generated by the sparse sampling strategy was outside the spiral trajectory, a new path with shortest distance would be generated to connect the spiral trajectory and the sparse sampling data. Thus by connecting all the sparse samples with the spiral trajectory, a randomly perturbed spiral trajectory was generated. Finally, the corresponding gradient waveforms on two dimensions were designed based on the proposed randomly perturbed spiral trajectory by using the time-optimal gradient method (50) which is able to design gradient waveforms with minimum time for arbitrary trajectory. The RF pulses of each channel for the sparse parallel transmission was then designed by using the spatial domain method (15).
An example of the 2-dimensional sparse parallel transmission pulses on the proposed randomly perturbed spiral k-space trajectory was designed and a numerical calculation of the block equation was performed to investigate the feasibility of the proposed method and the accuracy of the excitation profile. In this experiment, the desired excitation pattern was a cylinder with 6 cm diameter and the flip angle was 90°. The excitation was performed by using a 4-element RF coil array. The sensitivity pattern of each element of the coil array is shown in Figure 2. The k-space extension was 0.5 cycle/cm and 1,200 samples were chosen using the random undersampling schemes. The sparse parallel transmission with the reduction factor of 4 was performed to maximize the acceleration capability of the design. Sparse parallel transmission with the reduction factor of 2 and a non-parallel transmission were also performed for comparison in terms of excitation accuracy. Furthermore, for validation of the proposed sparse parallel excitation method, excitation using regular spiral trajectory which had a similar length to that of sparse parallel excitation at the reduction factor of 4 was performed.

To fairly evaluate the excitation accuracy and the variation, the maximum value of the passband error was used. For 90° excitation, the desired normalized magnetization in passband is 1. Therefore the maximum passband error is defined as:
[1] |
In this equation, Mxyn denotes the magnetization of each position in the passband of the transverse plane of the excitation profile, while N denotes the number of the excitation positions in the passband. The maximum value reflects the worst case in the excitation profile, indicating the performance of the excitation. The smaller the error is, the more accurate the excitation is.
Results
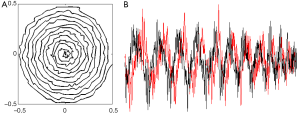
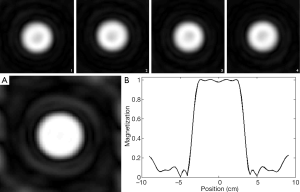
In the sparse parallel transmission at the reduction factor of 4, the pattern of the randomly perturbed spiral k-space trajectory is shown in Figure 3A. It is illustrated that the samples are along a spiral trajectory, but randomly perturbed by incoherent data. The corresponding gradient waveforms designed based on this optimal trajectory are shown in Figure 3B. Both the gradients and the RF pulses satisfied the limitation of hardware of commercially available human MRI scanners. It is noticed that the rapid change of the gradient waveforms may present a challenging requirement on the hardware performance. Results of the excitation profiles of 4 individual RF pulses and the combined excitation profile are shown in Figure 4. The 1D plot along the central line of the 2D excitation pattern (combined) is shown in Figure 4B. The excitation error is approximately 0.2 calculated by using the Eq. [1].
In the comparison study, sparse parallel transmission at the reduction factor of 1 (i.e., no reduction) and 2 were also performed using the same RF coil array and the same parameters. The 1D and 2D excitation profiles of the two experiments are shown in Figure 5. At the reduction factors of 1 and 2, the excitation errors are all in the range of 0.2 calculated by using Eq. [1]. This result indicates that the excitation errors of the sparse parallel transmission pulses are at the same level of the conventional non-parallel transmission pulses, demonstrating that the proposed perturbed spiral k-space trajectory is feasibility and efficiency in fast MR excitations.
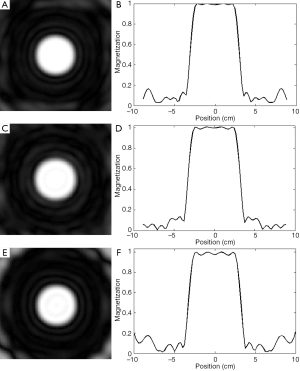
Figure 5E,F shows the results of excitations using conventional spiral k-space trajectory which has a similar length to that of sparse parallel excitation at the reduction rate of 4. Its passband error calculated from Eq. [1] was approximately 0.3, showing a degraded excitation accuracy over that of the proposed sparse parallel transmission on randomly perturbed spiral trajectory.
Discussion and conclusions
The method of designing sparse parallel transmission RF pulses on a randomly perturbed spiral sparse k-space trajectory is proposed and investigated. The optimal k-trajectory traveling through the sparse k-space samples shortens the corresponding gradient waveforms and pulse width. The promising result of Bloch simulation has demonstrated the feasibility and efficiency of this method. The small ripples on both the in-slice and out-of-slice regions are partially due to the imperfection of the k-space undersampling and RF pulses, which need to be improved for better excitation accuracy. The comparison result of the sparse parallel transmissions at the reduction factors of 2 and 4, and the non-parallel transmission demonstrates that the performance of the sparse parallel transmission at high reduction factors is at the same level of the non-parallel transmission strategy. Furthermore, this method can be also applied to non-parallel pulse designs and 3D spatial selective pulse designs.
Acknowledgements
This work was partially supported by NIH grants EB008699, K99EB015487 and P41 EB013598, a QB3 Research Award, a Springer Med Fund Award, and a National Natural Science Foundation of China Grant (51228702).
Disclosure: The authors declare no conflict of interest.
References
- Roemer PB, Edelstein WA, Hayes CE, et al. The NMR phased array. Magn Reson Med 1990;16:192-225. [PubMed]
- Adriany G, Van de Moortele PF, Wiesinger F, et al. Transmit and receive transmission line arrays for 7 Tesla parallel imaging. Magn Reson Med 2005;53:434-45. [PubMed]
- Wu B, Wang C, Krug R, et al. 7T human spine imaging arrays with adjustable inductive decoupling. IEEE Trans Biomed Eng 2010;57:397-403. [PubMed]
- Wu B, Zhang X, Wang C, et al. Flexible transceiver array for ultrahigh field human MR imaging. Magn Reson Med 2012;68:1332-8. [PubMed]
- Zhang X, Ugurbil K, Chen W. Microstrip RF surface coil design for extremely high-field MRI and spectroscopy. Magn Reson Med 2001;46:443-50. [PubMed]
- Zhang X, Ugurbil K, Chen W. A microstrip transmission line volume coil for human head MR imaging at 4T. J Magn Reson 2003;161:242-51. [PubMed]
- Kraff O, Bitz AK, Kruszona S, et al. An eight-channel phased array RF coil for spine MR imaging at 7 T. Invest Radiol 2009;44:734-40. [PubMed]
- Metzger GJ, Snyder C, Akgun C, et al. Local B1+ shimming for prostate imaging with transceiver arrays at 7T based on subject-dependent transmit phase measurements. Magn Reson Med 2008;59:396-409. [PubMed]
- Hardy CJ, Cline HE, Giaquinto RO, et al. 32-element receiver-coil array for cardiac imaging. Magn Reson Med 2006;55:1142-9. [PubMed]
- Li Y, Xie Z, Pang Y, et al. ICE decoupling technique for RF coil array designs. Med Phys 2011;38:4086-93. [PubMed]
- Yan X, Zhang X, Feng B, et al. 7T transmit/receive arrays using ICE decoupling for human head MR imaging. IEEE Trans Med Imaging 2014. [Epub ahead of print]. [PubMed]
- Brown R, Deniz CM, Zhang B, et al. Design and application of combined 8-channel transmit and 10-channel receive arrays and radiofrequency shimming for 7-T shoulder magnetic resonance imaging. Invest Radiol 2014;49:35-47. [PubMed]
- Gudino N, Heilman JA, Riffe MJ, et al. On-coil multiple channel transmit system based on class-D amplification and pre-amplification with current amplitude feedback. Magn Reson Med 2013;70:276-89. [PubMed]
- Zhu Y. Parallel excitation with an array of transmit coils. Magn Reson Med 2004;51:775-84. [PubMed]
- Grissom W, Yip CY, Zhang Z, et al. Spatial domain method for the design of RF pulses in multicoil parallel excitation. Magn Reson Med 2006;56:620-9. [PubMed]
- Katscher U, Börnert P. Parallel RF transmission in MRI. NMR Biomed 2006;19:393-400. [PubMed]
- Katscher U, Börnert P, Leussler C, et al. Transmit SENSE. Magn Reson Med 2003;49:144-50. [PubMed]
- Yip CY, Grissom WA, Fessler JA, et al. Joint design of trajectory and RF pulses for parallel excitation. Magn Reson Med 2007;58:598-604. [PubMed]
- Zelinski AC, Angelone LM, Goyal VK, et al. Specific absorption rate studies of the parallel transmission of inner-volume excitations at 7T. J Magn Reson Imaging 2008;28:1005-18. [PubMed]
- Zhang Z, Yip CY, Grissom W, et al. Reduction of transmitter B1 inhomogeneity with transmit SENSE slice-select pulses. Magn Reson Med 2007;57:842-7. [PubMed]
- Mei CS, Panych LP, Yuan J, et al. Combining two-dimensional spatially selective RF excitation, parallel imaging, and UNFOLD for accelerated MR thermometry imaging. Magn Reson Med 2011;66:112-22. [PubMed]
- Morrell GR. An analytic framework for the evaluation of coil configurations for parallel transmission MRI with subsampled cartesian excitation k-space. IEEE Trans Med Imaging 2010;29:523-30. [PubMed]
- Setsompop K, Wald LL, Alagappan V, et al. Parallel RF transmission with eight channels at 3 Tesla. Magn Reson Med 2006;56:1163-71. [PubMed]
- Liu Y, Ji JX. Minimal-SAR RF pulse optimization for parallel transmission in MRI. Conf Proc IEEE Eng Med Biol Soc 2008;2008:5774-7.
- Deng W, Yang C, Stenger VA. Accelerated multidimensional radiofrequency pulse design for parallel transmission using concurrent computation on multiple graphics processing units. Magn Reson Med. 2011;65:363-9. [PubMed]
- Kyriakos WE, Hoge WS, Mitsouras D. Generalized encoding through the use of selective excitation in accelerated parallel MRI. NMR Biomed 2006;19:379-92. [PubMed]
- Xu D, King KF, Zhu Y, et al. A noniterative method to design large-tip-angle multidimensional spatially-selective radio frequency pulses for parallel transmission. Magn Reson Med 2007;58:326-34. [PubMed]
- Pang Y, Zhang X. Precompensation for mutual coupling between array elements in parallel excitation. Quant Imaging Med Surg 2011;1:4-10. [PubMed]
- Chen D, Bornemann F, Vogel MW, et al. Sparse Parallel Transmit Pulse Design Using Orthogonal Matching Pursuit Method. Proc Intl Soc Mag Reson Med 2009;17:171.
- Pang Y, Zhang X. Sparse parallel transmission using optimized sparse k-space trajectory by simulated annealing. Proc Intl Soc Mag Reson Med 2010;18:4921.
- Pauly J, Nishimura D, Macovski A. A k-space analysis of small-tip-angle excitation. 1989. J Magn Reson 2011;213:544-57. [PubMed]
- Xu D, King KF, Zhu Y, et al. A noniterative method to design large-tip-angle multidimensional spatially-selective radio frequency pulses for parallel transmission. Magn Reson Med 2007;58:326-34. [PubMed]
- Lustig M, Donoho D, Pauly JM. Sparse MRI: The application of compressed sensing for rapid MR imaging. Magn Reson Med 2007;58:1182-95. [PubMed]
- Chang CH, Ji J. Improved compressed sensing MRI with multi-channel data using reweighted l(1) minimization. Conf Proc IEEE Eng Med Biol Soc 2010;2010:875-8.
- Çukur T, Lustig M, Saritas EU, et al. Signal compensation and compressed sensing for magnetization-prepared MR angiography. IEEE Trans Med Imaging 2011;30:1017-27. [PubMed]
- Doneva M, Börnert P, Eggers H, et al. Compressed sensing for chemical shift-based water-fat separation. Magn Reson Med 2010;64:1749-59. [PubMed]
- Donoho DL. Compressed sensing. IEEE Trans Inform Theory 2006;52:1289-306.
- Pang Y, Zhang X. Interpolated compressed sensing for 2D multiple slice fast MR imaging. PLoS One 2013;8:e56098. [PubMed]
- Tsaig Y, Donoho DL. Extensions of Compressed Sensing. Signal Processing 2006;86:549-71.
- Yu Y, Hong M, Liu F, et al. Compressed sensing MRI using Singular Value Decomposition based sparsity basis. Conf Proc IEEE Eng Med Biol Soc 2011;2011:5734-7.
- Madelin G, Chang G, Otazo R, et al. Compressed sensing sodium MRI of cartilage at 7T: preliminary study. J Magn Reson 2012;214:360-5. [PubMed]
- Michailovich O, Rathi Y, Dolui S. Spatially regularized compressed sensing for high angular resolution diffusion imaging. IEEE Trans Med Imaging 2011;30:1100-15. [PubMed]
- Otazo R, Kim D, Axel L, et al. Combination of compressed sensing and parallel imaging for highly accelerated first-pass cardiac perfusion MRI. Magn Reson Med 2010;64:767-76. [PubMed]
- Hong M, Yu Y, Wang H, et al. Compressed sensing MRI with singular value decomposition-based sparsity basis. Phys Med Biol 2011;56:6311-25. [PubMed]
- Ji JX, Zhao C, Lang T. Compressed sensing parallel magnetic resonance imaging. Conf Proc IEEE Eng Med Biol Soc 2008;2008:1671-4.
- Kim YC, Narayanan SS, Nayak KS. Accelerated three-dimensional upper airway MRI using compressed sensing. Magn Reson Med 2009;61:1434-40. [PubMed]
- Li W, Griswold M, Yu X. Fast cardiac T1 mapping in mice using a model-based compressed sensing method. Magn Reson Med 2012;68:1127-34. [PubMed]
- Liang D, Liu B, Wang J, et al. Accelerating SENSE using compressed sensing. Magn Reson Med 2009;62:1574-84. [PubMed]
- Liang D, Ying L. Compressed-sensing dynamic MR imaging with partially known support. Conf Proc IEEE Eng Med Biol Soc 2010;2010:2829-32.
- Lustig M, Kim SJ, Pauly JM. A fast method for designing time-optimal gradient waveforms for arbitrary k-space trajectories. IEEE Trans Med Imaging 2008;27:866-73. [PubMed]


