Body coil reference for inverse reconstructions of multi-coil data—the case for real-time MRI

Introduction

Since the development of the nuclear magnetic resonance (NMR) phased array (1) researchers seek to develop the optimal coil combination. With the advent of parallel imaging, which introduces undersampled acquisitions from multiple independent receive coils, such work also addresses the consequences of aberrant phase information which is due to a unique phase offset in each coil of a receive array. As a consequence, any combination or combined analysis of such multi-coil datasets may lead to spatially localized phase singularities which in magnitude images present as “black holes”. For a selection of relevant contributions see (2-8).

The occurrence of a phase singularity is a rare event and poorly predictable. In multi-coil magnetic resonance imaging (MRI) reconstructions it may result from a direct combination of respective datasets or a reduction of physical coil elements to virtual channels by means of a principal component analysis. In addition, it may also be elicited by inverse reconstructions which implicitly combine multi-coil data by jointly estimating the desired image and all its coil sensitivities. Following the observation that unaffected phase information may be available from a volumetric body coil scan (5), this study describes a simple way to avoid phase singularities in MRI reconstructions that lead to a nonlinear inverse problem. For example, this applies to model-based reconstructions of parametric maps which involve multiple unknowns as well as to anatomical real-time MRI at high temporal resolution (9). The nonlinearity of the latter problem is caused by the fact that body movements not only change the anatomical information within a series of images, but also the complex sensitivity maps of the used receive coils. Moreover, the high degree of undersampling precludes a linearization of the task by a separate pre-determination of the sensitivity maps as typically accomplished for conventional parallel MRI with very mild acceleration factors and fully sampled centers of k-space. Instead, the desired image and its coil sensitivities have to be simultaneously estimated in order to take full advantage of the few available data. Further physical and mathematical details of the techniques used here have been reported for both anatomical real-time MRI (9) and model-based phase-contrast flow MRI in real-time (10,11).

In this work, it is demonstrated that phase singularities or “black holes” may be precluded by “seeding” the iterative optimization process with a complex reference image acquired with the body coil. Such a scan may be obtained—at no extra cost or time—during the usual prep scan period of a real-time MRI recording by automatically switching between coil conditions, for example, between some leading prep scans with the body coil and subsequent prep scans with the user-selected receive coils. As all radiofrequency excitations are performed by the body coil, the choice of a receive coil does not affect the steady-state longitudinal magnetization prepared during initial scanning.

Methods

All MRI measurements were performed on a 3 T MRI system (Magnetom Prisma fit, Siemens Healthineers, Erlangen, Germany) with use of the standard 64-channel head coil or an 18-element thorax coil in conjunction with suitable elements of the spine coil array. Apart from a large number of trials during technical development, the final data for this work was obtained by recruiting 6 subjects without known illness among the students of the local University. Written informed consent, according to the recommendations of the local ethics committee, was obtained from all subjects prior to MRI. All subjects underwent real-time MRI of the head and abdomen as well as real-time flow MRI of abdominal vessels.

Anatomical real-time MRI was accomplished using highly undersampled radial fast low-angle shot (FLASH) acquisitions and image reconstruction by nonlinear inversion (NLINV) with temporal regularization to the immediately preceding frame (9). Briefly, the method benefits from an encoding scheme which consists of complementary sets of radial spokes for typically 5 successive frames. Serial image reconstruction employs the iteratively regularized Gauss-Newton method (12) for solving the nonlinear inverse optimization problem which jointly estimates a complex anatomic image and all coil sensitivity maps. The algorithm applies Tikhonov L2 regularization and enforces the coil sensitivity maps to be smooth. Most importantly, the Gauss-Newton method downsizes all regularization terms by a factor of two in each iterative step in order to ensure predominance of the data consistency term and optimize temporal fidelity.

Here, extensions of anatomic real-time MRI to real-time phase-contrast flow MRI (13,14) further explore a model-based reconstruction technique (10,11) which jointly computes a common magnitude image and a quantitative velocity map (as well as all coil sensitivity maps) directly from the two sets of flow-encoded data. Acquisition parameters for real-time MRI and real-time flow MRI are listed in Table 1.

Table 1 Acquisition parameters for anatomical and phase-contrast real-time MRI
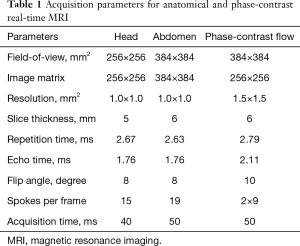
Full table

Online reconstructions of real-time images with up to 50 frames per second and negligible latency (depending on image matrix) are achieved by a highly parallelized version of the NLINV algorithm and its implementation on a computer (sysGen/TYAN Octuple-GPU, Sysgen, Bremen, Germany) with 8 graphical processing units (GeForce GTX TITAN, Nvidia, Santa Clara, CA, USA). This reconstruction computer is fully integrated into the software architecture of the MRI system as a “user-invisible” by-pass system.

So far, NLINV reconstructions from multi-coil data were accomplished by initializing the iterative optimization, i.e., the first Gauss-Newton step of the first image of a serial acquisition, by a complex “seed” image and zero for all coil sensitivities. This initial guess was obtained from a few prep scans with complementary sets of spokes (typically 5). The k-space data were taken from the first virtual channel of a principal component analysis of the multi-coil data, combined into a single k-space, and subjected to a Fourier transformation. The resulting complex image was then taken as seed for the numerical optimization. In this scenario, depending on the actual experimental conditions, the presence of phase offsets in individual receive coils may cause phase singularities that persist during Gauss-Newton iterations.

To correct for improper phase results under all circumstances, it is proposed to acquire body coil data which offer volumetric phase information. Such scans are implemented as initial part of the prep scan period before automatically switching to the user-defined set of receive coils. All acquisition parameters are identical for body coil and multi-coil data including the degree of undersampling. During development it turned out that multi-coil NLINV reconstructions without phase singularities can be achieved by using the data of a single body coil element. The final implementation therefore relies on a body coil dataset which represents the combination of, for example, 5 successive acquisitions in case of a complementary 5-turn encoding scheme. The resulting body coil image serves as initial guess for the complex image in multi-coil NLINV reconstructions. It is only used once for the very first iteration of the first serial image.

In general, the body coil acquisitions take only about a few hundred milliseconds (e.g., 5 frames) as leading part of the prep scan period which is usually applied to establish steady-state conditions. The procedure is insensitive to signal changes during the approach to steady-state or to the influence of motion as, for example, encountered for free-breathing abdominal examinations.

Results

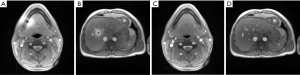
Figures 1,2 demonstrate the successful application of a body coil reference image for avoiding the development of a phase singularity and corresponding black hole in transverse sections of the abdomen, head and liver, respectively. The selected frames originate from real-time MRI movies which were contaminated from the beginning on, i.e., the NLINV reconstruction of the very first frame. However, the use of the volumetric phase information from the body coil reference eliminates the problem by “pushing” the iterative optimization (i.e., the joint estimation of the image and all coil sensitivities) into a physically meaningful solution. At the same time the procedure ensures rapid convergence in only a few Gauss-Newton iterations.

Figure 1 Nonlinear inverse reconstructions (magnitude and color-coded phase images) of multi-coil real-time MRI data (A,B) without and (C,D) with initialization by a body coil reference. Serial transverse images of the abdomen were obtained at 50 ms resolution. For further details see Table 1. Arrows indicate the positions of the black hole and corresponding phase singularity before and after removal. MRI, magnetic resonance imaging.

Figure 2 Nonlinear inverse reconstructions (magnitude images) of multi-coil real-time MRI data (A,B) without and (C,D) with initialization by a body coil reference. Serial transverse images of the head and liver were obtained at 40 ms and 50 ms resolution, respectively. For further details see Table 1. MRI, magnetic resonance imaging.

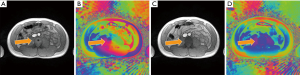
Apart from the occurrence of a singularity in uncorrected phase images, it should be noted that affected magnitude images not only show a central black hole, but further suffer from circular hyperintensities which, depending on the local anatomy and MRI appearance, may be mistaken as a pathologic alteration. Similarly, singularities impair the reliability of information obtained by quantitative mapping as, for example, shown in Figure 3 for model-based phase-contrast flow MRI in real-time. While the resulting magnitude image reveals the same black hole pattern as shown in Figures 1,2, the problem is apparently avoided in the corresponding phase-difference velocity map (Figure 3B). However, a comparison with the unaffected reconstruction achieved by initialization with a body coil reference image (Figure 3D) unravels locally degraded image quality such as spatial blurring in the uncorrected velocity map. This observation hints to incomplete convergence of the algorithm due to the presence of a phase singularity which obviously is far from the true numerical optimum. This observation is further supported by a pronounced quantitative underestimation of flow velocities in affected maps. For the case shown in Figure 3, the mean peak flow velocity in the lower descending aorta (during a 10 s real-time MRI study) is reduced by 35% from 74.0±5.3 cm/s for the corrected reconstruction to 48.6±3.9 cm/s for the contaminated reconstruction. The accuracy of real-time flow MRI assessments has previously been validated (10-13).

Figure 3 Nonlinear inverse model-based reconstructions (magnitude images and phase-difference velocity maps) of multi-coil real-time flow MRI data of the descending aorta and inferior vena cava (A,B) without and (C,D) with initialization by a body coil reference. The encoding velocity and temporal resolution were 200 cm/s and 50 ms, respectively. For further details see Table 1. MRI, magnetic resonance imaging.

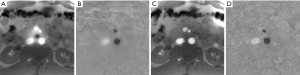
Because the occurrence of a phase singularity is a rare event, it precludes a statistical treatment. However, for the real-time MRI methods examined here, the use of a body coil reference image for iterative reconstruction eliminated black holes whenever observed.

Discussion

The proposed method solves a fundamental problem in inverse MRI reconstructions when using data from multiple receive coils. It turns out that a single reference image obtained by a volumetric body coil is sufficient to guide the numerical optimization and avoid phase singularities or “black holes”. Removal of such problems is of utmost importance as their appearance may resemble a disease-related qualitative or quantitative alteration in the reconstructed image. The method is simple, easy to implement and further improves the robustness of real-time MRI studies or other advanced reconstruction techniques using arbitrary combinations of application-optimized coil arrays.

Acknowledgments

None.

Footnote

Conflicts of Interest: The authors have no conflicts of interest to declare.

References

1. Roemer PB, Edelstein WA, Hayes CE, Souza SP, Mueller OM. The NMR phase array. Magn Reson Med 1990;16:192-225. [Crossref] [PubMed]
2. Walsh DO, Gmitro AF, Marcellinn MW. Adaptive reconstruction of phased array MR imagery. Magn Reson Med 2000;43:682-90. [Crossref] [PubMed]
3. Bydder M, Larkman DJ, Hajnal JV. Combination of signals from array coils using image-based estimation of coil sensitivity profiles. Magn Reson Med 2002;47:539-48. [Crossref] [PubMed]
4. Inati SJ, Hansen MS, Kellman P. A solution to the phase problem in adaptive coil combination. Proc Intl Soc Mag Reson Med 2013;21:2672.
5. Jellus V, Kannengiesser SAR. Adaptive coil combination using a body coil scan as phase reference. Proc Intl Soc Mag Reson Med 2014;22:4406.
6. Parker DL, Payne A, Todd N, Hadley JR. Phase reconstruction from multiple coil data using a virtual reference coil. Magn Reson Med 2014;72:563-9. [Crossref] [PubMed]
7. Vegh V, O’Brien K, Barth M, Reutens DC. Selective channel combination of MRI signal phase. Magn Reson Med 2016;76:1469-77. [Crossref] [PubMed]
8. Robinson SD, Dymerska B, Bogner W, Barth M, Zaric O, Goluch S, Grabner G, Deligianni X, Bieri O, Trattnig S. Combining phase images from array coils using a short echo time reference scan (COMPOSER). Magn Reson Med 2017;77:318-27. [Crossref] [PubMed]
9. Uecker M, Zhang S, Voit D, Karaus A, Merboldt KD, Frahm J. Real-time MRI at a resolution of 20 ms. NMR Biomed 2010;23:986-94. [Crossref] [PubMed]
10. Tan Z, Roeloffs VB, Voit D, Joseph AA, Untenberger M, Merboldt KD, Frahm J. Model-based reconstruction for real-time phase-contrast flow MRI: improved spatiotemporal accuracy. Magn Reson Med 2017;77:1082-93. [Crossref] [PubMed]
11. Tan Z, Hohage T, Kalentev O, Joseph AA, Wang X, Voit D, Merboldt KD, Frahm J. An eigenvalue approach for the automatic scaling of unknowns in model-based reconstructions: application to real-time phase-contrast flow MRI. NMR Biomed 2017. [Crossref] [PubMed]
12. Joseph AA, Merboldt KD, Voit D, Zhang S, Uecker M, Lotz J, Frahm J. Real-time phase-contrast MRI of cardiovascular blood flow using undersampled radial fast low-angle shot and nonlinear inverse reconstruction. NMR Biomed 2012;25:917-24. [Crossref] [PubMed]
13. Untenberger M, Tan Z, Voit D, Joseph AA, Roeloffs V, Merboldt KD, Schätz S, Frahm J. Advances in real-time phase-contrast flow MRI using asymmetric radial gradient echoes. Magn Reson Med 2016;75:1901-8. [Crossref] [PubMed]
14. Bakushinsky AB, Kokurin MY. Iterative methods for approximate solution of inverse problems. Dordrecht: Springer Science & Business Media, 2005.