A robust deformable image registration enhancement method based on radial basis function

Introduction

Respiratory motion can cause deleterious effects during the course of image-guided radiation therapy (IGRT), such as image artifacts during simulation (1-4), inaccurate target volume delineation during treatment planning (5,6), and erroneous patient positioning and dose deposition during treatment delivery (7,8). Motion modeling, in conjunction with deformable image registration (DIR), is often used to assess and correct for the effects of respiratory motion on radiation therapy treatment (9-11), wherein the respiratory motion is estimated by using DIR to estimate the correspondences between the images of different respiratory phases. The performance of DIR is highly variable between different applications, depending upon both image quality (artifacts, image intensity and contrast, etc.) and registration process (user experience and skills in parameter selection, etc.). DIR errors are commonly seen and expected in clinical applications, affecting the accuracy of motion modeling and subsequently its applications in radiation therapy motion management (12).

The sources and characteristics of DIR errors vary for different DIR algorithms as they employ different transformation models, matching criteria, and optimization methods. DIR algorithm is often categorized into two groups based on the matching information used: feature-based and intensity-based. The former focuses on geometrical match of image landmarks while the latter matches two images based on similarity in image intensity, treating all image voxels equally (11,13). Intensity-based DIR algorithms typically perform better at regions with good contrast than regions lacking of contrast (14,15). Studies have shown that visual similarity of the low-contrast regions does not always indicate accurate registration (16). For example, a good match between diaphragms and lung boundaries does not guarantee an accurate displacement vector field (DVF) within the lungs. In addition, hybrid DIR algorithms that use both image intensity and landmark pairs for image matching have also been recently developed (17-20) and shown great promises for DIR applications (21).

Despite various DIR algorithms have been proposed in research, many commercial DIR software currently used in the clinic are intensity-based, equipped with no or limited functions of feature-based DIR enhancement that utilizes user-specified measured displacements between landmark pairs. On the other hand, many sophisticated hybrid DIR algorithms are not fully ready yet for routine clinical applications. These hybrid DIR algorithms either perform feature-based DIR first whose results are then used as a starting point or constraints for subsequent intensity-based DIR, or take a coupled approach to perform feature-based and intensity-based DIR simultaneously. The final registration performance relies on the quality of the feature-based registration. These methods lack of robustness for routine clinical applications because the number of landmarks required by these methods is hardly available in practice. Therefore, a flexible and robust clinical post-processing tool that can enhance the output DVFs from commercial DIR software by utilizing readily available and reliable landmarks is highly desirable.

One of the challenges of developing such tool is the lack of knowledge of how a change in displacement at a voxel affects displacements at surrounding voxels. In the proposed method, we chose to derive this correlation from the initial DVFs, and represent it in the form of Radial basis function (RBF) expansion coefficients of the voxels. RBF is originally used for multivariate interpolation of scattered data on irregular grids. This property is very important to the application of our method because we envision that the landmarks with available measured displacements are randomly distributed across the volume of interest. Using Wendland’s RBF allows the method to work with this randomness. To perform RBF interpolation, RBF expansion coefficients are first derived among the known data points. Then new data can be fitted by a sum of RBF multiplied by the corresponding expansion coefficients (22,23). The expansion coefficients can be viewed as a description of how each data point correlates with surrounding data points at a given set of known data points. Specifically, we chose Wendland’s RBF to establish this local correlation with the following consideration. Wendland’s RBF has local support which is utilized to characterize the deformable nature of the lung motion as the motion at a certain location should be minimally impacted by the motion of tissues far away. By using Wendland’s RBF, we focused on characterizing motion correlation among local voxels and discarded the minimal impact of motion at voxels further away. In practice, using the locally supported Wendland’s RBF made matrix A (introduced in Eq. [3] in Methods section below) sparse, allowing potential computational acceleration in the future.

The aim of this work is to develop and evaluate a robust DIR enhancement method based on RBF expansion. Based on viewpoint presented above, in our method, we treat the RBF expansion coefficients from initial DVFs as an estimation of correlation between displacements at nearby voxels. Then the estimated correlation, i.e., the RBF expansion coefficients are updated under the guidance of sparsely available measured displacements. Lastly, the updated correlation is used to generate DVFs with enhanced accuracy. The robustness of the developed method was evaluated on an in-house developed digital lung phantom for five existing DIR algorithms.

Methods

RBF-based DIR enhancement method

The basic idea is to use measured/known displacements of landmarks (or image features) to enhance the physiological plausibility of DIR and subsequently reduce DIR errors in a time-efficient and robust manner for clinical applications. The designed framework is considered robust because it allows flexibility and has minimal restrictions on its input data. The two inputs of the method include the initial DVF (i.e., pre-enhancement DVF) which can be generated using any DIR algorithm, and the measured landmark displacements which can be of any number of landmarks obtained by any means (manually, automatically, or combined). The DIR enhancement method consists of three steps. The general idea is, first, to derive the contribution of each voxel to the displacements at nearby voxels, represented by the expansion coefficient map. Then the contribution is modified such that the RBF interpolated displacements at measured points agree with the measured displacements. In the last step, the enhanced DVF is derived from interpolation with the updated expansion coefficient map. Details are described below:

• The initial DVF is reshaped to an n-by-3 vector, where n is the number of voxels in the region of interest, labeled as u_pre.



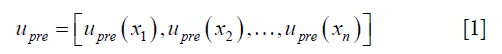
where 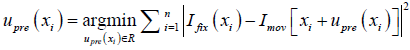, determined by the DIR algorithm that generated the initial DVF. It is then converted to a pre-enhancement expansion coefficient vector (n-by-3), λ_pre,



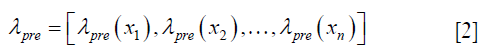
using the 3D Wendland’s compactly supported RBF with second derivative continuity. λ_pre is calculated by solving the following equation,



where A = (ϕ_i,j)_n×n, n is the number of the voxels in the region of interest, and ϕ_i,j is defined by the following equation:



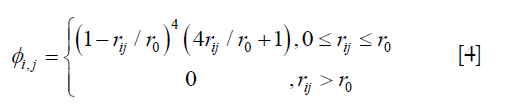
where r_i,j is the Euclidean distance between voxels i and j, r₀ is the range of support for the Wendland’s RBF. r₀ was determined by testing different values at 10 mm intervals from 20 mm to 60 mm. The enhanced DVFs generated with different r₀ were compared with the ground-truth DVF in the digital phantom in terms of residual registration error. It was determined that r₀ =40 mm would give the best overall results in registration of the lungs. It should be noted that the optimal r₀ value may be related to tissue properties and thus should be determined for each organ and tissue.

Each row in Eq. [3], as expressed in Eq. [5], represents how displacement at x_i is represented by the expansion coefficients at the nearby locations within a distance of r₀,



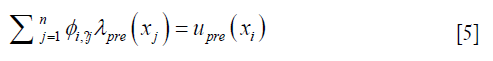
where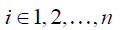

• The measured deformation vectors of landmarks are used to correct errors in the original coefficient map u_pre, and to generate the enhanced expansion coefficient map, λ_post, by satisfying the following constraint,



where A_truth = (ϕ_i,j)_m×n is a submatrix of A , consisting of the rows representing the measured points, m is the number of the voxels where the measured displacements are available, i.e., ϕ_i,j represents RBF between the ith landmark voxel and the jth voxel in the region of interest, and u_truth is an m-by-3 vector consisting of the measured displacements.

Each row in Eq. [6], as expressed in Eq. [7] dictates how the enhanced λ_post should satisfy the measured displacements,



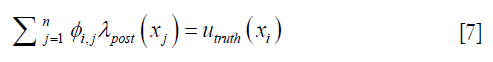
where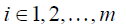

As Eq. [6] represents an underdetermined linear system, a constraint is introduced to determine the solution λ_post,



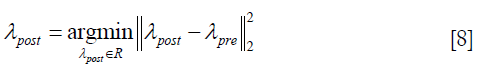
λ_post is derived by solving Eq. [6] with constraint as shown in Eq. [8], using QR factorization in MATLAB (MathWorks, Inc., Natick, MA, USA), which solves an underdetermined system with minimized 2-norm.

• The post-enhancement expansion coefficient map, λ_post, is used to construct the post-enhancement DVF, u_post using the following equation.



In the proposed method, it is optional to down-sample the initial DVF to improve the time-efficiency of the method. If down-sampling is performed, the full post-enhancement DVF is generated via linear interpolation of the down-sampled post-enhancement DVF.

Digital phantom of the lungs

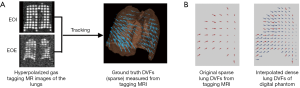
The RBF-based DIR enhancement method was evaluated using an in-house developed lung digital phantom. The phantom consists of two volumetric images of the thorax at the end-of-inhalation (EOI) and the end-of-exhalation (EOE) phases, and the corresponding DVF between the two phases which serve as the ground-truth DVF for DIR evaluations. This digital phantom was developed based on a hyperpolarized gas (Helium-3 or Xenon-129) tagging magnetic resonance imaging (MRI) technique which provides in vivo, direct measurement of lung deformation during respiration (24-26).

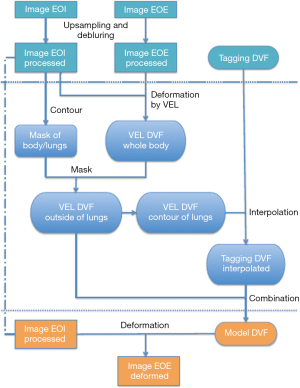
The generation of the digital phantom is illustrated in Figure 1 and described as follows. Subjects were imaged at the EOI and EOE phases using a hyperpolarized gas tagging MRI technique as well as a high-resolution (2.5 mm isotropic) 3D proton MRI technique. A sparse tagging displacement vector field (tDVF) was derived from the hyperpolarized gas tagging magnetic resonance (MR) images by tracking the displacements of the tagging grids between the EOI and EOE phases, as shown in Figure 2A. The 3D proton MR images of EOI and EOE were preprocessed via up-sampling (1 mm × 1 mm axial, 2.5 mm axial) and deblurring to obtain a new set of proton MR images with improved image quality as the base images for digital phantom generation. First, an estimated DVF of the thorax was generated by performing DIR between EOI and EOE image of the improved proton MRI using Velocity AI (VEL), labeled as VEL DVF. Secondly, VEL DVF inside of lungs were replaced by the sparse tagging DVF from tagging MRI, followed by an interpolation of the sparse lung DVF into a dense lung DVF using a multi-step natural neighbor algorithm, as shown in Figure 2B. Thirdly, DVF outside the lungs from the proton MRI and the DVF inside the lungs from the tagging MRI were combined to generate the model DVF which is considered as the ground-truth DVF of the entire thorax. The model DVF was then applied to the EOI images to generate the EOE image (deformed, not the original), completing the generation of the digital phantom. As the model DVF of the phantom was generated based on the in vivo, direct measurement of lung deformation during respiration, it can be used as independent reference to evaluate DVFs estimated by DIR.

Figure 1 Workflow of the generation of the digital phantom using hyperpolarized gas tagging MRI and the corresponding proton MRI at two respiratory phases (EOI and EOE). EOI, end-of-inhalation; EOE, end-of-exhalation; DVF, displacement vector field; VEL, velocity; MRI, magnetic resonance imaging.

Figure 2 Generation of the model DVF of the digital phantom within the lungs. (A) Illustration of the determination of the ground truth lung DVFs based on the hyperpolarized gas tagging MR images at EOI and EOE phases; (B) example of the original sparse lung DVFs measured from hyperpolarized gas tagging MRI and the interpolated dense lung DVFs of the digital phantom. EOI, end-of-inhalation; EOE, end-of-exhalation; DVF, displacement vector field; MRI, magnetic resonance imaging.

Evaluation of DIR enhancement method using digital phantom

The DIR enhancement method was tested on five DIR algorithms: VEL (Varian Medical Systems, Palo Alto, CA, USA), MIM (MIM Software, Beachwood, OH, USA), Improved Lucas-Kanade (ILK) and Original Horn and Schunck (OHS) (both are open source, available in DIRART toolbox in MATLAB), and Elastix (ELA) (open source, available online: http://elastix.isi.uu.nl/). DIR was performed between the EOI and EOE images of the digital phantom to generate the initial DVFs, u_pre. These initial DVFs cover a wide range of initial registration error levels and thus give a good indication of how our DIR enhancement method will perform at different initial error levels. We would like to emphasize that our study is not focused on evaluation of the five algorithms. Although we have fine-tuned the algorithms to get best registration results, the u_pre of the five algorithms should not be interpreted as representing the performance of the five algorithms because a fair comparison between DIR algorithms involve more consideration that fall beyond the scope of this study. The landmarks’ displacements, u_truth, were randomly selected from within the ground-truth DVF, i.e., a set of randomly selected voxels within the lungs were designated as landmark voxels with known displacements. The down-sampling factor used in the digital phantom study was 6, resulting in a total of 6,595 control points.

To evaluate the performance of the DIR enhancement method, pre- and post-enhancement DVFs were compared against the ground-truth DVF, and the corresponding 3D registration errors were determined for each voxel, e_3D,i, and for the entire volume, e_3D, which were calculated as follows respectively,

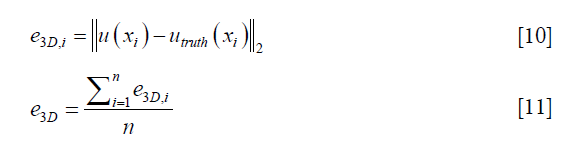
where u(x_i) represents either the pre- or post-enhancement displacement vector at the ith voxel, u_truth(x_i) is the ground-truth displacement vector at the i^th voxel, and n is the number of voxels. Intensity difference maps between the original and the synthesized EOI images (by applying the post-enhancement DVFs onto the original EOE images) were also generated to evaluate the effect of DIR enhancement on the appearance of the deformed image. Further, we studied how the number of landmarks (i.e., the density of the landmarks) would affect the performance of DIR enhancement. To ensure that down-sampling does not affect the validity of the DIR method, we investigated whether the locations of the landmarks affect the performance of DIR enhancement. Due to computational limitation, we had to down-sample the u_pre. After down-sampling, voxels where the landmarks are located (randomly chosen in the digital phantom study) may not be retained in the down-sampled u_pre. To demonstrate that the down-sampling would not affect the validity of our method, we intentionally tested three scenarios with different landmark locations characterized by on-grid ratios of 100%, 50%, and 0%, where 100% means all landmarks are located at voxels retained in down-sampled u_pre, and 0% means no landmarks are located at voxels retained in down-sampled u_pre.

Results

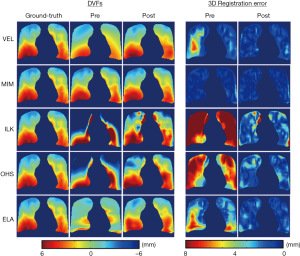
Figure 3 shows the representative results of DIR enhancement for the five DIR algorithms. The most prominent effect of registration enhancement (i.e., registration error reduction) is observed in the right lung (left side), where the initial DVFs contain large areas of registration errors as indicated by the DVF difference maps. After DIR enhancement, registration errors were significantly reduced. In all cases expect for ILK near the lung boundary, registration errors disappeared nearly completely in the post-enhancement images. Similar enhancement was also observed in the left lung (right side), despite that the enhancements were small for VEL and MIM since their initial DVFs were already close to the ground-truth DVF. It should be noted that the DIR enhancement method did not completely remove all DIR errors, especially in areas where the initial DIR errors were substantial. The quantitative performance of the DIR enhancement method is presented in Table 1 as measured by the pre- and post-enhancement 3D registration error per voxel, e_3D,pre and e_3D,post. The DIR enhancement algorithm results in an average DIR error reduction of 2.5±2.3 mm (percentage error reduction: 51.1%±29.1%) across the five cases.

Figure 3 Pre- and post-enhancement DVFs in the SI direction and the corresponding 3D registration error maps for the five DIR algorithms. DVF, displacement vector field; VEL, Velocity AI; ILK, Improved Lucas-Kanade; OHS, Original Horn and Schunck; ELA, Elastix; SI, superior inferior.

Table 1 Pre- and post-enhancement 3D registration error per voxel (mm)
Full table

For the evaluation of the landmark distribution wherein the landmarks were randomly selected for 5 times, the coefficient of variation (CV) in the mean 3D registration errors of the post-enhancement DVFs (the ratio of the standard deviation of post-enhancement error to the mean post-enhancement error) was 3.3% for VEL, 1.2% for MIM, 7.0% for ILK, 2.1% for OHS, and 1.7% for ELA, indicating that the DIR enhancement method is generally insensitive to the distribution of the landmarks.

Figure 4 shows the intensity difference maps between the original and the synthesized EOI images (by deforming the EOE images via DIR, with and without DIR enhancement). It can be appreciated that the DIR enhancement is less obvious in image intensity than in the DVFs (Figure 3). This is no surprise since the intensity similarity does not imply the accuracy of the underline DVFs. Yet, the DIR enhancement is apparent in certain areas where the initial registration errors are significant, such as the areas indicated by the circles for ILK and OHS. On average of the five DIR algorithms, the DIR enhancement method led to a 0.37% reduction per voxel in intensity error.

Figure 4 Pre-enhancement (top) and post-enhancement (bottom) intensity difference maps between the original and the synthesized EOI images. VEL, Velocity AI; ILK, Improved Lucas-Kanade; OHS, Original Horn and Schunck; ELA, Elastix; EOI, end-of-inhalation.

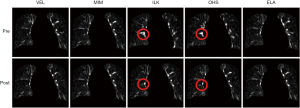
Figure 5 shows the effects of the number of landmarks on the performance of the DIR enhancement method, showing the absolute (Figure 5A) and normalized (Figure 5B) registration error as a function of the landmark density in terms of number of landmarks per liter volume. Normalized registration error is defined as the percentage ratio of post-enhancement registration error e_3D,post to pre-enhancement registration error e_3D,pre. e_3D is the residual registration error per voxel averaged over the entire volume as defined by Eq. [11]. It can be seen than that e_3D,post decreased as landmark density increased in a nearly inverse exponential manner for the five evaluated DIR algorithms. The level of enhancement depends upon the DIR method (i.e., the initial registration error): the greater the initial registration error, the greater the level of DIR enhancement. For example, ILK exhibited an initial registration error of nearly 8 mm which was reduced to approximately 2 mm after applying our DIR enhancement method. It was noticed that once the landmark density exceeded certain values (for example, 100 landmarks/liter), the DIR enhancement became marginal with more landmarks, indicating that a reasonable landmark density may be sufficient to achieve acceptable registration accuracy for the entire volume.

Figure 5 Absolute (A) and normalized (B) post-enhancement 3D registration errors as a function of the density of landmarks. VEL, Velocity AI; ILK, Improved Lucas-Kanade; OHS, Original Horn and Schunck; ELA, Elastix.

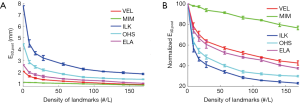
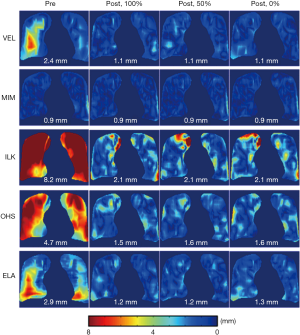
Figure 6 shows the effects of landmarks’ location in relation to the down-sampled DVF grids on the performance of the DIR enhancement method. The results showed that DIR enhancements were generally comparable between the three scenarios for all five DIR algorithms. The differences in the post-enhancement mean 3D registration error between the three on-grid ratios were all less than 0.1 mm, despite small variations in error distributions between the three scenarios for some DIR methods, such as ILK and OHS. These results indicate that the DIR enhancement method was largely insensitive to the landmark locations in relation to the down-sampled grids. Therefore, down-sampling of the initial DVF can be robustly carried out without compromising the validity of the DIR enhancement method.

Figure 6 Post-enhancement 3D registration errors (mean error shown on figures) for the 3 simulated scenarios wherein the percentage of landmarks located on the down-sampled DVF grids (i.e., landmark on-grid ratio) is 100%, 50%, and 0% respectively. VEL, velocity; ILK, Improved Lucas-Kanade; OHS, Original Horn and Schunck; ELA, Elastix; DVF, displacement vector field.

Discussion

Results shown in Figure 5 suggested that it is possible to effectively reduce DIR errors by utilizing only a relatively small number of landmarks, for example, 50–100 landmarks/liter of lung volumes. This finding is informative because it is often unclear how many landmarks are needed in order to achieve the most possible DIR enhancement. Identifying more landmarks often requires significantly increased efforts, which cannot be justified if the associated benefit to DIR enhancement is only marginal. In addition, when registration error is smaller than the image resolution the registration results are typically considered clinically acceptable (12). However, we should be cautious since different clinical applications may have different levels of sensitivity to DIR errors. For example, dose warping may be more sensitive to registration error than contour propagation.

It should be noted that although our method requires landmarks, it does not necessarily mean that users need to manually obtain and input these landmarks when using the method. These landmarks can be automatically determined using many existing feature extraction methods. Our method focuses on the processing with given landmarks, not on the process of obtaining landmarks. In our future study, we will incorporate automatic feature extraction into our DIR enhancement method. The difference between our hybrid DIR method and many other hybrid DIR methods is that our method is flexible in terms of the type, quantity and distribution of landmarks. In our method, the landmarks can be any image features with known/measurable corresponding displacements between the source and target images. Our method focuses on the processing with given set of landmarks, and therefore does not restrict, neither depend on, the method of landmark determination. In our digital phantom study, the landmarks are voxels randomly selected whose ground-truth displacements are fed into the algorithm as measured displacements. In this case, the landmarks may not represent any actual image features.

Post-enhancement residual DIR errors were observed in some cases, especially in the peripheral regions of the lungs, as shown in Figure 6. They could have been caused by the instability of the RBF interpolation near the boundaries of the lungs. Since most voxels in the lung boundary regions are not on the down-sampled DVF grids, the voxels near the boundaries have to be extrapolated, causing more uncertainties than interpolation.

Regarding the spacing between landmarks dense distribution of landmarks may not benefit DIR enhancement as explained previously due to the redundant information. In a small region where the displacements are expected to be smooth and continuous, extra landmarks are unlikely to provide more information than a single landmark. Therefore, imposing a limit on the minimum spacing between the landmarks may be practically useful to improve the time-efficiency of the DIR-enhancement method. This is of interest in our future studies to develop methods to best handle various heterogeneous distributions of landmarks.

In this work, the Wendland’s compactly supported function was used such that the displacement of a landmark can influence its nearby region within a reasonable range. There are two assumptions in the application of this function: (I) displacement is smooth in a relatively homogenous region; and (II) displacement of one voxel has minimal impact on the displacement of another voxel far away. Furthermore, the use of RBF allows for potential acceleration of the process because the RBF values are all zeros for voxels greater than a certain range, resulting in a very sparse matrix A and therefore leaving great potential for improvement on storage and calculation efficiency.

Our study has limitations. First, the DIR enhancement method was only evaluated using a digital phantom. In the next step, we plan to evaluate the new method using publicly available landmark databases, for example, the DIR-Lab (https://www.dir-lab.com/) as a start (16). Secondly, the landmarks used in this study are not actual anatomical landmarks such as vessel bifurcations, which may lead to some differences in deriving the deformation fields using these landmarks. The effects are to be evaluated systematically in a separate investigation. Thirdly, we intentionally did not specify the method of landmark extraction in this study because the landmark extraction is a separate process in our design. Fourthly, our evaluation is limited only within the lungs in this study. We did not evaluate it at the lung/chest wall interface where the sliding motion could be a major factor affecting the accuracy of the DIR. To validate the method at the boundary between lungs and chest wall, we need ground truth of the sliding motion. However, to our best knowledge, there is no phantom that can provide such ground truth information, and therefore we did not perform this validation in our current study. It is an important topic for our future study with an appropriate phantom.

Conclusions

In this study, we demonstrated the feasibility of a robust RBF-based method for enhancing DIR accuracy using sparsely distributed landmarks. This method has been shown robust and effective in reducing DVF errors using different numbers and distributions of landmarks for various DIR algorithms. It is potentially an easily implementable tool to enhance DIR accuracy for DIR-related applications.

Acknowledgments

Funding: This work is partly supported by a startup fund from the Hong Kong Polytechnic University and funding from NIH (1R21CA165384 and 1R21CA195317).

Footnote

Conflicts of Interest: The authors have no conflicts of interest to declare.

References

1. Liu Y, Yin FF, Chen NK, Chu ML, Cai J. Four dimensional magnetic resonance imaging with retrospective k-space reordering: a feasibility study. Med Phys 2015;42:534-41. [Crossref] [PubMed]
2. Tian Y, Stützer K, Enghardt W, Priegnitz M, Helmbrecht S, Bert C, Fiedler F. Experimental investigation of irregular motion impact on 4D PET-based particle therapy monitoring. Phys Med Biol 2016;61:N20-34.
3. Cai J, Read PW, Larner JM, Jones DR, Benedict SH, Sheng K. Reproducibility of interfraction lung motion probability distribution function using dynamic MRI: statistical analysis. Int J Radiat Oncol Biol Phys 2008;72:1228-35. [Crossref] [PubMed]
4. Yamamoto T, Langner U, Loo BW Jr, Shen J, Keall PJ. Retrospective analysis of artifacts in four-dimensional CT images of 50 abdominal and thoracic radiotherapy patients. Int J Radiat Oncol Biol Phys 2008;72:1250-8. [Crossref] [PubMed]
5. Cai J, McLawhorn R, Read PW, Larner JM, Yin FF, Benedict SH, Sheng K. Effects of breathing variation on gating window internal target volume in respiratory gated radiation therapy. Med Phys 2010;37:3927-34. [Crossref] [PubMed]
6. Ge H, Cai J, Kelsey CR, Yin FF. Quantification and minimization of uncertainties of internal target volume for stereotactic body radiation therapy of lung cancer. Int J Radiat Oncol Biol Phys 2013;85:438-43. [Crossref] [PubMed]
7. Mutaf YD, Scicutella CJ, Michalski D, Fallon K, Brandner ED, Bednarz G, Huq MS. A simulation study of irregular respiratory motion and its dosimetric impact on lung tumors. Phys Med Biol 2011;56:845-59. [Crossref] [PubMed]
8. Van den Begin R, Engels B, Gevaert T, Duchateau M, Tournel K, Verellen D, Storme G, De Ridder M. Impact of inadequate respiratory motion management in SBRT for oligometastatic colorectal cancer. Radiother Oncol 2014;113:235-9. [Crossref] [PubMed]
9. Colgan R, McClelland J, McQuaid D, Evans PM, Hawkes D, Brock J, Landau D, Webb S. Planning lung radiotherapy using 4D CT data and a motion model. Phys Med Biol 2008;53:5815-30. [Crossref] [PubMed]
10. Li T, Thorndyke B, Schreibmann E, Yang Y, Xing L. Model-based image reconstruction for four-dimensional PET. Med Phys 2006;33:1288-98. [Crossref] [PubMed]
11. Ruhaak J, Polzin T, Heldmann S, Simpson IJA, Handels H, Modersitzki J, Heinrich MP. Estimation of large motion in lung CT by integrating regularized keypoint correspondences into dense deformable registration. IEEE Trans Med Imaging 2017;36:1746-57. [Crossref] [PubMed]
12. Brock KK. Deformable Registration Accuracy Consortium. Results of a multi-institution deformable registration accuracy study (MIDRAS). Int J Radiat Oncol Biol Phys 2010;76:583-96. [Crossref] [PubMed]
13. Shusharina N, Sharp G. Analytic regularization for landmark-based image registration. Phys Med Biol 2012;57:1477-98. [Crossref] [PubMed]
14. Liu F, Hu Y, Zhang Q, Kincaid R, Goodman KA, Mageras GS. Evaluation of deformable image registration and a motion model in CT images with limited features. Phys Med Biol 2012;57:2539-54. [Crossref] [PubMed]
15. Yeo UJ, Supple JR, Taylor ML, Smith R, Kron T, Franich RD. Performance of 12 DIR algorithms in low-contrast regions for mass and density conserving deformation. Med Phys 2013;40:101701. [Crossref] [PubMed]
16. Castillo R, Castillo E, Guerra R, Johnson VE, McPhail T, Garg AK, Guerrero T. A framework for evaluation of deformable image registration spatial accuracy using large landmark point sets. Phys Med Biol 2009;54:1849-70. [Crossref] [PubMed]
17. Cao K, Ding K, Reinhardt JM, Christensen GE. Improving intensity-based lung CT registration accuracy utilizing vascular information. Int J Biomed Imaging 2012;2012:285136. [Crossref] [PubMed]
18. Johnson HJ, Christensen GE. Consistent landmark and intensity-based image registration. IEEE Trans Med Imaging 2002;21:450-61. [Crossref] [PubMed]
19. Panta RK, Segars P, Yin FF, Cai J. Establishing a framework to implement 4D XCAT phantom for 4D radiotherapy research. J Cancer Res Ther 2012;8:565-70. [Crossref] [PubMed]
20. Yin Y, Hoffman EA, Ding K, Reinhardt JM, Lin CL. A cubic B-spline-based hybrid registration of lung CT images for a dynamic airway geometric model with large deformation. Phys Med Biol 2011;56:203-18. [Crossref] [PubMed]
21. Ehrhardt J, Lorenz C. 4d modeling and estimation of respiratory motion for radiation therapy. Berlin: Springer, 2013.
22. Shusharina N, Sharp G. Image registration using radial basis functions with adaptive radius. Med Phys 2012;39:6542-9. [Crossref] [PubMed]
23. Allasia G, Cavoretto R, De Rossi A. Local interpolation schemes for landmark-based image registration: a comparison. Math Comput Simul 2014;106:1-25. [Crossref]
24. Cai J, Altes TA, Miller GW, Sheng K, Read PW, Mata JF, Zhong X, Cates GD Jr, de Lange EE, Mugler JP 3rd, Brookeman JR. MR grid-tagging using hyperpolarized helium-3 for regional quantitative assessment of pulmonary biomechanics and ventilation. Magn Reson Med 2007;58:373-80. [Crossref] [PubMed]
25. Cai J, Miller GW, Altes TA, Read PW, Benedict SH, de Lange EE, Cates GD, Brookeman JR, Mugler JP 3rd, Sheng K. Direct measurement of lung motion using hyperpolarized helium-3 MR tagging. Int J Radiat Oncol Biol Phys 2007;68:650-3. [Crossref] [PubMed]
26. Cai J, Sheng K, Benedict SH, Read PW, Larner JM, Mugler JP 3rd, de Lange EE, Cates GD Jr, Miller GW. Dynamic MRI of grid-tagged hyperpolarized helium-3 for the assessment of lung motion during breathing. Int J Radiat Oncol Biol Phys 2009;75:276-84. [Crossref] [PubMed]