Quantitative assessment of nonsolid pulmonary nodule volume with computed tomography in a phantom study

Introduction

Significant research has been conducted over the last 15 years on the use of volumetric measurements extracted from computed tomography (CT) scans as an improved measure of nodule size and as a quantitative imaging biomarker for lung cancer detection and therapeutic response. Volume has been examined for its potential for earlier determination of change in nodule size compared to a measurement of maximum diameter from a single slice (1) typically used in clinical practice. Numerous studies have been conducted to examine and quantify the interrelated effects of imaging protocols, nodule characteristics, and estimation methods on the measurement error of lung nodule volume, as summarized in two reviews on the subject published in 2009 (2) and 2014 (3) and presented in subsequent publications (4-11). However, most of the aforementioned studies have focused on the measurement of solid pulmonary nodules, defined as those that completely obscure the lung parenchyma (12). The volumetric assessment of subsolid nodules, defined as those that incompletely obscure the lung parenchyma (12), is a relatively under-examined area of research. Subsolid nodules can be subdivided according to their composition: nonsolid lesions that consist of ground-glass opacity (GGO) only; and part-solid lesions that contain both ground-glass and soft tissue elements (13). The volumetry of nonsolid nodules, otherwise known as pure ground glass, is the focus of this study.

Nonsolid nodules can be the first imaging finding in a patient with a neoplasia. Small persistent nonsolid nodules are often atypical adenomatous hyperplasia (AAH) and focal fibrosis, whereas nonsolid and part-solid nodules that increase in size typically indicate malignancy, which can include adenocarcinoma in situ (AIS), minimally invasive adenocarcinoma (MIA), and invasive adenocarcinoma, as well as lympho-proliferative disease (13). Nonsolid nodules are often slow-growing nodules with higher volume doubling times than are seen in solid nodules. Hasegawa et al. (14) reported mean volume doubling times of 813, 457, and 149 days, respectively, for ground-glass opacities, GGO with a solid component, and solid nodules respectively, all of which were significantly different.

The surveillance of nonsolid nodules with CT is the modality of choice for the identification of malignant lesions, with recently published guidelines from the Fleischner Society (15) calling for newly detected nonsolid lesions with diameter ≥6 mm to be followed up with CT for 6–10 months to confirm persistence, followed by CT scans every 2 years for 5 years to assess stability. The Fleischner guidelines also suggest considering follow-up at 2 and 4 years for certain suspicious nodules <6 mm in diameter (15). If an error of observation or measurement of the longest diameter is made by the radiologist, for example a 6.5-mm diameter measured as 5 mm then an inappropriate classification into “no further follow-up indicated” would be rendered. Ultimately this could result in a failure to diagnose a growing lung cancer. It is therefore important to examine imaging and lesion factors affecting the measurement of nonsolid nodules at these size levels, so that clinicians are better informed to determine whether a measured change in nodule size is likely to be associated with a true change in size and not just a random variation in the estimate that falls within the bounds of measurement error.

In addition to nodule size, another important factor to examine is nodule density, a measure of X-ray attenuation quantified using Hounsfield units (HU). Solid nodules were reported to have densities within about −195 to 190 HU (16), whereas nonsolid nodules were reported to have much lower densities with range of values depending on histological subtype; in a study by Kim et al. (17) nodules with atypical adenomatous hyperplasia ranged within −736 to −615 HU, nonspecific organizing pneumonia/fibrosis ranged between −792 to −258 HU, and adenocarcinomas or bronchioloalveolar cell carcinomas had densities ranging widely between −775 to −100 HU. In a phantom study by Scholten et al. (18) substantial differences in absolute percent error were observed between −800 and −630 HU densities for 5 and 10 mm in diameter spherical nodules, based on CT scans reconstructed with filtered back projection (FBP). It is not clear what the effect on measurement error would be for non-spherical nodules at these sizes and densities, or for CT scans reconstructed using iterative reconstruction (IR) algorithms, which have re-emerged in clinical scanners as part of the ongoing effort to reduce patient radiation exposure while maintaining image quality (19,20). Different types of IR include adaptive (or statistical as they are sometimes referred to) algorithms, which use predictor models of statistical noise in iterative procedures to reduce noise on FBP reconstructed scans, and model-based algorithms which incorporate more complex system models of data statistics, X-ray physics, and system optics in the image reconstruction process (21). Additionally, it would be beneficial to quantify the interrelated effects of nonsolid nodule characteristics (size, shape, density) and reconstruction algorithm with a wide range of dose levels to determine any reductions in exposure that can be achieved while still maintaining measurement consistency.

A number of studies have focused on the volumetry of nonsolid nodules and the effect of the factors mentioned above. We limited our review of related work to phantom studies, which enable the analysis of both accuracy and precision due to the availability of a reference standard regarding nodule size and allow the acquisition of multiple repeated scans without concern to patient exposure. Li et al. (6), Doo et al. (22), and Siegelman et al. (23) examined the volumetry of low-density nodules across different imaging protocols, but the lowest nodule density was limited to −630 HU. Scholten et al. (18) and Linning et al. (24) did not examine the effect of different reconstruction methods beyond FBP. Oda et al. (25) only focused on standard-dose diagnostic CT scans. Kim et al. (11) evaluated the influence of imaging protocols on semi-automated pulmonary nodule volumetry. They used 10 and 12 mm diameter nodules, a wide range of densities (−800 to 100 HU), and examined dose protocols as low as about 0.7 mGy. Study limitations included scanning the phantom only once, using only spherical nodules, and not examining nodules below one centimeter in diameter.

The focus of our work was to determine the properties of nonsolid nodules and related imaging protocols under which reliable volumetric measurements can be extracted. Toward that goal, we conducted a comprehensive phantom CT study that addressed the limitations of related work mentioned above by: (I) including a combination of nodule characteristics (densities as low as −800 HU, sizes of 10- and 5-mm in diameter, and spherical and spiculated shapes) and imaging protocols (radiation dose ranging from standard dose of 4.1 mGy to as low as 0.3 mGy and different state-of-the-art reconstruction methods) with a range of parameters that test the boundaries of reliable measurement; (II) extracting fifteen repeat acquisitions per each protocol to allow for analysis of precision with improved statistical power; (III) conducting analyses based on metrics of accuracy and precision recommended by the Quantitative Imaging Biomarkers Alliance (QIBA) consortium metrology group (26,27) in an effort to standardize such analyses and enable comparisons with other studies.

Methods

Anthropomorphic phantom and synthetic nodules

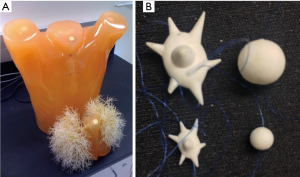
Twelve synthetic nodules manufactured by CIRS (Norfolk, Virginia, USA) were placed within the vasculature of an anthropomorphic phantom (Lungman N1, Kyotokagaku, Japan) shown in Figure 1. The nodules were combinations of two sizes (5, 10 mm in nominal diameter), two shapes (spherical, spiculated), and three densities (−800, −630, −10 HU). The −800 and −630 HU densities represented the low end to middle of the range of the range of nonsolid nodules in clinical practice whereas −10HU was within the typical density range of solid nodules. Spiculated nodules were included since clinically they were shown to have increased probability of malignancy (15) and in terms of measurement they could be a factor contributing to measurement error (6,28). All nodules were placed within foam inserts to avoid any vessel attachment and provide an approximation to the density of the lung parenchyma. Nodules were placed in the periphery of the lung cavity within the phantom. A reference standard on the true volume of each nodule was established using high-resolution micro CT imaging (Scanco100 Medical µCT, Scanco USA, Wayne, PA, USA) as described in Li et al. (29).

Figure 1 Anthropomorphic phantom torso with vasculature insert (A) and examples of the synthetic nodule shapes used in the study (B). The nodules shown include spherical and spiculated nodules at nominal diameters of 5 and 10 mm.

Imaging protocols

The phantom was scanned with a Toshiba Aquilion ONE Vision (Toshiba Medical Systems Corporation, Otawara, Japan) multi-detector row CT (MDCT) system. Imaging protocols had kVp and tube current time product (mAs) combinations designed to produce CTDI_vol ranging within (0.2–0.3 mGy), (0.6–0.7 mGy), (0.9–1.1 mGy), (1.7–1.8 mGy), and (4.0–4.1 mGy). Reconstruction method in the context of this study refers to the combination of reconstruction algorithm (FBP or IR) and any associated reconstruction kernels. Data was reconstructed with 0.5 mm image thickness and no overlap, using three reconstruction methods: a traditional FBP with a FC13 kernel, an adaptive IR algorithm [adaptive iterative dose reduction 3D (AIDR 3D)] employing the FC13 kernel, and a model-based IR algorithm [Forward projected model-based Iterative Reconstruction SoluTion (FIRST)]. AIDR 3D and FIRST were operated using default settings; AIDR 3D was operated with “AIDR 3D STD” and FIRST with the “IR MILD” setting for 120 kVp scans and the “IR STD” setting for 80, and 100 kVp scans, based on manufacturer recommendations. AIDR 3D is described elsewhere (30) and is available commercially. FIRST IR was made available at the time of this study though a collaboration of one of the authors (J Siegelman) with the manufacturer. It has recently been made commercially available. No within scan tube current modulation was employed in this study as control of the exposure level per nodule was one of the primary factors being tested.

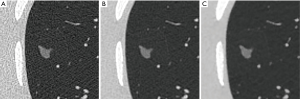
Using the image protocols and repeat scans described above, a dataset of 675 reconstructed CT series was created (3 kVp settings ×5 mAs settings ×3 reconstruction algorithms ×15 repeats). Due to 10 series having missing or corrupt data, 665 CT series were available for sizing 12 nodules. Analysis was performed on a total of 7,980 volume estimates from the 665 reconstructed CT series. Regions of interest around an example nodule, extracted from different reconstructed scans are shown in Figure 2.

Figure 2 CT images through the central slice of the −630 HU, 10 mm, spiculated synthetic nodule, reconstructed with: (A) FBP, (B) AIDR 3D, (C) FIRST reconstruction algorithms. These images were captured at window/level 1,800/−478 and were extracted from scans acquired with 120 kVp and 15 mAs (1.7 mGy). FBP, filtered back projection; AIDR, adaptive iterative dose reduction; FIRST, Forward projected model-based Iterative Reconstruction SoluTion; HU, Hounsfield units.

Volume estimation

Nodule volume measurements were derived from the reconstructed CT data using a previously validated matched filter-based estimator (31). The specific volumetric method was chosen because the focus of the study was to examine the effect of imaging protocols and nodule characteristics without additional sources of error from segmentation-based method or from inter-operator variability. The matched-filter based method used in the study is a low-bias estimator since it is informed of the nodule’s object. Briefly, the estimator was informed of the nodule’s approximate centroid and shape, by using simulated nodule templates which propagated through a model of the MDCT system. This matched-filter approach has the advantage of incorporating both knowledge of the nodule properties and the imaging process into the volume estimation process allowing for improved volume estimates.

Templates were generated within ±50% of nominal diameter and 1% step size, and had initial intensity profiles determined by the average pixel value of two ROIs, one within the nodule and one within the background. The angles of rotation for the spiculated nodules were estimated prior to matching using an automated normalized cross-correlation method (32). During the matching procedure, templates were moved around a centroid-offset (±1 pixel, 0.5 step size), and their intensity profile was varied around the estimated nodule intensities (±50 HU, 5 HU step size) and background intensities (±50 HU, 10 HU step size). Across each combination of these variables, a squared absolute difference cost function between the template and the nodule volume of interest (VOI) was minimized to determine the best match. Powell’s method of coordinate descent (33) was used to iterate toward the best-matched template. In comparison to the original approach (31), which employed an exhaustive search, Powell’s iterative search method led to improved computational efficiency and allowed for the use of smaller increments over wider ranges for the estimation parameters (size, HU, and nodule center).

Statistical analysis

Prior to statistical analysis, all volume estimates were log-transformed (natural log) to make the data better suited for subsequent analyses such as ANOVA which assumes homoscedasticity (26,34). Analyses included the extraction of metrics to describe bias and repeatability, as recommended by the QIBA metrology group (27,34). Linearity analysis was not performed due to inclusion of only two nodules sizes (5 and 10 mm).

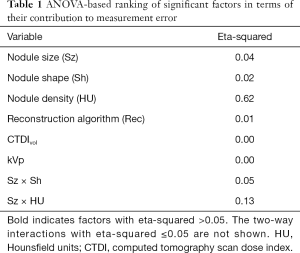
Bias was defined as the difference between the expected value of the measurements and the reference standard. For easier interpretation, bias was converted into percent bias (PB). PB, as well as the standard deviation of percent error (SPE), were measured across subgroups of volume estimates. Subgroups were selected based on n-way ANOVA with two-way interaction analysis of the estimation error. Factors in this analysis included nodule size, nodule shape, nodule density, reconstruction method, CTDI_vol, kVp, and the interaction of these factors. The implemented model treated variables as fixed factors. Eta-squared (35) was used for ranking substantial contribution to overall error. The eta-squared, interpreted as the proportion of the total variance that is attributed to an explanatory variable, was calculated as the ratio of the between-group sum of squares to the total sum of squares. PB and SPE were calculated across factors with eta-squared >0.05.

Repeatability represents the measurement precision under near identical imaging conditions. The repeatability coefficient (RC) is defined as the least significant difference between two repeated measurements at a two-sided significance of α=0.05. Under certain assumptions presented in Li et al. (6), the RC was estimated as 1.96, where is the estimate of the within-subject variance (6). The 95% CI of RC was calculated based on chi-square statistics as defined in Raunig et al. (34). Values for RC were converted to percentage (RC%) for easier interpretation. Note that RC% is a measure of error with lower values indicating better repeatability.

Results

Results shown in Table 1 indicate that density was the largest contributor to overall measurement error. Nodule size was not found to be significant; however, the interaction of nodule size and density was a large contributor. The interaction of nodule size and nodule shape was also found to be significant. The effect of nodule size as an individual factor was probably reduced due to the use of thin reconstructed image thickness (0.5 mm) protocols. Previous studies have shown that the effect of nodule size is more pronounced for thicker slice protocols (6). CTDI_vol was not shown to be a significant factor (eta-squared close to zero), despite the wide range in dose values and inclusion of 0.3 mGy scans. Reconstruction algorithm and kVp were also not significant. It has to be noted that this analysis ranks the most significant factors in terms of their influence on measurement accuracy, since the input to ANOVA consisted of the difference between log-transformed volume measurements and reference standard.

Table 1 ANOVA-based ranking of significant factors in terms of their contribution to measurement error
Full table

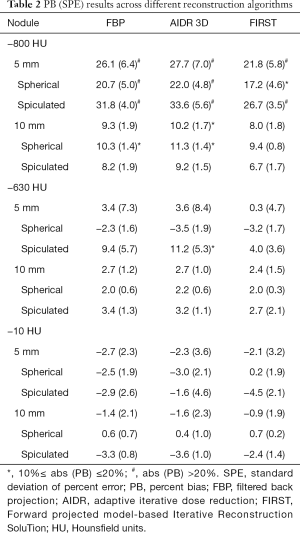
PB and SPE values across reconstruction method are tabulated in Table 2. Analysis was done per density, nodule size and shape, and across reconstruction methods based on the ANOVA analysis above. Results show that reconstruction method had a minor impact on PB for 10-mm nodules regardless of density, with differences of ±2.5% or less across algorithms. For the 5-mm nominal diameter nodules, the differences in PB among reconstruction methods were on the order of ±2.8% or less for the solid nodules an on the order of ±7% for the nonsolid nodules. Across densities, the −800 HU nodules showed higher error compared to higher density nodules for all reconstruction methods, with differences in PB on the order of 20% or more for the 5-mm nodules and 6% or so for the 10-mm nodules. The model-based FIRST IR algorithm showed smaller PB by 3–5% compared to the other two algorithms for the 5-mm, low density (−800 and −630 HU) nodules, but for the rest of 5-mm and all 10-mm nodules, differences were less than 1.8%. Across shapes, PB was generally higher for the spiculated nodules compared to spherical (differences ranging from 0.4 to ~14%) except for the −800 HU, 10 mm nodules where PB on spherical was slightly higher.

Table 2 PB (SPE) results across different reconstruction algorithms
Full table

Overall, the volume estimates of the 10-mm nodules with −630 and −10 HU densities were highly accurate across reconstruction methods, with PB within ±3.6%. However, for the −800 HU nodules with 10 mm in diameter, the maximum PB increased to 11.3%. Looking at the same breakdown for the 5-mm nodules, PB for the −630 and −10 HU densities the maximum was 11.2% whereas for the −800 HU nodules, maximum PB increased to 34%.

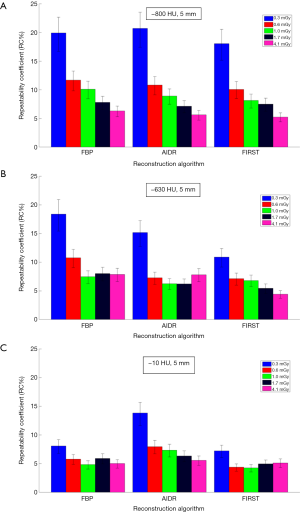
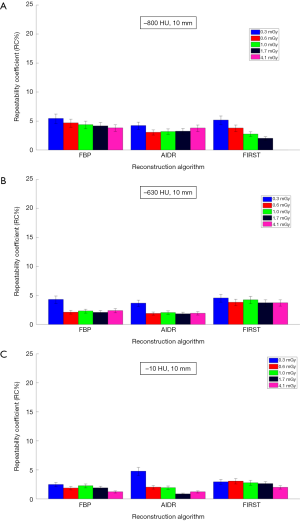
Figures 3,4 show repeatability results for each nodule size and density combination across CTDI_vol and reconstruction methods. We examined CTDI_vol and reconstruction methods based on findings from a recent study on the volumetry of low contrast objects (liver lesions) which showed that both of these factors had a significant effect on precision (36). It can be seen that for the 10-mm in diameter nodules that RC% was on the order of 5% or less and varied slightly (±3%) across CTDI_vol, reconstruction methods, or densities. For the 5-mm in diameter nodules, RC% was overall higher than for the 10-mm, ranging from about 4% to 20% depending on density and CTDI_vol, and to a lesser degree on reconstruction method. More specifically, excluding the 0.3 mGy dose which produced the highest error, the RC% range across all reconstruction methods for a given CTDI_vol setting was in the order of 4% or less. The effect of dose was relatively small, with RC% for the −800, −630 and −10 HU nodules decreasing by about 5%, 3% and 2% or less respectively, as CTDI_vol increased from 0.6 to 4.1 mGy for a given reconstruction method. Across reconstruction methods, differences in RC% were small (3% or less for a given CTDI_vol) with the exception of 0.3 mGy were larger differences were observed.

Figure 3 RC% across reconstruction algorithm (FBP, AIDR, FIRST) and CTDI_vol (0.3 to 4.1 mGy) for the 5 mm in diameter nodules of −800 (A), −630 (B) and −10 HU (C) density. Values were calculated from pooled volume estimates of all objects in the main subset, replicates, and kVp settings. FBP, filtered back projection; AIDR, adaptive iterative dose reduction; FIRST, Forward projected model-based Iterative Reconstruction SoluTion; HU, Hounsfield units; CTDI, computed tomography scan dose index; RC, repeatability coefficient.

Figure 4 RC% across reconstruction algorithm (FBP, AIDR, FIRST) and CTDI_vol (0.3 to 4.1 mGy) for the 10 mm in diameter nodules of −800 (A), −630 (B) and −10 HU (C) density. Values were calculated from pooled volume estimates of all objects in the main subset, replicates, and kVp settings. FBP, filtered back projection; AIDR, adaptive iterative dose reduction; FIRST, Forward projected model-based Iterative Reconstruction SoluTion; HU, Hounsfield units; CTDI, computed tomography scan dose index; RC, repeatability coefficient.

Discussion

The focus of the study was on the assessment of volumetric CT for nodules with densities spanning the range of solid and nonsolid nodules across different dose protocols and state-of-the-art reconstruction methods. We were particularly interested to quantify the impact of IR algorithms for measuring volume for low contrast tasks in the presence of high amounts of noise. At the same time, we wanted to provide some insight into any potential limit in the “measurability” of lung nodules, by stretching the range of dose protocols to as low as 0.3 mGy, the range of nodule sizes to 5 mm, and densities as low as −800 HU. Assessment was performed to quantify the accuracy and precision of volume estimates; both of these properties need to be within acceptable boundaries for a clinically useful biomarker (23).

Our findings show that the volume of the 10 mm nodules of all densities was measured with both high accuracy (PB within 11%) and high precision (RC% within 5%). Clinically, 11% PB or less in measuring volume would translate to a 3.5% PB or less in measuring the longest nodule diameter from baseline, with the ability to distinguish between a 10.00-mm and a larger than 10.35 mm diameter nodule. Excluding the −800 HU nodules, accuracy within 5% was achievable. In fact, density was the factor found to contribute the most to overall error in our analysis of significant factors. The impact of density on accuracy was also observed in the study by Scholten et al. (18) where substantial differences in absolute percent error were observed between −800 and −630 HU densities for 10 mm nodules. Precision for the 10-mm nodules was unaffected by CTDI_vol or reconstruction methods in the scanner examined in our study. This result is consistent with the findings reported by Kim et al. (11) on volumetry of nonsolid nodules using a Philips iCT scanner with low dose protocols and three different reconstruction methods (FBP, iDose, IMR). Our findings can be used to inform possible amendments to the QIBA profile for lung nodule volume assessment and monitoring in low-dose CT screening (current draft includes 6–12 mm nodules in diameter) and suggest the inclusion of nonsolid nodules in the target population. This document includes performance claims mainly based on studies of solid nodules. Our findings support the inclusion of the 10-mm nonsolid nodules in the category of “measurable” nodules for which the profile is applicable.

The study findings for the 5-mm diameter nodules show a substantial effect of density. The volume estimates for the −630 and −10 HU nodules showed relatively low bias (PB within 11%), but PB within 20–30% for the −800 HU nodules. Similarly, precision for the −630 and −10 HU nodules was relatively high (RC% less than 12%) for CTDI_vol ≥0.6 mGy and was not affected substantially by the choice of reconstruction method, whereas for the −800 HU, 5 mm nodules RC% varied more widely across dose and/or reconstruction method. These findings suggest that reliable surveillance of 5 mm in diameter nodules with densities of −630 HU and larger is possible using low-dose volumetric CT and the protocols used in this study. It has to be noted that these findings are based on thin slice protocols (slice thickness was 0.5 mm). Based on the importance of slice thickness on nodule volumetry, particularly for sub-centimeter nodules, it would be expected that findings could be different for protocols using thicker slices.

Dose did not have a significant effect on volumetric accuracy in our study, despite the inclusion of CTDI_vol as low as 0.3 mGy. Furthermore, the interaction of dose with reconstruction method was not significant in terms of accuracy. This differs from the work of Doo et al. (22) which reported on volume measurements of −630 and 100 HU spherical nodules using the same FBP and AIDR 3D reconstruction algorithms as in our study, significant improvement in average percent error was reported when using AIDR 3D in low-dose CT acquisitions, particularly for the 5-mm nodules. Other than the use of only spherical nodules and a different measurement method (commercially available semi-automated segmentation algorithm) in that study, this discrepancy can possibly be due to their use of a different reconstruction filter compared to those in our study (FC05 vs. FC13 in our study); FC05 is sharper than FC13 and has a beam hardening correction algorithm employed; for data reconstructed with a filter having these properties, the benefit of IR on measurement accuracy could be more pronounced. In terms of precision, dose, across the range investigated in our study, did not have any effect on the 10-mm in diameter nodules, but did have an effect on the 5-mm nodules in a limited way. RC% increased substantially at 0.3 mGy and varied across CTDI_vol values for the 800 HU, 5 mm in diameter nodules. Variability across CTDI_vol for these nodules was reduced for the higher densities. In terms of the effect of dose and its interaction with reconstruction methods on precision for the 5-mm nodules, our findings showed that repeatability was generally consistent from 0.6 to 4.1 mGy for the −630 and −10 HU densities, regardless of IR, and was only affected substantially when CTDI_vol fell to 0.3 mGy. For the −800 HU, 5 mm nodules, repeatability varied more widely across both CTDI_vol and reconstruction methods.

Reconstruction algorithm had a density-dependent effect on volumetric accuracy. Findings showed that for the −800 and −630 HU nodules, the model-based FIRST IR algorithm reduced bias compared to the other reconstruction methods for these low-density 5-mm nodules. These findings, combined with the discussion on dose above, suggest that low contrast nodules of small size and with locally uniform background (non-attached nodules in this study), may benefit from the use of model-based IR methods. Such reconstruction methods are usually designed to adaptively reduce noise while preserving edges in the image. It has been shown that IR algorithms can improve the detection of low-contrast lesions compared to FBP (37). However, further study is needed to quantify any specific benefits on volumetric estimation across a wider range of nodule properties such as the contrast, size and especially local background.

It has to be pointed out that the results reported above are from a phantom study using a matched filter-based volume estimator that is informed of nodule shape; measurement error in a clinical study with potentially more complex shapes and backgrounds would be expected to be higher. In general, it is assumed that this estimator provides an estimate of the lower-bound of measurement error. However, this method is not ideal; measurement error would in principle be lower if the estimator could match the exact properties of the different reconstruction method, which were not available in the context of this study. In terms of comparisons with a segmentation-based method, we recently reported results of a study (38) where nodules measurements from a subset of the scans investigated in this study, were segmented using a publicly available 3D segmentation tool. Results show that the measurement method did not substantially affect the accuracy of measurements for the 10-mm nodules with CTDI_vol ≥0.6 mGy, but it did affect the accuracy of the 5-mm nodule measurements. Segmentation-based volume estimation had lower PB than the matched-filter based estimator for −800 HU nodules but larger PB for −630 and −10 HU nodules. Direct comparisons between measurements methods regarding precision for different densities could not be made since the reported RC% was calculated from pooled nodule measurements and not per density or size. Overall, the segmentation method showed reduced repeatability with RC% differences between the methods being dependent on dose and reconstruction algorithm. For 0.6 mGy, RC% differences between methods were on the order of 14% for FBP and fell to ~4% with the model-based FIRST IR method. The effect of reconstruction method was smaller for 1.7 mGy scans, with differences in RC% 5% for FBP and 2% for FIRST IR. The above comparisons involve a specific segmentation-based volume estimation method and may not apply to other segmentation-based methods.

This work could inform the developers of guidelines and protocols such as the QIBA, organized by the Radiological Society of North America. The volumetric CT committee of QIBA is currently preparing a set of documents (called QIBA Profiles) specifying protocols and conditions for achieving volume measurements and determining change in volume within defined error bounds. However, most of the supporting data used to develop Profiles has been derived from studies focusing primarily on solid nodules. In fact, the QIBA profile for lung nodule volume assessment and monitoring in low dose CT screening which focuses on small nodules (6 to 12 mm in diameter) applies specifically to solid nodules. Similarly, the QIBA profile for CT tumor volume change for advanced disease (which focuses on nodules larger than 10 mm in diameter) applies to “tumors with sufficiently conspicuous margins”, a criterion that often does not apply to human visual assessment of nonsolid nodules. Our findings could help amend such guidelines to include protocols for improved and more consistent measurement of nonsolid nodules.

Conclusions

In summary, the findings of this comprehensive phantom study show that the density of lung nodules can substantially affect volumetry from CT, with the effect being more pronounced for smaller size. Overall, reasonable values of both accuracy and precision were achieved for volumetric measurements of all 10-mm nodules and for the 5-mm nodules with −630 HU or higher density, when derived from scans acquired at 0.6 mGy or higher. Model-based IR algorithm resulted in a more accurate measurement for the 5-mm, low-density (−800, −630 HU) nodules. Dose did not affect volumetric accuracy and only affected slightly the precision of 5-mm low-density nodules. These findings can be informative toward the creation of standardized guidelines for the volumetry of nonsolid nodules and establishing expected bounds for measurement error.

Acknowledgements

The project was supported in part through a Critical Path grant from the U.S. Food and Drug Administration. BP Berman (FDA) was supported through an appointment to the Research Participation Program at the Center for Devices and Radiological Health administered by the Oak Ridge Institute for Science and Education through an interagency agreement between the U.S. Department of Energy and the U.S. Food and Drug Administration. Dr. Siegelman was partly funded by Toshiba through a research collaboration agreement.

Footnote

Conflicts of Interest: K Schultz is employed by Toshiba Medical Research Institute, Inc., USA (TMRU). Toshiba was responsible for performing the CT reconstructions from the Toshiba scanner. J Siegelman was partly funded by Toshiba through a research collaboration agreement and is currently employed by the Takeda Pharmaceutical Company.

Disclosure: The mention of commercial products, their sources, or their use in connection with material reported herein is not to be construed as either an actual or implied endorsement of such products by the Department of Health and Human Services.

* Now at Takeda Pharmaceuticals, Cambridge, Massachussetts, USA

References

1. Eisenhauer EA, Therasse P, Bogaerts J, Schwartz LH, Sargent D, Ford R, Dancey J, Arbuck S, Gwyther S, Mooney M, Rubinstein L, Shankar L, Dodd L, Kaplan R, Lacombe D, Verweijk J. New response evaluation criteria in solid tumours: Revised RECIST guideline (version 1.1). Eur J Cancer 2009;45:228-47. [Crossref] [PubMed]
2. Gavrielides MA, Kinnard LM, Myers KJ, Petrick N. Non-calcified lung nodules: Volumetric assessment with thoracic CT. Radiology 2009;251:26-37. [Crossref] [PubMed]
3. Gavrielides MA, Li Q, Zeng R, Myers KJ, Sahiner B, Petrick N. Volumetric analysis of non-calcified lung nodules with thoracic CT: an updated review of related work over the last 5 years. J Radiol Radiat Ther 2014;2:1040.
4. Buckler AJ, Danagoulian J, Johnson K, Peskin A, Gavrielides MA, Petrick N, Obuchowski NA, Beaumont H, Hadjiiski L, Jarecha R, Kuhnigk JM, Mantri N, McNitt-Gray M, Moltz JH, Nyiri G, Peterson S, Tervé P, Tietjen C, von Lavante E, Ma X, St Pierre S, Athelogou M. Inter-Method Performance Study of Tumor Volumetry Assessment on Computed Tomography Test-Retest Data. Acad Radiol 2015;22:1393-408. [Crossref] [PubMed]
5. Gavrielides MA, Li Q, Zeng R, Myers KJ, Sahiner B, Petrick N. Volume estimation of multidensity nodules with thoracic computed tomography. J Med Imaging (Bellingham) 2016;3:013504. [Crossref] [PubMed]
6. Li Q, Gavrielides MA, Sahiner B, Myers KJ, Zeng R, Petrick N. Statistical analysis of lung nodule volume measurements with CT in a large-scale phantom study. Med Phys 2015;42:3932-47. [Crossref] [PubMed]
7. Young S, Kim HJ, Ko MM, Ko WW, Flores C, McNitt-Gray MF. Variability in CT lung-nodule volumetry: Effects of dose reduction and reconstruction methods. Med Phys 2015;42:2679-89. [Crossref] [PubMed]
8. Athelogou M, Kim HJ, Dima A, Obuchowski N, Peskin A, Gavrielides MA, Petrick N, Saiprasad G, Colditz Colditz D, Beaumont H, Oubel E, Tan Y, Zhao B, Kuhnigk JM, Moltz JH, Orieux G, Gillies RJ, Gu Y, Mantri N, Goldmacher G, Zhang L, Vega E, Bloom M, Jarecha R, Soza G, Tietjen C, Takeguchi T, Yamagata H, Peterson S, Masoud O, Buckler AJ. Algorithm Variability in the Estimation of Lung Nodule Volume From Phantom CT Scans: Results of the QIBA 3A Public Challenge. Acad Radiol 2016;23:940-52. [Crossref] [PubMed]
9. Scholten ET, de Jong PA, Jacobs C, van Ginneken B, van Riel S, Willemink MJ, Vliegenthart R, Oudkerk M, de Koning HJ, Horeweg N, Prokop M, Mali WP, Gietema HA. Interscan variation of semi-automated volumetry of subsolid pulmonary nodules. Eur Radiol 2015;25:1040-7. [Crossref] [PubMed]
10. Kim H, Park CM, Chae HD, Lee SM, Goo JM. Impact of radiation dose and iterative reconstruction on pulmonary nodule measurements at chest CT: a phantom study. Diagn Interv Radiol 2015;21:459. [Crossref] [PubMed]
11. Kim H, Park CM, Song YS, Lee SM, Goo JM. Influence of radiation dose and iterative reconstruction algorithms for measurement accuracy and reproducibility of pulmonary nodule volumetry: A phantom study. Eur J Radiol 2014;83:848-57. [Crossref] [PubMed]
12. Ridge CA, Yildirim A, Boiselle PM, Franquet T, Schaefer-Prokop CM, Tack D, Gevenois PA, Bankier AA. Differentiating between subsolid and solid pulmonary nodules at CT: inter-and intraobserver agreement between experienced thoracic radiologists. Radiology 2016;278:888-96. [Crossref] [PubMed]
13. Herold CJ. Management of solid and sub-solid lung nodules. Available online: https://cancerimagingjournal.biomedcentral.com/articles/10.1186/1470-7330-14-S1-O24
14. Hasegawa M, Sone S, Takashima S, Li F, Yang Z, Maruyama Y, Watanabe T. Growth rate of small lung cancers detected on mass CT screening. Br J Radiol 2000;73:1252-9. [Crossref] [PubMed]
15. MacMahon H, Naidich DP, Goo JM, Lee KS, Leung AN, Mayo JR, Mehta AC, Ohno Y, Powell CA, Prokop M, Rubin GD, Schaefer-Prokop CM, Travis WD, Van Schil PE, Bankier AA. Guidelines for management of incidental pulmonary nodules detected on CT images: from the Fleischner Society 2017. Radiology 2017;284:228-43. [Crossref] [PubMed]
16. Xu DM, van Klaveren RJ, de Bock GH, Leusveld AL, Dorrius MD, Zhao Y, Wang Y, de Koning HJ, Scholten ET, Verschakelen J, Prokop M, Oudkerk M. Role of baseline nodule density and changes in density and nodule features in the discrimination between benign and malignant solid indeterminate pulmonary nodules. Eur J Radiol 2009;70:492-8. [Crossref] [PubMed]
17. Kim HY, Shim YM, Lee KS, Han J, Yi CA, Kim YK. Persistent Pulmonary Nodular Ground-Glass Opacity at Thin-Section CT: Histopathologic Comparisons 1. Radiology 2007;245:267-75. [Crossref] [PubMed]
18. Scholten ET, Jacobs C, van Ginneken B, Willemink MJ, Kuhnigk JM, van Ooijen PM, Oudkerk M, Mali WP, de Jong PA. Computer-aided segmentation and volumetry of artificial ground-glass nodules at chest CT. AJR Am J Roentgenol 2013;201:295-300. [Crossref] [PubMed]
19. Mayo-Smith WW, Hara AK, Mahesh M, Sahani DV, Pavlicek W. How I do it: managing radiation dose in CT. Radiology 2014;273:657-72. [Crossref] [PubMed]
20. Padole A, Ali Khawaja RD, Kalra MK, Singh S. CT radiation dose and iterative reconstruction techniques. AJR Am J Roentgenol 2015;204:W384-92. [Crossref] [PubMed]
21. Deák Z, Grimm JM, Treitl M, Geyer LL, Linsenmaier U, Körner M, Reiser MF, Wirth S. Filtered back projection, adaptive statistical iterative reconstruction, and a model-based iterative reconstruction in abdominal CT: an experimental clinical study. Radiology 2013;266:197-206. [Crossref] [PubMed]
22. Doo KW, Kang EY, Yong HS, Woo OH, Lee KY, Oh YW. Accuracy of Lung Nodule Volumetry in Low-Dose CT with Iterative Reconstruction: An Anthropomorphic Thoracic Phantom Study. Br J Radiol 2014;87:20130644. [Crossref] [PubMed]
23. Siegelman JW, Supanich MP, Gavrielides MA. Pulmonary nodules with ground-glass opacity can be reliably measured with low-dose techniques regardless of iterative reconstruction: results of a phantom study. AJR Am J Roentgenol 2015;204:1242-7. [Crossref] [PubMed]
24. Linning E, Daqing M. Volumetric measurement pulmonary ground-glass opacity nodules with multi-detector CT: effect of various tube current on measurement accuracy—a chest CT phantom study. Acad Radiol 2009;16:934-9. [Crossref] [PubMed]
25. Oda S, Awai K, Murao K, Ozawa A, Yanaga Y, Kawanaka K, Yamashita Y. Computer-Aided Volumetry of Pulmonary Nodules Exhibiting Ground-Glass Opacity at MDCT. AJR Am J Roentgenol 2010;194:398-406. [Crossref] [PubMed]
26. Obuchowski NA, Reeves AP, Huang EP, Wang XF, Buckler AJ, Kim HJ, Barnhart HX, Jackson EF, Giger ML, Pennello G, Toledano AY, Kalpathy-Cramer J, Apanasovich TV, Kinahan PE, Myers KJ, Goldgof DB, Barboriak DP, Gillies RJ, Schwartz LH, Sullivan DC. Algorithm Comparison Working Group. Quantitative imaging biomarkers: A review of statistical methods for computer algorithm comparisons. Stat Methods Med Res 2015;24:68-106. [Crossref] [PubMed]
27. Sullivan DC, Obuchowski NA, Kessler LG, Raunig DL, Gatsonis C, Huang EP, Kondratovich M, McShane LM, Reeves AP, Barboriak DP, Guimaraes AR, Wahl RL. RSNA-QIBA Metrology Working Group. Metrology standards for quantitative imaging biomarkers. Radiology 2015;277:813-25. [Crossref] [PubMed]
28. Petrou M, Quint LE, Nan B, Baker LH. Pulmonary nodule volumetric measurement variability as a function of CT slice thickness and nodule morphology. AJR Am J Roentgenol 2007;188:306-12. [Crossref] [PubMed]
29. Li Q, Gavrielides MA, Nagaraja S, Hagen MJ, Zeng R, Myers KJ, Sahiner B, Petrick N, editors. A micro CT based tumor volume reference standard for phantom experiments. Arlington: Quantitative Medical Imaging, 2013.
30. Angel E. AIDR 3d White Paper, Toshiba Medical. Available online: https://medical.toshiba.com/download/aidr-3d-wp-aidr-3d
31. Gavrielides MA, Zeng R, Kinnard LM, Myers KJ, Petrick N. Information-theoretic approach for analyzing bias and variance in lung nodule size estimation. IEEE Trans Med Imaging 2010;29:1795-807. [Crossref] [PubMed]
32. Gavrielides MA, Li Q, Zeng R, Myers KJ, Sahiner B, Petrick N. Minimum detectable change in lung nodule volume in a phantom CT study. Acad Radiol 2013;20:1364-70. [Crossref] [PubMed]
33. Powell MJ. An efficient method for finding the minimum of a function of several variables without calculating derivatives. Comput J 1964;7:155-62. [Crossref]
34. Raunig DL, McShane LM, Pennello G, Gatsonis C, Carson PL, Voyvodic JT, Wahl RL, Kurland BF, Schwarz AJ, Gönen M, Zahlmann G, Kondratovich MV, O'Donnell K, Petrick N, Cole PE, Garra B, Sullivan DC. QIBA Technical Performance Working Group. Quantitative imaging biomarkers: A review of statistical methods for technical performance assessment. Stat Methods Med Res 2015;24:27-67. [Crossref] [PubMed]
35. Cohen J. Eta-squared and partial eta-squared in fixed factor ANOVA designs. Educ Psychol 1973;33:107-12.
36. Li Q, Liang Y, Huang Q, Zong M, Berman B, Gavrielides MA, Schwartz LH, Zhao B, Petrick N. Volumetry of low-contrast liver lesions with CT: Investigation of estimation uncertainties in a phantom study. Med Phys 2016;43:6608-20. [Crossref] [PubMed]
37. Saiprasad G, Filliben J, Peskin A, Siegel E, Chen J, Trimble C, Yang Z, Christianson O, Samei E, Krupinski E, Dima A. Evaluation of Low-Contrast Detectability of Iterative Reconstruction across Multiple Institutions, CT Scanner Manufacturers, and Radiation Exposure Levels. Radiology 2015;277:124-33. [Crossref] [PubMed]
38. Gavrielides MA, DeFilippo G, Berman BP, Li Q, Petrick N, Schultz K, Siegelman J. editors. Estimation of non-solid lung nodule volume with low-dose CT protocols: effect of reconstruction algorithm and measurement method. SPIE Medical Imaging, 2017. Available online: https://www.spiedigitallibrary.org/conference-proceedings-of-spie/10132/1/Estimation-of-non-solid-lung-nodule-volume-with-low-dose/10.1117/12.2255982.short?SSO=1