Correction of geometric distortion in Propeller echo planar imaging using a modified reversed gradient approach

Introduction

The Propeller (periodically rotated overlapping parallel lines with enhanced reconstruction) MR imaging sequence (1,2) has emerged as an attractive technique which finds increasing clinical usage (3,4), with diffusion-weighted investigations being the most popular application target (5-7). By collecting the spatially encoded signals in a series of circularly rotating blades to fill out the entire k-space, the central k-space is covered by all single rotating blades which can then be used to reconstruct low-resolution images (1,2). With the coarse morphological information obtained from these low-resolution images, Propeller MR imaging facilitates in-plane motion correction (8) and inter-shot phase correction as needed for multishot diffusion-weighted imaging (9). Therefore, the Propeller technique is believed to offer precise depiction of the diffusion parameters relatively free from artifacts encountered in conventional diffusion imaging based on single-shot echo-planar imaging (EPI) (10).

As opposed to the original design which used fast spin-echo for signal readout to achieve robustness (1,2), Propeller with EPI readout for each single blade, termed Propeller-EPI in this study, bears the advantages of reduced specific absorption rate, better multi-slice capability, and more efficient data acquisition (9). Accompanied by these benefits in Propeller-EPI are the inevitable trade-off factors inherent in EPI, most noteworthy being the higher sensitivity to susceptibility-induced field distortions. Field map correction (9), short-axis readout (11), and parallel imaging acceleration (12) have been proposed to reduce the geometric distortions resulting from these off-resonance effects, with the hope that visualization of diffusion-weighted images could be achieved with better reliability (13).

In this work, we propose an alternative method to achieve further correction of the geometric distortions due to the EPI readout. The approach based on a modified reversed gradient method (14,15) is particularly suitable for Propeller-EPI, as the requirement of two EPI images with opposite phase-encoding gradient polarities is easily fulfilled when the Propeller-EPI acquisition is executed with 360° (as opposed to 180°) rotational coverage. We report the implementation of this method and demonstrate its effectiveness using both phantom and human experiments at high spatial resolution.

Materials and methods

The reversed gradient method

The original reversed gradient method is based on the acquisition of two EPI images obtained using phase encoding gradients reversed in polarity, thus creating opposite spatial displacements y₁ in image i₁ and y₂ in image i₂, respectively, along the phase encoding direction (14). The true position of the pixel is given by:

and with true intensity:

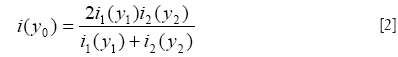
In reality, to find the matching pixel pair for y₁ and y₂, one usually works backwards by stepping through pixel locations in the corrected image coordinate system (y) to search for corresponding values having equal line integrals along the phase encoding direction on the two original distorted images (15). Namely, one needs to search for y₁ in image i₁ and y₂ in image i₂ such that:

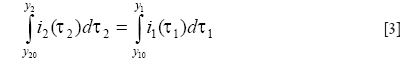
where y₁₀ and y₂₀ stand for the initial pair of pixels corresponding to the same location in images i₁ and i₂, from which the integration in Eq.[3] starts. The identification of the pixel pair y₁₀ and y₂₀ could be achieved with simple edge detection methods and is often straightforward. Proceeding Eq.[3] with all the phase encoding lines achieves the geometric correction for the entire EPI image.

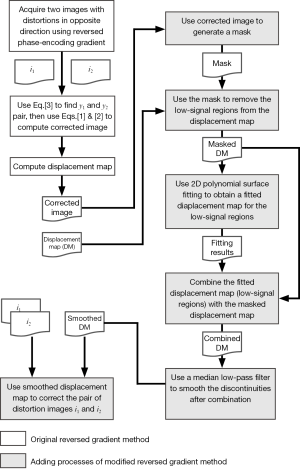
Modification using the displacement map concept

One problem of the reversed gradient method is that the search for matching pair pixel pair for y₁ and y₂ fails in low signal regions (16), because Eq.[3] can always be satisfied regardless of their original true locations. Fortunately, since any useful images contain some regions with detectable signals, the reversed gradient approach works well at least for these regions, for which the information could be used to remedy the erroneous estimates of y₁ and y₂ in other regions.

In this work, we assume that the variation of field inhomogeneities is slow, such that the pixel displacement resulting from susceptibility effects is a spatially smooth function. This assumption allows a modification of the pixel-by-pixel displacement map by using 2D polynomial surface fitting followed by a low-pass filter, with the low signal regions eliminated using a simple mask before the fitting procedure. The smoothed displacement map, instead of the original value obtained from Eq.[3], is then used to correct geometrical and intensity distortions using Eqs.[1] and [2]. The flow chart of the modified reversed gradient method is shown in Figure 1.

Figure 1 Step-by-step processes of the modified reversed gradient method utilizing the smoothed displacement map concept employed in this study

Imaging experiments

We collected phantom image data using single-shot spin-echo EPI to first show the effectiveness of the modified reversed gradient approach. The scanning parameters consisted of flip angle of 90°, TR/TE =1,650/120 ms, FOV 240 mm, slice thickness 5 mm, NEX 6, and a 256×256 imaging matrix. Two scans were performed, with the phase encoding gradient reversed in polarity in the second scan.

For demonstration of Propeller-EPI with modified reversed gradient reconstruction, healthy subjects were scanned using six-direction diffusion tensor imaging, with each single blade acquired using single-shot spin-echo EPI. The imaging parameters were TR/TE =1,200/96 ms, FOV =240 mm, b-factor 700 s/mm², slice thickness 3 mm, and NEX =4. The blade size was 15% of the reconstruction matrix, or 37×256 for a 256×256 reconstruction matrix. For each single signal average, a total of 24 blades were acquired for one image for a 360° circular coverage of the k-space, which corresponded to a rotating angle of 15° between adjacent blades. Note that the 24 blades showing geometric distortions became 12 corrected blades after the execution of the modified reversed gradient method. In addition, fast-spin echo images (TR/TE =1,200/95 ms, NEX =1) with fat suppression at the same slice location were acquired for comparison of geometry and contrast.

In order to push the limits of Propeller-EPI with the modified reversed gradient method, one more data set was obtained from a healthy adult using a 384×384 reconstruction matrix. The imaging parameters were TR/TE =2,500/80 ms, FOV =240 mm, slice thickness 3 mm, and NEX =4. The blade size was again kept at 15% of the reconstruction matrix. Parallel imaging with SENSE (17) was used with acceleration factors of 2 and 4 in two separate scans, thus the echo train length during the actual scan was 37 and 19, respectively. A total of 36 blades were used for a 360° circular coverage of the k-space, with a rotating angle of 10°. Only T2-weighted images were obtained, with fast spin-echo at the same slice location acquired also for comparison.

All the imaging experiments were performed on a 3.0 Tesla MR scanner (Philips Achieva, Best, the Netherlands) with a 8-channel head coil. Following acquisition, the complex k-space data were digitally transferred to a personal computer for off-line image reconstruction.

Image reconstruction

Reconstruction of the Propeller-EPI images was achieved by first separating the single-blade data into two sets, each with a 180° k-space coverage. Thus these two sets formed the reversed gradient image pair. The modified reversed gradient method was applied to these data to generate geometrically corrected single-blade data. Subsequently these single-blade data were combined using Propeller reconstruction method as reported previously (2,9), including in-plane spatial registration, phase correction, triangular windowing, Cartesian space regrinding, density compensation, followed by Fourier transformation. For the parallel imaging experiments, SENSE reconstruction preceded the reversed gradient calculations (12). Note that in order to demonstrate the robustness of the post-processing correction alone, no field map was acquired in this study. All reconstruction software was developed in-house under the Matlab^® platform (MathWorks, Natick, MA).

Results

Figure 2 shows the results from the single-shot EPI phantom experiment. While the original reversed gradient method is seen to correct most of the susceptibility-induced geometric distortions, some erroneous corrections could be found in the signal-free regions. With the modified approach proposed in this study using the smoothed displacement map, the corrected image becomes much closer to the original shape and intensity of the phantom.

Figure 2 Phantom images acquired with single-shot EPI with opposite phase gradient polarities, showing distortions along opposite direction (A,B). The reversed gradient corrected image (C) showed erroneous corrections at the signal-free regions (arrows). In the modified reversed gradient method, the original displacement map (D) was used to derive the new smoothed displacement map (E), yielding better geometric correction results (F)

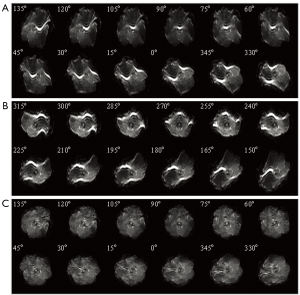
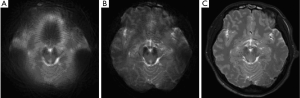
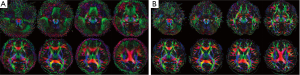
Figure 3 shows the original single-blade images from the slice at the pons level in the human experiments. The anatomic details could barely be identified from the 12 pairs of the single-blade images (Figure 3A,B) acquired using single-shot EPI which exhibits strong geometric distortions. Corrections using the modified reversed gradient method yield substantially improved consistency among all different single-blade images, although the tissue structure still looks blurred (Figure 3C). After Propeller reconstruction (Figure 4A, without using modified reversed gradient correction; Figure 4B, with the use of modified reversed gradient correction), the same image slice as in Figure 3 now shows sufficient morphological details as can be clearly identified visually as being comparable to the fast spin-echo image shown in Figure 4C nearly the cerebellum, except some signal loss around the auditory canals and the frontal lobe. The corresponding color-coded fractional anisotropy maps from eight slice locations obtained using Propeller-EPI without and with the use of modified reversed gradient corrections are shown in Figure 5A,B, respectively, which demonstrate major differences in the amount of blurring that exemplify the effectiveness of the modified reversed gradient correction algorithm when used in Propeller-EPI without the assistance from field map acquisitions.

Figure 3 The 12 pairs of original low-resolution single-blade images acquired using single-shot EPI (A,B), with the phase-encoding direction all set to be vertical. The rotational angles shown on the top-left corner stand for the angle between the anatomic anterior-posterior direction and the horizontal axis of these images. Prominent distortions are clearly seen to obscure the anatomic details. With corrections using the modified reversed gradient method, the 12 single-blade corrected images show much better mutual consistency (C)

Figure 4 Propeller reconstruction from single-blade EPI images of the same slice as in Figure 3 without (A) and with (B) modified reversed gradient correction. Comparison with the fast spin-echo image shown in (C) clearly demonstrates the effectiveness of the proposed approach

Figure 5 Colored fractional anisotropy maps corresponding to eight slice locations from a healthy subject obtained using Propeller-EPI without (A) and with (B) the use of modified reversed gradient corrections (red: left-right; blue: superior-inferior; green: anterior-posterior). Note the major difference in the amount of blurring in the frontal lobe, near the paranasal sinus, and near the skull base. The white matter fiber bundles such as the corticospinal tracts and the genu of the corpus callosum are prominently better visualized with the modified reversed gradient corrections

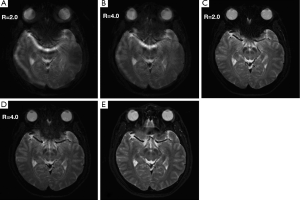
The T2-weighted images obtained at 384×384 matrix with high spatial resolution (nominal in-plane pixel width =0.625 mm) are shown in Figure 6. The Propeller-EPI images without using modified reversed gradient correction (Figure 6A,B) exhibit artifacts near the paranasal sinus that obscure the presence of blood vessels, whereas those after modified reversed gradient correction (Figure 6C,D) much better preserve the original geometry as compared with the fat-suppressed fast spin-echo image acquired at the same level (Figure 6E). The results also show that the reversed gradient method is fully compatible with parallel imaging.

Figure 6 T2-weighted images at 384×384 matrix size obtained using Propeller-EPI without (A,B) and with (C,D) modified reversed gradient correction. SENSE acceleration was used with acceleration factors R =2 (A,C) and R =4 (B,D), respectively. While parallel imaging at increased R is shown to somehow improve preservation of the geometry, the modified reversed gradient method is seen to be more effective especially near the skull base, as compared with the fast spin-echo image at the same slice location (E). The reversed gradient method is seen to be fully compatible with parallel imaging

Discussion

The results from our study show that corrections of EPI geometric and intensity distortions arising from susceptibility effects using the modified reversed gradient method indeed benefits from the smoothed displacement map. Through effectively reduced artifacts in low signal regions, reconstruction reliability is greatly improved. The employment of 2D polynomial surface fitting does not add noticeable increase in the computational loads (14,15), as only low order polynomial function is required due to the spatially slow variations of the main magnetic field near the air-tissue interface. The entire reconstruction routine is also computationally economic, although further acceleration can be achieved via parallel computation (18).

One potential application area of Propeller-EPI with reversed gradient corrections is high-resolution diffusion tensor imaging at high field strengths (19). Susceptibility effects worsen as field strength increases, making geometric distortions in single-shot EPI more annoying. Although Propeller imaging based on fast spin-echo acquisition is also capable of obtaining diffusion tensor images without geometric distortions (2,5-7), the increased RF specific absorption rate (20) makes it somewhat less desirable than EPI-based acquisition sequences. As a consequence, Propeller-EPI is an attractive alternative for diffusion tensor imaging (9,11,12,21), or even brain function imaging (22). In addition, the requirement of image pairs with opposite phase encoding gradient polarities can be easily fulfilled if multiple signal averages are used in Propeller-EPI to increase SNR in high-resolution imaging, making the reversed gradient calculations directly applicable.

Compared with corrections based on field map acquisition (23), there are several important advantages of our modified reversed gradient approach that are worthy of mentioning. First of all, no additional acquisition is necessary, hence the total examination time can be shorter. This could become critical in high-resolution imaging applications, where the use of multiple signal averages to exchange for SNR is accompanied by long scan time, resulting in location inconsistency between the field maps and the actual images. Secondly, the modified reversed gradient method also corrects EPI distortions arising from eddy current effects (24), as long as the distortions are opposite in the image pairs when the phase encoding gradient is reversed in polarity. In contrast, off-resonance corrections using field map do not take eddy current effects into consideration.

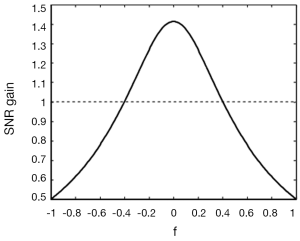
One currently unsolved issue in Propeller-EPI with the modified reversed gradient correction is the SNR alterations in the reconstructed images. With the reversed gradient method used alone for single-shot EPI, the SNR gain has been shown to depend on the local magnetic field inhomogeneity (14), in that higher local gradient value causes lower SNR in corrected image of this region. Morgan et al. (14) gives:

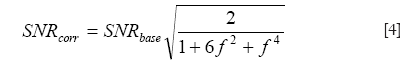
where SNR_corr and SNR_base are the SNRs of the corrected and uncorrected images, and

is a short-hand notation standing for the background gradient relative to the imaging gradient, respectively. Figure 7 plots the relationship between SNR_corr and SNR_base, where it is seen that for f =0, the gain in SNR reduces to the familiar formula given as the square root of the number of signal averages (two in this case). As background gradient becomes stronger, as in the case of air-tissue interfaces, the SNR gain reduces drastically. When the reversed gradient method is used for Propeller-EPI, the colored noise pattern due to the over-sampling of the k-space center (9) makes it even more complicated and is beyond the scope of this article.

Figure 7 The SNR gain from the reversed gradient corrections in single-shot EPI, plotted as a function of the factor f standing for the background field gradient relative to the imaging gradient. It is seen that the SNR gain decreases substantially as background gradient increases

We conclude that the modified reversed gradient method is an effective approach for Propeller-EPI. The substantially improved image quality makes it attractive for imaging applications at high spatial resolution.

Acknowledgements

Supported in part by the National Science Council under grants NSC 96-2314-B-011-001 (YRL) and NSC 101-2221-E-002-013-MY3 (HWC).

Disclosure: Presented in part at the 2006 Annual Meeting of the International Society for Magnetic Resonance in Medicine. The authors declare no conflict of interest.

References

1. Pipe JG. Motion correction with PROPELLER MRI: application to head motion and free-breathing cardiac imaging. Magn Reson Med 1999;42:963-9.
2. Pipe JG, Farthing VG, Forbes KP. Multishot diffusion-weighted FSE using PROPELLER MRI. Magn Reson Med 2002;47:42-52.
3. Lane BF, Vandermeer FQ, Oz RC, et al. Comparison of sagittal T2-weighted BLADE and fast spin-echo MRI of the female pelvis for motion artifact and lesion detection. AJR Am J Roentgenol 2011;197:W307-13.
4. Huang TY, Tseng YS, Tang YW, et al. Optimization of PROPELLER reconstruction for free-breathing T1-weighted cardiac imaging. Med Phys 2012;39:4896-902.
5. Deng J, Miller FH, Salem R, et al. Multishot diffusion-weighted PROPELLER magnetic resonance imaging of the abdomen. Invest Radiol 2006;41:769-75.
6. Juan CJ, Chang HC, Hsueh CJ, et al. Salivary glands: echo-planar versus PROPELLER Diffusion-weighted MR imaging for assessment of ADCs. Radiology 2009;253:144-52.
7. Attenberger UI, Runge VM, Stemmer A, et al. Diffusion weighted imaging: a comprehensive evaluation of a fast spin echo DWI sequence with BLADE (PROPELLER) k-space sampling at 3 T, using a 32-channel head coil in acute brain ischemia. Invest Radiol 2009;44:656-61.
8. Forbes KP, Pipe JG, Karis JP, et al. Brain imaging in the unsedated pediatric patient: comparison of periodically rotated overlapping parallel lines with enhanced reconstruction and single-shot fast spin-echo sequences. AJNR Am J Neuroradiol 2003;24:794-8.
9. Wang FN, Huang TY, Lin FH, et al. PROPELLER EPI: an MRI technique suitable for diffusion tensor imaging at high field strength with reduced geometric distortions. Magn Reson Med 2005;54:1232-40.
10. Winston GP. The physical and biological basis of quantitative parameters derived from diffusion MRI. Quant Imaging Med Surg 2012;2:254-65.
11. Skare S, Newbould RD, Clayton DB, et al. Propeller EPI in the other direction. Magn Reson Med 2006;55:1298-307.
12. Chuang TC, Huang TY, Lin FH, et al. PROPELLER-EPI with parallel imaging using a circularly symmetric phased-array RF coil at 3.0 T: application to high-resolution diffusion tensor imaging. Magn Reson Med 2006;56:1352-8.
13. Chen B, Moreland J, Zhang J. Human brain functional MRI and DTI visualization with virtual reality. Quant Imaging Med Surg 2011;1:11-6.
14. Morgan PS, Bowtell RW, McIntyre DJ, et al. Correction of spatial distortion in EPI due to inhomogeneous static magnetic fields using the reversed gradient method. J Magn Reson Imaging 2004;19:499-507.
15. Chang H, Fitzpatrick JM. A technique for accurate magnetic resonance imaging in the presence of field inhomogeneities. IEEE Trans Med Imaging 1992;11:319-29.
16. Kannengiesser SA, Wang Y, Haacke EM. Geometric distortion correction in gradient-echo imaging by use of dynamic time warping. Magn Reson Med 1999;42:585-90.
17. Pruessmann KP, Weiger M, Scheidegger MB, et al. SENSE: sensitivity encoding for fast MRI. Magn Reson Med 1999;42:952-62.
18. Huang TY, Tang YW, Ju SY. Accelerating image registration of MRI by GPU-based parallel computation. Magn Reson Imaging 2011;29:712-6.
19. Jeong HK, Gore JC, Anderson AW. High-resolution human diffusion tensor imaging using 2-D navigated multishot SENSE EPI at 7 T. Magn Reson Med 2013;69:793-802.
20. Massire A, Cloos MA, Luong M, et al. Thermal simulations in the human head for high field MRI using parallel transmission. J Magn Reson Imaging 2012;35:1312-21.
21. Aksoy M, Skare S, Holdsworth S, et al. Effects of motion and b-matrix correction for high resolution DTI with short-axis PROPELLER-EPI. NMR Biomed 2010;23:794-802.
22. Krämer M, Jochimsen TH, Reichenbach JR. Functional magnetic resonance imaging using PROPELLER-EPI. Magn Reson Med 2012;68:140-51.
23. Reber PJ, Wong EC, Buxton RB, et al. Correction of off resonance-related distortion in echo-planar imaging using EPI-based field maps. Magn Reson Med 1998;39:328-30.
24. Bastin ME, Armitage PA. On the use of water phantom images to calibrate and correct eddy current induced artefacts in MR diffusion tensor imaging. Magn Reson Imaging 2000;18:681-7.