
Deep learning-based rotational object detection algorithm for automatic Cobb angle measurement in X-ray images of scoliosis
Introduction
Scoliosis is a common spinal deformity characterized by lateral curvature of the spine, visible from both the frontal and lateral perspectives, typically forming a “C” or “S” shape (1). This condition can occur at any age but is most prevalent during childhood and adolescence, particularly during the teenage years (2). The Cobb angle, introduced in 1948 by American orthopedic surgeon John Robert Cobb (3), is widely used in clinical practice and research to measure the severity of scoliosis and is considered the "gold standard" for scoliosis diagnosis. The Cobb angle is determined by measuring the angle between the most tilted upper and lower vertebrae on an X-ray. Traditionally, marking and measuring the Cobb angle are manually performed by physicians. However, it has been noted that manual measurement is more time-consuming and less efficient in clinical practice compared to automated methods. Kuklo et al. found that manual measurements exhibit lower reproducibility and accuracy compared to automated measurements, particularly in postoperative scenarios where reliability significantly decreases (4). Tanure et al. discovered that manual Cobb angle measurements are highly dependent on the subjective judgment of the physician, leading to inconsistencies in subsequent measurements (5). Therefore, developing an accurate automated prediction technique for the Cobb angle in scoliosis is of paramount clinical significance.
In related research, numerous deep learning algorithms have been applied to the prediction of the Cobb angle in scoliosis. Wu et al. proposed a method using BoostNet for landmark detection of the spine, which forms the basis for detecting and calculating the Cobb angle (6). Imran et al. introduced an adjusted progressive side-output U-Net model for fully automated segmentation of vertebrae relevant to scoliosis measurement (7). Additionally, in the application of object detection algorithms for spinal pathology detection, Guo et al. proposed a method based on an improved YOLOv8 with the smallest number of parameters (YOLOv8n) architecture for detecting and automatically grading lumbar disc herniation (LDH) and lumbar central canal stenosis (LCCS), demonstrating that the YOLOv8n model is effective for vertebral detection (8). Furthermore, predicting the Cobb angle based on rotational object detection is an effective approach. The YOLO series models have gained widespread attention in various fields for rotational object detection. Zhang et al. proposed an improved YOLO model for remote sensing detection, using rotational bounding boxes for one-step detection of objects in remote sensing images (9). Cheng et al. introduced a YOLOv5-based rotational object detection method for remote sensing images, incorporating an angle loss into the loss function to detect the rotation angle of objects (10). These studies indicate that the YOLOv8n-oriented bounding box (OBB) model will provide reliable results for rotational object detection of spinal vertebrae.
This paper introduces a novel approach based on an enhanced YOLOv8n-OBB rotational object detection model, achieving automated and highly accurate Cobb angle measurement from scoliosis X-ray images. Uniquely, this method also enables precise evaluation of scoliosis severity. Compared to existing techniques, the proposed method significantly improves multiple network modules, markedly enhancing the accuracy in detecting rotated spinal structures and effectively addressing limitations in existing rotational object detection and angle prediction methodologies. This advancement carries significant implications for clinical practice. The main contributions are as follows:
- Development of a novel automated method for precise Cobb angle measurement from spinal X-ray images, effectively reducing subjective biases and inefficiencies associated with manual measurement.
- Significant enhancements of YOLOv8n-OBB through novel improvements in feature extraction and rotational object detection modules, substantially improving detection accuracy for rotated spinal structures.
- Innovative implementation of automatic Cobb angle assessment using a rotational object detection network, validated rigorously on both self-constructed and publicly available datasets. The method demonstrates notable superiority in accuracy and reliability compared to existing methods, providing critical theoretical foundations and practical guidance for clinical diagnosis and management of scoliosis.
We present this article in accordance with the CLEAR reporting checklist (available at https://qims.amegroups.com/article/view/10.21037/qims-24-2138/rc).
Methods
In our study on predicting the Cobb angle using rotational object detection, three specific steps were implemented: experimental preparation, rotational object detection and vertebra localization, and bone edge marking with Cobb angle calculation. The first step primarily involved dataset preparation and model parameter settings. In the second step, based on YOLOv8, an improved model of YOLOv8-DSF combined with C2f-DCNv2, C2f-FADC, and DSS modules to detect the rotational targets of spinal vertebrae and facilitate their precise localization was employed. In the third step, once the specific vertebrae positions were determined, the Cobb angle was calculated based on bone edge markings. This process enabled the automated identification and output of the corresponding Cobb angle and its precise location from input X-ray images.
Data materials and preparation
Our research utilized X-ray images of the spine in the anteroposterior (AP) position from patients exhibiting varying degrees of scoliosis. A total of 319 high-quality X-ray images detailing instances of scoliosis were collected from Tongji Hospital, Tongji Medical College, Huazhong University of Science and Technology and Henan Provincial People’s Hospital. All images were divided into training, testing, and validation sets at a ratio of 6:2:2. A subset of spine images from the Accurate Automated Spinal Curvature Estimation (AASCE) challenge dataset was further incorporated into the study (6), which have been meticulously selected by medical professionals and are considered representative to a certain extent.
The study was conducted according to the ethical guidelines of Declaration of Helsinki and its subsequent amendments. The study was approved by the Ethics Committee of Henan Provincial People’s Hospital (No. 2024-108) and the requirement for individual consent for this retrospective analysis was waived.
The collected images typically cover spine segments consisting of 17 or more relevant vertebrae, encompassing 12 thoracic vertebrae (T1–12) and 5 lumbar vertebrae (L1–5). The annotations for rotating bounding boxes used in the rotating object detection were manually annotated by medical experts.
As illustrated in Figure 1, the dataset preprocessing workflow amalgamates X-ray images sourced from hospital archives with those selected by medical professionals, thus forming an enriched dataset for rotational object detection. Given that the typical resolution of a full AP spinal X-ray is around 512×1,024 and the variability in resolution among individual images, standardization is imperative for the efficacy of model training. Additionally, the publicly accessible AASCE challenge dataset encompasses only cropped spinal images. This necessitates the cropping of X-ray images acquired from hospitals, a process that standardizes the data, as well as a process that assists in concealing personal patient information, thereby enhancing privacy protection. Subsequent to the extraction of the complete spine from these images, they are normalized to a uniform resolution of 512×1,024.
Rotating target detection and vertebra positioning
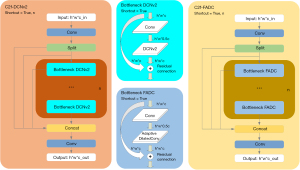
Several methods employ deep learning neural networks for predicting the Cobb angle in scoliosis. Techniques such as image segmentation and object detection have been particularly noted for their utility in estimating this angle, drawing significant interest from the research community (11,12). Drawing on the works of Wang et al., a rotated object detection strategy is used to initially identify spinal vertebrae (13). This approach sets the stage for the subsequent accurate calculation of the Cobb angle. Building on the YOLOv8 structure but differing from it, YOLOv8-DSF utilizes its rotational object detection head for this task. Multiple modules are added to the original architecture to propose a new rotation object detection architecture YOLOv8-DSF for detecting the position of the spine and simultaneously locating the key coordinates of the four corners of each vertebra. Firstly, several improvements are made to the C2f layer, resulting in the new C2f-DCNv2 and C2f-frequency-adaptive dilated convolution (FADC) layers. Furthermore, the new dynamic scale sequence feature fusion (DSS) module was implemented to enhance the localization and recognition of rotational object image features with respect to the neck section. Some Concat modules were also replaced with Zoom_cat modules to improve the model’s ability to fuse feature maps at different scales. The detailed introduction of the introduced modules is as follows:
- C2f-DCNv2. Within the backbone structure, as influenced by Zhu et al. (14). As shown in Figure 2, the C2f layer following the P4 Conv layer was enhanced to develop the innovative C2f-DCNv2 layer. In the YOLOv8 architecture, the conventional second Conv layer has been substituted with the DCNv2 layer in the bottleneck structure. Instead, the modified sampling output indirectly gives rise to a transformation in the kernel’s shape (15). In DCNv1, the operation is used to expand , as depicted in 16). Moreover, DCNv2 extends this concept by incorporating a weight coefficient for each sampling point, as outlined in
Eq. [2], with being a fractional value ranging from 0 to 1. - C2f-FADC. Following the P5 layer, it is suggested that YOLOv8-DSF has integrated the novel C2f-FADC layer in Figure 2. As depicted in Figure 3, the C2f-FADC layer employs FADC, a technique extensively utilized in computer vision to increase the receptive field by interspersing gaps among successive elements. Building on the findings of Chen et al., FADC dynamically adjusts dilation rates spatially based on local frequency, enabling adaptive responses. This feature is particularly beneficial in the detection and localization of vertebrae, because spinal scoliosis causes various deformations, including bending, expansion, and compression of vertebrae (17). Consequently, enhancing the receptive field of the convolution significantly aids in precise vertebrae localization.
- DSS and Zoom_cat. Inspired by ASF-YOLO (18), the Concat module has been replaced in the Neck structure with the Zoom_cat module, as shown in Figure 2. For large-sized feature maps, after processing through a convolutional module to adjust their channel counts, they are then downsampled; conversely, smaller-sized feature maps are upsampled following convolution. This method transforms feature maps of three different sizes into a uniform size, facilitating their concatenation, as depicted in
Eq. [3]. , , and denote the large, medium, and small-sized feature maps, respectively. This approach ensures a more balanced feature integration across different scales.

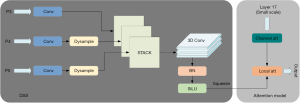
As depicted in Figure 4, the DSS module has been incorporated into the Neck architecture. As an ultra-lightweight and efficient upsampler (19), Dysample reduces the computational resources required by the DSS module to a large extent. It also minimizes inference latency, memory usage, and parameter count. Subsequently, images of the same size from P3, P4, and P5 layers are stacked and fed into a three-dimensional (3D) convolution layer. A combination of features across multiple scales is produced in this stage that offers targeted performance for varying sizes and rotational angles of spinal vertebrae. The images processed through the DSS module can be represented by Eqs. [4,5]. Here, denotes a two-dimensional (2D) image with width and height , and is the scale parameter controlling the standard deviation of the Gaussian filter used in the convolution.
Edge marking and cobb angle calculation
For the purpose of identifying vertebrae and locating the vertex coordinates of each bone, YOLOv8’s OBB detection head is employed (20). In this study, the format of four vertices was chosen to define the bounding boxes, specified as . These coordinates are subsequently rearranged in a specific sequence to outline the vertices, as illustrated in Figure 5. Upon obtaining the aforementioned coordinates, it is necessary to eliminate a certain number of anomaly detection boxes. A confidence threshold was additionally established: detection boxes with a confidence level below this threshold are discarded. In this vertebra detection task, the confidence threshold is set to 0.6. This procedure ensures that only the most probable detection results are considered, enhancing the accuracy of the vertebral localization. To avoid cross-interference between vertex coordinates, the vertices on the same side are reordered based on the y-values of each point from top to bottom, following the results above. Once each group of vertex coordinates is clearly defined, the slope of the upper and lower boundary vertices of each rectangular box can be calculated using Eq. [6]. These slopes are then organized into a list: . Since the detection boxes are rectangular and the top and bottom boundaries are always parallel, only the slope of the upper boundary needs to be calculated. This structured approach ensures that the vertices are properly aligned and free from overlapping errors.
After obtaining the list of slopes, the entire list of calculating the angle between each pair of slopes and recording their indices is iterated, as shown in Eq. [7]. When identifying the three largest angles, our approach follows three rules to exclude outliers: (I) if two angles share overlapping indices with more than one index in common, the angle with the smaller span is discarded, and the next largest angle is selected; (II) if a large angle exceeds 90 degrees, the supplementary angle will replace this angle in the list for comparison; (III) if the boundary vertex coordinates coincide, consequently resulting in a zero denominator in Eq. [6], the corresponding slope is set to infinity to avoid anomalies during angle calculation. The overall process for predicting the Cobb angle is illustrated in Figure 6.
Results
Experiments setup
Our methodology was implemented using the PyTorch DL framework (https://pytorch.org/). Detailed insights are provided by Ultralytics in their research report (21) about the process of model training with the utilization of the aforementioned hybrid dataset. A smaller parameter model of YOLOv8n-OBB as a baseline for research would be more beneficial with consideration to the specific application scenarios of Cobb angle prediction in certain medical institutions. According to the report, training YOLOv8 typically requires over 500 epochs; however, given that the experiments did not employ a pre-trained model, the training regimen was set to 1,000 epochs. This approach ensures robust model training while balancing computational efficiency.
In terms of optimizer selection, Adam demonstrates superior performance when training our custom dataset (22), whereas SGD is more effective with large datasets (23). Accordingly, our model opted for the Adam optimizer configured with an initial learning rate of 1×10−2, momentum of 0.937, and weight decay of 5×10−4. Training was conducted on hardware consisting of an Intel(R) Xeon(R) Silver 4214R CPU @ 2.40 GHz with a single GPU GeForce RTX 3080 Ti (12 GB). The software environment was set up with PyTorch 1.10.0 (https://pytorch.org/get-started/previous-versions/), Python 3.8 (https://www.python.org/downloads/), and CUDA 11.3 (https://developer.nvidia.com/cuda-11.3.0-download-archive), with a batch size of 16. This configuration ensures optimal resource utilization while accommodating the computational demands of our model training.
Ablation experiment
Evaluation metrics
To assess the accuracy of the redesigned model, our experiments utilized a suite of widely recognized metrics for evaluation. The key performance indicators encompassed precision (P), recall (R), mAP50, and mAP50–95. The precision-recall curve (P-R curve) that plots recall on the x-axis and precision on the y-axis illustrates the relationship between these two metrics (24). Average precision is calculated as the area under the P-R curve, serving to balance and reflect the performance of Precision and Recall comprehensively. As an average of the average precision across different categories, mean average precision (mAP) provides a holistic representation of model performance, as shown in Eq. [10]. Additionally, mAP50 refers to the mAP calculated with an Intersection over Union (IoU) threshold of 0.50, which is particularly valuable for objects that are relatively easier to detect due to their distinct features. Meanwhile, mAP50–95 represents the average mAP calculated across an IoU range from 0.50 to 0.95, offering a broader assessment of the model’s overall performance.
Result evaluation
To evaluate our model’s performance in rotational object detection of vertebrae prior to predicting the Cobb angle in scoliosis, ablation experiments were conducted by training and evaluating the YOLOv8n-OBB model with different modules. The results are presented in Table 1.
Table 1
| Model | Instances | P | R | mAP50test | mAP50–95test | PARAMS (m) |
|---|---|---|---|---|---|---|
| YOLOv8n-OBB (baseline) | 1,088 | 0.59 | 0.597 | 0.568 | 0.372 | 6.8 |
| Single | ||||||
| C2f-DCNv2 + OBB | 1,088 | 0.593 | 0.592 | 0.601 | 0.406 | 6.8 |
| C2f-FADC + OBB | 1,088 | 0.599 | 0.596 | 0.611 | 0.414 | 6.8 |
| DSS + OBB | 1,088 | 0.601 | 0.594 | 0.491 | 0.29 | 6.8 |
| Couple | ||||||
| C2f-DCNv2 + C2f-FADC + OBB | 1,088 | 0.608 | 0.6 | 0.498 | 0.306 | 6.8 |
| C2f-DCNv2 + DSS + OBB | 1,088 | 0.597 | 0.586 | 0.546 | 0.349 | 7.0 |
| C2f-FADC + DSS + OBB | 1,088 | 0.598 | 0.586 | 0.616 | 0.419 | 6.9 |
| All | ||||||
| YOLOv8-DSF | 1,088 | 0.591 | 0.595 | 0.626 | 0.424 | 7.0 |
DCN, deformable convolutional networks; DSF, C2f-DCNv2 + C2f-FADC + DSS + OBB; DSS, dynamic scale sequence feature fusion; FADC, frequency-adaptive dilated convolution; IoU, Intersection over Union; mAP50, the mAP calculated with an IoU of 0.50; mAP50–95, the average mAP calculated across an IoU range from 0.50 to 0.95; OBB, oriented bounding box; P, precision; PARAMS, parameter quantity; R, recall; YOLOv8n, YOLOv8 with the smallest number of parameters.
Initially, our experiment integrated each module (C2f-DCNv2, C2f-FADC, DSS) individually into the YOLOv8n-OBB model. The P on the test set increased by 0.3%, 0.9%, and 1.1%, whereas the mAP50 improved by 3.3%, 4.3%, and −7.8%, and the mAP50-95 improved by 3.4%, 4.2%, and −8.2%, respectively, on each module. The addition of a single module had no significant impact on the model’s size. Interestingly, the DSS module alone seemed to degrade the model’s performance. However, when multiple modules were integrated simultaneously, the results were counterintuitive. When integrating C2f-DCNv2 and C2f-FADC, C2f-DCNv2 and DSS, and C2f-FADC and DSS modules together into the YOLOv8n-OBB model, the P improved by 1.8%, 0.7%, and 0.8%, respectively. The mAP50 scores changed by −7.0%, −2.0%, and 4.8%, whereas the mAP50–95 scores changed by −6.6%, −2.3%, and 4.7%, respectively. The parameter count increased by 0.1 to 0.2 million (M) compared to the baseline. These results suggest that the combination of C2f-FADC and DSS modules may have a mutual influence, potentially enhancing the network’s ability to extract multi-scale information due to the FADC complementing the DSS module.
For our model, YOLOv8-DSF, which integrates all three modules simultaneously, the line graph in Figure 7 shows that it consistently performed well in ablation experiments. Compared to the baseline YOLOv8n-OBB model, our model achieved approximately 10% higher mAP50 scores and over 13% higher mAP50–95 scores. In terms of model size and parameters, our model is only 2% larger than the baseline, indicating that our model achieved better recognition accuracy with a relatively smaller size. Additionally, our model’s loss decreased more significantly within the same timeframe during training. Our model, therefore, demonstrates strong competitiveness in vertebral detection tasks for scoliosis.

Cobb angle calculation result evaluation
Evaluation metrics
In order to comprehensively evaluate the effectiveness of the model in predicting the Cobb angle for scoliosis, the predicted Cobb angles were compared with the true values annotated by professional doctors. To measure this difference, mean absolute error (MAE) and symmetric mean absolute percentage error (SMAPE) were chosen to evaluate the predicted Cobb angle versus the actual Cobb angle for each spinal X-ray image. The calculations are detailed in Eqs. [11,12]:
The factor in Eq. [11] represents the predicted values, given by . Similarly, the actual values are denoted by . The MAE values for the three primary Cobb angles, the upper Cobb angle, and the lower Cobb angle on a single spine can be calculated separately. For each X-ray image, there may not always be three Cobb angles present. According to Eq. [12], the denominator cannot be zero. Therefore, in cases where the actual and predicted values are both zero, the SMAPE value for that angle is set to zero. Finally, the average SMAPE value across all images is calculated, providing a reliable assessment of the model’s accuracy in predicting Cobb angles.
Result evaluation
In the Cobb angle prediction experiments, all the aforementioned models were evaluated with the test results presented in Table 2. MAE1, MAE2, and MAE3, respectively, represent the MAE for the primary Cobb angle, upper Cobb angle, and lower Cobb angle. MAE_Avg denotes the average MAE of the three angles—it can express the overall error between the different predicted values and the true values of the three Cobb angles in a relatively intuitive manner. SMAPE represents the SMAPE for each set of Cobb angles in the entire test set.
Table 2
| Model | MAE1 | MAE2 | MAE3 | MAE_Avg | SMAPE |
|---|---|---|---|---|---|
| YOLOv8n-OBB (baseline) | 13.20 | 10.65 | 18.49 | 14.12 | 26.17 |
| Single | |||||
| C2f-DCNv2 + OBB | 10.15 | 11.04 | 14.93 | 12.04 | 25.41 |
| C2f-FADC + OBB | 12.91 | 12.95 | 8.98 | 11.61 | 25.74 |
| DSS + OBB | 8.18 | 9.86 | 15.04 | 11.03 | 19.06 |
| Couple | |||||
| C2f-DCNv2 + C2f-FADC + OBB | 11.57 | 8.22 | 11.95 | 10.58 | 18.90 |
| C2f-DCNv2 + DSS + OBB | 5.31 | 3.25 | 7.38 | 5.31 | 10.19 |
| C2f-FADC + DSS + OBB | 9.03 | 11.48 | 12.52 | 11.01 | 15.94 |
| All | |||||
| YOLOv8-DSF | 4.79 | 3.59 | 6.90 | 5.09 | 8.43 |
DCN, deformable convolutional networks; DSF, C2f-DCNv2 + C2f-FADC + DSS; DSS, dynamic scale sequence feature fusion; FADC, frequency-adaptive dilated convolution; MAE, mean absolute error; OBB, oriented bounding box; SMAPE, symmetric mean absolute percentage error; YOLOv8n, YOLOv8 with the smallest number of parameters.
When individual modules (C2f-DCNv2, C2f-FADC, DSS) were integrated into the YOLOv8n-OBB model, the MAE_Avg for the three Cobb angles decreased by 2.08, 2.51, and 3.09, respectively. Specifically, C2f-DCNv2 reduced the error most for the primary Cobb angle, C2f-FADC for the lower Cobb angle, and the DSS module for the upper Cobb angle. This indicates that each module has a targeted impact on different positions of the Cobb angle detection. With regard to the SMAPE metric, the errors relative to the baseline were respectively reduced by 0.76, 0.43, and 6.28, suggesting that each module enhances the accuracy of Cobb angle detection to some extent.
Once two different modules were combined, the combinations of C2f-DCNv2 with C2f-FADC, C2f-DCNv2 with DSS, and C2f-FADC with DSS consequently reduced the MAE_Avg by 3.54, 8.81, and 3.11 in sequence, compared to the baseline. The SMAPE metric also indicated significant improvements in the accuracy of Cobb angle detection when pairs of modules were added.
The results in Table 2 show that our model of YOLOv8-DSF, which integrates all three modules simultaneously, significantly outperformed the baseline. Our model reduced the MAE_Avg by 9.03 compared to the baseline. Additionally, our model performed exceptionally well in procedures of predicting the primary, upper, or lower Cobb angles. The SMAPE metric showed a nearly 67% reduction in error. These results indicate that our model surpasses the baseline across all metrics, demonstrating strong competitiveness in Cobb angle prediction tasks.
The accuracy of the YOLOv8-DSF model in predicting Cobb angles for scoliosis was validated to a certain extent by testing it with the dataset from the AASCE Medical Image Computing and Computer Assisted Intervention (MICCAI) 2019 challenge. In Table 3, the tests results are compared with other predictions of Cobb angles for scoliosis.
Table 3
| Method | MAE1 | MAE2 | MAE3 | MAE_Avg | SMAPE |
|---|---|---|---|---|---|
| Khanal et al. (25) | – | – | – | – | 25.69 |
| Wang et al. (26) | 26.38 | 30.27 | 35.61 | 30.75 | 23.43 |
| Chen et al. (27) | – | – | – | – | 23.59 |
| Dubost et al. (28) | – | – | – | – | 22.96 |
| Horng et al. (29) | 9.71 | 25.97 | 33.01 | 22.89 | 16.48 |
| Wang et al. (30) | – | – | – | – | 12.97 |
| Ours | 2.83 | 4.74 | 6.38 | 4.65 | 12.69 |
–, the method’s author has not disclosed their test results or model code. AASCE, Accurate Automated Spinal Curvature Estimation; MAE, mean absolute error; MICCAI, medical image computing and computer assisted intervention; SMAPE, symmetric mean absolute percentage error.
Khanal et al. approached the task by initially detecting each vertebral body as an individual object in a way that enabled more precise positioning of the vertebrae’s four corner landmarks but yielded a SMAPE score of only 25.69 (25). In a similar vein, our method also treats each vertebral body as a distinct target for detection. However, with improved accuracy, our method particularly excels in detecting the pathological rotation of vertebrae associated with scoliosis. This approach significantly enhanced performance, achieving a lower SMAPE score of 12.69 on the same dataset. Dubost et al. developed a technique using two convolutional neural networks to segment the spinal cord’s midline in a cascading manner and to estimate the Cobb angle by smoothing the midline (28). Though innovative, this method did not perform as well in accurately locating vertebral boundaries compared to methods that directly detect vertebral targets, registering a SMAPE score of 22.96. Wang et al. proposed a pyramid feature aggregation method for multitask learning that allows angle estimation in a single stage without prior landmark collection (30). Nonetheless, our findings indicate that a more precise outcome is achieved by first collecting landmarks and then predicting angles.
Discussion
Throughout the experimental evaluation described above, our new model, YOLOv8-DSF, demonstrated significant potential in predicting Cobb angles for scoliosis. This method initially conducts rotational target detection to locate the corresponding vertebral corners of each spinal segment. Subsequently, the located landmarks undergo a filtration process, followed by slope calculation and selection, culminating in the prediction of the Cobb angles.
During the process of detecting spinal vertebrae using deep learning models, the increase in parameter count for YOLOv8 did not significantly enhance the detection of vertebrae. Consequently, our approach employed YOLOv8n-OBB with minimal parameter count as the baseline. By integrating modules such as DSS, C2f-FADC, and C2f-DCNv2 on top of this baseline, the parameter increase was a mere 0.1 M. This demonstrates that our model achieves superior performance with a smaller footprint, simultaneously consuming fewer hardware resources in clinical applications. By optimizing resource use while improving predictive accuracy, our approach facilitates easier deployment in clinical settings.
The parameter ablation study of YOLOv8-DSF reveals that the model achieved an mAP50 score of 0.626 and an mAP50–95 score of 0.424 on our dataset, representing an improvement of over 10% compared to the baseline. During the experimental process, as displayed in Table 1, the introduction of the DSS module alone may lead to a decrease in detection performance relative to the baseline. However, when module pairs or the full implementation within YOLOv8-DSF are introduced, the inclusion of the DSS module indeed enhances detection effectiveness. This indicates that there is a synergistic relationship between modules in visual detection and image processing.
We conducted an ablation study for the first time using our dataset to evaluate the accuracy of Cobb angle prediction in scoliosis assessment. Compared to the baseline, YOLOv8-DSF achieved an average MAE (MAE_Avg) score of 5.09 and a SMAPE score of 8.43. As shown in Table 2, the introduction of the DSS module alone significantly improved the MAE1 score for the upper Cobb angle, whereas the introduction of the C2f-FADC module alone significantly enhanced the MAE3 score for the lower Cobb angle. This suggests that different modules may focus on different aspects of scoliosis imaging, warranting further research to fully understand their impacts.
By utilizing the publicly available AASCE MICCAI 2019 challenge dataset, a comparison of Cobb angle prediction accuracy was additionally conducted between our model and other models. As shown in Table 3, our model achieved an MAE_Avg of 4.65 and a SMAPE score of 12.69, demonstrating a significant advantage over other methods. However, compared to the results tested on our proprietary dataset, the SMAPE score showed a decline. This discrepancy may be due to the dataset selection process for the AASCE MICCAI 2019 challenge, where only high-quality X-ray images were retained to reduce the impact of noise in the original dataset, and additional X-ray images were incorporated. The current practice might cause the model to underperform when predicting lower-quality X-ray images. Therefore, future work should focus on expanding the dataset for training to ensure the model maintains optimal performance across X-rays of varying quality.
In addition, inspired by the work of Polzer et al. (31), our vertebra detection method demonstrates significant potential in the automatic identification of vertebral fractures and subsequent stability assessment. By utilizing our method to accurately localize vertebrae in X-ray images and integrating it with the fracture detection approach with CT images proposed by Polzer et al., we can achieve effective multimodal image validation. This combined approach is expected to substantially enhance the accuracy of vertebral detection. Thus, our future research will focus on advancing multimodal image fusion techniques to further improve the performance of vertebral detection systems.
There remains immense potential to enhance model performance in works with ongoing expansion of the dataset. Our research can further improve the model’s object detection capabilities and the accuracy of Cobb angle predictions by employing methods such as incremental learning. This approach will support the continuous advancement of model performance and its clinical applicability.
Conclusions
In this research, a new network architecture YOLOv8-DSF was proposed for predicting the Cobb angle in scoliosis using an improved YOLOv8-based rotational object detection approach. Specifically, the C2f-FADC and C2f-DCNv2 layers were used in the backbone, integrating deformable convolutional networks and dilated convolutions. Additionally, in the Neck, the DSS module was incorporated along with the Zoom_cat and attention_model to fuse spatial scale features, thereby enhancing the detection performance of spinal vertebrae. This approach significantly improves the accuracy and reliability of vertebral rotational object detection compared to the original YOLOv8n-OBB.
Extensive experiments demonstrate that our model achieves an mAP50 score of 0.626 and an mAP50–95 score of 0.424 on our dataset, both exhibiting over a 10% improvement compared to the baseline. In terms of Cobb angle prediction accuracy, the MAE_Avg between manual measurements and our model’s automatic predictions on the test dataset is only 5.09, and the SMAPE is just 8.43. In tests conducted using the public dataset, the SMAPE score achieved was 12.69, which also demonstrates a significant advantage compared to other methods. These results collectively highlight the significant advantages of our model in rotational target detection performance and the accuracy of Cobb angle prediction. The smaller parameter size also facilitates clinical deployment and resource conservation. YOLOv8-DSF demonstrates exceptional potential in predicting scoliosis Cobb angles from X-ray images.
Acknowledgments
None.
Footnote
Reporting Checklist: The authors have completed the CLEAR reporting checklist. Available at https://qims.amegroups.com/article/view/10.21037/qims-24-2138/rc
Funding: None.
Conflicts of Interest: All authors have completed the ICMJE uniform disclosure form (available at https://qims.amegroups.com/article/view/10.21037/qims-24-2138/coif). The authors have no conflicts of interest to declare.
Ethical Statement: The authors are accountable for all aspects of the work in ensuring that questions related to the accuracy or integrity of any part of the work are appropriately investigated and resolved. The study was conducted according to the ethical guidelines of Declaration of Helsinki and its subsequent amendments. The study was approved by the Ethics Committee of Henan Provincial People's Hospital (No. 2024-108) and the requirement for individual consent for this retrospective analysis was waived.
Open Access Statement: This is an Open Access article distributed in accordance with the Creative Commons Attribution-NonCommercial-NoDerivs 4.0 International License (CC BY-NC-ND 4.0), which permits the non-commercial replication and distribution of the article with the strict proviso that no changes or edits are made and the original work is properly cited (including links to both the formal publication through the relevant DOI and the license). See: https://creativecommons.org/licenses/by-nc-nd/4.0/.
References
- Lechner R, Putzer D, Dammerer D, Liebensteiner M, Bach C, Thaler M. Comparison of two- and three-dimensional measurement of the Cobb angle in scoliosis. Int Orthop 2017;41:957-62. [Crossref] [PubMed]
- Schreiber S, Parent EC, Hill DL, Hedden DM, Moreau MJ, Southon SC. Patients with adolescent idiopathic scoliosis perceive positive improvements regardless of change in the Cobb angle - Results from a randomized controlled trial comparing a 6-month Schroth intervention added to standard care and standard care alone. SOSORT 2018 Award winner. BMC Musculoskelet Disord 2019;20:319. [Crossref] [PubMed]
- Botterbush KS, Zhang JK, Chimakurty PS, Mercier P, Mattei TA. The life and legacy of John Robert Cobb: the man behind the angle. J Neurosurg Spine 2023;39:839-46. [Crossref] [PubMed]
- Kuklo TR, Potter BK, Polly DW Jr, O'Brien MF, Schroeder TM, Lenke LG. Reliability analysis for manual adolescent idiopathic scoliosis measurements. Spine (Phila Pa 1976) 2005;30:444-54. [Crossref] [PubMed]
- Tanure MC, Pinheiro AP, Oliveira AS. Reliability assessment of Cobb angle measurements using manual and digital methods. Spine J 2010;10:769-74. [Crossref] [PubMed]
- Wu H, Bailey C, Rasoulinejad P, Li S. Automatic Landmark Estimation for Adolescent Idiopathic Scoliosis Assessment Using BoostNet. Springer International Publishing; 2017:127-35.
- Imran A, Huang C, Tang H, Fan W, Cheung K, To M, Qian Z, Terzopoulos D. Fully-Automated Analysis of Scoliosis from Spinal X-Ray Images. 2020 IEEE 33rd International Symposium on Computer-Based Medical Systems (CBMS), Rochester, MN, USA 2020:114-9.
Guo Y Huang X Chen W Nakamoto I Chen H Feng J Wu J. Lumbar Spine Symptom Detection and Automatic Grading Based on Improved Yolov8n. Available online: https://ssrn.com/abstract=4713044.- Zhang S, Wang X, Li P, Wang L, Zhu M, Zhang H, Zeng Z. An Improved YOLO Algorithm for Rotated Object Detection in Remote Sensing Images. Chongqing, China: 2021 IEEE 4th Advanced Information Management, Communicates, Electronic and Automation Control Conference (IMCEC); 2021:840-845. doi:
10.1109/IMCEC51613.2021.9482265 . - Cheng X, Zhang C. C2-YOLO: Rotating Object Detection Network for Remote Sensing Images with Complex Backgrounds. Padua, Italy: 2022 International Joint Conference on Neural Networks (IJCNN); 18-23 July 2022. doi:
10.1109/IJCNN55064.2022.9891999 . - Lin Y, Zhou HY, Ma K, Yang X, Zheng Y. Seg4Reg Networks for Automated Spinal Curvature Estimation. Springer International Publishing; 2020:69-74. doi:
10.1007/978-3-030-39752-4_7 . - Chen K, Peng C, Li Y, Cheng D, Wei S. Accurate Automated Keypoint Detections for Spinal Curvature Estimation. Springer International Publishing; 2020:63-8. doi:
10.1007/978-3-030-39752-4_6 . - Wang MX, Kim JK, Choi JW, Park D, Chang MC. Deep learning algorithm for automatically measuring Cobb angle in patients with idiopathic scoliosis. Eur Spine J 2024;33:4155-63. [Crossref] [PubMed]
- Zhu X, Hu H, Lin S, Dai J. Deformable convnets v2: More deformable, better results. Long Beach, CA, USA: Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition; 2019:9300-8. doi:
10.1109/CVPR.2019.00953 . - Wang CY, Liao HYM, Wu YH, Chen PY, Hsieh JW, Yeh IH. CSPNet: A new backbone that can enhance learning capability of CNN. Seattle, WA, USA: Proceedings of the IEEE/CVF conference on computer vision and pattern recognition workshops; 2020:1571-1580. doi:
10.1109/CVPRW50498.2020.00203 . - Dai J, Qi H, Xiong Y, Li Y, Zhang G, Hu H, et al. Deformable convolutional networks. Venice, Italy: Proceedings of the IEEE international conference on computer vision; 2017:764-773. doi:
10.1109/ICCV.2017.89 . - Chen L, Gu L, Zheng D, Fu Y. Frequency-adaptive dilated convolution for semantic segmentation. Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition; 2024. doi:
10.1109/CVPR52733.2024.00328 . - Kang M, Ting CM, Ting FF, Phan RCW. ASF-YOLO: A novel YOLO model with attentional scale sequence fusion for cell instance segmentation. Image and Vision Computing 2024;147:105057.
- Liu W, Lu H, Fu H, Cao Z. Learning to upsample by learning to sample. Proceedings of the IEEE/CVF International Conference on Computer Vision; 2023. doi:
10.1109/ICCV51070.2023.00554 . - Murrugarra-Llerena J, Kirsten LN, Zeni LF, Jung CR. Probabilistic Intersection-Over-Union for Training and Evaluation of Oriented Object Detectors. IEEE Trans Image Process 2024;33:671-81. [Crossref] [PubMed]
- Jocher G, Chaurasia A, Qiu J. (2023) YOLO by Ultralytics. Available online: https://github.com/ultralytics/ultralytics
- Kingma DP, Ba J. Adam: A method for stochastic optimization. arXiv preprint arXiv:14126980. 2014. 3rd International Conference for Learning Representations, San Diego, 2015.
- Bottou L. Large-Scale Machine Learning with Stochastic Gradient Descent. In: Lechevallier Y, Saporta, G. (eds) Proceedings of COMPSTAT'2010. Physica-Verlag HD. Available online: https://link.springer.com/chapter/10.1007/978-3-7908-2604-3_16#citeas
- Boyd K, Eng KH, Page CD. Area under the Precision-Recall Curve: Point Estimates and Confidence Intervals. In: Blockeel H, Kersting K, Nijssen S, Železný F. editors. Machine Learning and Knowledge Discovery in Databases. ECML PKDD 2013. Lecture Notes in Computer Science(), vol 8190. Berlin: Springer Berlin Heidelberg; 2013:451-66.
- Khanal B, Dahal L, Adhikari P, Khanal B. Automatic Cobb Angle Detection Using Vertebra Detector and Vertebra Corners Regression. In: Cai Y, Wang L, Audette M, Zheng G, Li S. editors. Computational Methods and Clinical Applications for Spine Imaging. CSI 2019. Lecture Notes in Computer Science(), vol 11963. Cham: Springer; 2020:81-7.
- Wang L, Xu Q, Leung S, Chung J, Chen B, Li S. Accurate automated Cobb angles estimation using multi-view extrapolation net. Med Image Anal 2019;58:101542. [Crossref] [PubMed]
- Chen B, Xu Q, Wang L, Leung S, Chung J, Li S. An Automated and Accurate Spine Curve Analysis System. IEEE Access 2019;7:124596-605.
- Dubost F, Collery B, Renaudier A, Roc A, Posocco N, Niessen W, et al. Automated Estimation of the Spinal Curvature via Spine Centerline Extraction with Ensembles of Cascaded Neural Networks. In: Cai Y, Wang L, Audette M, Zheng G, Li S. editors. Computational Methods and Clinical Applications for Spine Imaging. CSI 2019. Lecture Notes in Computer Science(), vol 11963. Cham: Springer; 2020:88-94.
- Horng MH, Kuok CP, Fu MJ, Lin CJ, Sun YN. Cobb Angle Measurement of Spine from X-Ray Images Using Convolutional Neural Network. Comput Math Methods Med 2019;2019:6357171. [Crossref] [PubMed]
- Wang J, Wang L, Liu C. A Multi-task Learning Method for Direct Estimation of Spinal Curvature. In: Cai Y, Wang L, Audette M, Zheng G, Li S. editors. Computational Methods and Clinical Applications for Spine Imaging. CSI 2019. Lecture Notes in Computer Science(), vol 11963. Cham: Springer; 2020:113-8.
- Polzer C, Yilmaz E, Meyer C, Jang H, Jansen O, Lorenz C, Bürger C, Glüer CC, Sedaghat S. AI-based automated detection and stability analysis of traumatic vertebral body fractures on computed tomography. Eur J Radiol 2024;173:111364. [Crossref] [PubMed]





