
Detection-guided deep learning-based model with spatial regularization for lung nodule segmentation
Introduction
Lung cancer has been one of the deadliest forms of cancer throughout the 20th century. In 2023, it accounted for the second-highest number of new cancer cases and remained the leading cause of cancer-related deaths (1). Early-stage lung cancer often presents with no clear symptoms, making lung nodules critical markers for identifying the disease. Consequently, the early detection of lung nodules is paramount for the prompt diagnosis and treatment of lung cancer, significantly enhancing the chances of patient survival. Computed tomography (CT) imaging plays a pivotal role in the early detection of lung tumors, providing radiologists with the ability to identify and examine suspicious lesions at their most treatable stage. Typically, CT scans are initially reviewed by radiologists to check for the presence of nodules, which are then categorized as benign or malignant based on their size, shape or its appearance over time. This process, however, can be time-consuming and labor-intensive, often involving the review of hundreds or even thousands of image slices per scan, and may lead to varying interpretations among different radiologists. Image segmentation techniques offer a solution by precisely delineating nodules from the surrounding lung tissue, offering valuable data on their size, shape, and growth rate. Therefore, the development of accurate and automated lung nodule segmentation methods is crucial. These technologies not only assist radiologists in the identification and classification of nodules but also significantly reduce their workload, and have the potential to increase efficiency, leading to improved diagnostic accuracy and patient care.
In recent decades, various medical image segmentation methods have been developed, enhancing the precision of medical diagnoses. Thresholding techniques segregate an image into two parts using a predefined intensity threshold (2,3). Morphology methods (4) leverage predefined shapes scanning images to identify areas that closely match these criteria for segmentation. Variational techniques minimize specific energy functions to ensure the segmented boundaries align accurately with the image’s target structures, exemplified by the Mumford-Shah model (5). The Chan-Vese method is a special case of the Mumford-Shah model that uses level sets to segment images that do not necessarily have clear edges (6,7). Graph cut methods represent an image as a weighted undirected graph and employ algorithms to enhance sub-graph similarity while distinguishing between different sub-graphs (8,9). Recent advancements also include unsupervised machine learning techniques like K-means (10), k-Nearest Neighbor (KNN) (11), and probabilistic models (12), further broadening the toolkit available for medical image segmentation.
With the advancement of computer technology, deep learning models, particularly convolutional neural networks (CNNs) (13) have surpassed traditional methods in efficacy across numerous computer vision tasks. Traditional techniques often depend on manual feature selection and prior knowledge, whereas deep learning models autonomously learn to extract relevant features directly from data. Among these, U-Net (14) has become a benchmark model in medical image segmentation for its efficiency and simplicity. This model utilizes an encoder-decoder framework with added skip connections, allowing for the detailed capture and preservation of spatial data. The encoder reduces feature dimensions to capture hierarchical information, while the decoder restores these features to their original resolution. The skip connections help preserve spatial information and aid in the precise localization of structures. The U-Net based methods, such as ResUNet (15) and ResUNet++ (16), further enhances segmentation accuracy. Concurrently, semantic segmentation models like DeepLab (17,18) have set new standards on public datasets for semantic segmentation like PASCAL VOC 2012 (19) by incorporating structures such as Xception (20) and atrous spatial pyramid pooling (ASPP) (17), showing potential for application in medical images. These developments underscore the potential of deep learning models for medical image analysis.
While numerous lung nodule segmentation methods have been introduced, the task remains daunting. A primary challenge is the limited size of clinical datasets for lung nodule segmentation, as nodules are infrequent compared to the prevalence of normal lung tissue in imaging studies. Additionally, lung nodules exhibit a wide variety in shape, size, and attenuation, complicating their classification and segmentation. Generally, lung nodules can be classified into several types: isolated nodules, juxtapleural nodules, cavitary nodules, ground-glass opacity (GGO) nodules, and calcific nodules (21). As depicted in Figure 1, juxtapleural nodules are connected to the lung pleura and chest wall and exhibit similar attenuation to it. Cavitary nodules pose challenges for accurate segmentation due to variations in attenuation in the setting of central lucency. Calcific and GGO nodules display high and low attenuation values, respectively. Moreover, the presence of numerous small nodules, which can fall into any of these categories, adds another layer of complexity to achieving accurate segmentation. Given the predominance of small size of nodules within clinical datasets relative to the size of CT scans, our approach concentrates on segmenting small regions of interest (ROI) around these nodules. Focusing on ROIs, identified either by radiologists or automated systems, allows for the prioritization of suspect nodules for in-depth analysis and clinical decision-making. It is usually integrated with computer-aided detection (CAD) systems, which allows for streamlined workflows and enables more precise delineation of nodules and more efficient utilization of computational resources in automated nodule detection and analysis. Such targeted efficiency is vital in clinical environments where swift diagnostic and treatment decision-making are paramount for radiologists.

In the field of deep learning, several strategies have been developed to overcome segmentation challenges and address the scarcity of training data. Recent innovations include applying transfer learning (TL) from extensive datasets (22,23), multitask learning to leverage shared features across tasks like classification and segmentation (24), and employing data augmentation, cross-validation, and regularization to mitigate overfitting.
This paper presents a multitask deep learning model that unites segmentation and classification tasks, leveraging shared information through feature combination blocks. The model undergoes pre-training on the large-scale public LUNA16 dataset before adapting to a smaller, private clinical dataset through an optimal TL strategy and enhancement by spatial regularization. The key contributions of this paper include:
- We propose a multitask model that enhances segmentation performance through integrated classification features;
- We introduce a feature combination block for efficient, flexible feature utilization without information loss, avoiding unnecessary upsampling and downsampling;
- We apply soft threshold dynamic (STD) regularization for refined segmentation predictions, incorporating classification outputs as prior information for enhanced segmentation accuracy;
- We adopt an optimal TL strategy facilitating effective use of pre-training data for segmentation on a smaller clinical dataset;
- Our results demonstrate the superiority of our model over other classic medical image segmentation models, supported by experimental evidence of improved performance through feature combination, spatial regularization, and TL.
The remaining part of this paper is organized as follows: In Methods, we introduce the datasets and explain the proposed methodology. In Results, we present our experimental results including comparative study, experiments of TL and ablation study. In Discussion, we discuss related literature studies and limitations of our methods. In Conclusion, we summarize the proposed method and conclude this work. We present this article in accordance with the CLEAR reporting checklist (available at https://qims.amegroups.com/article/view/10.21037/qims-2024-2511/rc).
Methods
Dataset
The study was conducted in accordance with the Declaration of Helsinki and its subsequent amendments. Two kinds of datasets are used in our experimental evaluation: one for pre-training, and the other one for TL and performance evaluation. Because the annotated clinical lung nodule dataset is typically limited in size, we use the public Lung Nodule Analysis 2016 (LUNA16) dataset (25) for pre-training. This dataset is a subset of the LIDC-IDRI dataset (26), containing 1,018 CT scans annotated by four radiologists. In LUNA16, scans thicker than 3 mm and those with inconsistent slice spacing or missing slices were removed, resulting in 888 scans (25). For each scan, multiple annotations were merged so that their positions and diameters were averaged. Our method focuses on segmenting lung nodules within a predefined region of interest (ROI) containing lung nodules. In total, we obtained 2,523 nodules. For each nodule, we found the location of the centroid and then cropped a three-dimensional (3D) region centered around the centroid so that each cropped region contained only one nodule. The first two dimensions of the 3D region are 128×128 and the third dimension depends on the lesion size. Note the proposed method is based on two-dimensional segmentation and some 2D slices without nodule are retained for pre-training.
We evaluated the performance of the proposed method on a small lung nodule dataset from Cleveland Clinic Foundation (CCF). It is collected from 7 patients and annotated by one radiologist. Similarly, 3D regions (128×128 along the first two dimensions) were cropped around each lesion without overlap. In total, the dataset from 7 patients consists of 56 lesions, 45 of which were randomly selected and used for training and 5-fold cross-validation. The remaining 11 lesions were used as a testing set for performance evaluation. In the CCF dataset, each CT scan typically contains hundreds of slices, while lung nodules only appear in about ten slices. Since the proposed model is 2D-based and has a classification component, most slices without nodules are excluded from the dataset but we do keep some slices that have no nodules to train the classifier. Some empty slices adjacent to the lung nodule are retained so that the ratio of slices with and without nodules is balanced. This resulted in a total of 814 slices remaining after the clean-up.
The image intensity of the LUNA16 dataset ranged from 0 to 255, while the intensity of the CCF dataset ranged from 0 to 1,000. To make the pre-trained model compatible with TL, both datasets were normalized according to the equation below so that their intensities are between 0 and 1. Additionally, we applied random flips in the data augmentation process.
Model architecture
The proposed multitask model aims to leverage classification information to improve the segmentation performance. The architecture is illustrated in Figure 2, and the size of the output of each block is also shown. The orange blocks (C1–C5) correspond to a ResNet-50 binary classifier whose final activation function is Sigmoid. In our model, the classifier learns to output a score between zero and one, representing the probability of the existence of a nodule. Because the classification task is relatively simpler than segmentation, we choose ResNet-50 to guarantee efficiency without losing accuracy. The blue blocks (S1–S9) correspond to a ResU-Net based segmentation model. The original ResU-Net model (15) consists of an encoder (blocks S1 to S5) and a decoder (blocks S6 to S9). In the encoder part, the size of the features gets smaller gradually and the number of channels gets larger to capture some high-level features. This means the encoder part works similarly to ResNet-50, and therefore it is appropriate to combine the features of ResNet-50 and the U-Net encoder. The feature combination blocks are represented by green arrows in Figure 2, which will be introduced later. Finally, after getting the classification output, we embed it into the sigmoid layer before the segmentation output. Different from feature combination, we expect the classification output to affect the segmentation output.

In the model, we modified the ResU-Net to achieve better performance. Originally, each ResU-Net block includes two BN-ReLU-Conv blocks (a batch normalization layer, a ReLU, and a convolution layer). The first convolution layer has a stride of 2 to reduce the size of features. We replaced it with a depth-wise separable convolutional layer used in Xception modules (20) to reduce computational cost and improve performance. This decomposition involves splitting the standard 3×3 convolutional layer into a 3×3 channel-wise spatial convolution followed by a 1×1 point-wise convolution. Additionally, inspired by ResUNet++ (16), we added an ASPP module respectively at the end of the encoder and decoder (S5 and S9), which can also significantly improve performance. ASPP typically consists of four atrous convolutions with different dilation rates to help increase the receptive field and capture multi-scale information. It is suggested that the dilation rates should not have common factor relationships like 2, 4, 8, etc. (27), so we chose dilation rates of 1, 5, 10, and 15.
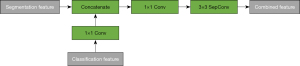
Feature combination block
Since we expect the multitask model to leverage the features of the classification model in order to improve the performance of the segmentation model, it is necessary to design an appropriate scheme to merge the classification and segmentation features. In our method, we only combine the features with the same size so that there is no up-sampling and down-sampling. Therefore, the combination strategy is flexible and depends on the specific model architecture. The combined blocks are indicated in Figure 3, in which the final layers are used as the combined feature. Instead of concatenating two features directly, we first let the classification feature go through a 1×1 convolutional layer (the number of output channels is equal to that of the input channel) so that it is transformed into a segmentation feature. Then the two features are concatenated. We apply another 1×1 convolutional layer so that the number of channels is reduced to the number of segmentation channels. Because the number of channels of the input features remains unchanged, the second 1×1 convolutional layer will learn to fuse the concatenated features. Finally, the combined feature is fed into a 3×3 depth-wise separable convolutional layer with the same number of input and output channels, which is the number of segmentation channels.
Embedded STD regularization
Apart from feature combination, we utilize the result of classification as spatial regularization to improve segmentation. To combine the deep learning framework with spatial regularization, Liu et al. (28,29) provided variational explanations for some widely used activation functions in deep learning, including softmax, ReLU, and sigmoid. For instance, the sigmoid function can be expressed as: and it can be represented as the argument that solves the following convex optimization problem when the parameter ε is equal to 1:
Where is the feature map input and means the inner product of a and b. The optimal solution x will be equal to Sig(u/ε), which can be proved by simply computing the derivative of the energy function. One can easily add regularization terms used in image processing and computer vision to achieve smoothness. STD (30) regularization was adopted to control the length of the boundary so the edges have little smoothness instead of being bumpy:
where means convolution, k represents a discrete Gaussian kernel with standard deviation σ and λ is a parameter. The STD regularization term has been proved to approximate the boundary length (31) and has a similar effect as total variation (TV) regularization. It involves convolution and inner product operation, which are cheaper to compute. Compared to TV regularization, which is non-smooth, STD regularization is more efficient in deep learning due to its smooth nature, making it compatible with neural networks and easier to solve. Furthermore, the new term (last term) is concave so that problem in (Eq. [3]) can be solved with an efficient and iterative algorithm. Given the input u which is the output of the last hidden layer, the initial value x0 can be set as x0=Sig(u). Then for each t-th step, the value of the next step can be computed as:
It is important to note that the network with STD regularization differs from post-processing methods like conditional random fields (CRF) because it is integrated into the back-propagation process and influences gradient updating. In practice, parameters such as ε, λ, and σ can be made learnable, allowing them to be automatically tuned by the neural network.
Combining the classification output with STD regularization, the new optimization problem can be expressed as in (Eq. [5]). Suppose the classification output is denoted as c which is between zero and one, representing the probability that the patch contains nodule(s). When c=0 there is no nodule in the patch and when c=1 there is at least one nodule. We add a new term to the STD regularization. Note measures the size/volume of the nodule. When c is close to 0, the classification indicates a low probability of having nodules and the additional term controls the size of the nodules. On the other hand, when c is close to or equal to one, the classifier is confident that there is something resembling a nodule. In this case, 1–c is small, and has almost no effect. Thus, the new term has the effect of reducing the size of the nodule in the prediction if the classification indicates a high chance of not having nodules (c being close to or equal to 0). This is very helpful in reducing false positives and avoiding identifying other tissues as nodules. It effectively combines classification output into segmentation to help improve segmentation results. In the neural network, the c in (Eq. [5]) is excluded from backpropagation to avoid affecting the classification result.
Both λ1 and σ control the effect of smoothness. When we use STD regularization in our models, we set λ1 to be equal to one and tune λ2 and σ automatically. Since the new term and its derivatives are constant, the solution of (Eq. [5]) is efficient and similar to that of (Eq. [3]). The new iterative scheme is shown in (Eq. [6]). The initial value could be set as Sig(u), and x will converge quickly within ten steps.
Implementation details
We implemented our model using an NVIDIA GeForce RTX 3080 Laptop GPU. First, we pre-trained the model with the LUNA16 dataset for 200 epochs with a batch size of 10. The initial learning rate was set to 0.001 without decay. Then, we trained the model with the CCF dataset for 50 epochs with a batch size of 10, which was sufficient considering its small size. The initial learning rate was 0.001 with a decay of 0.75 for every five epochs. We used Adam as the optimizer with a weight decay of 1e−8. The loss function for segmentation was a combination of binary cross-entropy (BCE) and Dice loss. The binary classification also used BCE loss. During model training, the overall loss was calculated as follows:
In our experiments, both λ1 and λ2 were set to be one.
To utilize the information learned from LUNA16, we conducted a series of experiments to determine the most effective TL strategy. We concluded that the best results are achieved when the model is fully fine-tuned, meaning no layers are frozen. Additionally, STD regularization was not applied during pre-training.
Evaluation metrics
To ensure a comprehensive evaluation of the models’ performance, we employ several commonly used metrics: precision (positive predictive value or PPV), sensitivity (or recall), Dice score (also called F1 score), and intersection over union (IoU). In the case of binary segmentation, they are defined as follows:
where TP represents true positive, i.e., the number of truly classified pixels whose true values are positive. Similarly, TN, FP, and FN are true negative, false positive, and false negative. Suppose the truth value of the lung nodule area is positive and that of the non-infected is negative, precision measures the accuracy rate of nodules in terms of prediction. Sensitivity measures the accuracy rate of nodules in terms of ground truth. Dice score combines precision and sensitivity, measuring the similarity between the predicted lung infections and the ground truth. IoU is another metric measuring the similarity of two finite sets, defined as their intersection divided by their union. In some cases, IoU is also related to volumetric overlap error (VOE) by IoU = 1 − VOE.
Another widely used evaluation metric in medical image segmentation is Hausdorff distance (HD), measuring the maximum distance from points in one contour to the closest point in the other contour. It provides a straightforward metric for comparison between the segmented region and the ground truth. Suppose the contours of the prediction and ground truth domains are X and Y, their HD is defined as
where is defined as and is computed with Euclidean distance in our experiments.
To comprehensively evaluate the results, we also use average symmetric surface distance (ASSD), which quantifies the average distance between the surfaces of two segmented objects. Compared to HD, it measures how well the boundary of the segmented object and the ground truth align with each other on average. It is defined as
where |X| means the length of the contour X.
Results
Comparative study
To evaluate the performance of our proposed model, we first compared our model without TL with other commonly used segmentation models. The average performance of each model on the CCF dataset is shown in Table 1. We observe that our model outperforms other models in terms of precision, Dice score, IoU and ASSD. While the proposed model achieves a relatively low sensitivity, our precision value is significantly higher than others and therefore gets the best overall performance.
Table 1
| Model | Precision | Sensitivity | Dice | IoU | HD (mm) | ASSD (mm) |
|---|---|---|---|---|---|---|
| UNet | 0.832 | 0.821 | 0.753 | 0.688 | 4.591 | 0.341 |
| ResUNet | 0.821 | 0.855† | 0.779 | 0.708 | 3.594 | 0.290 |
| ResUNet++ | 0.844 | 0.845 | 0.777 | 0.712 | 3.784 | 0.303 |
| DeepLabv3+ | 0.802 | 0.831 | 0.748 | 0.658 | 3.318 | 0.265 |
| Proposed model | 0.870† | 0.827 | 0.801† | 0.735† | 2.929† | 0.211† |
†, the best performance. ASSD, average symmetric surface distance; CCF, Cleveland Clinic Foundation; HD, Hausdorff distance; IoU, intersection over union.
We also visualized the segmentation results for comparison. We demonstrate four examples of the CCF dataset from different patients in Figure 4 with the prediction of the compared models and corresponding dice scores of them. The first example is a typical juxtapleural nodule with some heterogeneous attenuation. Although all five models successfully identified it, UNet, ResUNet and ResUNet++ captured the parts with relatively higher intensity and resulted in lower Dice scores. In the second example, UNet and ResUNet failed to identify the tiny nodule, while our model segmented the nodule accurately. In the third and fourth examples, our model captured the shapes of the nodules accurately resulting in the best Dice score among the models.

Experiments for TL strategies
During pre-training, the neural network model learns useful feature representations from the large datasets. Therefore, the parameters of some layers are usually frozen during the training process to prevent them from being updated based on the gradients computed from the loss function. By freezing some layers, the learned features are not overwritten during the fine-tuning process. Additionally, freezing layers can reduce computational cost and the risk of overfitting since there are fewer parameters to update. The choice of which layers to freeze depends on factors such as the similarity between the small and large datasets. In an encoder-decoder based model, the early convolutional layers in the encoder block are typically responsible for extracting low-level features like edges and textures, which are often generalizable across different datasets. These layers can be frozen if the pre-trained weights are from a dataset similar to the target training data. The final layers in the encoder block can capture high level and task-specific features, and the decoder layers are responsible for upsampling and combining features from different resolutions.
To ensure the best result using TL, we conducted experiments to determine the optimal TL strategy, as shown in Table 2. We froze S1 (the first segmentation encoder block), S5 (the last segmentation encoder block), S9 (the final segmentation decoder block), and C1 (the first classification block). Since both the pre-training and the fine-tuning involve binary classification, we also tested the case when freezing C5 (the fully connected layer of the classification part). The results in Table 2 indicate that fully fine-tuning without freezing any layers outperforms all the other strategies, demonstrating that there are essential differences between LUNA16 and the CCF dataset. However, the ablation study in the next section shows that the model still benefits from pre-training on LUNA16.
Table 2
| Model | Precision | Sensitivity | Dice | IoU | HD (mm) | ASSD (mm) |
|---|---|---|---|---|---|---|
| W/o freezing | 0.828 | 0.885 | 0.814† | 0.744† | 3.188† | 0.280† |
| Freeze S1 | 0.804 | 0.889† | 0.798 | 0.728 | 3.611 | 0.310 |
| Freeze S5 | 0.817 | 0.888 | 0.810 | 0.741 | 3.608 | 0.296 |
| Freeze S9 | 0.879† | 0.709 | 0.708 | 0.627 | 4.644 | 0.401 |
| Freeze C1 | 0.824 | 0.879 | 0.802 | 0.734 | 3.394 | 0.287 |
| Freeze C5 | 0.815 | 0.884 | 0.799 | 0.728 | 3.226 | 0.295 |
Ablation study
We conducted an ablation study to assess the effect of each component in our model, as presented in Table 3, in which the backbone means the blocks C1–C5 and S1–S9 in Figure 2. In the first row, we implemented the proposed backbone without feature combination blocks and STD regularization. This means the segmentation part works independently without being combined with classification. The results show a Dice score of 0.755, a HD of 3.509 mm, and an ASSD of 0.276 mm. In the second row, we implemented the proposed model without STD regularization and observed better performance in all metrics except ASSD. This highlights the improvement brought by the feature combination blocks. In the third row, we applied STD regularization into our model but set the value of λ2 in (Eq. [5]) as zero to show the effect of the third term in (Eq. [5]). Comparing the second and third rows, it is evident that STD regularization leads to a noticeable improvement in precision and Dice score. In the fourth row, we implemented the model to show the effect of the fourth term in (Eq. [5]). Compared with the second and the third rows, all the metrics except sensitivity are significantly improved. Finally, we applied the TL strategy in our model, achieving a Dice score of 0.814 and IoU of 0.744. Although TL leads to slightly worse HD and ASDD, it again shows the difference between the two datasets and that the model still benefits from TL.
Table 3
| Model | Precision | Sensitivity | Dice | IoU | HD (mm) | ASSD (mm) |
|---|---|---|---|---|---|---|
| Backbone w/o combination | 0.820 | 0.848 | 0.755† | 0.693† | 3.509† | 0.276† |
| Backbone w/o STD | 0.823 | 0.849† | 0.764 | 0.704 | 4.020 | 0.285 |
| Backbone + STD with λ2=0 | 0.846 | 0.847 | 0.787 | 0.720 | 3.927 | 0.287 |
| Backbone + STD | 0.870† | 0.827 | 0.801 | 0.735 | 2.929 | 0.211 |
| Backbone + STD + TL | 0.828 | 0.885 | 0.814 | 0.744 | 3.188 | 0.280 |
Discussion
In this study we propose a multitask model with TL for lung nodule segmentation, which outperforms other methods. Multitask learning is a technique in which a model is trained to perform multiple tasks simultaneously. By leveraging information from related tasks, multitasking learning can improve performance and generalization ability, which is helpful when training data is limited. Additionally, multitask learning can serve as a form of regularization by introducing additional constraints on the model.
When training a multitask model, it is essential to combine the features of different tasks to allow them to share information; otherwise, the tasks would operate independently. The feature combination, or information fusion scheme, usually depends on the architecture of deep neural networks. Conventional multitask models with a single channel (32,33) typically share parameters across different tasks in the hidden layers. The final outputs include predictions for different tasks, which may be generated in the middle or final layers of the model. However, tasks in computer vision, such as segmentation, detection, and classification, often emphasize different feature types. Sharing too many parameters could limit the model’s performance across tasks. To address this issue, some models (34) split the single channel into double channels for two tasks or use separate architectures (24). Misra et al. (35) evaluated the performance of two-task architectures split at different layers and concluded that the optimal multitask architecture depends on the individual tasks. It is essential to design feature combination blocks for split architecture so that the multiple tasks can share information and improve each other, otherwise the different tasks will work separately. Pure concatenation and linear combination (35) were naturally used and showed positive effects. Another way is to apply more hidden layers in feature combination blocks. The model in (24) upsampled the smaller feature so that the features have the same size and can be combined. However, like down-sampling, up-sampling could also cause loss of information because it involves replicating or interpolating existing information to fill in the gaps.
In our feature combination blocks, we avoid up-sampling and down-sampling by only combining the features with the same size. Before concatenating, we apply one more hidden layer to transform the classification feature to segmentation feature. Apart from feature combination, we incorporate the classification output into the spatial regularization of the segmentation output, which enables us to further utilize the multitask results and enhance interoperability.
While our model demonstrates promising results, there remains ample room for improvement, particularly when applied to small clinical datasets. Our model, especially the classification component, is designed to be simple and efficient for such datasets. However, we recognize that there is considerable flexibility in altering both the classification and segmentation components. The model is expected to be improved by combining other more advanced encoder-decoder based models. Additionally, the spatial regularization may need to be modified to further enhance the model’s performance on specific datasets. Currently the spatial regularization is designed to make the boundary smooth and reduce noise, and the classification output is used to control the overall size of the output. If the proposed model is applied to data other than lung nodule such as cartilage and vessel, we may not need smoothness but other spatial priors like connectivity or shape priors.
Conclusions
In this paper, we present a multitask deep learning model designed and implemented for segmenting small clinical lung nodule datasets. Our model integrates segmentation and classification components through feature combination blocks to facilitate information sharing between the two tasks. We incorporate spatial regularization adaptively guided by the classification output in the segmentation process. Additionally, we employ TL by pre-training the model on LUNA16, a large public dataset. Our experimental results demonstrate that the proposed model surpasses other classic models in the clinical dataset. We conduct a series of experiments by freezing different hidden layers during fine-tuning to determine the optimal TL strategy. Furthermore, our ablation study showcases the enhancements provided by various components within our model.
Acknowledgments
None.
Footnote
Reporting Checklist: The authors have completed the CLEAR reporting checklist. Available at https://qims.amegroups.com/article/view/10.21037/qims-2024-2511/rc
Funding: This work was supported by
Conflicts of Interest: All authors have completed the ICMJE uniform disclosure form (available at https://qims.amegroups.com/article/view/10.21037/qims-2024-2511/coif). M.Y. serves as an unpaid editorial board member of Quantitative Imaging in Medicine and Surgery. The other authors have no conflicts of interest to declare.
Ethical Statement: The authors are accountable for all aspects of the work in ensuring that questions related to the accuracy or integrity of any part of the work are appropriately investigated and resolved. The study was conducted in accordance with the Declaration of Helsinki and its subsequent amendments.
Open Access Statement: This is an Open Access article distributed in accordance with the Creative Commons Attribution-NonCommercial-NoDerivs 4.0 International License (CC BY-NC-ND 4.0), which permits the non-commercial replication and distribution of the article with the strict proviso that no changes or edits are made and the original work is properly cited (including links to both the formal publication through the relevant DOI and the license). See: https://creativecommons.org/licenses/by-nc-nd/4.0/.
References
- Siegel RL, Miller KD, Wagle NS, Jemal A. Cancer statistics, 2023. CA Cancer J Clin 2023;73:17-48. [Crossref] [PubMed]
- Otsu N. An automatic threshold selection method based on discrimination and least squares criteria. Trans Inst Electr Comm Eng Jpn 1980;D63:349-56.
- Wellner PD. Adaptive thresholding for the digitaldesk. Xerox, EPC1993-110 404 1993.
- Zana F, Klein JC. Segmentation of vessel-like patterns using mathematical morphology and curvature evaluation. IEEE Trans Image Process 2001;10:1010-9. [Crossref] [PubMed]
- Mumford DB, Shah J. Optimal approximations by piecewise smooth functions and associated variational problems. Commun Pure Appl Math 1989;577-685. [Crossref]
- Chan T, Vese L. An active contour model without edges. International Conference on Scale-space Theories in Computer Vision 1999:141-51.
- Chan TF, Vese LA. Active contours without edges. IEEE Trans Image Process 2001;10:266-77. [Crossref] [PubMed]
- Yi F, Moon I. Image segmentation: A survey of graph-cut methods. 2012 International Conference on Systems and Informatics (ICSAI2012) 2012:1936-41.
- Irshad H, Veillard A, Roux L, Racoceanu D. Methods for nuclei detection, segmentation, and classification in digital histopathology: a review—current status and future potential. IEEE Rev Biomed Eng 2013;7:97-114. [Crossref] [PubMed]
- Dhanachandra N, Manglem K, Chanu YJ. Image segmentation using k-means clustering algorithm and subtractive clustering algorithm. Procedia Comput Sci 2015;54:764-71. [Crossref]
- Rangel BM, Fernández MA, Murillo JC, Ortega JC, Arreguín JM. KNN-based image segmentation for grapevine potassium deficiency diagnosis. 2016 International Conference on Electronics, Communications and Computers (CONIELECOMP) 2016:48-53.
- Cuadra MB, Cammoun L, Butz T, Cuisenaire O, Thiran JP. Comparison and validation of tissue modelization and statistical classification methods in T1-weighted MR brain images. IEEE Trans Med Imaging 2005;24:1548-65. [Crossref] [PubMed]
- Krizhevsky A, Sutskever I, Hinton GE. ImageNet classification with deep convolutional neural networks. Advances in Neural Information Processing Systems 2012;
- Ronneberger O, Fischer P, Brox T. U-net: Convolutional networks for biomedical image segmentation. Medical Image Computing and Computer-assisted Intervention-MICCAI 2015: 234-41.
- Zhang Z, Liu Q, Wang Y. Road extraction by deep residual u-net. IEEE Geosci Remote Sens Lett 2018;15:749-53. [Crossref]
- Jha D, Smedsrud PH, Riegler MA, Johansen D, De Lange T, Halvorsen P, Johansen HD. Resunet++: An advanced architecture for medical image segmentation. 2019 IEEE International Symposium on Multimedia (ISM) 2019. doi:
10.1109/ISM46123.2019.00049 .10.1109/ISM46123.2019.00049 - Chen LC, Papandreou G, Kokkinos I, Murphy K, Yuille AL. DeepLab: Semantic Image Segmentation with Deep Convolutional Nets, Atrous Convolution, and Fully Connected CRFs. IEEE Trans Pattern Anal Mach Intell 2018;40:834-48. [Crossref] [PubMed]
- Chen LC, Zhu Y, Papandreou G, Schroff F, Adam H. Encoder-decoder with atrous separable convolution for semantic image segmentation. Proceedings of the European Conference on Computer Vision (ECCV) 2018:801-18.
- Everingham M, Winn J. The pascal visual object classes challenge 2012 (voc2012) development kit. Pattern Analysis, Statistical Modelling and Computational Learning. Tech Rep 2011;8:2-5.
- Chollet F. Xception: Deep learning with depth-wise separable convolutions. Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition 2017:1251-8.
- Liu H, Cao H, Song E, Ma G, Xu X, Jin R, Jin Y, Hung CC. A cascaded dual-pathway residual network for lung nodule segmentation in CT images. Phys Med 2019;63:112-21. [Crossref] [PubMed]
- Liu J, Dong B, Wang S, Cui H, Fan DP, Ma J, Chen G. COVID-19 lung infection segmentation with a novel two-stage cross-domain transfer learning framework. Med Image Anal 2021;74:102205. [Crossref] [PubMed]
- Riaz Z, Khan B, Abdullah S, Khan S, Islam MS. Lung Tumor Image Segmentation from Computer Tomography Images Using MobileNetV2 and Transfer Learning. Bioengineering (Basel) 2023;10:981. [Crossref] [PubMed]
- Wu YH, Gao SH, Mei J, Xu J, Fan DP, Zhang RG, Cheng MM. JCS: An Explainable COVID-19 Diagnosis System by Joint Classification and Segmentation. IEEE Trans Image Process 2021;30:3113-26. [Crossref] [PubMed]
- Setio AAA, Traverso A, de Bel T, Berens MSN, Bogaard CVD, Cerello P, et al. Validation, comparison, and combination of algorithms for automatic detection of pulmonary nodules in computed tomography images: The LUNA16 challenge. Med Image Anal 2017;42:1-13. [Crossref] [PubMed]
- Armato SG 3rd, McLennan G, Bidaut L, McNitt-Gray MF, Meyer CR, Reeves AP, et al. The Lung Image Database Consortium (LIDC) and Image Database Resource Initiative (IDRI): a completed reference database of lung nodules on CT scans. Med Phys 2011;38:915-31. [Crossref] [PubMed]
- Wang P, Chen P, Yuan Y, Liu D, Huang Z, Hou X, Cottrell G. Understanding convolution for semantic segmentation. 2018 IEEE Winter Conference on Applications of Computer Vision (WACV) 2018:1451-60.
- Liu J, Wang X, Tai XC. Deep convolutional neural networks with spatial regularization, volume and star-shape priors for image segmentation. J Math Imaging Vis 2022;64:625-45. [Crossref]
- Jia F, Liu J, Tai XC. A regularized convolutional neural network for semantic image segmentation. Anal Appl 2021;19:147-65. [Crossref]
- Esedoḡ Lu S, Otto F. Threshold dynamics for networks with arbitrary surface tensions. Commun Pure Appl Math 2015;68:808-64. [Crossref]
- Zhang J, Guo W. A New Regularization for Deep Learning-Based Segmentation of Images with Fine Structures and Low Contrast. Sensors (Basel) 2023;23:1887. [Crossref] [PubMed]
- Tjon E, Moh M, Moh TS. Eff-ynet: A dual task network for deepfake detection and segmentation. 2021 15th International Conference on Ubiquitous Information Management and Communication (IMCOM) 2021:1-8.
- Shen T, Gou C, Wang J, Wang FY. Simultaneous segmentation and classification of mass region from mammograms using a mixed-supervision guided deep model. IEEE Signal Process Lett 2019;27:196-200. [Crossref]
- He K, Lian C, Zhang B, Zhang X, Cao X, Nie D, Gao Y, Zhang J, Shen D. HF-UNet: Learning Hierarchically Inter-Task Relevance in Multi-Task U-Net for Accurate Prostate Segmentation in CT Images. IEEE Trans Med Imaging 2021;40:2118-28. [Crossref] [PubMed]
- Misra I, Shrivastava A, Gupta A, Hebert M. Cross-stitch networks for multi-task learning. Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition 2016:3994-4003.


