
Enhancing perihematomal edema segmentation: integrating prior knowledge with deep learning for enhanced accuracy and interpretability
Introduction
Spontaneous intracerebral hemorrhage (SICH) is a prevalent subtype of intracranial hemorrhage, typically occurring in the basal ganglia region, with a mortality rate reaching up to 40% (1,2). Even among survivors, the disability rate remains high (3). SICH is caused by the rupture of a blood vessel within the brain parenchyma, leading to blood leakage into the surrounding tissues. This condition results in the formation of a hematoma, accompanied by varying degrees of perihematomal edema (PHE) in the adjacent brain tissue. Studies have demonstrated that PHE, as a significant secondary injury following SICH, is closely associated with the functional outcomes of patients with SICH (4). Therefore, accurate segmentation of PHE is clinically crucial for evaluating patient prognosis and formulating treatment plans. Specifically, accurate PHE segmentation provides rich PHE characterization information, which is critical for clinicians when choosing intervention modalities such as surgical decompression or pharmacological management to reduce intracranial pressure. Through timely diagnosis and effective utilization of this precise PHE characterization information, the progression and severity of PHE can be better controlled, thereby reducing mortality and preventing intracranial hypertension and cerebral hernia. However, although computed tomography (CT) is the most commonly used imaging diagnostic tool for patients with SICH, localizing the PHE region on CT images is extremely challenging. In CT images, hemorrhagic regions typically appear as high-signal bright zones that contrast sharply with the surrounding tissues, whereas PHE is depicted as a low-density region with low contrast against the surrounding tissues, increasing the difficulty of segmentation. Additionally, the morphology and location of PHE within the skull are highly complex, and there is a significant overlap in CT values between PHE regions and other brain tissues, such as cerebrospinal fluid and microangiopathy (5,6). These factors make manual segmentation of PHE very challenging, limiting its widespread application in clinical trials and large-scale population studies.
In order to address the problem of PHE segmentation, researchers have proposed several automatic or semi-automatic segmentation methods. One of the earliest approaches was introduced by Loncaric et al. (7), which employs iterative morphological processing for PHE segmentation. Bardera et al. (8) utilized a novel level set method for this purpose. Chen et al. (9) proposed a method based on region growing edema clustering, specifically designed for segmenting PHE in SICH patients. Loncaric et al. (10) introduced a combination of fuzzy clustering and image labeling algorithms for PHE segmentation of CT images, which was later enhanced into a fuzzy expert system (11). In recent years, with the rapid advancement of technological innovation, image processing technology has made significant progress (12). Coupled with breakthroughs in neural networks for medical image analysis (13-15), several deep learning (DL)-based methods have been proposed. Ironside et al. (16) utilized U-Net (17) for PHE segmentation, achieving mean volumetric Dice similarity coefficients (DSC) of 0.838±0.294 and 0.843±0.293 with manual and semi-automated segmentation methods as reference standards, respectively, for the fully automated segmentation algorithm. However, the performance fluctuates significantly, with a standard deviation of nearly 0.3. Similarly, Dhar et al. (18) reported a median DSC score of 0.54 for PHE segmentation, with an interquartile range (IQR) of 0.39 to 0.65. The quantitative results reported above further underscore the challenging nature of pixel-by-pixel PHE segmentation on CT images. Despite the progress made by these methods, there are still many challenges in accurately delineating PHE boundaries. This is mainly attributed to the low contrast between PHE and surrounding tissues and overlapping CT values. These issues lead to less than consistent segmentation results, which may affect the reliability of clinical decisions and limit the application of these methods in daily clinical practice.
From the above, it is evident that DL methods still encounter significant challenges in PHE segmentation. It is crucial to recognize that SICH is not a monophasic event that ceases immediately. The hematoma continues to expand during the first 24 hours post-onset (19). The final intracranial hemorrhage results from hematoma expansion. A widely accepted explanation for the mechanism of hematoma expansion is the Fisher model of neuropathology (20). Fisher proposed that the final hematoma in an intracranial hemorrhage is caused by secondary shearing between adjacent blood vessels, where one ruptured blood vessel triggers subsequent bleeding. Additionally, blood flows in various directions from ruptured blood vessels into the cerebral parenchyma, influencing the hematoma’s location and shape, and creating a unique spatial distribution of intracranial hemorrhage (21). Although hematomas are typically accompanied by varying degrees of PHE in adjacent brain tissue, their unique spatial distribution is influenced by the direction of blood flow from the ruptured blood vessel, as illustrated in Figure 1. Thus, there are strong spatial contextual relationships between PHEs in neighboring slices due to hematoma expansion, and these relationships are established through the process of hematoma expansion.
These contextual relationships provide valid a priori information for PHE segmentation. In this study, we leverage the contextual relationships of PHE between consecutive slices as a priori knowledge for segmentation. We propose a novel approach to tackle the challenges in PHE segmentation, aiming to enhance both the accuracy and interpretability of the results. By designing an innovative module, we offer new perspectives and methodologies for PHE segmentation in SICH. Our main contributions are summarized as follows:
- We introduced an a priori module called Perihematomal Edema Synergistic Enhancement (PESE), which is designed to enhance the overall intracranial characterization of PHE changes in SICH. This module thereby strengthens the a priori knowledge representation of the overall characterization of PHE changes.
- Our proposed PESE module offers new insights into PHE segmentation in SICH by synergistically integrating a priori information from PHE-associated slices. Experimental results demonstrate that this method effectively enhances segmentation performance.
- The proposed PESE module is interpretable, enhancing the transparency and comprehensibility of the decision-making process in this section.
- The proposed architecture performs well across most evaluation metrics for segmentation results when compared to other methods.
We present this article in accordance with the TRIPOD+AI reporting checklist (available at https://qims.amegroups.com/article/view/10.21037/qims-24-2404/rc).
Methods
The study was conducted in accordance with the Declaration of Helsinki (as revised in 2013). In the field of automatic medical image segmentation, the self-configuring no new U-Net (nnU-Net) framework has demonstrated exceptional performance across a wide range of tasks (22-24). To address the challenges of PHE segmentation, we designed a module dedicated to 3-dimensional (3D) data that utilizes prior knowledge of PHE to enhance spatial features. By feeding these features into the 3D network, the network can utilize the 3D information more efficiently, thus improving the accuracy and effectiveness of segmentation. To integrate this module, a robust 3D network architecture is required. Therefore, we selected two 3D architectures based on U-Net (17) within the nnU-Net (25) framework for ablation experiments to evaluate the performance of different models in the PHE segmentation task. Through these experiments, we identified the best performing model and used it as the basis for our development of the Perihematomal Edema Synergistic Enhancement Network (PESE-Net). The main architecture of PESE-Net is shown in Figure 2 and its core component, the PESE module, is shown in Figure 3.
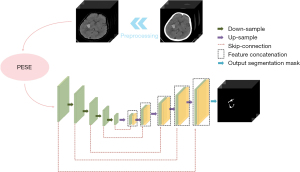
The specific procedure of the PESE module can be expressed as follows:
Where X represents the input medical image data, is the feature adjustment mapping function, is the slice similarity-based PHE-associated slice generation method, and ϕ is the dynamic similarity threshold. PESE represents the output after synergistically fusing the overall change features and spatial information of PHE.
Specifically, is a mapping function used to adjust the input 3D medical image data features, allowing subsequent operations to process these features more efficiently. The expression is as follows:
Where is an operator that rearranges the elements of F according to the specified new dimensions. Specifically, F contains input information for multiple batches of medical images, each with a certain depth d, channel count c, height h, and width w. The variable b represents the number of training batches. Fnode represents the 2-dimensional (2D) slice features rearranged according to the operation.
Overall, PESE-Net comprises two primary components: the slice similarity-based PHE-associated slice generation method and the operation to synergistically fuse the overall change features and spatial information of PHE, which is described in detail below.
Slice similarity-based PHE-associated slice generation method
We propose the slice similarity-based PHE-associated slice generation method for selecting PHE-associated slices in SICH images. This method generates PHE-associated slices by analyzing the similarity between slices. In SICH, the initial hematoma spreads to neighboring tissues, resulting in a high similarity of hematoma features between adjacent slices. Since the spreading of hematoma is usually accompanied by the generation of PHE and the hematoma exhibits high signal characteristics in CT, these features become easy to identify and compare when analyzing slice similarity. By examining the similarity of hematoma features in adjacent slices, we can use them as reference points to indirectly capture the dynamics of PHE. Although certain regions without hematoma features may also exhibit high similarity, we aimed to better filter out low-signal irrelevant regions not related to hematoma by dynamically adjusting the similarity thresholding strategy, focusing on identifying hematoma-associated slices, and thus identifying PHE-associated slices. This approach not only leverages the known relationship between hematoma and PHE but also enhances the effectiveness of identifying PHE-associated slices by optimizing the model. Ultimately, we aimed to better extract PHE-associated slice features and apply them to the operation to synergistically fuse the overall change features and spatial information of PHE to fully utilize these PHE features.
is the slice similarity-based PHE-associated slice generation method, which can be expressed as:
where p and q are 2D slice features in the dataset Fnode. Spq represents the calculated similarity between features p and q, with ϕ as the dynamic similarity threshold. The condition ensures that no loops are formed.
To calculate Spq, we need to determine the adaptive hematoma segmentation threshold T. From the above content, we determine that we identify PHE-associated slices by recognizing hematoma-associated slices. By determining T, we can better separate high signal hematoma regions, leading to more accurate slice similarity calculations. The method for calculating T is as follows:
where T is the adaptive hematoma segmentation threshold, is the optimization function used to determine the optimal value of the hematoma segmentation threshold, and is the percentile adjusted based on the coefficient of variation (CV).
The adaptive hematoma segmentation threshold is detailed below as the internal parameter of . Since hematomas appear as high signal regions on CT images, we initially extract pixel values between the 90th and 99th percentiles to identify these high-signal regions.
Where and represent the 90th and 99th percentiles of the image , respectively.
To quantify the degree of change in the high signal region, we calculate the CV:
where M is the mean of the high signal region and S is the standard deviation of the high-signal region. CV provides a measure of the relative variability of the data, enabling efficient adjustment of the threshold within the high-signal region. In the analysis of high signal hematoma regions, CV facilitates dynamic hematoma segmentation by adjusting the threshold to more accurately capture changes in hematoma signals.
To determine the optimal hematoma segmentation threshold, we find the percentile that maximizes the sum of binarized pixel values by performing calculations over a range of percentile high-signal hematoma regions:
where p is the current calculated percentile, and represents the binarization of pixel values. By optimizing the function , we can determine the optimal hematoma segmentation threshold to efficiently segment high signal hematoma regions.
To calculate Spq, we use T for binarization and evaluate the similarity of slices by calculating the DSC:
where indicates that if p is greater than the threshold T, it returns 1; otherwise, it returns 0. The variable smooth is a smoothing term, initially set to 1×10−5. When both the prediction and the target are background, the binarization result may be zero. Adding smooth avoids division by zero, ensuring stability.
A fixed similarity threshold cannot accommodate the diversity and complexity of different datasets. Therefore, we propose a dynamic similarity threshold method based on the trend of increasing similarity to more accurately evaluate the high similarity between adjacent slices. To calculate the dynamic similarity threshold ϕ, we first compute the DSC change between adjacent slices:
where ∆Spq represents the DSC change between adjacent slices.
Then, by calculating the average of the increasing DSC trend, we derive ϕ:
where N is the number of increasing DSC trends.
This method, through the calculation of ϕ, effectively enhances the accuracy of similarity evaluation, ensuring that associations are established only between slices with high similarity.
The operation to synergistically fuse the overall change features and spatial information of PHE
The operation to synergistically fuse the overall change features and spatial information of PHE is based on the concept of a graph convolutional network. A novel feature-weighting strategy effectively integrates these features. The specific operations are as follows:
where i and j are indices of features in PHE-associated slices; G[j] represents the updated value of the feature at index j; Xc is a copy of X, used to retain the original features; N(j) represents the set of features adjacent to the feature at index j; is a threshold filtering operation for background suppression; and Wn[i,j] represents the normalized weight between the features at indices i and j. The variable adaptive weight is an adaptive weight, initialized to 1.0, which keeps the features to be fused unchanged initially and gradually optimizes during training.
When the feature at index j has neighboring features (), it is updated as follows:
This method allows information from neighboring features to propagate to the feature at index j, thereby achieving an update.
If the feature at index j has no neighboring features (), it remains unchanged:
To calculate Wn, we first need to define the adjacency matrix A and the degree matrix D. The adjacency matrix A is defined as follows:
where E represents the set of all PHE-associated slices.
The degree matrix D is defined as:
where D is a diagonal matrix, and the diagonal element D[i,i] represents the degree of the feature at index i, which is the number of PHE-associated slice features adjacent to the feature at index i. N is the total number of PHE-associated slices.
The normalization formula for Wn is:
Where denotes the inverse square root of D. Wn is used to balance the influence between features during the transmission of PHE-associated slice features.
The specific formula for the operation is:
where is an indicator function, which takes the value 1 when the condition is met, otherwise 0. The variable t is a preset threshold of 0.0, used to filter background pixels and thus fuse more important feature information.
Through the aforementioned detailed steps, PESE-Net effectively integrates PHE-associated slice features with prior knowledge, thus enhancing the feature representation of PHE regions and its overall intracranial expression characteristics. This integration process provides robust scientific support for PHE segmentation.
Datasets
To evaluate the performance of the proposed method for PHE segmentation, we trained and validated it using the publicly available PHE-SICH-CT-IDS dataset, as published by Ma et al. (26). This dataset, as provided by the original creators, comprises CT scans from 120 patients. The scans were acquired using a PHILIPS Brilliance iCT scanner (Philips, Best, Netherlands) with the following parameters: tube voltage of 120 kV, tube current of 300 mA, matrix size of 512×512, slice thickness of 5.00 mm, and slice spacing of 5.00 mm. Each CT scan included an average of approximately 35 slices. This dataset applied the following inclusion and exclusion criteria to ensure its quality and relevance:
- Inclusion criteria:
- Diagnosis of spontaneous intracranial hemorrhage.
- Hemorrhage occurring in the basal ganglia region of the brain.
- Time from SICH symptom onset to hospital admission and scanning within 12 hours.
- Age over 18 years.
- Patients who did not undergo surgical treatment after admission and reexamined their head CT within 72 hours.
- Exclusion criteria:
- Poor image quality.
- History of neurosurgical procedures.
- Coagulation disorders or a history of anticoagulant use.
- Secondary intracerebral hemorrhage (ICH) or bleeding into the ventricles.
The characteristics of the patients included in the dataset are summarized in Table 1, which provides detailed information on age, sex, comorbidities, hemorrhage location, years of data collection, and the time from symptom onset to imaging.
Table 1
| Characteristics | Description |
|---|---|
| Age (years) | |
| Mean ± standard deviation | 55.91±15.57 |
| Median (IQR) | 56.0 (20.5) |
| Sex | |
| Male | 73 (60.83%) |
| Female | 47 (39.17%) |
| Comorbidities | |
| Hypertension | 96 (80.00%) |
| Diabetes | 12 (10.00%) |
| Coronary heart disease | 2 (1.67%) |
| Renal insufficiency | 1 (0.83%) |
| Hemorrhage location | |
| Left basal ganglia region | 60 (50.00%) |
| Right basal ganglia region | 59 (49.17%) |
| Both basal ganglia regions | 1 (0.83%) |
| Years of data collection | December 2020 to April 2023 |
| Time from SICH symptom onset to hospital admission and scanning | Within 12 hours |
IQR, interquartile range; SICH, spontaneous intracerebral hemorrhage.
During the data preprocessing stage, we ensured all data were consistent and complete. We identified that 8 cases had undergone transformations in window width and window position, which were inconsistent with the rest of the data. To maintain consistency in data processing and ensure the reliability of the experimental results, we opted to exclude these 8 cases. For model training and testing, we divided the data in a ratio close to 8:2, specifically using 90 cases for training and 22 cases for testing. This division resulted in a total of 6,470 CT images, including 3,235 CT slice images and 3,235 ground truth images of PHE. The ground truth of the PHE region in each slice is manually outlined on each CT image layer by radiologists using the open-source software LIFEx v5.10, with cerebral window settings (level =40, width =120).
Implementation details
In this study, our model was trained on the Pytorch platform using an NVIDIA A100 40GB GPU (NVIDIA, Santa Clara, CA, USA). For data preprocessing, we standardized the training, validation, and testing datasets. Initially, we applied a cerebral window setting (level =40, width =120) to the input medical images and performed normalization to enhance the contrast of PHE in CT images. This cerebral window setting is specifically designed for PHE, causing the pixels of the skull to appear highlighted. We then conducted cranial stripping by removing the largest connected region of these highlighted pixels layer by layer. In this experiment, we set n_conv_per_stage of UNet and n_blocks_per_stage of ResidualUNet to the same value, while keeping other parameters constant. This ensured that the computational load and feature extraction capability of each stage were similar, maintaining comparable depth and complexity between UNet and ResidualUNet for a fair comparison. nnU-Net, a U-Net-based adaptive segmentation framework, was chosen for its excellent auto-configuration features for network training and data augmentation. To fully utilize the patient data, a 5-fold cross-validation strategy was applied throughout the training process.
Results
Evaluation metrics
To quantitatively evaluate the segmentation performance of the proposed method, we employ the following segmentation evaluation metrics: DSC, Hausdorff distance (HD), relative volume difference (RVD), and normalized surface Dice (NSD) (27). DSC was utilized to measure the region overlapping error between ground truth and segmentation results, whereas HD was used to evaluate the coincidence between segmented surface and target surface. RVD quantifies the differences between the predicted and labeled PHE volumes, and NSD further evaluates the discrepancy between the target and predicted boundaries. They are defined as:
where P represents the segmentation result predicted by the segmentation method, and T represents the ground truth annotated by humans. is the number of voxels in the intersection of P and T. and are the total number of voxels in P and T, respectively. and are the surfaces (boundaries) of P and T, respectively. d(p,t) is the Euclidean distance between point p and point t. sup and inf represent the supremum (maximum value) and infimum (minimum value), respectively. ABS represents the absolute value. is the dilated region within a distance from . is the number of voxels in the intersection of and . is the number of voxels in the intersection of and . The variable is a predefined tolerance value for assessing the closeness between a segmented surface and a real surface. It is set to 1 in order to provide a reasonable criterion when measuring surface overlap that takes into account subtle differences without being overly stringent, while remaining consistent with the literature.
Additionally, we utilized the R2 value (coefficient of determination) to measure the goodness of fit in estimating PHE volume. The PHE volume was calculated using the method for ICH volume calculation described in (28), which involves multiplying the voxel counts of the PHE by the pixel spacing in the x, y, and z dimensions. The R2 value is derived by comparing the estimated PHE volume with the true PHE volume, indicating the degree of fit between the model-estimated and true PHE volumes.
Furthermore, we introduce residual plots. These plots help to analyze the distribution of errors and biases across different models over various ranges of true PHE volumes by illustrating the differences between the models’ estimated and true PHE volumes. This analysis aids in evaluating the stability and reliability of the model’s estimated PHE volume.
Interpretability analysis of the PESE module
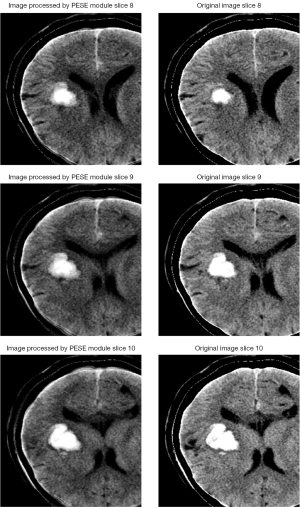
As illustrated by the adjacent CT slice images of the same patient in Figure 4, the hematoma slices of the original image (right side of Figure 4) exhibit strong similarity, indicating significant a priori knowledge between the hematoma features. Even though there may be uncertainty in determining PHE, this a priori knowledge can be leveraged to enhance the features of the area surrounding the hematoma, as PHE typically occurs in this region. The images processed by the PESE module (left side of Figure 4) demonstrate that the contrast of the tissue around the hematoma is substantially enhanced, potentially improving the recognizability of PHE. This enhancement of the surrounding tissue may provide crucial feature information, even in cases where PHE judgment is unclear.
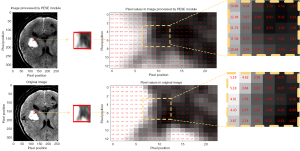
As shown in Figure 5, the PESE module substantially enhances the pixel values in the region surrounding the hematoma. This comparison allows for a more intuitive understanding of the role of the PESE module, and the enhancement effect offers valuable interpretability for PHE segmentation, despite potential uncertainties in PHE recognition.
Comparison with other segmentation methods on the test dataset
To demonstrate the advantages of the proposed network, we validated it on the test dataset and compared our proposed PESE-Net with other network models. Specifically, we utilized U-Net-based 2D (17) and 3D (29) models, named nnUnet2D and nnUnet3D, respectively. Additionally, we utilized residual-based (30) 2D and 3D U-Net models, named ResidualUnet2D and ResidualUnet3D, respectively, along with the Attention-Unet (31) network. We conducted a comprehensive comparison of these network models with the proposed method. Based on the previously described process for selecting the PESE-Net base model, we conducted ablation experiments on the 3D architectures in nnU-Net, namely ResidualUnet3D and nnUnet3D, with the detailed results shown in Table 2. The experimental results indicate that ResidualUnet3D outperforms nnUnet3D in all aspects and is therefore selected as the base model for PESE-Net. We compared this PESE-Net with other network models to verify its advantages in the PHE segmentation task. Table 3 presents the segmentation results for each model. Our proposed model achieved DSC, HD, RVD, and NSD values of 45.2259%±19.2139%, 26.7355±16.8963, 0.5230±0.2553, and 0.6053±0.2118, respectively. The experimental results indicate that the PESE-Net model outperforms other network models in the PHE segmentation task, effectively segmenting PHE and highlighting its substantial advantages.
Table 2
| Model | DSC (%) | HD | RVD | NSD |
|---|---|---|---|---|
| PESE + nnUnet3D | 43.7034±18.8393 | 30.3314±18.0216 | 0.5236±0.2691 | 0.5846±0.2031 |
| PESE + ResidualUnet3D | 45.2259±19.2139 | 26.7355±16.8963 | 0.5230±0.2553 | 0.6053±0.2118 |
The data are presented as mean ± standard deviation. DSC, Dice similarity coefficient; HD, Hausdorff distance; NSD, normalized surface Dice; PESE-Net, PESE Network; PESE, Perihematomal Edema Synergistic Enhancement; RVD, relative volume difference.
Table 3
| Model | DSC (%) | HD | RVD | NSD |
|---|---|---|---|---|
| nnUnet2D | 38.9372±21.5253 | 30.5380±18.1791 | 0.5875±0.2781 | 0.5220±0.2402 |
| ResidualUnet2D | 37.8204±19.9692 | 32.1208±19.3245 | 0.6163±0.2434 | 0.5189±0.2177 |
| ResidualUnet3D | 44.7613±18.7310 | 27.1460±17.4162 | 0.5359±0.2469 | 0.6010±0.2019 |
| Attention-Unet | 39.4966±21.9986 | 33.1634±20.0513 | 0.5925±0.2671 | 0.5273±0.2509 |
| nnUnet3D | 43.3731±18.4456 | 29.3114±17.2133 | 0.5483±0.2350 | 0.5863±0.2027 |
| PESE-Net | 45.2259±19.2139 | 26.7355±16.8963 | 0.5230±0.2553 | 0.6053±0.2118 |
The data are presented as mean ± standard deviation. DSC, Dice similarity coefficient; HD, Hausdorff distance; NSD, normalized surface Dice; PESE-Net, Perihematomal Edema Synergistic Enhancement Network; RVD, relative volume difference.
To further visualize the results presented in Table 3, we provide comparative box plots of all models based on the DSC, HD, RVD, and NSD metrics in Figure 6. As shown in the figure, the box plots for our model are relatively short, indicating minimal fluctuation and a high degree of stability in the results. Additionally, most data points are concentrated in the central region of the box, suggesting that our model consistently performs well across these evaluation metrics. These observations further confirm that PESE-Net substantially enhances the stability of PHE segmentation by effectively leveraging the contextual relationship of PHE between consecutive slices as prior knowledge.

Figure 7 presents the visualization of segmentation results comparing the proposed model with other models. It is evident that PESE-Net surpasses the other methods in terms of segmentation accuracy, particularly near the PHE boundary. PESE-Net substantially reduces false positive pixels in its predictions compared to other models. This advantage may be attributed to PESE-Net’s capability to effectively leverage the PHE contextual relationships between consecutive slices as prior knowledge for segmentation. These results suggest that PESE-Net demonstrates superior accuracy and reliability in handling PHE segmentation tasks.

In the diagnosis of SICH, the accuracy of PHE volume estimation has some reference value in assessing a patient’s prognosis (18).
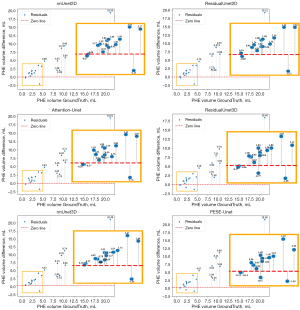
To more comprehensively assess the models’ performance in estimating PHE volumes, we utilized residual plots. In the residual plot shown in Figure 8, the zero line represents perfect prediction, and the closer the data points are to this line, the more accurate the model estimation is. By observing the PHE volume prediction bias plots for all models, we found that all models tend to predict PHE volumes that are generally less than the true volumes. We speculate that this may be due to unclear boundaries and low contrast in the PHE regions, making it difficult for the models to accurately identify these areas. By calculating the total bias of PHE volume in the 0–5 mL range for all models, we found that our model has a total bias of 12.61 mL, which is the smallest among all models. In comparison, the total biases for the other models are as follows: nnUnet3D, 15.27 mL; nnUnet2D, 16.46 mL; ResidualUnet3D, 12.70 mL; ResidualUnet2D, 17.04 mL; and Attention-Unet, 15.68 mL. By observing the PHE volume prediction bias plots for each model in the 0–5 mL range, we can see that our model exhibits relatively smaller prediction bias in this range. Therefore, we believe our model has an advantage in predicting small volume PHE.
Discussion
SICH is among the diseases with the highest morbidity and mortality rates globally. Its detrimental effects arise not only from the direct compression of surrounding brain tissue by the hematoma but, more critically, from the subsequent formation of PHE. As a secondary injury, PHE can lead to intracranial hypertension, cerebral herniation, and even death. Accurate segmentation of PHE is clinically vital for evaluating the prognosis of SICH patients and developing treatment plans. We employed the 3D U-Net model of nnU-Net as the base network model and integrated the newly designed PESE module, which effectively extracts PHE-associated slice features based on prior knowledge of PHE surrounding the hematoma. Additionally, the PESE module performs the operation to synergistically fuse the overall change features and spatial information of PHE, followed by the adaptive fusion of features from PHE-associated slices. The experimental results demonstrate the effectiveness of our proposed PESE module.
To the best of our knowledge, most segmentation tasks in the field of PHE segmentation currently focus on innovations in network models. However, due to the grayscale overlap and fuzzy boundaries between PHE and surrounding tissues, existing DL methods struggle to accurately segment PHE. To address these challenges, we propose integrating PHE-related a priori knowledge with DL methods to enhance the accuracy and robustness of PHE segmentation. In our study, we introduce PESE-Net, which effectively leverages the contextual relations of PHE between consecutive slices as a priori knowledge for PHE segmentation. This approach fully exploits the rich spatial features present in continuous slices of PHE, providing a comprehensive understanding of its complex spatial feature distribution. Additionally, our network offers a deep insight into the distribution of these features through the slice similarity-based PHE-associated slice generation method and the operation to synergistically fuse the overall change features and spatial information of PHE. These methods more effectively enhance the overall change features of PHE within the cranium and are well-suited for segmenting the complex features associated with PHE. In our study, we primarily focused on improving the accuracy and robustness of PHE segmentation by integrating machine learning (ML) models with prior knowledge of PHE. ML models excel in handling large datasets and recognizing complex patterns, providing consistent and automated segmentation results. This capability is particularly important in large-scale studies or clinical environments where manual segmentation is challenging. Although our study does not directly compare the performance of ML models with radiologists, we recognize the potential of ML models to complement the work of radiologists. By providing fast and consistent segmentation results, ML models can alleviate the workload of radiologists and offer support in situations where rapid processing of large amounts of data is required. In future research, we will further explore the application of PESE-Net to other medical image segmentation tasks. We plan to extend its application to PHE-related medical imaging datasets to validate its performance across different dimensions and more complex scenarios. Furthermore, we will investigate the potential of PESE-Net in multimodal medical image processing by integrating various types of imaging data [e.g., MRI, CT, and positron emission tomography (PET)] for joint feature enhancement, aiming to improve segmentation accuracy and diagnostic precision.
This study has several limitations: (I) the dataset used in this study, PHE-SICH-CT-IDS, does not provide detailed information on the medical treatment of edema, such as the use of hyperosmolar agents. This lack of information may introduce bias in the study results; therefore, future research should consider these factors to ensure a more comprehensive analysis; (II) in CT images, PHE appears as a low-density region with low contrast with surrounding tissues, which increases the difficulty of segmentation. In addition, PHE has a complex morphology and its CT values significantly overlap with other brain tissues, making PHE segmentation challenging. In contrast, MRI is generally superior to CT in identifying underlying structural lesions and quantifying PHE (32). Future studies could explore segmentation of PHE data using MRI to improve the accuracy of its segmentation and quantitative analysis; (III) our model currently focuses on enhancing PHE features. In future studies, we plan to automate this module to integrate features of various lesions in medical images for automated enhancement. This will enable our enhancement module to be widely used in various medical image processing tasks; (IV) our module is currently only applied in neural networks. In the future, we hope to apply it to medical imaging devices used by clinicians to help them visualize lesions more clearly and thus better plan surgery and treatment strategies.
Conclusions
In this study, we proposed PESE-Net by integrating the ResidualUnet3D model of nnU-Net with the proposed PESE a priori module. The PESE module leverages the PHE contextual relationships between consecutive slices as a priori knowledge for PHE segmentation. Experimental results demonstrate that incorporating the PESE module substantially enhances the performance of the base model on PHE segmentation, achieving effective segmentation and stable volume estimation of PHE regions. By embedding an a priori module into the underlying network architecture, PESE-Net achieves notable improvements in segmentation performance without altering the network structure. This finding underscores the importance of judiciously utilizing data prior information in medical image processing. Compared to relying solely on more complex network structures, incorporating a priori knowledge not only enhances the accuracy and robustness of the model but also offers a more practical solution with limited computational resources. More importantly, the PESE module is interpretable, surpassing most non-interpretable modules in other DL methods. Therefore, future research could further explore systematic integration of prior knowledge to optimize model performance and advance the field of medical image processing.
Acknowledgments
None.
Footnote
Reporting Checklist: The authors have completed the TRIPOD+AI reporting checklist. Available at https://qims.amegroups.com/article/view/10.21037/qims-24-2404/rc
Funding: This work was supported by
Conflicts of Interest: All authors have completed the ICMJE uniform disclosure form (available at https://qims.amegroups.com/article/view/10.21037/qims-24-2404/coif). All authors report that this work was supported by the Science & Technology Development Program of Jilin Province, China (No. 20230401100YY). The authors have no other conflicts of interest to declare.
Ethical Statement: The authors are accountable for all aspects of the work in ensuring that questions related to the accuracy or integrity of any part of the work are appropriately investigated and resolved. The study was conducted in accordance with the Declaration of Helsinki (as revised in 2013).
Open Access Statement: This is an Open Access article distributed in accordance with the Creative Commons Attribution-NonCommercial-NoDerivs 4.0 International License (CC BY-NC-ND 4.0), which permits the non-commercial replication and distribution of the article with the strict proviso that no changes or edits are made and the original work is properly cited (including links to both the formal publication through the relevant DOI and the license). See: https://creativecommons.org/licenses/by-nc-nd/4.0/.
References
- Feigin VL, Lawes CM, Bennett DA, Barker-Collo SL, Parag V. Worldwide stroke incidence and early case fatality reported in 56 population-based studies: a systematic review. Lancet Neurol 2009;8:355-69. [Crossref] [PubMed]
- Steiner T, Al-Shahi Salman R, Beer R, Christensen H, Cordonnier C, Csiba L, et al. European Stroke Organisation (ESO) guidelines for the management of spontaneous intracerebral hemorrhage. Int J Stroke 2014;9:840-55. [Crossref] [PubMed]
- van Asch CJ, Luitse MJ, Rinkel GJ, van der Tweel I, Algra A, Klijn CJ. Incidence, case fatality, and functional outcome of intracerebral haemorrhage over time, according to age, sex, and ethnic origin: a systematic review and meta-analysis. Lancet Neurol 2010;9:167-76. [Crossref] [PubMed]
- Gebel JM Jr, Jauch EC, Brott TG, Khoury J, Sauerbeck L, Salisbury S, Spilker J, Tomsick TA, Duldner J, Broderick JP. Relative edema volume is a predictor of outcome in patients with hyperacute spontaneous intracerebral hemorrhage. Stroke 2002;33:2636-41. [Crossref] [PubMed]
- Appelboom G, Bruce SS, Hickman ZL, Zacharia BE, Carpenter AM, Vaughan KA, Duren A, Hwang RY, Piazza M, Lee K, Claassen J, Mayer S, Badjatia N, Connolly ES Jr. Volume-dependent effect of perihaematomal oedema on outcome for spontaneous intracerebral haemorrhages. J Neurol Neurosurg Psychiatry 2013;84:488-93. [Crossref] [PubMed]
- Li N, Worthmann H, Heeren M, Schuppner R, Deb M, Tryc AB, Bueltmann E, Lanfermann H, Donnerstag F, Weissenborn K, Raab P. Temporal pattern of cytotoxic edema in the perihematomal region after intracerebral hemorrhage: a serial magnetic resonance imaging study. Stroke 2013;44:1144-6. [Crossref] [PubMed]
- Loncaric S, Dhawan AP, Broderick J, Brott T. 3-D image analysis of intra-cerebral brain hemorrhage from digitized CT films. Comput Methods Programs Biomed 1995;46:207-16. [Crossref] [PubMed]
- Bardera A, Boada I, Feixas M, Remollo S, Blasco G, Silva Y, Pedraza S. Semi-automated method for brain hematoma and edema quantification using computed tomography. Comput Med Imaging Graph 2009;33:304-11. [Crossref] [PubMed]
- Chen M, Hu Q, Liu Z, Zhou S, Li X. Segmentation of cerebral edema around spontaneous intracerebral hemorrhage. Appl Math Inf Sci 2013;7:563-570. [Crossref]
- Loncaric S, Cosic D, Dhawan AP. Hierarchical segmentation of CT head images. Proceedings of 18th Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Amsterdam, Netherlands, 1996, pp. 736-737.
- Loncaric S, Kovacevic D, Cosic D. Fuzzy expert system for edema segmentation. In: Proceedings of the 9th Mediterranean Electrotechnical Conference (MELECON’98) 1998;2:1476-1479.
- Udendhran R, Balamurugan M, Suresh A, Varatharajan R. Enhancing image processing architecture using deep learning for embedded vision systems. Microprocess Microsyst 2020;76:103094. [Crossref]
- Yang H, Shan C, Bouwman A, Kolen AF, de With PHN. Efficient and Robust Instrument Segmentation in 3D Ultrasound Using Patch-of-Interest-FuseNet with Hybrid Loss. Med Image Anal 2021;67:101842. [Crossref] [PubMed]
- Zhao Y, Wang X, Che T, Bao G, Li S. Multi-task deep learning for medical image computing and analysis: A review. Comput Biol Med 2023;153:106496. [Crossref] [PubMed]
- Wei L, Liu H, Xu J, Shi L, Shan Z, Zhao B, Gao Y. Quantum machine learning in medical image analysis: A survey. Neurocomputing 2023;525:42-53. [Crossref]
- Ironside N, Chen CJ, Mutasa S, Sim JL, Ding D, Marfatiah S, Roh D, Mukherjee S, Johnston KC, Southerland AM, Mayer SA, Lignelli A, Connolly ES. Fully Automated Segmentation Algorithm for Perihematomal Edema Volumetry After Spontaneous Intracerebral Hemorrhage. Stroke 2020;51:815-23. [Crossref] [PubMed]
- Ronneberger O, Fischer P, Brox T. U-net: Convolutional networks for biomedical image segmentation. In: Navab N, Hornegger J, Wells W, Frangi A, (eds). Medical Image Computing and Computer-Assisted Intervention – MICCAI 2015: 18th International Conference, Munich, Germany, October 5-9, 2015, Proceedings, Part III 2015;234-241.
- Dhar R, Falcone GJ, Chen Y, Hamzehloo A, Kirsch EP, Noche RB, Roth K, Acosta J, Ruiz A, Phuah CL, Woo D, Gill TM, Sheth KN, Lee JM. Deep Learning for Automated Measurement of Hemorrhage and Perihematomal Edema in Supratentorial Intracerebral Hemorrhage. Stroke 2020;51:648-51. [Crossref] [PubMed]
- Aguilar MI, Brott TG. Update in intracerebral hemorrhage. Neurohospitalist 2011;1:148-59. [Crossref] [PubMed]
- Fisher CM. Pathological observations in hypertensive cerebral hemorrhage. J Neuropathol Exp Neurol 1971;30:536-50. [Crossref] [PubMed]
- Mutlu N, Berry RG, Alpers BJ. Massive cerebral hemorrhage: clinical and pathological correlations. Arch Neurol 1963;8:644-61. [Crossref] [PubMed]
- Liu R, Wang SB, Du SS, Meng KN, Wang RZ, Bai L, Chen Q, Gong GZ, Yin Y. A comparative study of automatic hippocampal segmentation in whole-brain radiotherapy applying DPNU-Net, Mask-RCNN, and nnU-Net models. J Radiat Res Appl Sci 2025;18:101274. [Crossref]
- Chen Q, Wang Y, Xu J, Li Q. Semi-supervised 3D Tooth Segmentation Using nn-UNet with Axial Attention. In: Wang Y, Chen X, Qian D, Ye F, Wang S, Zhang H, (eds). Semi-supervised Tooth Segmentation. STS 2023. Lecture Notes in Computer Science. Springer 2025;14623:96.
- Haylaz E, Gumussoy I, Duman SB, Kalabalik F, Eren MC, Demirsoy MS, Celik O, Bayrakdar IS. Automatic Segmentation of the Nasolacrimal Canal: Application of the nnU-Net v2 Model in CBCT Imaging. J Clin Med 2025;14:778. [Crossref] [PubMed]
- Isensee F, Jaeger PF, Kohl SAA, Petersen J, Maier-Hein KH. nnU-Net: a self-configuring method for deep learning-based biomedical image segmentation. Nat Methods 2021;18:203-11. [Crossref] [PubMed]
- Ma D, Li C, Du T, Qiao L, Tang D, Ma Z, Shi L, Lu G, Meng Q, Chen Z, Grzegorzek M, Sun H. PHE-SICH-CT-IDS: A benchmark CT image dataset for evaluation semantic segmentation, object detection and radiomic feature extraction of perihematomal edema in spontaneous intracerebral hemorrhage. Comput Biol Med 2024;173:108342. [Crossref] [PubMed]
- Yang J, Wickramasinghe U, Ni B, Fua P. Implicitatlas: learning deformable shape templates in medical imaging. In: Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition 2022;15861-71.
- Ironside N, Chen CJ, Mutasa S, Sim JL, Marfatia S, Roh D, Ding D, Mayer SA, Lignelli A, Connolly ES. Fully Automated Segmentation Algorithm for Hematoma Volumetric Analysis in Spontaneous Intracerebral Hemorrhage. Stroke 2019;50:3416-23. [Crossref] [PubMed]
- Çiçek Ö, Abdulkadir A, Lienkamp SS, Brox T, Ronneberger O. 3D U-Net: learning dense volumetric segmentation from sparse annotation. In: Medical Image Computing and Computer-Assisted Intervention – MICCAI 2016: 19th International Conference, Athens, Greece, October 17-21, 2016, Proceedings, Part II 2016;424-432.
- He K, Zhang X, Ren S, Sun J. Deep residual learning for image recognition. In: Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition 2016;770-778.
- Oktay O, Schlemper J, Folgoc LL, Lee M, Heinrich M, Misawa K, Mori K, McDonagh S, Hammerla NY, Kainz B, Glocker B, Rueckert D. Attention u-net: learning where to look for the pancreas. arXiv preprint arXiv:1804.03999 2018.
- Kidwell CS, Wintermark M. Imaging of intracranial haemorrhage. Lancet Neurol 2008;7:256-67. [Crossref] [PubMed]




