
A study on indirect tumor localization using lung phantom during radiation therapy
Introduction
Organ motion due to respiratory movements is one of the most common and challenging issues in the process of radiation therapy (1,2). This is because respiratory motion can induce three-dimensional motion in tumors, with tumors located closer to the diaphragm exhibiting greater displacement (3). Respiratory motion can cause tumors to displace, requiring a larger radiation field to encompass the tumor’s entire range of motion. This increased treatment area can lead to damage to surrounding healthy tissues. To determine the optimal radiation field, patients undergo computed tomography (CT) simulation prior to treatment based on their clinical diagnosis (4).
Real-time tumor tracking requires the use of tumor localization techniques, which can be categorized into direct localization (5) and indirect localization (6). Direct localization relies on imaging systems or the insertion of metal markers for image-guided positioning (7,8). While this method offers high accuracy, the invasiveness of ionizing radiation can limit treatment time and may result in issues such as marker tracking loss due to tumor motion caused by respiration.
Indirect localization involves transforming the tumor’s motion trajectory into highly correlated respiratory surrogates, such as surface displacement of the thoracoabdominal region (9,10). Optical imaging is used to capture the surface displacement of irradiation targets attached to the skin surface, and a tumor conversion formula is established based on their motion trajectory to assess internal tumor displacement (11,12). Predicting tumor motion using respiratory surrogates requires a high degree of displacement correlation. Additionally, during radiation therapy, the tumor’s motion pattern may vary due to different breathing patterns, leading to discrepancies between the tumor motion conversion formula and the actual tumor trajectory (13). Therefore, the tumor conversion formula requires multiple validations to reduce uncertainty.
The ultrasound monitoring system is a non-invasive and non-radioactive in vivo imaging monitoring system. Ultrasound imaging has been employed for tumor monitoring in various anatomical sites, such as the brain (14) and prostate (15). However, ultrasound imaging of lung tumors, due to the inability for direct monitoring, requires the identification of highly correlated respiratory surrogates to track lung tumor motion (16). The diaphragm serves as an excellent in vivo surrogate. Ultrasound can directly capture the motion images of the diaphragm, which exhibit a high degree of correlation with lung tumor motion (17,18).
This study was conducted in collaboration with the Department of Radiation Oncology at Taipei Medical University Hospital. In previous study, the phantom used in experiments had issues with water leakage, which posed a risk to experimental equipment and compromised the accuracy of the results. Additionally, the phantom only simulated the chest cavity, without including an abdominal simulation. The primary aim of this research was to update the phantom to better simulate real human conditions and address the leakage issues present in previous phantom. The novel phantom includes both chest and abdominal cavities. Improvements such as the addition of sealing rings and enhanced manufacturing precision have been made to prevent water leakage issues. Additionally, it aims to improve the tumor superior-inferior (SI) to medial-lateral (ML) direction conversion formula developed by our team (19). By integrating mask region-based convolutional neural networks (Mask R-CNN) ultrasound image tracking algorithm (M-UITA) with 4-dimensional computed tomography (4DCT) (20), we simultaneously monitored the motion trajectories of both the tumor and diaphragm phantoms. A new tumor motion transformation formula was derived, with a particular focus on improving the ML-direction transformation. Subsequently, cone-beam computed tomography (CBCT) was employed to compare and validate the tumor motion conversion position discrepancies between the previously published formula and the one developed in this paper. We present this article in accordance with the TRIPOD reporting checklist (available at https://qims.amegroups.com/article/view/10.21037/qims-24-1777/rc).
Methods
The study was conducted in accordance with the Declaration of Helsinki (as revised in 2013). The study was approved by the Ethics Committee of Taipei Medical University Hospital (No. IRB 201902015) and informed consent was obtained from all individual participants.
Experimental apparatus
Experimental phantom
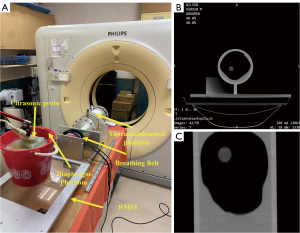
This study designed experimental phantom for three different areas: the thoracoabdominal region, lung, and diaphragm. The thoracoabdominal phantom followed the design approach proposed by Kim et al. (21). It utilized an acrylic hollow cylindrical structure with a silicone membrane partitioning the interior into two compartments, simulating the diaphragm. These two compartments were filled with water to emulate the thoracic and abdominal cavities. To prevent leakage from the phantom, four sealing rings are installed on the piston push rod, and sealing rings are also applied to the front and rear cover plates. The connection between the lung phantom and the breathing hole is secured tightly with a sealing tape and a strap. The lung phantom comprised three layers: an outer layer simulating the lung’s external covering using a balloon, a middle layer filled with sponge inside the balloon to mimic lung structure, and an inner layer employing a 3 mm wooden ball to replicate a lung tumor phantom (22), as shown in Figure 1A,1B.
The diaphragm phantom involved affixing a rubber belt to the inner edge of a plastic container, serving as the target for ultrasound image tracking. The plastic container was filled with agarose and water to act as an ultrasound transmission medium and simulate the internal tissue structures of the human body. When the ultrasound probe is in direct contact with the body surface, there is no relative displacement between the probe and the body surface; however, as the human lungs contract and expand, a relative displacement occurs between the lungs and the surface of the body. To simulate this relative displacement, the diaphragm phantom in this study was designed with two layers: the top layer simulates the body surface, and the bottom layer simulates the internal organs. When Respiratory Motion Simulation System (RMSS) received the respiratory signal and moved, the probe remained fixed in the groove on the top layer phantom surface, preventing its movement. Meanwhile, the bottom layer moved in response to the respiratory signal received by RMSS, as shown in Figure 2A. The respiratory belt used in 4DCT was unable to detect the deformation of the abdominal phantom. Therefore, following the reference to our team’s previous research, a rubber ball was employed as a substitute for the abdominal phantom (19), as shown in Figure 2B.
RMSS
The RMSS developed by our team previously can simulate motion in three different regions: the thoracoabdominal area, the lungs, and the diaphragm, as shown in Figure 3. Its operating principle involves inputting prerecorded real human respiratory signals into the RMSS to induce SI motion. This causes the plastic container (diaphragm phantom) placed above the RMSS platform to exhibit SI respiratory motion, and the motion of the diaphragm phantom is measured using an ultrasound probe. Simultaneously, a plate is moved by the RMSS to compress a rubber ball (abdominal region), causing it to deform and produce anterior-posterior (AP) motion. The extent of this deformation is sensed by the respiratory belt of the 4DCT. Additionally, the plate also drives a piston, which compresses and deforms a balloon (lungs), generating SI, AP, and ML motion. In this study, 4DCT was employed to measure the three-axis displacement of a wooden ball (tumor phantom) inside the balloon due to the deformation of the balloon. The motion trajectories of the three different phantoms at the same time are correlated and correspond to the states of inhalation and exhalation.
Diaphragm image tracking
This study uses ultrasound to capture the motion images of the diaphragm phantom. Additionally, it combines the previously developed Mask R-CNN model used by our team to create the M-UITA for tracking the diaphragm phantom’s movement. This algorithm extracts 1,800 real human diaphragm ultrasound images as the training dataset and sets up a deep learning environment using Anaconda, an open-source distribution of Python and R programming languages, for Mask-RCNN training. After training, the ultrasound image tracking algorithm calculates the average coordinates of the diaphragm identified by Mask R-CNN to achieve the goal of tracking diaphragm displacement (20).
Capture of input signals from the respiratory motion simulator
This study prepared four sets of pre-recorded human respiratory signals, obtained from healthy volunteers, along with one set of sine wave signals. The respiratory signals, each lasting 60 seconds, were captured using ultrasound to record diaphragm motion. The four distinct human respiratory signals (23) are as follows: A signal represents baseline shift, B signal corresponds to deep breath, C signal imitates staged breathing, and D signal represents slow breathing. Additionally, the sine signal has an amplitude of ±20 mm and a frequency of 0.25 Hz. All of the pre-recorded respiratory signals are shown in Figure 4.
The tumor motion conversion model
This study used 4DCT for scanning the lung phantom while concurrently tracking the diaphragm using ultrasound imaging. When the ultrasound detected real-time motion signals in the SI direction of the diaphragm phantom, M-UITA was used to track the diaphragm phantom’s position. Additionally, with reference to the tumor motion conversion model proposed by our team, motion and position signals in the SI and ML directions of the tumor phantom were obtained (19).
Ultrasound and 4DCT signal processing
A specific time window was defined for acquiring both ultrasound and 4DCT data. 4DCT utilizes spiral CT scanning to generate three-dimensional (3D) anatomical images of the patient. The fourth dimension in 4DCT represents time, captured by a synchronized respiratory belt that records external respiratory signals. The CT scanner continuously advances with a pitch of 0.5 mm every 1.5 seconds, recording the acquisition time for each image slice. This allows 4DCT to capture the dynamic movement of the tumor phantom at different points in the respiratory cycle, as shown in Figure 5A. The respiratory belt records the AP displacement signal generated by the abdominal phantom’s ball motion and the corresponding time. The respiratory belt data synchronizes the timing of CT scans during the tumor phantom scan, ensuring consistent duration for each respiratory cycle, as shown in Figure 5B. For this experiment, data was collected during the ninth to twelfth respiratory cycles.
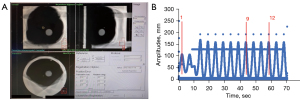
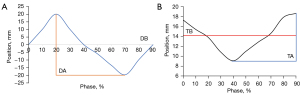
The diaphragm signals were extracted from the ultrasound probe within the defined time window. And each respiratory cycle was further divided into ten phases (0% to 90%) based on the respiratory signal. For each phase, diaphragm signals from all cycles at that position were averaged to obtain the average respiratory waveform, as shown in Figure 6A. The averaged respiratory waveform provides the Diaphragm amplitude (DA) and the diaphragm baseline (DB) parameters for the motion of diaphragm phantom. DA is the difference between the minimum and maximum diaphragm position on the average diaphragm motion trace. DB is the average of the signal over a whole respiratory cycle. In 4DCT, images obtained from the spiral CT scan must be sorted based on respiratory phases, which are divided into ten phases ranging from 0% to 90% in this study. The images of each phase group are recombined into a three-dimensional image, allowing for the acquisition of three-dimensional images at different phases ranging from 0% to 90%. Compared to traditional 3DCT scans, 4DCT offers significant advantages. It exhibits fewer motion artifacts due to the inclusion of a time axis, which allows for the consideration of respiratory motion during image acquisition (24). The 4DCT can capture tumor motion in three dimensions. However, in this study, due to CBCT can only capture images in two directions in real-time. Therefore, only the tumor motion signals in SI and ML directions were extracted from the 4DCT. The pathway in the SI direction provides tumor amplitude (TA) and tumor baseline (TB) of the tumor phantom motion, as shown in Figure 6B. TA is the difference between the minimum and maximum tumor position and TB is the average tumor position.
Establishment of the tumor motion conversion model formula
The ultrasound images provide DA and DB. Furthermore, the 4DCT data offer parameters related to the motion of tumor phantom, such as TA, TB, and linear functions relating the SI to ML displacement of the tumor phantom when moving upwards and downwards. First, we set the zero coordinates of the system through RMSS. The tumor motion conversion model consists of two steps. The first step involves using M-UITA to identify the conversion formula for the SI position from the diaphragm phantom to the tumor phantom. Subtracting DB from the diaphragm phantom in the SI direction coordinates calculates the displacement of the diaphragm. Then, based on the ratio of TA to DA, calculate the actual displacement of the tumor. Finally, add TB to calculate the real-time position of the tumor phantom in the SI direction, as in Eq. [1]. The second step is the conversion of the SI position of the tumor phantom to the ML position of the tumor phantom. This step involves using line fitting to calculate M and b, as in Eq. [2].
SIdiaphragm: the ultrasound captures the real-time position of the diaphragm phantom in the SI direction; SItumor: the real-time position of the tumor phantom in the SI direction; DA: diaphragm amplitude; DB: diaphragm baseline; TA: tumor amplitude; TB: tumor baseline.
MLtumor: the real-time position of the tumor phantom in the ML direction; SItumor: the real-time position of the tumor phantom in the SI direction; M: slope; b: offset.
It’s worth noting that while our previous tumor motion conversion model directly linearly processed ten phases when the tumor phantom moved up and down, in this study, Eq. [2] was improved. As the tumor phantom shows some degree of hysteresis and moves up and down in response to respiratory motion, this study took a different approach. The 10 averaged phases from the 4DCT were further divided into two sets, each containing five phases. One set included the 0–40% phases, while the other consisted of the 50–90% phases. Subsequently, phase data in these separate sets were processed linearly to derive the formula for converting the tumor phantom’s motion from the SI to the ML direction.
Experimental verification
In this study, the development process of the tumor motion conversion model consisted of two stages. The first part involved developing the tumor motion conversion model. It primarily used an ultrasound device (Fukuda Denshi, UF-4000, Broadsound Corporation) to acquire respiratory motion images of the diaphragm phantom. The M-UITA was used to identify the trajectory of the diaphragm phantom, which was synchronized with the Philips Brilliance CT Big Bore machine to obtain 4DCT images of the tumor phantom in 10 phases, aiming to develop the tumor phantom’s motion conversion model. The second part focused on validating the positional accuracy of the tumor phantom’s motion conversion model. The Elekta Synergy System machine was used to compare the tumor phantom’s motion path predicted by the motion conversion model with the actual motion path images obtained through CBCT. The experimental design involved placing the tumor model in three different positions: anterior, middle, and posterior, to represent three types of lung tumor motion models. To verify the accuracy of the tumor phantom’s motion conversion model under different respiratory conditions, each model was tested with four prerecorded human respiratory signals and sine signal.
Experimental setup of the tumor motion model
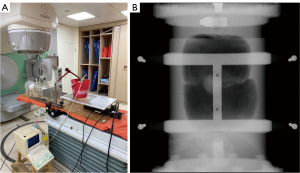
The tumor phantoms and RMSS were set up on the 4D-CT system. The tumor phantoms are classified into three types: Phantom I, Phantom II, and Phantom III, representing tumors located in the lower right lung, upper left lung, and center lung, respectively. The respiratory belt was secured to the abdominal ball to receive signals, and the ultrasound probe was positioned on the diaphragm phantom, as shown in Figure 7A. The ultrasound device detected the movement signals of the diaphragm phantom and used M-UITA to identify its motion position. For the lung phantom, a region was scanned using 4DCT, generating ten sets of axial section images at phases ranging from 0% to 90%, as shown in Figure 7B. After reconstruction, these ten sets of images were combined to create ten coronal composite images, as shown in Figure 7C. The respiratory belt detected deformation signals in the AP direction of the abdominal ball and recorded the data.
Experimental setup for verification of tumor tracking error
The tumor phantom and RMSS were set up on the bed of CBCT. CBCT does not require the use of a respiratory belt as an activation signal, thus the rubber ball was not placed. The ultrasound probe is positioned on the diaphragm phantom. The experimental setup is shown in Figure 8A. The ultrasound detects the motion signals of the diaphragm phantom, and the M-UITA is used to identify the position of diaphragm motion. Using the tumor motion conversion model equations Eq. [1] & Eq. [2], this is transformed into the motion paths of the tumor phantom in the SI and ML directions. These paths are then compared to the actual tumor phantom motion position signals (continuous image frames) obtained by CBCT for verification. CBCT captures images continuously at intervals of 0.18 seconds. The CBCT images record images of all tumor phantom positions within the duration of the scan and the corresponding time. CBCT imaging is performed only in the SI and ML directions, as shown in Figure 8B. Therefore, this experiment verifies the position conversion error only in the SI and ML directions for the tumor motion conversion model.
Results
Tumor motion conversion model refine
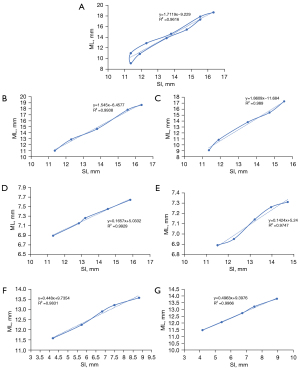
The results were compared with the previous conversion formula, as shown in Figure 9. Using the previous formula, the calculated R2 was 0.93–0.98, while the improved formula resulted in an R2 of 0.97–0.99.
Motion conversion model error results
Each point on the real-time trajectories represents the barycenter position of the tumor phantom in the images captured by CBCT. The imaging resolution of CBCT in this experiment is 0.3 mm/pixel. Figures 10,11 illustrate the conversion error results specifically for pattern E of Phantom III. Figure 10 provides an overall comparison of the coronal plane trajectories. Figure 11A,11B show the actual and estimated real-time tumor phantom motion trajectories in the SI and ML directions, respectively. This data chart demonstrates that the conversion accuracy is effective and robust under different respiratory conditions.
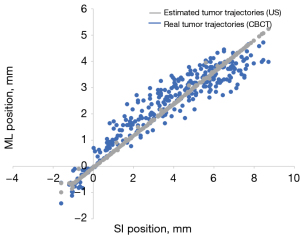
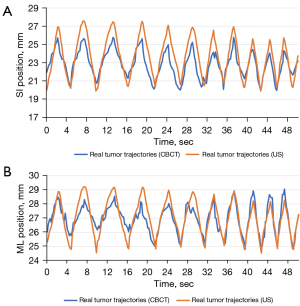
Table 1 displays the positional conversion errors for Phantom I and Phantom III under various breathing patterns. Phantom II is not discussed due to the minimal displacement of the tumor phantom. Each CBCT scan took approximately 60 seconds, resulting in 350 images. The conversion positional error in Table 1 represents the absolute error between the actual tumor phantom displacement observed during CBCT scans and the estimated target trajectories from the tumor conversion model calculated by Eqs. [1,2]. The numbers outside of the brackets represent the median positional error. The numbers inside the brackets represent the lower and upper bounds of positional error for each respiratory cycle. The percentage represents the size of the error relative to the average amplitude. The conversion positional errors in the SI direction range from 0.30 to 1.68 mm and 6.31% to 13.91%, while in the ML direction, they range from 0.25 to 2.05 mm and 6.99% to 18.43%. The error percentage in the SI direction is smaller than that in the ML direction. This is because the ML direction is calculated based on the SI values, resulting in accumulated errors. The obtained data were statistically analyzed using two-tailed Student’s t-tests. A probability value of P<0.05 was considered indicative of a significant difference.
Table 1
| Tumor phantom | Respiratory patterns | Position errors (mm) | Position errors (%) | |||
|---|---|---|---|---|---|---|
| SI | ML | SI | ML | |||
| I | Sin | 1.17 (0.47–1.72)*** | 0.62 (0.36–1.23)*** | 7.67 | 8.22 | |
| A | 0.76 (0.13–1.44)* | 1.21 (0.38–2.24)*** | 9.03 | 15.44 | ||
| B | 1.68 (0.93–2.39)*** | 2.05 (1.96–3.08)*** | 6.55 | 15.98 | ||
| C | 0.99 (0.52–1.64)*** | 0.77 (0.41–1.17)* | 13.91 | 17.27 | ||
| D | 1.09 (0.67–1.50)*** | 1.01 (0.71–1.16)*** | 13.15 | 18.43 | ||
| III | Sin | 0.61 (0.33–1.04)*** | 0.25 (0.19–0.57)*** | 6.78 | 6.99 | |
| A | 0.30 (0.18–0.55)* | 0.73 (0.30–1.04)*** | 6.56 | 16.44 | ||
| B | 0.46 (0.25–0.71)*** | 0.56 (0.33–1.48)*** | 6.31 | 15.43 | ||
| C | 0.38 (0.27–1.21)*** | 0.55 (0.35–0.83)* | 9.97 | 14.80 | ||
| D | 0.84 (0.58–1.51)* | 0.84 (0.42–1.25)** | 12.90 | 15.36 | ||
Data are presented as median (Min–Max) unless otherwise indicated. A signal represents baseline shift, B signal corresponds to deep breath, C signal imitates staged breathing, and D signal represents slow breathing. *, P<0.05; **, P<0.01; ***, P<0.001. ML, medial-lateral; SI, superior-inferior.
Figure 12 compares the conversion positional errors between the ML conversion formula developed in this study and the previous ML formula used by our team. It is evident from Figure 12 that the ML formula developed in this research yields smaller conversion positional errors compared to the previous formula. The larger positional error for input signal B can be partially attributed to the higher amplitude of the input signal waveform and the continuous piston movement, which led to a reduction in lung phantom displacement due to increased internal water pressure. However, it’s important to note that the conversion formula is based on the motion of the diaphragm phantom, so the estimated tumor displacement may differ in magnitude from the measured diaphragm phantom displacement.
Table 2 presents a comparison of positional error parameters. The median values of baseline errors in this study range from 0.12 to 1.72 mm, while the median values of amplitude errors range from 0.23 to 1.96 mm. In the previous conversion formula, the median values of baseline errors range from 0.14 to 1.91 mm, and the median values of amplitude errors range from 0.25 to 2.06.
Table 2
| Tumor phantom |
Respiratory patterns | Position errors (mm) | |||
|---|---|---|---|---|---|
| Previous work baseline | Previous work amplitude | Current work baseline | Current work amplitude | ||
| I | Sin | 0.22 (0.11–0.63) | 0.59 (0.19–1.04) | 0.15 (0.07–0.54) | 0.51 (0.13–0.92) |
| A | 0.42 (0.02–1.57) | 2.06 (0.15–4.05) | 0.35 (0.01–1.44) | 1.96 (0.09–3.86) | |
| B | 1.91 (0.8–0.62) | 1.44 (0.61–2.52) | 1.72 (7.10–6.83) | 1.32 (0.49–2.30) | |
| C | 1.03 (0.39–1.65) | 1.83 (1.29–2.59) | 0.94 (0.34–1.54) | 1.65 (1.04–2.38) | |
| D | 1.14 (0.82–1.68) | 0.48 (0.29–0.81) | 1.00 (0.71–1.50) | 0.42 (0.24–0.61) | |
| III | Sin | 0.14 (0.06–0.45) | 0.25(0.06–0.81) | 0.12 (0.04–0.36) | 0.23 (0.04–0.71) |
| A | 0.23 (0.08–0.49) | 0.46 (0.11–0.97) | 0.19 (0.05–0.42) | 0.42 (0.07–0.89) | |
| B | 0.32 (0.04–0.65) | 0.71 (0.09–1.41) | 0.27 (0.02–0.56) | 0.67 (0.07–1.30) | |
| C | 0.36 (0.12–0.83) | 0.51 (0.06–0.96) | 0.29 (0.08–0.71) | 0.40 (0.04–0.84) | |
| D | 0.64 (0.03–1.15) | 1.01 (0.23–1.56) | 0.52 (0.02–1.00) | 0.94 (0.17–1.44) | |
Data are presented as median (Min–Max) unless otherwise indicated. A signal represents baseline shift, B signal corresponds to deep breath, C signal imitates staged breathing, and D signal represents slow breathing.
Discussion
Our team’s previous design of the phantom had issues with ineffective sealing in the interior compartments, resulting in significant water leakage during the experiment when the piston was in continuous motion. This could potentially lead to problems such as moisture damage and cleanliness issues with the CT equipment. Furthermore, the previous phantom directly propelled the piston to drive the lung phantom, which, despite having a large displacement, could not accurately simulate the actual respiratory motion of the lungs. Therefore, this study aimed to address the problems in the previous phantom design, resolving the issue of water leakage in the phantom and achieving a more faithful representation of the realistic respiratory motion inside the human body.
The tumor phantom motion conversion formula previously developed by our team relied on linear processing of the 10-phase data extracted from 4DCT to obtain the ML conversion formula. However, as respiratory motion causes the tumor phantom’s displacement trajectory to be elliptical, linear processing of the phase data alone is insufficient to accurately predict the precise position trajectory. In this study, the conversion equation was developed based on the elliptical displacement trajectory of the tumor phantom. The 10-phase data extracted from the 4DCT were divided into two sets of five phases, one for upward (0–40% phase) and one for downward motion (50–90% phase), and their phase data was processed separately to derive the ML conversion formula. The correlation (R2) of the tumor phantom’s phase in 4DCT was generally higher in this study, with the highest correlation reaching R2=0.99.
In this study, comparison was made with traditional tracking techniques in conventional X-ray radiation therapy. Pepin et al. (25) tested the CyberKnife® Synchrony® system for synchronized breathing tracking, revealing a total error of 6.9 mm in the SI direction, 4.6 mm in the AP direction, and 3.5 mm in the ML direction. Hoogeman et al. (26) measured the accuracy of the CyberKnife® Synchrony® system during treatment of actual patients, finding that the system’s external-internal correlation errors were 0.2–1.9 mm in the SI direction, 0.1–1.9 mm in the ML direction, and 0.2–2.5 mm in the AP direction. Our study compared with indirect tumor tracking techniques. Fassi et al. (9) utilized a surface sensing system combined with internal-external correlation models for tumor tracking, reporting median tracking errors of 0.7–2.2 mm in the SI direction and 1.2–2.4 mm in the ML direction. Fakhraei et al. (10) proposed a patient-specific model to estimate tumor location during radiation therapy using chest surface displacement as a surrogate signal. Validation on a respiratory phantom and five lung cancer patients showed localization errors of less than 1 mm in the left-right (LR) and AP directions, and less than 2 mm in the SI direction for the phantom, and under 1.1 mm in the LR and AP directions and up to 6.4 mm in the SI direction for patients. Compared to using implanted markers (8,27) to track tumor motion, using ultrasound to monitor diaphragm motion for predicting tumor displacement is non-invasive. The indirect tumor tracking method developed in this study yielded median tracking errors of 0.30 to 1.68 mm in the SI direction and 0.25–2.05 mm in the ML direction. A limitation of this study is that it exclusively considered the SI and ML directions, neglecting the AP direction, and the tumor motion model was developed and validated using the same phantom dataset, which may limit its generalizability. Future studies should explore the conversion formula between diaphragm and tumor motions in the AP direction and validate the model on independent datasets, including practical patient data, to improve its robustness and applicability.
Conclusions
This study developed a novel thoracoabdominal phantom and refined a tumor motion conversion formula for the ML direction. Validation using CBCT confirmed improved accuracy compared to previous models. The developed conversion model in this study is not limited to the use of ultrasound to irradiate the diaphragm. It can be employed with any organ or tissue highly correlated with the tumor, provided that clear ultrasound images can be captured.
Acknowledgments
The authors would like to express their appreciation to the Taipei Medical University Hospital, Taiwan for providing the financial and facilities support for this study.
Footnote
Reporting Checklist: The authors have completed the TRIPOD reporting checklist. Available at https://qims.amegroups.com/article/view/10.21037/qims-24-1777/rc
Funding: This work was supported by
Conflicts of Interest: All authors have completed the ICMJE uniform disclosure form (available at https://qims.amegroups.com/article/view/10.21037/qims-24-1777/coif). The authors have no conflicts of interest to declare.
Ethical Statement: The authors are accountable for all aspects of the work in ensuring that questions related to the accuracy or integrity of any part of the work are appropriately investigated and resolved. The study was conducted in accordance with the Declaration of Helsinki (as revised in 2013). The study was approved by the Ethics Committee of Taipei Medical University Hospital (No. IRB 201902015) and informed consent was obtained from all individual participants.
Open Access Statement: This is an Open Access article distributed in accordance with the Creative Commons Attribution-NonCommercial-NoDerivs 4.0 International License (CC BY-NC-ND 4.0), which permits the non-commercial replication and distribution of the article with the strict proviso that no changes or edits are made and the original work is properly cited (including links to both the formal publication through the relevant DOI and the license). See: https://creativecommons.org/licenses/by-nc-nd/4.0/.
References
- Meijer KM, van Dijk IWEM, Huijskens SC, Daams JG, Balgobind BV, Bel A. Pediatric radiotherapy for thoracic and abdominal targets: Organ motion, reported margin sizes, and delineation variations - A systematic review. Radiother Oncol 2022;173:134-45. [Crossref] [PubMed]
- Goitein M. Organ and tumor motion: an overview. Semin Radiat Oncol 2004;14:2-9. [Crossref] [PubMed]
- Saito M, Suzuki H, Sano N, Ashizawa K, Yoshizawa K, Shibata Y, Ueda K, Komiyama T, Marino K, Aoki S, Saito R, Maehata Y, Onishi H. Evaluation of the target dose coverage of stereotactic body radiotherapy for lung cancer using helical tomotherapy: A dynamic phantom study. Rep Pract Oncol Radiother 2020;25:200-5. [Crossref] [PubMed]
- Shafiei F, Fekri-Ershad S. Detection of Lung Cancer Tumor in CT Scan Images Using Novel Combination of Super Pixel and Active Contour Algorithms. Traitement Du Signal 2020;37:1029-35.
- Makela AV, Schott MA, Sehl OC, Gevaert JJ, Foster PJ, Contag CH. Tracking the fates of iron-labeled tumor cells in vivo using magnetic particle imaging. Nanoscale Adv 2022;4:3617-23. [Crossref] [PubMed]
- Remy C, Bouchard H. Uncertainty-driven determination of target measurement times for indirect tracking validation in adaptive radiotherapy. Phys Med Biol 2022;
- Park JC, Park SH, Kim JH, Yoon SM, Kim SS, Kim JS, Liu Z, Watkins T, Song WY. Four-dimensional cone-beam computed tomography and digital tomosynthesis reconstructions using respiratory signals extracted from transcutaneously inserted metal markers for liver SBRT. Med Phys 2011;38:1028-36. [Crossref] [PubMed]
- Montanaro T, Nguyen DT, Keall PJ, Booth J, Caillet V, Eade T, Haddad C, Shieh CC. A comparison of gantry-mounted x-ray-based real-time target tracking methods. Med Phys 2018;45:1222-32. [Crossref] [PubMed]
- Fassi A, Schaerer J, Fernandes M, Riboldi M, Sarrut D, Baroni G. Tumor tracking method based on a deformable 4D CT breathing motion model driven by an external surface surrogate. Int J Radiat Oncol Biol Phys 2014;88:182-8. [Crossref] [PubMed]
- Fakhraei S, Ehler E, Sterling D, Chinsoo Cho L, Alaei P. A Patient-Specific correspondence model to track tumor location in thorax during radiation therapy. Phys Med 2023;116:103167. [Crossref] [PubMed]
- Dai Z, He Q, Zhu L, Zhang B, Jin H, Yang G, Cai C, Tan X, Jian W, Chen Y, Zhang H, Wu J, Wang X. Automatic prediction model for online diaphragm motion tracking based on optical surface monitoring by machine learning. Quant Imaging Med Surg 2023;13:2065-80. [Crossref] [PubMed]
- Li G. Advances and potential of optical surface imaging in radiotherapy. Phys Med Biol 2022;
- Zhao B, Yang Y, Li T, Li X, Heron DE, Huq MS. Statistical analysis of target motion in gated lung stereotactic body radiation therapy. Phys Med Biol 2011;56:1385-95. [Crossref] [PubMed]
- Pirhadi A, Salari S, Ahmad MO, Rivaz H, Xiao Y. Robust landmark-based brain shift correction with a Siamese neural network in ultrasound-guided brain tumor resection. Int J Comput Assist Radiol Surg 2023;18:501-8. [Crossref] [PubMed]
- Sihono DSK, Ehmann M, Heitmann S, von Swietochowski S, Grimm M, Boda-Heggemann J, Lohr F, Wenz F, Wertz H. Determination of Intrafraction Prostate Motion During External Beam Radiation Therapy With a Transperineal 4-Dimensional Ultrasound Real-Time Tracking System. Int J Radiat Oncol Biol Phys 2018;101:136-43. [Crossref] [PubMed]
- Fontanarosa D, van der Meer S, Bamber J, Harris E, O’Shea T, Verhaegen F. Review of ultrasound image guidance in external beam radiotherapy: I. Treatment planning and inter-fraction motion management. Phys Med Biol 2015;60:R77-114. [Crossref] [PubMed]
- Hindley N, Keall P, Booth J, Shieh CC. Real-time direct diaphragm tracking using kV imaging on a standard linear accelerator. Med Phys 2019;46:4481-9. [Crossref] [PubMed]
- Mostafaei F, Tai A, Gore E, Johnstone C, Haase W, Ehlers C, Cooper DT, Lachaine M, Li XA. Feasibility of real-time lung tumor motion monitoring using intrafractional ultrasound and kV cone beam projection images. Med Phys 2018;45:4619-26. [Crossref] [PubMed]
- Ting LL, Chuang HC, Liao AH, Kuo CC, Yu HW, Tsai HC, Tien DC, Jeng SC, Chiou JF. Tumor motion tracking based on a four-dimensional computed tomography respiratory motion model driven by an ultrasound tracking technique. Quant Imaging Med Surg 2020;10:26-39. [Crossref] [PubMed]
- Ting LL, Guo ML, Liao AH, Cheng ST, Yu HW, Ramanathan S, Zhou H, Boominathan CM, Jeng SC, Chiou JF, Kuo CC, Chuang HC. Development and evaluation of ultrasound image tracking technology based on Mask R-CNN applied to respiratory motion compensation system. Quant Imaging Med Surg 2023;13:6827-39. [Crossref] [PubMed]
- Kim J, Lee Y, Shin H, Ji S, Park S, Kim J, Jang H, Kang Y. Development of deformable moving lung phantom to simulate respiratory motion in radiotherapy. Med Dosim 2016;41:113-7. [Crossref] [PubMed]
- Ehrbar S, Perrin R, Peroni M, Bernatowicz K, Parkel T, Pytko I, Klöck S, Guckenberger M, Tanadini-Lang S, Weber DC, Lomax A. Respiratory motion-management in stereotactic body radiation therapy for lung cancer - A dosimetric comparison in an anthropomorphic lung phantom (LuCa). Radiother Oncol 2016;121:328-34. [Crossref] [PubMed]
- Ting LL, Chuang HC, Liao AH, Kuo CC, Yu HW, Zhou YL, Tien DC, Jeng SC, Chiou JF. Experimental verification of a two-dimensional respiratory motion compensation system with ultrasound tracking technique in radiation therapy. Phys Med 2018;49:11-8. [Crossref] [PubMed]
- Vedam SS, Keall PJ, Kini VR, Mostafavi H, Shukla HP, Mohan R. Acquiring a four-dimensional computed tomography dataset using an external respiratory signal. Phys Med Biol 2003;48:45-62. [Crossref] [PubMed]
- Pepin EW, Wu H, Zhang Y, Lord B. Correlation and prediction uncertainties in the cyberknife synchrony respiratory tracking system. Med Phys 2011;38:4036-44. [Crossref] [PubMed]
- Hoogeman M, Prévost JB, Nuyttens J, Pöll J, Levendag P, Heijmen B. Clinical accuracy of the respiratory tumor tracking system of the cyberknife: assessment by analysis of log files. Int J Radiat Oncol Biol Phys 2009;74:297-303. [Crossref] [PubMed]
- Schmidt ML, Hoffmann L, Møller DS, Knap MM, Rasmussen TR, Folkersen BH, Poulsen PR. Systematic intrafraction shifts of mediastinal lymph node targets between setup imaging and radiation treatment delivery in lung cancer patients. Radiother Oncol 2018;126:318-24. [Crossref] [PubMed]







