MRI signal simulation of liver DDVD (diffusion derived ‘vessel density’) with multiple compartments diffusion model

Fu-Zhao Ma; Ben-Heng Xiao; Yì Xiáng J. Wáng

doi:10.21037/qims-2024-2693

Letter to the Editor

MRI signal simulation of liver DDVD (diffusion derived ‘vessel density’) with multiple compartments diffusion model

Fu-Zhao Ma, Ben-Heng Xiao, Yì Xiáng J. Wáng

Department of Imaging and Interventional Radiology, Faculty of Medicine, The Chinese University of Hong Kong, Hong Kong SAR, China

Correspondence to: Yì Xiáng J. Wáng, PhD. Department of Imaging and Interventional Radiology, Faculty of Medicine, The Chinese University of Hong Kong, 30-32 Ngan Shing Street, Shatin, New Territories, Hong Kong SAR, China. Email: yixiang_wang@cuhk.edu.hk.

Submitted Nov 29, 2024. Accepted for publication Jan 08, 2025. Published online Jan 21, 2025.

doi: 10.21037/qims-2024-2693

Our exploration of diffusion-weighted imaging (DWI) in liver fibrosis evaluation revealed that diffusion-derived ‘vessel density’ (DDVD) can reflect microvascular perfusion. Liver blood vessels including sub-pixel microvessels show high signal when there is no motion probing gradient (b=0 s/mm²) and low signal when even very low b-values (such as b=1, b=2 s/mm²) are applied (1,2). Thus, the signal difference between images when the motion probing gradient is ‘off’ and ‘on’ reflects the extent of tissue vessel density in physiological sense, and we term this as DDVD. DDVD is derived from Eq. [1]:

$D D V D (b_{0}, b_{2}) = \frac{S b_{0}}{R O I a r e a_{0}} - \frac{S b_{2}}{R O I a r e a_{2}} [u n i t : \frac{a r b i t r a r y u n i t (a u)}{p i x e l}]$ [1]

where $R O I a r e a_{0}$ and $R O I a r e a_{2}$ refer to the number of pixels in the selected region-of-interest (ROI) on b=0 and b=2 s/mm² DWI, respectively. $S b_{0}$ refers to the measured sum signal intensity within the ROI when b=0, and $S b_{2}$ refers to the measured sum signal intensity within the ROI when b=2 s/mm², thus $S b / R O I a r e a$ equates to the mean signal intensity within the ROI. $S b_{2}$ and $R O I a r e a_{2}$ can also be approximated by other low b-values (such as b=10 s/mm²) DWI. If we consider a pixel to be an individual ROI, DDVD pixelwise map can be constructed pixel-by-pixel with this same principle (3).

The analysis of DDVD requires only two b-values (with one being b=0 s/mm²and the other being non-zero low b-value), with a significantly shorter scanning time than contrast enhanced computed tomography/magnetic resonance imaging (CT/MRI) while without the need of a contrast agent injection. DDVD measure based on this simple principle is useful as a straightforward imaging biomarker in diverse clinical scenarios. DDVD is a useful parameter for distinguishing livers with and without fibrosis, and livers with more severe fibrosis tend to have even lower DDVD measurements than those with milder liver fibrosis (1,2). He et al. (4) and Li et al. (5) reported that placenta DDVD as a perfusion biomarker allows excellent separation of normal and early pre-eclampsia pregnancies. Lu et al. (6) reported that placenta regional DDVD is significantly higher in pregnant women with placenta accreta spectrum disorders than women with normal placenta, and especially higher in patients with placenta percreta. Hu et al. (7) described that liver hemangiomas can be mostly differentiated from liver mass-forming lesions [hepatocellular carcinomas (HCCs) and focal nodular hyperplasia] solely based on DDVD map. Chen et al. (8) described a proof-of-concept study that a combination of DDVD map and high b-value DWI identifies the exitance and the size of penumbras. As absolute magnetic resonance (MR) signal intensity is influenced by various factors, including B0/B1 spatial inhomogeneity, coil loading, receiver gain, etc., we use the ratio of a lesion to its adjacent native tissue (such as the ratio of HCC’s DDVD to liver DDVD) to minimize these scaling factors (5,9,10).

In this letter, applying the multiple compartments diffusion MRI model, we conduct signal simulation for DDVDs of liver parenchyma and liver simple cyst.

Multiple compartments diffusion model

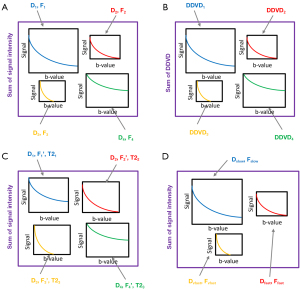
In DWI, each imaged tissue block can be considered to have multiple compartments with different levels of diffusion (Figure 1A). According to the Stejskal-Tanner Eq. [2], each compartment’s signal intensity exhibits mono-exponential decay with the b-value:

$S_{i} (b) = S_{i 0} \cdot e^{- b D_{i}}$ [2]

Figure 1 In diffusion weighted imaging, each imaged tissue block can be considered to have multiple compartments with different levels of diffusion. (A) For a tissue block, hereby it is assumed that there are four compartments, with each having its own diffusion coefficient (D₁, D₂, D₃, D₄) and the related proportion (F₁, F₂, F₃, F₄, F₁+F₂+F₃+F₄=1). (B) The same as multiple compartments model, DDVD of the whole tissue block can also be considered to be comprised of multiple compartments. Four compartments (DDVD₁, DDVD₂, DDVD₃, DDVD₄) are assumed. (C) In a tissue block, in addition to each diffusion compartment having its own diffusion coefficient, each diffusion component also has its own T2 relaxation time (denoted as T2₁, T2₂, T2₃, T2₄). (D) For the liver, a three compartments model is commonly used. The three compartments include: slow compartment [diffusion coefficient is D_slow (D_s), and proportion is F_slow (F_s)], fast compartment [diffusion coefficient is D_fast (D_f), and proportion is F_fast (F_f)], and very fast compartment [diffusion coefficient is D_vfast (D_vf), and proportion is F_vfast(F_vf)]. DDVD, diffusion derived ‘vessel density’.

Where $b$ is the motion probing factor, $S_{i 0}$ is the signal intensity of the compartment when no motion probing gradient is applied, and $D_{i}$ is the diffusion coefficient of the compartment. The signal intensity of the entire tissue block can be considered as the sum of the signal intensities of all compartments:

$S (b) = \sum_{i} S_{i} (b) = S_{0} \cdot \sum_{i} F_{i} \cdot e^{- b D_{i}}$ [3]

$S_{i} (b)$ is the signal intensity of each compartment, $S_{0}$ is the signal intensity of the entire tissue block when the b-value is 0, and $F_{i}$ is the fraction of each compartment. In this letter, symbol $\sum_{i} = \sum_{i = 1}^{n}$ . The following equation must be satisfied for $F_{i}$ :

$\sum_{i} F_{i} = 1$ [4]

DDVD can also be considered as the sum of the differences in signal intensity for each compartment (Figure 1B).

$D D V D (b_{1}, b_{2}) = \sum_{i} D D V D_{i} (b_{1}, b_{2})$ [5]

$= \sum_{i} S_{i} (b_{1}) - S_{i} (b_{2})$ [6]

$= S_{0} \cdot \sum_{i} F_{i} \cdot (e^{- b_{1} D_{i}} - e^{- b_{2} D_{i}})$ [7]

$D D V D_{i}$ represents the $D D V D$ value of each compartment. Therefore, the discussion of the $D D V D$ for an entire tissue block can be separated into the discussion of the $D D V D_{i}$ for each compartment. This allows us to determine the contribution of each compartment to the $D D V D$ value under different b-values and to observe the trend of $D D V D$ change as the b-value changes.

We have been using the first b-value being zero in previous studies, thus $D D V D (0, b_{2})$ equals:

$D D V D (0, b_{2}) = S_{0} \cdot \sum_{i} F_{i} \cdot (1 - e^{- b_{2} D_{i}})$ [8]

In the following discussion, we will continue to use this formula to explore the corresponding changes in the DDVD value when the second b-value ( $b_{2}$ ) changes.

T2 effects between different tissue components

Even when each type of tissue block is considered being composed of only a single diffusion compartment, related to the ‘T₂ shine-through’ effect, the differences in T₂ relaxation times among different tissue components result in variations in $S_{0}$ . This means that the brightness of each tissue component on the DWI at b-value =0 differs, giving signal dependence on the b-value, according to (11-14):

$S (b) = S_{0} \cdot e^{- T E / T_{2}} \cdot e^{- b D}$ [9]

Here, $S_{0}$ is a scalar independent of T₂ and diffusion, $T E$ is the echo time, $T_{2}$ is the T₂relaxation time of the tissue, and $D$ is the diffusion coefficient of the tissue as a whole. Therefore, the signal intensity is not solely determined by diffusion but is also influenced by the T2 values of the tissue components.

T2 effect between different T2 values of different compartments of a tissue block

With a tissue block having multiple diffusion compartments, and the T₂ effect introduces another influence. If we consider that each component has its own T₂ relaxation time, with a corresponding $E_{2 i} = e^{- \frac{T E}{T_{2 i}}}$ , the expression for signal intensity should be (Figure 1C):

$S (b) = {S^{'}}_{0} \cdot \sum_{i} {F^{'}}_{i} \cdot E_{2}_{i} \cdot e^{- b D_{i}}$ [10]

Here, $S_{0}^{'}$ and $F_{i}^{'}$ are the original parameters without considering the T₂ effect. After re-normalization, we obtain the following equation:

$S (b) = {S^{'}}_{0} \cdot (\sum_{i} {F^{'}}_{i} \cdot E_{2}_{i}) \cdot \sum_{i} \frac{{F^{'}}_{i} \cdot E_{2}_{i}}{\sum_{i} {F^{'}}_{i} \cdot E_{2}_{i}} \cdot e^{- b D_{i}}$ [11]

After simplification, we can further obtain:

$\begin{matrix} S (b) = S_{0} \cdot \sum_{i} F_{i} \cdot e^{- b D_{i}} \end{matrix}$ [12]

The measured F_i, D_i, and S₀are always and already modulated by T₂ effect, and the measured values will change following the adjustment of the time of echo (TE) parameter. This type of T₂ effect will affect the measured F_i(i.e., the measured proportions of different diffusion compartments), while this T₂ effect will not affect the measure of D_i.

Tri-exponential diffusion model

It has been suggested that liver’s DWI signal attenuation follows a tri-exponential model, which was found to better describe the intravoxel incoherent motion (IVIM) signal decay in the liver when the b-value is within the 0–800 s/mm² range (15-19). The tri-exponential IVIM model comprises three compartments: a slow diffusion compartment, a fast perfusion-related compartment, and a very fast perfusion-related compartment, and thus the signal intensity decay can be represented as (Figure 1D):

$S (b) = S_{0} \cdot (F_{s} \cdot e^{- b D_{s}} + F_{f} \cdot e^{- b D_{f}} + F_{V f} \cdot e^{- b D_{V f}})$ [13]

where $D_{s}$ denotes the slow diffusion coefficient, $D_{f}$ and $D_{V f}$ represent the fast and very fast perfusion-related pseudo-diffusion coefficients, respectively. $F_{s}$ , $F_{f}$ , and $F_{V f}$ are the fractions of each compartment. The measured values of the diffusion coefficients in literature vary substantially (17).

Numerical simulation of the liver DDVD

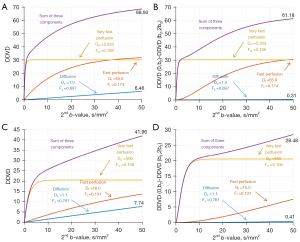
Considering the tri-exponential diffusion model, we attempt to simulate the numerical results of liver DDVD by varying the b₂value. Due to the significant differences between the diffusion coefficients and based on our earlier research (20), we gradually increase b₂from 0 to 10 s/mm² and then to 50 s/mm² to observe the numerical changes in liver DDVD.

In order to numerically simulate the liver’s DDVD, specific parameter values are required. In the literature, the measurements of $D_{s}$ , $F_{V f}$ , $F_{f}$ , and $F_{s}$ are relatively stable, while the measurements of $D_{V f}$ and $D_{f}$ show substantial variations (Table 1) (15-19). To show that our numerical simulation analysis is robust across variations of the reported parameter values, we use two sets of parameter measurements described by Riexinger et al. (18,19). As shown in Table 1, the first set has higher measurements for $D_{V f}$ and $D_{f}$ , while the second set has lower measurements for $D_{V f}$ and $D_{f}$ . The final simulation results of the DDVD curve indicate that the pattern of changes in DDVD values still follow our prediction even considering the substantial variations in tri-exponential diffusion model parameter values.

Table 1

Tri-exponential decay model liver diffusion parameter values reported by Riexinger et al. (18) (for Test 1) and Riexinger et al. (19) (for Test 2)

Source	B₀	TE	D_s	F_s	D_f	F_f	D_vf	F_vf
Test 1	3.0T	100 ms	1.0	0.697	65.9	0.174	2,333	0.159
Test 2	3.0T	45 ms	1.1	0.761	16.0	0.131	500	0.108

Test 1 had higher F_f and F_vf measures, and much higher D_f and D_vf measures. Test 1 used a much longer TE. For acquired signal, a longer TE has the same effect as shorter T2, which have been noted to promote the ‘apparent’ values of perfusion related parameters relative to the ‘apparent’ values measured with a shorter TE (21,22). D_s, D_f, D_vf unit in ×10⁻³ mm²/s. B₀, field strength of the main magnetic field; TE, time of echo.

Liver DDVD numerical simulation when the b₂ is less than 10 s/mm²

For the diffusion and fast perfusion compartments, because of the much lower diffusion coefficient relative to that of the very fast compartment, the value at exponential term is small enough to take one order Taylor expansion and their $D D V D_{i}$ can be approximated as:

$\begin{matrix} D D V D_{i} = S_{0} \cdot F_{i} \cdot (1 - e^{- b_{2} D_{i}}) = S_{0} b_{2} F_{i} D_{i} \end{matrix}$ [14]

Eq. [14] indicates that the DDVD values of these two compartments will increase linearly with b₂. Regardless the significant variation in the measured values of $D_{f}$ (ranging from 16×10⁻³ to 65.9×10⁻³ mm²/s) (15-19), the Eq. [14] remains valid. Additionally, since $D_{s}$ is very small, the contribution of diffusion to DDVD is minimal and can be neglected.

For the very fast perfusion compartment, regardless of the numerical system used, the amount of related DDVD growth will gradually become close to zero with b₂ changes to 10 s/mm². In such a case, $D D V D_{i}$ will approach a fixed value:

$D D V D_{V f} = S_{0} \cdot F_{V f}$ [15]

Therefore, when b₂ is less than 10 s/mm², liver DDVD can be written as:

$D D V D (0, b_{2}) = S_{0} \cdot (F_{V f} (1 - e^{- b_{2} D_{v f}}) + b_{2} F_{f} D_{f})$ [16]

The second term has a limited impact on the value and can be considered a correction term. When the very fast perfusion compartment has nearly completely plateaued, the above equation can be simplified to:

$D D V D (0, b_{2}) = S_{0} \cdot (F_{V f} + b_{2} F_{f} D_{f})$ [17]

At this point, the measured $D D V D (0, b_{2})$ fully reflects the perfusion information with minimal influence from diffusion. DDVD is predominantly affected by F_vf, F_fand D_f. More importantly, the most unstable measurement, $D_{v f}$ , does not contribute to the value of $D D V D (0, b_{2})$ (Figure 2).

Figure 2 Numerical simulation of liver DDVD with a higher D_vf and D_f measurement as described in the study by Riexinger et al. (18). D_vf =2,333×10⁻³ mm²/s, F_vf =0.159; D_f =65.9×10⁻³ mm²/s, F_f =0.174 and D_s =1.0×10⁻³ mm²/s, F_s =0.697. Yellow line is for very fast compartment, red line is for fast compartment, and blue line is for the slow diffusion compartment. Violet line is the sum of three lines, thus representing the liver sum (measured) DDVD. The red point in (A,B) denotes the approximated estimation of liver DDVD equaling S₀∙(F_vf + b₂F_fD_f), when b₂ is approximately between 1 and 10 s/mm². Liver (summed) DDVD at b₂=2 and 10 s/mm² are closer to our recent measurements [according to Ju et al. (20), 3.0T DDVD at b₂ of 2 s/mm² was 37.8 au/pixel, 3.0T DDVD at b₂=10 s/mm² was 51.5 au/pixel]. In (A), when b₂=2 s/mm², DDVD is dominated by contributions by F_vf (88.2%), followed by F_fand D_f. In (B), when b₂=10 s/mm², DDVD is dominated by contributions by F_vf (63.8%), F_f and D_f. The estimation of DDVD based on the first-order approximation is still valid until b₂=10 s/mm², indicating that the contributions of F_f and D_f are comparable. In (C), when b₂=50 s/mm², three compartments all contribute to DDVD. DDVD in arbitrary unit (au)/pixel. DDVD, diffusion derived ‘vessel density’.

Liver DDVD numerical simulation when the b₂ is between 10 and 50 s/mm²

For the diffusion compartment, the linear approximation remains valid, and its related DDVD variation follows Eq. [14]. The influence of this compartment on the DDVD value has gradually increased and can no longer be ignored but still remains a linear pattern (note that: this also works for the diffusion of other organs as D_s has a limited dynamic range and no matter which organ or structure, the change in $D D V D_{i}$ corresponding to diffusion can always be approximated as a straight line).

For the very fast compartment which has plateaued and its influence on the DDVD remains unchanged, its related DDVD contribution follows Eq. [15]. Considering the sum of all sub-compartments, the liver DDVD can be represented as:

$D D V D (0, b_{2}) = S_{0} \cdot (F_{V f} + F_{f} (1 - e^{- b_{2} D_{f}}) + b_{2} F_{s} D_{s})$ [18]

According to the numerical simulation of two sets of data (i.e., lower D_vf measure and high D_vf, Figure 3), following the increase of b₂ from 0 to 50 s/mm², liver (summed) DDVD had an initial phase of rapid increase, followed by a slow increase. Prior to the inflection point, the DDVD signal change is dominated by the very fast compartment; after the inflection point, the DDVD signal change is dominated by the fast compartment. When the values of $D_{v f}$ and $D_{f}$ have a greater difference, the difference of the DDVD growth slopes before and after the inflection point is also greater. On the other hand, if the values of $D_{v f}$ and $D_{f}$ have a smaller difference, the DDVD growth curve around the inflection point will be smoother.

Figure 3 Numerical simulation of liver DDVD with a lower D_vf and D_fmeasurement as described in the study by Riexinger et al. (19). (A-C) D_vf =500×10⁻³ mm²/s, F_vf =0.108; D_f =16.0×10⁻³ mm²/s, F_f =0.131 and D_s =1.1×10⁻³ mm²/s, F_s =0.761. Yellow line is for very fast compartment, red line is for fast compartment, and blue line is for the slow diffusion compartment. Violet line is the sum of three lines, thus representing the liver sum (measured) DDVD. The red point in (B) denotes the approximated estimation of liver DDVD equaling S₀∙(F_vf+ b₂F_fD_f). DDVD in arbitrary unit/pixel. DDVD, diffusion derived ‘vessel density’.

An attempt to offset the impact of diffusion on DDVD value

According to the simulation results shown in Figure 4. When b₂is relatively large, the impact of diffusion on DDVD measure can no longer be ignored. Since we intend to use DDVD to measure perfusion related information, following the parameters shown in Eq. [18], we proposed to use the following equation to mitigate the impact of diffusion on DDVD (3):

$D D V D (0, b_{2}) - D D V D (b_{2}, 2 b_{2})$ [19]

Figure 4 Numerical simulation of liver DDVD and a mitigation approach for the slow diffusion effect. Estimations in (A,B) utilized a higher D_vf and D_f measurement as described in the study by Riexinger et al. (18), and the results are closer to our actual measurements described in the study by Ju et al. (20). Estimations in (C,D) utilized a lower D_vf and D_f measurement as described in the study by Riexinger et al. (19). Following the mitigation approach for the slow diffusion effect by DDVD(b₀, b₂) – DDVD(b₂, 2×b₂), the summed signal decreased slightly to moderately from original DDVD [for example, at b₂=50 s/mm², (A)→(B): 68.50→61.18, (C)→(D): 41.96→28.48] while the signal of slow diffusion decreased to an unmeasurable level [for example, at b₂=50 s/mm², (A)→(B): 6.46→0.31, (C)→(D): 7.74→0.41]. Violet line is the sum of three lines, orange line is for very fast compartment, red line is for fast compartment, and blue line is for the slow diffusion compartment. D_s, D_f, D_vf unit in ×10⁻³ mm²/s. DDVD in arbitrary unit/pixel. DDVD, diffusion derived ‘vessel density’.

For the diffusion compartment, as the relationship between b₂and DDVD always follow an appropriately linear pattern, thus Eq. [19] is approximated by:

$(b_{2} - 0) \cdot F_{s} D_{s} - (2 b_{2} - b_{2}) \cdot F_{s} D_{s} = 0$ [20]

For the signal growth of very fast perfusion, when $b_{2}$ is relatively ‘high’ (such as 30 s/mm²), it can be assumed that:

$D D V D_{V f} (b_{2}, 2 b_{2}) = 0$ [21]

Considering the sum of very fast compartment, fast compartment, and slow (diffusion) compartment, Eq. [19] can be re-written as:

$D D V D (0, b_{2}) - D D V D (b_{2}, 2 b_{2}) = S_{0} \cdot (F_{V f} + F_{f} (1 - 2 e^{- b_{2} D_{f}} + e^{- b_{2} D_{f}}))$ [22]

The simulation results for Eq. [19] shown in Figure 4 demonstrate that, after the application of Eq. [19], the diffusion compartment is well eliminated.

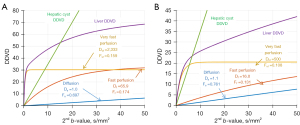
Numerical simulation in the case of liver simple cyst

It’s possible that a liver simple cyst is comprised of a single compartment. Given the lack of perfusion, cyst DWI signal follows a mono-exponential decay due to its relatively non-restricted diffusion. In the meantime, the corresponding diffusion coefficient should be less than 2.5×10⁻³ mm²/s (23,24).

In addition to its diffusion property, liver simple cyst has a markedly longer T2 relaxation time compared with that of the liver. Thus, cysts consistently display a higher signal on DWI images, irrespective of the b-value. Liver cyst DDVD can be represented as:

$D D V D_{c y s t} (0, b_{2}) = S_{0, c y s t} \cdot b_{2} \cdot D_{s, c y s t}$ [23]

The intercept of Y-axis (Y-axis is DDVD and X-axis is b₂) will always be zero in an idealized measurement. Though the coefficient $S_{0, c y s t}$ is very high, the relationship between $b_{2}$ and DDVD_cyst will follow a linear line, the slope of the line is determined by (S_0,cyst × D_s,cyst), where T2 contributes to S_0,cyst(Figure 5).

Figure 5 Numerical simulation of liver DDVD and liver simple cyst DDVD. (A) simulation utilizing a higher measurement of liver D_vfand D_f as described in the study by Riexinger et al. (18). (B) simulation utilizing a lower measurement of liver D_vf and D_f as described in the study by Riexinger et al. (19). Yellow line is for very fast compartment, red line is for fast compartment, and blue line is for the slow diffusion compartment. Violet line is the sum of three lines, thus representing the liver sum (measured) DDVD. The green line represents the liver cyst DDVD which is considered to contain solely a slow diffusion compartment. According to the current estimation and under idealized conditions (when without positioning shift between the DW images of two b-values), the measured DDVD value of the cyst exceeds that of the liver at approximately b₂=15 s/mm² (A). D_s, D_f, D_vfunit in ×10⁻³ mm²/s. DDVD in arbitrary unit/pixel. DDVD, diffusion derived ‘vessel density’.

Acknowledgments

Funding: This study received funding from a Hong Kong GRF Project (No. 14112521).

Footnote

Conflicts of Interest: All authors have completed the ICMJE uniform disclosure form (available at https://qims.amegroups.com/article/view/10.21037/qims-2024-2693/coif). Y.X.J.W. serves as the Editor-in-Chief of Quantitative Imaging in Medicine and Surgery. Y.X.J.W. is the founder of Yingran Medicals Ltd., which develops medical image-based diagnostics software. B.H.X. contributed to the development of Yingran Medicals Ltd. The other author has no conflicts of interest to declare.

Ethical Statement: The authors are accountable for all aspects of the work in ensuring that questions related to the accuracy or integrity of any part of the work are appropriately investigated and resolved.

Open Access Statement: This is an Open Access article distributed in accordance with the Creative Commons Attribution-NonCommercial-NoDerivs 4.0 International License (CC BY-NC-ND 4.0), which permits the non-commercial replication and distribution of the article with the strict proviso that no changes or edits are made and the original work is properly cited (including links to both the formal publication through the relevant DOI and the license). See: https://creativecommons.org/licenses/by-nc-nd/4.0/.

References

Wáng YXJ. Living tissue intravoxel incoherent motion (IVIM) diffusion MR analysis without b=0 image: an example for liver fibrosis evaluation. Quant Imaging Med Surg 2019;9:127-33. [Crossref] [PubMed]
Xiao BH, Huang H, Wang LF, Qiu SW, Guo SW, Wáng YXJ. Diffusion MRI Derived per Area Vessel Density as a Surrogate Biomarker for Detecting Viral Hepatitis B-Induced Liver Fibrosis: A Proof-of-Concept Study. SLAS Technol 2020;25:474-83. [Crossref] [PubMed]
Yao DQ, Zheng CJ, Deng YY, Lu BL, Lu T, Hu GW, Li XM, Xiao BH, Ma FZ, Sabarudin A, King AD, Wáng YXJ. Potential diverse applications of diffusion-derived vessel density (DDVD) pixel-by-pixel mapping. Quant Imaging Med Surg 2024;14:2136-45. [Crossref] [PubMed]
He J, Chen C, Xu L, Xiao B, Chen Z, Wen T, Wáng YXJ, Liu P. Diffusion-Derived Vessel Density Computed From a Simplified Intravoxel Incoherent Motion Imaging Protocol in Pregnancies Complicated by Early Preeclampsia: A Novel Biomarker of Placental Dysfunction. Hypertension 2023;80:1658-67. [Crossref] [PubMed]
Li CY, Chen L, Ma FZ, Chen JQ, Zhan YF, Wáng YXJ. High performance of the diffusion magnetic resonance imaging biomarker diffusion-derived ‘vessel density’ (DDVD) for separating placentas associated with pre-eclampsia from placentas in normal pregnancy. Quant Imaging Med Surg 2025;15:1-14. [Crossref]
Lu T, Wang L, Li M, Wang Y, Chen M, Xiao BH, Wáng YXJ. Diffusion-derived vessel density (DDVD) computed from a simple diffusion MRI protocol as a biomarker of placental blood circulation in patients with placenta accreta spectrum disorders: A proof-of-concept study. Magn Reson Imaging 2024;109:180-6. [Crossref] [PubMed]
Hu GW, Li CY, Zhang G, Zheng CJ, Ma FZ, Quan XY, Chen W, Sabarudin A, Zhu MSY, Li XM, Wáng YXJ. Diagnosis of liver hemangioma using magnetic resonance diffusion-derived vessel density (DDVD) pixelwise map: a preliminary descriptive study. Quant Imaging Med Surg 2024;14:8064-82. [Crossref] [PubMed]
Chen JQ, Li CY, Wang W, Yao DQ, Jiang RF, Wáng YXJ. Diffusion-derived vessel density (DDVD) for penumbra delineation in brain acute ischemic stroke: initial proof-of-concept results using single NEX DWI. Quant Imaging Med Surg 2024;14:9533-42. [Crossref] [PubMed]
Li XM, Yao DQ, Quan XY, Li M, Chen W, Wáng YXJ. Perfusion of hepatocellular carcinomas measured by diffusion-derived vessel density biomarker: Higher hepatocellular carcinoma perfusion than earlier intravoxel incoherent motion reports. NMR Biomed 2024;37:e5125. [Crossref] [PubMed]
Lu BL, Yao DQ, Wáng YXJ, Zhang ZW, Wen ZQ, Xiao BH, Yu SP. Higher perfusion of rectum carcinoma relative to tumor-free rectal wall: quantification by a new imaging biomarker diffusion-derived vessel density (DDVD). Quant Imaging Med Surg 2024;14:3264-74. [Crossref] [PubMed]
Stejskal EO, Tanner JE. Spin Diffusion Measurements: Spin Echoes in the Presence of a Time Dependent Field Gradient. J Chem Phys 1965;42:288-92. [Crossref]
Le Bihan D, Breton E, Lallemand D, Grenier P, Cabanis E, Laval-Jeantet M. MR imaging of intravoxel incoherent motions: application to diffusion and perfusion in neurologic disorders. Radiology 1986;161:401-7. [Crossref] [PubMed]
Le Bihan D, Turner R, Moonen CT, Pekar J. Imaging of diffusion and microcirculation with gradient sensitization: design, strategy, and significance. J Magn Reson Imaging 1991;1:7-28. [Crossref] [PubMed]
Jerome NP, d'Arcy JA, Feiweier T, Koh DM, Leach MO, Collins DJ, Orton MR. Extended T2-IVIM model for correction of TE dependence of pseudo-diffusion volume fraction in clinical diffusion-weighted magnetic resonance imaging. Phys Med Biol 2016;61:N667-80.
Cercueil JP, Petit JM, Nougaret S, Soyer P, Fohlen A, Pierredon-Foulongne MA, Schembri V, Delhom E, Schmidt S, Denys A, Aho S, Guiu B. Intravoxel incoherent motion diffusion-weighted imaging in the liver: comparison of mono-, bi- and tri-exponential modelling at 3.0-T. Eur Radiol 2015;25:1541-50. [Crossref] [PubMed]
Chevallier O, Zhou N, Cercueil JP, He J, Loffroy R, Wáng YXJ. Comparison of tri-exponential decay versus bi-exponential decay and full fitting versus segmented fitting for modeling liver intravoxel incoherent motion diffusion MRI. NMR Biomed 2019;32:e4155. [Crossref] [PubMed]
Chevallier O, Wáng YXJ, Guillen K, Pellegrinelli J, Cercueil JP, Loffroy R. Evidence of Tri-Exponential Decay for Liver Intravoxel Incoherent Motion MRI: A Review of Published Results and Limitations. Diagnostics (Basel) 2021;11:379. [Crossref] [PubMed]
Riexinger AJ, Martin J, Rauh S, Wetscherek A, Pistel M, Kuder TA, Nagel AM, Uder M, Hensel B, Müller L, Laun FB. On the Field Strength Dependence of Bi- and Triexponential Intravoxel Incoherent Motion (IVIM) Parameters in the Liver. J Magn Reson Imaging 2019;50:1883-92. [Crossref] [PubMed]
Riexinger A, Martin J, Wetscherek A, Kuder TA, Uder M, Hensel B, Laun FB. An optimized b-value distribution for triexponential intravoxel incoherent motion (IVIM) in the liver. Magn Reson Med 2021;85:2095-108. [Crossref] [PubMed]
Ju ZG, Leng XM, Xiao BH, Sun MH, Huang H, Hu GW, Zhang G, Sun JH, Zhu MSY, Guglielmi G, Wáng YXJ. Influences of the second motion probing gradient b-value and T2 relaxation time on magnetic resonance diffusion-derived ‘vessel density’ (DDVD) calculation: the examples of liver, spleen, and liver simple cyst. Quant Imaging Med Surg 2025;15:74-87. [Crossref]
Lemke A, Laun FB, Simon D, Stieltjes B, Schad LR. An in vivo verification of the intravoxel incoherent motion effect in diffusion-weighted imaging of the abdomen. Magn Reson Med 2010;64:1580-5. [Crossref] [PubMed]
Ma FZ, Wáng YXJ T. (2) relaxation time elongation of hepatocellular carcinoma relative to native liver tissue leads to an underestimation of perfusion fraction measured by standard intravoxel incoherent motion magnetic resonance imaging. Quant Imaging Med Surg 2024;14:1316-22. [Crossref] [PubMed]
Gatidis S, Schmidt H, Martirosian P, Schwenzer NF. Development of an MRI phantom for diffusion-weighted imaging with independent adjustment of apparent diffusion coefficient values and T2 relaxation times. Magn Reson Med 2014;72:459-63. [Crossref] [PubMed]
Kalaitzakis G, Boursianis T, Gourzoulidis G, Gourtsoyianni S, Lymperopoulou G, Marias K, Karantanas A, Maris TG. Apparent diffusion coefficient measurements on a novel diffusion weighted MRI phantom utilizing EPI and HASTE sequences. Phys Med 2020;73:179-89. [Crossref] [PubMed]

Cite this article as: Ma FZ, Xiao BH, Wáng YXJ. MRI signal simulation of liver DDVD (diffusion derived ‘vessel density’) with multiple compartments diffusion model. Quant Imaging Med Surg 2025;15(2):1710-1718. doi: 10.21037/qims-2024-2693

MRI signal simulation of liver DDVD (diffusion derived ‘vessel density’) with multiple compartments diffusion model

Multiple compartments diffusion model

Tri-exponential diffusion model

Numerical simulation of the liver DDVD

Table 1

Liver DDVD numerical simulation when the b₂ is less than 10 s/mm²

Liver DDVD numerical simulation when the b₂ is between 10 and 50 s/mm²

Numerical simulation in the case of liver simple cyst

Acknowledgments

Footnote

References

Article Options

Download Citation

Share

Multiple compartments diffusion model

Tri-exponential diffusion model

Numerical simulation of the liver DDVD

Table 1

Liver DDVD numerical simulation when the b2 is less than 10 s/mm2

Liver DDVD numerical simulation when the b2 is between 10 and 50 s/mm2

Numerical simulation in the case of liver simple cyst

Acknowledgments

Footnote

References

Article Options

Download Citation

Share

Liver DDVD numerical simulation when the b₂ is less than 10 s/mm²

Liver DDVD numerical simulation when the b₂ is between 10 and 50 s/mm²