
Texture analysis combined with machine learning in radiographs of the knee joint: potential to identify tibial plateau occult fractures
Introduction
As an important weight-bearing joint of the human body, the knee joint has a high likelihood of trauma. Among them, the incidence of tibial plateau fracture accounts for about 1% of all fractures and 8% of fractures in the elderly (1). Occult fracture is a type of fracture characterized by a trabecular fracture of the phalanx, also known as hidden fracture, subchondral bone contusion, and hidden intraosseous fracture (2,3). X-ray examination is a convenient and economical imaging method, especially preferred in clinical work, particularly in the examination of emergency orthopedic patients. When an occult fracture occurs, due to subtle changes in bones, routine X-ray examination often fails to detect changes in bone structure, except for indirect signs such as soft tissue swelling and joint capsule effusion, which can easily lead to missed diagnoses, delaying patient treatment and even exacerbating the condition (4). Magnetic resonance imaging (MRI) has great advantages in detecting hidden fractures (2). However, due to the time-consuming and many contraindications of MRI, it is rarely used in the emergency examination of patients with bone trauma. Patients diagnosed with occult fractures through MRI often have a period of time since the first examination. During this period, incorrect treatment by doctors or patient negligence may lead to deterioration of the condition. Therefore, improving the early diagnosis rate of occult fractures has a positive effect on improving the prognosis of patients.
Texture analysis (TA) can extract many image features that are not visible to the naked eye and reflect heterogeneity within the lesion (5). Due to the large amount of data involved in TA, the corresponding algorithm is applied for feature extraction and model construction. Once trained, these features can lead to strong inferences known as machine learning (ML) (6). By learning from past calculations and extracting the rules from massive databases, it can help humans generate reliable and repeatable decisions (7). By using the ML method to filter out key information for diagnosing diseases from a large number of texture features, auxiliary diagnosis, classification, or grading of diseases can be facilitated. In recent years, radiomics has been widely studied and used in the differential diagnosis of tumors with multiple systems, pathological grading, prognosis prediction and efficacy evaluation (8-15). In musculoskeletal imaging, most studies have mainly focused on the diagnosis of diseases such as osteoporosis, fractures and osteoarthritis and have achieved many results (16-22). However, there are currently few studies using X-ray images for TA to predict occult fractures, and it is particularly necessary to explore ML models for predicting the risk of occult fractures based on plain films.
This study had two primary objectives: One is to extract texture features from knee X-ray images and compare the performance of various ML methods in classifying occult tibial plateau fractures. The other is to select the best feature selection method to identify key features for diagnosing occult tibial plateau fractures, ultimately establishing the most effective prediction model for assessing the risk of these fractures. We present this article in accordance with the TRIPOD+AI reporting checklist (available at https://qims.amegroups.com/article/view/10.21037/qims-24-799/rc).
Methods
Patient selection
This retrospective study was conducted in accordance with the Declaration of Helsinki (as revised in 2013) and approved by the local institutional review board of Sichuan Orthopedic Hospital (No. KY-2024-039-01). Due to the retrospective nature of the study, the requirement for written informed consent was waived.
Figure 1 shows the flow chart of the inclusion and exclusion of case-control studies. From 2018 to 2022, patients underwent emergency X-ray examination in Sichuan Orthopedic Hospital due to knee joint trauma and showed negative fractures but subsequent MRI confirmed occult fractures of the tibial plateau or no fractures were included in the study. The interval between X-ray and MRI examination was not more than one week. Exclusion criteria included nonstandard position of the radiographs, obvious osteoporosis and hyperostosis of the knee joint or other conditions, such as tumor, postoperative, and unclosed epiphyseal plate, that affect the density of the tibial plateau. All imaging labels were jointly marked by two radiologists with more than ten years of experience in musculoskeletal imaging diagnosis. In cases of disagreement between the two radiologists during image interpretation, a consensus was reached after consulting a third physician with similar qualifications.
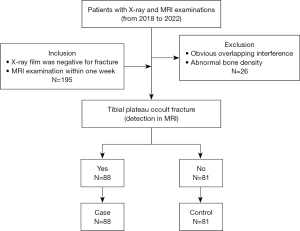
Our study collected 195 patients with negative knee X-ray fractures but MRI showing occult fractures or no fractures of the tibial plateau. Eight patients were excluded due to severe osteoarthritis, 6 patients were excluded due to obvious osteoporosis, 6 patients were excluded due to an abnormal lateral position, 3 patients were excluded due to an unclosed epiphyseal plate of the tibial plateau, 2 patients were excluded due to a growth obstacle line of the tibial plateau, and 1 patient was excluded due to an intramedullary bone island of the tibial plateau. Finally, 169 patients were enrolled in the study, including 88 patients in the occult fracture group (case group) and 81 patients in the non-fracture group (control group).
Imaging devices and procedures
The X-ray examinations were conducted on two different devices (Aristos FX-Plus, Siemens Healthineers; or SONIALVISION safire, Shimadzu Medical Systems). When anteroposterior position examination was being performed, the patient lay on their back on the photography bed, with their lower limbs extended and their toes facing upwards. The centerline was perpendicular to the midpoint of the lower edge of the patella, with an irradiation field of 24 cm × 18 cm, tube voltage of 60±3 kV, and tube current of 5–6 mAs. When lateral position examination of the knee joint was being performed, the patient lay on their side on the photography bed, and the opposite knee was bent forward and placed in front of the subject side. The outer side of the tested knee was closely attached to the bed surface, with knee joint flexion of approximately 135°. The centerline was tilted 5° to 7° toward the head side, shooting directed through the anterior 1/3 of the junction of the lower edge of the patella and the popliteal fossa, with an irradiation field of 24 cm × 18 cm, tube voltage of 60±3 kV, and tube current of 5–6 mAs.
MRI examinations were performed with a 1.5T scanner (Signa Exploere, GE Healthcare) using a specialized coil for the knee joint. The patient was placed in a supine position with advanced feet, and the knee joint was rotated outward by 10–15°. The scanning center was the lower edge of the patella, and the scanning range included the complete knee joint. The MRI protocol included five sequences: sagittal fast spin echo (FSE) sequence fat-saturation T2-weighted imaging (T2WI) [repetition time/time to echo (TR/TE) =4,111 ms/84 ms], sagittal FSE fat-suppressed proton density weighted imaging (PDWI) (TR/TE =2,640 ms/36 ms), coronal FSE fat-saturation T1-weighted imaging (T1WI) (TR/TE =654 ms/11 ms), coronal FSE fat-suppressed PDWI (TR/TE =2,500 ms/37 ms), and transverse FSE fat-suppressed PDWI (TR/TE =2,450 ms/33 ms). The thickness/spacing of the sagittal, coronal and transverse slices were 3.5 mm/0.8 mm, 3.0 mm/0.6 mm and 4 mm/1 mm, respectively; the scanning field of view was 160 mm × 160 mm; the matrix was 320×256.
Texture parameter extraction
A total of 169 patients’ knee radiographs were imported into the Radiant DICOM Viewer (version 2020.2.3), and the images were set to uniform size and exported in BMP format. Then, the image was imported into MaZda software (version 4.6). Before extracting texture features, all images were normalized at the grayscale level in the range of [m-3s, m+3s] (m is the average grayscale value of the image, s is the standard deviation) to reduce the impact of differences in image contrast and brightness on the results. Region of interest (ROI) delineation was performed along the proximal tibial cortex on anteroposterior and lateral X-ray images, with the upper boundary being the tibial plateau joint surface and the lower boundary being 2 cm below the epiphyseal line. In the process of the depiction, hyperplastic osteophytes should be avoided, and a substantially thickened cortex should be delineated along its inner edge. Two radiologists with more than 10 years of experience in musculoskeletal imaging diagnosis manually delineated the ROI on each case and took the average value of the two as the final result.
A total of 291 quantitative parameters were extracted for each ROI using six feature calculation methods, including gray level histogram (GLH), gray-level run-length matrix (GLRLM), absolute gradient (GRA), gray-level co-occurrence matrix (GLCOM), autoregressive model (ARM), and wavelet transform (WAV). Samples with missing features were removed during data cleaning, resulting in a final dataset of 82 case samples and 78 control samples. Each sample contained a total of 582 texture features, 291 from anteroposterior views and 291 from lateral views. To distinguish between anteroposterior and lateral features, we attached “(C)” to the name of each lateral X-ray texture feature, such as WavEnHH_S-5 (C).
Feature selection and model construction
Feature engineering was performed in the Jupyter notebook (version 5.7.4). We applied six methods for feature selection, which were divided into three categories, including F_classif in filtered analysis of variance, wrapped least absolute shrinkage and selection operator (LASSO) and recursive feature elimination (RFE), as well as embedded random forest (RF), gradient boosting decision tree (GBDT) and eXtreme gradient boosting (XGBoost). The results of these six methods were compared with the feature selection methods [mutual information (MI), Fisher, probability of classification error + average correction coefficient (POE +ACC)] of MaZda software. It is worth mentioning that we only focused on specific hyperparameters that had been identified as crucial and could significantly impact the model performance (23). The F_classif method utilized the SelectPercentile() function, with the percentile threshold set to 5, to select the top 5% of features that had the highest correlation with the target variable. Other settings remained at their default values. The LASSO model used the cross-validated version LassoCV. The regularization parameter alpha was selected as the best value in a geometric sequence with a length of 50 and ranging from 10−3 to 10, which was uniformly distributed in logarithmic space. The cross-validation parameter (cv) was set to 10, and the maximum number of iterations (max_iter) was set to 100,000. For the RFE model, the optimal number of features was set to 40 using the parameter “n_features_to_select”, and a grid search was performed to optimize the parameters of the random forest basic model. The maximum number of iterations named “n_estimators” of the weak classifier in the GBDT model was set to 30, while the other settings were kept as default. In the RF model, the parameter named “n_estimators” was set to 10. For the XGBoost model, the default settings were used. For each model, we evaluated their effectiveness using three traditional classifiers: logistic regression, support vector machine (SVM) and Gaussian naive Bayes (GaussianNB). In the logistic regression model, default settings were used. For the SVM model, the kernel function was set to the Gaussian radial basis function (RBR), while other parameters were set to their default values. In the GaussianNB model, we assumed that the data follow a Gaussian distribution. In order to ensure the validation of the model, the ten-fold cross-validation method was used to conduct data analysis. Accuracy and F1-score were used to assess the predictive power of the models. We also plotted the receiver operating characteristic (ROC) curve and calculated the area under the curve (AUC) along with its 95% confidence interval (CI). The process of our study is schematically summarized in Figure 2.

Statistical analysis
The statistical analysis was performed in SPSS (version 22). Quantitative data that conformed to a normal distribution were described using the mean (± standard deviation), and the independent sample t-test was used for intergroup comparison. Quantitative data that did not conform to a normal distribution were represented by the median (P25, P75), and the Mann-Whitney U test was used for comparison between groups. The comparison of the rates was conducted using the Chi-squared test. Differences were considered significant at the two-sided P<0.05.
Results
Clinical characteristics and imaging findings
A total of 169 patients were included in this study. There were 88 patients (55 males and 33 females) in the case group, with a mean age of 36.6±14.3 years, and 81 patients (41 males and 40 females) in the control group, with an average age of 40.6±13.5 years. There was no significant difference in age or sex ratio between the case group and the control group (P=0.061 and 0.160, respectively). The X-ray images of the patients in the case group and the control group showed that the tibial plateau bone cortex was continuous, and the bone texture was clear, without distortion and interruption. In the subsequent MRI examinations, the case group exhibited linear or band shadows of T1 low signal, T2 low signal and PDWI high signal in the medullary cavity of the tibial plateau, accompanied by high signal bone marrow edema (Figure 3), including 66 (66/88, 75.0%) cases with cruciate ligament injury, 34 (34/88, 38.6%) cases with lateral collateral ligament injury and 30 (30/88, 34.1%) cases with meniscus injury. All cases were accompanied by joint capsule effusion to varying degrees. In the control group, there were 17 (17/81, 21.0%) patients with anterior cruciate ligament injury, 14 (14/81, 17.3%) patients with lateral collateral ligament injury, and 12 (12/81, 14.8%) patients with meniscus injury. As in the case group, all cases in the control group had different degrees of joint capsule effusion. The incidences of cruciate ligament injury, collateral ligament injury and meniscus injury in the case group were significantly higher than those in the control group (P=0.000, 0.002, and 0.004, respectively). The patient clinical characteristics and imaging findings in each group are summarized in Table 1.
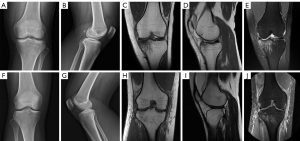
Table 1
| Variables | Case group (n=88) | Control group (n=81) | t/χ2 | P value |
|---|---|---|---|---|
| Age (years) | 36.6±14.3 | 40.6±13.5 | −1.887 | 0.061 |
| Sex | 1.979 | 0.160 | ||
| Male | 55 (62.5) | 41 (50.6) | ||
| Female | 33 (37.5) | 40 (49.4) | ||
| Cruciate ligament injury | 66 (75.0) | 17 (21.0) | 49.234 | 0.000 |
| Collateral ligament injury | 34 (38.6) | 14 (17.3) | 9.456 | 0.002 |
| Meniscus injury | 30 (34.1) | 12 (14.8) | 8.391 | 0.004 |
| Joint capsule effusion | 88 (100.0) | 81 (100.0) | – | – |
Data are presented as mean ± SD or n (%). SD, standard deviation.
Performance evaluation of ML models
Table 2 describes the classification accuracy, F1-score and AUC of six ML feature selection methods and three MaZda feature selection methods. From this table, we can see that LASSO yielded the finest outcome with an average accuracy rate and F1-score of 0.81 and 0.80, respectively, while GBDT followed closely with an average accuracy of 0.80 and F1 score of 0.79. In the metric of accuracy, the most ideal method in MaZda was the MI method, which reached 0.77. In the metric of F1 value, the best method in MaZda was Fisher, with a value of 0.78, but both methods had lower values than the LASSO method.
Table 2
| Models (FSM_CM) | Performance | ||
|---|---|---|---|
| Accuracy | F1-score | AUC (95% CI) | |
| Logistic | |||
| F_classif | 0.74 | 0.72 | 0.874 (0.706–0.923) |
| LASSO | 0.81†,‡ | 0.79† | 0.916 (0.776–0.927)† |
| RFE | 0.74 | 0.72 | 0.790 (0.688–0.871) |
| GBDT | 0.79 | 0.78 | 0.722 (0.633–0.883) |
| RF | 0.79 | 0.79 | 0.755 (0.622–0.881) |
| XGBoost | 0.77 | 0.75 | 0.797 (0.643–0.867) |
| Fisher | 0.73 | 0.72 | 0.844 (0.679–0.879) |
| POE + ACC | 0.66 | 0.67 | 0.778 (0.616–0.792) |
| MI | 0.76 | 0.73 | 0.734 (0.664–0.860) |
| SVM | |||
| F_classif | 0.78 | 0.76 | 0.844 (0.790–0.906) |
| LASSO | 0.80† | 0.80†,‡ | 0.920 (0.830–0.943)†,‡ |
| RFE | 0.78 | 0.77 | 0.890 (0.817–0.910) |
| GBDT | 0.80† | 0.79† | 0.887 (0.747–0.910) |
| RF | 0.79 | 0.78 | 0.839 (0.706–0.909) |
| XGBoos | 0.76 | 0.76 | 0.842 (0.678–0.872) |
| Fisher | 0.76 | 0.76 | 0.818 (0.762–0.882) |
| POE + ACC | 0.65 | 0.64 | 0.734 (0.591–0.804) |
| MI | 0.77 | 0.77 | 0.839 (0.685–0.909) |
| GaussianNB | |||
| F_classif | 0.76 | 0.78 | 0.895 (0.832–0.937)† |
| LASSO | 0.79 | 0.75 | 0.880 (0.822–0.932) |
| RFE | 0.78 | 0.78 | 0.847 (0.775–0.915) |
| GBDT | 0.77 | 0.77 | 0.818 (0.615–0.888) |
| RF | 0.65 | 0.61 | 0.860 (0.734–0.909) |
| XGBoost | 0.75 | 0.73 | 0.769 (0.573–0.937) |
| Fisher | 0.76 | 0.78 | 0.888 (0.832–0.937) |
| POE + ACC | 0.71 | 0.73 | 0.818 (0.629–0.853) |
| MI | 0.76 | 0.74 | 0.867 (0.6430–898) |
†, the top three experimental results under each indicator; ‡, the optimal outcomes. AUC, area under the curve; FSM, feature selection model; CM, classification model; CI, confidence interval; LASSO, least absolute shrinkage and selection operator; RFE, recursive feature elimination; RF, embedded random forest; GBDT, gradient boosting decision tree; XGBoost, eXtreme gradient boosting; POE + ACC, probability of classification error + average correction coefficient; MI, mutual information; SVM, support vector machine; GaussianNB, Gaussian naive Bayes.
In the AUC metric, the LASSO model had the highest AUC of 0.920 (95% CI: 0.830–0.943) when the classification evaluation model was SVM. The combination of LASSO and logistic regression was second only to the former, with an AUC of 0.916 (95% CI: 0.776–0.927). Compared with the feature selection methods in MaZda, other ML feature selection models in this study also achieved improved model performance on the AUC evaluation metric. For example, in MaZda, when the classification model was GaussianNB, the Fisher method in MaZda had the highest AUC of 0.888 (95% CI: 0.832–0.937), which was lower than that of the LASSO model. The ROC curve is depicted in Figure 4 to show how well each feature selection technique performs at various classification levels.
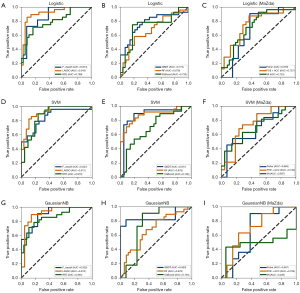
The logistic regression model and SVM model performed similarly in this classification task, but there were differences between the two models in terms of computational efficiency and interpretability. In this case, the optimal classification model could not be directly distinguished by only comparing the numerical results of the three metrics. Therefore, we added the statistical test analysis of the logistic regression model and SVM model on the basis of the original experimental results to select the better model. To select the appropriate statistical test method, based on the original experimental data, we increased the number of experiments of three measures under each classification model to 16, which reduced the impact of random error and made the results more reliable. Then, we first performed a normality test on the experimental data, and the results are presented in Table 3. The normality test results for all six groups of data were within the lower limit of significance, indicating that all data could be considered as having an approximately normal distribution. Therefore, the independent samples t-test could be conducted.
Table 3
| CM metric | Logistic regression | SVM | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| N | Normal parametersa,b | Most extreme differences | Test statistic | Asymp.sig (2-tailed) | Normal parametersa,b | Most extreme differences | Test statistic | Asymp.sig (2-tailed) | ||||||||||
| Mean | Std | Absolute | Positive | Negative | Mean | Std | Absolute | Positive | Negative | |||||||||
| Accuracy | 16 | 0.793 | 0.049 | 0.160 | 0.160 | −0.115 | 0.160 | 0.200c,d | 0.805 | 0.051 | 0.119 | 0.119 | −0.119 | 0.119 | 0.200c,d | |||
| F1-score | 16 | 0.773 | 0.053 | 0.147 | 0.131 | −0.147 | 0.147 | 0.200c,d | 0.808 | 0.047 | 0.137 | 0.137 | −0.130 | 0.137 | 0.200c,d | |||
| AUC | 16 | 0.880 | 0.031 | 0.122 | 0.102 | −0.122 | 0.122 | 0.200c,d | 0.907 | 0.050 | 0.135 | 0.135 | −0.113 | 0.135 | 0.200c,d | |||
a, test distribution is normal; b, calculated from data; c, Lilliefors significance correction; d, this is a lower bound of the true significance. CM, classification model; AUC, area under the curve; SVM, support vector machine; Std, standard deviation.
Table 4 shows the results of the independent sample t-test for the performance comparison of the logistic regression and SVM classification models. The results showed that the accuracy, F1-score and AUC of SVM were higher than those of logistic regression, but the differences were not statistically significant (P=0.481, 0.059 and 0.326, respectively). There was no significant difference between the logistic regression model and SVM model in the metrics of accuracy, F1-score and AUC performance in this classification task.
Table 4
| Metric | Logistic | SVM | t | P value |
|---|---|---|---|---|
| Accuracy | 0.793±0.049 | 0.805±0.051 | −0.714 | 0.481 |
| F1-score | 0.773±0.053 | 0.808±0.047 | −1.965 | 0.059 |
| AUC | 0.880±0.031 | 0.907±0.050 | −0.999 | 0.326 |
Data are presented as mean ± SD. SVM, support vector machine; AUC, area under the curve; SD, standard deviation.
Based on the results of the independent samples t-test for the logistic regression model and SVM model, it can be concluded that there was no significant difference in the performance between these two models in this classification task. Considering both the model performance and computational complexity, the logistic regression model was more suitable for the classification task in this study. When the feature selection model was LASSO and the classification model was logistic regression, this combination achieved the best classification performance.
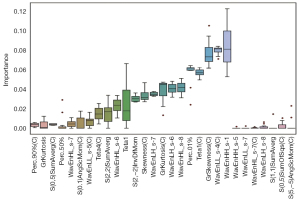
The importance of the predicted features of the LASSO model is shown in Figure 5, and 29 features out of 582 were chosen after several iterations of parameter tuning. We discovered that the model performed best in the optimization phase when there were 22 specified feature subsets. Consequently, only the top 22 features were left as follows: ‘Perc.90%(C)’, ‘GrKurtosis’, ‘S(0,5)SumAverg(C)’, ‘Perc.50%’, ‘WavEnHL_s-7’, ‘S(0,1)AngScMom(C)’, ‘WavEnLL_s-5(C)’, ‘Teta4(C)’, ‘S(2,2)SumAverg’, ‘WavEnHL_s-6’, ‘Teta1’, ‘S(2, 2)InvDfMom’, ‘Skewness(C)’, ‘WavEnLH_s-7’, ‘GrKurtosis(C)’, ‘WavEnLH_s-6’, ‘WavEnHL_s-8’, ‘Perc.01%’, ‘Teta1(C)’, ‘GrSkewness(C)’, ‘WavEnLL_s-4(C)’, and ‘WavEnHH_s-1’.
In the logistic regression classification task, the dependent variable was a binary variable, and its value was (positive result: there is a risk of occult fracture) or (negative result: there is no risk of occult fracture). The independent variables that affected the value of were the 22 features finally selected by the LASSO model. To implement the logistic regression classifier, each feature was associated with a regression coefficient. Through training, the logistic regression coefficients and the intercept could be obtained. By combining the intercept with the regression coefficients of each feature, we could determine the probability of via logistic regression equation as follows:
In Eq. [1], the expression of l is given as follows:
where to correspond to the 22 feature variables listed in Figure 5. By applying the regression equation to each record, a value ranging between 0 and 1 was obtained, which represented the probability of the sample belonging to the case group (). In this experiment, a threshold of 0.5 was given. That is, if the value of Eq. [1] is greater than the threshold, it indicates that the sample belongs to the case group (). Otherwise, the sample belongs to the control group ().
Discussion
In the clinical work-up, we found that plain X-ray could hardly detect hidden fractures of the knee joint. On subsequent MR examination, we established the existence of the fracture. Almost all of the patients had other imaging abnormalities, such as ligament injury, meniscus injury, and joint capsule effusion. Delayed recognition of hidden fractures may aggravate the patient’s condition. In this study, we deeply investigated whether TA based on X-ray images cold identify hidden fractures of the knee joint and combined it with ML to explore and construct the best predictive model.
We applied six feature selection methods, compared them with three methods of MaZda software, and selected the best one. In the accuracy measurement, the LASSO model showed the best performance, with a value of 0.81. It also achieved the best classification performance in F1-score and AUC measurements, with values of 0.80 and 0.920, respectively. This showed that LASSO had an excellent ability to identify cases with hidden fracture risk of the knee joint compared with the other five ML feature selection models (accuracy range, 0.65–0.80; F1 score range, 0.61–0.79; AUC range, 0.722–0.895). Among the three feature selection models of MaZda software, in the accuracy metric, the most ideal method was the MI method, which reached 0.77. In the metrics of F1-score and AUC, the best method in MaZda was Fisher, reaching 0.78 and 0.888, respectively. All indicators were lower than those of the LASSO method.
Combined with accuracy, F1-score, AUC and ROC curve analysis, it was observed that when the feature selection model was LASSO and the classification model was SVM, the combination of LASSO and SVM yielded the best classification performance. The performance of the combination of LASSO and logistic regression was slightly inferior. Careful comparison of the results of the two combinations on the three metrics showed that the performances of the two combinations were very similar. First, in terms of the accuracy metric, the logistic regression model was slightly superior to the SVM model. Second, in terms of the F1-score and AUC evaluation metrics, the SVM model was slightly superior to the logistic regression model, but the difference was no more than 0.01. Through subsequent statistical tests, we found that there was no significant difference in performance. The logistic regression model had strong interpretability. By calculating the coefficients of the logistic regression equation, we can directly interpret the impact of features on the results, which allows us to better understand the results of the model and explain them. In addition, logistic regression is a parametric model, while SVM needs to solve the quadratic optimization problem, which involves the selection of support vectors and the calculation of kernel functions, and the calculation complexity is relatively high. The logistic regression model was generally more efficient than the SVM model when dealing with large-scale data. Therefore, considering both the model performance and computational complexity, the logistic regression model was more suitable for the classification task in this study.
In existing research on artificial intelligence (AI)-assisted diagnosis of fracture, many studies have focused on the application of deep learning methods to identify or diagnose fractures in hip joints, wrists, lumbar vertebrae and other structures (23-30). For example, a neural network was applied to the diagnosis and classification of knee joint fractures and achieved high accuracy (30). In a previous study, scholars believed that AI improved the sensitivity of radiologists and non-radiologists in detecting fractures in various parts and may even enhance their specificity (31). Kuo et al. (32) conducted a META analysis and found that the performance of AI in diagnosing fractures was comparable to that of clinicians. In the realm of diagnosing occult fractures, some scholars have found that the convolutional neural network model can detect occult fractures of the scaphoid (27). However, there is a lack of research on an intelligent auxiliary diagnostic model for occult fractures of the knee joint. Deep learning is a subset of AI that differs from traditional ML in that the former does not require manual feature extraction but instead uses neural networks to automatically perform high-dimensional abstract learning on data (7,33). Feature engineering is considered time-consuming, labor-intensive, and inflexible, but it is an important part of medical image analysis (34). In the past decade, the improvement of computing power in ML models and the development of new models have brought new solutions to problems in various fields of radiology (35). To the best of our knowledge, only a few studies, such as ours, have investigated and compared different feature selection and ML modeling methods based on radiomics. For example, in one study, the prediction performance of 14 feature selection methods and 12 classifiers was evaluated in two lung cancer cohorts (36).
This study utilized the Lasso feature selection method to select 22 texture features, including 4 parameters from GLH, 4 parameters from GLCOM, 3 parameters from GRA, 3 parameters from ARM, and 8 parameters from WAV. We further constructed logistic regression equations using the 22 selected key features, which can greatly improve recognition accuracy and reduce computational burden. The method proposed in this paper will be further used to support practical clinical work. Specifically, we use the classic waterfall model of software development as a guide, first identifying the specific requirements of the system, including user preferences, and thus determining the system design, followed by system development, testing, and finally the implementation and maintenance of the system. The key to the practical application of this method is system design and system implementation. How to embed the algorithm into the existing system and ensure the operability of the system is the key issue. In terms of algorithm integration design, we will pay attention to the business process of the existing platform, and then consider the user’s preference to establish the design scheme. We will develop corresponding questionnaires to investigate and analyze this. At the same time, in addition to the development stage, the later implementation also pays attention to the preparation of explanatory documents and cases, and also strengthens the training of users. We will also further optimize the system based on user feedback.
This study has several limitations. First, this is a retrospective case‒control study with a limited number of patients, which may introduce more selection bias and stochastic effects. Second, as the X-ray images are two-dimensional overlapping images, we did not discuss and analyze occult fractures in other parts of the knee joint, such as the femoral condyle, patella, and proximal fibula. We only considered the tibial plateau, which was least affected by overlap. Third, this study focused solely on evaluating the predictive performance of the radiomics model and did not incorporate additional statistically significant clinical features. As a result, there is a lack of discussion regarding the integration of clinical and radiomics models. Fourth, the image segmentation in this study was performed manually, introducing a certain degree of subjectivity. Fifth, this study did not prove that the ML model can distinguish between occult tibial plateau fractures and simple bone marrow edema, which has certain limitations and needs to be further explored in the future. Finally, the application of reliable prediction models requires the support of a large number of data sets, and this study currently lacks prospective large-sample, multi-center data to verify the accuracy and universality of the research model.
Conclusions
In summary, this study used the texture features of X-ray images of the knee joint combined with ML to diagnose occult tibial plateau fractures. We first compared the performance of various ML methods and found that the LASSO feature selection method combined with the logistic classifier constructed the model with the best performance, the 22 key features screened out are then used to establish a logistic regression equation. This study is expected to provide a theoretical basis for clinical practice in developing automated software to help doctors identify patients at risk of occult tibial plateau fractures based on the first plain radiograph and formulate further diagnosis and treatment plans. The study is expected to significantly reduce the early missed diagnosis rate of occult tibial plateau fractures, lower patients’ medical costs, and enhance patient prognosis. It holds substantial clinical application value and warrants further research and application in the diagnosis of occult fractures in other regions, such as the spine and femoral neck. Based on the research results presented in this paper, in future theoretical studies, we will expand our research framework on multi-center and multimodal data. On the other hand, ML intelligent segmentation algorithms can be further explored. In clinical practice, we can further collect the feedback information from doctors to optimize our algorithms, while strengthening software development and application.
Acknowledgments
Funding: None.
Footnote
Reporting Checklist: The authors have completed the TRIPOD+AI reporting checklist. Available at https://qims.amegroups.com/article/view/10.21037/qims-24-799/rc
Conflicts of Interest: All authors have completed the ICMJE uniform disclosure form (available at https://qims.amegroups.com/article/view/10.21037/qims-24-799/coif). The authors have no conflicts of interest to declare.
Ethical Statement: The authors are accountable for all aspects of the work in ensuring that questions related to the accuracy or integrity of any part of the work are appropriately investigated and resolved. This retrospective study was conducted in accordance with the Declaration of Helsinki (as revised in 2013) and approved by the local institutional review board of Sichuan Orthopedic Hospital (No. KY-2024-039-01). Due to the retrospective nature of the study, the requirement for written informed consent was waived.
Open Access Statement: This is an Open Access article distributed in accordance with the Creative Commons Attribution-NonCommercial-NoDerivs 4.0 International License (CC BY-NC-ND 4.0), which permits the non-commercial replication and distribution of the article with the strict proviso that no changes or edits are made and the original work is properly cited (including links to both the formal publication through the relevant DOI and the license). See: https://creativecommons.org/licenses/by-nc-nd/4.0/.
References
- Reátiga Aguilar J, Rios X, González Edery E, De La Rosa A, Arzuza Ortega L. Epidemiological characterization of tibial plateau fractures. J Orthop Surg Res 2022;17:106. [Crossref] [PubMed]
- Shu Z, Lei J, Ding C. Diagnostic Value Comparison between Multislice Spiral Computerized Tomography and Magnetic Resonance Imaging under Artificial Intelligence Algorithm in Diagnosing Occult Fractures of the Knee Joint. Contrast Media Mol Imaging 2022;2022:3282409. [Crossref] [PubMed]
- Vellet AD, Marks PH, Fowler PJ, Munro TG. Occult posttraumatic osteochondral lesions of the knee: prevalence, classification, and short-term sequelae evaluated with MR imaging. Radiology 1991;178:271-6. [Crossref] [PubMed]
- Ma Q, Jiao Q, Wang S, Dong L, Wang Y, Chen M, Wang S, Ying H, Zhao L. Prevalence and Clinical Significance of Occult Fractures in the Extremities in Children. Front Pediatr 2020;8:393. [Crossref] [PubMed]
- Zhang YP, Zhang XY, Cheng YT, Li B, Teng XZ, Zhang J, Lam S, Zhou T, Ma ZR, Sheng JB, Tam VCW, Lee SWY, Ge H, Cai J. Artificial intelligence-driven radiomics study in cancer: the role of feature engineering and modeling. Mil Med Res 2023;10:22. [Crossref] [PubMed]
- Corrias G, Micheletti G, Barberini L, Suri JS, Saba L. Texture analysis imaging "what a clinical radiologist needs to know". Eur J Radiol 2022;146:110055. [Crossref] [PubMed]
- Janiesch C, Zschech P, Heinrich K. Machine learning and deep learning. Electron Markets 2021;31:685-95.
- Zheng Y, Zhou D, Liu H, Wen M. CT-based radiomics analysis of different machine learning models for differentiating benign and malignant parotid tumors. Eur Radiol 2022;32:6953-64. [Crossref] [PubMed]
- Xu H, Zou X, Zhao Y, Zhang T, Tang Y, Zheng A, Zhou X, Ma X. Differentiation of Intrahepatic Cholangiocarcinoma and Hepatic Lymphoma Based on Radiomics and Machine Learning in Contrast-Enhanced Computer Tomography. Technol Cancer Res Treat 2021;20:15330338211039125. [Crossref] [PubMed]
- Novak J, Zarinabad N, Rose H, Arvanitis T, MacPherson L, Pinkey B, et al. Classification of paediatric brain tumours by diffusion weighted imaging and machine learning. Sci Rep 2021;11:2987. [Crossref] [PubMed]
- Li X, Miao Y, Han L, Dong J, Guo Y, Shang Y, Xie L, Song Q, Liu A. Meningioma grading using conventional MRI histogram analysis based on 3D tumor measurement. Eur J Radiol 2019;110:45-53. [Crossref] [PubMed]
- Xv Y, Wei Z, Lv F, Jiang Q, Guo H, Zheng Y, Zhang X, Xiao M. Multiparameter computed tomography (CT) radiomics signature fusion-based model for the preoperative prediction of clear cell renal cell carcinoma nuclear grade: a multicenter development and external validation study. Quant Imaging Med Surg 2024;14:7031-45. [Crossref] [PubMed]
- Cao H, Shangguan L, Zhu H, Hu C, Zhang T, Han Z, Wei P. Prognostic Analysis of 131I Efficacy After Papillary Thyroid Carcinoma Surgery Based on CT Radiomics. J Clin Endocrinol Metab 2024;109:3036-45. [Crossref] [PubMed]
- Hussain L, Huang P, Nguyen T, Lone KJ, Ali A, Khan MS, Li H, Suh DY, Duong TQ. Machine learning classification of texture features of MRI breast tumor and peri-tumor of combined pre- and early treatment predicts pathologic complete response. Biomed Eng Online 2021;20:63. [Crossref] [PubMed]
- Hsieh HP, Wu DY, Hung KC, Lim SW, Chen TY, Fan-Chiang Y, Ko CC. Machine Learning for Prediction of Recurrence in Parasagittal and Parafalcine Meningiomas: Combined Clinical and MRI Texture Features. J Pers Med 2022;12:522. [Crossref] [PubMed]
- Li J, Fu S, Gong Z, Zhu Z, Zeng D, Cao P, Lin T, Chen T, Wang X, Lartey R, Kwoh CK, Guermazi A, Roemer FW, Hunter DJ, Ma J, Ding C. MRI-based Texture Analysis of Infrapatellar Fat Pad to Predict Knee Osteoarthritis Incidence. Radiology 2022;304:611-21. [Crossref] [PubMed]
- Wang M, Chen X, Cui W, Wang X, Hu N, Tang H, Zhang C, Shen J, Xie C, Chen X. A Computed Tomography-based Radiomics Nomogram for Predicting Osteoporotic Vertebral Fractures: A Longitudinal Study. J Clin Endocrinol Metab 2023;108:e283-94. [Crossref] [PubMed]
- Hong N, Park H, Kim CO, Kim HC, Choi JY, Kim H, Rhee Y. Bone Radiomics Score Derived From DXA Hip Images Enhances Hip Fracture Prediction in Older Women. J Bone Miner Res 2021;36:1708-16. [Crossref] [PubMed]
- Xue Z, Wang L, Sun Q, Xu J, Liu Y, Ai S, Zhang L, Liu C. Radiomics analysis using MR imaging of subchondral bone for identification of knee osteoarthritis. J Orthop Surg Res 2022;17:414. [Crossref] [PubMed]
- Poullain F, Champsaur P, Pauly V, Knoepflin P, Le Corroller T, Creze M, Pithioux M, Bendahan D, Guenoun D. Vertebral trabecular bone texture analysis in opportunistic MRI and CT scan can distinguish patients with and without osteoporotic vertebral fracture: A preliminary study. Eur J Radiol 2023;158:110642. [Crossref] [PubMed]
- Muehlematter UJ, Mannil M, Becker AS, Vokinger KN, Finkenstaedt T, Osterhoff G, Fischer MA, Guggenberger R. Vertebral body insufficiency fractures: detection of vertebrae at risk on standard CT images using texture analysis and machine learning. Eur Radiol 2019;29:2207-17. [Crossref] [PubMed]
- Hodgdon T, Thornhill RE, James ND, Beaulé PE, Speirs AD, Rakhra KS. CT texture analysis of acetabular subchondral bone can discriminate between normal and cam-positive hips. Eur Radiol 2020;30:4695-704. [Crossref] [PubMed]
- Urakawa T, Tanaka Y, Goto S, Matsuzawa H, Watanabe K, Endo N. Detecting intertrochanteric hip fractures with orthopedist-level accuracy using a deep convolutional neural network. Skeletal Radiol 2019;48:239-44. [Crossref] [PubMed]
- Bae J, Yu S, Oh J, Kim TH, Chung JH, Byun H, Yoon MS, Ahn C, Lee DK. External Validation of Deep Learning Algorithm for Detecting and Visualizing Femoral Neck Fracture Including Displaced and Non-displaced Fracture on Plain X-ray. J Digit Imaging 2021;34:1099-109. [Crossref] [PubMed]
- Gao Y, Soh NYT, Liu N, Lim G, Ting D, Cheng LT, Wong KM, Liew C, Oh HC, Tan JR, Venkataraman N, Goh SH, Yan YY. Application of a deep learning algorithm in the detection of hip fractures. iScience 2023;26:107350. [Crossref] [PubMed]
- Lindsey R, Daluiski A, Chopra S, Lachapelle A, Mozer M, Sicular S, Hanel D, Gardner M, Gupta A, Hotchkiss R, Potter H. Deep neural network improves fracture detection by clinicians. Proc Natl Acad Sci U S A 2018;115:11591-6. [Crossref] [PubMed]
- Langerhuizen DWG, Bulstra AEJ, Janssen SJ, Ring D, Kerkhoffs GMMJ, Jaarsma RL, Doornberg JN. Is Deep Learning On Par with Human Observers for Detection of Radiographically Visible and Occult Fractures of the Scaphoid? Clin Orthop Relat Res 2020;478:2653-9. [Crossref] [PubMed]
- Germann C, Meyer AN, Staib M, Sutter R, Fritz B. Performance of a deep convolutional neural network for MRI-based vertebral body measurements and insufficiency fracture detection. Eur Radiol 2023;33:3188-99. [Crossref] [PubMed]
- Yoon AP, Lee YL, Kane RL, Kuo CF, Lin C, Chung KC. Development and Validation of a Deep Learning Model Using Convolutional Neural Networks to Identify Scaphoid Fractures in Radiographs. JAMA Netw Open 2021;4:e216096. [Crossref] [PubMed]
- Lind A, Akbarian E, Olsson S, Nåsell H, Sköldenberg O, Razavian AS, Gordon M. Artificial intelligence for the classification of fractures around the knee in adults according to the 2018 AO/OTA classification system. PLoS One 2021;16:e0248809. [Crossref] [PubMed]
- Guermazi A, Tannoury C, Kompel AJ, Murakami AM, Ducarouge A, Gillibert A, Li X, Tournier A, Lahoud Y, Jarraya M, Lacave E, Rahimi H, Pourchot A, Parisien RL, Merritt AC, Comeau D, Regnard NE, Hayashi D. Improving Radiographic Fracture Recognition Performance and Efficiency Using Artificial Intelligence. Radiology 2022;302:627-36. [Crossref] [PubMed]
- Kuo RYL, Harrison C, Curran TA, Jones B, Freethy A, Cussons D, Stewart M, Collins GS, Furniss D. Artificial Intelligence in Fracture Detection: A Systematic Review and Meta-Analysis. Radiology 2022;304:50-62. [Crossref] [PubMed]
- Abrol A, Fu Z, Salman M, Silva R, Du Y, Plis S, Calhoun V. Deep learning encodes robust discriminative neuroimaging representations to outperform standard machine learning. Nat Commun 2021;12:353. [Crossref] [PubMed]
- Drotár P, Gazda J, Smékal Z. An experimental comparison of feature selection methods on two-class biomedical datasets. Comput Biol Med 2015;66:1-10. [Crossref] [PubMed]
- Wichmann JL, Willemink MJ, De Cecco CN. Artificial Intelligence and Machine Learning in Radiology: Current State and Considerations for Routine Clinical Implementation. Invest Radiol 2020;55:619-27. [Crossref] [PubMed]
- Parmar C, Grossmann P, Bussink J, Lambin P, Aerts HJWL. Machine Learning methods for Quantitative Radiomic Biomarkers. Sci Rep 2015;5:13087. [Crossref] [PubMed]


