
Accelerated Cartesian cardiac T2 mapping based on a calibrationless locally low-rank tensor constraint
Introduction
Cardiac T2 mapping has become an established method for the assessment of myocardial edema, inflammation, and infiltration in various cardiac diseases, including myocarditis, acute myocardial infarction, hypertrophic cardiomyopathy (HCM), amyloidosis, Fabry disease, and autoimmune cardiomyopathies (1-4). However, the commonly used single-shot balanced steady-state free precession (bSSFP) T2 mapping technique has a relatively low spatial resolution (~2 mm, especially along the phase-encoding direction) since the scan time for each image is limited by the duration of the cardiac quiescent period. Increasing spatial resolution without an extension of the acquisition window may improve the sensitivity in detecting localized myocardial damage (4,5).
Several high-resolution cardiac T2 mapping methods have been developed based on either three-dimensional (3D) imaging or two-dimensional (2D) non-Cartesian imaging (6-10). Bustin et al. (6) devised a free-breathing 3D whole-heart T2 mapping technique with an isotropic 1.5-mm3 resolution, leveraging a Cartesian variable density trajectory and a patch-based low-rank reconstruction. Dorniak et al. (7) developed a respiratory motion-registered whole-heart T2 mapping with a 1.6-mm3 resolution via a 3D radial bSSFP readout. Due to the superior signal-to-noise ratio (SNR) of 3D imaging, 3D T2 mapping approaches can achieve isotropic high-resolution imaging over the whole heart. However, these methods often cause a substantially increased scan time, which limits their use in clinical practice. Alternatively, increasing the in-plane resolution of 2D cardiac T2 mapping can be achieved without lengthening the scan time. For example, Hamilton et al. (8) developed simultaneous T1 and T2 mapping using cardiac magnetic resonance fingerprinting with a variable-density spiral trajectory, yielding a resolution of 1.6 mm × 1.6 mm. Darçot et al. (9) introduced a golden-angle radial spoiled gradient echo (GRE) sequence to accelerate 2D cardiac T2 mapping, improving the resolution to 1.17 mm × 1.17 mm. Shao et al. (10) introduced a simultaneous myocardial T1 and T2 mapping technique with a resolution of 1.7 mm × 1.7 mm based on a radial GRE sequence. Note that a shared feature for these above-mentioned methods is the use of non-Cartesian trajectories, such as radial and spirals, in accelerating the k-space sampling. However, it is well-known that these trajectories are more susceptible to reconstruction errors caused by eddy currents, gradient delay, and off-resonance effects (9,11). Cartesian sampling is less susceptible to these hardware-related defects, yet its application in high-resolution cardiac T2 mapping has not been fully studied. If Cartesian sampling can be used to increase the spatial resolution of cardiac T2 mapping, the technique with the Cartesian sampling may be more easily deployed in clinical practice.
A challenge for accelerating Cartesian cardiac T2 mapping, in particular uniform Cartesian undersampled cardiac T2 mapping, is that the undersampling artifacts are not incoherent and thus more difficult to mitigate than are those generated from non-Cartesian sampling. Furthermore, cardiac T2 mapping has a small number of raw images (3–4 images) and a relatively low SNR due to T2-weighting, both of which make precise reconstruction of the T2 maps more challenging. Traditionally, sparsity-based regularization (12,13) and low-rank-based regularization (14,15) have been used to accelerate parameter mapping. These methods leverage the sparsity of the image in a certain transform domain and the internal correlation of signals in the spatial domain to accelerate parameter mapping. Recently, learning-based methods have emerged as the new state of the art (16-18). Various data-driven (17) and model-driven (19) supervised methods have been applied to accelerate parameter mapping and have further improved the mapping quality compared with that of traditional methods. However, supervised learning methods (16,20) require fully sampled data to train the model, which is currently lacking in the application of high-resolution cardiac parameter mapping. Unsupervised or self-supervised learning methods (21,22) are alternatives to supervised methods and do not require fully sampled data for training. However, although these methods have demonstrated promising initial results, they remain in the exploratory stages and require further validation of their effectiveness and reliability. Therefore, the development of iterative methods with novel quality-improving image constraints remains critical to the task of refining high-resolution cardiac parametric mapping.
We thus developed a novel improved-resolution Cartesian cardiac T2 mapping method based on a calibrationless space-contrast-coil locally low-rank tensor (SCC-LLRT) constraint. The constraint was inspired by multiple recent works in which the enforcement of low rankness over multiple dimensions was demonstrated to improve the reconstruction performance (15,23,24) compared with that of typical spatial-contrast low-rank enforcement. To undersample k-space, we use shift undersampling improves parametric mapping efficiency and resolution (SUPER), which is a uniform Cartesian undersampling pattern that has been applied in cardiac (25) and brain T1 mapping (26).
Methods
The study was conducted in accordance with the Declaration of Helsinki (as revised in 2013) and was approved by the institutional review boards of Shanghai Jiao Tong University (No. E20230312I) and the Ruijin Hospital Lu Wan Branch (2016 Clinical Trial Ethics Review No.133). All participants provided written informed consent before the scan.
Pulse sequence
Figure 1A shows the proposed pulse sequence, which was modified from the T2-prepared single-shot bSSFP T2 mapping sequence with linear phase encode ordering (27). The sequence is electrocardiography (ECG)-triggered, and each echo train is acquired during diastole. Each bSSFP readout is preceded by five radiofrequency pulses with linearly increasing flip angles (FAs). Four-fold undersampling was performed based on the nested SUPER-sensitivity encoding (SENSE) pattern (25) with an additional 87.5% partial Fourier acquisition. This pattern involves nesting a shift undersampling pattern within a static undersampling pattern, in which sampling lines 1, 5, and 9 are used at odd contrast points while lines 3, 7, and 11 are used at even contrast points. Previous studies (25) have demonstrated that the nested SUPER-SENSE pattern effectively reduces aliasing artifacts in achieving four-fold acceleration for T1 mapping as compared to conventional shift undersampling. The central 24 k-space lines are fully sampled at every contrast. The sequence consists of four images acquired with a T2-prepared time of 0, 24, 40, and 55 ms.
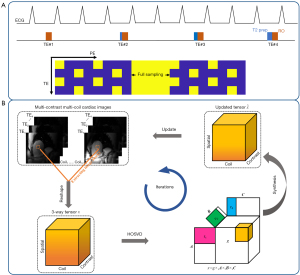
SCC-LLRT-constrained reconstruction
Unlike previous locally low-rank (LLR) reconstruction algorithms that only leverage the low- rankness of the spatial-contrast signals (28), the proposed SCC-LLRT constraint assumes the multicontrast multicoil signal collected in a local area of the image is a low-rank three-way tensor. The cost function for the SCC-LLRT constrained reconstruction problem is given by the following:
where is the measured k-space data, D is the undersampling operator, is the discrete Fourier transform, is the multicontrast multicoil images, is the matrix Frobenius norm, is a set of nonoverlapping image blocks in the spatial domain, is the tensor extraction operator that reshapes the image block b into a 3-way tensor, is the number of nonzero elements along the kth mode in the core tensor, and is the corresponding limit of the nonzero elements. We solve the problem in Eq. [1] using a projection onto convex sets (POCS) algorithm that alternates between the ensurance of data fidelity and the enforcement of the SCC-LLRT property. In each iteration, the algorithm sequentially executes the following steps:
- Step 1: given , the initial guess, employ the higher-order singular value decomposition (HOSVD) algorithm to generate a rank Tucker decomposition (29) for . Perform soft-thresholding of the core tensor by the threshold α to further enforce the tensor low rankness (Figure 1B).
- Step 2: synthesize the three-way tensor and assemble the tensor blocks.
- Step 3: enforce data consistency by replacing the data in the sampled k-space locations with the measured data as follows:
where is the zero filling in the sampled k-space locations, and is the augmentation of the vector into full-sized k-space by zero-filling. In Step 1, the set of nonoverlapping blocks are randomly shuffled to avoid blocky artifacts, as suggested by Zhang et al. (28). Note that the proposed algorithm is calibrationless, as it does not involve coil sensitivity encoding in the formulation. The calibrationless formulation simplifies the reconstruction process and may improve its robustness in the presence of a limited field of view (FOV) (30).
Implementation
To accelerate the reconstruction, the multicoil raw data were compressed to 12 virtual coils based on principal component analysis (PCA). In Step 1 of SCC-LLRT, the multi-contrast multi-coil images were initialized with generalized autocalibrating partially parallel acquisition (GRAPPA) (31) reconstruction. Image reconstruction quality was optimized empirically by a tuning of the parameters. After parameter tuning, the SCC-LLRT algorithm employed a 5×5 block size, a rank (6,4,4) Tucker decomposition for the LLRT enforcement, 300 iterations for the POCS algorithm, and a threshold of 0.001 for the soft-thresholding operator.
We compared the performance of our algorithm with that of GRAPPA, LLR, and nonlinear inversion (NLINV) in reconstructing the improved-resolution T2 maps. The LLR reconstruction method only considers low rankness in the spatial-contrast domain and uses the self-calibration formulation for embedded parallel imaging. The algorithm was implemented using the code provided by Zhang et al. (28). The NLINV algorithm simultaneously reconstructs the coil sensitivity maps and the images by imposing separate regularizations over the two variables without using contrast information. The algorithm was implemented using the code provided by Uecker et al. (32). The reconstruction parameters of these methods were separately optimized to maximize the reconstruction quality and ensure fair comparisons.
For all methods, after the reconstruction of the multicoil multicontrast images, coil sensitivities were estimated based on eigenvector maps (30) through use of the reconstructed images, which were then merged along the coil dimension by a least squares estimation. Nonrigid image registration (33) was used to register all images and was followed by voxel-wise curve fitting to generate the T2 maps. All reconstructions were performed offline with MATLAB R2022a (MathWorks, Natick, MA, USA) on a Linux server equipped with four 24-core Xeon Platinum 8260 CPUs (Intel, Santa Clara, CA, USA). For LLR and NLINV, the reconstruction time for a single improved-resolution T2 map was 139 and 219 s, respectively.
Phantom imaging
Phantom imaging was performed to compare the accuracy and precision of the improved-resolution SUPER T2 mapping with those of regular T2 mapping. Phantoms were prepared using two different mixed solutions of NiCl2 and agar gel to approximate the T2 values of a normal (T2=48 ms) and edematous (T2=61 ms) myocardium. The T2 value of each vial was measured by a spin-echo sequence with 6 TEs (from 9 to 80 ms). The spin-echo sequence protocol was conducted under the following parameters: repetition time (TR) =10,000 ms, FOV =120 mm × 168 mm, matrix size =68×96, and bandwidth =600 Hz/pixel. Imaging was performed on a 3-T scanner (uMR790, United Imaging Healthcare, Shanghai, China) with a 32-channel head coil. The improved-resolution SUPER T2 mapping sequence was conducted under the following parameters: TR/TE =3.05 ms/1.41 ms; FOV =300 mm × 360 mm; slice thickness =8 mm; matrix size =212×256; acquisition window =195.2 ms; FA =70°; bandwidth =1,085 Hz/pixel; T2-prepared time =0, 24, 40, 55 ms; phase resolution =100%; partial echo factor =83%; partial Fourier factor =87.5%; and lines acquired per heartbeat =64. The regular T2 mapping sequence was conducted under the following parameters: TR/TE =2.77 ms/1.28 ms; FOV =300 mm × 360 mm; slice thickness =8 mm; matrix size =160×192; phase resolution =80%; GRAPPA factor =2; autocalibration signal lines =24; acquisition window =188.4 ms; FA =35°; T2-prepared time =0, 30, 55 ms; and lines acquired per heartbeat =68. Other parameters were the same between the two sequences. Simulated heart rates ranged from 60 to 100 beats per minute (bpm). The improved-resolution T2 map was reconstructed with SCC-LLRT, while the regular-resolution T2 map was reconstructed with GRAPPA (31). We quantitatively compared the T2 precision of GRAPPA, LLR, NLINV, and SCC-LLRT according to their reconstructed improved-resolution T2 maps. Precision was considered to be the average of the mean standard deviations (SDs) of T2 values within the two-vial phantom over different simulated heart rates.
Healthy participants
A total of 13 healthy participants (7 males; age 25±3 years) were imaged under breath-holding on a 3-T scanner (uMR790, United Imaging Healthcare) with a 12-channel torso coil and 24-channel spine coil. Both the proposed SUPER T2 mapping and the regular T2 mapping techniques were completed in three short-axis slices under the same parameters as those of the phantom study. The acquisition resolution for SUPER T2 mapping was 1.4 mm × 1.4 mm (interpolated to 0.7 mm × 0.7 mm), whereas that for regular T2 mapping was 2.34 mm × 1.88 mm (interpolated to 0.94 mm × 0.94 mm). To test the reproducibility of the proposed method, 8 healthy participants (5 males) underwent 2 scans spaced 7–10 days apart.
SCC-LLRT was compared with GRAPPA, LLR, and NLINV in the reconstruction of the improved-resolution images. The image quality of these reconstruction algorithms was assessed through qualitative scoring by experienced readers. For comparison of improved-resolution T2 mapping against regular-resolution T2 mapping, the mean T2 value, precision, and test-retest reproducibility of each myocardial segment were evaluated according to the American Heart Association (AHA) model. Precision was assessed as the SD of the measured T2 in each segment. The reproducibility was assessed by the absolute difference between the mean T2s measured at the two time points.
Patients
A total of 20 patients (8 females; age 51±17 years) were imaged under breath-holding on a 3-T scanner (uMR890, United Imaging Healthcare) with a 12-channel torso coil and 32-channel spine coil in Ruijin Hospital Lu Wan Branch. Clinical indications included hypertensive cardiomyopathy (n=8), HCM (n=2), dilated cardiomyopathy (n=2), Fabry disease (n=1), cardiac amyloidosis (n=1), athletic heart syndrome (n=1), ischemic cardiomyopathy (n=1), arrhythmia (n=1), and others (n=3). Both the proposed SUPER T2 mapping and the regular T2 mapping techniques were completed in three short-axis slices. Late gadolinium enhancement (LGE) imaging was performed 10 minutes after contrast agent injection. The improved-resolution SUPER T2 mapping sequence was conducted under the following parameters: TR/TE =3.08 ms/1.55 ms, FOV =340 mm × 380 mm, slice thickness =8 mm, matrix size =228×256, acquisition window =187.9 ms, FA =35°, bandwidth =1,200 Hz/pixel, partial Fourier factor =75%, and lines acquired per heartbeat =61. The regular T2 mapping sequence was conducted under the following parameters: TR/TE =2.72 ms/1.29 ms, FOV =340 mm × 380 mm, slice thickness =8 mm, matrix size =172×192, FA =35°, phase resolution =75%, acquisition window =209.4 ms, and lines acquired per heartbeat =77. The other parameters were the same as those used for two sequences in scanning healthy participants. Changes of the above parameters were made to match the protocol of the clinical T2 mapping sequence. The LGE imaging sequence was conducted under the following parameters: TR/TE =5.25 ms/2.17 ms, FA =15°, FOV =340 mm × 380 mm, slice thickness =8 mm, matrix size =258×288, in-plane resolution =1.32 mm × 1.32 mm, phase resolution =100%, GRAPPA factor =2, autocalibration signal lines =24, and the acquisition window during diastasis =152.25 ms.
Qualitative scoring
Qualitative scoring was performed to evaluate the performance of the different reconstruction methods and the different T2 mapping techniques. To objectively compare LLR, NLINV, and SCC-LLRT, T2 maps generated from these methods were randomized for each healthy participant. Two experienced readers (H.C. and Z.C., both with more than 3 years’ experience in cardiovascular magnetic resonance) who were blinded to the randomization order independently evaluated each T2 map to grade the severity of artifacts, noise, and the overall image quality. A five-point scale (1, nondiagnostic; 2, poor; 3, fair; 4, good; 5, excellent) was used for the evaluation. To compare regular-resolution T2 mapping with improved-resolution T2 mapping, three criteria, namely the sharpness of myocardial boundaries, the conspicuity of the papillary muscles and fine structures, and artifacts, were graded by the same readers using the same five-point scale. This assessment was performed in both healthy participants and patients. The scores from the two readers were averaged to obtain the final score.
Statistical analysis
The paired t test was used to assess statistical differences in regional T2 mean, SD, and the T2 difference between two scans (7–10 days apart) for different methods or measurements. The Wilcoxon signed-rank test was used to assess statistical differences in qualitative scores. Intraclass correlation coefficient (ICC) analysis was used to assess interreader agreement. Bland-Altman and linear regression analyses were performed to assess the agreement between the improved-resolution SUPER T2 mapping and the regular T2 mapping results for both healthy participants and patients. A P value less than 0.05 was considered statistically significant.
Results
Phantom imaging
Table 1 lists the T2 values of the two-vial phantom measured by the regular-resolution T2 mapping and improved-resolution SUPER T2 mapping at different heart rates. The difference between the T2 values measured by the two techniques was less than 6 ms across different heart rates. Higher heart rates caused a reduction in T2 value for both methods due to the incomplete signal recovery at high heart rates (34). The difference in T2 value between the highest and lowest heart rates for the improved-resolution T2 mapping was 6 ms for both vials. The T2 values measured by the improved-resolution technique were slightly closer to the reference values measured by the spin-echo sequences. SCC-LLRT exhibited lower mean T2 SDs (0.95±0.18 ms) for the two-vail phantom compared to GRAPPA (1.57±0.50 ms; P=0.005), LLR (1.23±0.57 ms; P=0.196), and NLINV (2.31±0.25 ms; P<0.001), suggesting a superior noise suppression performance of SCC-LLRT.
Table 1
| Vial | Reference T2 | Method | HR 60 | HR 70 | HR 80 | HR 90 | HR 100 |
|---|---|---|---|---|---|---|---|
| 1 | 48±0.4 | Regular-Res | 55±0.7 | 54±0.6 | 53±0.6 | 52±0.6 | 51±0.6 |
| Improved-Res | 54±0.7 | 52±0.6 | 50±0.6 | 49±0.7 | 48±0.6 | ||
| 2 | 61±0.5 | Regular-Res | 68±1.0 | 67±0.9 | 65±1.0 | 66±1.0 | 64±0.9 |
| Improved-Res | 65±0.6 | 63±0.5 | 60±0.5 | 60±0.5 | 59±0.5 |
Data are presented as mean ± standard deviation. bpm, beats per minute; HR, heart rate; Res, resolution.
Healthy participants
Figure 2 shows the results of the three short-axis slices reconstructed by GRAPPA, LLR, NLINV, and SCC-LLRT for the improved-resolution T2 mapping data from one healthy participant. In this example, SCC-LLRT more effectively suppressed aliasing artifacts as compared to GRAPPA and LLR. Additionally, it appears that SCC-LLRT better suppressed noise as compared to NLINV. The results of qualitative comparisons between LLR, NLINV, and SCC-LLRT for the 13 healthy participants are summarized in Table 2. SCC-LLRT significantly reduced artifacts (4.50±0.39) as compared with LLR (2.31±0.60; P<0.001) and NLINV (3.65±0.56; P<0.01), better suppressed noise (4.12±0.35) as compared with NLINV (2.65±0.50; P<0.001), and improved the overall image quality (4.38±0.40) as compared with LLR (2.54±0.41; P<0.001) and NLINV (3.04±0.50; P<0.001). The ICCs of the two readers were 0.87 [95% confidence interval (CI): 0.75–0.93] for artifacts, 0.70 (95% CI: 0.43–0.85) for noise, and 0.84 (95% CI: 0.69–0.92) for overall image quality; meanwhile, the interreader agreement of each reconstruction method (LLR, NLINV, and SCC-LLRT) for these three criteria was 0.69 (95% CI: 0.41–0.84), 0.81 (95% CI: 0.63–0.90), and 0.65 (95% CI: 0.41–0.86), respectively.
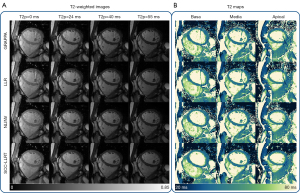
Table 2
| Method | Artifacts | Noise | Overall quality |
|---|---|---|---|
| LLR | 2.31±0.60* | 4.23±0.50† | 2.54±0.41* |
| NLINV | 3.65±0.56* | 2.65±0.50* | 3.04±0.50* |
| SCC-LLRT | 4.50±0.39† | 4.12±0.35 | 4.38±0.40† |
Data are presented as mean ± standard deviation. *, significant difference compared to SCC-LLRT. †, the method with the best performance. LLR, locally low rank; NLINV, nonlinear inversion; SCC-LLRT, space-contrast-coil locally low-rank tensor.
Figure 3 shows a comparison of the regular-resolution and improved-resolution T2 mapping techniques in three short-axis slices for one healthy participant. The results of qualitative comparisons between the two methods over 13 healthy participants are listed in Table 3. The improved-resolution T2 maps, compared to the regular resolution, significantly improved the sharpness of myocardial boundaries (4.46±0.60 vs. 3.04±0.50; P<0.001) and the conspicuity of the papillary muscles and fine structures (4.46±0.63 vs. 2.65±0.30; P<0.001). There was no significant difference in the suppression of image artifacts between the improved-resolution and regular-resolution T2 maps (4.54±0.36 vs. 4.46±0.53; P=0.79). The ICCs of the two readers for the sharpness of myocardial boundaries, the conspicuity of papillary muscles and fine structures, and artifacts were 0.83 (95% CI: 0.63–0.92), 0.87 (95% CI: 0.71–0.94), and 0.73 (95% CI: 0.48–0.86), respectively.

Table 3
| Criterion | Regular resolution | Improved resolution | P value |
|---|---|---|---|
| Sharpness of myocardial boundaries | 3.04±0.50* | 4.46±0.60† | <0.001 |
| Conspicuity of papillary muscles and fine structures | 2.65±0.30* | 4.46±0.63† | <0.001 |
| Artifacts | 4.46±0.53 | 4.54±0.36† | 0.79 |
Data are presented as mean ± standard deviation. *, significant difference compared to improved resolution. †, the method with the best performance.
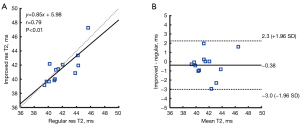
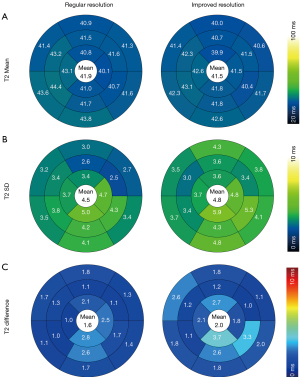
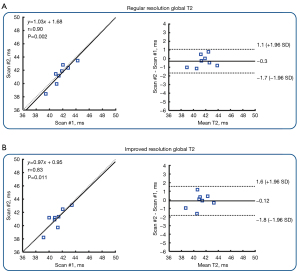
Figure 4 shows the result of correlation and Bland-Altman analysis of 13 healthy participants in global T2 values. The T2 values estimated by the improved-resolution T2 mapping significantly correlated with those of the regular-resolution T2 mapping (r=0.79; P<0.01). A mean bias of −0.38 ms was found between the two techniques. Figure 5 shows the average of the T2 values (panel A), T2 SDs (panel B), and the T2 difference between two scans (7–10 days apart; panel C) in the 16 AHA myocardial segments of all healthy participants. There was no significant difference in terms of mean T2 values for the whole myocardium between the improved-resolution and regular-resolution T2 mapping techniques (41.5±2.1 vs. 41.9±2.0 ms; P=0.36). The T2 SD for the whole myocardium was slightly higher for the improved-resolution T2 mapping technique (4.8±1.4 vs. 4.5±1.0 ms; P=0.09). Although the interscan T2 difference appeared slightly higher for the improved-resolution T2 mapping technique in most segments, the interscan absolute T2 difference for the whole myocardium was not significantly different between the two methods (2.0±0.5 vs. 1.6±0.5 ms; P=0.27). Figure 6 shows the correlation and agreement of global T2 values over the test-retest scans in 8 healthy participants. The global T2 values of the two scans were significantly correlated for both regular-resolution T2 mapping (r=0.90; P=0.002) and improved-resolution T2 mapping (r=0.83; P=0.011). The mean bias between the two scans was −0.30 ms for the regular-resolution T2 mapping technique and −0.12 ms for the improved-resolution T2 mapping technique.
Patients
Figure 7 shows the T2 maps and slice-matched LGEs acquired in two patients. Patient 1 was a 74-year-old female with ischemic cardiomyopathy and asymmetrical septal hypertrophy, and patient 2 was a 66-year-old female with cardiac amyloidosis. The improved-resolution T2 map technique exhibited a clearer delineation of the high-T2 area (arrowheads) in patient 1 as compared with the regular-resolution T2 mapping technique. For patient 2, there was a slight and diffuse T2 increase in the septum compared with the lateral wall myocardium (improved-resolution: 49±1.3 vs. 41±1.4 ms; regular resolution: 50±2.8 vs. 44±2.1 ms), potentially due to inflammation caused by amyloidosis (3). The results of qualitative comparisons between the regular-resolution and improved-resolution T2 mapping techniques over 20 patients are listed in Table 4. The improved-resolution T2 maps, compared those of the regular-resolution sequence, significantly improved the sharpness of myocardial boundaries (4.97±0.11 vs. 3.70±0.21; P<0.001) and the conspicuity of papillary muscles and fine structures (4.95±0.21 vs. 3.55±0.42; P<0.001); however, there was no significant difference in suppression of image artifacts between the two methods (4.75±0.38 vs. 4.55±0.42; P=0.72). The ICCs of the two readers for the sharpness of myocardial boundaries, the conspicuity of papillary muscles and fine structures, and artifacts were 0.81 (95% CI: 0.57–0.91), 0.74 (95% CI: 0.38–0.88), and 0.71 (95% CI: 0.45–0.85).

Table 4
| Criterion | Regular resolution | Improved resolution | P value |
|---|---|---|---|
| Sharpness of myocardial boundaries | 3.70±0.21* | 4.97±0.11† | <0.001 |
| Conspicuity of papillary muscles and fine structures | 3.55±0.42* | 4.95±0.21† | <0.001 |
| Artifacts | 4.55±0.42 | 4.75±0.38† | 0.72 |
Data are presented as mean ± standard deviation. *, significant difference compared to improved resolution. †, the method with the best performance.
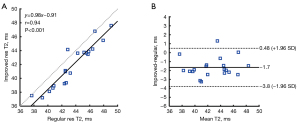
Figure 8 shows the result of the correlation and Bland-Altman analysis of the patients. The T2 values estimated by the improved-resolution T2 mapping significantly correlated with those of the regular-resolution T2 mapping (r=0.94; P<0.001). A mean bias of −1.7 ms was found for the improved-resolution T2 mapping with respect to the regular-resolution T2 mapping.
Discussion
In this paper, we propose a novel technique for cardiac T2 mapping that combines Cartesian SUPER undersampling and a calibrationless reconstruction based on the SCC-LLRT constraint. Reconstructions in healthy participants demonstrated that T2 maps obtained with SCC-LLRT had fewer artifacts and improved overall image quality as compared those obtained with the NLINV reconstruction and the conventional LLR-constrained reconstruction. In vivo imaging showed that as compared with the regular T2 mapping, the proposed method exhibited sharper myocardial boundaries and better depiction of fine structures, with similar accuracy, precision, and reproducibility.
Compared to previously described 2D high-resolution cardiac T2 mapping methods (8-10), our method offers several advantages. First, we use Cartesian sampling and bSSFP readouts, whereas other methods employ radial/spiral sampling and GRE readouts, which can lead to stronger eddy currents, off-resonance effects, streak artifacts, and low SNR and often entail a more complex reconstruction. Second, we use the SCC-LLRT constraint for reconstruction, which demonstrated superior performance in suppressing aliasing artifacts and noise compared with several alternative methods. Finally, the LLR tensor constraint in the space-contrast-coil domain enables a calibrationless reconstruction, which simplifies the reconstruction workflow and eliminates errors caused by inaccurate coil sensitivity estimation.
Another high-dimensional low-rankness-based algorithm, high-dimensionality undersampled patch-based reconstruction (HD-PROST) (24) was previously proposed for accelerating multicontrast magnetic resonance imaging (MRI). Our algorithm shares similarities to HD-PROST, for instance, the use of the low-rank constraint of 3D tensors. However, how the 3D tensor is constructed differs substantially between the two methods. HD-PROST constructs a 3D tensor that encompasses space, patch, and contrast dimensions, using local and nonlocal patch similarity as a regularization constraint to improve the reconstruction. This strategy entails a search of similar patches within spatial domain, which can increase the computational time. Furthermore, HD-PROST requires that the coil sensitivity calibration incorporate SENSE into the reconstruction. In contrast, SCC-LLRT leverages the joint low-rank property over space, contrast, and coil dimensions, which integrates parallel imaging with low-rank constrained reconstruction. Because parallel imaging is integrated, SCC-LLRT does not require a separate coil sensitivity calibration. Moreover, SCC-LLRT does not search for similar patches in each iteration, facilitating a relatively rapid execution.
The improved-resolution cardiac T2 mapping technique can potentially benefit a variety of clinical situations that involve the development and resolution of focal edema, such as in the treatment of myocarditis, acute myocardial infarction, and HCM and the postablation monitoring of patients. Myocarditis often causes focal T2 elevations, typically in the subepicardial layer, due to the presence of myocardial inflammation (2,35). After treatment, the T2-elevated area gradually shrinks over a period of several months, during which a higher-resolution T2 mapping can serve as a means to monitoring the progress (36). As has been reported by Amano et al., HCM can also cause focal edemas (5). In their study, 54 patients with HCM were examined, 21 of whom had edema, which was frequently located outside the regions of LGE and had a focal appearance. Thus, an improved-resolution T2 assessment can be particularly important for an accurate assessment of myocardial injury in these patients. Finally, edema can be detected in MRI-guided left ventricular ablation by T2 mapping soon after the ablation has begun, with the edematous area quickly expanding within a few hours (37). Improved-resolution T2 mapping can provide imaging guidance in determining where the ablation has been successfully performed and whether the extent of ablation is sufficient for the patient. Traditionally, clinicians have preferred dark-blood turbo spin echo (TSE) for the assessment of focal edemas, mainly due to its higher resolution and a better contrast compared with regular T2 mapping. However, T2 mapping is quantitative and less affected by artifacts (27). A robust and accurate higher-resolution cardiac T2 mapping method has superior performance in detecting focal edemas and thus may reduce the need for separate applications of dark-blood TSE and T2 mapping for the detection of focal and diffuse edemas, respectively.
In addition to reconstruction methods, there are new sequences that may also improve the resolution and scan efficiency of cardiac T2 mapping. For example, Zhu et al. proposed a novel cardiac imaging method based on bSSFP with wave encoding to accelerate imaging (38). They reported that wave-bSSFP in cardiac T1 mapping provided improved resolution. By combining this novel sequence framework with our SCC-LLRT reconstruction algorithm, we can likely further improve the resolution or reduce the duration of the acquisition window. Furthermore, several recent studies have employed deep learning to accelerate MR parametric mapping (39-41). In cardiac MR parametric mapping, obtaining fully sampled data for training labels is challenging. Therefore, the images reconstructed using our proposed method from undersampled data can serve as a proxy to fully sampled data for the training of learning-based reconstruction networks. A benefit of learning-based methods is the fast computation. Currently, our algorithm requires 8.64 minutes of reconstruction to reconstruct a single T2 map. Although this computational time is reasonable for an iterative algorithm that involves tensor decomposition, it is still too long for clinical deployment. The training of learning-based methods, such as unrolling network learning tensor low-rank priors (17,42), has the potential to significantly improve reconstruction efficiency and render the improved-resolution cardiac T2 mapping technique more feasible for routine clinical applications.
Our proposed method and related study involved several limitations which should be mentioned. First, despite the mitigation of noise by the proposed SCC-LLRT algorithm, the method still shows a lower precision when compared with regular T2 mapping. Further optimization of the algorithm or the image acquisition schemes is needed to improve the precision of the T2 maps at such a high resolution. However, we note that a slight decrease of precision is unlikely to significantly affect the clinical assessment of edema. Second, motion correction was not incorporated into the reconstruction process but rather applied after the raw images were reconstructed. We found that an approach using separate reconstruction and motion correction can yield a decent T2 mapping quality in our dataset despite the common occurrence of motion across the patient cohort. However, motion can theoretically decrease the signal correlation between neighboring voxels, potentially compromising the reconstruction quality of the proposed approach. Further exploration into the effects of severe motion on the performance of this approach is essential, and the development of integrated approaches that combine motion correction with reconstruction techniques is critical. Third, the proposed technique merely increases the in-plane resolution. Since the slice thickness is 8 mm, there is still large room for improvement in the through-plane resolution. To this end, a fast and accurate 3D T2 mapping technique with which the SCC-LLRT algorithm can still be used to reduce scan time may be useful. Fourth, as a proof-of-concept study, we only validated the method by scanning a small sample size of 13 healthy participants and 20 patients on two scanners. Additional multicenter studies with a greater number of patients are necessary to confirm the broader application of this novel method.
Conclusions
We propose the combination of a SCC-LLRT-constrained reconstruction algorithm with Cartesian SUPER undersampling to accelerate cardiac T2 mapping. The results from our study showed that the proposed method can achieve an overall similar accuracy, precision, and scan-rescan reproducibility as compared the regular-resolution T2 mapping while improving image resolution. The higher resolution increases the sharpness of myocardial borders and the conspicuity of fine details, which may have the potential to improve the diagnostic confidence of cardiac T2 mapping for small lesions.
Acknowledgments
Funding: This work was partially supported by
Footnote
Conflicts of Interest: All authors have completed the ICMJE uniform disclosure form (available at https://qims.amegroups.com/article/view/10.21037/qims-24-740/coif). X.T. was a full-time master’s student at Shanghai Jiao Tong University during his participation in this study. After graduating in March 2023, he joined Shanghai United Imaging Healthcare Co. Ltd. as a full-time employee. The other authors have no conflicts of interest to declare.
Ethical Statement: The authors are accountable for all aspects of the work in ensuring that questions related to the accuracy or integrity of any part of the work are appropriately investigated and resolved. This study was conducted in accordance with the Declaration of Helsinki (as revised in 2013) and was approved by the institutional review boards of Shanghai Jiao Tong University (No. E20230312I) and the Ruijin Hospital Lu Wan Branch (2016 Clinical Trial Ethics Review No.133). All participants provided written informed consent before being scanned.
Open Access Statement: This is an Open Access article distributed in accordance with the Creative Commons Attribution-NonCommercial-NoDerivs 4.0 International License (CC BY-NC-ND 4.0), which permits the non-commercial replication and distribution of the article with the strict proviso that no changes or edits are made and the original work is properly cited (including links to both the formal publication through the relevant DOI and the license). See: https://creativecommons.org/licenses/by-nc-nd/4.0/.
References
- Camporeale A, Diano A, Tondi L, Pica S, Pasqualin G, Ciabatti M, Graziani F, Pieroni M, Lombardi M. Cardiac Magnetic Resonance Features of Fabry Disease: From Early Diagnosis to Prognostic Stratification. Rev Cardiovasc Med 2022;23:177. [Crossref] [PubMed]
- Sanchez Tijmes F, Thavendiranathan P, Udell JA, Seidman MA, Hanneman K. Cardiac MRI Assessment of Nonischemic Myocardial Inflammation: State of the Art Review and Update on Myocarditis Associated with COVID-19 Vaccination. Radiol Cardiothorac Imaging 2021;3:e210252. [Crossref] [PubMed]
- Kotecha T, Martinez-Naharro A, Treibel TA, Francis R, Nordin S, Abdel-Gadir A, Knight DS, Zumbo G, Rosmini S, Maestrini V, Bulluck H, Rakhit RD, Wechalekar AD, Gilbertson J, Sheppard MN, Kellman P, Gillmore JD, Moon JC, Hawkins PN, Fontana M. Myocardial Edema and Prognosis in Amyloidosis. J Am Coll Cardiol 2018;71:2919-31. [Crossref] [PubMed]
- Amano Y, Yanagisawa F, Tachi M, Hashimoto H, Imai S, Kumita S. Myocardial T2 Mapping in Patients With Hypertrophic Cardiomyopathy. J Comput Assist Tomogr 2017;41:344-8. [Crossref] [PubMed]
- Amano Y, Aita K, Yamada F, Kitamura M, Kumita S. Distribution and Clinical Significance of High Signal Intensity of the Myocardium on T2-Weighted Images in 2 Phenotypes of Hypertrophic Cardiomyopathy. J Comput Assist Tomogr 2015;39:951-5. [Crossref] [PubMed]
- Bustin A, Milotta G, Ismail TF, Neji R, Botnar RM, Prieto C. Accelerated free-breathing whole-heart 3D T2 mapping with high isotropic resolution. Magn Reson Med 2020;83:988-1002. [Crossref] [PubMed]
- Dorniak K, Di Sopra L, Sabisz A, Glinska A, Roy CW, Gorczewski K, Piccini D, Yerly J, Jankowska H, Fijałkowska J, Szurowska E, Stuber M, van Heeswijk RB. Respiratory Motion-Registered Isotropic Whole-Heart T(2) Mapping in Patients With Acute Non-ischemic Myocardial Injury. Front Cardiovasc Med 2021;8:712383. [Crossref] [PubMed]
- Hamilton JI, Pahwa S, Adedigba J, Frankel S, O'Connor G, Thomas R, Walker JR, Killinc O, Lo WC, Batesole J, Margevicius S, Griswold M, Rajagopalan S, Gulani V, Seiberlich N. Simultaneous Mapping of T1 and T2 Using Cardiac Magnetic Resonance Fingerprinting in a Cohort of Healthy Subjects at 1.5T. J Magn Reson Imaging 2020;52:1044-52. [Crossref] [PubMed]
- Darçot E, Yerly J, Colotti R, Masci PG, Chaptinel J, Feliciano H, Bianchi V, van Heeswijk RB. Accelerated and high-resolution cardiac T(2) mapping through peripheral k-space sharing. Magn Reson Med 2019;81:220-33. [Crossref] [PubMed]
- Shao J, Zhou Z, Nguyen KL, Finn JP, Hu P. Accurate, precise, simultaneous myocardial T1 and T2 mapping using a radial sequence with inversion recovery and T2 preparation. NMR Biomed 2019;32:e4165. [Crossref] [PubMed]
- Feng L. Golden-Angle Radial MRI: Basics, Advances, and Applications. J Magn Reson Imaging 2022;56:45-62. [Crossref] [PubMed]
- Lima da Cruz G, Bustin A, Jaubert O, Schneider T, Botnar RM, Prieto C. Sparsity and locally low rank regularization for MR fingerprinting. Magn Reson Med 2019;81:3530-43. [Crossref] [PubMed]
- Wang X, Rosenzweig S, Roeloffs V, Blumenthal M, Scholand N, Tan Z, Holme HCM, Unterberg-Buchwald C, Hinkel R, Uecker M. Free-breathing myocardial T1 mapping using inversion-recovery radial FLASH and motion-resolved model-based reconstruction. Magn Reson Med 2023;89:1368-84. [Crossref] [PubMed]
- Cao T, Ma S, Wang N, Gharabaghi S, Xie Y, Fan Z, Hogg E, Wu C, Han F, Tagliati M, Haacke EM, Christodoulou AG, Li D. Three-dimensional simultaneous brain mapping of T1, T2, T2* and magnetic susceptibility with MR Multitasking. Magn Reson Med 2022;87:1375-89. [Crossref] [PubMed]
- Christodoulou AG, Shaw JL, Nguyen C, Yang Q, Xie Y, Wang N, Li D. Magnetic resonance multitasking for motion-resolved quantitative cardiovascular imaging. Nat Biomed Eng 2018;2:215-26. [Crossref] [PubMed]
- Hamilton JI, Currey D, Rajagopalan S, Seiberlich N. Deep learning reconstruction for cardiac magnetic resonance fingerprinting T1 and T2 mapping. Magn Reson Med 2021;85:2127-35. [Crossref] [PubMed]
- Li P, Hu Y. Learned Tensor Low-CP-Rank and Bloch Response Manifold Priors for Non-Cartesian MRF Reconstruction. IEEE Trans Med Imaging 2023;42:3702-14. [Crossref] [PubMed]
- Qu WY, Cheng J, Zhu YJ, Liang D. Deep MR parametric imaging with the learned L+S model and attention mechanism. IET Image Process 2023;17:969-78.
- Le JV, Mendes JK, McKibben N, Wilson BD, Ibrahim M, DiBella EVR, Adluru G. Accelerated cardiac T1 mapping with recurrent networks and cyclic, model-based loss. Med Phys 2022;49:6986-7000. [Crossref] [PubMed]
- Lyu J, Wang G, Hossain MS. Iterative Temporal-spatial Transformer-based Cardiac T1 Mapping MRI Reconstruction. ACM Transactions on Multimedia Computing, Communications and Applications 2024;20:1-18.
- Liu F, Kijowski R, El Fakhri G, Feng L. Magnetic resonance parameter mapping using model-guided self-supervised deep learning. Magn Reson Med 2021;85:3211-26. [Crossref] [PubMed]
- Hamilton JI. A Self-Supervised Deep Learning Reconstruction for Shortening the Breathhold and Acquisition Window in Cardiac Magnetic Resonance Fingerprinting. Front Cardiovasc Med 2022;9:928546. [Crossref] [PubMed]
- Yi Z, Liu Y, Zhao Y, Xiao L, Leong ATL, Feng Y, Chen F, Wu EX. Joint calibrationless reconstruction of highly undersampled multicontrast MR datasets using a low-rank Hankel tensor completion framework. Magn Reson Med 2021;85:3256-71. [Crossref] [PubMed]
- Bustin A, Lima da Cruz G, Jaubert O, Lopez K, Botnar RM, Prieto C. High-dimensionality undersampled patch-based reconstruction (HD-PROST) for accelerated multi-contrast MRI. Magn Reson Med 2019;81:3705-19. [Crossref] [PubMed]
- Hu C, Peters DC. SUPER: A blockwise curve-fitting method for accelerating MR parametric mapping with fast reconstruction. Magn Reson Med 2019;81:3515-29. [Crossref] [PubMed]
- Yang F, Zhang J, Li G, Zhu J, Tang X, Hu C. Regularized SUPER-CAIPIRINHA: Accelerating 3D variable flip-angle T1 mapping with accurate and efficient reconstruction. Magn Reson Med 2023;90:1380-95. [Crossref] [PubMed]
- Giri S, Chung YC, Merchant A, Mihai G, Rajagopalan S, Raman SV, Simonetti OP. T2 quantification for improved detection of myocardial edema. J Cardiovasc Magn Reson 2009;11:56. [Crossref] [PubMed]
- Zhang T, Pauly JM, Levesque IR. Accelerating parameter mapping with a locally low rank constraint. Magn Reson Med 2015;73:655-61. [Crossref] [PubMed]
- Kolda TG, Bader BW. Tensor Decompositions and Applications. Siam Rev 2009;51:455-500.
- Uecker M, Lai P, Murphy MJ, Virtue P, Elad M, Pauly JM, Vasanawala SS, Lustig M. ESPIRiT--an eigenvalue approach to autocalibrating parallel MRI: where SENSE meets GRAPPA. Magn Reson Med 2014;71:990-1001. [Crossref] [PubMed]
- Griswold MA, Jakob PM, Heidemann RM, Nittka M, Jellus V, Wang J, Kiefer B, Haase A. Generalized autocalibrating partially parallel acquisitions (GRAPPA). Magn Reson Med 2002;47:1202-10. [Crossref] [PubMed]
- Uecker M, Hohage T, Block KT, Frahm J. Image reconstruction by regularized nonlinear inversion--joint estimation of coil sensitivities and image content. Magn Reson Med 2008;60:674-82. [Crossref] [PubMed]
- Xue H, Shah S, Greiser A, Guetter C, Littmann A, Jolly MP, Arai AE, Zuehlsdorff S, Guehring J, Kellman P. Motion correction for myocardial T1 mapping using image registration with synthetic image estimation. Magn Reson Med 2012;67:1644-55. [Crossref] [PubMed]
- Si D, Kong X, Guo R, Cheng L, Ning Z, Chen Z, Chen S, Herzka DA, Ding H. Single breath-hold three-dimensional whole-heart T2 mapping with low-rank plus sparse reconstruction. NMR Biomed 2023;36:e4924. [Crossref] [PubMed]
- Urzua Fresno C, Sanchez Tijmes F, Shaw KE, Huang F, Thavendiranathan P, Khullar S, Seidman MA, Hanneman K. Cardiac Imaging in Myocarditis: Current Evidence and Future Directions. Can Assoc Radiol J 2023;74:147-59. [Crossref] [PubMed]
- Ding H, Schar M, Zviman MM, Halperin HR, Beinart R, Herzka DA. High-resolution quantitative 3D T2 mapping allows quantification of changes in edema after myocardial infarction. J Cardiovasc Magn Reson 2013;15:181.
- Krahn PRP, Singh SM, Ramanan V, Biswas L, Yak N, Anderson KJT, Barry J, Pop M, Wright GA. Cardiovascular magnetic resonance guided ablation and intra-procedural visualization of evolving radiofrequency lesions in the left ventricle. J Cardiovasc Magn Reson 2018;20:20. [Crossref] [PubMed]
- Zhu Y, Wang C, Su S, Qiu Z, Yan Z, Liang D, Wang Y, Wang H. High resolution single-shot myocardial imaging using bSSFP with wave encoding. Med Phys 2023;50:7039-48. [Crossref] [PubMed]
- Lu Q, Li J, Lian Z, Zhang X, Feng Q, Chen W, Ma J, Feng Y. A model-based MR parameter mapping network robust to substantial variations in acquisition settings. Med Image Anal 2024;94:103148. [Crossref] [PubMed]
- Jun Y, Shin H, Eo T, Kim T, Hwang D. Deep model-based magnetic resonance parameter mapping network (DOPAMINE) for fast T1 mapping using variable flip angle method. Med Image Anal 2021;70:102017. [Crossref] [PubMed]
- Sabidussi ER, Klein S, Caan MWA, Bazrafkan S, den Dekker AJ, Sijbers J, Niessen WJ, Poot DHJ. Recurrent inference machines as inverse problem solvers for MR relaxometry. Med Image Anal 2021;74:102220. [Crossref] [PubMed]
- Zhang Y, Li P, Hu Y T. (2)LR-Net: An unrolling network learning transformed tensor low-rank prior for dynamic MR image reconstruction. Comput Biol Med 2024;170:108034. [Crossref] [PubMed]


