
Dilated multi-scale residual attention (DMRA) U-Net: three-dimensional (3D) dilated multi-scale residual attention U-Net for brain tumor segmentation
Introduction
Cancer is a disease that causes pathological and physiological alterations during cell division, and is a major cause of death worldwide. In 2020, there were an estimated 19.3 million new cancer cases and 10 million cancer-related deaths worldwide (1). The incidence rate of brain tumors worldwide is only 1.6%, and the mortality rate is only approximately 2.5%; however the risk of death for patients with brain tumors is significantly higher than that of other cancer patients (1).
Brain tumors, which can be either benign or malignant, are defined as the abnormal growth and unnatural division of cells in brain tissue. The most prevalent type of malignant brain tumor is glioma, which is further classified into high-grade glioma (HGG) and low-grade glioma (LGG) based on the extent of the malignancy. Glimoas can be categorized into the following three tumor sub-regions: the necrotic tumor core (NCR), enhancing tumor (ET), and peritumoral edema (ED) regions. The sizes of gliomas also vary, and their forms can exhibit lobulation and other characteristics. Consequently, it is difficult to precisely segregate brain gliomas and their internal sub-regions.
Multi-modal imaging, or magnetic resonance imaging (MRI), is characterized by its ability to produce distinct imaging sequences using various contrast techniques, such as T1-weighted (T1), T1-weighted contrast-enhanced (T1CE), T2-weighted (T2), and fluid-attenuated inversion recovery (FLAIR) (2). The analysis of these four modalities can lead to a more thorough understanding of brain tumors, as various modalities present distinct characteristic information. Thus, computer-aided diagnosis and treatment based on MRI images is one of the most popular research areas in brain tumor image segmentation.
Researchers frequently employed conventional machine-learning techniques to perform segmentation tasks in the early phases of brain tumor segmentation (BraTS) research. However, as the morphology and appearance of brain tumors can vary widely, it can be challenging to properly capture these distinctions. Additionally, these methodologies are frequently constrained by subjective criteria and specific domain knowledge.
U-Net and its three-dimensional (3D) version, U-Net (3,4), are convolutional neural network (CNN) architectures widely used for medical image segmentation, such as BraTS (5,6). Pereira et al. used two slightly different U-Nets to perform pixel-level classification of small two-dimensional image slices of brain tumors (7), specifically for LGG and HGG. However, this method is time consuming. Dong et al. used U-Net to segment slices of each 3D multi-modal MRI image (8). This method has fast training and testing speeds, and low computational requirements, but it also has a large number of parameters. Further, U-Net-based methods often fail to fully use the contextual information of 3D images.
Milletari et al. developed V-Net (9), an improved model based on 3D U-Net. V‑Net introduces residual connections and batch normalization (BN) operations, effectively alleviating gradient vanishing and network degradation issues. This allows the features learned at each layer of the network to be directly passed to subsequent layers, while avoiding excessive computation and parameters. V-Net performs well overall; however, its ability to segment the tumor core (TC) region, which is of great interest in medical diagnosis, is average. Oktay et al. proposed attention U-Net (10), which introduces attention gates based on 3D U-Net to help the network focus on regions of interest, and which was shown to have improved local segmentation performance for relatively small volumes. However, its overall segmentation performance is average. Isensee et al. used an ensemble of multiple 3D U-Nets (11,12), trained on a large dataset, which has strong feature learning capabilities. The use of region-based training, additional training data co-training, post-processing to enhance tumor detection by targeting false positives, and combining dice and cross-entropy losses significantly improves the performance of this method. However, repeated training also slightly increases the probability of network overfitting (13).
Xu et al. used an architecture composed of a shared feature extractor that branches out into three relatively smaller 3D U-Nets to segment each sub-region of layered tumors (14). Each 3D U-Net contains a feature bridging module that is coupled with attention blocks to achieve high overall segmentation performance for different brain tumor regions. However, this network has a long training time, which limits the scalability of architecture variants and data. Ruba et al. combined 3D U-Net with the local symmetry inter-sign operator (15), which showed good performance in the segmentation of sub-regions within tumors, as well as good sensitivity (Sens) and specificity. Additionally, this method was found to be more efficient than other methods in terms of its training and testing times. However, its effectiveness is better in HGG compared to LGG, and its generalizability may also be affected by the slightly poorer performance on LGG datasets. Li et al. proposed an enhanced 3D U-Net with enhanced encoding and decoding modules to improve the extraction and use of image features (16). They also accelerated the convergence speed of the model by using a hybrid loss function. However, this method loses some information between blocks during block processing, resulting in poor segmentation performance for the whole tumor (WT) region.
To address these issues comprehensively, we introduced two new convolutional modules to the encoding path of the traditional 3D U-Net. These modules have high feature extraction levels and a low parameter count, reducing the loss of shallow and deep features. We also added and modified the channel attention (CA) mechanism in 3D U-Net to enable it to adapt to 3D brain tumor data, removing redundant information, effectively highlighting useful information, and allocating computing resources reasonably. The main contributions of this study are as follows:
- We proposed a 3D dilated multi-scale residual attention U-Net (DMRA-U-Net) model based on 3D U-Net for MRI BraTS. The DMRA U-Net uses dilated convolution residual (DCR) modules to replace the original convolution layers in the shallow encoding path of 3D U-Net to more efficiently use shallow features. The multi-scale convolution residual (MCR) modules replace the original convolution layers in the bottom encoding path of 3D U-Net to extract richer and more comprehensive feature expression, reducing the loss or blurring of overall information.
- We added a CA module between the encoding and decoding paths to alleviate the difficulty of extracting and retaining important features when processing deep feature maps.
- We conducted extensive experiments on four BraTS datasets (i.e., BraTS 2018, 2019, 2020, and 2021), and the results showed that DMRA U-Net has good segmentation performance for the WT, TC, and ET regions. The performance of DMRA U-Net was also comparable to that of other BraTS methods.
Methods
In this section, we first introduce the structure of the DMRA U-Net for BraTS. We then detail the basic structure and function of the DCR module, MCR module, and CA module, respectively. The study was conducted in accordance with the Declaration of Helsinki (as revised in 2013).
Overall architecture
We constructed the DMRA U-Net by combining the proposed DCR, MCR, and modified CA modules with a traditional 3D U-Net. Figure 1 shows the model structure of the DMRA U-Net. With skip connections between each layer of the encoder and decoder, the DMRA U-Net uses the same encoder-decoder architecture as that of the traditional 3D U-Net. The left-side encoding path is mainly used to input the tumor feature maps from the MRI, which reduces the size of the feature maps after a series of operations. While the right-side decoding path recovers the size of the feature map by jump-joining and transposition convolution, which increases the feature map to match the size of the input image for end-to-end segmentation. The four input channels of the DMRA U-Net correspond to the following four modalities of MRI (i.e., T1, T1CE, T2, and FLAIR), and the three output channels correspond to the three brain tumor regions to be segmented (i.e., the WT region, the TC region, and the ET region).
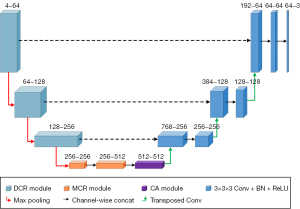
The DMRA U-Net model uses input data 4×128×128×128 in size. For the down-sampling operations, maximum pooling with a kernel size of 2 and a stride of 2 is used to reduce the image size by half, such that the size at the bottom of the network becomes 512×16×16×16. The up-sampling operations are performed using transpose convolution with a kernel size of 2 and a stride of 2 to double the image size and restore the spatial information and original dimensions of the input. The output data size for the DMRA U-Net model is 3×128×128×128. Unlike the traditional 3D U-Net, DCR modules are used in the first three layers of the encoding path instead of the original 3D convolutions. At the bottom of the encoding path, there are two MCR modules followed by a CA module. The operations in the decoding path are consistent with those of the traditional 3D U‑Net. Specific details about the DCR and MCR modules are described in detail in the following sections.
DCR module
The original convolutional layers in the shallow layers of the encoding path (i.e., the first three layers) are replaced with the DCR module to more effectively use shallow features while preserving lower computational complexity and the memory consumption of the model. Figure 2 shows the basic structure of the module. The DCR module provides more discriminative representations without adding extra parameters than standard convolution processes. Consequently, we decided to add the DCR module for the BraTS tasks.
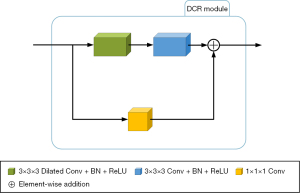
The DCR module is divided into a convolutional path and a residual path. First, in the convolutional path, a 3×3×3 dilated convolution is added with a stride of 1 (17), padding of 2, dilation rate of 2, and bias set to “false” for the initial feature extraction of the input feature map to this module. Next, BN and rectified linear unit (ReLU) operations are performed once each, consecutively (18,19). A 3×3×3 convolution is then applied to further extract image features with a stride of 1, padding of 1, dilation rate of 1, and bias set to “false.” BN and ReLU operations are then performed once each, resulting in the output of the convolutional path. Second, in the residual path, a 1×1×1 convolution is added with a stride of 1, padding of 1, and bias set to “false.” This convolution is used to adjust the channel number of the original feature map to match the output feature map of the convolutional path. Finally, the output feature maps from the convolutional path and the residual path are added at the pixel level, producing the final output of the DCR module.
Dilated convolution convolves the weights in the convolution kernel with positions distributed at certain intervals in the input tensor. This enlarges the effective receptive field of the convolution kernel, increasing the perception range and improving the feature extraction ability of the network while maintaining the same kernel size and number of parameters. The equation for calculating the equivalent kernel size of the dilated convolution is expressed as follows:
where is the effective kernel size, is the original kernel size, and is the dilation rate of the dilated convolution, which refers to the spacing between the weights in the convolutional kernel. When the dilation rate is 1, the dilated convolution is equivalent to regular convolution.
The equation for calculating the receptive field of the dilated convolution is expressed as follows:
where is the receptive field size of the current layer, is the receptive field size of the previous layer, is the effective kernel size of the current layer, is the stride of any previous layer, and is the product of the strides of all previous layers.
The introduction of the BN layer has a regularizing effect and improves the generalizability of the model. The BN layer then estimates the mean and variance of each input to the network, and standardizes the input data, allowing each layer in the network to learn more stably. Finally, the BN layer addresses the issue of gradient disappearance and ensures better gradient propagation in deep neural networks. The process and equation of the BN layer are expressed as follows:
where is a batch of values input to the BN layer, is the average of values in the input, is the variance of values in the input, is the normalized result, is the final output of the BN layer, is the learnable scale parameter, and is the learnable shift parameter.
After performing the aforementioned operations of mean, variance, normalization, scaling, and shifting on the input data to the network, the BN layer obtains the final output, .
MCR module
The MCR module is used to replace the original convolutional layer at the bottom of the encoding path to simultaneously process features of different scales, obtain a richer and more comprehensive feature set, and decrease information loss or blurring. Figure 3 shows the basic architecture of the MCR module.
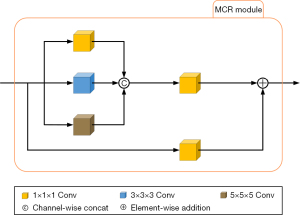
The MCR module is divided into multi-scale convolutional paths and residual paths. First, in the multi-scale convolutional path, the input data is simultaneously passed through three convolutional paths; the first path is a 1×1×1 3D convolution with a stride of 1, padding of 0, and bias set to “true”; the second path is a 3×3×3 3D convolution with a stride of 1, padding of 1, and bias set to “true”; the third path is a 5×5×5 3D convolution with a stride of 1, padding of 2, and bias set to “true”. The output results of the then three convolutional paths are concatenated along the channel dimension, after which, a 1×1×1 3D convolution is performed with a stride of 1, padding of 0, and bias set to “true”. This 1×1×1 convolution can combine features at the channel level to integrate information from different channels. Second, in the residual path, a 1×1×1 3D convolution is added to obtain the output of the residual path. Finally, the output feature maps of the multi-scale convolutional path and the residual path are added pixel by pixel, and the result is the final output of the MCR module.
CA module
We modified the CA module and positioned it between the encoder and decoder of the 3D U-Net (20) to address difficulties related to the extraction and retention of important features when processing deep feature maps. Figure 4 shows the basic architecture of the CA module.
Unlike the CA module designed by the original authors (20), we replaced some of the original operations for 2D data in the CA module with operations that can be adapted to 3D data, and made some other minor changes. Our CA module has two paths. In the first path, the input feature map is first passed through two parallel maximum pooling layers and average pooling layers, transforming the feature map from a size of C × D × H × W to a size of C×1×1 ×1. It then passes through a shared fully connected layer. The fully connected layer first compresses the number of channels of the feature map to 1/r times that of the original, where r is the reduction ratio, which was set to 16 in this study. Next, it passes through a ReLU activation function, and then expands back to the original number of channels, yielding two results, after which the ReLU activation function is not applied to the results. The two output results are element-wise added, and then passed through a sigmoid activation function to obtain the output weight of the first path. In the second path, no operation is performed on the input feature map. Finally, the output weight of the first path is element-wise multiplied with the original feature map of the second path to obtain the final output of the CA module.
Statistical analysis
The t-test, also known as the Student’s t-test, was used to compare whether there was a significant difference between the means of two samples. The P value is the probability value of the t-distribution, which measures the level of confidence in rejecting the null hypothesis. Thus, the smaller the P value, the higher the level of confidence in rejecting the null hypothesis. A P value less than 0.05 indicated that the results obtained from the two methods were statistically significant.
Experiments
Datasets
In this study, we used the BraTS 2018–2021 datasets (21,22), which are publicly available brain glioma datasets provided by the Medical Image Computing and Computer Assisted Intervention (MICCAI) Society, to train and evaluate our proposed model. The datasets comprised multi-modal brain MRI scans, including T1, T1CE, T2, and FLAIR scans, from multiple medical centers. Each MRI sequence has 155 images, and each image is sized 240×240 pixels. Detailed information about the BraTS datasets is provided in Table 1. As Table 1 shows, the training sets of BraTS 2018 and BraTS 2019 were further classified into HGG and LGG sets. However, since 2020, the form of the BraTS dataset has undergone a number of changes, and the training dataset no longer distinguishes between HGG and LGG data.
Table 1
| Dataset | Training | Validation | ||
|---|---|---|---|---|
| HGG | LGG | Total | ||
| BraTS 2018 | 210 | 75 | 285 | 66 |
| BraTS 2019 | 259 | 76 | 335 | 125 |
| BraTS 2020 | – | – | 369 | 125 |
| BraTS 2021 | – | – | 1251 | 219 |
BraTS, brain tumor segmentation; HGG, high-grade gliomas; LGG, low-grade gliomas.
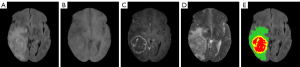
The dataset has four label categories: Label 0, which represents the healthy background region; Label 1, which represents the NCR region; Label 2, which represents the ED region; and Label 4, which represents the ET region. Figure 5 provides an example of a sample from the BraTS 2018 training dataset, where each label is represented by a corresponding color: Label 1 (i.e., the NCR region) is shown in red; Label 2 (i.e., the ED region) is shown in green; and Label 4 (i.e., the ET region) is shown in yellow. The BraTS dataset also has three segmentation result labels, which are used to segment the WT region, TC region, and ET region. The WT region includes green, yellow, and red labels; the TC region includes red and yellow labels, and the ET region only includes the yellow label.
Data preprocessing
Due to uncertainties related to brain tumor morphology and location, as well as the blurriness of boundaries and manual annotation biases, the preprocessing of brain tumor images is particularly important. Previous studies have shown that data augmentation techniques can significantly affect a model’s generalizability to BraTS (23-25). The data augmentation methods adopted in this study can be used to randomly scale, flip, and rotate input data during the training process to increase data diversity and help improve model generalizability and robustness. First, we adjusted 1% of the non-zero outliers in each image. Second, minimum-maximum normalization was applied to all images. Third, we cropped the MRI image of each sample from a size of 155×240×240 pixels to a size of 128×128×128 pixels. We applied a centrosymmetric cropping technique on the image portion of the target size, ensuring that the cropped location was equally spaced from the original image’s edge along all axes. With this cropping technique, the important portions of the brain tumor image are preserved while a significant number of useless background pixels are removed, alleviating the class imbalance of brain tumors and reducing computation. Finally, with an 80% probability, we performed the following data augmentation operations on each sample image in turn: the code has a 20% chance to discard any one of the channels of this image; we randomly scaled the intensity values of the image, with scaling factors between [0.9, 1.1]; and we randomly rotated and flipped the image.
Evaluation metrics
There are various evaluation metrics for medical image segmentation. We evaluated the performance of the model using commonly used metrics in medical segmentation, including the dice similarity coefficient (DSC), Hausdorff distance (HD), and Sens.
The DSC is a measure of set similarity commonly used to calculate the similarity between two samples. The value of the DSC ranges from 0 to 1, where a value closer to 1 indicates a higher similarity between segmentation contours. The DSC is expressed as:
where is the set of predicted labels, is the set of true labels, is the true positive voxel count, is the false positive voxel count, is the true negative voxel count, and is the false negative voxel count.
The HD is the maximum distance from a set to the nearest point in another set. It is often used in image segmentation tasks because it is sensitive to the segmented boundaries. A smaller HD indicates greater similarity between two sets. The HD is expressed as:
where is the one-way HD from set to , and is the one-way HD from set to . The longest distance between and is selected, which represents the HD between set and set .
Sens refers to the proportion of actual positive samples that the model successfully identifies as positive, and is also known as the true positive rate or recall. It measures the ability of a model to correctly identify positive samples. The value of the Sens ranges from 0 to 1, with higher values indicating that the model is better at identifying positive samples. Sens is expressed as:
Parameter settings
Setting appropriate parameters can help prevent the model from getting trapped in local minima, accelerate the convergence speed, and achieve better segmentation results. In this study, we used the stochastic gradient descent (SGD) optimization algorithm with an initial learning rate of 1×10−4, a momentum of 0.9, a normalization function of BN, and a loss function of dice loss. The batch size was set to 1, and the number of epochs was set to 300. During the training phase, the BraTS 2018 dataset was randomly divided into a training set and a validation set at a ratio of 8:2. After every 3 epochs of training, 1 epoch of validation was performed. During the testing phase, as the providers of the datasets did not provide ground truth labels for the validation and testing patients in this series of datasets, and the BraTS 2019 dataset added 50 cases to the BraTS 2018 dataset (including 49 HGG cases and 1 LGG case), these additional 50 cases from the BraTS 2019 dataset were selected as the test set to evaluate the performance of the model. In addition, this study also selected 34 additional samples from the BraTS 2020 training set, which were added to the BraTS 2019 dataset, as the second test set. From the BraTS 2021 dataset, the last 50 samples (with identification numbers ranging from 01617 to 01666) from the training set were selected as the third test set. The models trained on the BraTS 2018 dataset were directly tested on these three datasets for the statistical analysis. The specific dataset divisions are shown in Table 2.
Table 2
| Dataset | Training set | Validation set | Testing set |
|---|---|---|---|
| BraTS 2018 | 228 | 57 | – |
| BraTS 2019 | – | – | 50 |
| BraTS 2020 | – | – | 34 |
| BraTS 2021 | – | – | 50 |
BraTS, brain tumor segmentation.
Our experiments were conducted on a NVIDIA A100-PCIE graphics card with a memory of 40 GB. The model was implemented using Python 3.9.0 and the PyTorch 1.12.0+cu113 deep-learning framework.
Results
To validate the effectiveness of our proposed DMRA U-Net, we conducted comparative experiments with other methods on the BraTS 2019 dataset, and the final segmentation results are shown in Table 3. Table 3 provides a comparison of the DSC, HD, and Sens between our proposed model and other methods for the WT, TC, and ET regions. As Table 3 shows, the DSC significantly improved from 0.8567, 0.8614, and 0.8752 (3D U-Net) to 0.9012, 0.8867, and 0.8813 (DMRA U-Net) for the WT, TC, and ET regions, respectively; the HD significantly decreased from 50.69, 29.77, and 20.88 mm (3D U-Net) to 28.86, 13.34, and 10.88 mm (DMRA U-Net) for the WT, TC, and ET regions, respectively; the Sens significantly improved from 0.9394, 0.9380, and 0.9164 (3D U-net) to 0.9429, 0.9452, and 0.9303 (DMRA U-Net) for the WT, TC, and ET regions, respectively. In addition, we compared our results (listed in Table 3) with the results of the most recent models that used the BraTS 2019 dataset. The results showed that the DMRA U-Net proposed in this study ranked first in four metrics. More specifically, it achieved the highest DSC in the TC region (1.9% higher than the previous highest score), the best HD in the TC region (1.59 mm lower than the previous lowest score), the best HD in the ET region (0.85 mm lower than the previous lowest score), and the best Sens in the TC region [1.9% higher than the previous highest score in a published paper (33)]. Notably, the DSC for the WT region (0.9012) of our method was close to the best score (0.9060), and the Sens for the ET region (0.9303) was close to the best score (0.946). The above comparisons showed the powerful ability of our model to undertake semantic segmentation.
Table 3
| Methods | DSC | HD (mm) | Sens | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| WT | TC | ET | WT | TC | ET | WT | TC | ET | |||
| DANet (26) | 0.842 | 0.853 | 0.797 | – | – | – | 0.885 | 0.915 | 0.839 | ||
| R2U-Net (27) | 0.843 | 0.861 | 0.787 | – | – | – | 0.875 | 0.895 | 0.843 | ||
| AttUNet (28) | 0.849 | 0.866 | 0.789 | – | – | – | 0.878 | 0.918 | 0.848 | ||
| H2NF-Net (29) | 0.8879 | 0.8537 | 0.8277 | – | – | – | – | – | – | ||
| Context aware 3D U-Net (30) | 0.8912 | 0.8467 | 0.7910 | – | – | – | 0.8998 | 0.8555 | 0.8428 | ||
| Two-stage-VAE 3D U-Net (31) | 0.8729 | 0.8357 | 0.8205 | 11.42 | 19.96 | 15.67 | – | – | – | ||
| nnU-Net (12) | 0.9060 | 0.8426 | 0.7767 | – | – | – | – | – | – | ||
| Res 3D U-Net (32) | 0.8734 | 0.8687 | 0.8780 | 56.96 | 32.92 | 21.34 | 0.9609 | 0.9232 | 0.9287 | ||
| MRAB 3D U-Net (33) | 0.8241 | 0.8673 | 0.8587 | 35.26 | 14.93 | 15.28 | 0.9821 | 0.9263 | 0.8733 | ||
| Enhanced 3D U-Net (16) | 0.778 | 0.875 | 0.903 | 56.26 | 18.62 | 11.73 | 0.906 | 0.926 | 0.946 | ||
| 3D U-Net | 0.8567 | 0.8614 | 0.8752 | 50.69 | 29.77 | 20.88 | 0.9394 | 0.9380 | 0.9164 | ||
| DMRA U-Net (ours) | 0.9012 | 0.8867 | 0.8813 | 28.86 | 13.34 | 10.88 | 0.9429 | 0.9452 | 0.9303 | ||
DSC, dice similarity coefficient; HD, Hausdorff distance; Sens, sensitivity; BraTS, brain tumor segmentation; WT, whole tumor; TC, tumor core; ET, enhancing tumor; DA, dual attention; R2, recurrent residual; Att, attention; H2NF, hybrid high-resolution and non-local feature; 3D, three-dimensional; VAE, variational auto-encoder; nn, no new; Res, residual; MRAB, multipath residual attention block; DMRA, dilated multi-scale residual attention.
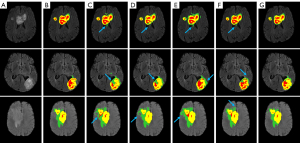
Additionally, we visualized the BraTS results of our proposed DMRA U-Net model as shown in Figure 6. Each row in Figure 6 represents a sample. From left to right, the seven columns display the FLAIR image of the patient sample, the ground truth, the segmentation of the 3D U-Net, the segmentation of the residual 3D U-Net (Res 3D U-Net), the segmentation of the multipath residual attention block 3D U-Net (MRAB 3D U-Net), the segmentation of the Enhanced 3D U-Net (16), and the segmentation of the proposed DMRA U-Net. As Figure 6 shows, the traditional 3D U-Net exhibits poor segmentation performance around the edges of the brain tumor and the surrounding regions as indicated by the blue arrows. This is due to the single information extraction approach of the 3D U-Net, leading to the emergence of numerous false positive voxels. Other state-of-the-art methods improve the segmentation performance compared to 3D U-Net; however, there are still a few false positive voxels, and the segmentation among different regions inside the tumor is not ideal. Conversely, the DMRA U-Net finely delineates the various regions in the tumor without obvious under- or over-segmentation, and significantly reduces false positive mis-segmentation around the tumor periphery.
Discussion
We conducted ablation experiments on the new dataset from BraTS 2019 to evaluate the effectiveness of our model in BraTS. Specifically, we used 3D U-Net as the baseline model. We also conducted a detailed comparative statistical analysis between 3D U-Net and DMRA U-Net.
The encoding path of the traditional 3D U-Net has many issues, including weak feature extraction capabilities, that make it difficult to avoid information loss, and fixed convolution operations that struggle to adapt to both local and global features in medical image data. Thus, in this study, we retained the U-shaped structure of the 3D U-Net, but redesigned the encoding path by replacing the original convolution operations with a new DCR module and a MCR module. This improved was done to improve the segmentation performance of the model in BraTS tasks.
In addition, many researchers have shown that segmentation methods based on attention mechanisms significantly improve segmentation accuracy. However, few researchers have considered the shortcomings of spatial attention (SA) mechanisms in removing truly redundant information when dealing with small-sized deep feature maps. We attempted to combine CA, SA, and CA and SA, and ultimately chose the CA mechanism, which is better able to process deep feature maps. We also made some modifications to reduce the computational complexity of our proposed model while ensuring the effectiveness of the CA module.
Ablation experiments on the hyperparameters
In terms of the selection of optimization algorithms, we experimented with different algorithms for training, including Adaptive Moment Estimation (Adam), Adam with Weight Decay Fix (AdamW), and SGD (Table 4). As Table 4 shows, the model trained with the SGD algorithm achieved optimal results in five out of nine metrics on the BraTS 2019 dataset, attaining the best segmentation performance. Therefore, we ultimately chose the SGD algorithm for the core experiments.
Table 4
| Optimization algorithms | DSC | HD (mm) | Sens | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| WT | TC | ET | WT | TC | ET | WT | TC | ET | |||
| Adam | 0.8933 | 0.8877 | 0.8802 | 31.74 | 15.34 | 12.44 | 0.9735 | 0.9419 | 0.9220 | ||
| AdamW | 0.8792 | 0.8870 | 0.8819 | 34.90 | 14.46 | 9.19 | 0.9678 | 0.9219 | 0.9037 | ||
| SGD (ours) | 0.9012 | 0.8867 | 0.8813 | 28.86 | 13.34 | 10.88 | 0.9429 | 0.9452 | 0.9303 | ||
BraTS, brain tumor segmentation; DSC, dice similarity coefficient; HD, Hausdorff distance; Sens, sensitivity; WT, whole tumor; TC, tumor core; ET, enhancing tumor; Adam, adaptive moment estimation; AdamW, adaptive moment estimation with weight decay; SGD, stochastic gradient descent.
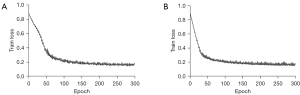
A small batch size can achieve better generalization while preventing a significant increase in training time. We showed this by training the model on the BraTS 2018 dataset, and testing it on the BraTS 2019 dataset. The specific training times and test results are shown in Table 5. As Table 5 shows, increasing the batch size from 1 to 2 reduced the average training time per epoch by 7.85 seconds, but led to a decrease in eight out of nine metrics on the BraTS 2019 dataset. Additionally, we recorded the impact of batch size settings on the convergence behavior of the model during training as shown in Figure 7. As Figure 7 shows, when the batch size is 1, the model’s convergence speed in the early stages of training is significantly faster compared to the control group with a batch size of 2. This is because a small batch size allows for more frequent updates of the model parameters, with each update based on different small sample sets, enabling quicker exploration of the loss function surface. Due to limitations in our experimental equipment, we did not conduct ablation experiments with a batch size bigger than 2.
Table 5
| Batch size | Training time/epoch (s)(mean ± SD) | DSC | HD (mm) | Sens | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| WT | TC | ET | WT | TC | ET | WT | TC | ET | ||||
| 2 | 102.95±9.05 | 0.8872 | 0.8728 | 0.8473 | 36.95 | 14.17 | 9.04 | 0.9032 | 0.8967 | 0.8302 | ||
| 1 (ours) | 110.80±6.54 | 0.9012 | 0.8867 | 0.8813 | 28.86 | 13.34 | 10.88 | 0.9429 | 0.9452 | 0.9303 | ||
DSC, dice similarity coefficient; HD, Hausdorff distance; Sens, sensitivity; WT, whole tumor; TC, tumor core; ET, enhancing tumor; SD, standard deviation.
Ablation experiments on the DCR module
First, we performed ablation tests to assess the effectiveness of the DCR module in the shallow encoding path of the 3D U-Net. We replaced the original convolution layers in the first, second, and third layers of the encoding path with the DCR module, and the segmentation results obtained are shown in Table 6. As Table 6 shows, replacing specific original convolution layers in the encoding path with the DCR module alleviated the problem of inefficient use of shallow features in BraTS tasks and achieved good segmentation results.
Table 6
| Metrics | 3D U-Net | 3D U-Net + DCR |
|---|---|---|
| DSC | ||
| WT | 0.8567 | 0.8902 |
| TC | 0.8614 | 0.8725 |
| ET | 0.8752 | 0.8763 |
| HD (mm) | ||
| WT | 50.69 | 47.71 |
| TC | 29.77 | 27.14 |
| ET | 20.88 | 19.84 |
| Sens | ||
| WT | 0.9394 | 0.9517 |
| TC | 0.9380 | 0.9364 |
| ET | 0.9164 | 0.9161 |
DCR, dilated convolution residual; BraTS, brain tumor segmentation; 3D, three-dimensional; DSC, dice similarity coefficient; WT, whole tumor; TC, tumor core; ET, enhancing tumor; HD, Hausdorff distance; Sens, sensitivity.
Ablation experiments on the MCR module
Next, we tested the effectiveness of the MCR module in the deep encoding path. We replaced two original convolutions in the fourth layer of the 3D U-Net encoding path with the MCR module, and the segmentation results obtained are shown in Table 7. As Table 7 shows, the 3D U-Net + MCR model outperformed the 3D U-Net model in almost all evaluation metrics in all regions, with a decrease of only 0.86% in Sens for the TC region. This indicates that replacing the two original convolutions in the lowest layer of the encoding path with the MCR module enables a richer and more comprehensive feature set to be obtained through different receptive field sizes, reducing information loss or blurring.
Table 7
| Metrics | 3D U-Net | 3D U-Net + MCR |
|---|---|---|
| DSC | ||
| WT | 0.8567 | 0.8953 |
| TC | 0.8614 | 0.8833 |
| ET | 0.8752 | 0.8839 |
| HD (mm) | ||
| WT | 50.69 | 42.27 |
| TC | 29.77 | 14.99 |
| ET | 20.88 | 13.97 |
| Sens | ||
| WT | 0.9394 | 0.9441 |
| TC | 0.9380 | 0.9294 |
| ET | 0.9164 | 0.9166 |
MCR, multi-scale convolution residual; BraTS, brain tumor segmentation; 3D, three-dimensional; DSC, dice similarity coefficient; WT, whole tumor; TC, tumor core; ET, enhancing tumor; HD, Hausdorff distance; Sens, sensitivity.
Ablation experiments on the CA module
Moreover, we individually validated the CA module, which is capable of adapting to 3D volumetric data, into the 3D U-Net. We tested the performance of the module without the SA module (20) designed by the original authors. We added the CA module between the encoding and decoding paths of the 3D U-Net, and the segmentation results obtained are shown in Table 8. As Table 8 shows, the addition of the CA module led to a slight decrease in HD, but a significant improvement in the other evaluation metrics. The DSC significantly improved from 0.8567, 0.8614, and 0.8752 (3D U-net) to 0.8747, 0.8697, and 0.8859 (3D U-Net + CA) for the WT, TC and ET regions, respectively. Further, we conducted a quantitative analysis comparing attention modules, such as the convolutional block attention module (CBAM) and squeeze-and-excitation (SE) module (20,34). The modified CA module emerged slightly ahead in overall segmentation performance. The addition of our CA module addressed the issues related to extracting and preserving important features when processing with deep feature maps.
Table 8
| Metrics | 3D U-Net | 3D U-Net + CA | 3D U-Net + CBAM | 3D U-Net + SE |
|---|---|---|---|---|
| DSC | ||||
| WT | 0.8567 | 0.8747 | 0.8884 | 0.8871 |
| TC | 0.8614 | 0.8697 | 0.8510 | 0.8690 |
| ET | 0.8752 | 0.8859 | 0.8666 | 0.8718 |
| HD (mm) | ||||
| WT | 50.69 | 52.57 | 53.08 | 47.78 |
| TC | 29.77 | 33.90 | 30.76 | 36.21 |
| ET | 20.88 | 21.39 | 26.03 | 28.82 |
| Sens | ||||
| WT | 0.9394 | 0.9394 | 0.9139 | 0.9060 |
| TC | 0.9380 | 0.8930 | 0.9104 | 0.9256 |
| ET | 0.9164 | 0.8697 | 0.8795 | 0.8827 |
CA, channel attention; BraTS, brain tumor segmentation; 3D, three-dimensional; CBAM, convolutional block attention module; SE, squeeze-and-excitation; DSC, dice similarity coefficient; WT, whole tumor; TC, tumor core; ET, enhancing tumor; HD, Hausdorff distance; Sens, sensitivity.
Comprehensive ablation experiments on all modules
After verifying the performance of each module independently, we conducted a comprehensive multi-module ablation experiment on the BraTS 2019 dataset, the results of which are shown in Table 9. As Table 9 shows, our proposed final model achieved the best segmentation performance in terms of most of the evaluation metrics in the multi-module ablation experiment. The DSC scores for WT, TC, and ET segmentation were 0.9012, 0.8867, and 0.8813, respectively, which were 4.5%, 2.5%, and 0.6% higher than the 3D U-Net, respectively. Additionally, the dual-module combination of DCR and MCR surpassed the 3D U-Net by 3.4%, 1.1%, and −0.07% in DSC scores for WT, TC, and ET, respectively. This indicates that the DCR, MCR, and CA modules all possess strong independent stability and can be combined effectively, improving the model’s ability to perform BraTS tasks.
Table 9
| Metrics | 3D U-Net | 3D U-Net + DCR | 3D U-Net + DCR + MCR | 3D U-Net + DCR + MCR + CA (ours) |
|---|---|---|---|---|
| DSC | ||||
| WT | 0.8567 | 0.8902 | 0.8912 | 0.9012 |
| TC | 0.8614 | 0.8725 | 0.8728 | 0.8867 |
| ET | 0.8752 | 0.8763 | 0.8745 | 0.8813 |
| HD (mm) | ||||
| WT | 50.69 | 47.71 | 43.29 | 28.86 |
| TC | 29.77 | 27.14 | 16.48 | 13.34 |
| ET | 20.88 | 19.84 | 18.80 | 10.88 |
| Sens | ||||
| WT | 0.9394 | 0.9517 | 0.9454 | 0.9429 |
| TC | 0.9380 | 0.9364 | 0.9249 | 0.9452 |
| ET | 0.9164 | 0.9161 | 0.8957 | 0.9303 |
DCR, dilated convolution residual; MCR, multi-scale convolution residual; CA, channel attention; BraTS, brain tumor segmentation; 3D, three-dimensional; DSC, dice similarity coefficient; WT, whole tumor; TC, tumor core; ET, enhancing tumor; HD, Hausdorff distance; Sens, sensitivity.
Statistical analysis results
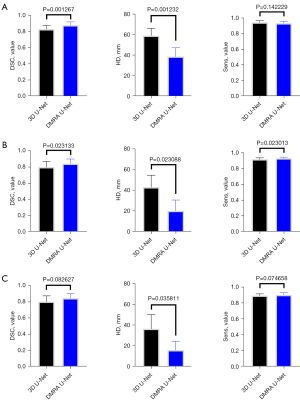
Finally, to further assess the performance of DMRA U-Net, we conducted comprehensive tests with the DMRA U-Net model, which was trained on the BraTS 2018 dataset. The tests were performed on the BraTS 2019, BraTS 2020 and BraTS 2021 datasets. We compared various metrics between the DMRA U-Net model and the 3D U-Net model, and the statistical analysis results are shown in Figure 8. All the calculations and drawings were performed using GraphPad Prism (version 8.0). An unpaired one-tailed Student’s t-test was used to compare the statistical difference between two groups. As Figure 8 shows, except for the t-test values of Sens for the WT region, the DSC for the ET region, and the Sens for the ET region, the t-test values of all other values were less than 0.05, and thus statistically significant.
Conclusions
The results showed that our model achieved good overall segmentation performance for the WT, TC, and ET regions. However, our model did not achieve the best segmentation performance in the ET region. This may be due to the relatively small volume and large variability among the samples in the ET region. The sizes and positions of the ET region vary across different samples in the dataset. We intend to explore the design of post-processing operations in the future to address the shortcomings of our model in handling the relatively small and less stable ET region in terms of volume and information. Currently, precise BraTS techniques can segment clear and detailed brain tumor images. These images can offer accurate parameter assessments in clinical applications, helping doctors monitor treatment effects and disease progression more precisely. In the future, we plan to expand our BraTS methods to include the application of clinical parameters such as the volume of enhanced lesions and the Response Assessment in Neuro-Oncology criteria (35,36).
Acknowledgments
Funding: This work was supported by
Footnote
Conflicts of Interest: All authors have completed the ICMJE uniform disclosure form (available at https://qims.amegroups.com/article/view/10.21037/qims-24-779/coif). The authors have no conflicts of interest to declare.
Ethical Statement: The authors are accountable for all aspects of the work in ensuring that questions related to the accuracy or integrity of any part of the work are appropriately investigated and resolved. The study was conducted in accordance with the Declaration of Helsinki (as revised in 2013).
Open Access Statement: This is an Open Access article distributed in accordance with the Creative Commons Attribution-NonCommercial-NoDerivs 4.0 International License (CC BY-NC-ND 4.0), which permits the non-commercial replication and distribution of the article with the strict proviso that no changes or edits are made and the original work is properly cited (including links to both the formal publication through the relevant DOI and the license). See: https://creativecommons.org/licenses/by-nc-nd/4.0/.
References
- Chhikara B S, Parang K. Global Cancer Statistics 2022: the trends projection analysis. Chem Biol Lett 2023;10:451.
- Plewes DB, Kucharczyk W. Physics of MRI: a primer. J Magn Reson Imaging 2012;35:1038-54. [Crossref] [PubMed]
- Ronneberger O, Fischer P, Brox T. U-Net: Convolutional Networks for Biomedical Image Segmentation. In: Navab N, Hornegger J, Wells W, Frangi A. editors. Medical Image Computing and Computer-Assisted Intervention – MICCAI 2015. Lecture Notes in Computer Science, Springer, 2015;9351:234-41.
- Çiçek Ö, Abdulkadir A, Lienkamp SS, Brox T, Ronneberger O. 3D U-Net: Learning Dense Volumetric Segmentation from Sparse Annotation. In: Ourselin S, Joskowicz L, Sabuncu M, Unal G, Wells W. editors. Medical Image Computing and Computer-Assisted Intervention – MICCAI 2016. Lecture Notes in Computer Science, Springer, 2016;9901:424-32.
- Wu B, Zhang F, Xu L, Shen S, Shao P, Sun M, Liu P, Yao P, Xu RX. Modality pre-serving U-Net for segmentation of multimodal medical images. Quant Imaging Med Surg 2023;13:5242-57. [Crossref] [PubMed]
- Liang J, Yang C, Zeng M, Wang X. TransConver: transformer and convolution parallel network for developing automatic brain tumor segmentation in MRI images. Quant Imaging Med Surg 2022;12:2397-415. [Crossref] [PubMed]
- Pereira S, Pinto A, Alves V, Silva CA. Brain Tumor Segmentation Using Convolutional Neural Networks in MRI Images. IEEE Trans Med Imaging 2016;35:1240-51. [Crossref] [PubMed]
- Dong H, Yang G, Liu F, Mo Y, Guo Y. Automatic Brain Tumor Detection and Seg-mentation Using U-Net Based Fully Convolutional Networks. In: Valdés Hernández M, González-Castro V. editors. Medical Image Understanding and Analysis. MIUA 2017. Communications in Computer and Information Science, Springer, 2017;723:506-17.
- Milletari F, Navab N, Ahmadi SA. V-net: Fully convolutional neural networks for volumetric medical image segmentation. 2016 Fourth International Conference on 3D Vision (3DV), Stanford, CA, USA, 2016:565-71.
Oktay O Schlemper J Folgoc LL Lee M Heinrich M Misawa K Mori K McDonagh S Hammerla NY Kainz B Attention u-net: Learning where to look for the pancreas. arXiv: 1804.03999,2018 .- Isensee F, Kickingereder P, Wick W, Bendszus M, Maier-Hein KH, editors. No new-net. Brainlesion: Glioma, Multiple Sclerosis, Stroke and Traumatic Brain Injuries, Springer, 2019:234-44.
- Isensee F, Jäger PF, Full PM, Vollmuth P, Maier-Hein KH. nnU-Net for brain tumor segmentation. nnU-Net for Brain Tumor Segmentation. In: Crimi A, Bakas S. editors. Brainlesion: Glioma, Multiple Sclerosis, Stroke and Traumatic Brain Injuries. BrainLes 2020. Lecture Notes in Computer Science, Springer, 2021;12659:118-32.
- Santos CFGD, Papa JP. Avoiding overfitting: A survey on regularization methods for convolutional neural networks. ACM Computing Surveys (CSUR) 2022;54:1-25. [Crossref]
- Xu H, Xie H, Liu Y, Cheng C, Niu C, Zhang Y. Deep Cascaded Attention Network for Multi-task Brain Tumor Segmentation. In: Shen D, Liu T, Peters TM, Staib LH, Es-sert C, Zhou S, Yap PT, Khan A. editors. Medical Image Computing and Computer Assisted Intervention – MICCAI 2019. Lecture Notes in Computer Science, Springer, 2019;11766:420-8.
- Ruba T, Tamilselvi R, Beham MP. Brain tumor segmentation in multimodal MRI images using novel LSIS operator and deep learning. J Ambient Intell Human Comput 2023;14:13163-77. [Crossref]
- Li Z, Wu X, Yang X. A Multi Brain Tumor Region Segmentation Model Based on 3D U-Net. Appl Sci 2023;13:9282. [Crossref]
- Yu F, Koltun V, Funkhouser T. Dilated residual networks. Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), 2017:472-80.
- Ioffe S, Szegedy C. Batch normalization: Accelerating deep network training by reducing internal covariate shift. Proceedings of the 32nd International Conference on Machine Learning, PMLR, 2015;37:448-56.
- Nair V, Hinton GE, editors. Rectified linear units improve restricted boltzmann machines. Proceedings of the 27th International Conference on Machine Learning (ICML-10). 2010:807-14.
- Woo S, Park J, Lee JY, Kweon IS. CBAM: Convolutional block attention module. Proceedings of the European Conference on Computer Vision (ECCV), 2018:3-19.
- Menze BH, Jakab A, Bauer S, Kalpathy-Cramer J, Farahani K, Kirby J, et al. The Multimodal Brain Tumor Image Segmentation Benchmark (BRATS). IEEE Trans Med Imaging 2015;34:1993-2024. [Crossref] [PubMed]
- Bakas S, Akbari H, Sotiras A, Bilello M, Rozycki M, Kirby JS, Freymann JB, Fara-hani K, Davatzikos C. Advancing The Cancer Genome Atlas glioma MRI collections with expert segmentation labels and radiomic features. Sci Data 2017;4:170117. [Crossref] [PubMed]
- Nalepa J, Marcinkiewicz M, Kawulok M. Data Augmentation for Brain-Tumor Segmentation: A Review. Front Comput Neurosci 2019;13:83. [Crossref] [PubMed]
- Wang Y, Ji Y, Xiao H. A data augmentation method for fully automatic brain tumor segmentation. Comput Biol Med 2022;149:106039. [Crossref] [PubMed]
- Biswas A, Bhattacharya P, Maity SP, Banik R. Data augmentation for improved brain tumor segmentation. IETE Journal of Research 2023;69:2772-82. [Crossref]
- Fu J, Liu J, Tian H, Li Y, Bao Y, Fang Z, Lu H. Dual attention network for scene segmentation. Proceedings of the IEEE/CVF Conference on Computer Vision and Pat-tern Recognition (CVPR), 2019:3146-54.
- Alom MZ, Yakopcic C, Hasan M, Taha TM, Asari VK. Recurrent residual U-Net for medical image segmentation. J Med Imaging (Bellingham) 2019;6:014006. [Crossref] [PubMed]
- Schlemper J, Oktay O, Schaap M, Heinrich M, Kainz B, Glocker B, Rueckert D. Attention gated networks: Learning to leverage salient regions in medical images. Med Image Anal 2019;53:197-207. [Crossref] [PubMed]
- Jia H, Cai W, Huang H, Xia Y. H2NF-Net for Brain Tumor Segmentation Using Multimodal MR Imaging: 2nd Place Solution to BraTS Challenge 2020 Segmentation Task. In: Crimi A, Bakas S. editors. Brainlesion: Glioma, Multiple Sclerosis, Stroke and Traumatic Brain Injuries. BrainLes 2020. Lecture Notes in Computer Science, Springer, 2021;12659:56-68.
- Ahmad P, Qamar S, Shen L, Saeed A. Context aware 3D UNet for brain tumor seg-mentation. In: Crimi A, Bakas S. editors. Brainlesion: Glioma, Multiple Sclerosis, Stroke and Traumatic Brain Injuries. BrainLes 2020. Lecture Notes in Computer Science, Springer, 2021;12658:207-18.
- Lyu C, Shu H. A Two-Stage Cascade Model with Variational Autoencoders and Attention Gates for MRI Brain Tumor Segmentation. Brainlesion 2020;2020:435-47. [PubMed]
- Raza R, Bajwa UI, Mehmood Y, Anwar MW, Jamal MH. dResU-Net: 3D deep residual U-Net based brain tumor segmentation from multimodal MRI. Biomedical Signal Processing and Control 2023;79:103861. [Crossref]
- Akbar AS, Fatichah C, Suciati N. Single level UNet3D with multipath residual attention block for brain tumor segmentation. Journal of King Saud University-Computer and Information Sciences 2022;34:3247-58. [Crossref]
- Hu J, Shen L, Sun G. Squeeze-and-excitation networks. Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), 2018:7132-41.
- Chang K, Beers AL, Bai HX, Brown JM, Ly KI, Li X, et al. Automatic assessment of glioma burden: a deep learning algorithm for fully automated volumetric and bidimensional measurement. Neuro Oncol 2019;21:1412-22. [Crossref] [PubMed]
- Nalepa J, Kotowski K, Machura B, Adamski S, Bozek O, Eksner B, Kokoszka B, Pekala T, Radom M, Strzelczak M, Zarudzki L, Krason A, Arcadu F, Tessier J. Deep learning automates bidimensional and volumetric tumor burden measurement from MRI in pre- and post-operative glioblastoma patients. Comput Biol Med 2023;154:106603. [Crossref] [PubMed]



