
Automatic measurement of anatomical parameters of the lumbar vertebral body and the intervertebral disc on radiographs by deep learning
Introduction
Low back pain (LBP), a typical symptom of the bone and muscle system in clinic, is a serious public health problem globally. About 84% of individuals experience LBP at least once in their life (1), and its high prevalence and disability rate impose an enormous economic burden on patients and society (2,3). Studies have shown that diseases affecting lumbar muscles, lumbar vertebrae, and lumbar intervertebral disc could lead to LBP (4,5), among which lumbar disc degeneration is the leading cause of LBP (6), accounting for about 39% (7,8). The intervertebral disc height (IDH) is an index of intervertebral disc degeneration and regeneration (9,10), and a decrease or loss of the standard height is associated with lumbar disc degeneration and LBP (5,11,12). In addition, an accurate measurement of anatomical parameters of the vertebral body and intervertebral disc as well as biomechanical parameters of sagittal alignment of the lumbar spine is crucial for the diagnosis and treatment of spinal disorders, for example, in the design of spinal implant (13-15), vertebral deformity and fracture (16-19), and prognosis evaluation (20,21).
At present, many studies have measured and analyzed anatomical parameters such as the shape and angles of the vertebral body and intervertebral disc on lumbar X-ray (22-24), computed tomography (CT) (25,26), and magnetic resonance imaging (MRI) (27) images. Results have shown that understanding such data may help explain the biomechanical mechanisms of spinal diseases, with potential clinical significance (25). However, these data directly depend on the size of the examined sample as well as the accuracy of manual measurement. Furthermore, the measurement process is vulnerable to a non-negligible degree of intra- and inter-observer variability, and requires substantial time. Therefore, a user-independent, automated method for characterizing spinal anatomy is urgently needed to evaluate lumbar disorders quantitatively.
With the substantial progress of imaging equipment and the rise of big data, artificial intelligence (AI), which efficiently performs high-throughput data calculation and analysis, has attracted extensive attention recently. In particular, the emergence of popular deep learning (DL) algorithms makes it possible to mine potentially quantifiable information in medical images. Researchers have extracted the anatomical parameters of the spine from images based on DL through automatic segmentation and detection for evaluating spinal deformity (28), compressive fracture (29), spondylolisthesis (30), surgical evaluation (31), and so on. However, the above models have failed to be productized and used in practical clinical applications. Our main objective is to develop an automatic measurement model based on lateral lumbar radiographs and DL to quantify the anatomical parameters of the vertebral body and intervertebral disc, and to evaluate its performance with the aim of providing an automatic lumbar spine measurement tool for clinical use. We present this article in accordance with the GRRAS reporting checklist (available at https://qims.amegroups.com/article/view/10.21037/qims-23-1859/rc).
Methods
The study was conducted in accordance with the Declaration of Helsinki (as revised in 2013). This study was approved by the Ethics Committee of Gansu Provincial Hospital of Traditional Chinese Medicine (No. 2020-112-01). Since the data were retrieved from the Picture Archiving and Communication System (PACS), the requirement for informed consent of this retrospective analysis was waived.
Dataset preparation
We retrospectively reviewed 1,460 standing lateral lumbar radiographs in the PACS of Department of Radiology, Gansu Provincial Hospital of Traditional Chinese Medicine from September 2019 to March 2021. Due to medical conditions that may affect the vertebral anatomy, we performed a quality check on images to ensure they were suitable for model building and testing. The exclusion criteria were as follows: (I) a history of spinal surgery with implant (screws, plates, or cement); (II) severe spinal deformity; (III) severe hyperosteogeny; (IV) poor image quality or other issues affecting the annotation. After selection, a total of 1,318 images were included in the study, which were annotated by 3 experienced radiologists [R1 (P.W.), R2 (X.C.), and R3 (W.W.) with more than 5 years of work experience] with purposely developed software (all the above personnel have received unified relevant training). The annotated images were randomly allocated into 3 subsets of 722 (55%), 305 (23%), and 291 (22%) for model training, validation, and testing, respectively. To ensure an unbiased evaluation of performance, the training and testing datasets did not overlap. A month later, R1 reannotated the 291 test set images to evaluate intra-observer consistency.
Landmark annotation and parameter measurement
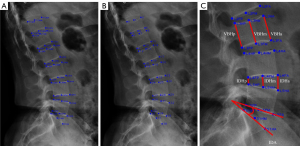
The radiologists annotated each vertebra by the 6-point morphology method (31,32), including 2 anterior, 2 posterior, and 2 middle points of the top and bottom vertebral plates from T12 to S1. In case the outer contour of the vertebral body did not entirely overlap, the midpoint was selected at the center between the upper and lower contours. This method ignores bone spurs and osteophytes, so we excluded images from patients with severe vertebral hyperosteogeny. The average of the values obtained by the 3 radiologists was used as a reference standard compared with the model’s prediction. Landmarks on each vertebral body have specific names, which were used to calculate clinically relevant parameters: vertebral body height (VBH) from T12 to L5, including anterior height (VBHa), middle height (VBHm), and posterior height (VBHp); IDH from T12 to S1, including anterior height (IDHa), middle height (IDHm), and posterior height (IDHp); and intervertebral disc angle (IDA) from T12 to S1. The specific name of each landmark and the measurement methods for the parameters are shown in Figure 1.
Model construction
In our previous study (33), the proposed model had a missed detection of the lumbar vertebral body. Specifically, the S1 vertebral body was detected separately, resulting in the separation of the S1 vertebral body and L5 vertebral body detection. In order to solve this problem, we added the global layer structure to High-Resolution Net (HRNet) (34).
The method automatically detecting the landmark of the vertebrae on lateral lumbar radiographs in this paper mainly used the HRNet model as the primary backbone model, in combination with the Distribution-Aware coordinate (DAC) method (35). The overall method pipeline is shown in Figure 2. To address the situation of detecting a separation between vertebrae, we incorporated the positional relationship between lumbar vertebrae in the model by adding a global layer structure to the vertebrae detection phase. At the first stage, the landmarks of the lumbar spine were detected by HRNet and DAC methods, which were mainly used for the positioning of each vertebral body. Then, each vertebral body was cut according to the spinal thermal diagram and sent to the second stage to obtain the landmark localization of each vertebral body needed. Next, the HRNet model and DAC method are described, respectively.
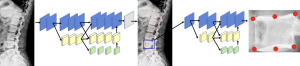
The HRNet model can maintain high resolution from beginning to end through parallel branches with multiple resolutions to achieve the purpose of solid semantics and accurate location. Preserving the details of lumbar spine images is helpful for analysis and diagnosis, so we used HRNet as the training model.
Specifically for the global layer, we used 1 feature channel to predict all landmarks of the lumbar spine. In other words, we add a positional constraint to the vertebral body detection part of the lumbar spine, which allows the model to focus more on learning the vertebral body and the intervertebral body positions. It can be described by the mathematical formula as follows:
where F denotes the convolution kernel, which is 1x1 in size, * denotes the convolution operation, and Ci denotes the feature channel for the ith critical point.
More specifically, the feature channels of each landmark are concatenated. Then, the convolution operation is performed to produce a characteristic channel with global feature information, which can better enhance the position information between vertebrae.
Generally, HRNet was used as a first stage model to locate each vertebra on the spine and as a second stage model to detect landmarks on the vertebrae. Specially, we designed the group layer for the lumbar feature at stage 1. We used 7-channel numbers to indicate group layers according to the number of vertebrae. Each channel including 5 landmarks could easily describe the vertebrae. The advantage of this operation is enhanced ability of vertebrae location. The output of stage 1 is a heatmap of all vertebrae. At the second stage, the output layer of HRNet has 6 channels to detect the landmarks of the vertebrae.
However, the decoding progress from heatmap to original image space may lead to quantization error. The coordinates of the landmark from the heatmap translate into the original coordinates. This process can minimize the error. Thus, on inference, we adopted the DAC method as a post-technique to improve accuracy.
Expressly, to obtain the accurate location at the sub-pixel level, we assumed the predicted heatmap follows a 2-dimensional (2D) Gaussian distribution, same as the ground-truth heatmap. Therefore, the predicted heatmap can be represented as:
where denotes the coordinate position on the predicted heatmap, is the target landmark location, and is a set constant which controls the range of the Gaussian distribution. In order to fit the above-mentioned Gaussian distribution and ultimately obtain the predicted landmark locations, we need to compute first and second order derivatives as in the following steps. We log transformed G to facilitate inference while keeping the original location of the maximum activation as:
The landmark P in the thermodynamic diagram is expanded by the Taylor formula. The first-order partial derivative of formula P was determined as:
The second-order partial derivative of formula P was determined as:
The landmark P in place in the thermodynamic diagram is expanded by the Taylor formula:
to obtain more accurate prediction point coordinates.
The calculation method of clinical anatomical parameters applied in this study was as follows (Figure 1):
(I) VBH
We measured VBH expressed as:
where i indicates a given vertebra; k represents the 3 landmarks on the top vertebrae, l represents the corresponding 3 landmarks on the bottom vertebrae, and indicates the distance of the vertebra corresponding to the landmark and the landmark.
(II) IDH
We measured the IDH between neighbor vertebrae, which is obtained as:
where is the number defining the gap between neighbor vertebrae; is the 3 landmarks on bottom location for the vertebra, t represents the 3 landmarks on top location for the vertebra, and indicates the distance of the disc corresponding to the landmark and the landmark.
(III) IDA
We measured the angle between neighbor vertebrae, which is obtained as:
where is the vector on top edge for the vertebra, is the vector on bottom edge for the vertebra, and is a dot product.
Statistical analysis
All data analyses were performed with Python (Scipy, Statsmodels, and Pingouin). General patient data, including gender and age distribution, were represented by statistical description. The data of measured values were expressed as mean ± standard deviation (SD). The percentage within 1, 1.5, 2, 2.5, and 3 mm landmark-to-landmark distance thresholds was used to assess the inter-observer and intra-observer reliability of landmark annotation (36,37). The performance of the model measurement was evaluated in terms of mean absolute error (MAE), percentage of correct keypoints (PCK), intraclass correlation coefficient (ICC), regression analysis, and Bland-Altman plot. The PCK is defined as the percentage of prediction landmarks that fall within the r-radius neighborhood of reference standard landmark (36,37). Paired t-test was performed to analyze the difference between the reference standard and the model in terms of prediction. Differences were considered statistically significant with P<0.05, and ICC >0.75 indicated good reliability. The specific statistical methodology is shown in Table 1.
Table 1
| Statistical methods | Statistical significance |
|---|---|
| Median ± 95% CI (age); percentage (gender ratios) | General patient data, including gender and age distribution |
| The percentages within 1, 1.5, 2, 2.5, and 3 mm landmark-to-landmark distance thresholds | Reliability of landmark annotations |
| PCK | Landmark performance of the model |
| SD | Model measurement performance |
| MAE | |
| ICC (95% CI) | |
| Regression analysis and Bland-Altman plot | |
| Paired t-test |
PCK is defined as the percentage of prediction landmarks that fall within the r-radius neighborhood of reference standard landmark. CI, confidence interval; PCK, percentage of correct keypoints; SD, standard deviation; MAE, mean absolute error; ICC, intraclass correlation coefficient.
Results
General patient data
A total of 1,318 lateral lumbar radiographs were included in this study. The proportions of the training, validation, and test sets were 55%, 23%, and 22%, respectively. There were no significant differences among the included datasets in terms of gender composition and age. The general data of the included patients are shown in Table 2.
Table 2
| Characteristic | Training set | Validation set | Test set |
|---|---|---|---|
| Image number | 722 (55) | 305 (23) | 291 (22) |
| Male | 312 (43.2) | 128 (42.0) | 118 (40.5) |
| Female | 410 (56.8) | 177 (58.0) | 173 (59.5) |
| Age (years) | 42 (42–44) | 42 (41–45) | 45 (43–47) |
| Male | 36 (38–42) | 38 (38–43) | 38 (38–43) |
| Female | 47 (44–47) | 47 (43–47) | 48 (45–48) |
Data are expressed as number (percentage) or median (95% CI). CI, confidence interval.
Reliability of landmark annotation
The percentage of intra-observer landmark distance within the 3 mm threshold was 96%. The percentage of inter-observer landmark distance within the 3 mm threshold was 94% (R1 and R2), 92% (R1 and R3), and 93% (R2 and R3), respectively (Table 3).
Table 3
| Threshold (mm) | |||||
|---|---|---|---|---|---|
| 1 | 1.5 | 2 | 2.5 | 3 | |
| Intra-observer reliability | 59 | 73 | 86 | 92 | 96 |
| Inter-observer reliability | |||||
| R1 vs. R2 | 40 | 63 | 79 | 89 | 94 |
| R1 vs. R3 | 37 | 62 | 76 | 85 | 92 |
| R2 vs. R3 | 38 | 59 | 75 | 86 | 93 |
R1, R2 and R3 represent the three radiologists of the annotated landmarks.
Performance of the model
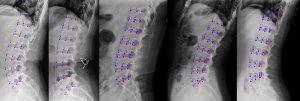
For the landmark prediction, the total PCK of the model within the 3 mm distance threshold ranged from 69% to 98% (Table 4, Figure 3). The model had relatively poor ability in predicting the anatomical landmarks of T12 and S1 vertebrae, especially for the PCK at the 1 mm distance threshold (64% and 44%, respectively). Representative examples of the model for landmark prediction are shown in Figure 4.
Table 4
| Threshold (mm) | T12 | L1 | L2 | L3 | L4 | L5 | S1 | Total |
|---|---|---|---|---|---|---|---|---|
| 1 | 64 | 71 | 75 | 78 | 77 | 64 | 44 | 69 |
| 1.5 | 82 | 87 | 89 | 91 | 91 | 83 | 67 | 86 |
| 2 | 90 | 95 | 95 | 97 | 96 | 92 | 80 | 93 |
| 2.5 | 94 | 98 | 98 | 99 | 98 | 96 | 88 | 97 |
| 3 | 96 | 99 | 99 | 99 | 99 | 98 | 94 | 98 |
PCK is defined as the percentage of prediction landmarks that fall within the r-radius neighborhood of reference standard landmark. PCK, percentage of correct keypoints.
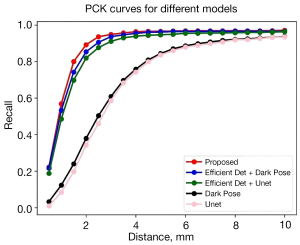
In addition, we conducted a comparison test with the previously proposed model (33) and other typical landmark localization models (Figure 5). The results show that the model proposed in this paper outperformed other models for vertebral detection and lumbar spine landmark localization. The final result showed that these 2-stage models achieved higher accuracy but slower inference. The better results of the 2-stage method are mainly due to the accurate detection of the vertebral body in the first stage, which allows the second stage to achieve landmark localization based on local blocks, allowing the convolutional neural network (CNN) to focus on a single vertebral body.
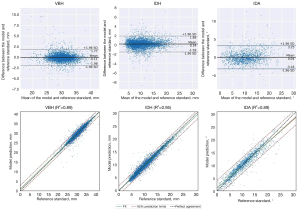
As for the model measurement, compared with the reference standard, model-predicted values for VBH, IDH, and IDA were 30.22±3.01 mm, 10.40±3.91, mm and 10.63°±4.74°, respectively, with ICCs from 0.93 to 0.98. There was no significant difference between the model and the reference standard (all P>0.05). However, the SDs of differences between model and reference standard were 0.95 mm, 0.89 mm, and 1.64°, respectively, in terms of VBH, IDH, and IDA (with MAEs of 0.61 mm, 0.63 mm, and 1.15°, respectively), which were non-negligible (Table 5).
Table 5
| Parameters | Radiologist | Mean | Model | P value | ICC (95% CI) | SD | MAE |
|---|---|---|---|---|---|---|---|
| VBH (mm) | 30.09±2.98a | 30.11±2.93 | 30.22±3.01 | 0.07 | 0.98 (0.97–0.98) | 0.95 | 0.61 |
| 30.11±2.94b | |||||||
| 30.14±2.94c | |||||||
| IDH (mm) | 10.57±3.99a | 10.55±3.96 | 10.40±3.91 | 0.06 | 0.94 (0.90–0.96) | 0.89 | 0.63 |
| 10.56±3.98b | |||||||
| 10.51±3.96c | |||||||
| IDA (°) | 10.62±4.97a | 10.67±4.96 | 10.63±4.74 | 0.81 | 0.93 (0.91–0.94) | 1.64 | 1.15 |
| 10.70±4.96b | |||||||
| 10.70±4.98c |
Data are mean ± SD, P (paired t-test) <0.05 indicates statistical significance between the model and the reference standard. a, b, and c represent manual measurements performed by 3 different radiologists. For the sake of simplicity, the anterior, middle, and posterior vertebral heights (VBHa, VBHm, and VBHp respectively), as well as disc heights and angles (IDHa, IDHm, IDHp, and IDA, respectively) were all pooled together. ICC (95% CI), intra-class correlation coefficient (95% confidence interval); SD, standard deviation; MAE, mean absolute error; VBH, vertebral body height; IDH, intervertebral disc height; IDA, intervertebral disc angle; VBHa, vertebral body anterior height; VBHm, vertebral body middle height; VBHp, vertebral body posterior height; IDHa, intervertebral disc anterior height; IDHm, intervertebral disc middle height; IDHp, intervertebral disc posterior height.
To further assess differences and correlations between model and reference standard in measuring VBH, IDH, and IDA, Bland-Altman plot and regression analyses were performed (Figure 6). The results showed that the parameters exhibited clear linear correlations, with coefficients of determination R2 ranging from 0.89 to 0.95. Bland-Altman plot analysis showed low mean differences between model and reference standard, specifically, 0.11 mm, 0.14 mm, and 0.04°, in VBH, IDH, and IDA, respectively, thus demonstrating no consistent bias between the 2 methods.
Discussion
Understanding the anatomical parameters of the lateral lumbar spine is of great significance for spinal anatomy and clinical research. This paper presented a new approach based on the HRNet and DAC methods to recognize vertebral landmarks and measure VBH, IDH, and IDA on lateral lumbar radiographs with different resolutions and fields of view. Compared with the reference standard, our findings revealed: (I) the model could automatically identify and locate the landmarks of lumbar vertebrae, and the total PCK of all landmarks at the 3 mm distance threshold was 98%; (II) the model demonstrated good accuracy and reliability in measuring VBH, IDH, and IDA with ICCs ranging from 0.93 to 0.98.
In our previous study (33), we proposed the method of EfficientDet combined with U-net for automatic lumbosacral anatomical parameters measurements from lateral lumbar radiographs. EfficientDet is responsible for vertebral frame detection, and U-net identifies the landmarks in each vertebral body; however, the occasional separation of detected vertebral bodies can occur. To solve the problem and improve the accuracy and detection range of vertebral landmark localization, we explored the detection capability of different models and conducted comparison tests. The landmark localization algorithm DarkPose was also used for vertebral detection, and the results of the comparison test (Figure 5) showed that DarkPose has a more robust landmark localization capability than U-net. From the comparison test, it is easy to see that the 2-stage approach of vertebral body detection network cascaded with a landmark localization network is more accurate than the 1-stage approach. The vertebral position is detected first in the 2-stage method, reducing the target range and improving image resolution. In addition, based on the detected vertebral position, the landmarks contained in a single vertebral body are recognized, which reduces the task difficulty, unlike the 1-stage method that directly recognizes all landmarks. The end-to-end method of DarkPose + DarkPose proposed in this paper makes full use of the advantages of DarkPose and the 2-stage method to achieve the best results in vertebral body detection and landmark localization.
To date, studies based on the DL model have mostly analyzed spinal diseases, including adolescent idiopathic scoliosis (38), lumbar spondylolisthesis (39), and fractures (32). In this study, the proposed method can automatically identify landmarks and measure anatomical parameters of the vertebral body and intervertebral disc from T12 to S1 without affecting the diagnostic results of radiologists. Describing the geometric features of the lumbar spine may have a specific prompt, and a predictive effect in some lumbar diseases such as vertebral compression fractures and lumbar degenerative changes (including disc space narrowing and degenerative spondylolisthesis) that are missed or delayed while handling many X-ray images depending on visual assessment alone. Although our findings could not be directly quantitatively compared with previous studies due to the nature of reported results, the accuracy of landmark prediction seems to be similar to or even better than that shown in other reports (40,41).
In order to ensure the accuracy of the dataset used for model training, we computed the percentage within the 3 mm landmark to determine distance thresholds for evaluating the intra- and inter-observer reliabilities of the annotation. The results showed that the percentage of intra-observer landmark distance at the 3 mm threshold was 96%, and inter-observer within 3 mm ranged from 92% to 94% (Table 3). Chen et al. (42) reported that a mean distance for inter-observer landmarks falling within the range of 3 mm was satisfactory for clinical analysis, suggesting our manual annotations are relatively reliable. However, intra- and inter-observer distances falling within 1 mm performed relatively poorly (37–40%). In terms of model prediction, qualitative analysis showed excellent visual performance of the method (Figure 4); however, quantitative comparison with the reference standard still showed some undeniable discrepancies (Table 5), especially for T12 and S1, which would have an impact on the clinical application of the method. Nevertheless, it is worth noting that this work not only provided a methodological contribution, but clearly highlighted the remarkable potential of the DL model in the quantitative evaluation of the lumbar spine.
Other studies have also proposed DL models based on locating landmarks (38-40,43,44). Nguyen et al. (39) proposed a DL system based on CNN to measure segmental motion angles and evaluate severity in the Meyerding classification. Bland-Altman analysis showed a mean difference of 0.079 between the system and reference standard for IDA, whereas ours had a value of 0.04 (Figure 6). Galbusera et al. (44) proposed a method for automatically identifying vertebral landmarks (L3–L4) based on an artificial neural network. The average distance between the predicted anterior cranial corner of L4 and the correspondent manually identified point was 7.03±4.03 pixels (corresponding in average to 8.63% of VBHL4). The vertebral body detection range (T12–S1) and corresponding landmark identification were further supplemented and improved in this study. Moreover, these identified prediction landmarks may allow the model to extract more clinical parameters related to lumbar spine diseases, including lumbar lordosis and sacral inclination.
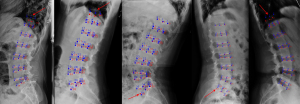
We also analyzed the failure cases of the proposed method (Figure 7). Unsatisfactory prediction results were mainly attributed to failed identification of the landmarks of T12 and S1 vertebral bodies, but the positioning of vertebral bodies was highly accurate. This phenomenon is mainly due to overlapping other anatomical structures such as the lung and the pelvis with vertebrae, with the resulting lack of local contrast. The effectiveness and accuracy of the predictive model based on the neural network are mainly related to the size and quality of the training set rather than the learning algorithm itself. In order to accurately describe the geometric features of the vertebral body, high-precision recognition of landmarks requires high image quality, which also explains and limits the availability of images. In the current model, we used data enhancement, for example, ±10° rotation, to ensure the variety of images and increase the detection accuracy in the training process. However, this was not enough to cover all cases in the clinical environment, which is one of the reasons for poor prediction by the model.
As with other studies, there are some limitations. Firstly, as mentioned before, we evaluated the quality of the included images and excluded some images affecting the landmark annotation, limiting the size of the data set used for model training and its application in clinical practice. Secondly, due to the retrospective nature of the study, we did not correlate the lumbar spine measurement parameters with the corresponding clinical diseases and scores. Thirdly, for the measurement results, statistical tests found no significant differences between model and radiologists, but the SD and ICC values indicate there is still room for improvement. We will further expand the data for training or improve the algorithm for refining the key points that are relatively poorly identified by the model, so as to improve the model accuracy. In the later stage, we focused on the application of the model in the clinic and the development of structured reports on the lumbar spine, and eventually productized the model into a web site interface that can be used by anyone.
Conclusions
The newly proposed model based on the HRNet and DAC methods can accurately identify landmarks and automatically measure various anatomical parameters of the vertebral body and intervertebral disc on lateral lumbar radiographs. It has a significant potential for assisting clinical workers in facilitating the measurement and improving the evaluation of lumbar disorders quantitatively after further training. Certainly, it is helpful for clinical research studies and the establishment of structured reports on the lumbar spine.
Acknowledgments
Funding: This work was supported by
Footnote
Reporting Checklist: The authors have completed the GRRAS reporting checklist. Available at https://qims.amegroups.com/article/view/10.21037/qims-23-1859/rc
Conflicts of Interest: All authors have completed the ICMJE uniform disclosure form (available at https://qims.amegroups.com/article/view/10.21037/qims-23-1859/coif). G.C. is a consultant of Hangzhou Jianpei Technology Co., Ltd. L.H. is an employee of Hangzhou Jianpei Technology Co., Ltd. The other authors have no conflicts of interest to declare.
Ethical Statement: The authors are accountable for all aspects of the work in ensuring that questions related to the accuracy or integrity of any part of the work are appropriately investigated and resolved. The trial was conducted in accordance with the Declaration of Helsinki (as revised in 2013). The study was approved by Gansu Provincial Hospital of Traditional Chinese Medicine (No. 2020-112-01). The requirement for informed consent was waived because retrospective imaging data were used.
Open Access Statement: This is an Open Access article distributed in accordance with the Creative Commons Attribution-NonCommercial-NoDerivs 4.0 International License (CC BY-NC-ND 4.0), which permits the non-commercial replication and distribution of the article with the strict proviso that no changes or edits are made and the original work is properly cited (including links to both the formal publication through the relevant DOI and the license). See: https://creativecommons.org/licenses/by-nc-nd/4.0/.
References
- Fortunati M, Rossi-Mossuti F, Muroi C. Everyone Has Low Back Pain: Degenerative Lumbar Spinal Disorders and Their Treatment Options. Praxis (Bern 1994) 2020;109:87-95.
- Hoy D, Brooks P, Blyth F, Buchbinder R. The Epidemiology of low back pain. Best Pract Res Clin Rheumatol 2010;24:769-81. [Crossref] [PubMed]
- Buchbinder R, van Tulder M, Öberg B, Costa LM, Woolf A, Schoene M, Croft PLancet Low Back Pain Series Working Group. Low back pain: a call for action. Lancet 2018;391:2384-8. [Crossref] [PubMed]
- Ogon I, Takashima H, Morita T, Oshigiri T, Terashima Y, Yoshimoto M, Takebayashi T, Yamashita T. Association between Spinopelvic Alignment and Lumbar Intervertebral Disc Degeneration Quantified with Magnetic Resonance Imaging T2 Mapping in Patients with Chronic Low Back Pain. Spine Surg Relat Res 2020;4:135-41. [Crossref] [PubMed]
- Karunanayake AL, Pathmeswaran A, Wijayaratne LS. Chronic low back pain and its association with lumbar vertebrae and intervertebral disc changes in adults. A case control study. Int J Rheum Dis 2018;21:602-10. [Crossref] [PubMed]
- Sääksjärvi S, Kerttula L, Luoma K, Paajanen H, Waris E. Disc Degeneration of Young Low Back Pain Patients: A Prospective 30-year Follow-up MRI Study. Spine (Phila Pa 1976) 2020;45:1341-7. [Crossref] [PubMed]
- Zheng CJ, Chen J. Disc degeneration implies low back pain. Theor Biol Med Model 2015;12:24. [Crossref] [PubMed]
- Simon J, McAuliffe M, Shamim F, Vuong N, Tahaei A. Discogenic low back pain. Phys Med Rehabil Clin N Am 2014;25:305-17. [Crossref] [PubMed]
- Seitsalo S, Schlenzka D, Poussa M, Osterman K. Disc degeneration in young patients with isthmic spondylolisthesis treated operatively or conservatively: a long-term follow-up. Eur Spine J 1997;6:393-7.
- Miyakoshi N, Abe E, Shimada Y, Okuyama K, Suzuki T, Sato K. Outcome of one-level posterior lumbar interbody fusion for spondylolisthesis and postoperative intervertebral disc degeneration adjacent to the fusion. Spine (Phila Pa 1976) 2000;25:1837-42. [Crossref] [PubMed]
- Pfirrmann CW, Metzdorf A, Elfering A, Hodler J, Boos N. Effect of aging and degeneration on disc volume and shape: A quantitative study in asymptomatic volunteers. J Orthop Res 2006;24:1086-94. [Crossref] [PubMed]
- Siepe CJ, Hitzl W, Meschede P, Sharma AK, Khattab MF, Mayer MH. Interdependence between disc space height, range of motion and clinical outcome in total lumbar disc replacement. Spine (Phila Pa 1976) 2009;34:904-16. [Crossref] [PubMed]
- Zhou SH, McCarthy ID, McGregor AH, Coombs RR, Hughes SP. Geometrical dimensions of the lower lumbar vertebrae--analysis of data from digitised CT images. Eur Spine J 2000;9:242-8. [Crossref] [PubMed]
- van der Houwen EB, Baron P, Veldhuizen AG, Burgerhof JG, van Ooijen PM, Verkerke GJ. Geometry of the intervertebral volume and vertebral endplates of the human spine. Ann Biomed Eng 2010;38:33-40. [Crossref] [PubMed]
- Yao J, Dong B, Sun J, Liu JT, Liu F, Li XW, Yuan PW, Zhang JB. Accuracy and Reliability of Computer-aided Anatomical Measurements for Vertebral Body and Disc Based on Computed Tomography Scans. Orthop Surg 2020;12:1182-9. [Crossref] [PubMed]
- Tatoń G, Rokita E, Wróbel A. Application of geometrical measurements in the assessment of vertebral strength. Pol J Radiol 2013;78:15-8. [Crossref] [PubMed]
- Hsu WE, Su KC, Chen KH, Pan CC, Lu WH, Lee CH. The Evaluation of Different Radiological Measurement Parameters of the Degree of Collapse of the Vertebral Body in Vertebral Compression Fractures. Appl Bionics Biomech 2019;2019:4021640. [Crossref] [PubMed]
- Diacinti D, Pisani D, Barone-Adesi F, Del Fiacco R, Minisola S, David V, Aliberti G, Mazzuoli GF. A new predictive index for vertebral fractures: the sum of the anterior vertebral body heights. Bone 2010;46:768-73. [Crossref] [PubMed]
- Gao L, Fan T, Chen Y, Qiu S. Reference values for vertebral shape in young Chinese women: implication for assessment of vertebral deformity. Eur Spine J 2010;19:1162-8. [Crossref] [PubMed]
- McGirt MJ, Eustacchio S, Varga P, Vilendecic M, Trummer M, Gorensek M, Ledic D, Carragee EJ. A prospective cohort study of close interval computed tomography and magnetic resonance imaging after primary lumbar discectomy: factors associated with recurrent disc herniation and disc height loss. Spine (Phila Pa 1976) 2009;34:2044-51. [Crossref] [PubMed]
- Zárate-Kalfópulos B, Reyes-Tarrago F, Navarro-Aceves LA, García-Ramos CL, Reyes-Sánchez AA, Alpízar-Aguirre A, Rosales-Olivarez LM. Characteristics of Spinopelvic Sagittal Alignment in Lumbar Degenerative Disease. World Neurosurg 2019;126:e417-21. [Crossref] [PubMed]
- Liu X, Hou Y, Shi H, Zhao T, Sun C, Shi J, Shi G. A retrospective cohort study on the significance of preoperative radiological evaluation of lumbar degenerative diseases for surgical reference. Quant Imaging Med Surg 2023;13:5100-8. [Crossref] [PubMed]
- Shao Z, Rompe G, Schiltenwolf M. Radiographic changes in the lumbar intervertebral discs and lumbar vertebrae with age. Spine (Phila Pa 1976) 2002;27:263-8. [Crossref] [PubMed]
- Mahato NK. Disc spaces, vertebral dimensions, and angle values at the lumbar region: a radioanatomical perspective in spines with L5-S1 transitions: clinical article. J Neurosurg Spine 2011;15:371-9. [Crossref] [PubMed]
- Been E, Li L, Hunter DJ, Kalichman L. Geometry of the vertebral bodies and the intervertebral discs in lumbar segments adjacent to spondylolysis and spondylolisthesis: pilot study. Eur Spine J 2011;20:1159-65. [Crossref] [PubMed]
- Tan S, Yao J, Yao L, Ward MM. High precision semiautomated computed tomography measurement of lumbar disk and vertebral heights. Med Phys 2013;40:011905. [Crossref] [PubMed]
- Natalia F, Meidia H, Afriliana N, Young JC, Yunus RE, Al-Jumaily M, Al-Kafri A, Sudirman S. Automated measurement of anteroposterior diameter and foraminal widths in MRI images for lumbar spinal stenosis diagnosis. PLoS One 2020;15:e0241309. [Crossref] [PubMed]
- Galbusera F, Niemeyer F, Wilke HJ, Bassani T, Casaroli G, Anania C, Costa F, Brayda-Bruno M, Sconfienza LM. Fully automated radiological analysis of spinal disorders and deformities: a deep learning approach. Eur Spine J 2019;28:951-60. [Crossref] [PubMed]
- Al-Helo S, Alomari RS, Ghosh S, Chaudhary V, Dhillon G, Al-Zoubi MB, Hiary H, Hamtini TM. Compression fracture diagnosis in lumbar: a clinical CAD system. Int J Comput Assist Radiol Surg 2013;8:461-9. [Crossref] [PubMed]
- Liao S, Zhan Y, Dong Z, Yan R, Gong L, Zhou XS, Salganicoff M, Fei J. Automatic Lumbar Spondylolisthesis Measurement in CT Images. IEEE Trans Med Imaging 2016;35:1658-69. [Crossref] [PubMed]
- Briot K, Kolta S, Fechtenbaum J, Said-Nahal R, Benhamou CL, Roux C. Increase in vertebral body size in postmenopausal women with osteoporosis. Bone 2010;47:229-34. [Crossref] [PubMed]
- Hsieh CI, Zheng K, Lin C, Mei L, Lu L, Li W, Chen FP, Wang Y, Zhou X, Wang F, Xie G, Xiao J, Miao S, Kuo CF. Automated bone mineral density prediction and fracture risk assessment using plain radiographs via deep learning. Nat Commun 2021;12:5472. [Crossref] [PubMed]
- Zhou S, Yao H, Ma C, Chen X, Wang W, Ji H, He L, Luo M, Guo Y. Artificial intelligence X-ray measurement technology of anatomical parameters related to lumbosacral stability. Eur J Radiol 2022;146:110071. [Crossref] [PubMed]
- Sun K, Xiao B, Liu D, Wang J. Deep high-resolution representation learning for human pose estimation. 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA 2019:5686-696.
- Zhang F, Zhu X, Dai H, Ye M, Zhu C. Distribution-Aware Coordinate Representation for Human Pose Estimation. 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 2020:7091-100.
- Payer C, Štern D, Bischof H, Urschler M. Integrating spatial configuration into heatmap regression based CNNs for landmark localization. Med Image Anal 2019;54:207-19. [Crossref] [PubMed]
- Ye Q, Shen Q, Yang W, Huang S, Jiang Z, He L, Gong X. Development of automatic measurement for patellar height based on deep learning and knee radiographs. Eur Radiol 2020;30:4974-84. [Crossref] [PubMed]
- Renganathan G, Manaswi N, Ghionea I, Cukovic S. Automatic Vertebrae Localization and Spine Centerline Extraction in Radiographs of Patients with Adolescent Idiopathic Scoliosis. Stud Health Technol Inform 2021;281:288-92. [Crossref] [PubMed]
- Nguyen TP, Chae DS, Park SJ, Kang KY, Yoon J. Deep learning system for Meyerding classification and segmental motion measurement in diagnosis of lumbar spondylolisthesis. Biomed Signal Process Control 2021;65:102371.
- Cina A, Bassani T, Panico M, Luca A, Masharawi Y, Brayda-Bruno M, Galbusera F. 2-step deep learning model for landmarks localization in spine radiographs. Sci Rep 2021;11:9482. [Crossref] [PubMed]
- Wu H, Bailey C, Rasoulinejad P, Li S. Automated comprehensive Adolescent Idiopathic Scoliosis assessment using MVC-Net. Med Image Anal 2018;48:1-11. [Crossref] [PubMed]
- Chen HC, Lin CJ, Wu CH, Wang CK, Sun YN. Automatic Insall-Salvati ratio measurement on lateral knee x-ray images using model-guided landmark localization. Phys Med Biol 2010;55:6785-800. [Crossref] [PubMed]
- Kim KC, Cho HC, Jang TJ, Choi JM, Seo JK. Automatic detection and segmentation of lumbar vertebrae from X-ray images for compression fracture evaluation. Comput Methods Programs Biomed 2021;200:105833. [Crossref] [PubMed]
- Fabio Galbusera, Tito Bassani, Francesco Costa, et al. Artificial neural networks for the recognition of vertebral landmarks in the lumbar spine. Comput Methods Biomech Biomed Eng Imaging Vis 2018;6:447-52.



