
Assessing the impact of nodule features and software algorithm on pulmonary nodule measurement uncertainty for nodules sized 20 mm or less
Introduction
Pulmonary nodules are increasingly being detected due to ever-improving resolution of computed tomography (CT) scanners, increased uptake of low-dose CT screening for lung cancer, and the expanded eligibility criteria for the screening (1). Pulmonary nodule size and growth assessment are cornerstones of nodule management protocols. These management protocols typically set minimum nodule size thresholds for initiating growth assessment, with variations in timing for follow-up CTs based on nodule size.
While it is implicitly understood that optimizing management protocols for growth assessment represents a tradeoff between waiting long enough to overcome measurement uncertainty versus waiting so long that prognosis is substantially impacted, there is no empirical evidence for estimating these time intervals. Assessment of change in nodule size is impacted by both real change in nodule size and measurement uncertainty (2). Nodule size (3-5), shape (6), margin characteristics (7,8), patient motion (5), and scanner protocols (9) have been reported to contribute to measurement uncertainty, although often with conflicting results (3-5,10-14). Better understanding of factors associated with nodule measurement uncertainty would allow for a data-driven personalized choice for timing of the follow-up CT.
Previous studies used either nodule phantoms (13,14), clinically stable nodules (3,4,10), three scans with two close in time and one at a much longer interval (12), or two scans of patients in a short interval (coffee-break scans) (5,11) to assess measurement uncertainty. Criticisms of these studies were that phantoms did not accurately reflect the appearance of in-vivo nodules, and studies using real in-vivo nodules with only two time points were not statistically robust. Our goal was to assess features associated with measurement uncertainty of pulmonary nodules, 20 mm or less, and the extent of their impact. We present this article in accordance with the GRRAS reporting checklist (available at https://qims.amegroups.com/article/view/10.21037/qims-23-1501/rc).
Methods
We reviewed prospectively collected solid nodules with repeated CT imaging series of the same nodule in the same person obtained within minutes obtained during routine fine needle aspiration CT-guided biopsy procedures performed between 2015 and 2021. The study was conducted in accordance with the Declaration of Helsinki (as revised in 2013) and was considered to be exempt human research by the Institutional Review Board of the Icahn School of Medicine at Mount Sinai (No. 19-1417) because this retrospective study was minimal risk and used de-identified image data. Individual consent was waived for this retrospective study as no identifiable patient information was used. Patients were not exposed to radiation other than routinely used during the procedure itself.
The inclusion/exclusion criteria were as follows. Only CT scans of patients who underwent fine needle aspiration CT-guided biopsy procedures performed between 2015 and 2021 were considered. These were further refined to only include those with CT scans of nodules which were biopsied with average diameter 20 mm or less, having at least four CT scan series meeting the following quality criteria: obtained prior to insertion of the biopsy needle into the nodule, slice thickness of ≤1.0 mm, at least 2 images above and below the nodule, and without image artifacts within 5 mm of the nodule.
Before inserting the biopsy needle, patients practiced holding their breath under observation by the radiologist performing the procedure (DY, more than 25 years of biopsy experience). An initial CT scan was obtained at the beginning of the procedure; subsequent scans were localized only to the area around the nodule and needle, in accordance with typical clinical protocol. After inserting the biopsy needle, a series of CT images were obtained in a single breath-hold with each advance of the needle using Siemens Somatom AS using 100 kVp, 120 mA, pitch factor 1.5, reconstructed with slice thickness of 1.0 mm. This provides a set of independently acquired repeated CT scans from which to assess measurement uncertainty.
Software algorithms for nodule volume measurement
Two algorithms representing two fundamentally different approaches to nodule segmentation and volume measurement were used to measure three-dimensional nodule volume (15,16). Algorithm #1 (15) requires two points specified by a single investigator (A.J.) on the CT image indicating the longest diameter of the nodule; nodules were segmented using automated image filtering, thresholding, and morphological techniques (15); volume was measured from the segmented image. Algorithm #2 (16) used level-set techniques with image features to segment the nodule using a single seed point, the midpoint of the two points specified for algorithm #1; volume was measured using the 3D model of each nodule.
Resulting segmentations were reviewed by a single investigator (A.J., 13 years of experience) to identify situations with under- or over-segmentation near attached structures.
Each algorithm k produced volume Vijk for nodule i and CT series j. As multiple CT series j (j=1… m) for ith nodule (i=1…n) were obtained within minutes, differences in the measured volumes of the ith nodule for each different CT series using algorithm k, Vijk were due to measurement uncertainty not actual nodule change.
Measurement uncertainty
Measurement uncertainty as defined by the Radiological Society of North America, Quantitative Imaging Biomarkers Alliance (RSNA-QIBA) (17) is given by the CoV of the volume measurements defined as the standard deviation of the volume measurements for nodule i using Algorithm k, divided by the mean of the same volume measurements Eq. [1]:
A higher indicates greater volume measurement variability. The RSNA-QIBA Small Nodule Profile specified CoV of nodule volume limits for nodules with longest dimension in axial plane between 6 to 12 mm; CoV of nodule volume limits were 29% for 6 mm (113.1 mm3), 23% for 7 mm (179.6 mm3), 19% for 8 mm (268.1 mm3), 16% for 9 mm (381.7 mm3), 14% for 10 mm (523.6 mm3), 12% for 11 mm (696.9 mm3), and 11% for 12 mm (904.8 mm3) diameter nodules.
The standard deviation of the volume measures, Sik, for the ith nodule for Algorithm k is given by:
The mean volume for the ith nodule for each algorithm (k=1, 2) is the sum of the repeated volumes, Vijk, j=1…m, divided by the number of repeated CT series (m) for the ith nodule:
Automated measurement algorithms provide nodule volumes, but lung screening protocols typically provide recommendations based on nodule diameter; nodule diameter was estimated for the ith nodule for each algorithm k, , as the diameter of a sphere with average volume, in equation [3]:
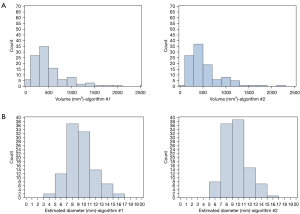
As algorithm #1 produces a different volume for a given nodule than algorithm #2, frequency counts based on estimated diameter categories for each of the two algorithms may differ.
Nodule features
- Each nodule volume computed by both algorithms.
- Nodule location by lobe visually determined as right upper lobe (RUL), right middle lobe (RML), right lower lobe (RLL), left upper lobe (LUL), or left lower lobe (LLL).
- Blood vessel attachment to each nodule visually determined by a single observer (A.J.), denoted as present or absent.
- Costal pleural attachment of the nodule visually determined by a single observer (A.J.), denoted as present or absent.
Nodule surface area calculated from the 3D nodule segmentation (18). A sphere has the smallest surface area for a given volume, so any deviation from a sphere for a given volume increases the surface area of the nodule. - Variability of nodule volume was assessed in each of the CT scanner three acquisition dimensions (mm): x, y, and z. For supine patient position the x dimension provides measurements from right to left, y dimension from anterior to posterior, and the z dimension from superior to inferior.
Statistical analyses of the impact of nodule features on measurement uncertainty
Summary statistics of nodule volume and CoV of nodule volume by the two algorithms were calculated. Pearson (r) and Spearman (p) correlation coefficients and scatterplots were used to assess the relationship between CoV of nodule volume and nodule diameter. Normality of the data was evaluated using a Shapiro-Wilk test and skewed variables were logarithmically transformed. A Wilcoxon rank-sum test was used to compare the distribution of CoV of nodule volume of the two algorithms. Agreement of the volume measurements using the two algorithms was evaluated using intraclass correlation coefficient (ICC) and Bland-Altman plots. The mean difference was computed as the average of the volume difference for each individual nodule: . Multiple linear regressions were used to model the relationship between nodule features and CoV of nodule volume for both algorithms. Variance inflation factor was used to assess multi-collinearity. P values <0.05 were considered statistically significant. All statistical analyses were performed using R (version 4.1; the R Foundation for Statistical Computing) (19) and SAS (version 9.4; SAS Institute, Cary, NC, USA).
Results
There were 169 nodules that met the inclusion criteria. Of these, 115 (68.0%) were segmented using algorithm #1 and 133 (78.7%) were segmented using algorithm #2, and 107 (63.3%) by both algorithms (Figure 1). Of the 169 nodules, 8 were correctly segmented by algorithm #1 but not algorithm #2, and 26 were correctly segmented by algorithm #2 but not algorithm #1. Of the 107 nodules in 107 patients, 33 nodules had four repeated CT series, 68 nodules had five series, and 6 nodules had six series. Using Eqs. [1–3] for each algorithm, mean volume, standard deviation, and CoV of the nodule volume were calculated (Table 1). As volumes differed for each algorithm, frequency distributions of estimated diameters differed (Table 1, Figure 2).
Table 1
| Volume (mm3); estimated diameter (mm) |
Algorithm #1 | Algorithm #2 | |||||||
|---|---|---|---|---|---|---|---|---|---|
| N Obs | Mean volume (mm3) | Std Dev of volume* (mm3) | CoV of volume** (%) | N Obs | Mean volume (mm3) | Std Dev of volume* (mm3) | CoV of volume** (%) | ||
| <113 mm3 (<6.0 mm) | 8 | 78.55 | 6.24 | 7.49 | 1 | 73.37 | 7.72 | 10.53 | |
| 113–267 mm3 (6.0–7.9 mm) | 20 | 200.85 | 12.26 | 6.45 | 20 | 197.67 | 31.98 | 17.36 | |
| 268–381 mm3 (8.0–8.9 mm) | 23 | 322.36 | 18.59 | 5.83 | 24 | 326.28 | 38.80 | 12.18 | |
| 382–523 mm3 (9.0–9.9 mm) | 18 | 436.34 | 31.89 | 7.10 | 23 | 450.35 | 52.72 | 11.70 | |
| 524–696 mm3 (10.0–10.9 mm) | 15 | 578.97 | 36.28 | 6.24 | 16 | 608.00 | 57.26 | 9.43 | |
| 697–1,149 mm3 (11.0–12.9 mm) | 14 | 883.09 | 41.24 | 4.57 | 15 | 892.19 | 63.07 | 7.12 | |
| ≥1,150 mm3 (13.0–20 mm) | 9 | 1,574.25 | 81.66 | 5.02 | 8 | 1,496.90 | 79.38 | 5.20 | |
Diameter was estimated from the measured volume under the assumption of a perfect sphere. *, average of standard deviation of volume for each nodule for that particular size category; **, average of CoV of volume for each nodule in that particular size category. N Obs, number of observations; Std Dev, standard deviation; CoV, coefficient of variation.
Nodule volume measurements from the two algorithms had excellent agreement interclass correlation coefficient (ICC) =0.98. The mean volume using algorithm #1 was 515.23 mm3 and using algorithm #2, 535.53 mm3; mean difference in volume between the two algorithms was 20.3 mm3, with algorithm #2 reporting volumes larger than algorithm #1 on average (95% Bland-Altman limits of agreement: −140.1 to 180.7 mm3) as shown on the Bland-Altman plot (Figure 3). Figure 3 showed an overall trend that as the mean volume of both algorithms (x-axis) increased, the difference in mean volume of the two algorithms (y-axis), decreased, although there were outliers at larger volumes.
Nodule volume measurement uncertainty
The standard deviation of the volume measurements increased with increasing nodule volume for both algorithms, from 6.24 to 81.66 for algorithm #1 and from 7.72 to 79.38 (Table 1) for algorithm #2. , the CoV of the ith nodule volume using algorithm k, is standardized by mean nodule volume. Thus, unlike the standard deviation, , it decreased with increasing nodule volume for both algorithms. The trend was more apparent for algorithm #2 (Table 2, Figure 4).
Table 2
| Volume (mm3); estimated diameter (mm) |
CoV of volume | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Algorithm #1 | Algorithm #2 | ||||||||||
| N Obs | CoV of volume** (%) | Median (%) | Lower quartile (%) | Upper quartile (%) | N Obs | CoV of volume** (%) | Median (%) | Lower quartile (%) | Upper quartile (%) | ||
| <113 mm3 (<6.0 mm) | 8 | 7.49 | 8.21 | 3.6 | 10.61 | 1 | 10.53 | 10.53 | 10.53 | 10.53 | |
| 113–267 mm3 (6.0–7.9 mm) | 20 | 6.45 | 5.67 | 3.48 | 9.95 | 20 | 17.36 | 11.48 | 5.80 | 27.83 | |
| 268–381 mm3 (8.0–8.9 mm) | 23 | 5.83 | 5.11 | 2.71 | 7.8 | 24 | 12.18 | 11.41 | 4.50 | 14.68 | |
| 382–523 mm3 (9.0–9.9 mm) | 18 | 7.10 | 5.25 | 3.01 | 10.98 | 23 | 11.70 | 11.26 | 4.80 | 15.01 | |
| 524–696 mm3 (10.0–10.9 mm) | 15 | 6.24 | 4.92 | 1.88 | 11.95 | 16 | 9.43 | 9.24 | 3.15 | 14.40 | |
| 697–1,149 mm3 (11.0–12.9 mm) | 14 | 4.57 | 2.89 | 2.32 | 4.36 | 15 | 7.12 | 7.06 | 3.84 | 10.42 | |
| ≥1,150 mm3 (13.0–20 mm) | 9 | 5.02 | 4.90 | 3.92 | 6.37 | 8 | 5.20 | 4.61 | 3.10 | 6.64 | |
Diameter was estimated from the measured volume under the assumption of a perfect sphere. **, average of CoV of volume for each nodule in that particular size category. CoV, coefficient of variation; N Obs, number of observations.
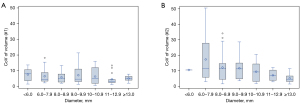
For both algorithms, CoV of nodule volume (Table 2) were well below the RSNA-QIBA Small Nodule Profile limits (17). CoV of nodule volume was significantly lower for algorithm #1 than algorithm #2 (median CoV of nodule volume of 4.6% vs. 8.7%, P<0.001), both overall and for each nodule volume category.
Effect of nodule characteristics on volume measurement uncertainty
Table 3 shows the CoV of nodule volume by nodule features for the 107 nodules. Of the 107 nodules, 49 (45.8%) were in the upper/middle lobe and 58 (54.2%) were in the lower lobe. Blood vessel attachments were seen in 62 (57.9%) of the 107 nodules and costal pleural attachments seen in 9 (8.4%). Median nodule surface area was 450.5mm2 and 589.7mm2 for algorithm #1 and algorithm #2
Table 3
| Nodule feature | N | CoV of nodule volume | ||||||
|---|---|---|---|---|---|---|---|---|
| Algorithm #1 | Algorithm #2 | |||||||
| Median (%) | Lower quartile (%) | Upper quartile (%) | Median (%) | Lower quartile (%) | Upper quartile (%) | |||
| Nodule location | ||||||||
| LLL | 25 | 5.36 | 3.14 | 9.95 | 12.96 | 6.84 | 18.79 | |
| LUL | 16 | 4.30 | 2.99 | 9.90 | 9.24 | 4.67 | 14.23 | |
| RLL | 33 | 4.90 | 2.97 | 10.98 | 10.53 | 4.14 | 14.63 | |
| RML | 12 | 3.86 | 3.09 | 6.54 | 7.03 | 3.53 | 10.06 | |
| RUL | 21 | 4.04 | 2.95 | 5.68 | 7.79 | 4.99 | 11.5 | |
| Upper/middle lobe* | 49 | 4.04 | 2.95 | 6.42 | 7.58 | 4.95 | 12.66 | |
| Lower lobe** | 58 | 5.23 | 2.97 | 10.87 | 11.24 | 4.68 | 15.19 | |
| Blood vessel attachment | ||||||||
| Yes | 62 | 4.46 | 2.90 | 7.28 | 6.62 | 3.84 | 13.32 | |
| No | 45 | 4.70 | 3.05 | 10.87 | 10.72 | 7.06 | 20.57 | |
| Costal pleural attachment | ||||||||
| Yes | 9 | 6.37 | 2.90 | 11.79 | 11.37 | 9.23 | 13.03 | |
| No | 98 | 4.59 | 2.97 | 8.12 | 8.16 | 4.15 | 14.48 | |
| Surface area | 107 | 450.5 | 323.7 | 628.6 | 589.7 | 438.4 | 780.9 | |
*, upper/middle lobe represents the sum of LUL, RML and RUL; **, lower lobe represents the sum of LLL and RLL. CoV, coefficient of variation; LLL, left lower lung, LUL, left upper lung, RLL, right lower lung, RML, right middle lung, RUL, right upper lung.
For algorithm #1, univariable analyses of CoV of nodule volume (Table 4), using the log-transform of CoV of nodule volume, showed a negative association with estimated nodule volume (β=−0.0002, P=0.35) and log-transform of the nodule surface area (β=−0.18, P=0.15), but neither was statistically significant. Nodule location as well as attachments to blood vessels or pleura were not significantly associated with CoV of nodule volume.
Table 4
| Nodule characteristics | Univariate | ||
|---|---|---|---|
| Estimate (β) | Std. error | P value | |
| Volume (mm3) | −0.0002 | 0.0002 | 0.35 |
| Nodule location | |||
| Upper/middle lobe | Ref. | ||
| Lower lobe | 0.15 | 0.14 | 0.28 |
| Blood vessel attachment | −0.15 | 0.14 | 0.28 |
| Costal pleural attachment | 0.29 | 0.25 | 0.25 |
| Log (nodule surface area) | −0.18 | 0.13 | 0.15 |
Reference category were absent of blood vessel attachment and absent of costal pleural attachment. Std., standard.
For algorithm #2, univariable analyses of CoV of nodule volume (Table 4), using the log-transformed CoV of nodule volume, was negatively associated with estimated nodule volume (β=-0.0007, P=0.001). Nodules without attachment to blood vessels (P=0.002) and smaller nodule surface area (P<0.001) were significantly associated with increasing log-transformed CoV of nodule volume (Table 5). As a strong positive association between surface area and estimated nodule volume (r=0.98) was identified, two separate multivariable regression models were fitted to avoid multicollinearity. When nodule characteristics were considered together using a multiple linear regression model, smaller nodule volume (P=0.02) and nodules without attachment to blood vessels (P=0.02) remained significantly associated with increasing CoV of nodule volume [r2=0.16, Akaike information criterion (AIC) =−55.97] (Table 5, model 1). When nodule surface area was included as an independent variable together with nodule location, blood vessels, and pleural attached nodules in a separate multivariable model (Table 5, model 2), nodule surface area remained as the only significant factor associated with CoV of nodule volume (r2=0.20, AIC =−61.58). Using nodule surface area instead of nodule volume in the adjusted model significantly improved the model fit (r2) from 0.16 to 0.20.
Table 5
| Nodule characteristics | Univariate | Multivariable (Model 1) | Multivariable (Model 2) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Estimate (β) | Std. error | P value | Estimate (β) | Std. error | P value | Estimate (β) | Std. error | P value | |||
| Volume (mm3) | −0.0007 | 0.0002 | 0.0012 | −0.0005 | 0.0002 | 0.017 | – | – | – | ||
| Nodule location | |||||||||||
| Upper/middle lobe | Ref. | Ref. | Ref. | ||||||||
| Lower lobe | 0.18 | 0.16 | 0.26 | 0.10 | 0.15 | 0.50 | 0.10 | 0.15 | 0.49 | ||
| Blood vessel attachment | −0.48 | 0.15 | 0.002 | −0.37 | 0.16 | 0.02 | −0.27 | 0.16 | 0.09 | ||
| Costal pleural attachment | 0.34 | 0.28 | 0.23 | 0.25 | 0.27 | 0.35 | 0.34 | 0.26 | 0.20 | ||
| Log (nodule surface area) | −0.75 | 0.17 | <0.0001 | – | – | – | −0.48 | 0.14 | 0.001 | ||
Reference category were absent of blood vessel attachment and absent of costal pleural attachment. Std., standard.
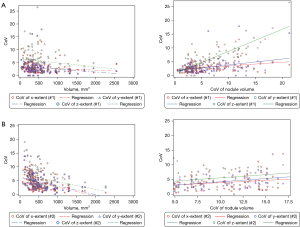
Analyses of CoV for the x, y, and z measurements (mm, x: right to left, y: anterior to posterior, z: superior to inferior) for all nodules are shown in Table 6 and Table 7 for algorithms #1 and #2 respectively. Using algorithm #1, median CoV of x, y, z measurements were 2.5% (IQR: 1.6–3.8%), 2.5% (IQR: 1.6–3.6%), and 4.7% (IQR: 2.7–7.4%), respectively. Correlation between the CoV of nodule volume and the CoV of the x, y, z measurements were 0.29 (P=0.0021), 0.25 (P=0.009), and 0.80 (P<0.001) (Figure 5A). Using algorithm #2, median CoV of x, y, z measurements were 3.2% (IQR: 2.0–6.11%), 3.8% (IQR: 2.4–6.1%), and 5.2% (IQR: 3.5–8.0%), respectively. Correlation between the CoV of nodule volume and the CoV of the x, y, z measurements was 0.46 (P<0.001), 0.52 (P<0.001), and 0.58, respectively (P<0.001) (Figure 5B). There was a strong relationship between CoV of nodule volume and CoV of z measurements in algorithm #1, while it was low for CoV of x and y measurements. However, for algorithm #2, the relationship between CoV of nodule volume and CoV of the x, y, and z measurements was low-moderate.
Table 6
| Nodule characteristics | Univariate | Multivariable | |||||
|---|---|---|---|---|---|---|---|
| Estimate (β) | Std. error | P value | Estimate (β) | Std. error | P value | ||
| x-measurement (right to left across patient) | |||||||
| Volume (mm3) | −0.0002 | 0.0001 | 0.09 | −0.0003 | 0.0001 | 0.06 | |
| Nodule location | |||||||
| Upper/middle lobe | Ref. | Ref. | |||||
| Lower lobe | 0.22 | 0.11 | 0.06 | 0.17 | 0.11 | 0.13 | |
| Blood vessel attachment | −0.04 | 0.12 | 0.71 | 0.10 | 0.12 | 0.40 | |
| Costal pleural attachment | 0.72 | 0.19 | 0.0003 | 0.72 | 0.22 | 0.001 | |
| y-measurement (anterior to posterior) | |||||||
| Volume (mm3) | −0.0005 | 0.0001 | <0.001 | −0.0005 | 0.0001 | <0.001 | |
| Nodule location | |||||||
| Upper/middle lobe | Ref. | Ref. | |||||
| Lower lobe | 0.14 | 0.11 | 0.23 | 0.04 | 0.12 | 0.73 | |
| Blood vessel attachment | −0.10 | 0.12 | 0.41 | 0.02 | 0.12 | 0.84 | |
| Costal pleural attachment | 0.09 | 0.23 | 0.70 | 0.18 | 0.22 | 0.42 | |
| z-measurement (superior to inferior) | |||||||
| Volume (mm3) | −0.0003 | 0.0002 | 0.11 | −0.0001 | 0.0002 | 0.52 | |
| Nodule location | |||||||
| Upper/middle lobe | Ref. | Ref. | |||||
| Lower lobe | 0.36 | 0.13 | 0.01 | 0.37 | 0.14 | 0.01 | |
| Blood vessel attachment | −0.21 | 0.13 | 0.12 | −0.20 | 0.14 | 0.16 | |
| Costal pleural attachment | 0.33 | 0.24 | 0.16 | 0.18 | 0.26 | 0.49 | |
Reference categories were absent of blood vessel attachment and absent of costal pleural attachment. CoV, coefficient of variation; Std., standard.
Table 7
| Nodule characteristics | Univariate | Multivariable | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Estimate (β) | Std. error | P value | Estimate (β) | Std. error | P value | ||||
| x-measurement (right to left across patient) | |||||||||
| Volume (mm3) | −0.001 | 0.0002 | <0.001 | 0.0009 | 0.0002 | <0.001 | |||
| Nodule location | |||||||||
| Upper/middle lobe | Ref. | Ref. | |||||||
| Lower lobe | 0.20 | 0.14 | 0.14 | 0.05 | 0.12 | 0.68 | |||
| Blood vessel attachment | −0.41 | 0.13 | 0.003 | −0.24 | 0.12 | 0.06 | |||
| Costal pleural attachment | 0.22 | 0.24 | 0.38 | 0.17 | 0.21 | 0.41 | |||
| y-measurement (anterior to posterior) | |||||||||
| Volume (mm3) | −0.0007 | 0.0002 | <0.001 | −0.0007 | 0.0002 | <0.001 | |||
| Nodule location | |||||||||
| Upper/middle lobe | Ref. | Ref. | |||||||
| Lower lobe | 0.15 | 0.13 | 0.25 | 0.02 | 0.12 | 0.84 | |||
| Blood vessel attachment | −0.13 | 0.13 | 0.30 | 0.02 | 0.13 | 0.89 | |||
| Costal pleural attachment | 0.04 | 0.23 | 0.85 | 0.07 | 0.21 | 0.74 | |||
| z-measurement (superior to inferior) | |||||||||
| Volume (mm3) | −0.0004 | 0.0001 | 0.0022 | −0.0003 | 0.0002 | 0.025 | |||
| Nodule location | |||||||||
| Upper/middle lobe | Ref. | Ref. | |||||||
| Lower lobe | 0.25 | 0.11 | 0.02 | 0.19 | 0.11 | 0.08 | |||
| Blood vessel attachment | −0.18 | 0.11 | 0.09 | −0.12 | 0.11 | 0.26 | |||
| Costal pleural attachment | 0.15 | 0.19 | 0.44 | 0.12 | 0.19 | 0.52 | |||
Reference categories were absent of blood vessel attachment and absent of costal pleural attachment. CoV, coefficient of variation; Std., standard.
Discussion
Current protocols for management of lung nodules utilize fixed nodule size and growth thresholds, implicitly designed to overcome measurement uncertainty without regard to specific characteristics of a patient’s nodule. Our goal is to understand the nodule- and patient-specific factors that affect measurement uncertainty with a view towards personalizing follow-up interval recommendations. Using two different automated volume measurement algorithms to calculate the CoV of nodule volume of our zero-change database of 107 nodules, we provided a best-case scenario for minimizing variation in size by reducing other possible sources of variation—same scanner and CT scan parameters, coached breathing, and having the patient remain on the table between scans. As a result, the measurement uncertainty for both algorithms given by the CoV of nodule volume (Table 1) was well below the RSNA-QIBA Small Nodule Profile limits and lower than the 15% reported by Smith et al. (4) and other studies (5,6,10-12). Algorithm #1 had a significantly lower median CoV of nodule volume than algorithm #2 (4.6% vs. 8.7%, P<0.001) (Table 2), which may be explained by the additional complexity of algorithm #2, which allowed this algorithm to segment a broader range of nodules (133 successfully segmented nodules vs. 115 for algorithm #1) at the expense of greater measurement uncertainty (Table 1). Additionally, algorithm #1 uses morphological filtering operations with a spherical kernel to remove attached structures, which has the side effect of smoothing the nodule surface, reducing variation. The trend of decreasing CoV of nodule volume with increasing nodule volume for both algorithms may be due to uncertainty in segmenting the nodule surface. The link between surface area and uncertainty was described in a previous study, which found a “zone of transition” on the surface of the nodule that proportionally decreased with increasing nodule size (20).
There are several notable findings from this study. First is confirmation of the relationship between nodule size and extent of uncertainty. Second, substantial differences in the performance of the two software programs exist. Third, there was evidence for nodule complexity impacting the measurement uncertainty. Fourth, we found a more significant relationship of measurement uncertainty to changes in the z-measurement which suggests spatial warping, previously demonstrated for older generations of scanners (9), illustrated in Figure 6, but may be due to other factors such as cardiac motion. Taken together our findings strongly suggest that the extent of measurement uncertainty represents a complex interaction between the device used to produce the image, the software used to make the measurement, and characteristics of the nodule and patient.
Although this study focused on measurement uncertainty, bias, defined as the deviation from the true measurement, is an additional component of measurement error. While algorithm #1 had lower measurement uncertainty, we do not know if it has a lower bias as the true volume of in-vivo nodules is unknown; thus, we do not know which algorithm is best overall. Previous nodule measurement challenges with a variety of different algorithms, one including the same algorithms as the ones in this study (21), and another study including similar algorithms (22), also showed differences between algorithms in both measurement uncertainty and bias.
Limitations of our study are that we evaluated a single scanning protocol on a single CT machine, and differences between scanners and protocols within the same scanner are likely to influence these results. We plan to obtain more cases from different scanners and with additional reconstruction protocols to investigate the impact of these aspects on volume measurement uncertainty. In addition, the scanning protocol utilized a pitch factor of 1.5, which is higher than typically recommended for lung cancer screening protocols (23). While a previous study found that lower pitch factor reduces uncertainty in synthetic nodules (24), the difference for a thin-slice scan was less than 5%. We plan to evaluate additional nodule characteristics, such as heterogeneity of density, to determine their impact and develop a more comprehensive model; however, we evaluated the nodule features we believed to have the greatest impact. In addition, this approach is only useful for measuring uncertainty and not accuracy; we will need to use phantom measurements and various approaches to modeling and simulation for additional understanding. We believe that, for estimating change assessment for a particular software and imaging setting, uncertainty likely will be the dominating effect. Finally, we used a single observer to both provide initial seed points for both algorithms and to evaluate whether the algorithms successfully segmented nodules; another observer may have selected different seed points and had different criteria for segmentation success. If multiple observers evaluated the segmentations and we only selected nodules that all observers agreed had “good” segmentations, we would have both reduced the size of the dataset and eliminated nodules that the observers disagreed on, which would reduce the measurement uncertainty further. In addition, as shown in the example nodule in Figure 6, irrespective of the segmentation, there is a clear difference in the number of slices the nodule appears between the two scans.
Conclusions
The results of this study have important implications on nodule management protocols. Recently, an approach to quantifying change in prognosis due to time delays that typically occur because of typical diagnostic algorithms has been reported (25). The primary reason for the requirement of any time delay for assessing growth relates to overcoming measurement uncertainty. Thus, the necessary components for balancing between these two competing elements of for determining optimal, and even personalized time delays, are only now beginning to emerge.
Acknowledgments
This work has been presented at the IASLC World Conference on Lung Cancer 2023 (September 9–12, 2023).
Funding: This work was supported by
Footnote
Reporting Checklist: The authors have completed the GRRAS reporting checklist. Available at https://qims.amegroups.com/article/view/10.21037/qims-23-1501/rc
Conflicts of Interest: All authors have completed the ICMJE uniform disclosure form (available at https://qims.amegroups.com/article/view/10.21037/qims-23-1501/coif). A.J. received support as the Principal Investigator from a grant from the Prevent Cancer Foundation for this work. He also served as a co-chair on an unpaid basis of the RSNA QIBA Small Lung Nodule Volume committee from Jan 2023 to Feb 2024. R.Y. received support for this work from a grant from the Prevent Cancer Foundation. K.J.M. served as a co-chair on an unpaid basis of the RSNA QIBA Small Lung Nodule Volume committee from Jan 2023 to Feb 2024. She is the owner of Puente Solutions LLC, a for-profit company. She receives consulting fee from Annalise.ai; HeartLung; InformAI; Median iBiopsy; Malcova; Mt. Sinai School of Medicine; Sira; Voronoi; and VoxelCloud. C.I.H. is the President and serves on the board of the Early Diagnosis and Treatment Research Foundation. She receives no compensation from the Foundation. The Foundation is established to provide grants for projects, conferences, and public databases for research on early diagnosis and treatment of diseases. C.I.H. is also a named inventor on a number of patents and patent applications relating to the evaluation of pulmonary nodules on CT scans of the chest which are owned by Cornell Research Foundation (CRF). Since 2009, C.I.H. does not accept any financial benefit from these patents including royalties and any other proceeds related to the patents or patent applications owned by CRF. She is on the advisory board of Lunglife AI without compensation. D.Y. is a named inventor of General Electric on a number of patents and patent applications related to the evaluation of chest diseases including measurements of chest nodules. He has received financial compensation for the licensing of these patents. In addition, he is a consultant and co-owner of Accumetra, a private company developing tools to improve the quality of CT imaging. He is on the advisory board and owns equity in HeartLung, a company that develops software related to CT scans of the chest. He is on the medical advisory board of Median Technology that is developing technology related to analyzing pulmonary nodules and is on the medical advisory board of Carestream, a company that develops radiography equipment. He is also on the advisory board of Lunglife AI. The other author has no conflicts of interest to declare.
Ethical Statement: The authors are accountable for all aspects of the work in ensuring that questions related to the accuracy or integrity of any part of the work are appropriately investigated and resolved. The study was conducted in accordance with the Declaration of Helsinki (as revised in 2013) and was considered to be exempt human research by the Institutional Review Board of the Icahn School of Medicine at Mount Sinai (No. 19-1417) because this retrospective study was minimal risk and used de-identified image data. Individual consent was waived for this retrospective study as no identifiable patient information was used.
Open Access Statement: This is an Open Access article distributed in accordance with the Creative Commons Attribution-NonCommercial-NoDerivs 4.0 International License (CC BY-NC-ND 4.0), which permits the non-commercial replication and distribution of the article with the strict proviso that no changes or edits are made and the original work is properly cited (including links to both the formal publication through the relevant DOI and the license). See: https://creativecommons.org/licenses/by-nc-nd/4.0/.
References
- US Preventive Services Task Force. Krist AH, Davidson KW, Mangione CM, Barry MJ, Cabana M, Caughey AB, Davis EM, Donahue KE, Doubeni CA, Kubik M, Landefeld CS, Li L, Ogedegbe G, Owens DK, Pbert L, Silverstein M, Stevermer J, Tseng CW, Wong JB. Screening for Lung Cancer: US Preventive Services Task Force Recommendation Statement. JAMA 2021;325:962-70. [Crossref] [PubMed]
- Sullivan DC, Obuchowski NA, Kessler LG, Raunig DL, Gatsonis C, Huang EP, Kondratovich M, McShane LM, Reeves AP, Barboriak DP, Guimaraes AR, Wahl RLRSNA-QIBA Metrology Working Group. Metrology Standards for Quantitative Imaging Biomarkers. Radiology 2015;277:813-25. [Crossref] [PubMed]
- Liang M, Yip R, Tang W, Xu D, Reeves A, Henschke CI, Yankelevitz DF. Variation in Screening CT-Detected Nodule Volumetry as a Function of Size. AJR Am J Roentgenol 2017;209:304-8. [Crossref] [PubMed]
- Smith GT, Rahman AR, Li M, Moore B, Gietema H, Veronesi G, Massion PP, Walker RC. Reproducibility of Volumetric Computed Tomography of Stable Small Pulmonary Nodules with Implications on Estimated Growth Rate and Optimal Scan Interval. PLoS One 2015;10:e0138144. [Crossref] [PubMed]
- Gietema HA, Schaefer-Prokop CM, Mali WP, Groenewegen G, Prokop M. Pulmonary nodules: Interscan variability of semiautomated volume measurements with multisection CT-- influence of inspiration level, nodule size, and segmentation performance. Radiology 2007;245:888-94. [Crossref] [PubMed]
- Gietema HA, Wang Y, Xu D, van Klaveren RJ, de Koning H, Scholten E, Verschakelen J, Kohl G, Oudkerk M, Prokop M. Pulmonary nodules detected at lung cancer screening: interobserver variability of semiautomated volume measurements. Radiology 2006;241:251-7. [Crossref] [PubMed]
- Han D, Heuvelmans MA, Vliegenthart R, Rook M, Dorrius MD, de Jonge GJ, Walter JE, van Ooijen PMA, de Koning HJ, Oudkerk M. Influence of lung nodule margin on volume- and diameter-based reader variability in CT lung cancer screening. Br J Radiol 2018;91:20170405. [Crossref] [PubMed]
- Iwano S, Okada T, Koike W, Matsuo K, Toya R, Yamazaki M, Ito S, Ito J, Naganwa S. Semi-automatic volumetric measurement of lung cancer using multi-detector CT effects of nodule characteristics. Acad Radiol 2009;16:1179-86. [Crossref] [PubMed]
- Henschke CI, Yankelevitz DF, Yip R, Archer V, Zahlmann G, Krishnan K, Helba B, Avila R. Tumor volume measurement error using computed tomography imaging in a phase II clinical trial in lung cancer. J Med Imaging (Bellingham) 2016;3:035505. [Crossref] [PubMed]
- Kostis WJ, Yankelevitz DF, Reeves AP, Fluture SC, Henschke CI. Small pulmonary nodules: reproducibility of three-dimensional volumetric measurement and estimation of time to follow-up CT. Radiology 2004;231:446-52. [Crossref] [PubMed]
- Wormanns D, Kohl G, Klotz E, Marheine A, Beyer F, Heindel W, Diederich S. Volumetric measurements of pulmonary nodules at multi-row detector CT: in vivo reproducibility. Eur Radiol 2004;14:86-92. [Crossref] [PubMed]
- Goodman LR, Gulsun M, Washington L, Nagy PG, Piacsek KL. Inherent variability of CT lung nodule measurements in vivo using semiautomated volumetric measurements. AJR Am J Roentgenol 2006;186:989-94. [Crossref] [PubMed]
- Gavrielides MA, Zeng R, Kinnard LM, Myers KJ, Petrick N. Information-theoretic approach for analyzing bias and variance in lung nodule size estimation with CT: a phantom study. IEEE Trans Med Imaging 2010;29:1795-807. [Crossref] [PubMed]
- Nietert PJ, Ravenel JG, Leue WM, Miller JV, Taylor KK, Garrett-Mayer ES, Silvestri GA. Imprecision in automated volume measurements of pulmonary nodules and its effect on the level of uncertainty in volume doubling time estimation. Chest 2009;135:1580-7. [Crossref] [PubMed]
- Reeves AP, Chan AB, Yankelevitz DF, Henschke CI, Kressler B, Kostis WJ. On measuring the change in size of pulmonary nodules. IEEE Trans Med Imaging 2006;25:435-50. [Crossref] [PubMed]
- Krishnan K, Ibanez L, Turner WD, Jomier J, Avila RS. An open-source toolkit for the volumetric measurement of CT lung lesions. Opt Express 2010;18:15256-66. [Crossref] [PubMed]
- CT Volumetry Technical Committee. QIBA Profile: Small Lung Nodule Volume Assessment and Monitoring in Low Dose CT Screening. 2018. Available online: https://qibawiki.rsna.org/images/a/a2/QIBA_CT_Vol_SmallLungNoduleAssessmentInCTScreening_2018.11.20.docx
- Reeves AP, Xie Y, Jirapatnakul A. Automated pulmonary nodule CT image characterization in lung cancer screening. Int J Comput Assist Radiol Surg 2016;11:73-88. [Crossref] [PubMed]
- R Core Team. R: A Language and Environment for Statistical Computing. R Foundation for Statistical Computing, Vienna, Austria, 2017.
- Zhang L, Yankelevitz DF, Henschke CI, Jirapatnakul AC, Reeves AP, Carter D. Zone of transition: a potential source of error in tumor volume estimation. Radiology 2010;256:633-9. [Crossref] [PubMed]
- Reeves AP, Jirapatnakul AC, Biancardi AM, Apanasovich TV, Moltz JH, Kuhnigk JM. The VOLCANO’09 Challenge: Preliminary Results. The Second International Workshop on Pulmonary Image Analysis 2009:353-64.
- Athelogou M, Kim HJ, Dima A, Obuchowski N, Peskin A, Gavrielides MA, et al. Algorithm Variability in the Estimation of Lung Nodule Volume From Phantom CT Scans: Results of the QIBA 3A Public Challenge. Acad Radiol 2016;23:940-52. [Crossref] [PubMed]
- American Association of Physicists in Medicine. Lung Cancer Screening CT Protocols Version 6.
0. 2023. Available online: https://www.aapm.org/pubs/CTProtocols/documents/LungCancerScreeningCT.pdf - Chen B, Barnhart H, Richard S, Colsher J, Amurao M, Samei E. Quantitative CT: technique dependence of volume estimation on pulmonary nodules. Phys Med Biol 2012;57:1335-48. [Crossref] [PubMed]
- Yankelevitz DF, Yip R, Henschke CI. Impact of Duration of Diagnostic Workup on Prognosis for Early Lung Cancer. J Thorac Oncol 2023;18:527-37. [Crossref] [PubMed]




