
Quantitative susceptibility mapping based basal ganglia segmentation via AGSeg: leveraging active gradient guiding mechanism in deep learning
Introduction
Quantitative susceptibility mapping (QSM) is a computational imaging technique that enables the estimation of tissue susceptibility distribution from magnetic resonance imaging (MRI) phase data. It has demonstrated potential in both biomedical research and clinical diagnosis of brain iron metabolism, cerebral blood oxygenation, and pathological conditions detection (1). Due to its ability to quantify the paramagnetic nonheme iron in brain tissue, QSM can provide higher contrast and resolution for basal ganglia structures than other conventional computational imaging techniques (2). The basal ganglia including the caudate nucleus (CN), putamen (PU), globus pallidus (GP), substantia nigra (SN), and red nucleus (RN) are involved in various aspects of motor control, cognitive functions, emotion regulation, and sensory processing. They have already been demonstrated to play essential roles in neurodegenerative diseases including Alzheimer’s disease (AD) (3), Parkinson’s disease (PD) (4), and multiple sclerosis (MS) (5). Conventional methods for basal ganglia localization and segmentation heavily depend on the layer-by-layer manual annotation by experts, resulting in a tedious amount of workload. Therefore, a highly efficient and robust automatic approach for basal ganglia segmentation is essential for further research and clinical applications and is a fundamental composition of computer-aided diagnostic systems.
Regions of interest (ROIs) segmentation in medical images is a fundamental and valuable issue that has been extensively studied in the past few years. Before the advent of deep learning in this field, the atlas-based approach was considered as a significant solution (6). The atlas-based segmentation approach employs a predefined template and registers it to the individual QSM map through different algorithms, yielding the label of corresponding ROIs. Magon et al. have proposed a label-fusion segmentation and performed a deformation-based shape analysis of deep gray matter (DGM) in MS (7). The authors in study (8) proposed a multi-atlas tool for automated segmentation of brain DGM nuclei and demonstrated the superiority of accuracy over other single-atlas based approaches. This study employed QSM and T1 images that were registered separately to a common template space using a symmetric diffeomorphic registration algorithm. The template space was defined by the average of 10 atlases with manually labeled ROIs in DGM structures. The excellent performance of the method at that time hints at the potential value of multi-contrast data fusion for segmenting tasks. It is worth noting that atlas-based methods share similar advantages and disadvantages. Although highly mathematically interpretable, they require counter-intuitive parameter tuning for each individual subject, which is daunting and time-consuming. The final results of atlas-based methods are strongly influenced by the similarity between atlas and registered subjects, including the contrast difference, signal-to-noise ratio (SNR), and even acquisition parameter setting (9). Presently, registration atlases are primarily collected from healthy human data, which results in significant differences between patient data, decreasing the accuracy of registration in clinical applications (10). The distribution of lesions is diverse in various brain diseases (e.g., brain tumors, cerebral hemorrhage, and calcification), making registration challenging, particularly when the lesion size is large.
Recently, deep learning methods have become increasingly popular and successful in the field of medical image segmentation, due to their ability in learning complex and hierarchical features from large-scale data and achieving high accuracy. They have been proven to outperform conventional segmentation algorithms based on image continuity and atlas registration in multiple subproblems of medical image segmentation, such as lung nodules (11), brain tumors (12), liver tumors (13), retinal vessels (14), and various normal or pathological regions. U-shaped networks with down-sampling processes in their encoders and up-sampling processes in decoders are widely adopted as the backbone of various segmentation networks together with the core idea of skip-connection (15). Multiple kinds of attention mechanisms have been demonstrated to be useful in guiding the segmentation network to focus on the lesion area, structure edge (16), or adjusting channel weights (17). To balance computation cost and segmentation accuracy, 2.5D networks have been proposed by Zhang et al. to segment lesions in (18) to treat biomedical images as multiple patches or fuse adjacent slices to complete Z-axis context information. Zhang et al. proposed a 3D network with spatial information along the Z-axis as strong prior to promote the segmentation process (19). Nevertheless, the way to extract features is priory settled down without learning, and it cannot obtain cross-slice information since it only samples adjacent slices. Transformer-based neural networks like Swin-Transformer (20) or TransBTS (21) have been proven to outperform Convolutional Neural Network (CNN) in many biomedical tasks along with the noticeable increment of computation cost and inference time.
Deep learning methods have also been gradually applied to the task of basal ganglia segmentation. For instance, Raj et al. proposed a 2-D fully convolutional neural network to segment GP and PU from QSM (22). The 2D network requires reasonable computation costs, yet it loses significant spatial information in the inter-slice correlation. As a 3D extension of UNet, the VNet has demonstrated its effectiveness on various 3D medical imaging datasets, including the challenging task of segmenting gliomas from brain MRI (23). Solomon et al. applied a modified attention-gated UNet with deformable convolution kernels to segment GP from 7T MRI (24). Guan et al. proposed a 3-D network to segment sub-cortical nuclei which adopts spatial and channel attention modules in both encoder and decoder stages to focus the network on target regions (25). Wang et al. trained a 3D network with attention gates to segment basal ganglia and employed them for automatic PD detection (26). With the targeted adjustments and improvements of deep learning techniques on DGM segmentation tasks, the localization and segmentation of basal ganglia have been gradually developed. However, the boundary contour of nuclei remains a challenge to distinguish due to the lack of intensity contrast difference between surrounding tissues. Additional difficulty during the segmenting process could be encountered since the original susceptibility values are covered up by the artifacts that exist near the large susceptibility variation.
Given the aforementioned challenges, aiming to improve the robustness towards susceptibility artifacts and equip the model with better ability to generate precise boundary contour of nuclei, it is crucial to reconsider and integrate following two key ideas into the network design. Firstly, MRI signals inherently comprise two types of original images, namely magnitude images and phase images, while QSM relies on phase image post-processing. Magnitude images often possess boundary information that is not present in QSM, and can serve as an additional information source while the susceptibility values are covered up by artifacts. In many traditional image processing methods, images from different modalities or contrasts are sometimes fused and enhanced to suit specific downstream tasks. Deep learning methods should also incorporate targeted designs accordingly. Secondly, medical images exhibit 3D characteristics. Similar to inter-frame information acquired between continuous frames in video segmentation, inter-layer information in medical images contains valuable continuity and steep change information, often reflecting rich boundary structural details. However, this aspect has not been extensively explored. Building upon these two concepts, we propose AGSeg, a dual-branch network based on active gradient guidance, featuring magnitude information completion for basal ganglia segmentation. AGSeg employs a dual-branch architecture as its backbone, providing an efficient framework to incorporate inter-layer information while reflecting the original design intention within a reasonable number of model parameters. The design of active gradient module (AGM) allows the network to actively select the sample interval for gradient map acquisition, increasing the network’s generalization ability. The introduction of the magnitude information complete (MIC) module exploits the magnitude information lost in the reconstruction process of QSM and increases the network’s robustness to clinical data.
Methods
The detailed architecture of the proposed AGSeg is shown in Figure 1. In this section, a detailed elaboration of the proposed AGSeg is provided. The MIC module is first described to emphasize the significance of integrating magnitude information as an auxiliary input. Then, the concept of active gradient map guidance is introduced. Lastly, the dual-branch architecture is presented, which also explains the overall architecture and data flow inside AGSeg. AGSeg takes QSM and Magnitude map as two individual inputs and outputs the final segmentation prediction and its corresponding gradient maps. The manual annotation of segmentation maps and their gradient maps are used as labels in the same training stage. The study was conducted in accordance with the Declaration of Helsinki (as revised in 2013). The study was approved by Medical Ethics Committee of Xiamen University (No. EC-20230515-1006) and informed consent was taken from all subjects.

MIC module
Extensively explored within traditional image-processing research, fusion-based enhancement methods have been employed for generating contrast-shifted images intended for various downstream tasks (27,28). The primary goal of conventional fusion techniques is to amplify the contrast between ROIs and the background, thereby facilitating localization and segmentation. In deep learning-based segmentation, the foreground, and background are typically differentiated in the tail part of the network using activation functions such as Softmax or Sigmoid. However, the network-produced feature maps encompass voluminous high dimensional data distributed across numerous channels, leading the ultimate segmentation decision criterion to encompass more than mere visual contrast within the spatial domain. Consequently, it is crucial to develop an automatic mechanism that can be controlled by the network through gradient descent to fuse different images from different sources and generate enhanced feature maps for downstream tasks accordingly. Based on this rationale, we introduce the MIC module, elucidated in detail in Figure 2.

Aiming to fully harness magnitude information, the MIC module accepts two distinct inputs: the magnitude map () and its corresponding QSM (). Convolutions with kernel size as 3×3×3 are used to extract features from Mag and QSM while increasing the channel numbers to contain extracted features. The extracted feature maps are channel-wisely concatenated to form the input of the squeeze and excitation (SE) block (17). SE block will generate two channel-wise corresponding mask vectors to adjust the weights of each channel thus emphasizing some channels while reducing the importance of others. The residual block (RB) was composed of three 3×3×3 convolutions with skip connection to form residual path. Detail composition of RB is also depicted in Figure 1. The weighted feature maps of Mag and QSM will be channel-wisely concatenated to generate the final enhanced output. This fusion mechanism is replicated identically twice, each instantiation possessing distinct parameters, which engender two disparate enhanced feature maps after the training process. These two enhanced feature maps are derived through distinct parameters which signifies diverse enhancement emphases. They are respectively employed as the initial inputs for the Seg-branch and Grad-branch. Through the MIC module, the magnitude information during the reconstruction of QSM is re-explored. As the parameters within the module are acquired via automatic learning based on gradient descent, the module effectively amplifies disparities between foreground and background across numerous channels according to the network’s own criteria for distinguishing target ROIs.
AGM
The basal ganglia consist of several nuclei, which present a continuous intensity distribution in the spatial domain. However, MRI signals exhibit discreteness along each direction as a stack of continuous slices. The inter-slice information frequently contains continuous or steep change information, particularly at the nuclei boundary. Such information can serve as prior knowledge to guide the segmentation process. In this work, the inter-slice information along the Z-axis is further exploited through the formulation of the AGM and the gradient fuiding module (GGM). The detailed architectures of these modules are illustrated in Figure 3. The AGM is specifically designed to generate gradients of the given subject in order to emphasize the inter-layer features, which typically include valuable edge information of the target regions.
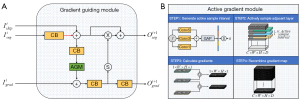
The overall pipeline of the AGM can be described in four steps. For explanatory purposes, the batch size is assumed to be one in the following description. Firstly, suppose the shape of the input feature map is , the input feature maps flow to an inception block with Conv5, Conv3, and Conv1 composed in parallel. The outputs of each conv block (CB) are elemental-wisely summed up as the input of the global average pooling block. The feature maps are flattened to a vector () with the length of the original channel number . The values of the flattened vector are first normalized across the channel dimension. A Softmax function is utilized to map this vector into the probability distribution between 0 and 1. Subsequently, a set of predefined thresholds (ranging from 0 to 1) is employed to classify this vector into five classes, each representing a specific sample interval (). Secondly, the input feature maps are actively sampled based on the generated sample interval, where each element in the vector becomes an individual interval for the corresponding channel. Consequently, the residues between selected layers are computed to infer the required gradient map. Zero paddings are performed for those slice pairs that are out of the patch. The existence of the residue path can make sure the original information in the featuremap of the seg-branch is not affected by the zero-padded slices. Finally, the derived gradient maps are concatenated along the Z-axis to formulate a new 3D volume with an identical shape to the original inputs. The transfer function of AGM () for each channel can be expressed by the Eq. [1].
where represents the intensity value at the position of layer, denotes the auto-selected sample interval and is the hyper-parameter to adjust the influence of gradient guidance in the segmentation network. AGM acts as a fundamental cross-domain translation module, mapping the input feature maps into the gradient domain. We can observe that when the sample interval inside AGM was fixed into a constant number through the ablation experiment, the model performance noticeably dropped. The distribution of sample intervals () is also recorded and visualized and details are explained in Discussion section.
GGM
With AGM as a powerful tool to access inter-slice information, an efficient method is crucial to exploit these valuable features to guide segmentation processes. Thus, we propose the GGM with detailed architectures shown in Figure 3. GGM servers as the information exchange pathway between Seg-branch and Grad-branch.
It provides edge information through gradient guidance while employing multi-level featuremaps to calculate gradient maps at different fields of view (FoV). The GGM receives three inputs including the skipping featuremap , segmentation featuremap from the previous stage in Seg-branch, and gradient featuremap . Subsequently, it generates two outputs, one for the Seg-branch and the other for the Grad-branch, denoted as and . Through AGM, featuremaps from Seg-branch at each down/up sampling level can generate gradient maps with corresponding size and FoV, which can help the Grad-branch to extract contours of ROIs from the initial gradient map. Reversely, the activated attention map from Grad-branch enhances the significance of the structure edge by performing element-wise multiplication between the attention mask and the featuremap from Seg-branch. In this way, the accessed inter-slice information is further exploited. The information exchange paths inside the GGM can be described by Eqs. [2] and [3].
where and represent the outputs delivered to Grad-branch and Seg-branch, and are elemental-wise summation and multiplication, represents the convolution operation with kernel size as 3×3×3, denotes the operation of acquiring gradient maps through AGM. denotes the sigmoid function used to activate featuremap into binary distribution where only foreground and background are distinguished.
Network architecture
The detailed architecture of the proposed AGSeg is presented in Figure 1 with a dual-branch framework as its main backbone. Corresponding enhanced feature maps are generated through the MIC module by automatically fusing the input Magnitude image and QSM map. The upper part of Figure 1 represents the Seg-branch which aims to extract both global and local features through a U-shaped down/up sample network and skip-connection to reconstruct the final segmentation map. The lower part of Figure 1 represents the active Grad-branch with the function of providing edge attention guidance to the Seg-branch while simultaneously reconstructing the gradient map for the target nuclei from the initial gradient map. Both Seg-branch and Grad-branch are constructed based on the core idea of multi-scale frameworks (23). High-level features with global information are extracted at the start of each branch. Low-level features are grasped through 3 stages of down-sample operation achieved by convolution with a stride equal to two.
To accommodate GPU memory limitations, the batch size used for training is set to one, which poses a challenge for frequently used batch normalization. To address this issue, group normalization is employed as a replacement for batch normalization (29). The key distinction between CB and RB shown in Figure 1 is that the latter takes the input of RB as a residual and performs element-wise summation with the result of CB, thereby mitigating network degradation issues that may occur in deep neural networks (30). The up-sample operations are conducted inside GGMs through trilinear interpolation and skip-connection. GGM plays an essential role in exchanging feature maps between branches, which sends the gradient map of multi-level feature maps calculated by AGM to the Grad-branch and also takes the edge attention guidance back to the Seg-branch. Compared with the decoder, the down-sampling part of the encoder owns more convolutions, which brings more parameters concentrated on the encoder. This design can be helpful to freeze main parameters and retrain remaining parts when transferring the model into a newly met dataset.
Experimental data preparation
A mixed dataset was collected in this work to train, validate, and test the model performance while ensuring the comparison between each method is fair. The overall dataset was divided into five independent parts for training and evaluating segmentation accuracy for 5-fold validation.
3T Dataset was a public dataset acquired on a Siemens Prisma platform with 64 channel head/neck coil using a muti-echo 3D GRE sequence with the following parameters (31): FoV =211×224×160 mm3, matrix size =210×224×160, flip angle =20°, repetition time (TR) =44 ms, echo time (TE) =7.7/13.4/18.8/25.3/31.7/28.2 ms, spatial resolution =1×1×1 mm3. Multiple scans in various orientations were acquired, with 144 measurements collected in total. Laplacian-based method was applied in the phase unwrapping stage and V-SHARP was used to remove the background field (32). The individual parcellation maps generated through the registration method were offered. Manual adjustments were performed by several professional researchers to generate the final ground truth parcellation maps. Similar to other medical image segmentation tasks, the ground truth was stored as a 4D matrix where the foreground and background of each class are represented by the binary-coded index inside each channel. This dataset is now publicly available at: https://qmri.sjtu.edu.cn/resources.
7T Dataset was composed of 44 measurements acquired from a 7T (Philips Achieva, 32 channel head coil) scanner and the following parameters: FoV= 224×224×126 mm3, matrix size =224×224×110, TR =28/45 ms, TE =5/2 ms, ∆TE =5/2 ms, 5–16 echoes, spatial resolution =1×1×1 mm3, flip angle =9°. Phase processing steps were conducted including phase unwrapping with a Laplacian-based method and background field removal with iRSHARP (33). The COSMOS map was generated as the final QSM after the multi-orientation data was registered to the supine position. Manual segmentation labels were annotated by experienced radiologists and double-checked. This dataset was used for the second stage of training to verify the feasibility of transfer learning. Comparison experiments were also conducted on the 7T Dataset. This dataset is publicly available at: https://github.com/Sulam-Group/LPCNN.
Clinical 3T Dataset collected for the generalization test consisted of 19 measurements acquired from a 3T GE MR750 scanner with parameters as follows: FoV =256×256×140 mm3, spatial resolution =1×1×1 mm3, TR =24 ms, TE =3.6/5.8/8.2/10.6 ms, 8 echoes, 24 channel coil. Same phase pre-process steps and background field removal methods as the 7T Dataset were applied, structural feature based collaborative reconstruction (SFCR) was performed to reconstruct the final single-orientation QSM (34). This dataset was used for the generalization experiment to find out the performance of AGSeg on newly-met data. To find out the effectiveness of fine-tuning on small data sizes, transfer learning was also performed on a randomly selected measurement. More details about transfer learning can be found in the following sections.
United imaging healthcare (UIH) 5T Dataset includes healthy human brain data collected through a uMR Jupiter 5T platform, 48 channel coil with parameters as follows: FoV =224×200×120 mm3, spatial resolution =0.33×0.33×1 mm3, TR =35 ms, TE =3.6/10.2/16.8/23.4/30 ms, 5 echoes. The same phase pre-process steps and background field removal methods as the 7T Dataset were applied, and the final QSM data was generated by SFCR. This dataset was used for the generalization experiment with respect to data acquired at different magnetic field strengths.
Evaluation and statistical analysis
The major aim of medical image segmentation is to achieve accurate ROI localization and segmentation. To evaluate the final result, a combination of quantitative and qualitative analyses is employed here. The segmentation performance is quantitatively evaluated using the Dice similarity coefficient (DSC) and 95% Hausdorff distance (HD95). The DSC measures the spatial volume overlap between the prediction and corresponding ground truth, while the HD95 focuses on the similarity of boundaries. Formulas to calculate DSC and HD95 values are shown in Eqs. [4] and [5].
Where P and T denote the prediction and the ground truth of segmentation, p and t are the foreground (non-zero) voxels of prediction and ground truth, and h is the distance between two sets, which are calculated by .
Comprehensive statistical analysis was performed based on the acquired results of both ablation study and comparison experiments. In this section, the detailed results of various experiments are listed. The ablation studies are designed to demonstrate the effectiveness of the proposed modules as well as the sample methods. Furthermore, comparison experiments between AGSeg and other prevalent basal ganglia segmentation algorithms are also performed on diverse datasets acquired from various magnetic strengths. Regression studies were performed on both the results of AGSeg and compared methods. The average susceptibility values and total volume of predicted nuclei were chosen as statistical indicators to reflect the accuracy of segmentation results. Additionally, experiments conducted on the clinical datasets were undertaken to demonstrate the AGSeg’s generalization ability and its sensitivity to transfer learning.
Implementation details
The original magnitude images and susceptibility maps are randomly cropped into sub-volumes of size 128×128×128 as training samples. Center cropping is applied to make sure that target ROIs exist in the generated sub-volumes. Random rotation along 3-dimensions is adopted with the rotation angle and the corresponding ratio . The initial learning rate was set to 1×104 and decayed exponentially.
In this work, all network models were implemented using Python with Pytorch backend and were trained on a workstation with NVIDIA Titan X GPU, Intel Xeon CPU E5 2.10 GHz, and 64 GB RAM. AdamW was chosen as the network optimizer. Experiments in this section including ablation studies and comparison experiments are designed to mainly prove the effectiveness of proposed mechanisms while demonstrating the superior performance of AGSeg. Four existing basal ganglia segmentation methods including three deep learning-based and one atlas-based method were selected for comparison. Deep learning-based methods are DeepQSMSeg (25), CAUNet (35), and VNet (23), whose codes were rewritten according to the original paper. The atlas-based method was tested by uploading test files to their public system (8,36).
Loss function
AGSeg takes QSM and magnitude map as two individual inputs and outputs the final segmentation prediction and its corresponding gradient maps. The manual annotation of segmentation maps and their gradient maps are used as labels in the training stage. The loss functions are identical in the overall training process. Dice loss () combined with voxel-wise focal loss () is adopted to describe and evaluate the training convergence state.
Where and are the focal and dice loss function with a detailed description in Eqs. [6] and [7]. and are the prediction and the ground-truth of the segmentation result at position .
where is a small constant to ensure that the denominator is not zero. The total loss function is the weighted summation of Seg-branch loss and Grad-branch loss to make sure that each branch is trained to function as designed. Denoted as: , where is the influential factor to adjust the weight of each branch to achieve balance during the training process.
Training strategy
As one particularity of QSM, the final results of the same object can differ much due to different parameter settings and processing procedures. A standard and universally applicable protocol in medical practice is still lacking, necessitating greater robustness and user-friendliness in the employed models. Transfer learning has been demonstrated as a powerful training strategy to boost model performance and robustness in various kinds of computer vision (CV) tasks. Therefore, the training process of AGSeg also exploits transfer learning. The AGSeg was first zero-initialized and trained on the 3T Dataset until the loss function value was no longer reduced. At this point, AGSeg was able to segment 3T QSM data properly and has already achieved reliable results. Then, all trainable parameters of the encoder part are frozen, and remaining only the decoder part to be trained in the next stage on the 7T Dataset. The loss function was able to step across the first convergence state and reduce again in the second training stage due to better contrast of 7T data. The second stage of the training process can be seen as a fine-tuning procedure that can efficiently transfer the well-trained model into a new dataset. This can be both helpful for the performance of the model on new datasets and make it easier for radiologists’ daily practice. To verify the effectiveness of transfer learning, the average dice curve was recorded. More details are shown in the Result section.
Results
Ablation study
Ablation experiments were conducted on a combination dataset comprising 3T and 7T QSM data to validate the effectiveness of the proposed modules. Five-fold cross-validation was employed, with 80% and 20% of the data randomly selected for the training and test datasets, respectively. The first ablation study aimed to verify the effectiveness of the MIC module and the Grad-branch by deleting corresponding blocks or replacing them with normal convolutions. For a fair comparison, AGSeg without relative blocks was removed and retrained on the same dataset under the same training strategy. Additionally, another study was conducted to demonstrate the necessity of active sampling intervals () in gradient map acquisition by comparing them to constant sample intervals. For all ablation studies, the DSC and HD95 were calculated for each DGM nucleus, and the average values were used as the final quantitative evaluation indices.
Table 1 presents the results of the first ablation study, showing that the mean DSC value of the modified AGSeg without the MIC module was dropped by 5.95% and the HD increased by 12.26%. This provides strong evidence of the effectiveness of MIC module. In the AGSeg_w/o Grad-branch, which omitted the gradient branch, we replaced the GGM in Seg-branch with trilinear interpolation to achieve upsampling function. Consequently, the modified AGSeg essentially transformed into an encoder-decoder network with a structure resembling VNet but with fewer parameters than the original VNet (23). The modification resulted in a 15.10% decrement in DSC and a 48.26% increment in HD. Despite the reduction in overall parameter capacity, these significant performance differences still highlighted the importance of the Grad-branch. Table 2 depicts the outcomes of the second ablation study, wherein alterations were made to the sample interval generation scheme. An obvious decline in performance is evident when fixing the sample intervals into constant numbers. While AGSeg’s performance might be deemed acceptable for a few nuclei when utilizing constant interval settings, significant false segmentation occurred, particularly around the nuclei boundary. However, models employing actively generated sample intervals demonstrated superior performance across almost all target nuclei, attributable to the adaptability to input feature maps facilitated by AGM.
Table 1
| Models | CN | GP | PU | SN | RN | AVG | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| DSC | HD95 | DSC | HD95 | DSC | HD95 | DSC | HD95 | DSC | HD95 | DSC | HD95 | ||||||
| AGNet_Origin | 0.872 | 2.016 | 0.913 | 1.693 | 0.891 | 1.807 | 0.839 | 2.462 | 0.856 | 2.070 | 0.874 | 2.009 | |||||
| AGNet_w/o MIC | 0.859 | 2.065 | 0.886 | 2.006 | 0.866 | 2.132 | 0.761 | 2.536 | 0.737 | 2.541 | 0.822 | 2.256 | |||||
| AGNet_w/o GB | 0.771 | 3.145 | 0.734 | 2.848 | 0.751 | 3.363 | 0.724 | 2.991 | 0.728 | 2.548 | 0.742 | 2.979 | |||||
CN, caudate nucleus; GP, putamen; PU, globus pallidus; SN, substantia nigra; RN, red nucleus; AVG, the average value of 5 target nuclei; DSC, Dice similarity coefficient; HD95, 95% Hausdorff distance; MIC, magnitude information complete.
Table 2
| Models | CN | GP | PU | SN | RN | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| DSC | HD95 | DSC | HD95 | DSC | HD95 | DSC | HD95 | DSC | HD95 | |||||
| ASI (AGSeg_Origin) | 0.8721 | 2.0165 | 0.9136 | 1.6933 | 0.8911 | 1.8070 | 0.8394 | 2.4623 | 0.8560 | 2.0700 | ||||
| CSI (n=1) | 0.8298 | 2.8927 | 0.8789 | 2.0749 | 0.8544 | 2.1326 | 0.8270 | 2.2366 | 0.8466 | 2.1687 | ||||
| CSI (n=2) | 0.8475 | 2.1498 | 0.8454 | 2.5698 | 0.8149 | 2.2189 | 0.7489 | 2.8786 | 0.7947 | 2.8165 | ||||
| CSI (n=5) | 0.8345 | 2.4863 | 0.8823 | 2.0498 | 0.7999 | 2.4490 | 0.7116 | 2.6472 | 0.7213 | 2.6046 | ||||
CN, caudate nucleus; GP, putamen; PU, globus pallidus; SN, substantia nigra; RN, red nucleus; DSC, Dice similarity coefficient; HD95, 95% Hausdorff distance; ASI, active sample interval; CSI, constant sample interval.
Figure 4 shows the segmentation results for a randomly selected subject from the test dataset before and after the ablation of corresponding blocks. Significant false positive/negative segmentation phenomenon can be observed over ROI boundaries, which are marked by arrows in Figure 4 After ablating the Grad-branch, the model tends to generate more false positive predictions and becomes severely bad at distinguishing GP and ventral pallidum (VeP). More False negative predictions appeared inside PU due to the existence of tiny artifacts, which do not exist in the magnitude images. Both quantitative and qualitative results can demonstrate the effectiveness of the proposed MIC module and Grad-branch.

Results on healthy human data
The performance of the well-trained AGSeg was evaluated on the 3T and 7T Dataset. AGSeg was compared with four existing methods for segmenting basal ganglia. The outcomes of comparison experiments are presented in Table 3. The analysis revealed that AGSeg achieved the highest Dice coefficient values for all target DGM nuclei, with an average value of 0.8744. It is worth noting that the HD values of AGSeg for SN and RN are slightly larger than those of DeepQSMSeg and CAUNet. This could be attributed to AGSeg’s tendency to produce more compact boundaries for small targets, leading to more volume overlap and reduced loss values. While this phenomenon may not be visually apparent, it can only be sensitively observed through the increment of the HD95 index.
Table 3
| Methods | AGSeg | DeepQSMSeg | CAUNet | V-Net | Multi-Atlas | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| DSC | HD95 | DSC | HD95 | DSC | HD95 | DSC | HD95 | DSC | HD95 | |||||
| CN | 0.8721 | 2.0165 | 0.8412 | 2.3586 | 0.8267 | 2.3622 | 0.8146 | 2.6631 | 0.7820 | 2.9636 | ||||
| PU | 0.8911 | 1.8070 | 0.8646 | 1.9773 | 0.8515 | 1.9497 | 0.8312 | 2.1464 | 0.7980 | 2.9316 | ||||
| GP | 0.9136 | 1.6933 | 0.8560 | 2.0365 | 0.8546 | 2.1593 | 0.8367 | 2.4973 | 0.8283 | 2.2315 | ||||
| SN | 0.8394 | 2.4623 | 0.7886 | 2.4115 | 0.7937 | 2.8907 | 0.7300 | 2.5863 | 0.7608 | 2.6698 | ||||
| RN | 0.8560 | 2.0700 | 0.8435 | 1.9969 | 0.8134 | 1.3962 | 0.7927 | 2.9212 | 0.7768 | 2.5963 | ||||
| AVG | 0.8744 | 2.0098 | 0.8388 | 2.1562 | 0.8280 | 2.1516 | 0.8010 | 2.5629 | 0.7892 | 2.6785 | ||||
DSC, Dice similarity coefficient; HD95, 95% Hausdorff distance; CN, caudate nucleus; GP, putamen; PU, globus pallidus; SN, substantia nigra; RN, red nucleus; AVG, the average value of 5 target nuclei.
Qualitative analysis results are shown in Figure 5. An enlarged view of ROIs and the difference map between prediction and the ground truth are given at the right edge of each image. Three slices are chosen per measurement to demonstrate the segmentation performance on nuclei. Specifically, the 1st and 4th rows indicate a basal ganglia level where the morphology of CN, PU, and GP can be observed. Both AGSeg and the compared methods successfully located and segmented the primary area of these nuclei. However, the boundary between CN and GP remained challenging and AGSeg can predict a more precise outline. This phenomenon is particularly noticeable when the image quality is not good enough or a low contrast exists at the boundaries of nuclei. The 2nd and 5th rows of Figure 5 display a mid-brain slice where the axial view of PU’s front part can be observed. It is difficult to distinguish GP and VeP because these two objects seem to be a unite one when observing from the axial view. More false positive predicted voxels can be observed from the difference map between the prediction of DeepQSMSeg and ground truth. Segmentation of SN and RN are depicted in the 3rd and the 6th row of Figure 5. It poses more challenges for deep learning-based methods due to their relatively small volume compared to other target nuclei. This situation presents a long-tail problem (37), under which AGSeg can predict a more accurate and compact contour of RN.

Regression analysis was conducted on AGSeg’s predictions and the corresponding ground truth. The average susceptibility and the total volume of each nucleus were compared to evaluate segmentation performance. Both indices are sensitive to variations in the boundary of segmented nuclei. The susceptibility values experience sharp changes inside and outside the nuclei near their boundaries, occasionally fluctuating between positive and negative values. Assuming the nuclei to approximate spherical entities, the increase in radius exhibits an approximate cubic function proportionality to the volume growth. This suggests that the accuracy of the nucleus boundary significantly influences the overall voxel count. Figure 6 clearly illustrates that these two indices closely align between the prediction and the ground truth, resulting in a regression curve of scatter points approximating a linear function with a slope close to 1. The corresponding regression function and values are also noted in Figure 6, which indicates a high segmentation accuracy of our model. For comparison, similar regression analysis was performed on the results of other deep learning-based segmentation algorithms. Figure 7 displays the regression analysis results for DeepQSMSeg. The regression lines of AGSeg are also attached as red lines. A noticeable deviation from a slope of 1 is observed in the fitted line of DeepQSMSeg. The scattered points representing mean magnetic susceptibility values and voxel counts of different nuclei cluster noticeably above or under the line of , indicating potential over/under estimation caused by the inaccurate predicted nuclei boundary. The smaller value also yields the lower robustness of DeepQSMSeg on the test dataset.


Results on clinical dataset
The generalization ability of AGSeg was further verified through experiments conducted on the Clinical 3T dataset comprising QSM data acquired from six patients with epilepsy and the 5T dataset collected from a UIH 5T MRI platform. All models were initially trained on the healthy human brain dataset and subsequently tested on these newly-met datasets without any finetuning. The segmentation results are depicted in Figure 8 for better visualization. It is noteworthy that the clinical data exhibited a lower SNR compared to the training data, and more pronounced artifacts were present in proximity to or within the target nuclei. The distribution of 5T data also differs much compared with training data, including but not limited to the difference of max/min value, standard deviation, SNR, and artifacts severity. Despite these challenges, AGSeg produced relatively more accurate segmentation results compared to other models. In contrast, the compared models struggled to accurately predict the segmentation of low-contrast volumes and showed shortcomings in handling artifacts of circular/striking shapes. This experiment also demonstrates the good generalization and robustness of AGSeg when dealing with new data acquired by different parameters that were not employed during the training stage or from subjects with abnormal tissues.

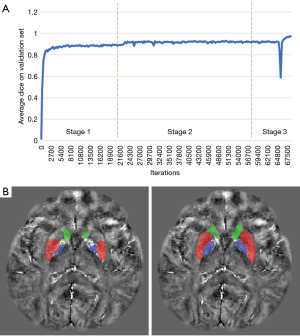
In Figure 9, the second and the third stages are both transfer learning stages. After demonstrating the effectiveness of transfer learning on the 7T Dataset in the second stage, the third stage was set to demonstrate the hypersensitivity of AGSeg towards transfer learning. A random subject from the clinical dataset was chosen and annotated to be the ground truth for transfer learning. The encoder side of AGSeg was frozen with gradients set to zero during the training process, leaving only the parameters in the decoder to be retrained. The convergence state of the overall training process can be depicted by the average DSC curve on the validation set, as visible in the third stage of Figure 9. A subject was arbitrarily chosen from the test clinical set, and the segmentation results generated by AGSeg before and after the transfer learning process were also incorporated in Figure 9. A notably more precise ROI boundary and reduced instances of false positive segmentation were achieved following a low-computation cost retraining process. This aspect holds potential significance for radiologists engaging in multi-center consultations and scientific research endeavors.
Discussion
The MIC module intends to incorporate lost magnitude information from the QSM reconstruction process into the segmentation procedure as an auxiliary information source. This auxiliary source holds the potential to empower the network in addressing artifacts present within the QSM maps. Even professional radiologists tend to extract information from various medical image modalities prior to arriving at a final diagnostic decision. The motivation behind this approach stems from the observation that different tissues or lesions might demonstrate similar features within a single modality. The strategy of multi-modality fusion has gained increasing attention from researchers due to its adeptness in enhancing accuracy and generalization ability. In forthcoming research endeavors, if feasible, additional medical image modalities can be introduced as more auxiliary information sources to comprehensively evaluate the capabilities of the MIC module.
The proposed AGM can capture inter-slice context information and exploit it through attention weights to guide the segmentation focus of the Seg-branch. How to capture the edge information more precisely plays a crucial role in generating better attention weights. It is feasible to improve training convergence and inference speed, as well as conserve computational resources by selecting a fixed and constant sample interval. However, this approach may lead to a reduction in the generalization ability of AGSeg, particularly in handling test data with varying voxel resolutions. Figure 10 provides a visualization of gradient maps of QSM (1st column) and gradient maps of five sets of target nuclei (2nd to 6th columns) obtained at different sample interval selections. It is evident that an appropriate choice of the sample interval yields reasonable feature texture in QSM gradient maps. An overly high selection of will result in a coarser edge band while an overly low selection causes the abnormal phenomenon of edge information vanishing. AGM possesses the capability to actively determine an optimal sample interval by employing latent code acquired from intrinsic attributes of input feature maps and the specific target.

For graph visualization, the distribution of is recorded when testing inputs of 128×128×128 patches, as depicted in the frequency distribution histogram in Figure 11. The histogram illustrates substantial variation in the chosen sample interval by each AGM. As shown in Figures 1,3, AGM1 and AGM4 are at the start and the end part of AGSeg, with the largest size of feature maps, they tend to extract long-interval features in some channels to get higher numerical gradients and coarser edge band. Conversely, AGM3 situated in the bottleneck part of AGSeg, operates on highly abstracted input feature maps, capturing features like texture or noise suppression. In this context, AGM3 prefers a lower sample interval to retain meaningful gradient maps without excessive loss of information. This agrees with the original design intent of selecting an appropriate sample interval based on input feature map attributes.

The segmentation accuracy has been notably enhanced through the incorporation of gradient guidance, concurrently augmenting the robustness of AGSeg against common lesions or pathological tissue. However, AGSeg’s training dataset exclusively comprises QSM data obtained from healthy human brains, thereby limiting its performance when confronted with extensive lesions like spongioblastoma or meningioma. Furthermore, the susceptibility values may exhibit substantial variation when being reconstructed through different post-process algorithmic pipelines or under disparate parameter settings. This variability can result in the failure of a properly functioning model when applied to novel data. These challenges are commonly encountered within routine clinical practice. In response to these challenges, AGSeg has been configured to demonstrate sensitivity in small data size transfer learning, as shown in Figure 9. This entails the freezing of parameters across nearly all blocks, with training solely focused on the final two residual blocks using multi-center acquired data. Such an approach expedites the convergence of AGSeg’s training process, facilitated by the inclusion of gradient guidance. Owing to dataset limitations and computation costs, AGSeg was exclusively trained on a healthy human dataset, utilizing magnitude images and QSM maps as dual-input modalities. In future endeavors, additional data from diverse modalities such as T1 or Flair could be incorporated as auxiliary inputs for AGSeg, providing supplementary information.
Up to this point, the training data for AGSeg comprises only five pairs of DGMN as the target ROI. However, the overarching concept of seeking edge priors holds potential for application in other medical image segmentation tasks, particularly when the target ROI is not exceptionally small. In our forthcoming research, we intend to extend this approach to various medical segmentation tasks involving diverse targets. The fusion mechanism of the magnitude image and QSM map, while implemented, may benefit from enhanced interpretability. In future iterations, causal learning techniques can be introduced to reveal the criterion of segmentation result, shedding light on how the multiple modalities are fused together. This may further improve our understanding of feature fusion mechanisms and offer more insights for neural network design.
Recently, ultra-large models such as ChatGPT and Segment-Anything Model (SAM) (38) have been demonstrated to be efficient in various tasks ranging from natural language processing (NLP) to CV. The impressive performance of these ultra-large models has underscored the potential for a unified model capable of addressing tasks within the realms of NLP and CV in the future. MedSAM, as a finetuned version of SAM in medical image datasets, has proven its utility in diverse medical image segmentation tasks (39). However, even the fine-tuning process requires an extremely high computation resource (e.g., 4 or more V100 GPUs for example), rendering it impractical for daily use by radiologists and most researchers. On the contrary, the whole training process of AGSeg only requires 12G of GPU memory, a capacity readily met by many contemporary PCs. Serving as an end-to-end model, AGSeg attains a comparable level of segmentation accuracy and inference speed with significantly fewer computational requirements, obviating the need for user prompts. Consequently, albeit designed for a relatively specific downstream segmentation task, the small-parameter model like AGSeg can indeed be practical in the routine applications of clinicians and researchers.
Conclusions
In this study, AGSeg is proposed, which is a MIC network for basal ganglia segmentation based on the active gradient guidance mechanism. The segmentation task is performed using a dual-branch architecture in AGSeg, which simultaneously reconstructs gradient maps to reveal inter-slice contour information and guides the overall segmentation process. To actively capture inter-layer context information, we introduce the AGM. The magnitude and susceptibility maps do not agree exactly in terms of structural consistency. To form effective information complementarity, we introduce the magnitude images as another input of AGSeg. By integrating the design of MIC module, AGSeg can take both magnitude images and QSM maps as dual inputs. The features from both information sources are selectively enhanced and fused to increase the robustness of AGSeg. A comprehensive evaluation of AGSeg was conducted on both healthy and clinical datasets, comparing it with several mainstream models. The results demonstrate that both the AGM and MIC modules can effectively enhance the accuracy and robustness of AGSeg. Furthermore, the experiments findings indicate that our proposed model outperforms existing models in terms of segmentation performance and generalization ability.
Acknowledgments
The authors thank Shanghai United Imaging Healthcare Co., Ltd. for their valuable support in acquiring data from the uMR Jupiter 5T platform.
Funding: This work was supported in part by
Footnote
Conflicts of Interest: All authors have completed the ICMJE uniform disclosure form (available at https://qims.amegroups.com/article/view/10.21037/qims-23-1858/coif). The authors have no conflicts of interest to declare.
Ethical Statement: The authors are accountable for all aspects of the work in ensuring that questions related to the accuracy or integrity of any part of the work are appropriately investigated and resolved. The study was conducted in accordance with the Declaration of Helsinki (as revised in 2013). The study was approved by Medical Ethics Committee of Xiamen University (No. EC-20230515-1006) and informed consent was taken from all subjects.
Open Access Statement: This is an Open Access article distributed in accordance with the Creative Commons Attribution-NonCommercial-NoDerivs 4.0 International License (CC BY-NC-ND 4.0), which permits the non-commercial replication and distribution of the article with the strict proviso that no changes or edits are made and the original work is properly cited (including links to both the formal publication through the relevant DOI and the license). See: https://creativecommons.org/licenses/by-nc-nd/4.0/.
References
- Kee Y, Liu Z, Zhou L, Dimov A, Cho J, de Rochefort L, Seo JK, Wang Y. Quantitative Susceptibility Mapping (QSM) Algorithms: Mathematical Rationale and Computational Implementations. IEEE Trans Biomed Eng 2017;64:2531-45. [Crossref] [PubMed]
- Chen Y, Liu S, Buch S, Hu J, Kang Y, Haacke EM. An interleaved sequence for simultaneous magnetic resonance angiography (MRA), susceptibility weighted imaging (SWI) and quantitative susceptibility mapping (QSM). Magn Reson Imaging 2018;47:1-6. [Crossref] [PubMed]
- Kim HG, Park S, Rhee HY, Lee KM, Ryu CW, Rhee SJ, Lee SY, Wang Y, Jahng GH. Quantitative susceptibility mapping to evaluate the early stage of Alzheimer's disease. Neuroimage Clin 2017;16:429-38. [Crossref] [PubMed]
- Thomas GEC, Leyland LA, Schrag AE, Lees AJ, Acosta-Cabronero J, Weil RS. Brain iron deposition is linked with cognitive severity in Parkinson's disease. J Neurol Neurosurg Psychiatry 2020;91:418-25. [Crossref] [PubMed]
- Zivadinov R, Tavazzi E, Bergsland N, Hagemeier J, Lin F, Dwyer MG, Carl E, Kolb C, Hojnacki D, Ramasamy D, Durfee J, Weinstock-Guttman B, Schweser F. Brain Iron at Quantitative MRI Is Associated with Disability in Multiple Sclerosis. Radiology 2018;289:487-96. [Crossref] [PubMed]
- Vrtovec T, Močnik D, Strojan P, Pernuš F, Ibragimov B. Auto-segmentation of organs at risk for head and neck radiotherapy planning: From atlas-based to deep learning methods. Med Phys 2020;47:e929-50. [Crossref] [PubMed]
- Magon S, Chakravarty MM, Amann M, Weier K, Naegelin Y, Andelova M, Radue EW, Stippich C, Lerch JP, Kappos L, Sprenger T. Label-fusion-segmentation and deformation-based shape analysis of deep gray matter in multiple sclerosis: the impact of thalamic subnuclei on disability. Hum Brain Mapp 2014;35:4193-203. [Crossref] [PubMed]
- Li X, Chen L, Kutten K, Ceritoglu C, Li Y, Kang N, Hsu JT, Qiao Y, Wei H, Liu C, Miller MI, Mori S, Yousem DM, van Zijl PCM, Faria AV. Multi-atlas tool for automated segmentation of brain gray matter nuclei and quantification of their magnetic susceptibility. Neuroimage 2019;191:337-49. [Crossref] [PubMed]
- Aljabar P, Heckemann RA, Hammers A, Hajnal JV, Rueckert D. Multi-atlas based segmentation of brain images: atlas selection and its effect on accuracy. Neuroimage 2009;46:726-38. [Crossref] [PubMed]
- Schipaanboord B, Boukerroui D, Peressutti D, van Soest J, Lustberg T, Dekker A, Elmpt WV, Gooding MJ. An Evaluation of Atlas Selection Methods for Atlas-Based Automatic Segmentation in Radiotherapy Treatment Planning. IEEE Trans Med Imaging 2019;38:2654-64. [Crossref] [PubMed]
- Tang H, Zhang C, Xie X. NoduleNet: Decoupled False Positive Reduction for Pulmonary Nodule Detection and Segmentation. Medical Image Computing and Computer Assisted Intervention – MICCAI 2019. Lecture Notes in Computer Science(), Springer, 2019:266–274.
- Isensee F, Jäger PF, Full PM, Vollmuth P, Maier-Hein KH. nnU-Net for Brain Tumor Segmentation. In: Crimi A, Bakas S. editors. Brainlesion: Glioma, Multiple Sclerosis, Stroke and Traumatic Brain Injuries. BrainLes 2020. Lecture Notes in Computer Science(), Springer, 2021:118-32.
- Bilic P, Christ P, Li HB, Vorontsov E, Ben-Cohen A, Kaissis G, et al. The Liver Tumor Segmentation Benchmark (LiTS). Med Image Anal 2023;84:102680. [Crossref] [PubMed]
- Jin Q, Meng Z, Pham TD, Chen Q, Wei L, Su R. DUNet: A deformable network for retinal vessel segmentation. Know-Based Syst 2019;178:149-62. [Crossref]
- Tajbakhsh N, Jeyaseelan L, Li Q, Chiang JN, Wu Z, Ding X. Embracing imperfect datasets: A review of deep learning solutions for medical image segmentation. Med Image Anal 2020;63:101693. [Crossref] [PubMed]
- Wang K, Zhang X, Zhang X, Lu Y, Huang S, Yang D. EANet: Iterative edge attention network for medical image segmentation. Pattern Recogn 2022;127:108636. [Crossref]
- Hu J, Shen L, Sun G. Squeeze-and-excitation networks. 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 2018:7132-41.
- Zhang H, Valcarcel AM, Bakshi R, Chu R, Bagnato F, Shinohara RT, Hett K, Oguz I. Multiple Sclerosis Lesion Segmentation with Tiramisu and 2.5D Stacked Slices. Med Image Comput Comput Assist Interv 2019;11766:338-46.
- Zhang J, Xie Y, Wang Y, Xia Y. Inter-Slice Context Residual Learning for 3D Medical Image Segmentation. IEEE Trans Med Imaging 2021;40:661-72. [Crossref] [PubMed]
- Liu Z, Lin Y, Cao Y, Hu H, Wei Y, Zhang Z, Lin S, Guo B. Swin transformer: Hierarchical vision transformer using shifted windows. Proceedings of the IEEE/CVF International Conference on Computer Vision (ICCV), 2021:10012-22.
- Wang W, Chen C, Ding M, Yu H, Zha S, Li J. TransBTS: Multimodal Brain Tumor Segmentation Using Transformer. In: de Bruijne M, Cattin PC, Cotin S, Padoy N, Speidel S, Zheng Y, Essert C, editors. Medical Image Computing and Computer Assisted Intervention – MICCAI 2021. Lecture Notes in Computer Science(), vol 12901. Springer, 2021:109-19.
- Raj SS, Malu G, Sherly E, Vinod Chandra SS, editors. A deep approach to quantify iron accumulation in the DGM structures of the brain in degenerative Parkinsonian disorders using automated segmentation algorithm. 2019 International Conference on Advances in Computing, Communication and Control (ICAC3); 2019.
- Milletari F, Navab N, Ahmadi SA. V-Net: Fully Convolutional Neural Networks for Volumetric Medical Image Segmentation. 2016 Fourth International Conference on 3D Vision (3DV), Stanford, CA, USA, 2016:565-71.
- Solomon O, Palnitkar T, Patriat R, Braun H, Aman J, Park MC, Vitek J, Sapiro G, Harel N. Deep-learning based fully automatic segmentation of the globus pallidus interna and externa using ultra-high 7 Tesla MRI. Hum Brain Mapp 2021;42:2862-79. [Crossref] [PubMed]
- Guan Y, Guan X, Xu J, Wei H, Xu X, Zhang Y. DeepQSMSeg: A Deep Learning-based Sub-cortical Nucleus Segmentation Tool for Quantitative Susceptibility Mapping. Annu Int Conf IEEE Eng Med Biol Soc 2021;2021:3676-9. [Crossref] [PubMed]
- Wang Y, He N, Zhang C, Zhang Y, Wang C, Huang P, Jin Z, Li Y, Cheng Z, Liu Y, Wang X, Chen C, Cheng J, Liu F, Haacke EM, Chen S, Yang G, Yan F. An automatic interpretable deep learning pipeline for accurate Parkinson's disease diagnosis using quantitative susceptibility mapping and T1-weighted images. Hum Brain Mapp 2023;44:4426-38. [Crossref] [PubMed]
- Dadarwal R, Ortiz-Rios M, Boretius S. Fusion of quantitative susceptibility maps and T1-weighted images improve brain tissue contrast in primates. Neuroimage 2022;264:119730. [Crossref] [PubMed]
- Wei H, Zhang C, Wang T, He N, Li D, Zhang Y, Liu C, Yan F, Sun B. Precise targeting of the globus pallidus internus with quantitative susceptibility mapping for deep brain stimulation surgery. J Neurosurg 2019;133:1605-11. [Crossref] [PubMed]
- Wu Y, He K. Group normalization. Proceedings of the European Conference on Computer Vision (ECCV), 2018:3-19.
- He K, Zhang X, Ren S, Sun J. Deep residual learning for image recognition. 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 2016:770-8.
- Shi Y, Feng R, Li Z, Zhuang J, Zhang Y, Wei H. Towards in vivo ground truth susceptibility for single-orientation deep learning QSM: A multi-orientation gradient-echo MRI dataset. Neuroimage 2022;261:119522. [Crossref] [PubMed]
- Li W, Wu B, Liu C. Quantitative susceptibility mapping of human brain reflects spatial variation in tissue composition. Neuroimage 2011;55:1645-56. [Crossref] [PubMed]
- Fang J, Bao L, Li X, van Zijl PCM, Chen Z. Background field removal for susceptibility mapping of human brain with large susceptibility variations. Magn Reson Med 2019;81:2025-37. [Crossref] [PubMed]
- Bao L, Li X, Cai C, Chen Z, van Zijl PC. Quantitative Susceptibility Mapping Using Structural Feature Based Collaborative Reconstruction (SFCR) in the Human Brain. IEEE Trans Med Imaging 2016;35:2040-50. [Crossref] [PubMed]
- Chai C, Wu M, Wang H, Cheng Y, Zhang S, Zhang K, Shen W, Liu Z, Xia S. CAU-Net: A Deep Learning Method for Deep Gray Matter Nuclei Segmentation. Front Neurosci 2022;16:918623. [Crossref] [PubMed]
- Mori S, Wu D, Ceritoglu C, Li Y, Kolasny A, Vaillant MA, Faria AV, Oishi K, Miller MI. MRICloud: delivering high-throughput MRI neuroinformatics as cloud-based software as a service. Comput Sci Eng 2016;18:21-35. [Crossref]
- Kang B, Xie S, Rohrbach M, Yan Z, Gordo A, Feng J, Kalantidis Y. Decoupling representation and classifier for long-tailed recognition. IEEE Trans Pattern Anal Mach Intell 2019;45:4274-88.
- Kirillov A, Mintun E, Ravi N, Mao H, Rolland C, Gustafson L, Xiao T, Whitehead S, Berg AC, Lo WY, Dollar P, Girshick R. Segment anything. Proceedings of the IEEE/CVF International Conference on Computer Vision (ICCV), 2023:4015-26.
- Ma J, He Y, Li F, Han L, You C, Wang B. Segment anything in medical images. Nat Commun 2024;15:654. [Crossref] [PubMed]


