
Accelerated four-dimensional free-breathing whole-liver water-fat magnetic resonance imaging with deep dictionary learning and chemical shift modeling
Introduction
Fat-suppressed magnetic resonance imaging (MRI) improves the diagnostic value of MRI by offering better identification of underlying lesions such as inflammation, edema, and tumors (1-4). On the other hand, fat quantification MRI has been a promising tool for the noninvasive assessment of several liver diseases, such as the detection and staging of liver fibrosis, quantification of liver steatosis, and liver fat measurement of nonalcoholic fatty liver disease (NAFLD) (5,6). Proton-density fat fraction (PDFF) has been a known biomarker for the assessment of liver steatosis (5). Multi-echo chemical shift encoded (CSE) MRI has been widely used for fat quantification and fat suppression in clinical liver examinations (7-10).
Clinical liver water-fat imaging, with either three-dimensional (3D) or multi-slice two-dimensional (2D) acquisitions, is routinely acquired in 12 to 34 seconds during a breath-hold (9,10). The relatively short acquisition time in a breath-hold limits the spatial resolution and spatial coverage (9,10). The acquisitions would require a scan time beyond a single breath-hold for further improvement in the spatial resolution, and/or spatial coverage. Multiple breath-holds imaging could result in slice mis-registration in 2D acquisitions and motion artifacts in 3D acquisitions. For children and patients with lung disorders, breath-holding presents additional challenge using conventional breath-hold imaging (11,12). Free-breathing motion-resolved imaging can be used to overcome these limitations, and is more desirable for patient comfort in clinical settings (13-16). Moreover, free-breathing water-fat imaging is of specific value in certain applications, such as the attenuation correction for positron emission tomography-MR (PET-MR) imaging (17) and target area outlining for MR image-guided interventional therapy (18). The acquisition for four-dimensional (4D) free-breathing water-fat imaging of whole-liver, however, could take up to several minutes (14,15,19-21). Using conventional respiratory gating approaches would further extend the total examination time (22). Therefore, acceleration of 4D free-breathing whole-liver water-fat imaging is highly desirable.
Several algorithms have been proposed to accelerate the acquisition and reduce the aliasing artifacts in the free-breathing water-fat imaging (13-15,23,24). A compressed sensing (CS)-based water-fat separation (CS-WF) algorithm combined with radial sampling has been proposed for 3D free-breathing abdominal water-fat imaging by quantifying fat and water directly from the k-space data (13,14). By introducing a respiratory motion dimension in the reconstruction process, the CS-WF algorithm effectively reduces motion-induced blurring artifacts. Another CS‐based reconstruction algorithm, which jointly estimates dynamic water, fat, and B0 inhomogeneity maps as well as a set of coil sensitivity maps, is capable of reconstructing images to accelerate 2D liver water-fat imaging (23). These CS-based algorithms achieved an acceleration factor from 3 to 5 in 3D multi-echo water-fat imaging (13-15). These CS-based iterative reconstruction algorithms, however, require empirical optimizations of the regularization parameters to improve the image quality and are computationally expensive.
Dictionary learning and deep learning (DL) have shown good performance in accelerating MRI and multi-contrast MRI (25-41). The coupled dictionary learning based multi-contrast MRI reconstruction (CDLMRI) algorithm exploits the dependency correlation between different contrasts to reconstruct the images from undersampled data by iteratively updating among coupled dictionary learning, coupled sparse denoising, and data consistency (DC) (25). In the DL-based magnetic resonance fingerprinting algorithm, a convolutional neural network is used to replace dictionary matching in the conventional magnetic resonance fingerprinting, and operates patch-wise to reconstruct the parametric maps (26). The parallel non-Cartesian convolutional recurrent neural networks (PNCRNN) algorithm learns the spatial-temporal correlations with the convolution recurrent neural networks and provides the state-of-the-art performance for non-Cartesian dynamic MRI reconstruction (30). These methods exploit prior spatial-temporal information of the data by combining the advantages of DL and dictionary learning, and show promising results in the accelerated free-breathing MRI. However, the method for accelerating free-breathing water-fat imaging by combining the DL methods with dictionary learning to exploit the prior information from the free-breathing multi-echo data in the spatial, respiratory motion, and echo dimensions has not been studied.
Contributions, innovations, and the organization of the paper
In this work, we proposed a high-dimensional model-guided deep dictionary learning (HMDDL) algorithm to accelerate the 4D free-breathing water-fat imaging for whole-liver. Two major contributions have been made in this study. First, a high-dimensional dictionary learning neural network (hdDLNN) has been proposed to suppress the undersampling artifacts in multi-echo images. The hdDLNN is an end-to-end trainable neural network, and utilizes the prior information from the dynamic multi-echo data in spatial, respiratory motion, and echo dimensions. By using the hdDLNN, the HMDDL could learn features among different echo images, thus exploiting the data sparsity in higher dimensions and achieving higher acceleration rate in 4D multi-echo imaging. Second, a high-dimensional MG reconstruction has been proposed to improve the qualities of 4D free-breathing water-fat separation and PDFF/ quantification. Free-breathing water-fat imaging is of specific value in certain applications (17,18). The MG reconstruction (36) is extended to solve an additional respiratory motion dimension for 4D water-fat imaging by exploring water and fat image features along spatial and respiratory motion dimensions. The proposed HMDDL was compared with the CS-WF (13,14) and the PNCRNN on the prospectively undersampled data at acceleration rates (R) of 6, 8, and 10. The water-fat chemical shift model in the HMDDL was also used in the PNCRNN for water-fat reconstruction. In the spirit of reproducible research, codes for HMDDL will be available at https://github.com/hmddl.
The rest of the paper is organized as follows. In the ‘Theory’ section, the reconstruction problem for free-breathing motion-resolved water-fat imaging as well as the HMDDL algorithm are described. In the ‘Methods’ section, the in-vivo data acquisition, the implementation details, the retrospectively and prospectively undersampling schemes, and the parameter optimization for network training are described. In the ‘Results’ section, the reconstructed water/fat images and PDFF/ maps from the representative subjects are demonstrated in figures. The statistical analyses are summarized in tables. In the ‘Discussion’ section, the innovations, advantages, and the limitations of the HMDDL are presented. The differences between HMDDL and other relevant algorithms are discussed. Finally, the conclusions are drawn in the ‘Conclusions’ section.
Theory
Problem statements
In the accelerated free-breathing motion-resolved Necho-echo water-fat imaging acquisition, the k-space data acquired at echo time are represented by the chemical shift model (21).
where is the undersampled Fourier operator based on the sampling pattern for the l-th echo, represents the undersampled multi-echo k-space data binned into Nbin different motion states, and each motion state is sampled by radial trajectory consist of Nproj spokes with Nread points in each spoke. , , and are the 2D complex-valued multi-echo images, water images, and fat images in different motion states, respectively. The relative amplitude and the chemical-shift frequency of the c-th fat spectral speak are and , respectively. C is the total number of fat spectral peaks, is the field map, and is the inverse of . Grouping and together in a column vector , the model can be written in a concise form , where A is the nonlinear operator mapping the water image and fat image to the k-space domain. The objective of the water-fat separation reconstruction is to obtain by solving .
HMDDL
In the HMDDL algorithm, the motion-resolved water-fat reconstruction task is separated into two sub-tasks. In the first sub-task, the objective is to obtain the motion-resolved multi-echo images x from the undersampled k-space data y. The optimization problem can be rewritten as:
where is the undersampled dynamic multi-echo k-space data, , is the desired dynamic multi-echo images, . is the total number of patches, is the total pixel number of the multi-echo image series, denotes the norm, and p can be selected from 0 to 1. In this paper, p value was selected as 1 to enforce the sparsity constraint on . is the operator that extracts the i-th patch from the real and imaginary parts of the complex-valued image , and are the sparse representation vectors corresponding to . is the patch size that can be expressed as , where , , and represent the patch sizes along spatial, respiratory motion, and echo dimensions, respectively. is the dictionary to be learned, and is the dictionary size. To handle the complex-valued data, we combined the real and imaginary sparse representation vectors into one vector, and used a larger dictionary to represent the transformation. Thus, the Eq. [3] can be transformed as:
where , . and represent the real and imaginary parts of , respectively. and are two sets of the sparse representation vectors corresponding to and .
The hdDLNN algorithm was proposed to solve the problem in Eq. [4]. The hdDLNN contains several iterations of de-aliasing network (DN) blocks and DC blocks. The DN block is used for the dictionary sparse coding, and the image de-aliasing. The DC block is used to ensure the data fidelity with the acquired k-space data. In the DN blocks, the patches are first extracted from the input multi-echo images along the spatial-motion-echo dimensions, then processed by the patch de-aliasing module (PDM) (41), and finally averaged into the reconstructed multi-echo images. In the PDM for the m-th iteration, the problem to derive the optimal sparse code from the patch under the trained dictionary can be formulated as:
where is the regularization coefficient determined by a coefficient estimation module (CEM) with the weights of (41). The dictionary and the weights of CEM are set as the learnable parameters. The optimal sparse code is calculated from the , the trained and the trained using the iterative soft thresholding algorithm (ISTA) (42). The output of DN block can be calculated as the weighted average (42,43). In the DC blocks, the is updated by using the gradient descent algorithm (43).
After getting the x in the first sub-task, the field maps, maps, as well as the water images and fat images can be obtained by using the graph-cut algorithm (44). The field maps and maps are used to generate the operator A, and the water images and fat images are used as the initial guesses of for the second sub-task.
In the second sub-task, the objective is to obtain the motion-resolved water/fat images from the undersampled k-space data y. The reconstruction problem can be written as:
where y are the undersampled k-space data with dimensions of , is a trainable regularization weight, is de-aliased generated by the CNN, and is a set of learned parameters. A high-dimensional MG reconstruction is proposed to solve this problem by exploring water and fat image features along both spatial and respiratory motion dimensions. The proposed MG reconstruction contains several iterations of DL blocks and model-guided (MG) blocks. The DL block is used to learn the mapping relationship between the reconstructed water-fat images and the ground-truth, and the MG block is used to guide the reconstruction by using the multi-peak fat model in Eq. [2]. The number of dimensions of and are . In the n-th DL block, the output can be expressed as:
In the n-th MG block, the optimization problem in Eq. [7] can be written as:
where is the Jacobian of at , is a trainable regularization weight. The iteratively regularized Gauss-Newton (IRGN) algorithm (36) was used to solve the problem in Eq. [8]:
The overall architecture of the HMDDL algorithm is shown in Figure 1A. The HMDDL mainly consists of the hdDLNN block and the MG reconstruction block, the detail structures of which are shown in Figure 1B and Figure S1, respectively. The implementation details of the HMDDL algorithm are summarized in Table 1.

Table 1
| Require: , , , |
| Input: , |
| Output: |
| 1. Estimating the sensitivity maps using ESPIRiT |
| 2. Setting |
| 3. For to do |
| 4. For to do |
| 5. |
| 6. |
| 7. |
| 8. End for |
| 9. |
| 10. |
| 11. End for |
| 12. Estimating the field map , map, and using graph-cut |
| 13. For to N do |
| 14. |
| 15. |
| 16. Updating using |
| 17. End for |
| 18. Return |
HMDDL, high-dimensional model-guided deep dictionary learning; CEM, coefficient estimation module; ISTA, iterative soft thresholding algorithm; IRGN, iteratively regularized Gauss-Newton algorithm.
Methods
Data acquisition
The 3D blipped golden-angle stack-of-stars multi-gradient-echo pulse sequence was designed for the prospective acquisition of the multi-channel data (36). The diagram of the sequence was shown in Figure S2. Sixteen healthy subjects (aged 30±6 years, body mass index 21.6±2.0 kg/m2) and 17 subjects with clinically diagnosed NAFLD (aged 32±9 years, body mass index 26.9±2.5 kg/m2) were scanned on a 3.0 T uMR790 scanner (Shanghai United Imaging Healthcare Co., Ltd., Shanghai, China). All patients were recruited from the faculty and student population of Shanghai Jiao Tong University. The study was conducted in accordance with the Declaration of Helsinki (as revised in 2013). The study was evaluated and approved by the Ethics Committee of the School of Biomedical Engineering, Shanghai Jiao Tong University. Written informed consent was obtained from the participants before each scan. A 12-channel abdominal coil was used for whole-liver signal collection. The parameters for free-breathing radial samplings were as follows: repetition time (TR) =5.17 ms, echo time (TE) =1.25/2.50/3.75 ms, flip angle =5°, bandwidth =1,200 Hz/pixel, slice thickness =5 mm, readouts =192, FOV =330×330 mm2, number of slices =40, spatial resolution =1.72×1.72×5 mm3, number of spokes per slice-encode =3,000, total scan time =10 min 21 s. A six-peak fat model was used with the following peak frequencies: −3.80, −3.40, −2.60, −1.94, −0.39, and 0.59 ppm (21). The relative amplitudes of the spectral peaks were: 0.087, 0.694, 0.128, 0.004, 0.039, and 0.048, respectively.
Respiratory motion detection and data sorting
The respiratory motion was extracted from the dataset using the first echo. The flow chart of the respiratory motion extraction is shown in Figure S3. The projection profiles were computed by performing 1D Fourier transform of the center points along slice direction. Respiratory motion detection was then performed using principal component analysis (PCA). The principal component with highest peak in the frequency range of 0.1–0.5 Hz was selected to represent the respiratory motion. The k-space raw data were then sorted into different bins according to the extracted motion (22), as shown in the Figure 2A,2B. The flow chart of the k-space data sorting strategy was shown in Figure S4.
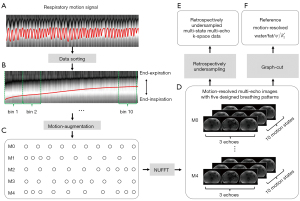
Motion augmentation
In order to improve the robustness of the network to different breathing and sampling patterns, five different breathing patterns were designed for motion-augmentation (30,41). The designed breathing patterns were shown in Figure 2C. M0 indicates the uniform breathing pattern; M1 indicates slow in the start but fast at the end of expiration; M2 indicates fast in the start but slow at the end of expiration; M3 indicates fast in the start and end but slow in the middle of expiration; M4 indicates slow in the start and end but fast in the middle of expiration. The original dynamic images were upsampled in the temporal dimension using interpolation, and then resampled according to the preset patterns to obtain motion-augmented ground truth data.
Retrospective undersampling scheme for training and validation data
The training and validation data of HMDDL were generated using the retrospectively acquired multi-channel radial data. In the fully sampling experiments, the total scan time for the golden-angle radial sampling was 10 min 21 s, and the total number of spokes per slice-encode was 3,000. After sorting the data into 10 respiratory motion states, the number of spokes per slice-encode at each state was 300, which satisfies the Nyquist sampling theorem. The flow chart of the retrospectively undersampled data generation was shown in Figure 2. First, the full-sampled multi-echo k-space raw data were sorted into 10 motion states after the respiratory motion extraction. Secondly, motion-augmentation was performed by using five designed breathing patterns. Thirdly, the full-sampled motion-resolved multi-echo images were reconstructed by using the NUFFT. Fourthly, the reference water/fat images were obtained from the full-sampled motion-resolved multi-echo images by using the graph-cut algorithm. Finally, the retrospectively undersampled data were generated by using the NUFFT on the full-sampled motion-resolved multi-echo images with designed undersampling trajectories. In this study, the sensitivity maps were estimated with the ESPIRiT algorithm (45).
Prospective undersampling scheme for test data
The performance of HMDDL was tested on the prospectively acquired multi-channel radial data. The first 500, 380, and 300 spokes per slice-encode of the raw data were used to reconstruct the motion-resolved water and fat images at the acceleration rates of R=6, 8, and 10, corresponding to the scan time of 1 min 44 s, 1 min 18 s, and 1 min 02 s, respectively. The multi-echo k-space data were undersampled along spatial, temporal, and echo dimension, as shown in Figure S5.
Network training and testing
Data acquired from ten healthy subjects and ten NAFLD subjects were selected for training. Data acquired from one healthy subject and two NAFLD subjects were selected for validation. Data acquired from five healthy subjects and five NAFLD subjects were selected for testing. For each subject, the middle 30 slices were selected for the reconstruction to avoid the slab profile artifacts. The number of slices used for the network training, validation and test was 600, 90, and 300, respectively. The training set and validation set were randomly shuffled before training.
In the HMDDL algorithm, the hdDLNN and MG reconstruction were trained separately for different sub-tasks. The parameters of hdDLNN were used as follows: patch size was selected as , , and , where and denote the size of the x-axis and y-axis directions in the spatial dimensions, respectively, and denotes the size in respiratory motion and echo dimensions. The dictionary size was 128. The number of iterations was 8. The loss function for training was defined as the sum of the mean squared error (MSE) of the dynamic multi-echo images. The Adam optimizer was used to train the networks with the following parameters: initial learning rate =0.001, , . The number of epochs was 100. For MG reconstruction, the loss function of training was defined as , where and are the sum of the MSE of the water images and fat images, respectively. The Adam optimizer was used to train the networks with the following parameters: initial learning rate =0.001, , , . The number of epochs was 150. The other parameters were , , and , where , , and are the number of filters, the number of outer iterations, and the number of inner iterations, respectively (36). In the PNCRNN algorithm, the network parameters were set as described in Zhang’s work (30).
Data analysis
The water/fat images and B0/ maps obtained from the fully-sampled data by using the graph-cut algorithm were used as the references. The comparison among HMDDL, PNCRNN, and CS-WF was performed in this study using the following metrics: peak signal-to-noise ratio (PSNR), structure similarity (SSIM), and root mean squared error (RMSE). The PSNR/SSIM values were calculated as the mean PSNR/SSIM for water images and fat images of all slices and motion states. Bland-Altman plots were used to statistically compare the water images, fat images, PDFF maps, and maps obtained by different algorithms. A paired t-test was used to identify the significant difference of PDFF/ measured with CS-WF/PNCRNN/HMDDL against references. A P value less than 0.05 was considered as a significant difference. The PDFF map was calculated as . For each subject, eight regions of interest (ROIs) were manually selected in the liver segments II, III, IVa, IVb, V, VI, VII, and VIII for the estimation of the average PDFF of the liver for each subject, where each ROI was 10 pixels by 10 pixels. These ROIs were also used for the PDFF and statistical analyses. The ROIs were drawn on the reference images while avoiding large vessels. The CS-WF, PNCRNN, and HMDDL were implemented by using MATLAB R2019b (MathWorks, Natick, MA, USA) and PyTorch, respectively. The computation was performed on a Linux server equipped with two Intel Xeon Platinum 8260 CPUs, 1024 GB RAM, and an NVIDIA A100 GPU.
Results
Table 2 summarizes the average PDFF and the range of values of the liver for each subject in the training and validation, and test sets. Figure 3 and Figure 4 show the water images, fat images, PDFF maps, and maps at the end-expiratory state reconstructed by using CS-WF, PNCRNN, and HMDDL at R=10 on a healthy subject and a NAFLD subject, respectively. The PSNR and SSIM values are listed below the corresponding water and fat images. The PDFF and values in the ROIs are calculated as the mean ± standard deviations, and are listed below the corresponding PDFF and maps. The artifacts in CS-WF and PNCRNN are reduced in HMDDL by visual inspection. In comparison with the CS-WF and PNCRNN, the texture details of the water images are improved by using HMDDL.
Table 2
| Sets | Healthy | NAFLD | |||||
|---|---|---|---|---|---|---|---|
| Subject, No. | PDFF (%) | R2* range (s−1) | Subject, No. | PDFF (%) | R2* range (s−1) | ||
| Training and validation sets | 1 | 2.71±1.76 | 24–64 | 12 | 5.03±1.13 | 30–86 | |
| 2 | 2.92±1.67 | 26–76 | 13 | 6.25±1.03 | 18–96 | ||
| 3 | 3.20±1.09 | 38–86 | 14 | 7.14±1.47 | 36–110 | ||
| 4 | 3.37±1.12 | 14–88 | 15 | 7.82±1.30 | 12–118 | ||
| 5 | 3.51±1.22 | 34–86 | 16 | 8.68±1.73 | 32–104 | ||
| 6 | 3.72±1.40 | 24–70 | 17 | 12.35±2.67 | 26–90 | ||
| 7 | 3.89±1.14 | 26–96 | 18 | 15.27±1.66 | 18–94 | ||
| 8 | 3.92±1.38 | 32–94 | 19 | 16.50±2.32 | 84–168 | ||
| 9 | 3.97±1.56 | 34–68 | 20 | 17.47±2.16 | 72–198 | ||
| 10 | 4.03±1.13 | 30–86 | 21 | 22.81±1.98 | 34–158 | ||
| 11 | 4.27±1.56 | 34–68 | 22 | 34.73±2.63 | 36–110 | ||
| 23 | 38.80±3.21 | 84–202 | |||||
| Test set | 24 | 2.62±1.23 | 54–90 | 29 | 6.85±1.61 | 16–98 | |
| 25 | 3.29±0.87 | 60–96 | 30 | 14.20±2.38 | 26–102 | ||
| 26 | 3.33±0.84 | 24–80 | 31 | 20.96±2.34 | 16–136 | ||
| 27 | 3.69±0.89 | 14–62 | 32 | 28.41±3.24 | 36–132 | ||
| 28 | 4.13±0.72 | 28–96 | 33 | 36.86±2.53 | 38–134 | ||
The PDFF values are presented as mean ± standard deviations. PDFF, proton-density fat fraction; NAFLD, nonalcoholic fatty liver disease.

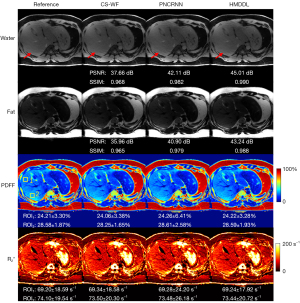
Figure 5 and Figure 6 show the Bland-Altman plots of PDFF maps and maps at R=10 for five test healthy subjects and five test NAFLD subjects, respectively. In comparison with the CS-WF and PNCRNN, the HMDDL provides smaller deviations for PDFF maps and maps.


Figure 7 and Figure 8 show the water/fat images, quantitative maps, and the corresponding errors at the end-expiratory state obtained by using CS-WF, PNCRNN, and HMDDL at R=10 on a healthy subject and a NAFLD subject, respectively. In comparison with the CS-WF, the HMDDL provides smaller errors in water images, fat images, and quantitative maps.


Figure 9 shows the quantitative results of PSNR and SSIM among CS-WF, PNCRNN, and HMDDL at R=6, 8, and 10 on all test subjects. In comparison with the CS-WF, the HMDDL improved the mean PSNR by 7.46, 9.22, and 9.93 dB at R=6, 8, and 10, respectively. In comparison with the PNCRNN, the HMDDL improved the mean PSNR by 2.62, 1.98, and 2.20 dB at R=6, 8, and 10, respectively. The quantitative results of PSNR, SSIM, and RMSE for CS-WF, PNCRNN, and HMDDL at R=10 on five test healthy subjects and five test NAFLD subjects were summarized in the Table 3. The paired t-test results for PDFF and for CS-WF, PNCRNN, and HMDDL at R=10 on five test healthy subjects and five test NAFLD subjects were summarized in the Table 4. The statistical analyses results at R=6 and 8 on all test subjects were summarized in the Tables S1-S4. The HMDDL provided higher PSNR values, higher SSIM values, and smaller RMSE values, compared with the CS-WF and the PNCRNN. The paired t-test showed that there was no significant difference between HMDDL and references for PDFF/ measurement at R up to 10. The reconstruction time of HMDDL for one slice is less than 0.4 seconds, which was two orders of magnitude less than that of CS-WF.
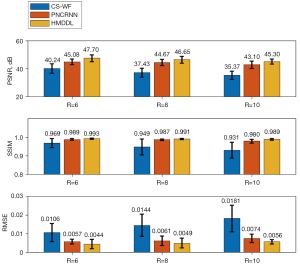
Table 3
| Metrics | Healthy | NAFLD | |||||
|---|---|---|---|---|---|---|---|
| CS-WF | PNCRNN | HMDDL | CS-WF | PNCRNN | HMDDL | ||
| PSNR (dB) | 34.94±3.18 | 42.67±2.74 | 44.98±2.00 | 35.80±2.68 | 43.43±1.59 | 45.63±1.72 | |
| SSIM | 0.920±0.047 | 0.979±0.012 | 0.989±0.004 | 0.942±0.034 | 0.981±0.008 | 0.989±0.004 | |
| RMSE | 0.0192±0.0080 | 0.0077±0.0025 | 0.0058±0.0013 | 0.0171±0.0059 | 0.0071±0.0020 | 0.0053±0.0010 | |
The PSNR, SSIM, and RMSE values are presented as mean ± standard deviations. CS-WF, compressed sensing-based water-fat separation; PNCRNN, parallel non-Cartesian convolutional recurrent neural networks; HMDDL, high-dimensional model-guided deep dictionary learning; NAFLD, nonalcoholic fatty liver disease; PSNR, peak signal-to-noise ratio; SSIM, structure similarity; RMSE, root mean squared error.
Table 4
| Metrics | Healthy | NAFLD | |||||
|---|---|---|---|---|---|---|---|
| CS-WF | PNCRNN | HMDDL | CS-WF | PNCRNN | HMDDL | ||
| Paired t-test for PDFF | 0.0021 | 0.8218† | 0.8775† | 0.8988† | 0.9756† | 0.9993† | |
| Paired t-test for R2* | 0.1937† | 0.8612† | 0.9819† | 0.8226† | 0.8224† | 0.9793† | |
†, the paired t-tests which do not reject the null hypothesis, indicating that there is no significant difference between the measurements and the reference values. CS-WF, compressed sensing-based water-fat separation; PNCRNN, parallel non-Cartesian convolutional recurrent neural networks; HMDDL, high-dimensional model-guided deep dictionary learning; NAFLD, nonalcoholic fatty liver disease; PDFF, proton-density fat fraction.
Discussion
A high-dimensional MG deep dictionary learning algorithm is proposed to accelerate free-breathing motion-resolved water-fat imaging. The proposed HMDDL combines the powers of deep dictionary learning and MG reconstruction by jointly using the hdDLNN and multi-peak fat model. This was the first time that deep dictionary learning in combination with MG reconstruction has been used to accelerate multi-echo water-fat imaging. The in-vivo experiments demonstrated that the proposed HMDDL could provide robust dynamic water-fat separation with high acceleration rate for every slice and motion state, in terms of both quantitative metrics and visualization results.
The HMDDL was mainly composed of hdDLNN and high-dimensional MG reconstruction. The hdDLNN utilized the end-to-end trainable neural network to learn the spatial-motion-echo prior information from the dynamic multi-echo data. The patches were extracted from the dynamic multi-echo images along spatial, temporal, and echo dimensions. These patches captured local variations and textures of the dynamic multi-echo images, and provided a better representation of specific details, edges, and textures in different dimensions than the overall view of the image. Due to the information redundancy of the image in different dimensions, the representation coefficients of these patches under a certain dictionary matrix were highly sparse compared to the conventional sparse transform of the whole image. Therefore, the artifacts in the initial input patches were removed by updating the dictionary and the sparse code. In combination with graph-cut, the hdDLNN achieved high qualities of the field maps, maps, water images, and fat images from the highly-undersampled k-space data. The MG reconstruction utilized the end-to-end trainable neural network to learn the mapping relationship between the undersampled dynamic water-fat images and reference dynamic water-fat images by exploring the features of images along both spatial and respiratory motion dimensions, which achieved further improvements of the image quality in the accelerated free-breathing water-fat imaging.
There are several advantages of the HMDDL algorithm. First, the HMDDL could shorten the scan time without much degradation of image quality in comparison with fully sampling acquisition. The HMDDL enables the acquisition for 4D free-breathing water-fat imaging within approximately 1 min which corresponds to the acceleration rate of 10. Fast free-breathing acquisition is desirable and useful for those patients with breath-hold difficulties such as serious-condition, pediatric, sedated, or elderly patients (11,12). Second, the HMDDL enables a motion-resolved 3D coverage of whole-liver with a spatial resolution of 1.72×1.72×5 mm3 and 10 respiratory motion states, which has the potential to capture the spatial distribution of fibrosis stages, PDFF, between different parts of the liver and can be used for disease differentiation. Moreover, high-quality dynamic water and fat images can be used to improve the accuracy of attenuation correction in PET-MR imaging (17), as well as for target area outlining for MR image-guided interventions (18). Third, the reconstruction time of HMDDL is two orders of magnitude less than that of conventional CS-based algorithms. In this study, the reconstruction time of HMDDL is less than 0.4 seconds for one slice, compared to approximately 60 seconds of the CS-based algorithms.
In this study, the HMDDL algorithm was compared with a CNN-based PNCRNN algorithm. The comparison results between the HMDDL and PNCRNN can be explained from a DL perspective to understand the underlying working mechanism of the proposed HMDDL algorithm. As shown in Figure S6, we discovered that the primary components of HMDDL can be represented using convolution and transpose convolution, which meant that fundamentally, the HMDDL could also be represented as a structure of convolutional neural networks. Compared with PNCRNN, the structure of HMDDL is derived from the dictionary learning theory, which endows greater interpretability to the intermediate variables compared to typical feature maps in conventional CNNs. Furthermore, the connections between convolutional layers follow specific patterns. The soft-thresholding operator acts as an activation function between layers, while the cascade of ISTA steps forms a skip-connection structure. This connectivity resembles ResNet’s architecture, effectively addressing degradation issues and yielding greater improvements as the network depth increases (46). While residual connections exist in CNN methods, the residuality within our proposed method is denser. Generally, these features may contribute to the superiority of the proposed HMDDL algorithm, which showed the importance of transferring the domain knowledge into the networks. Given the inherent connections between our proposed approach and CNN-based networks, we believe that CNN-based algorithms are also expected to improve performance by better utilizing domain knowledge.
Recently, several algorithms have been proposed for rapid fat and quantification using stack-of-stars MRI, such as model-guided deep learning for water-fat separation (MGDL-WF) (36), an uncertainty-aware physics-driven DL network (UP-Net) (47) and multitasking multi-echo MRI (MT-ME) (15). The MGDL-WF utilizes a U-net in combination with MG reconstruction to accelerate 3D static water-fat imaging. The proposed HMDDL extends the MG reconstruction to solve an additional respiratory motion dimension, achieving acceleration of 4D free-breathing dynamic water-fat imaging. The UP-Net utilizes generative adversarial networks (GAN) and U-net to suppress the radial undersampling artifacts, and achieves an acceleration rate around 3 for free-breathing water-fat imaging. Adding k-space DC layers might be helpful for UP-Net to address higher undersampling factors (47). Instead of using GAN, the proposed HMDDL uses a high-dimensional dictionary learning neural network to reduce the artifacts, and achieved an acceleration rate up to 10. Moreover, DC layers were added in the proposed HMDDL to ensure that the reconstructed water images and fat images were consistent with the k-space measurements. Compared with the MT-ME algorithm, the main difference of the proposed HMDDL is the use of DL network. The MT-ME algorithm utilizes traditional low-rank sparsity constraints to enable simultaneous multitasking imaging, and achieves an acceleration rate around 3 in free-breathing whole-liver multiparametric mapping. The proposed HMDDL learns the sparse features in the data by using deep neural networks, and achieves a higher acceleration rate. In addition, the traditional iteration-based reconstruction is time-consuming, which is less suitable for some applications that require real-time imaging.
Accurate field map is essential for the success of water-fat separation (48,49). In this study, the field maps and maps were reconstructed by using the hdDLNN in combination with graph-cut. The hdDLNN utilized the prior information in spatial-motion-echo dimensions, and achieved artifact-reduced dynamic multi-echo images from the highly undersampled k-space data. The graph-cut algorithm was then used to reconstruct the field maps and maps.
In the HMDDL algorithm, the qualities of dynamic water and fat images were further improved by using the high-dimensional MG reconstruction. The combination of hdDLNN and graph-cut is a straightforward approach to accelerate free-breathing water-fat imaging, in which hdDLNN and graph-cut were used for the artifact reduction and water-fat separation, respectively. One advantage of this combination is that hdDLNN might be more flexible to the data acquired with other imaging protocols. To further improve the image qualities, we used a multi-peak fat model (21) to guide the water-fat separation reconstruction by taking the advantage of the priori information of the multi-echo CSE model.
There are several limitations in this study. First, the optimization of the field map was not considered in the HMDDL. Incorporating the field map into the loss function generally requires a constraint on the smoothness of the field map. However, there are challenges in using spatial smoothness constraints in a DL algorithm, such as adding the Markov random field prior (49), adjusting the regularization parameters (13), etc. Secondly, HMDDL only utilizes the prior information in 2D spatial dimensions due to the limited GPU memory, and further utilization of the prior information in slice dimension can be considered in the future. Thirdly, the data were acquired from 16 healthy subjects and 17 NAFLD subjects, with relatively small samples of different steatosis stages and different breathing patterns. Validation of the proposed algorithm to more clinical cases with more different steatosis stages and breathing patterns is necessary. Furthermore, the k-space data were sorted into different motion states solely according to the extracted respiratory motion along the slice dimension. Respiratory motion variability, such as drifts and irregular breathing, were not considered in this study. Besides, the respiratory signal detection of subjects with irregular breathing pattern poses an additional challenge. This issue would be better addressed by improving the temporal resolution in the detection of respiratory signals, such as a koosh-ball trajectory (50) with superior-to-inferior navigation.
Conclusions
In this work, we propose the HMDDL algorithm to exploit the prior information of data in spatial-motion-echo dimensions by jointly using deep dictionary learning and chemical shift modeling. The HMDDL algorithm provides substantial improvement of the qualities of the water/fat images and PDFF/ maps, and reduces the reconstruction time, in comparison with the conventional compressed sensing-based algorithm on healthy subjects and NAFLD subjects. This technique can potentially be used for MR guided radiation therapy.
Acknowledgments
Funding: This work was supported in part by
Footnote
Conflicts of Interest: All authors have completed the ICMJE uniform disclosure form (available at https://qims.amegroups.com/article/view/10.21037/qims-23-1396/coif). The authors have no conflicts of interest to declare.
Ethical Statement: The authors are accountable for all aspects of the work in ensuring that questions related to the accuracy or integrity of any part of the work are appropriately investigated and resolved. The study was conducted in accordance with the Declaration of Helsinki (as revised in 2013). The study was evaluated and approved by the Ethics Committee of the School of Biomedical Engineering, Shanghai Jiao Tong University. Written informed consent was obtained from the participants before each scan.
Open Access Statement: This is an Open Access article distributed in accordance with the Creative Commons Attribution-NonCommercial-NoDerivs 4.0 International License (CC BY-NC-ND 4.0), which permits the non-commercial replication and distribution of the article with the strict proviso that no changes or edits are made and the original work is properly cited (including links to both the formal publication through the relevant DOI and the license). See: https://creativecommons.org/licenses/by-nc-nd/4.0/.
References
- Mulé S, Kharrat R, Zerbib P, Massire A, Nickel MD, Ambarki K, Reizine E, Baranes L, Zegai B, Pigneur F, Kobeiter H, Luciani A. Fast T2-weighted liver MRI: Image quality and solid focal lesions conspicuity using a deep learning accelerated single breath-hold HASTE fat-suppressed sequence. Diagn Interv Imaging 2022;103:479-85. [Crossref] [PubMed]
- Shanbhogue K, Tong A, Smereka P, Nickel D, Arberet S, Anthopolos R, Chandarana H. Accelerated single-shot T2-weighted fat-suppressed (FS) MRI of the liver with deep learning-based image reconstruction: qualitative and quantitative comparison of image quality with conventional T2-weighted FS sequence. Eur Radiol 2021;31:8447-57. [Crossref] [PubMed]
- Yoon JH, Lee JM, Yu MH, Kim EJ, Han JK, Choi BI. Fat-suppressed, three-dimensional T1-weighted imaging using high-acceleration parallel acquisition and a dual-echo Dixon technique for gadoxetic acid-enhanced liver MRI at 3 T. Acta Radiol 2015;56:1454-62. [Crossref] [PubMed]
- Chandarana H, Block TK, Rosenkrantz AB, Lim RP, Kim D, Mossa DJ, Babb JS, Kiefer B, Lee VS. Free-breathing radial 3D fat-suppressed T1-weighted gradient echo sequence: a viable alternative for contrast-enhanced liver imaging in patients unable to suspend respiration. Invest Radiol 2011;46:648-53. [Crossref] [PubMed]
- Yang Y, Xu K, Chen X, Ding J, Shi J, Li J. The Accuracy and Clinical Relevance of the Multi-echo Dixon Technique for Evaluating Changes to Hepatic Steatosis in Patients with Non-alcoholic Fatty Liver Disease Treated with Formulated Food. Magn Reson Med Sci 2023;22:263-71. [Crossref] [PubMed]
- Armstrong T, Zhong X, Shih SF, Felker E, Lu DS, Dale BM, Wu HH. Free-breathing 3D stack-of-radial MRI quantification of liver fat and R(2)* in adults with fatty liver disease. Magn Reson Imaging 2022;85:141-52. [Crossref] [PubMed]
- Gassenmaier S, Kähm K, Walter SS, Machann J, Nikolaou K, Bongers MN. Quantification of liver and muscular fat using contrast-enhanced Dual Source Dual Energy Computed Tomography compared to an established multi-echo Dixon MRI sequence. Eur J Radiol 2021;142:109845. [Crossref] [PubMed]
- Shimizu K, Namimoto T, Nakagawa M, Morita K, Oda S, Nakaura T, Utsunomiya D, Yamashita Y. Hepatic fat quantification using automated six-point Dixon: Comparison with conventional chemical shift based sequences and computed tomography. Clin Imaging 2017;45:111-7. [Crossref] [PubMed]
- Tang A, Tan J, Sun M, Hamilton G, Bydder M, Wolfson T, Gamst AC, Middleton M, Brunt EM, Loomba R, Lavine JE, Schwimmer JB, Sirlin CB. Nonalcoholic fatty liver disease: MR imaging of liver proton density fat fraction to assess hepatic steatosis. Radiology 2013;267:422-31. [Crossref] [PubMed]
- Meisamy S, Hines CD, Hamilton G, Sirlin CB, McKenzie CA, Yu H, Brittain JH, Reeder SB. Quantification of hepatic steatosis with T1-independent, T2-corrected MR imaging with spectral modeling of fat: blinded comparison with MR spectroscopy. Radiology 2011;258:767-75.
- Jaimes C, Kirsch JE, Gee MS. Fast, free-breathing and motion-minimized techniques for pediatric body magnetic resonance imaging. Pediatr Radiol 2018;48:1197-208. [Crossref] [PubMed]
- Jahnke C, Paetsch I, Achenbach S, Schnackenburg B, Gebker R, Fleck E, Nagel E. Coronary MR imaging: breath-hold capability and patterns, coronary artery rest periods, and beta-blocker use. Radiology 2006;239:71-8. [Crossref] [PubMed]
- Benkert T, Feng L, Sodickson DK, Chandarana H, Block KT. Free-breathing volumetric fat/water separation by combining radial sampling, compressed sensing, and parallel imaging. Magn Reson Med 2017;78:565-76. [Crossref] [PubMed]
- Schneider M, Benkert T, Solomon E, Nickel D, Fenchel M, Kiefer B, Maier A, Chandarana H, Block KT. Free-breathing fat and R(2) * quantification in the liver using a stack-of-stars multi-echo acquisition with respiratory-resolved model-based reconstruction. Magn Reson Med 2020;84:2592-605. [Crossref] [PubMed]
- Wang N, Cao T, Han F, Xie Y, Zhong X, Ma S, Kwan A, Fan Z, Han H, Bi X, Noureddin M, Deshpande V, Christodoulou AG, Li D. Free-breathing multitasking multi-echo MRI for whole-liver water-specific T1, proton density fat fraction, and R2* quantification. Magn Reson Med 2022;87:120-37. [Crossref] [PubMed]
- Starekova J, Zhao R, Colgan TJ, Johnson KM, Rehm JL, Wells SA, Reeder SB, Hernando D. Improved free-breathing liver fat and iron quantification using a 2D chemical shift-encoded MRI with flip angle modulation and motion-corrected averaging. Eur Radiol 2022;32:5458-67. [Crossref] [PubMed]
- Freitag MT, Fenchel M, Bäumer P, Heußer T, Rank CM, Kachelrieß M, Paech D, Kopka K, Bickelhaupt S, Dimitrakopoulou-Strauss A, Maier-Hein K, Floca R, Ladd ME, Schlemmer HP, Maier F. Improved clinical workflow for simultaneous whole-body PET/MRI using high-resolution CAIPIRINHA-accelerated MR-based attenuation correction. Eur J Radiol 2017;96:12-20. [Crossref] [PubMed]
- Carpenter CM, Pogue BW, Paulsen KD. Incorporation of Magnetic Resonance Water-Fat Separation into MR-guided near-infrared spectroscopy in the Breast. Multimodal Biomedical Imaging 2009;IV: [Crossref]
- Zhong X, Armstrong T, Nickel MD, Kannengiesser SAR, Pan L, Dale BM, Deshpande V, Kiefer B, Wu HH. Effect of respiratory motion on free-breathing 3D stack-of-radial liver R2* relaxometry and improved quantification accuracy using self-gating. Magn Reson Med 2020;83:1964-78. [Crossref] [PubMed]
- Luo H, Zhu A, Wiens CN, Starekova J, Shimakawa A, Reeder SB, Johnson KM, Hernando D. Free-breathing liver fat and R2* quantification using motion-corrected averaging based on a nonlocal means algorithm. Magn Reson Med 2021;85:653-66. [Crossref] [PubMed]
- Kim JR, Yoon HM, Cho YA, Lee JS, Jung AY. Free-breathing contrast-enhanced upper abdominal MRI in children: comparison between Cartesian acquisition and stack-of-stars acquisition with two different fat-suppression techniques. Acta Radiol 2021;62:541-50. [Crossref] [PubMed]
- Feng L, Axel L, Chandarana H, Block KT, Sodickson DK, Otazo R. XD-GRASP: Golden-angle radial MRI with reconstruction of extra motion-state dimensions using compressed sensing. Magn Reson Med 2016;75:775-88. [Crossref] [PubMed]
- Tan Z, Voit D, Kollmeier JM, Uecker M, Frahm J. Dynamic water/fat separation and B0 inhomogeneity mapping-joint estimation using undersampled triple-echo multi-spoke radial FLASH. Magn Reson Med 2019;82:1000-11. [Crossref] [PubMed]
- Sharma SD, Hu HH, Nayak KS. Accelerated T2*-compensated fat fraction quantification using a joint parallel imaging and compressed sensing framework. J Magn Reson Imaging 2013;38:1267-75. [Crossref] [PubMed]
- Song P, Weizman L, Mota JFC, Eldar YC, Rodrigues MRD. Coupled Dictionary Learning for Multi-Contrast MRI Reconstruction. IEEE Trans Med Imaging 2020;39:621-33.
- Balsiger F, Reyes M, Scheidegger O, Carlier PG, Marty B. Quantification of fat fraction and water T1 in neuromuscular diseases using deep learning-based magnetic resonance fingerprinting with water and fat separation. Imaging Neuromusc Dis 2019;25:S26-7.
- Yang Y, Sun J, Li H, Xu Z. ADMM-CSNet: A Deep Learning Approach for Image Compressive Sensing. IEEE Trans Pattern Anal Mach Intell 2020;42:521-38. [Crossref] [PubMed]
- Wang S, Su Z, Ying L, Peng X, Zhu S, Liang F, Feng D, Liang D. Accelerating magnetic resonance imaging via deep learning. Proc IEEE Int Symp Biomed Imaging 2016;2016:514-7. [Crossref] [PubMed]
- Lee D, Yoo J, Ye JC. Deep residual learning for compressed sensing MRI. 2017 IEEE 14th International Symposium on Biomedical Imaging (ISBI 2017), Melbourne, VIC, Australia, 2017:15-18.
- Zhang Y, She H, Du YP. Dynamic MRI of the abdomen using parallel non-Cartesian convolutional recurrent neural networks. Magn Reson Med 2021;86:964-73. [Crossref] [PubMed]
- Küstner T, Fuin N, Hammernik K, Bustin A, Qi H, Hajhosseiny R, Masci PG, Neji R, Rueckert D, Botnar RM, Prieto C. CINENet: deep learning-based 3D cardiac CINE MRI reconstruction with multi-coil complex-valued 4D spatio-temporal convolutions. Sci Rep 2020;10:13710. [Crossref] [PubMed]
- Küstner T, Pan JZ, Gilliam C, Qi H, Cruz G, Hammernik K, Blu T, Rueckert D, Botnar R, Prieto C, Gatidis S. Self-supervised motion-corrected image reconstruction network for 4D magnetic resonance imaging of the body trunk. Apsipa Trans Signal 2022;11:e12.
- Eldeniz C, Gan W, Chen S, Fraum TJ, Ludwig DR, Yan Y, Liu J, Vahle T, Krishnamurthy U, Kamilov US, An H. Phase2Phase: Respiratory Motion-Resolved Reconstruction of Free-Breathing Magnetic Resonance Imaging Using Deep Learning Without a Ground Truth for Improved Liver Imaging. Invest Radiol 2021;56:809-19.
- Abdi M, Feng X, Sun C, Bilchick KC, Meyer CH, Epstein FH. Suppression of artifact-generating echoes in cine DENSE using deep learning. Magn Reson Med 2021;86:2095-104.
- Abdi M, Bilchick KC, Epstein FH. Compensation for respiratory motion-induced signal loss and phase corruption in free-breathing self-navigated cine DENSE using deep learning. Magn Reson Med 2023;89:1975-89. [Crossref] [PubMed]
- Li S, Shen C, Ding Z, She H, Du YP. Accelerating multi-echo chemical shift encoded water-fat MRI using model-guided deep learning. Magn Reson Med 2022;88:1851-66. [Crossref] [PubMed]
- Schlemper J, Caballero J, Hajnal JV, Price AN, Rueckert D. A Deep Cascade of Convolutional Neural Networks for Dynamic MR Image Reconstruction. IEEE Trans Med Imaging 2018;37:491-503. [Crossref] [PubMed]
- Sun C, Zhang M, Wu R, Lu J, Xian G, Yu Q, Gong X, Luo R. A convolutional recurrent neural network with attention framework for speech separation in monaural recordings. Sci Rep 2021;11:1434. [Crossref] [PubMed]
- Ravishankar S, Bresler Y. MR image reconstruction from highly undersampled k-space data by dictionary learning. IEEE Trans Med Imaging 2011;30:1028-41. [Crossref] [PubMed]
- Lewis DJ, Singhal V, Majumdar A. Solving Inverse Problems in Imaging via Deep Dictionary Learning. IEEE Access 2019;7:37039-49.
- Wang Z, She H, Zhang Y, Du YP. Parallel non-Cartesian spatial-temporal dictionary learning neural networks (stDLNN) for accelerating 4D-MRI. Med Image Anal 2023;84:102701. [Crossref] [PubMed]
- Beck A, Teboulle M. A Fast Iterative Shrinkage-Thresholding Algorithm for Linear Inverse Problems. Siam J Imaging Sci 2009;2:183-202.
- Dabov K, Foi A, Katkovnik V, Egiazarian K. Image denoising by sparse 3-D transform-domain collaborative filtering. IEEE Trans Image Process 2007;16:2080-95.
- Hernando D, Kellman P, Haldar JP, Liang ZP. Robust water/fat separation in the presence of large field inhomogeneities using a graph cut algorithm. Magn Reson Med 2010;63:79-90. [Crossref] [PubMed]
- Uecker M, Lai P, Murphy MJ, Virtue P, Elad M, Pauly JM, Vasanawala SS, Lustig M. ESPIRiT--an eigenvalue approach to autocalibrating parallel MRI: where SENSE meets GRAPPA. Magn Reson Med 2014;71:990-1001. [Crossref] [PubMed]
- He K, Zhang X, Ren S, Sun J. Deep residual learning for image recognition. 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 2016:770-8.
- Shih SF, Kafali SG, Calkins KL, Wu HH. Uncertainty-aware physics-driven deep learning network for free-breathing liver fat and R(2) * quantification using self-gated stack-of-radial MRI. Magn Reson Med 2023;89:1567-85. [Crossref] [PubMed]
- Hernando D, Haldar JP, Sutton BP, Ma J, Kellman P, Liang ZP. Joint estimation of water/fat images and field inhomogeneity map. Magn Reson Med 2008;59:571-80.
- Xiang QS. Two-point water-fat imaging with partially-opposed-phase (POP) acquisition: an asymmetric Dixon method. Magn Reson Med 2006;56:572-84. [Crossref] [PubMed]
- Ding Z, Cheng Z, She H, Liu B, Yin Y, Du YP. Dynamic pulmonary MRI using motion-state weighted motion-compensation (MostMoCo) reconstruction with ultrashort TE: A structural and functional study. Magn Reson Med 2022;88:224-38. [Crossref] [PubMed]


