
Deep learning-based partial volume correction in standard and low-dose positron emission tomography-computed tomography imaging
Introduction
As a nuclear medicine imaging technology, positron emission tomography (PET) is a key imaging modality in the diagnosis and treatment planning of cancer patients (1,2). A sufficient dose of radioactive tracer should be injected into the patient to acquire high-quality PET images for diagnostic purposes at the cost of exposing the body to ionizing radiation (3-6). The dosage of the injected radiotracer should be decreased to an acceptable level to limit the radiation risk, based on the well-known as low as reasonably achievable (ALARA) principle (7). However, a reduction of standard of care radiotracer dose would result in poor PET image quality, as well as a noise-induced quantitative bias, considering the statistical characteristics of PET image formation (8-10). Moreover, the partial volume effect (PVE), which is the result of detector size and sensitivity limitation in PET imaging, leads to considerable bias, especially for structures of the order of the full width at half maximum (FWHM) of the point spread function (PSF) of the system, spill-in and spill-out across the neighboring regions, and ambiguity at tissue boundaries (7,8,11). In this light, prior to the quantitative evaluation of metabolism and physiology of the organs/lesions, partial volume correction (PVC) and noise suppression are desirable in PET studies.
The PVC techniques may be divided into two categories: reconstruction-based and post-reconstruction approaches (12-15). In the reconstruction-based method, anatomical information could be incorporated into an iterative image reconstruction method, as prior information, to compensate for the PVE across different anatomical regions. The salient differentiation between reconstruction-based PVC and post-reconstruction PVC can be delineated based on the framework through which PVC is imparted to the PET image. In the context of reconstruction-based PVC, the correction paradigm is inherently assimilated during the PET image reconstruction phase, leveraging concurrent anatomical delineations procured from magnetic resonance imaging (MRI). Such integration seeks to augment the fidelity of the PET representation by mitigating the spatial resolution degradation and blurring attributable to partial volume effects. the high spatial resolution and soft tissue contrast of MRI are leveraged to guide the reconstruction of PET images. Specifically, during the reconstruction process, the anatomical details obtained from MRI are utilized to provide a priori information or constraints. Conversely, post-reconstruction PVC techniques administer the correction subsequent to the PET image reconstruction, harnessing anatomical demarcations from structural modalities like MRI to circumscribe pertinent regions of interest. Subsequently, uptake quantifications within these demarcated zones undergo rectifications to counterbalance the influences of the partial volume effect. In essence, while reconstruction-based PVC synergizes MRI-derived anatomical insights during the PET image reconstruction continuum, post-reconstruction PVC rectifies uptake metrics within circumscribed anatomical confines informed by MRI (16-18). It is worth mentioning that only computed tomography (CT) images were solely used for the purpose of attenuation and scatter correction in the experimental setup or study (19,20).
Regarding the conventional noise reduction techniques in emission tomography (21-24), machine learning approaches have demonstrated an outstanding ability to restore the image quality in emission tomography (6,23,25,26). In this regard, Xu et al. developed a fully convolutional encoder-decoder residual deep network model to estimate standard-dose PET images from ultra-low-dose (LD) data. Their proposed deep network outperformed the non-local mean (NLM) and block-matching 3D filters in terms of peak signal-to-noise ratio (PSNR), structural similarity index (SSIM), and root mean squared error (RMSE) (27). Cui et al. introduced an unsupervised deep learning method for PET image denoising, which shows promise in enhancing the diagnostic capabilities of PET imaging. The network was provided with both the initial noisy PET image and the prior image of the patient as instructional labels. Their findings demonstrated that the proposed approach outperformed the conventional Gaussian, NLM, and block-matching 4D filters (28).
A number of approaches have been proposed for the correction of PVE in PET imaging (post-reconstruction methods), which include geometric transfer matrix (GTM) (29), multi-target correction (MTC) (30), region-based voxel-wise correction (RBV) (31), iterative Yang (IY) (32), reblurred Van-Cittert (RVC) (33), and Richardson-Lucy (RL) (33). The first four PVC methods are region-based and require anatomical information and/or regions of interest, while the latter two are deconvolution-based applied at the voxel level. Post-reconstruction PVC and de-noising approaches are frequently employed in PET imaging; however, a joint estimate of the partial volume corrected and de-noised PET images would be crucial particularly in LD PET imaging (34-37). In this regard, Xu et al. suggested a framework for a combined PET image de-noising, PVC, and segmentation by an analytical approach. Their findings demonstrated that the proposed framework could effectively eliminate noise and correct PVE (38). For joint PVC and noise reduction, Boussion et al. integrated deconvolution-based approaches (RL and RVC) with wavelet-based de-noising. This method improved the accuracy of tissue delineation and quantification without sacrificing functional information when tested on clinical and simulated PET images (34). Matsubara et al. predicted the PVC maps using the deepPVC model trained with both magnetic resonance (MR) and 11C-PiB PET images. Their results suggest that the deepPVC model learns valuable features from the MR and 11C-PiB PET images, allowing the prediction of PV-corrected maps (39).
Since most PVC approaches rely on anatomical information obtained from MRI scans (17), co-registration of PET and MRI data is required. The utilization of anatomical information in PVE correction would not be straightforward due to the absence of MRI image in most clinical routines, internal organ motion, patient uncontrolled movements, and changes in the appearance and size of structures in anatomical and functional imaging (34,40). In this study, we proposed a deep learning solution for joint PVC and noise reduction in LD PET imaging. Our investigation employs both LD and full-dose (FD) PET images independently as inputs for an adapted encoder-decoder U-Net architecture. For training our deep learning model, we utilized FD PET images subjected to six widely recognized PVC techniques, denoted as FD + PVC, as the intended targets. Notably, FD + PVC generated through six distinct methodologies served as our comparative benchmark. The essence of our proposed deep learning framework lies in its dual objectives: the concurrent mitigation of noise artifacts and implementation of PVC techniques on LD PET images. It should be noted that no PVC was performed on the LD PET images and these images were only considered as the input of the model to predict FD + PVC (simultaneous PVC and noise reduction).
Methods
The study was conducted in accordance with the Declaration of Helsinki (as revised in 2013). The Institutional Ethics Committee of Razavi Hospital at Imam Reza University in Mashhad, Iran, approved the study. Individual consent for the retrospective analysis was waived.
Data acquisition
Between January 2020 and January 2021, a total of 185 patients diagnosed with head and neck cancer were referred for 18F-FDG brain PET/CT scans as part of the initial staging of their cancer. However, 25 of these patients had to be excluded from the study. The reasons for exclusion included the presence of severe metal artifacts in the CT images, leading to suboptimal or erroneous PET attenuation and scatter correction in 8 cases, issues arising from bulk motion occurring between the CT and PET acquisition in 11 cases, motion artifacts within the PET imaging of 3 patients, and instances where the raw PET data, also known as list mode data, was found to be corrupted in 3 additional patients. For the purposes of this study, only clinical datasets without significant artifacts were deemed suitable for inclusion, and no additional criteria were imposed for data collection.
Clinical 18F-FDG brain PET/CT images (head and neck cancer) were collected for 20 min on a Biograph 16 PET/CT scanner (Siemens Healthineers, Germany) following a standard of care injection dose of 205±10 MBq for 160 patients (the patient data were randomly divided into training, validation, and test datasets; 100 subjects for training, 20 subjects for validation, and 40 subjects for test). A low-intensity CT scan (110 kVp, 145 mAs) was conducted before collecting the PET data to correct for the purpose of attenuation and scatter correction. The PET-CTAC images underwent scatter correction, utilizing the single-scatter simulation (SSS) method across two iterations. The entire corrections required for quantitative PET imaging including random, normalization, decay, etc., were performed within PET image reconstruction. This model scanner has a PSF equivalent to a Gaussian function with FWHM of 4–5 mm. In this regard, a PSF with an FWHM of 4.5 mm was considered for PVC methods. Written consents were acquired from patients participated in this study. The PET data were obtained in a list-mode format to allow for the generation of synthetic LD data by randomly selecting 5% of the events (i.e., under-sampling) within the acquisition time. A 5% reduction in imaging time retains an acceptable signal-to-noise ratio. A greater reduction might introduce excessive noise, while a lesser reduction may not offer significant dynamic value. Although noise does pose challenges to the networks, the signal-to-noise ratio remains adequate. Before embarking on the development of deep learning models, we applied six distinct PVC methods. For each method, we utilized two frameworks: one with LD input images and the other with FD input images. This resulted in a total of 12 models for the network. Subsequently, all the PET images were converted to standard uptake value (SUV) units. To manage the dynamic range of PET intensities, these images were uniformly normalized by a factor of 10 across the dataset.
It’s important to highlight that the intensity conversion of all PET images into SUV was based on body weights and injected doses, thereby preserving the quantitative value of the PET images. The absolute SUV value plays a crucial role in clinical studies. Hence, our measurements focused on gray matter without normalization to any specific region. We employed a general normalization factor of 10 to aid the network’s training. The overarching goal was to maintain the clinical significance of the PET images. To achieve accurate image quantification, normalization using a factor of 10 was deemed essential. This approach remains the sole method to retrieve the original SUV from the generated images. The quantitative parameters were then calculated/reported in SUV unit the results section. For deep learning training, the reconstructed PET images were up-sampled into a matrix of 144×144×120 with a voxel size of 2 mm × 2 mm × 2 mm. Total FOV is 576 mm × 576 mm × 480 mm, and FOV after cropping is X mm × Y mm × Z mm. Up-sampling did not affect quantification. The comparison with reference data were conducted in the up-sampled mode to avoid any errors introduced by the image resize. Table 1 summarizes specific patient demographics data in detail.
Table 1
| Variable | Training | Test | Validation |
|---|---|---|---|
| Number | 100 | 40 | 20 |
| Male/female | 59/41 | 23/17 | 12/8 |
| Age (years) | 63±8 | 60±18 | 63±4.5 |
| Weight (kg) | 71±6 | 69±12 | 72±11 |
Indication/diagnosis: head and neck cancer staging or follow-up examinations.
Partial volume correction approaches
The PETPVC toolbox (17) was used to execute PVC on the PET images of 160 patients, with 20 subjects for validation and 40 for testing. The PETPVC was created utilizing the Insight Segmentation and Registration Toolkit (Insight Software Consortium, USA) in a C++ environment. Based on the fact that they are commonly used in research and clinical trials, six methods were selected for their effectiveness, feasibility of implementation, and relevance to clinical practice, including GTM (29), MTC (30), RBV (31), IY (32), RVC (33), and RL (33). Labbé (LAB) and Müller-Gärtner (MG) techniques are not recommended and may not provide satisfactory results for PVC in amyloid PET data (41). The automated anatomical labeling (AAL) (42) brain PET template/atlas was employed and transferred/co-registered to the patients’ PET-CT scan to apply PVC. The process included loading images, transferring them to the atlas space through affine transfer, resampling, matching the atlas to the images, and zoning in the standard atlas space. To regionalize the patient space, the atlas was transferred to the patient space using the inverse of the affine transfer performed in the previous step. The patient’s image was registered to a template, and the transformation was used to transfer anatomical regions onto the target patient. This enabled the application of PVC using the AAL atlas as a reference and the training of deep learning models based on ground truth anatomical brain regions. The AAL brain mask was employed for four of these PVC techniques, namely GTM, MTC, RBV, and IY, since these techniques are region-based and require anatomical masks for implementing PVC. Brain area masks are used instead of an MR image; however, the MR image is still considered the most accurate. This process ensures that the masks, like the MR image, function as intended. The brain regions mask was not used for the two deconvolution-based algorithms, namely RVC and RL. The six PVC methods are briefly discussed in the following sections.
GTM
The GTM (29) is a region-based method for PVC, which depends on anatomical information in terms of boundaries between different regions. The GTM is formulated by Eq. [1].
Wherein T represents real activity uptakes in each anatomical (brain) area, G represents the spill-over of activity from one region to another, registered in a matrix of size N (numbers of regions), and r is the vector of mean activity in each region as measured from the input (original) PET data. The spill-over activity (Gi,j) of the region (i) into the region (j) is calculated through the smoothing area (i) with the system’s PSF and multiplying with the region (j). The remaining voxels are then added together and normalized by the total activity in the area (i). When the spill-over activity of all regions into all others have been computed, the true activity values (T) can be found by applying: T=G−1. The GTM method assumes that activity within an area is uniform, and a single value would represent its activity uptake.
IY
The IY methodology (32) is similar to Yang’s method (43), wherein instead of applying the GTM method, the mean values of individual areas are calculated from the input PET data itself. The mean value estimations are then adjusted by applying Eq. [2] in an iterative fashion.
Here, Tk,i is the estimated mean value of region (i) at the iteration (k), and fk is an estimation of the PVE corrected image at the iteration (k). In this equation, is a piece-wise version of the PET image with a mean value for each region. h(x) is the estimated average PET signal value in a region. Pi(x) is the PVC of a target in a voxel. Finally, the image Sk is a piece-wise constant image that represents average values for each region.
RBV
The RBV approach (31) is a hybrid methodology that employs the algorithm developed by Yang et al. (43) to accomplish both region- and voxel-based PVC. The mean activity levels in each region are first determined using the GTM approach. Afterward, Eq. [3] is employed to carry out a voxel-by-voxel PVC.
Here, stands for a synthetic image generated by the GTM technique (mean value is used for each region).
MTC
The MTC (30) is a combined region- and voxel-based PVC technique, where in the mean activity levels in each region are first determined using the GTM approach, and thereafter, the whole area is corrected voxel-by-voxel. The MTC PVC technique is implemented through Eq. [4].
where fC is the PVC corrected picture, ⊗ stands for the convolution operator, h denotes the system’s PSF, f denotes the input (original) image, Pi and Pj indicates the brain/anatomical regions, and Ti is the corrected mean value of region (i) obtained from the GTM technique. The variable j denotes the target region or structure under consideration. Each target region will have a corresponding value of j.
Deconvolution techniques
Without any requirement for anatomical information or segmentation, two deconvolution techniques are applied to reduce the PVE. However, the efficiency of these procedures is restricted, and in some situations, these methods may result in noise amplification. When no anatomical information is provided, they can improve the contrast of the image to some extent. The iterative implementation of the two standard deconvolution algorithms, namely RL and RVC, is given in Eq. [5] and Eq. [6] (33).
Here, α is the convergence rate parameter that defines the degree of change at each iteration. h(x) is a region’s estimated mean PET signal, while f(x) is the true PET signal in a voxel. fk(x) is the estimated PET signal after deconvolution in iteration k.
Deep neural network implementation
A modified encoder-decoder U-Net architecture, illustrated in Figure 1, was employed to apply PVC to PET images. The modified U-Net is a fully convolutional neural network with deep concatenation connections between different stages, which is based on the encoder-decoder structure (44). Convolution with 33 kernels and a rectified linear unit (ReLU) is used at each level. A 2×2 max-pooling is used for down-sampling and up-sampling blocks across various stages. In U-Net, “con” means “convolutional layer”, while “conv” means “convolution operation”. Max-pooling is usually done after a convolutional operation, but sometimes, it’s better to apply dropout before max-pooling to prevent overfitting and improve generalization. MATLAB software and the Deep Learning toolbox were used to design and train the network, while an NVIDIA GPU was used for training. The U-Net training was stopped based on two criteria: maximum epochs and minimum validation RMSE loss. Each PVC method was given a maximum of 15 epochs, with 340 iterations per epoch and a total of 5,100 maximum iterations. The minimum validation RMSE loss was determined for each method and compared with the normal and standard values. Performance during training and validation was evaluated using PSNR, RMSE, and SSIM. The Adam optimizer was used with a learning rate of 0.003 to train the network. The input to the network was either 5% LD or FD PET images to predict PVC PET images. The goal was to train this network to perform the PVE correction on PET images based on the different aforementioned PVC approaches (independently). Considering the six PVC techniques, a total of 12 separate models (6 for LD and 6 for FD input data) were developed.
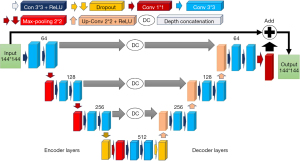
Performance evaluation
Five standard quantitative measures were performed to assess the quality of predicted PET images (FD + PVC) by different U-Net models. These metrics include PSNR (Eq. [7]), RMSE (Eq. [8]), SSIM (45) (Eq. [9]), voxel-wise mean relative bias (MRB) (Eq. [10]), and mean absolute relative bias (MARB) (Eq. [11]).
In Eq. [7], max value is the maximum possible pixel value in reference image, whereas MSE is the mean square error.
In the given context, J represents the predicted images obtained from each PVC method (FD + PVC), whereas I represent the reference image that shows FD + PVC PET images generated through various PVC methods. M×N denotes the total number of pixels present in the image. Our U-Net network was trained using uncorrected LD and FD PET images as inputs and FD PET images with correction as outputs.
Here, μx, μy represent the average of x, y images and , represent their variance. denotes the covariance of x and y images. c1=(k1L)2, c2=(k2L)2, k1=0.01 and k2=0.03 were selected by default to avoid division by very small numbers (L is the dynamic range of the pixel values).
Here, MRB and MARB are metrics used to evaluate the accuracy of U-Net’s predictions in PVC in PET imaging. It calculates the average relative bias on a per-voxel basis between the predicted output and the reference standard image. In Eq. [10] and Eq. [11], N indicates the total number of voxels in the volume of interest, Mi represents the measured value obtained from the PET scanner, and Ti represents the true value obtained from a reference standard. FD + PVC images generated by different methods are considered reference standards. PVC models have their own reference points, which are baselines and not necessarily ground truth. Furthermore, compared to the PVC atlas, MRB is only calculated once for the PVC register to estimate the average systematic bias introduced by partial volume effects in the region of interest (ROI) or the entire image, and MARB also shows the overall network bias.
For different PVC methods with either FD or LD input data, PSNR, RMSE, SSIM and MRB metrics were calculated and compared to the FD + PVC images predicted by the U-Net. These metrics are instrumental in evaluating accuracy, image quality, and clinical relevance. They also facilitate comparison with other studies. Among these, RMSE is particularly significant as it represents absolute errors in image intensity. Additionally, to enhance the assessment of the performance of different PVC models, we determined the voxel-wise MRB. Furthermore, given the AAL atlas transferred/co-registered to the patient’s space (to define 71 anatomical brain areas), the region-wise RMSE was determined for the individual brain regions. The left and right regions were combined to reduce the number of brain areas to 34 for the evaluation of the models. The brainstem is a crucial structure that links the spinal cord to the rest of the brain. Unlike other brain regions, it doesn’t have left and right counterparts.
Results
Figure 2 displays LD and FD PET images (first row) along with ground truth FD + PVC (second row) and U-Net models’ predicted FD + PVC images for various PVC algorithms (third and fourth rows). In the visual comparison presented in Figure 2, the U-Net generated RVC-predicted images that displayed reduced noise and a smoother appearance compared to images produced by other PVC models. Following this, the RBV, IY, and MTC methods demonstrated superior quality with diminished noise levels. The GTM image, contingent on the algorithm used, showcases enhanced anatomical details. On the other hand, the RL image appears noisier. A visual assessment indicates that images predicted by the U-Net from both LD and FD PET images share similar structural and detailed characteristics with the reference FD + PVC images. Visual inspection revealed that images predicted by the U-Net from both LD and FD PET images bear similar structures/details with respect to the reference FD + PVC images. The images in Figure 3 illustrate the contrast between the SUV maps for the FD and LD inputs for the first and second rows. After analyzing the difference SUV maps generated from various PVC images by the U-Net model, we identified similar systematic biases/trends in the models with LD and FD input PET images.
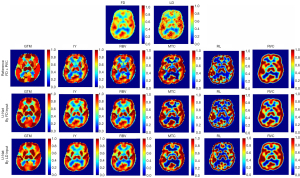

Figure 3 highlights that regions with positive values point to an uptick in SUV, denoting heightened metabolic activity. This could be indicative of disease progression or a therapeutic response. Conversely, regions with negative values hint at a decline in SUV and metabolic activity, potentially signaling disease regression or a positive response to treatment. Analyzing the SUV map of the difference between LD and FD input, there seems to be no notable difference across PVC algorithms. In the perspective of a nuclear medicine specialist, the RVC method slightly edges out in performance over other methods. Yet, there’s no discernible difference among the PVC methods in terms of pinpointing disease locations or differentiating head cancer across the cortices.
Tables 2,3 illustrate the results of the quantitative analysis of the predicted PET images in terms of PSNR, RMSE, SSIM, MRB and MARB metrics for the LD and FD input PET data, respectively. These tables compare quantitative image quality metrics [mean ± standard deviation (SD)] between FD + PVC predicted by the U-Net models and the ground truth FD + PVC PET images for the entire head region. It should be noted that network bias is absent when values are zero. Extreme positive or negative values indicate over or underestimation tendencies, respectively. Significant negative values suggest underestimation of activity.
Table 2
| Test dataset | LD vs. FD | GTM | IY | RBV | MTC | RL | RVC |
|---|---|---|---|---|---|---|---|
| PSNR | 22.04±0.09 | 15.18±1.34 | 18.62±1.09 | 16.24±1.63 | 13.51±2.11 | 10.31±1.47 | 24.73±1.01 |
| RMSE (SUV) | 0.89±0.16 | 1.65±0.66 | 1.30±0.47 | 1.60±0.61 | 2.71±1.41 | 5.00±2.39 | 0.99±0.45 |
| SSIM | 0.54±0.09 | 0.63±0.05 | 0.63±0.06 | 0.57±0.06 | 0.64±0.05 | 0.30±0.07 | 0.89±0.05 |
| MRB (%) | 0.01±0.56 | 0.96±25.11 | 0.67±15.77 | 1.89±16.67 | 3.15±29.29 | −2.06±6.77 | −0.01±2.59 |
| MARB (%) | 0.04±0.03 | 30.78±2.00 | 19.55±2.29 | 20.73± 2.31 | 17.13±3.13 | 23.05±4.75 | 16.26±1.95 |
FD, full-dose; PVC, partial volume correction; PET, positron emission tomography; LD, low-dose; GTM, geometric transfer matrix; IY, iterative Yang; RBV, region-based voxel-wise correction; MTC, multi-target correction; RL, Richardson-Lucy; RVC, reblurred Van-Cittert; PSNR, peak signal-to-noise ratio; RMSE, root mean squared error; SUV, standardized uptake value; SSIM, structural similarity index; MRB, mean relative bias; MARB, mean absolute relative bias.
Table 3
| Test dataset | GTM | IY | RBV | MTC | RL | RVC |
|---|---|---|---|---|---|---|
| PSNR | 14.38±2.62 | 17.75±2.24 | 17.18±3.18 | 15.45±3.48 | 13.92 ±3.11 | 29.23±4.24 |
| RMSE (SUV) | 1.64±0.62 | 1.35±0.48 | 1.48±0.55 | 2.45±1.34 | 3.27±1.71 | 0.79±0.48 |
| SSIM | 0.65±0.05 | 0.67±0.06 | 0.65±0.05 | 0.58±0.05 | 0.37±0.04 | 0.94±0.05 |
| MRB (%) | −3.27±13.49 | 3.44±17.1 | 1.15±17.06 | −1.55 ±24.48 | −2.06±6.86 | 1.42±2.87 |
| MARB (%) | 35.18±1.99 | 16.29±1.94 | 21.52±2.29 | 20.77±3.46 | 32.02±4.84 | 14.30±1.70 |
FD, full-dose; PVC, partial volume correction; PET, positron emission tomography; GTM, geometric transfer matrix; IY, iterative Yang; RBV, region-based voxel-wise correction; MTC, multi-target correction; RL, Richardson-Lucy; RVC, reblurred Van-Cittert; PSNR, peak signal-to-noise ratio; RMSE, root mean squared error; SUV, standardized uptake value; SSIM, structural similarity index; MRB, mean relative bias; MARB, mean absolute relative bias
The PVC methods exhibited varying levels of performance across different metrics. In terms of PSNR, RVC achieved 24.73 for LD and 29.23 for FD, whereas RL scored 10.31 for LD and 13.92 for FD. MTC recorded 13.51 for LD and 15.45 for FD, and RBV showed 16.24 for LD and 17.18 for FD.
Similarly, when considering RMSE, RVC yielded 0.99 for LD and 0.79 for FD, while RL resulted in 5 for LD and 3.27 for FD. MTC’s figures were 2.71 for LD and 2.45 for FD, and RBV displayed 1.60 for LD and 1.48 for FD.
Regarding SSIM, RVC obtained 0.89 for LD and 0.94 for FD, whereas RL achieved 0.30 for LD and 0.37 for FD. MTC recorded 0.64 for LD and 0.58 for FD, and RBV showed 0.57 for LD and 0.65 for FD.
Lastly, in terms of error, RVC had an MRB of −0.01 for LD and 1.42 for FD, while RL had −2.06 for LD and −2.06 for FD. MTC showed 3.15 for LD and −1.55 for FD, and RBV displayed 1.89 for LD and 1.15 for FD. IY had an MRB of 0.67 for LD and 3.44 for FD, and GTM recorded 0.96 for LD and −3.27 for FD.
The RVC model shows an improvement of 18.1% over the LD PET image in terms of PSNR and 20.2% in terms of RMSE. Our research findings indicate that the RVC model performed better than the LD input model, while the RL model performed the worst. The RVC model had a PSNR of 24.73 for LD and 29.23 for FD and an SSIM of 0.89 for LD and 0.94 for FD. On the other hand, the RL model had a PSNR of 10.31 for LD and 13.92 for FD, with an SSIM of 0.30 for LD and 0.37 for FD. Moreover, the RL model had the highest error rate among other PVC methods, with an RMSE parameter of 5 for LD and 3.27 for FD.
For the MARB parameter, both the RVC and IY methods with the FD input outperformed their LD counterparts, registering values of 14.30 and 16.29, respectively. Consequently, the overall network error for these two PVC models is less than that of the LD input. Additionally, the MARB values for the RVC model, 16.26 for LD and 14.30 for FD, were lower than those of other PVC methods. This underscores the network’s diminished error rate and its preeminent performance compared to other methods. Conversely, the RL and GTM methods logged the highest MARB values for the FD input, at 32.02 and 35.18, respectively.
Table 4 shows statistically significant differences between the FD + PVC predicted by the U-Net images by the LD and FD input models were analyzed using paired t-test analysis. A P value of less than 0.05 was considered statistically significant. The results of the paired t-test analysis showed that there were significant differences between the LD and FD input models. The study demonstrated several benefits of using deep neural networks for PVC on PET images.
Table 4
| Test dataset | GTM | IY | RBV | MTC | RL | RVC |
|---|---|---|---|---|---|---|
| RMSE (P value) | 0.04 | 0.03 | 0.05 | 0.40 | <0.001 | 0.05 |
| SSIM (P value) | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 |
| PSNR (P value) | 0.08 | 0.03 | 0.10 | <0.001 | <0.001 | <0.001 |
| MRB (P value) | 0.05 | 0.05 | 0.04 | 0.03 | 1.00 | 0.02 |
| MARB (P value) | <0.001 | <0.001 | 0.12 | <0.001 | <0.001 | <0.001 |
LD, low-dose; FD, full-dose; PVC, partial volume correction; GTM, geometric transfer matrix; IY, iterative Yang; RBV, region-based voxel-wise correction; MTC, multi-target correction; RL, Richardson-Lucy; RVC, reblurred Van-Cittert; RMSE, root mean squared error; SSIM, structural similarity index; PSNR, peak signal-to-noise ratio; MRB, mean relative bias; MARB, mean absolute relative bias.
Tables S1-S6 in the supplementary materials display mean values of PSNR, RMSE, and SSIM for LD and FD datasets for training, validation, and test datasets.
The summary of the region-wise (for the different brain regions) analysis of different deep learning-based PVC models is presented in Figures 4-7 for LD and FD PET input data, respectively. For the models with LD input data, the RMSE values for predicted FD + GTM were higher in Heschl’s gyri, thalamus, pallidum, putamen, caudate nucleus, amygdala, and olfactory, compared to that in the LD PET images. For the predicted FD + IY, FD + RBV, and FD + MTC PET images, higher RMSEs were observed in Heschl’s gyri, thalamus, pallidum, putamen, and caudate nucleus brain regions, compared to LD PET images. For the RL model, higher RMSEs were observed in all brain regions. On the other hand, the results indicated that for PSNR values, FD is approximately 18.18% better than LD for RVC and 35.02% better than LD for the RL method. For RMSE values, FD is approximate −20.20% better than LD for RVC and −34.60% better than LD for the RL method. Overall, the predicted PVC PET images from either LD or FD PET data exhibited similar results in the entire brain regions.
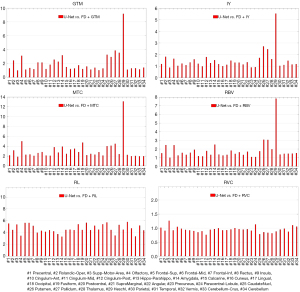
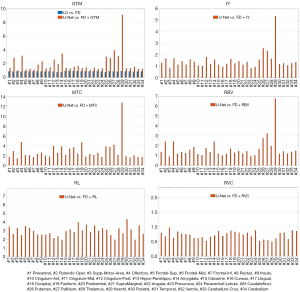
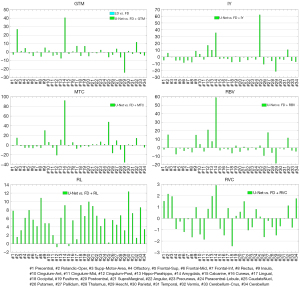
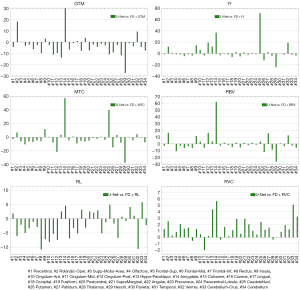
The study found that MRB values were higher in the amygdala region for predicted FD + GTM and in the amygdala and caudate nucleus regions for predicted FD + MTC PET images when compared to LD PET images. The RL model showed higher MRBs in all brain regions as compared to LD PET images. On the other hand, the RBV model showed similar MRB percentages in both modes, performing equally in both cases. In comparison, the RVC model produced better results in all brain regions when compared to LD PET, making it a better option for network learning.
Figures S1,S2 in supplementary materials show RMSE boxplots for the FD + PVC PET images predicted by different models from the LD and FD PET input data, respectively. The RMSE boxplots revealed that images predicted by the U-Net from LD and FD PET data contain similar levels of error, compared to the reference FD + PVC images.
Discussion
We set out to create a deep learning solution for the joint PVC and de-noising of LD PET data without using any anatomical images. The 2D networks are as effective as 3D networks for regression problems like PVC. This is because the size of the training dataset increases and the number of parameters is less, resulting in better optimization and less overfitting. Running PVC in two dimensions does not change the nature or physics of the underlying data (46). MR images must be segmented into specific brain regions for proper analysis. Registration using an atlas is crucial for accurate identification and closure of these regions. As an outcome, this framework could be used in PET/CT imaging applications where MRI images are not accessible for conventional PVC methods. To achieve this, we utilized FD and 5% LD PET data (as the input data) and FD PET images corrected for PVE using six frequently used PVC techniques to train a modified encoder-decoder U-Net network. To conduct PVC, the AAL brain atlas was used to delineate anatomical areas of the brain. The anticipated PVE corrected PET images from both LD and FD PET data revealed comparable image quality considering the visual assessment. The differences between LD and FD images (Table 2 and Figure 3) were significantly lower than those observed for PVC models since the errors due to the PVC did not exist in the comparison of the LD and FD images and it merely reflects the noise levels in the LD PET images. According to the P value table, the PVC PET images predicted by LD and FD PET input data showed comparable outcomes considering PSNR, SSIM, RMSE, and MRB throughout the brain regions. This suggests that these models can jointly reduce noise and perform PVC.
Since the RVC PVC strategy depends purely on a simple convolution procedure, which would not be challenging for the deep learning model to predict, the RVC model performed marginally better than the other PVC models. On the other hand, PVC techniques that rely on the brain areas mask to correct PET images exhibited greater quantification errors. Defining the exact anatomical brain regions binary would be highly challenging for the deep learning model, particularly when the input data is LD PET images. In this regard, significant RMSEs were observed for the MTC and RL PVC approaches, which cannot be ignored. As a result, the current deep learning models are inefficient for these two approaches. This limitation hinders the study’s potential and the use of deep learning techniques for these two approaches.
The GTM approach is a region-based method that performs PVC concurrently on different brain regions provided by the AAL brain map. The GTM approach tends to estimate a mean value for each region, based on which the spill-in and spill-out across different regions are then calculated. Since this approach assumes a uniform activity uptake for each region, the accuracy of the PVC by the deep learning model solely depends on the identification of anatomical regions. However, the MTC approach is a hybrid PVC that relies on both region-based and voxel-level processing to correct the PVE. The MTC method, in the first step, creates an estimation of the corrected image based on which voxel-based processing is conducted to generate the final PVC image. This procedure is relatively more complicated, compared to the RVC approach, and thus, a larger RMSE was observed for this method. Similarly, the RBV PVC approach, which is a combination of Yang’s voxel-wise correction (43) and the GTM approach, is a hybrid method; therefore, a similar RMSE to that of the RBV approach was observed. The RBV approach differs from the MTC method in that all areas are corrected at the same time while the MTC method performs PVC region by region (32,47). In the IY technique, which is a variation of the Yang’s approach, the voxel-wise uptake values are taken directly from the input PET images, as opposed to the GTM method which relies on regional mean values. The IY is often faster than the RBV and GTM methods to execute since it requires k convolution operation, where k is usually less than 10. However, the RBV method involves computing n convolutions, where n is the number of brain regions. Visually, the results of these two methods are similar. The PVC approaches discussed above are all based on anatomical information provided by the AAL brain map to calculate inter-region spill-over. Voxel-based PVC methods would also consider the intra-region spill-over and signal correction; thus, larger RMSEs were observed for these approaches.
Compared to the LD PET data, the predicted FD + GTM PET images in the Heschl’s gyri, thalamus, pallidum, putamen, caudate nucleus, amygdala, and olfactory regions showed an overestimation of activity. This observation could be due to fact that these regions have very close dimensions to the full width at half the maximum of the PSF of the system. In the predicted FD + IY, FD + RBV, and FD + MTC images, a larger over-estimation was observed in Heschl’s gyri, thalamus, pallidum, putamen, and caudate nucleus, in comparison with the input LD PET images. These regions are of small size with relatively high activity levels, wherein small boundary estimation errors by the deep learning models would lead to large errors in these areas. Similarly, a larger overestimation was observed in Heschl’s gyri, thalamus, pallidum, putamen, and caudate nucleus regions for IY, MTC, and RBV models, overall, the Heschl’s gyri, thalamus, pallidum, putamen, caudate nucleus, amygdala, and olfactory have relatively high activity levels and small dimensions, which render them more susceptible to errors associated with PVC since anatomical boundary estimation is challenging. A small deviation from the true anatomical boundary would lead to large errors. In addition to the small size, high intensity contrast of the Heschl’s gyri region with respect to the surrounding regions would make it very sensitive to the small PVC errors.
Since IY, RBV, and MTC techniques relied on a similar initial estimation generated by the GTM method, the models developed based on them exhibited comparable levels of error. For all brain regions, the RL model led to an overestimation of activity uptake, which might be attributable to the fact that this method does not rely on any initial PVC estimation. The RL technique assumes a Poisson noise model and performs PVC based on a multiplicative correction step. Noise amplification is observed in this algorithm when the number of iterations proceeds as there no regularization factor is applied. The PVE is the result of limited spatial resolution in PET imaging. In this light, the PSF should be set precisely to accurately model and compensate PVE in some PVC algorithms. Overall, the RVC model exhibited lower errors in the entire brain regions, compared to the LD PET image for either LD or FD PET input data since this method contains a simple deconvolution process which is not challenging for deep learning models to predict. The U-Net models were effective in recovering image information from LD PET images. Lower MRB values were observed with MTC and RL, suggesting they may be more effective for accurate image information recovery.
Comparing the PSNR, RMSE, and SSIM parameters from Tables 2,3 with those in Tables S5,S6, we notice that applying PVC to both LD and FD images introduced significant errors, leading to reductions in SSIM and PSNR values. Nevertheless, the U-Net network demonstrated its capability to accurately predict PVC images. Additionally, all PVC methods yielded significant improvements across the three parameters under discussion. Consequently, using deep learning, which presents fewer errors, proves more effective in enhancing PVC images.
The U-NET model used in image analysis can potentially cause overestimation due to two factors: small receptive field and boundary estimation errors. The receptive field determines the area of input data that affects the prediction at a given point. If the field is too small compared to the size of the structures being analyzed, it can result in incomplete information and inaccurate predictions. Boundary estimation errors can arise due to limitations in the training data or architectural choices made in the network design. Inaccurate boundary estimation can result in misclassification or misalignment of structures, leading to overestimation. These factors are especially important in the context of PET image analysis, where accurate boundary estimation is crucial for proper PVC.
Our study had certain limitations. Firstly, our dataset was relatively small, consisting of only 160 images. This constrained the number of images we could allocate for validation. Secondly, tumor evaluations were not conducted for the patients. Moreover, our research was not a multi-center study, and it exclusively focused on a single cohort of patients with head and neck cancer. We aim to address some of these limitations in our future research, which will include comparisons of our deep learning method with others, as well as acquiring patient-specific anatomical MR data to complement PET data. However, the registration of the AAL brain template to the patients’ PET data were meticulously verified by our group visually to avoid any misalignment errors. While we employed an atlas/template for PVC and achieved accurate registration, it’s important to highlight that our study does not incorporate MRI data. Thus, although our findings align with those derived from PVC images using MRI, we can’t definitively state that they’re equivalent. Furthermore, simulation studies are essential for a comprehensive comparison of various PVC algorithms. The absence of a ground truth in clinical studies, compared to simulation studies, complicates the task of contrasting the effectiveness of different PVC methods. However, drawing from clinical data for such evaluations is challenging due to the lack of a universally accepted ground truth tailored for PVC. However, future studies could test phantom data to overcome this challenge. Some of these algorithms might have intrinsic limitations/shortcomings which may adversely affect the performance of the deep learning models developed based on them. In this regard, some standard approaches, such as the unrolling technique (48) or deep ensemble methods (49) could be employed to develop a PVC deep learning model that is superior to each of the PVC algorithms alone. Both methods have shown promising results and are now standard techniques.
Conclusions
Based on several PVC methods as the reference, we demonstrated that deep neural networks could conduct PVC on PET scans without anatomical images. Regarding the complexity of PVC techniques, our observations show that the RVC, RL, and RBV methods exhibit comparable performance in terms of PSNR, RMSE, SSIM, and MRB parameters for LD and FD inputs. The deep learning-based PVC models exhibited similar performance for both FD and LD input PET data, which demonstrated that these models could perform joint PVC and noise reduction. Since these models do not require any anatomical images, such as MRI data, they could be used in dedicated brain PET, as well as PET/CT scanners.
In the future, we would focus on PET/MR data to compare the PVC methods. We will also test the unrolling technique to find out whether this method will be able to do PVC independently (without CT and MR images).
Acknowledgments
We want to express our sincere appreciation to our coworkers for their work on this project, especially Dr. Arman Rahmim for the invaluable technical assistance.
Funding: None.
Footnote
Conflicts of Interest: All authors have completed the ICMJE uniform disclosure form (available at https://qims.amegroups.com/article/view/10.21037/qims-23-871/coif). N.Z. is a full-time employee of Siemens Medical Solutions USA, Inc. The other authors have no conflicts of interest to declare.
Ethical Statement: The authors are responsible for ensuring that all aspects of the work are investigated and resolved concerning questions regarding accuracy or integrity. The study was conducted in accordance with the Declaration of Helsinki (as revised in 2013). The Institutional Ethics Committee of Razavi Hospital, Imam Reza University, Mashhad, Iran, approved the study. The requirement for individual consent for this retrospective analysis was waived.
Open Access Statement: This is an Open Access article distributed in accordance with the Creative Commons Attribution-NonCommercial-NoDerivs 4.0 International License (CC BY-NC-ND 4.0), which permits the non-commercial replication and distribution of the article with the strict proviso that no changes or edits are made and the original work is properly cited (including links to both the formal publication through the relevant DOI and the license). See: https://creativecommons.org/licenses/by-nc-nd/4.0/.
References
- Rahmim A, Zaidi H. PET versus SPECT: strengths, limitations and challenges. Nucl Med Commun 2008;29:193-207. [Crossref] [PubMed]
- Zaidi H, Karakatsanis N. Towards enhanced PET quantification in clinical oncology. Br J Radiol 2018;91:20170508. [Crossref] [PubMed]
- Sanaat A, Arabi H, Mainta I, Garibotto V, Zaidi H. Projection Space Implementation of Deep Learning-Guided Low-Dose Brain PET Imaging Improves Performance over Implementation in Image Space. J Nucl Med 2020;61:1388-96. [Crossref] [PubMed]
- Sanaei B, Faghihi R, Arabi H. Quantitative investigation of low-dose PET imaging and post-reconstruction smoothing. arXiv preprint 2021. doi:
10.48550/arXiv.2103.10541 . - Khoshyari-morad Z, Jahangir R, Miri-Hakimabad H, Mohammadi N, Arabi H. Monte Carlo-based estimation of patient absorbed dose in 99mTc-DMSA, -MAG3, and -DTPA SPECT imaging using the University of Florida (UF) phantoms. arXiv preprint 2021. doi:
10.48550/arXiv.2103.00619 . - Sanaat A, Shiri I, Arabi H, Mainta I, Nkoulou R, Zaidi H. Deep learning-assisted ultra-fast/low-dose whole-body PET/CT imaging. Eur J Nucl Med Mol Imaging 2021;48:2405-15. [Crossref] [PubMed]
- Berkhout WE. The ALARA-principle. Backgrounds and enforcement in dental practices. Ned Tijdschr Tandheelkd 2015;122:263-70. [Crossref] [PubMed]
- Basu S, Hess S, Nielsen Braad PE, Olsen BB, Inglev S, Høilund-Carlsen PF. The Basic Principles of FDG-PET/CT Imaging. PET Clin 2014;9:355-70. v. [Crossref] [PubMed]
- Arabi H, Zaidi H. Non-local mean denoising using multiple PET reconstructions. Ann Nucl Med 2021;35:176-86. [Crossref] [PubMed]
- Rana N, Kaur M, Singh H, Mittal BR. Dose Optimization in (18)F-FDG PET Based on Noise-Equivalent Count Rate Measurement and Image Quality Assessment. J Nucl Med Technol 2021;49:49-53. [Crossref] [PubMed]
- Arabi H, Asl ARK, editors. Feasibility study of a new approach for reducing of partial volume averaging artifact in CT scanner. 2010 17th Iranian Conference of Biomedical Engineering (ICBME); 2010: IEEE.
- Erlandsson K, Dickson J, Arridge S, Atkinson D, Ourselin S, Hutton BF MR. Imaging-Guided Partial Volume Correction of PET Data in PET/MR Imaging. PET Clin 2016;11:161-77. [Crossref] [PubMed]
- Cysouw MCF, Golla SVS, Frings V, Smit EF, Hoekstra OS, Kramer GM, Boellaard R. Partial-volume correction in dynamic PET-CT: effect on tumor kinetic parameter estimation and validation of simplified metrics. EJNMMI Res 2019;9:12. [Crossref] [PubMed]
- Belzunce MA, Mehranian A, Reader AJ. Enhancement of Partial Volume Correction in MR-Guided PET Image Reconstruction by Using MRI Voxel Sizes. IEEE Trans Radiat Plasma Med Sci 2019;3:315-26. [Crossref] [PubMed]
- Zeraatkar N, Sajedi S, Farahani MH, Arabi H, Sarkar S, Ghafarian P, Rahmim A, Ay MR. Resolution-recovery-embedded image reconstruction for a high-resolution animal SPECT system. Phys Med 2014;30:774-81. [Crossref] [PubMed]
- Cysouw MCF, Kramer GM, Schoonmade LJ, Boellaard R, de Vet HCW, Hoekstra OS. Impact of partial-volume correction in oncological PET studies: a systematic review and meta-analysis. Eur J Nucl Med Mol Imaging 2017;44:2105-16. [Crossref] [PubMed]
- Thomas BA, Cuplov V, Bousse A, Mendes A, Thielemans K, Hutton BF, Erlandsson K. PETPVC: a toolbox for performing partial volume correction techniques in positron emission tomography. Phys Med Biol 2016;61:7975-93. [Crossref] [PubMed]
- Ibaraki M, Matsubara K, Shinohara Y, Shidahara M, Sato K, Yamamoto H, Kinoshita T. Brain partial volume correction with point spreading function reconstruction in high-resolution digital PET: comparison with an MR-based method in FDG imaging. Ann Nucl Med 2022;36:717-27. [Crossref] [PubMed]
- Mostafapour S, Gholamiankhah F, Dadgar H, Arabi H, Zaidi H. Feasibility of Deep Learning-Guided Attenuation and Scatter Correction of Whole-Body 68Ga-PSMA PET Studies in the Image Domain. Clin Nucl Med 2021;46:609-15. [Crossref] [PubMed]
- Laurent B, Bousse A, Merlin T, Nekolla S, Visvikis D. PET scatter estimation using deep learning U-Net architecture. Phys Med Biol 2023; [Crossref]
- Arabi H, Zaidi H. Improvement of image quality in PET using post-reconstruction hybrid spatial-frequency domain filtering. Phys Med Biol 2018;63:215010. [Crossref] [PubMed]
- Arabi H, Zaidi H. Spatially guided nonlocal mean approach for denoising of PET images. Med Phys 2020;47:1656-69. [Crossref] [PubMed]
- Aghakhan Olia N, Kamali-Asl A, Hariri Tabrizi S, Geramifar P, Sheikhzadeh P, Farzanefar S, Arabi H, Zaidi H. Deep learning-based denoising of low-dose SPECT myocardial perfusion images: quantitative assessment and clinical performance. Eur J Nucl Med Mol Imaging 2022;49:1508-22. [Crossref] [PubMed]
- Sanaei B, Faghihi R, Arabi H. Does prior knowledge in the form of multiple low-dose PET images (at different dose levels) improve standard-dose PET prediction? arXiv preprint 2022. doi:
10.48550/arXiv.2202.10998 . - Arabi H, Zaidi H. Applications of artificial intelligence and deep learning in molecular imaging and radiotherapy. Eur J Hybrid Imaging 2020;4:17. [Crossref] [PubMed]
- Arabi H. AkhavanAllaf A, Sanaat A, Shiri I, Zaidi H. The promise of artificial intelligence and deep learning in PET and SPECT imaging. Phys Med 2021;83:122-37. [Crossref] [PubMed]
- Xu J, Gong E, Pauly J, Zaharchuk G. 200x low-dose PET reconstruction using deep learning. arXiv preprint 2017. doi:
10.48550/arXiv.1712.04119 . - Cui J, Gong K, Guo N, Wu C, Meng X, Kim K, Zheng K, Wu Z, Fu L, Xu B, Zhu Z, Tian J, Liu H, Li Q. PET image denoising using unsupervised deep learning. Eur J Nucl Med Mol Imaging 2019;46:2780-9. [Crossref] [PubMed]
- Rousset OG, Ma Y, Evans AC. Correction for partial volume effects in PET: principle and validation. J Nucl Med 1998;39:904-11.
- Erlandsson K, Wong A, Van Heertum R, Mann JJ, Parsey R. An improved method for voxel-based partial volume correction in PET and SPECT. Neuroimage 2006;31:T84.
- Thomas BA, Erlandsson K, Modat M, Thurfjell L, Vandenberghe R, Ourselin S, Hutton BF. The importance of appropriate partial volume correction for PET quantification in Alzheimer's disease. Eur J Nucl Med Mol Imaging 2011;38:1104-19. [Crossref] [PubMed]
- Erlandsson K, Buvat I, Pretorius PH, Thomas BA, Hutton BF. A review of partial volume correction techniques for emission tomography and their applications in neurology, cardiology and oncology. Phys Med Biol 2012;57:R119-59. [Crossref] [PubMed]
- Tohka J, Reilhac A. Deconvolution-based partial volume correction in Raclopride-PET and Monte Carlo comparison to MR-based method. Neuroimage 2008;39:1570-84. [Crossref] [PubMed]
- Boussion N, Hatt M, Reilhac A, Visvikis D, editors. Fully automated partial volume correction in PET based on a wavelet approach without the use of anatomical information. 2007 IEEE Nuclear Science Symposium Conference Record; 2007: IEEE.
- Azimi MS, Kamali-Asl A, Ay MR, Arabi H, Zaidi H, editors. A Novel Attention-based Convolutional Neural Network for Joint Denoising and Partial Volume Correction of Low-dose PET Images. 2021 IEEE Nuclear Science Symposium and Medical Imaging Conference (NSS/MIC); 2021: IEEE.
- Azimi MS, Kamali-Asl A, Ay MR, Arabi H, Zaidi H, editors. ATB-Net: A Novel Attention-based Convolutional Neural Network for Predicting Full-dose from Low-dose PET Images. 2021 IEEE Nuclear Science Symposium and Medical Imaging Conference (NSS/MIC); 2021: IEEE.
- Azimi MS, Kamali-Asl A, Ay MR, Zeraatkar N, Hosseini MS. ARABI H, Zaidi H. Comparative assessment of attention-based deep learning and non-local mean filtering for joint noise reduction and partial volume correction in low-dose PET imaging. Journal of Nuclear Medicine 2022;63:2729.
- Xu Z, Gao M, Papadakis GZ, Luna B, Jain S, Mollura DJ, Bagci U. Joint solution for PET image segmentation, denoising, and partial volume correction. Med Image Anal 2018;46:229-43. [Crossref] [PubMed]
- Matsubara K, Ibaraki M, Kinoshita T. DeepPVC: prediction of a partial volume-corrected map for brain positron emission tomography studies via a deep convolutional neural network. EJNMMI Phys 2022;9:50. [Crossref] [PubMed]
- Soret M, Bacharach SL, Buvat I. Partial-volume effect in PET tumor imaging. J Nucl Med 2007;48:932-45. [Crossref] [PubMed]
- Su Y, Blazey TM, Snyder AZ, Raichle ME, Marcus DS, Ances BM, et al. Partial volume correction in quantitative amyloid imaging. Neuroimage 2015;107:55-64. [Crossref] [PubMed]
- Tzourio-Mazoyer N, Landeau B, Papathanassiou D, Crivello F, Etard O, Delcroix N, Mazoyer B, Joliot M. Automated anatomical labeling of activations in SPM using a macroscopic anatomical parcellation of the MNI MRI single-subject brain. Neuroimage 2002;15:273-89. [Crossref] [PubMed]
- Yang J, Huang S, Mega M, Lin K, Toga A, Small G, Phelps M. Investigation of partial volume correction methods for brain FDG PET studies. IEEE Transactions on Nuclear Science 1996;43:3322-7.
- Bahrami A, Karimian A, Fatemizadeh E, Arabi H, Zaidi H. A new deep convolutional neural network design with efficient learning capability: Application to CT image synthesis from MRI. Med Phys 2020;47:5158-71. [Crossref] [PubMed]
- Wang Z, Bovik AC, Sheikh HR, Simoncelli EP. Image quality assessment: from error visibility to structural similarity. IEEE Trans Image Process 2004;13:600-12. [Crossref] [PubMed]
- Shiri I, Arabi H, Geramifar P, Hajianfar G, Ghafarian P, Rahmim A, Ay MR, Zaidi H. Deep-JASC: joint attenuation and scatter correction in whole-body (18)F-FDG PET using a deep residual network. Eur J Nucl Med Mol Imaging 2020;47:2533-48. [Crossref] [PubMed]
- Shidahara M, Thomas BA, Okamura N, Ibaraki M, Matsubara K, Oyama S, Ishikawa Y, Watanuki S, Iwata R, Furumoto S, Tashiro M, Yanai K, Gonda K, Watabe H. A comparison of five partial volume correction methods for Tau and Amyloid PET imaging with [18F]THK5351 and [11C]PIB. Ann Nucl Med 2017;31:563-9.
- Monga V, Li Y, Eldar YC. Algorithm unrolling: Interpretable, efficient deep learning for signal and image processing. IEEE Signal Processing Magazine 2021;38:18-44.
- Ganaie MA, Hu M, Malik AK, Tanveer M, Suganthan PN. Ensemble deep learning: A review. Engineering Applications of Artificial Intelligence 2022;115:105151.


