
A two-stage deep-learning framework for CT denoising based on a clinically structure-unaligned paired data set
Introduction
Computed tomography (CT) is a high-resolution medical imaging technique that is widely used for the detection and diagnosis of diseases, such as lung nodules. However, the radiation accumulated during CT has also raised concerns about potential health hazards (1,2). The radiation dose can be reduced by reducing the X-ray tube current or tube voltage; however, this also considerably lowers the quality of the resulting CT images and compromises the diagnostic workup (3).
Currently, low-dose CT (LDCT) is being successfully used for lung cancer screening in real clinical settings, as it can clearly depict and readily detect pulmonary nodules due to the naturally high contrast between a nodule and its surrounding air and the sparse structures in the lung. In addition, recent studies have shown the significant benefits of LDCT lung cancer screening. For example, the National Lung Screening Trial showed that compared to chest radiography, LDCT enabled the earlier detection of 13% more lung cancers and reduced 5-year lung cancer-related mortality by 20% (4). Similarly, the Dutch-Belgian Nederlands-Leuvens Longkanker Screenings Onderzoek trial showed that LDCT screening reduced 5-year mortality in lung cancer by up to 25% (5).
Based on these encouraging findings, there is now a global consensus that lung cancer should be screened using LDCT in high-risk populations, which has resulted in a surge in the number of LDCT treatments prescribed. In standard lung cancer LDCT, while lung nodules can be sensitively detected, soft-tissue lesions within the scope of scanning are hardly appreciable due to their considerably high noise level. From the perspective of health economics, if the noise level of LDCT could be further reduced without increasing the radiation dose, more lesions could be detected in the same test, which would be of great significance to the whole lung cancer screening population.
Current LDCT denoising methods can be broadly classified into three types according to their CT imaging processes: (I) projection-space denoising; (II) iterative reconstruction; and (III) image-space denoising. Projection-space denoising refers to the process of filtering projection-space data before performing image reconstruction and is a preprocessing algorithm. This technique merges photon statistics into CT data and smooths the data by optimizing the associated likelihood function using a statistical noise model (6,7) or by applying nonlinear filters that are adaptive to noise (8). Iterative reconstruction uses a reconstruction kernel to filter the input projection data, after which the filtered data are backprojected into the image space, and the final image is computed using an optimization-based framework (9), such as the total variation (TV) (10,11), non-local mean (NLM) (12,13), or low-rank (14) methods. Image-space denoising algorithms directly process the reconstructed CT images. Traditional methods, such as dictionary-based learning (15,16), and NLM (17,18) methods, and block-matching (19) algorithms have all achieved promising results.
In recent years, deep learning has demonstrated superiority over traditional methods in image-processing tasks (20-22) and has been applied to LDCT denoising (23). With the rapid development of deep-learning techniques, researchers have continued to improve methods to obtain CT images with higher quality based on the problems encountered during LDCT processing (24-33). Such methods include the introduction of generative adversarial networks (GANs) (25), perceptual losses (27), and attention mechanisms (32,33). The improvements provided by these methods have resulted in better LDCT denoising performance.
Many previous studies (24,25,27,33) have achieved impressive LDCT image denoising performance; however, almost all of these studies were based on structurally aligned synthetic or under-sampled paired data sets, which typically require processing of raw sinusoidal data and are difficult for most researchers to use. Clinically, LDCT and normal-dose CT (NDCT) scans with 100% pixel alignment derived from one patient cannot be obtained due to the involuntary physiological movements that occur during scanning, such as breathing, heartbeat, and intestinal peristalsis, even if the patient receives two consecutive scans within minutes. Additionally, ethics committees would never approve such a study design. However, when a possibly malignant disease (rather than a nodule only) is detected in LDCT, NDCT is usually prescribed within days for better characterization, diagnosis, staging, and treatment planning. Thus, many paired but not 100% pixelwise structure-unaligned LDCT and NDCT images are available for each patient in the real world.
We proposed a LDCT denoising method based on a clinically non-pixelwise structure-aligned but similar paired CT data set and two-stage training to obtain higher-quality CT images. We also employed the U-Net, residual structure, attention mechanism, and Wasserstein GAN (WGAN) strategies in the proposed method. The remainder of the article is organized as follows: (I) introduces the network framework and provides details of the proposed method, including the loss function and training method; (II) describes the data set used for the experiments and the related experimental setup; (III) sets out the experimental results of the proposed method; (IV) discusses the proposed method; (V) concludes with a summary of this article.
Methods
Figure 1 depicts the general framework of the proposed method, which consists of two stages: a pretraining stage, and a WGAN training stage. In the first stage, Gaussian noise perturbations are added to the initial NDCT scan to generate a pixelwise structurally aligned simulated LDCT scan to train the generator model. This process is completed using a pixel-level loss function to provide the model with structure recovery and denoising capabilities. In the second stage, the WGAN framework is trained on a clinically unaligned paired data set, and the generator adopts the model weights from the first stage to make the denoised CT images more consistent with the real NDCT images in terms of their data distributions. The network structure is described in detail in the next subsection.

Network architecture
U-Net-style networks have been successfully applied in various medical image-processing fields with stunning results (34,35). Hence, the generator in this article adopts a U-Net (36) style-network and introduces a residual structure (37) and an attention mechanism (38) to enhance the feature mapping and learning capabilities of the model, and to improve the stability of the model training process. The proposed network structure is depicted in detail in Figure 2, which shows the detailed structure of the generator that contains an encoder-decoder structure in the upper part of the figure. The encoder component includes four successive residual blocks and a downsampling operation. Notably, the residual connections of the residual blocks are features corrected using 1×1 convolution and batch normalization. The downsampling layer is a 2×2 maximum pooling layer, and the input of the decoder component is a single-channel CT image. The first residual block outputs a 32-channel feature map, each subsequent residual block multiplies the number of channels in the input, and the output of each residual block is connected to the decoding section.
The decoder component corresponds to the encoder component, with four consecutive upsampling blocks, a feature splicing layer, and residual blocks. Each upsampling block consists of a bilinear interpolation layer and a residual block, where the bilinear interpolation layer multiplies the size of the input feature map by 2. The feature splicing layer splices the output feature map provided by the upsampling blocks with the jump-connected feature map and inputs it into the residual blocks. The residual blocks of the decoder component halve the number of channels of the input feature map. Finally, the output layer uses a 3×3 convolution and adds the input CT image. Inspired by Cheng et al. (39), we used an attention module for feature correction in the multiscale jump connections of the model to address the semantic gap between the low- and high-level features and enhance the feature extraction capability of the model.
The discriminator uses the structure proposed by Yang et al. (27), which contains six convolutional layers and two fully connected layers. Each convolutional layer is followed by a leaky rectified linear unit (LReLU) activation function, alternating between one stride and two strides to reduce the size of the feature map. Moreover, the number of feature channels gradually increases to 256. The first fully connected layer has an output of size 1,024, which is followed by the LReLU activation function. The last fully connected layer has an output of size 1 and does not use the sigmoid activation function (40).
Attention mechanism
Attention mechanisms focus on useful information and reduce the weight of unimportant information. Previous image-processing research has achieved better effect enhancements through the introduction of attention mechanisms (32,34,41). Inspired by these works, we introduced attention mechanisms (38) into the proposed network, including channel attention and spatial attention mechanisms. Figure 3 shows their detailed structures. Each channel of the feature map can be considered a feature detector. Thus, channel attention focuses on the meaningful features in the input data, and channel attention feature maps can be generated using the interchannel relationships of the features. In the channel attention mechanism, both global max pooling and global average pooling are first applied to each input feature channel, allowing for more fine-grained channel attention. Then, the feature information obtained from the different pooling steps is aggregated through a shared fully connected layer. The final channel weight vector can be expressed as:
where GAve and GMax represent global average pooling and global max pooling operations, respectively, FC represents a shared fully connected layer, and fC represents the input feature map. The final output is the elementwise multiplication of fC and VCA, and is expressed as:
Channel attention focuses on the meaningful information in the input feature map, while spatial attention complements it by focusing on the important and useful information in the input feature map. For the computation of spatial attention, the spatial relationships of features are used to generate a spatial attention feature map of the input data. The same maximum pooling and flat pooling operations are used in the spatial attention mechanism to obtain different aggregations of spatial information. The final vector of spatial weights can be expressed as:
where Conv represents a convolution operation with 7×7 kernels, SAve and SMax represent the average pooling and max pooling operations implemented along the channel axes of the input feature map, respectively, and & denotes feature map concatenation. The final output is the elementwise multiplication of fC and VSA, and is expressed as:
Loss function
Pretraining phase
During the pretraining phase, we focused on improving the peak signal-to-noise ratio (PSNR) and structural similarity index measure (SSIM) values of the images generated by the model; the L1 and SSIM loss functions are used to provide the model with good structural recovery and denoising abilities. The loss function is expressed as follows:
where N denotes the number of pixels, and x and y denote the generated image and the reference image, respectively. Details of the SSIM formula are provided in the Appendix 1.
The feature information carried by an image is not captured by the pixel-level loss function, which usually causes excessive image smoothing and the loss of edges and details (42,43). The perceptual loss (42) takes the image features into account and optimizes the features extracted by the convolutional network as part of its objective function to reduce the feature-level difference between the generated image and the reference image. This function is semantically more similar than the pixel-level loss function, and is expressed as:
where C, H, and W represent the number of channels, height, and width of the feature layer in the deep neural network, respectively, ϕ(·) represents the feature extraction network, and Visual Geometry Group 19 (VGG–19) (44) was chosen for feature information extraction. The final loss function is:
WGAN training phase
GANs are implicit generative models that were proposed by Goodfellow et al. (45) in 2014, and they are difficult to train due to their loss functions and the lack of diversity in the sample generation process (46). Thus, Arjovsky et al. (40) proposed using Wasserstein distance as a measure of the difference between the generated image samples and real data, and their network is referred to as the WGAN. Based on this, Gulrajani et al. (47) introduced a gradient penalty to accelerate the convergence of the WGAN. The loss function used in this article is expressed as follows:
Where the first two terms of the formula are the Wasserstein distance estimation, and the last term is the gradient penalty term used for network regularization; E denotes the expectation operator; denotes the uniform sampling of pairs of estimated and reference images; the λ parameter denotes the regularization parameter used to balance the Wasserstein estimation and the gradient penalty term; Dd is the operation for distinguishing an estimated CT image from a ground-truth image; and Θ denotes the network parameters of G. Specifically, the generator D and discriminator G are trained alternately by fixing one and updating the other.
Image evaluation
We used three metrics to evaluate the performance of the proposed method: the PSNR, SSIM, and root mean square error (RMSE). The SSIM has been defined above. The PSNR is used to measure the noise level of an image and is a common metric for image quality evaluation; it is defined by the mean squared error (MSE). The mathematical expression for the MSE of two m × n images x and y if one is a noisy approximation of the other is as follows:
The PSNR is based on the MSE definition:
Where MAXx is the maximum value in the given image. The equation shows that the smaller the MSE, the larger the PSNR between images x and y, and the lower the noise level of the images.
The RMSE is an objective evaluation metric based on pixel error that reflects the degree of difference between image x and image y at the pixel level. The smaller the RMSE value, the smaller the difference between the generated image and the labeled image, and the better the image quality. The RMSE can be described by the following expression:
The P values for the various methods were calculated using the paired Student’s t-test. The significance threshold was set at 5% (P<0.05). The observed differences were statistically significant when their P values were below this threshold.
Radiologists then conducted the qualitative evaluation of the images. To assess image quality more comprehensively, two radiologists were asked to conduct a blind reading study. Twenty groups of images processed with different methods, each containing six images of the same image slice (Input, Labeled, CycleGAN, Pixel2Pixel, BM3D, and Proposed), were selected, and each image was rated according to the performance of the different methods in terms of noise suppression, artifact correction and detail preservation using a 10-point scale (on which 1= unacceptable, and 10= excellent). A combined quality score was also given to all the images.
Materials and experimental setup
The study was conducted in accordance with the Declaration of Helsinki (as revised in 2013) and was supported and approved by the Cancer Hospital Chinese Academy of Medical Sciences, Shenzhen Center. The requirement of informed consent was waived for all the included patients due to the retrospective study design.
Patient medical records were reviewed to identify patients who underwent both LDCT and NDCT at our institution between April 2019 and December 2022. The subject inclusion criteria were as follows: (I) the patients had finished both LDCT and NDCT with optimal image quality; and (II) the interval between their LDCT and NDCT treatments was less than 1 year without morphological changes. Ultimately, 64 patients were identified for inclusion in this study. The patients mainly had lung nodules, but some also had enlarged lymph nodes and liver cysts. The patients were divided randomly into two groups, a training group comprising 46 patients and a test group comprising 18 patients.
The CT images were obtained with a 256-detector row CT scanner (Revolution CT, GE Healthcare, Milwaukee, WI, USA). The CT images were reconstructed using standard algorithms with a reconstructed slice thickness of 1.25 mm. An X-ray tube voltage of 120 kV and a tube current of 20–80 mA were used for LDCT, and an X-ray tube voltage of 120 kV and a tube current of 150–500 mA were used for NDCT. All the acquired images were reviewed by two experienced radiologists (Y.X. and Z.L. who had more than 5 and 10 years of lung imaging experience, respectively). The data set comprised NDCT and LDCT images acquired from the 64 patients (200–350 CT slices per scan per patient) at different periods with resolutions of 512×512 in Digital Imaging and Communications in Medicine (DICOM) format. The CT dose information for the patient data is shown in Table 1.
Table 1
| Group | CT types | CT dose range (mGY) | Mean dose (mGY) |
|---|---|---|---|
| Training data | LDCT | 0.48–2.20 | 1.542±0.504 |
| NDCT | 7.44–18.09 | 12.044±2.919 | |
| Testing data | LDCT | 0.48–2.28 | 1.613±0.477 |
| NDCT | 8.84–18.87 | 12.624±3.537 |
The mean dose column presents the data as the mean ± standard deviation. CTDIvol, volume computed tomography dose index; LDCT, low-dose computed tomography; NDCT, normal-dose computed tomography.
During the pretraining phase, the model was optimized using the adaptive moment estimation optimizer with an initial learning rate of 1×10−3 and a tuple of (0.5, 0.999). To reduce the gradient fluctuations in the optimization step, the learning rate was also updated during training, with an update every 40 stages. The update rule for this phase was that each updated learning rate was 0.7 times the previous value, and the model was trained for a total of 200 epochs (the training time was approximately 22.8 hours). At each training step, the input image was randomly cropped to 128×128, and the batch size was set to 16.
During the WGAN training phase, the size of the image input was also 128×128, and the total number of training epochs was 200 (the training time was approximately 28 hours). The initial learning rate was set to 1×10−5, and it was updated every 40 epochs during the training process. The update rule was that the updated learning rate was 0.6 times the previous value. The batch size was set to 20, and each epoch was trained 3 times for the discriminator network and once for the generator network. The models were implemented in PyTorch (version 1.7.1) and run on a computer equipped with an NVIDIA GeForce GTX 2080Ti Graphics Processing Unit (GPU) (11.0 GB).
To evaluate the effectiveness of our approach, our method was compared with other state-of-the-art methods, including the CycleGAN, Pixel2Pixel, and block-matching and three-dimensional filtering (BM3D) algorithms. The CycleGAN network was used as the primary architecture in Chandrashekar et al.’s (48) algorithm for generating contrast-enhanced CT angiography, and Song et al.’s (49) algorithm for non-contrast CT liver segmentation. These works (48,49) demonstrated the dominant performance of the CycleGAN network for CT image reconstruction. We also included by Isola et al.’s (50) Pixel2Pixel network based on its effective performance in style-transfer tasks. The BM3D algorithm is excellent among the traditional denoising algorithms. In the comparison experiments, the models were trained with clinically structured non-aligned paired data sets.
Results
Qualitative evaluation
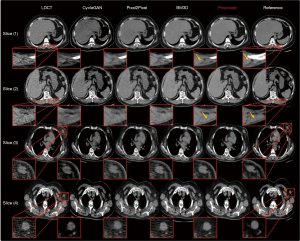
Representative slices from the test set were selected to verify the effectiveness of the proposed method. The overall subjective results of several methods are shown in Figure 4. The proposed method achieved the best noise removal results and produced the closest tissue texture to that of the reference image. The CycleGAN-processed image was considerably attenuated, causing significant changes to the image texture, which seriously affected the normal diagnostic workups. The Pixel2Pixel-processed image still retained a large amount of noise and produced a certain blurring effect, failing to achieve better results. The traditional BM3D algorithm achieved a certain level of noise reduction in the CT images, but the processed images introduced new textures and changed the original medical information in the images.
As stated above, two radiologists scored each image using a 10-point scale (on which 1= unacceptable, and 10= excellent) based on the performance of the different methods in terms of noise suppression, artifact correction and detail recovery. A combined quality score was also given to all images. As Table 2 shows, our method achieved the best scores in terms of noise suppression, artifact correction, and detail recovery, validating the effectiveness of our method from a subjective aspect.
Table 2
| Metric | Input | Label | CycleGAN | Pixel2Pixel | BM3D | Proposed |
|---|---|---|---|---|---|---|
| Noise suppression | – | – | 4.33±0.35 | 6.14±0.36 | 7.22±0.25 | 8.25±0.35 |
| Detail restoration | – | – | 4.88±0.40 | 4.88±0.40 | 6.42±0.29 | 8.77±0.20 |
| Artifact correction | – | – | 4.71±0.42 | 6.03±0.28 | 6.88±0.22 | 8.46±0.26 |
| Comprehension quality | 3.61±0.31 | 8.60±0.25 | 4.51±0.38 | 6.12±0.32 | 7.38±0.28 | 8.32±0.21 |
Data are presented as the mean ± standard deviation. CycleGAN, cycle generative adversarial network; Pixel2Pixel, image-to-image translation with conditional adversarial networks; BM3D, block-matching and 3D filtering; SD, standard deviation.
In addition to the overall image recovery effect, we also focused on the details of the recovered images (Figure 4). The slice 1 and slice 2 regions of interest (ROIs) clearly show that our method had excellent detail retention and recovery effects. The images processed by the comparison methods were worse than those of our method in terms of texture recovery and tissue structure maintenance. The ROIs in slices 3 and 4 show the patient’s nodule site, and the recovery effect of our method was closest to that of the reference image relative to the other comparison methods. CycleGAN removed the noise around the nodules; however, the intranodular portion underwent significant texture bias due to image attenuation. The images processed by Pixel2Pixel and BM3D still had much noise around the nodes.
Intensity distribution similarity
To assess the intensity distribution similarity between the processed images and the corresponding reference images (Figure 5), the liver and heart were chosen as ROIs for the test set. The probability density curves were fitted on these ROIs using the kernel density estimation function. Based on the results, the fitted curve produced using the proposed method best approximated the probability curve of the reference image. Notably, the of CycleGAN’s fitted curve showed the most severe deviation from the reference curve and possessed the lowest probability density peak, which is in line with the results in Figure 4. Both the BM3D and Pixel2Pixel algorithms yielded obvious deviations and lower peaks in their peaks fitted from the reference curve.

Quantitative evaluation
ROIs on the heart, liver, spleen, and muscle tissues in the test set were chosen for the quantitative calculation of the image evaluation metrics. Table 3 sets out the metric calculation results produced by the various methods on the ROIs. The image generated by CycleGAN had the lowest PSNR, which is consistent with it possessing the lowest probability density peak. Pixel2Pixel was not able to effectively learn the noise or produce the original structure of the images; thus, its PSNR, SSIM, and RMSE metrics were considerably lower than those of our method. The BM3D algorithm achieved better performance among the comparison methods, but our method still yielded an average improvement of approximately 7% in terms of the three evaluation indicators. Taken together, the statistical results showed that our proposed method exhibited the best denoising capability.
Table 3
| Metric | Methods | Heart | Liver | Spleen | Muscle | Mean |
|---|---|---|---|---|---|---|
| PSNR | CycleGAN | 39.05* | 37.45* | 37.46 | 39.26 | 38.31 |
| Pixel2Pixel | 46.99* | 46.69* | 38.60 | 33.33* | 41.40 | |
| BM3D | 46.37* | 44.38* | 48.48* | 45.70* | 46.23 | |
| Proposed | 49.54* | 47.65* | 48.12* | 45.26* | 47.64 | |
| SSIM | CycleGAN | 0.987* | 0.981* | 0.984 | 0.986* | 0.984 |
| Pixel2Pixel | 0.993* | 0.987 | 0.977* | 0.967* | 0.981 | |
| BM3D | 0.987* | 0.985* | 0.991* | 0.980* | 0.985 | |
| Proposed | 0.995* | 0.989* | 0.992* | 0.991* | 0.992 | |
| RMSE | CycleGAN | 0.0115* | 0.0138* | 0.0137* | 0.0110 | 0.0125 |
| Pixel2Pixel | 0.0046* | 0.0096* | 0.0098* | 0.0230* | 0.0117 | |
| BM3D | 0.0051* | 0.0064* | 0.0039* | 0.0054* | 0.0052 | |
| Proposed | 0.0033* | 0.0042* | 0.0040* | 0.0057* | 0.0043 |
*, P<0.05, corresponding to a significant difference. ROIs, regions of interest; CycleGAN, cycle generative adversarial network; Pixel2Pixel, image-to-image translation with conditional adversarial networks; BM3D, block-matching and 3D filtering; PSNR, peak signal-to-noise ratio; SSIM, structural similarity index measure; RMSE, root mean square error.
Further, to verify the effectiveness of the proposed two-stage training method, our method was compared with a network that used only WGAN training, denoted as WGAN (oneStep), and another network that used first-stage training, referred to as Proposed (firstStep). WGAN (oneStep) training is based on clinically structured unaligned paired data sets. The qualitative analysis (Figure 6) showed that the image processed by the proposed method (firstStep) retained the maximum amount of noise, while the results output by WGAN (oneStep) also retained visible noise and lost some of the tissue structure in comparison with the results of the proposed two-stage training method. Further, the quantitative analysis (Table 4) showed that the proposed method improved on the PSNR, SSIM, and RMSE metrics of the WGAN (oneStep), with an approximate average improvement of 4% and an approximate improvement of 7% compared to Proposed (firstStep). This was consistent with the results of the qualitative analysis. In summary, the proposed two-stage training method effectively enhanced the denoising ability of the used model, achieving good results in both noise removal and detail retention tasks.

Table 4
| Metric | Methods | Heart | Liver | Spleen | Muscle | Mean |
|---|---|---|---|---|---|---|
| PSNR | Proposed | 49.54* | 47.65* | 48.12* | 45.26* | 47.64 |
| WGAN (oneStep) | 48.06* | 46.77* | 46.86* | 45.30* | 46.75 | |
| Proposed (firstStep) | 47.08* | 45.77* | 46.23* | 44.35* | 45.86 | |
| SSIM | Proposed | 0.995* | 0.989* | 0.992* | 0.991* | 0.992 |
| WGAN (oneStep) | 0.992* | 0.986* | 0.988* | 0.990* | 0.989 | |
| Proposed (firstStep) | 0.992* | 0.984* | 0.988* | 0.988* | 0.988 | |
| RMSE | Proposed | 0.0033* | 0.0042* | 0.0040* | 0.0057* | 0.0043 |
| WGAN (oneStep) | 0.0039* | 0.0046* | 0.0046* | 0.0057* | 0.0047 | |
| Proposed (firstStep) | 0.0044* | 0.0052* | 0.0050* | 0.0062* | 0.0052 |
*, P<0.05, corresponding to a significant difference. WGAN, Wasserstein generative adversarial network; ROIs, regions of interest; PSNR, peak signal-to-noise ratio; SSIM, structural similarity index measure; RMSE, root mean square error.
Lesion detection evaluation
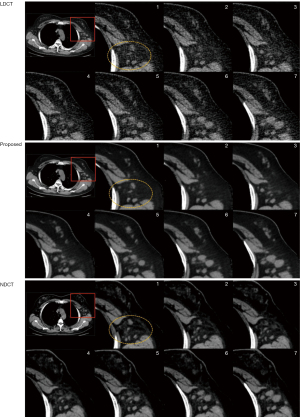
We also noted that the presence of noise around the lesions caused some masking and reduced their detectability in the LDCT images. Figure 7 shows consecutive CT images with multiple enlarged lymph nodes in the ROI of the left axillary artery. Compared with the original LDCT image, the denoised LDCT image provided a much better visualization of the lesion. This has strong clinical implications in terms of improving lesion detection and characterization in soft-tissue regions within the scanning range during LDCT screening.
Discussion
This article presented a method for LDCT denoising to obtain the corresponding NDCT image. Many deep learning-based studies have been conducted on LDCT image denoising with promising results. However, most of these studies have been based on synthesized or under-sampled paired image data sets with fully aligned structures, and these models cannot be used to process the clinically acquired data sets for which either LDCT or NDCT is available. Additionally, the performance of models trained using synthetic or under-sampled paired data sets may be inaccurate due to noise models. Our method is based on a clinically non-pixelwise structure-aligned paired CT data set collected from the real world. The proposed method effectively removes noise from LDCT images and has good detail retention, which could potentially enhance the lesion detection and characterization effects obtained for soft tissues within the scanning range of lung cancer LDCT screening. This might greatly reduce the economic cost to patients and improve the effectiveness of LDCT screening by detecting more lesions in soft tissue without increasing the required radiation hazards.
The proposed method outperformed other comparison methods both quantitatively and qualitatively. We introduced an attention mechanism that performs feature information integration on the multiscale spanning connections of the model to address the semantic gap between the underlying and higher-level features, thereby improving the quality of the generated LDCT images. These enhancements included improved denoising effects and detailed tissue structure retention. The results illustrated that the proposed two-stage training method is effective. The textural features of the CycleGAN-processed image were significantly different from those of the reference image and loses its medical significance. The subjective results and the SSIM results showed that the tissue of the Pixel2Pixel-processed image is poorly maintained, but this method achieved a certain denoising effect. The BM3D method had the best results among the compared methods but still had considerable noise around the nodules in the soft tissue. The WGAN training process focuses on fitting the data distribution between the LDCT and NDCT images. The WGAN (oneStep) achieved excellent denoising performance; however, it was significantly weaker than our method in terms of texture recovery and tissue structure maintenance, which is an important improvement provided by the two-stage training method over this one-stage training method.
Our study had several limitations. First, the proposed method is based on a two-dimensional reconstruction strategy that does not take the 3D relationships between consecutive CT images into account, and it ignores the spatial characteristics of the given CT data. Thus, this represents a direction for future work. Second, the significant anatomical differences between different body parts are not taken carefully into consideration, and this prior information may also have some influence on the results. Finally, while the proposed method outperformed other methods, the denoised LDCT images could still be improved to reach the level of real NDCT images.
Conclusions
In this article, we proposed a LDCT denoising method based on a non-pixelwise structure-aligned paired clinical data set collected in the real world to improve the lesion detection and characterization effects achieved for denoised LDCT images. This approach could potentially be used to detect more lesions in soft tissue during LDCT lung cancer screening. The model uses a U-Net-like structure and introduces an attention mechanism to enhance its denoising effect and detail retention ability to obtain higher-quality CT images. A two-stage training method is employed to give the model a good denoising capability while keeping the resulting CT images closer to the original NDCT images in terms of their attenuation distributions. The proposed method was validated in both quantitative and qualitative analyses, and it exhibited the best denoising capability compared with other methods and thus has good clinical implications.
Acknowledgments
Funding: This work was supported by
Footnote
Conflicts of Interest: All authors have completed the ICMJE uniform disclosure form (available at https://qims.amegroups.com/article/view/10.21037/qims-23-403/coif). The authors have no conflicts of interest to declare.
Ethical Statement: The authors are accountable for all aspects of the work in ensuring that questions related to the accuracy or integrity of any part of the work are appropriately investigated and resolved. This study was conducted in accordance with the Declaration of Helsinki (as revised in 2013) and was approved by the Cancer Hospital Chinese Academy of Medical Sciences, Shenzhen Center. The requirement of informed consent was waived for all the included patients due to the retrospective study design.
Open Access Statement: This is an Open Access article distributed in accordance with the Creative Commons Attribution-NonCommercial-NoDerivs 4.0 International License (CC BY-NC-ND 4.0), which permits the non-commercial replication and distribution of the article with the strict proviso that no changes or edits are made and the original work is properly cited (including links to both the formal publication through the relevant DOI and the license). See: https://creativecommons.org/licenses/by-nc-nd/4.0/.
References
- Berrington de González A, Darby S. Risk of cancer from diagnostic X-rays: estimates for the UK and 14 other countries. Lancet 2004;363:345-51. [Crossref] [PubMed]
- Miglioretti DL, Johnson E, Williams A, Greenlee RT, Weinmann S, Solberg LI, Feigelson HS, Roblin D, Flynn MJ, Vanneman N, Smith-Bindman R. The use of computed tomography in pediatrics and the associated radiation exposure and estimated cancer risk. JAMA Pediatr 2013;167:700-7. [Crossref] [PubMed]
- Jiang C, Zhang N, Gao J, Hu Z. Geometric calibration of a stationary digital breast tomosynthesis system based on distributed carbon nanotube X-ray source arrays. PLoS One 2017;12:e0188367. [Crossref] [PubMed]
- Aberle DR, Adams AM, Berg CD, Black WC, Clapp JD, Fagerstrom RM, Gareen IF, Gatsonis C, Marcus PM, Sicks JD. Reduced lung-cancer mortality with low-dose computed tomographic screening. N Engl J Med 2011;365:395-409. [Crossref] [PubMed]
- De Koning H, Van Der Aalst C, Ten Haaf K, Oudkerk M. PL02. 05 effects of volume CT lung cancer screening: mortality results of the NELSON randomised-controlled population based trial. J Thorac Oncol 2018;13:S185.
- Wang J, Li T, Lu H, Liang Z. Penalized weighted least-squares approach to sinogram noise reduction and image reconstruction for low-dose X-ray computed tomography. IEEE Trans Med Imaging 2006;25:1272-83. [Crossref] [PubMed]
- La Rivière PJ, Bian J, Vargas PA. Penalized-likelihood sinogram restoration for computed tomography. IEEE Trans Med Imaging 2006;25:1022-36. [Crossref] [PubMed]
- Manduca A, Yu L, Trzasko JD, Khaylova N, Kofler JM, McCollough CM, Fletcher JG. Projection space denoising with bilateral filtering and CT noise modeling for dose reduction in CT. Med Phys 2009;36:4911-9. [Crossref] [PubMed]
- Thibault JB, Sauer KD, Bouman CA, Hsieh J. A three-dimensional statistical approach to improved image quality for multislice helical CT. Med Phys 2007;34:4526-44. [Crossref] [PubMed]
- Hu Z, Zhang Y, Liu J, Ma J, Zheng H, Liang D. A feature refinement approach for statistical interior CT reconstruction. Phys Med Biol 2016;61:5311-34. [Crossref] [PubMed]
- Zhang Y, Zhang W, Lei Y, Zhou J. Few-view image reconstruction with fractional-order total variation. J Opt Soc Am A Opt Image Sci Vis 2014;31:981-95. [Crossref] [PubMed]
- Green M, Marom EM, Kiryati N, Konen E, Mayer A, editors. Efficient low-dose CT denoising by locally-consistent non-local means (LC-NLM). International Conference on Medical Image Computing and Computer-Assisted Intervention; 2016: Springer.
- Zhang Y, Xi Y, Yang Q. IEEE Trans Comput Imaging 2016;2:510-23. [Crossref] [PubMed]
- Cai JF, Jia X, Gao H, Jiang SB, Shen Z, Zhao H. Cine cone beam CT reconstruction using low-rank matrix factorization: algorithm and a proof-of-principle study. IEEE Trans Med Imaging 2014;33:1581-91. [Crossref] [PubMed]
- Chen Y, Yin X, Shi L, Shu H, Luo L, Coatrieux JL, Toumoulin C. Improving abdomen tumor low-dose CT images using a fast dictionary learning based processing. Phys Med Biol 2013;58:5803-20. [Crossref] [PubMed]
- Cui XY, Gui ZG, Zhang Q, Shangguan H, Wang AH. Learning-based artifact removal via image decomposition for low-dose CT image processing. IEEE Transactions on Nuclear Science 2016;63:1860-73.
- Li Z, Yu L, Trzasko JD, Lake DS, Blezek DJ, Fletcher JG, McCollough CH, Manduca A. Adaptive nonlocal means filtering based on local noise level for CT denoising. Med Phys 2014;41:011908. [Crossref] [PubMed]
- Zhang H, Ma J, Wang J, Liu Y, Han H, Lu H, Moore W, Liang Z. Statistical image reconstruction for low-dose CT using nonlocal means-based regularization. Part II: An adaptive approach. Comput Med Imaging Graph 2015;43:26-35. [Crossref] [PubMed]
- Kang D, Slomka P, Nakazato R, Woo J, Berman DS, Kuo C-CJ, Dey D, editors. Image denoising of low-radiation dose coronary CT angiography by an adaptive block-matching 3D algorithm. Medical Imaging 2013: Image Processing; 2013: SPIE.
- Wang P, Han K, Wei XS, Zhang L, Wang L, editors. Contrastive learning based hybrid networks for long-tailed image classification. Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition; 2021.
- Feng G, Hu Z, Zhang L, Lu H, editors. Encoder fusion network with co-attention embedding for referring image segmentation. Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition; 2021.
- Zamir SW, Arora A, Khan S, Hayat M, Khan FS, Yang M-H, Shao L, editors. Multi-stage progressive image restoration. Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition; 2021.
- Chen H, Zhang Y, Zhang W, Liao P, Li K, Zhou J, Wang G. Low-dose CT via convolutional neural network. Biomed Opt Express 2017;8:679-94. [Crossref] [PubMed]
- Chen H, Zhang Y, Kalra MK, Lin F, Chen Y, Liao P, Zhou J, Wang G, Low-Dose CT. With a Residual Encoder-Decoder Convolutional Neural Network. IEEE Trans Med Imaging 2017;36:2524-35. [Crossref] [PubMed]
- Hu Z, Jiang C, Sun F, Zhang Q, Ge Y, Yang Y, Liu X, Zheng H, Liang D. Artifact correction in low-dose dental CT imaging using Wasserstein generative adversarial networks. Med Phys 2019;46:1686-96. [Crossref] [PubMed]
- Wang Y, Liao Y, Zhang Y, He J, Li S, Bian Z, Zhang H, Gao Y, Meng D, Zuo W, Zeng D, Ma J. Iterative quality enhancement via residual-artifact learning networks for low-dose CT. Phys Med Biol 2018;63:215004. [Crossref] [PubMed]
- Yang Q, Yan P, Zhang Y, Yu H, Shi Y, Mou X, Kalra MK, Zhang Y, Sun L, Wang G, Low-Dose CT. Image Denoising Using a Generative Adversarial Network With Wasserstein Distance and Perceptual Loss. IEEE Trans Med Imaging 2018;37:1348-57. [Crossref] [PubMed]
- Yin X, Zhao Q, Liu J, Yang W, Yang J, Quan G, Chen Y, Shu H, Luo L, Coatrieux JL. Domain Progressive 3D Residual Convolution Network to Improve Low-Dose CT Imaging. IEEE Trans Med Imaging 2019;38:2903-13. [Crossref] [PubMed]
- Kang E, Chang W, Yoo J, Ye JC. Deep Convolutional Framelet Denosing for Low-Dose CT via Wavelet Residual Network. IEEE Trans Med Imaging 2018;37:1358-69. [Crossref] [PubMed]
- Wolterink JM, Leiner T, Viergever MA, Isgum I. Generative Adversarial Networks for Noise Reduction in Low-Dose CT. IEEE Trans Med Imaging 2017;36:2536-45. [Crossref] [PubMed]
- Meng M, Li S, Yao L, Li D, Zhu M, Gao Q, Xie Q, Zhao Q, Bian Z, Huang J, editors. Semi-supervised learned sinogram restoration network for low-dose CT image reconstruction. Medical Imaging 2020: Physics of Medical Imaging; 2020: SPIE.
- Huang Z, Chen Z, Zhang Q, Quan G, Ji M, Zhang C, Yang Y, Liu X, Liang D, Zheng H. CaGAN: A cycle-consistent generative adversarial network with attention for low-dose CT imaging. IEEE Transactions on Computational Imaging. 2020;6:1203-18.
- Li M, Hsu W, Xie X, Cong J, Gao W SACNN. Self-Attention Convolutional Neural Network for Low-Dose CT Denoising With Self-Supervised Perceptual Loss Network. IEEE Trans Med Imaging 2020;39:2289-301. [Crossref] [PubMed]
- Zhou H, Liu X, Wang H, Chen Q, Wang R, Pang ZF, Zhang Y, Hu Z. The synthesis of high-energy CT images from low-energy CT images using an improved cycle generative adversarial network. Quant Imaging Med Surg 2022;12:28-42. [Crossref] [PubMed]
- Xue H, Zhang Q, Zou S, Zhang W, Zhou C, Tie C, Wan Q, Teng Y, Li Y, Liang D, Liu X, Yang Y, Zheng H, Zhu X, Hu Z. LCPR-Net: low-count PET image reconstruction using the domain transform and cycle-consistent generative adversarial networks. Quant Imaging Med Surg 2021;11:749-62. [Crossref] [PubMed]
- Ronneberger O, Fischer P, Brox T, editors. U-net: Convolutional networks for biomedical image segmentation. International Conference on Medical Image Computing and Computer-Assisted Intervention; 2015: Springer.
- He K, Zhang X, Ren S, Sun J, editors. Deep residual learning for image recognition. Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition; 2016.
- Woo S, Park J, Lee JY, Kweon IS, editors. Cbam: Convolutional block attention module. Proceedings of the European Conference on Computer Vision (ECCV); 2018.
- Cheng S, Wang Y, Huang H, Liu D, Fan H, Liu S, editors. Nbnet: Noise basis learning for image denoising with subspace projection. Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition; 2021.
- Arjovsky M, Chintala S, Bottou L, editors. Wasserstein generative adversarial networks. International Conference on Machine Learning; 2017: PMLR.
- Anwar S, Barnes N, editors. Real image denoising with feature attention. Proceedings of the IEEE/CVF International Conference on Computer Vision; 2019.
- Johnson J, Alahi A, Fei-Fei L, editors. Perceptual losses for real-time style transfer and super-resolution. European Conference on Computer Vision; 2016: Springer.
- Ledig C, Theis L, Huszár F, Caballero J, Cunningham A, Acosta A, Aitken A, Tejani A, Totz J, Wang Z, editors. Photo-realistic single image super-resolution using a generative adversarial network. Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition; 2017.
- Simonyan K, Zisserman A. Very deep convolutional networks for large-scale image recognition. arXiv preprint arXiv:14091556. 2014.
- Goodfellow I, Pouget-Abadie J, Mirza M, Xu B, Warde-Farley D, Ozair S, Courville A, Bengio Y. Generative adversarial networks. Communications of the ACM. 2020;63:139-44.
- Arjovsky M, Bottou L. Towards principled methods for training generative adversarial networks. arXiv preprint arXiv:170104862. 2017.
- Gulrajani I, Ahmed F, Arjovsky M, Dumoulin V, Courville AC. Improved training of wasserstein gans. Advances in Neural Information Processing Systems 2017;30.
- Chandrashekar A, Shivakumar N, Lapolla P, Handa A, Grau V, Lee R, Oxford Abdominal Aortic Aneurysm (OxAAA) Study. A deep learning approach to generate contrast-enhanced computerised tomography angiograms without the use of intravenous contrast agents. Eur Heart J 2020;41:ehaa946.0154.
- Song C, He B, Chen H, Jia S, Chen X, Jia F. Non-contrast CT liver segmentation using CycleGAN data augmentation from contrast enhanced CT. Interpretable and Annotation-Efficient Learning for Medical Image Computing: Springer; 2020. p. 122-9.
- Isola P, Zhu JY, Zhou T, Efros AA, editors. Image-to-image translation with conditional adversarial networks. Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition; 2017.




