
Transferring U-Net between low-dose CT denoising tasks: a validation study with varied spatial resolutions
Introduction
The recent booming of deep learning (DL) techniques has substantially shifted the paradigm of low-dose computed tomography (LDCT) medical imaging, which aims at reducing the radiation dose of CT scans to as low as reasonably achievable (ALARA). Many studies (1-10) have investigated to seek for the advanced LDCT imaging solutions, especially for the way of generating and reconstructing CT images with higher signal-to-noise ratio (SNR) at lower radiation dose. Different from the well-known filtered back-projection (FBP) method and the iterative reconstruction (IR) method, the performance of DL approaches heavily relies on the training data, which is usually made by two sets of CT images: the expected images, i.e., the label images obtained at standard exposures; the images to be processed, i.e., the input CT images obtained at lower exposures. Afterwards, the training procedure makes the network learn to remove the noise on the LDCT images.
As required by the DL method, dedicated LDCT data always have to be gathered and prepared in advance. Take the worldwide recognized American Association of Physicists in Medicine (AAPM) LDCT imaging challenge data (11) as an example, those LDCT images were prepared for low-mAs CT imaging applications with conventional imaging spatial resolution, i.e., Δx >625 µm. In this study, Δx denoted the spatial resolution of the imaging system by default. When dealing with a different LDCT imaging task of varied spatial resolution (12), for instance, the small animal biological micro-CT imaging (13) with a spatial resolution of Δx <50 µm, it is hard to find such a well-recognized and open-sourced LDCT imaging data. Intuitively, it is viable to use the AAPM clinical LDCT image data in the low-dose micro-CT imaging applications (Figure 1). Herein, the similar object contents were assumed, namely, the anatomic structures of small animals were assumed to be similar to that of humans. Essentially, this leads to a very interesting question: can the neural network trained at one spatial resolution be transferred and applied directly onto another LDCT imaging task with different spatial resolution, provided that both the noise level and structural content are similar? If the answer to this question is positive, a specific LDCT imaging network can be easily extended without spending a lot of resources to retrain it. Consequently, many efforts such as the data preparation, network training, computation and human resources can be saved. To answer the above question, the LDCT imaging performance of a popular DL algorithm, e.g., U-Net (14), at six varied image spatial resolutions is validated in this study.
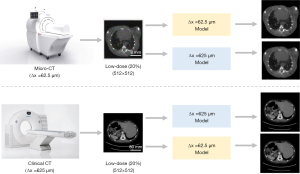
In the field of DL, some preprocessing is usually necessary if a pre-trained network model needs to be applied onto other tasks. And the most common method is transfer learning (15-18), which has been proven effective in improving the performance of neural networks on various tasks. Transfer learning can be especially useful in situations where a limited amount of data is available for the target task or when the new task is closely related to the original task. The application of the varied resolution network model in this study also involves limitations in data quantity and similarity of tasks. Therefore, some transfer learning processes have been applied to relevant network models in this study. Without changing the network structure, six sets of small amounts of target resolution image data were used to retrain the non-target resolution image model, and then applied to the denoising task of target resolution LDCT images. Through such transfer learning research, it is possible to investigate whether the generalization ability of network can be improved after the network retraining which was based on a small amount of target task data.
The rest of this article is organized as follows: the Methods section presents the CT imaging physics, numerical experiments, and details of the network training and retraining; the Results section presents the LDCT imaging results at six certain image resolutions and the network retraining results; the Discussion and Conclusions section present the discussions and a brief conclusion of this study.
Methods
CT imaging model
In CT imaging, the measured beam intensity I in detector element t at projection angle θ is expressed as
where I0,A denotes the number of incident X-ray photons, denotes the X-ray beam spectra, and denotes the Radon transform (19) of the object :
in which denotes the Dirac -function and represents an X-ray beamlet, , and . At last, CT images are reconstructed using the FBP algorithm along with Ramp filter.
Data preparation
In this study, a group of selected abdominal CT images were downloaded from the Cancer Imaging Archive (20) at https://www.cancerimagingarchive.net/ for network training and validation. The study was conducted in accordance with the Declaration of Helsinki (as revised in 2013). Before data preparations, these CT images having Hounsfield unit (HU) were converted into linear attenuation coefficient via formula: . Herein, the X-ray energy was assumed as 60 keV, and the at 60 keV was obtained from National Institute of Standards and Technology (NIST, USA).
Forward projection and FBP reconstructions were performed to generate the needed noisy CT images. In total, six spatial imaging resolutions (denoting the resolving capability of the image system) were manually selected: 62.5, 125, 250, 375, 500 and 625 µm. The main parameters are listed in Table 1. It should be noted that these resolution settings were not corresponding to certain imaging modalities, and each setting only represented a typical class of imaging modality. For example, the 62.5 µm setting denoted the typical spatial resolution of a small animal micro-CT scanner, and the 625 µm setting denoted the typical spatial resolution of a clinical CT scanner. With Poisson statistics, the used photons enable us to generate CT images with similar SNRs. No electronic noise was added in these numerical experiments. The X-ray source to detector distance (SDD) and the source to rotation center (SOD) were adjusted adaptively along with the resolution settings. Meanwhile, the dimension of the detector, denoted as , also varied along with . By default, was assumed in this work. For more details, please refer to our previous work (6,21). The animal experiment was approved by the Institutional Animal Care and Use Committee (IACUC) of the Shenzhen Institute of Advanced Technology at the Chinese Academy of Sciences and was conducted in compliance with the protocol (SIAT-IACUC-201228-YGS-LXJ-A1498; January 5, 2021) for the care and use of animals.
Table 1
| Spatial resolution | 62.5 μm | 125 μm | 250 μm | 375 μm | 500 μm | 625 μm |
|---|---|---|---|---|---|---|
| Input I0 (photons) | 3.6×104 | 1.5×104 | 1×104 | 1.5×104 | 2.5×104 | 5.6×104 |
| Label I0 (photons) | 1.8×105 | 7.5×104 | 5×104 | 7.5×104 | 1.25×105 | 2.8×105 |
| SDD (mm) | 150 | 300 | 600 | 900 | 1,200 | 1,500 |
| SOD (mm) | 75 | 150 | 300 | 450 | 600 | 750 |
The input and label photon numbers (I0) are listed in the first and second rows, the X-ray SDD and the SOD are listed in the third and fourth rows. CT, computed tomography; SDD, source to detector distance; SOD, source to rotation center.
The U-Net
In this study, the U-Net (14) proposed by Ronneberger et al. was trained. Specifically, there are 24 convolutional layers in total. The contracting branch contains 11 convolutional layers, and the number of feature channels in these layers is 32, 32, 32, 64, 64, 128, 128, 256, 256, 512 and 512, respectively. The size of the convolutional kernel is 3×3 for each layer in contracting branch, and 2×2 max pooling operations with stride 2 are applied for down-sampling. The expansive branch contains 13 convolutional layers, and the number of feature channels in these layers is 256, 256, 256, 128, 128, 128, 64, 64, 64, 32, 32, 32 and 1, respectively. The size of the convolutional kernel is 3×3 for the first layer to the twelfth layer in expansive branch, and the size of the convolutional kernel is 1×1 for the final layer in expansive branch. Additionally, 3×3 deconvolution operations with stride 2 are applied for up-sampling. The activation function was replaced by the leaky rectified linear unit (Leaky ReLU). Concatenations were added between the corresponding layers having the same image size. In addition, the mean-square-error (MSE) is selected as the network loss, which is defined as:
where y denotes the label CT images with normal dose, denotes the predicted image from the network, and m=n=512 denote the size of the images. All network training were implemented in Python with the TensorFlow library on a NVIDIA RTX A6000 GPU card.
Network training
In total, six U-Net models were trained with respect to the LDCT images having six different spatial resolutions. For a certain image resolution, 2,400 images were used for the U-Net training, 300 images were used for validation and 300 images were used for testing. Finally, the LDCT images with high resolution (Δx =62.5 µm) and the LDCT images with low resolution (Δx =625 µm) are validated by all these six network models, correspondingly. The peak signal to noise ratio (PSNR), normalized root mean square error (NRMSE) and structural similarity (SSIM) are measured to evaluate the denoising performance. The PSNR is defined as,
where MAXI denotes the maximum intensity value, and the MSE used here is calculated based on the ground truth. And the NRMSE can be denoted as
where is the mean of the cross-test predicted image, and the MSE used here is calculated based on the corresponding self-test result. In addition, the SSIM is used to measure the perceptual similarity between the cross-test LDCT and the self-test CT images, which is defined as
where denotes the self-test image, y denotes the cross-test image. And and denote the averages of and y, and denote the variance of and y, denotes the co-variance between and y, and c1 and c2 denote the two variables to stabilize the division operation.
Model retraining
Additionally, network retraining was performed for the 625 µm model by a small amount of LDCT images with 62.5 µm spatial resolution. To do so, six different amounts of data were utilized, corresponding to 5%, 10%, 15%, 20%, 25% and 30% of the original 2,400 training images. The number of images used in both validation and testing sets was fixed at 300. Afterwards, such retrained model was used to test the 62.5 µm LDCT images. Early stopping, namely, stopping the network training if the loss value does not decrease after a certain number of epochs, is used during the network retraining. Specifically, the number of retraining steps for the six groups was: 3,000 for 5% group, 5,000 for 10%, 15% and 20% groups, 6,000 for 25% group, and 7,000 for 30% group.
Results
Network loss
The training losses are plotted in Figure 2. It can be seen that the loss curves of six different resolutions exhibit similar trends, indicating the independence of the U-Net training to the spatial resolution. These CT images of different resolutions used for network training were generated with similar SNRs. The presented figure illustrates that despite the network model trained on high spatial resolution images exhibiting higher MSE values than the model trained on low resolution images, all training curves converge within an equal number of training steps. The final convergent values of these training loss curves in Figure 2 are different. We guess this might be due to the slightly different noise levels of the generated CT images at different spatial resolutions. Additionally, the network training time is listed in Table 2. Approximately, the total network training time is quite close from each other.
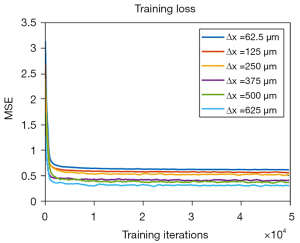
Table 2
| Model | Training steps | Computation time |
|---|---|---|
| 62.5 μm | 50,000 | 6 h 48 min |
| 125 μm | 50,000 | 6 h 52 min |
| 250 μm | 50,000 | 6 h 48 min |
| 375 μm | 50,000 | 6 h 47 min |
| 500 μm | 50,000 | 6 h 49 min |
| 625 μm | 50,000 | 6 h 48 min |
Results of high-resolution images
The high-resolution LDCT images (62.5 µm) were denoised by the U-Net model trained at the same resolution (denoted as self-test) and the U-Net model trained at other resolutions (denoted as cross-test). Results in Figure 3 demonstrate that the trained network can be used to denoise the LDCT images that have the same resolution without generating significant image artifacts. Herein, two different abdominal structures were compared. Results on Figure 4 are for the cross-tests with the other LDCT images having varied spatial resolutions. Two region-of-interests (ROIs), highlighted by the yellow and blue boxes, were selected. In addition, the difference maps with respect to the self-test result are depicted in the second and fourth rows. Obviously, these U-Net trained at different image spatial resolutions can be used to remove the image noise on the high resolution LDCT images. The PSNR values listed in Table 3 also indicate that all models can denoise the LDCT images having 62.5 µm spatial resolution.

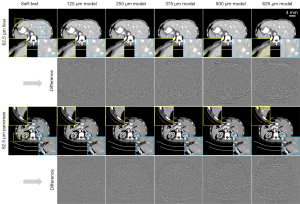
Table 3
| Test | PSNR (dB) | |||||
|---|---|---|---|---|---|---|
| 62.5 μm model | 125 μm model | 250 μm model | 375 μm model | 500 μm model | 625 μm model | |
| 62.5 μm-LDCT | 37.17±1.03 | 37.26±1.03 | 37.31±1.03 | 37.11±1.01 | 36.98±1.01 | 36.87±1.00 |
| 625 μm-LDCT | 37.06±1.01 | 37.43±1.04 | 37.71±1.05 | 37.73±1.06 | 37.71±1.06 | 37.75±1.06 |
The values are presented as mean ± standard deviation. LDCT, low-dose computed tomography; PSNR, peak signal to noise ratio.
Aside from the noise reduction, however, it can be noticed that some fake image contents were generated during the cross-test validations. For the tested high resolution LDCT images, more artificial textures show up at the edges of the images as the resolution used in U-Net model varies from 125 µm up to 625 µm, see the yellow ROIs on Figure 4. On the contrary, such artifacts are not significant for the blue ROIs located around the central vicinity. In addition, the number of residual artifacts become dramatic as the resolution discrepancy increases between the training model and the targeting validation model, see the difference images on Figure 4.
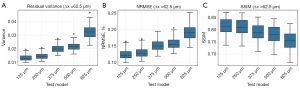
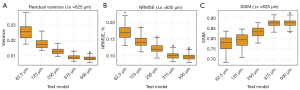
More quantitative analysis results are presented in Figure 5. In particular, the variance of the residual images is compared on Figure 5A, NRMSEs and SSIMs of the validation results are compared on Figure 5B,5C, respectively. In short, these quantitative results show high consistency with the above visual observations. As the resolution decreases, the residual variance and NRMSE values get larger, and the SSIM values get smaller, indicating a worse performance in maintaining the identical image information. In other words, cross tests with unmatched spatial resolution may introduce alien image information, e.g., random image artifacts, and thus degrades the overall image quality.
Results of low-resolution images
This study also explored the low-resolution (625 µm) LDCT imaging performance in a similar manner. Figure 6 depicts the self-test results. Likewise, the outcomes indicate that the trained network can be employed to effectively denoise the LDCT images having the same resolution. Herein, two different abdominal structures were compared. The cross-test results presented in Figure 7 demonstrate that the U-Net models trained with other resolution datasets can be used to denoise the low-resolution (625 µm) LDCT images. This is consistent with the results obtained from the validations of high-resolution (62.5 µm) LDCT data. Specifically, two ROIs were highlighted and the corresponding residual images are illustrated in the second and fourth rows. Table 3 presents the quantitative analysis results, which also demonstrate that all the U-Net models are capable of effectively denoise the low-resolution LDCT images.


In contrast to the high-resolution validations, the occurrence of artifacts on the periphery of the CT images was rare and less prominent in such low-resolution validations, see the yellow ROIs in Figure 7. However, the sharpness of the denoised low-resolution LDCT images gradually degrades as the spatial resolution of the training data increases from 500 to 62.5 µm, see the two highlighted ROIs on Figure 7. As the resolution disparity between the training data and testing data increases, the amount of residual artifacts also escalates, see the residual images in Figure 7.
The measured residual variance, NRMSEs, and SSIMs results were plotted in Figure 8, respectively. These quantitative results indicate a gradual degradation of the cross-test outcomes as the spatial resolution varies. These findings again demonstrate that the network validation using inconsistent resolutions would introduce artifacts to the denoised LDCT images, thereby diminishing the generalization capability among different network models.
Results of network retraining
With the purpose to enhance the LDCT denoising performance of the cross tests, network retraining was investigated with the low-resolution model (625 µm). Namely, the U-Net that has already been trained by the low-resolution LDCT images was retrained by a small fraction of high-resolution LDCT images (62.5 µm). The retraining losses are plotted in Figure 9. It should be noted that each group utilized different training data, and to avoid overfitting, the number of training steps performed by each group varied. Therefore, each group stopped training at the point of their lowest loss value, which was approximately similar across the groups.

Afterwards, LDCT images having 62.5 µm pixel size are validated by the fine-tuned low-resolution model (625 µm). Obviously, network retraining can significantly improve the LDCT denoising performance, especially in reducing the alien image artifacts around the edges of the object, see the zoom-in ROIs in Figure 10. As expected, increasing the amount of retraining data would benefit the final denoising performance, see the residual images in Figure 10.
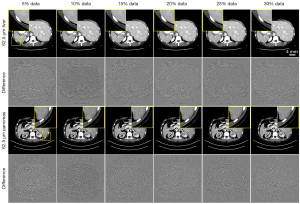
Quantitative analysis results are presented in Figure 11. It is found that the image quality gets almost unchanged when the amount of retrained data is about 20% of the total number of training samples. Interestingly, further increasing the amount of retrained data does not result in significant improvement of image quality. Eventually, results obtained from the retrained network show close image quality to the ones obtained from the cross-tests with 125 µm model.

Noise property
In this part, noise-only CT images are studied and presented (Figure 12). Visually, such noise-only CT images contain unique features and look quite different at varied spatial resolutions. For instance, the noise texture on Figure 12A is quite uniform for CT images having 62.5 µm pixel size. Whereas, residual streaking signals gradually become apparent at the edges of the noise-only CT images as the image resolution decreases, see Figure 12F. We speculate that such differences in noise texture may be the root cause for blocking the transfer of U-Net between different LDCT denoising tasks with varied spatial resolutions.

Discussion
In this work, the feasibility of using the same LDCT denoising neural network, which has been trained at a certain image resolution in advance, directly onto another LDCT imaging application having different image resolution has been investigated. Herein, the most popular image-domain based neural network U-Net was employed to remove the LDCT image noise. Evaluations were performed on the data generated from the clinical CT images having six spatial resolutions.
It was found that the U-Net can efficiently remove the CT image noise for self-test and cross-test. Its denoising capability is fairly independent of the image spatial resolution. Whereas, its denoising performance is strongly correlated with the image spatial resolution (assuming the same attenuation coefficients). We guess this is mainly due to the inconsistent CT image noise textures among different image resolutions. In particular, strong streaking noise textures are easily obtained at low image resolution, regardless of the angular sampling rate. As the image resolution increases, these streaking noise textures become less significant, and more uniformed noise maps are obtained. Because of these residual noise streaks, as a consequence, the immediate transformations of the U-Net between different LDCT image resolutions get challenged, especially when generating high-quality CT images. For instance, noticeable structural artifacts were presented at the edges of the object when denoising the high-resolution CT image by the U-Net trained with a lower resolution. As a contrary, in the process of denoising the low-resolution CT image by the higher resolution CT images trained U-Net, there were still some dispersion artifacts and image blurring in the middle area of the image.
Usually, the image denoising procedure would degrade the image resolution due to the blurring effect. As a consequence, balance and trade-off are often needed to remove most of the image noise while minimally impacting the image resolution. Specifically, some previous studies (22,23) have demonstrated that such image resolution degradation may depend on the object contrast: the image gets more blurred at the regions having low contrast. Despite of the important interplay between image noise and image resolution, however, this topic is beyond the main scope of this study, which only focuses on discussing the reproducibility of the denoising performance of a given network, which has already been trained in advance, among varied LDCT image datasets acquired from different imaging systems with varied resolutions. Usually, the resolution of an imaging system is defined and measured without considering the image noise.
Since it is quite difficult to completely remove such noise induced streaking features on CT images, especially for the diagnostic CT modalities (24) with spatial resolution Δx >500 µm, therefore, the current answer to the aforementioned question at the beginning of this article tends to be negative. Namely, the DL based neural network for LDCT imaging trained at one image resolution cannot be directly transferred and applied to another LDCT imaging task with a varied image resolution, even if the dose reduction ratio and the object content are similar. With the attempt to partially address this issue, network retraining was performed. It was found that only about 20% of the original samples is enough to improve the overall LDCT denoising performance. In future, if it is feasible to sufficiently remove such noise induced streaking features by utilizing novel CT image hardware, data acquisition strategies and other image reconstruction methods (25-29), we believe the same DL network could be directly transferred between different LDCT imaging applications having varied spatial resolutions without the need of additional network retraining. By that time, a great number of efforts and resources such as the data preparation and network training can all be saved.
This study has several limitations. First, only one single DL-based CT image denoising algorithm, i.e., the U-Net, was validated. For other CT image denoising networks, e.g., GAN based DL algorithms (30-32) and 3D U-Net (33), we do not know how the results would become and careful comparisons are needed in future. Second, the different resolution data in this study were only obtained through numerical experiments of clinical CT images, and more evaluations of LDCT physical experiments need to be investigated in the future.
Conclusions
In conclusion, the DL based LDCT image denoising algorithms maybe sensitive to the CT noise textures. As a result, it is not recommended to apply the same U-Net for LDCT denoising tasks performed at different spatial resolutions to generate the same high-quality LDCT images. An optional solution is to retrain the network model with a very small amount of the target resolution data. Such transfer learning can effectively avoid introducing additional image artifacts and hence improve the model’s denoising ability for LDCT denoising tasks with different resolutions.
Acknowledgments
Funding: This work was supported by
Footnote
Conflicts of Interest: All authors have completed the ICMJE uniform disclosure form (available at https://qims.amegroups.com/article/view/10.21037/qims-23-768/coif). D.L. serves as an unpaid editorial board member of Quantitative Imaging in Medicine and Surgery. The other authors have no conflicts of interest to declare.
Ethical Statement: The authors are accountable for all aspects of the work in ensuring that questions related to the accuracy or integrity of any part of the work are appropriately investigated and resolved. The study was conducted in accordance with the Declaration of Helsinki (as revised in 2013). The animal experiment was approved by the Institutional Animal Care and Use Committee (IACUC) of the Shenzhen Institute of Advanced Technology at the Chinese Academy of Sciences and was conducted in compliance with the protocol (No. SIAT-IACUC-201228-YGS-LXJ-A1498; January 5, 2021) for the care and use of animals.
Open Access Statement: This is an Open Access article distributed in accordance with the Creative Commons Attribution-NonCommercial-NoDerivs 4.0 International License (CC BY-NC-ND 4.0), which permits the non-commercial replication and distribution of the article with the strict proviso that no changes or edits are made and the original work is properly cited (including links to both the formal publication through the relevant DOI and the license). See: https://creativecommons.org/licenses/by-nc-nd/4.0/.
References
- Chen H, Zhang Y, Kalra MK, Lin F, Chen Y, Liao P, Zhou J, Wang G, Low-Dose CT. With a Residual Encoder-Decoder Convolutional Neural Network. IEEE Trans Med Imaging 2017;36:2524-35. [Crossref] [PubMed]
- Wu D, Kim K, El Fakhri G, Li Q. Iterative Low-Dose CT Reconstruction With Priors Trained by Artificial Neural Network. IEEE Trans Med Imaging 2017;36:2479-86. [Crossref] [PubMed]
- Zhu B, Liu JZ, Cauley SF, Rosen BR, Rosen MS. Image reconstruction by domain-transform manifold learning. Nature 2018;555:487-92. [Crossref] [PubMed]
- Yin X, Zhao Q, Liu J, Yang W, Yang J, Quan G, Chen Y, Shu H, Luo L, Coatrieux JL. Domain Progressive 3D Residual Convolution Network to Improve Low-Dose CT Imaging. IEEE Trans Med Imaging 2019;38:2903-13. [Crossref] [PubMed]
- Li Y, Li K, Zhang C, Montoya J, Chen GH. Learning to Reconstruct Computed Tomography Images Directly From Sinogram Data Under A Variety of Data Acquisition Conditions. IEEE Trans Med Imaging 2019;38:2469-81. [Crossref] [PubMed]
- Ge Y, Su T, Zhu J, Deng X, Zhang Q, Chen J, Hu Z, Zheng H, Liang D. ADAPTIVE-NET: deep computed tomography reconstruction network with analytical domain transformation knowledge. Quant Imaging Med Surg 2020;10:415-27. [Crossref] [PubMed]
- He J, Wang Y, Ma J. Radon Inversion via Deep Learning. IEEE Trans Med Imaging 2020;39:2076-87. [Crossref] [PubMed]
- Su T, Cui Z, Yang J, Zhang Y, Liu J, Zhu J, Gao X, Fang S, Zheng H, Ge Y, Liang D. Generalized deep iterative reconstruction for sparse-view CT imaging. Phys Med Biol 2022;
- Ma G, Zhao X, Zhu Y, Zhang H. Projection-to-image transform frame: a lightweight block reconstruction network for computed tomography. Phys Med Biol 2022;
- Tamura A, Mukaida E, Ota Y, Nakamura I, Arakita K, Yoshioka K. Deep learning reconstruction allows low-dose imaging while maintaining image quality: comparison of deep learning reconstruction and hybrid iterative reconstruction in contrast-enhanced abdominal CT. Quant Imaging Med Surg 2022;12:2977-84. [Crossref] [PubMed]
- McCollough C. TU-FG-207A-04: overview of the low dose CT grand challenge. Medical Physics 2016;43:3759-60.
- Sidky EY, Pan X. Report on the AAPM deep-learning sparse-view CT grand challenge. Med Phys 2022;49:4935-43. [Crossref] [PubMed]
- Touch M, Clark DP, Barber W, Badea CT. A neural network-based method for spectral distortion correction in photon counting x-ray CT. Phys Med Biol 2016;61:6132-53. [Crossref] [PubMed]
- Ronneberger O, Fischer P, Brox T. U-net: Convolutional networks for biomedical image segmentation. In: Medical Image Computing and Computer-Assisted Intervention–MICCAI 2015: 18th International Conference, Munich, Germany, October 5-9, 2015, Proceedings, Part III 18. Springer International Publishing, 2015: 234-241.
- Pan SJ, Yang Q. A survey on transfer learning. IEEE Transactions on Knowledge and Data Engineering 2010;22:1345-59.
- Torrey L, Shavlik J. Transfer learning. In: Handbook of research on machine learning applications and trends: algorithms, methods, and techniques. Hershey: IGI global, 2010: 242-264.
- Weiss K, Khoshgoftaar TM, Wang DD. A survey of transfer learning. Journal of Big Data 2016;3:9.
- Zhuang F, Qi Z, Duan K, Xi D, Zhu Y, Zhu H, Xiong H, He Q. A comprehensive survey on transfer learning. Proceedings of the IEEE 2020;109:43-76.
- Kak AC, Slaney M. Principles of Computerized Tomographic Imaging. Philadelphia: Society for Industrial and Applied Mathematics, 1988.
- Roth HR, Farag A, Turkbey E, Lu L, Liu J, Summers RM. Data from pancreas-CT. The cancer imaging archive. IEEE Transactions on Image Processing, 2016. doi:
10.7937/K9/TCIA.2016.tNB1kqBU . - Zhang X, Su T, Yang J, Zhu J, Xia D, Zheng H, Liang D, Ge Y. Performance evaluation of dual-energy CT and differential phase contrast CT in quantitative imaging applications. Med Phys 2022;49:1123-38. [Crossref] [PubMed]
- Li K, Tang J, Chen GH. Statistical model based iterative reconstruction (MBIR) in clinical CT systems: experimental assessment of noise performance. Med Phys 2014;41:041906. [Crossref] [PubMed]
- Li K, Garrett J, Ge Y, Chen GH. Statistical model based iterative reconstruction (MBIR) in clinical CT systems. Part II. Experimental assessment of spatial resolution performance. Med Phys 2014;41:071911. [Crossref] [PubMed]
- Hsieh J, Nett B, Yu Z, et al. Recent advances in CT image reconstruction Current Radiology Reports 2013;1:39-51. [J].
- Hsieh SS, Pelc NJ. The feasibility of a piecewise-linear dynamic bowtie filter. Med Phys 2013;40:031910. [Crossref] [PubMed]
- Liu F, Yang Q, Cong W, Wang G. Dynamic bowtie filter for cone-beam/multi-slice CT. PLoS One 2014;9:e103054. [Crossref] [PubMed]
- Willemink MJ, Persson M, Pourmorteza A, Pelc NJ, Fleischmann D. Photon-counting CT: Technical Principles and Clinical Prospects. Radiology 2018;289:293-312. [Crossref] [PubMed]
- Flohr T, Petersilka M, Henning A, Ulzheimer S, Ferda J, Schmidt B. Photon-counting CT review. Phys Med 2020;79:126-36. [Crossref] [PubMed]
- Leng S, Bruesewitz M, Tao S, Rajendran K, Halaweish AF, Campeau NG, Fletcher JG, McCollough CH. Photon-counting Detector CT: System Design and Clinical Applications of an Emerging Technology. Radiographics 2019;39:729-43. [Crossref] [PubMed]
- Wolterink JM, Leiner T, Viergever MA, Isgum I. Generative Adversarial Networks for Noise Reduction in Low-Dose CT. IEEE Trans Med Imaging 2017;36:2536-45. [Crossref] [PubMed]
- Hu Z, Jiang C, Sun F, Zhang Q, Ge Y, Yang Y, Liu X, Zheng H, Liang D. Artifact correction in low-dose dental CT imaging using Wasserstein generative adversarial networks. Med Phys 2019;46:1686-96. [Crossref] [PubMed]
- Zhou H, Liu X, Wang H, Chen Q, Wang R, Pang ZF, Zhang Y, Hu Z. The synthesis of high-energy CT images from low-energy CT images using an improved cycle generative adversarial network. Quant Imaging Med Surg 2022;12:28-42. [Crossref] [PubMed]
- Shan H, Zhang Y, Yang Q, Kruger U, Kalra MK, Sun L. IEEE Trans Med Imaging 2018;37:1522-34. [Crossref] [PubMed]


