
In vitro and clinical validation of different correction algorithms for the two-dimensional proximal isovelocity surface area method in a low-velocity flow field for quantifying tricuspid regurgitation
Introduction
Severe tricuspid regurgitation (TR) is associated with an increased mortality risk irrespective of pulmonary pressures and right ventricle (RV) dysfunction (1). However, these patients are often referred too late, and thus accurate severity grading may permit effective therapy at an earlier stage to improve survival (2). Current guidelines recommend a multiparametric approach that integrates qualitative, semiquantitative, and quantitative findings to estimate TR severity (3,4). The 2-dimensional proximal isovelocity surface area (2D PISA) method is the recommended approach for quantifying TR. This method relies on the accurate estimation of PISA, which is based on the measurement of its radius and subsequent calculation under the assumption of a hemispheric shape (Figure 1A,1B). However, previous in vitro studies demonstrated the hemispheric assumption is violated by variable regurgitant orifice and valve geometry (irregular PISA shape) as well as contour flattening (hemiellipsoid PISA shape) under low regurgitant velocities (5-10) (Figure 1C-1E), with the latter being the major source of error (11). Recent clinical studies comparing the 2D PISA method against other quantitative measurements also revealed significant underestimation of TR severity by 2D PISA (12,13).

Pilot studies proposed different algorithms to correct the underestimation caused by low peak regurgitant velocity (5,14) (Figure 1). For instance, Rodriguez et al. found that 2D PISA method progressively underestimated regurgitant flow when the velocity at PISA shell (Valiasing) approached the peak velocity through the regurgitant orifice (Vorifice) and proposed to correct the effective regurgitant orifice area (EROA) through multiplying by Vorifice/(Vorifice − Valiasing) (14). Deng et al. observed that when the pressure gradient was less than 40 mmHg, the effect of hemiellipsoid PISA shape could no longer be adjusted through decreasing the Valiasing but could be corrected empirically by dividing the EROA by a constant of 0.7 (5). However, these algorithms were proposed based on computational modeling and steady flow settings (constant flow rate through an orifice) and have yet to be validated either in pulsatile low-pressure models that mimic the flow environment of the right heart (changing instantaneous flow rate during every beat) or clinically for TR. The advantages and disadvantages of both the in vitro and in vivo methods are summarized in Figure 2. The in vitro method provides a gold standard reference but can only replicate a limited number of either flow conditions or valve geometry while the in vivo validation is valid for everyday clinical scenarios but does not have a universally-accepted reference standard.

Therefore, the aim of this study was (I) to examine the accuracy of different correction algorithms applied to the conventional 2D PISA method in pulsatile low-pressure models and (II) to compare the utility of these 2D PISA correction techniques to that of quantitative volumetric methods and vena contracta (VC) area in diagnosing severe TR.
Methods
In vitro validation
In vitro validation was performed on a multifunctional valve tester (PPD-1000, Shanghai Heartpartner Testing Equipment Co., Ltd., Shanghai, China) which consisted of a pulsatile bump, a ventricle chamber, a flow meter (transit-time ultrasonic flow probe, Transonic Systems, Inc., Ithaca, NY, USA) that measured the volume of fluid passing from the ventricle chamber into the arterial compliance module, the atrium chamber, and its compliance module (Figure 3A).

The circulatory fluid consisted of 30% glycerin, 70% water, and 1% corn starch added as ultrasound scattering particles in order to mimic the blood viscosity (15). Two millimeter-thick polytetrafluoroethylene plates with different regurgitant orifice areas (20, 30, or 80 mm2) were placed between the atrium and ventricle module. All orifices were circular. The bump was controlled via a computer that could adjust the speed and stroke length of the piston, which in turn determined the pressure wave form and stroke volume generated by the piston, respectively. The regurgitant volume (RVol) was defined as the difference between the stoke volume (SV) generated by the piston and the volume passing through the arterial end. The true EROA was calculated by dividing the RVol by the velocity-time integral (VTI) of the regurgitant jet as measured via continuous-wave (CW) Doppler (Figure 3B). The true EROAs acquired during three consecutive beats were averaged.
The heart rate was set to 72 beats per minute (a heart rate mimicking the normal human range was intended with lower heart rates being attempted, but it was difficult to maintain a steady pulsatile flow without beat-to-beat variation under a low-pressure and low-pulse-frequency condition). The regurgitant stroke volume was controlled between 14 to 40 mL per beat (the stroke volume was arbitrarily adjusted to select volumes that could maintain stable piston operation), and the resultant peak pressure gradient ranged from 7 to 45 mmHg. Two-dimensional and Doppler echocardiographic examination of the in vitro model was performed using an Acuson SC2000 Prime (Siemens Healthineers, Erlangen, Germany) with a 4V1c probe.
Conventional 2D PISA method and correction under a low-regurgitant-pressure gradient
The baseline was shifted to 11, 22, 32 and 43 cm/s for PISA measurement during 2D color Doppler echocardiography (CDE). An optimized PISA shell was defined as that most representative of a round shape (Figure 6).

Two previously described correction procedures were used to account for the contour flattening of the proximal flow convergence region under a low-regurgitant-pressure gradient (5,14) (Figure 1). One of these correction methods involves dividing the 2D PISA EROA by a factor of 0.7 and was referred to as EROA0.7. The other method involves multiplying the unadjusted EROA by Vorifice/(Vorifice − Valiasing), where Vorifice is the TR jet velocity, and Valiasing is the color aliasing velocity (EROAVo-Va); this method was referred to as EROAVo-Va. Meanwhile, uncorrected EROAs were referred to as EROAUC.
Clinical validation
For the clinical validation cohort, we enrolled 150 consecutive inpatients who were undergoing clinically indicated transthoracic echocardiography (TTE) for elective cardiac surgery and who presented with more-than-mild TR at Zhongshan Hospital, Fudan University, from June of 2018 to December of 2019. The TTE session was routinely ordered the day before surgery at Zhongshan Hospital. Patients with any of the following conditions were not included in the study: intracardiac shunts, concomitant valvular lesions (more-than-mild pulmonary stenosis or pulmonary insufficiency), presence of a prosthetic tricuspid valve, incomplete visualization of the flow convergence region, and inadequate acoustic window (Figure S1). This study was approved by the ethics committee of Zhongshan Hospital, Fudan University, and conducted in accordance with the Declaration of Helsinki (as revised in 2013). Written consent was obtained from every patient.
Echocardiographic examination
A 2D and 3D transthoracic echocardiographic examination was performed on a commercially available ultrasound platform (Vivid E95, GE Healthcare, Chicago, IL, USA) with either a 2D or 3D probe as appropriate. Intraoperative transesophageal echocardiography (TOE), which has better spatial resolution, is typically performed for every surgical patient as a clinical routine, but TOE was not employed as part of this study, as the time constraints on perioperative settings precluded the acquisition of a 3D dataset of the RV and 3D color Doppler images, which require fine tuning to achieve a balance between spatial and temporal resolution.
A minimum of six consecutive beats were collected to capture the complete respiratory cycle. Measurements were averaged from all the recorded images to eliminate the potential impact of respiratory variation and atrial fibrillation. The assessment of the TR mechanism involved the integration of findings from various cardiac structures, including the right atrium, tricuspid annulus, valve leaflets, subvalvular apparatus, and RV. The primary TR referred only to TR due to primary leaflet abnormality, as indicated in the regurgitation evaluation guidelines (3). Both image acquisition (Y.L. and B.C.) and analysis (Y.L. and Y.W.) were performed by experienced cardiologists.
2D echocardiography
2D echocardiography was performed according to the current guidelines (16). The baseline was shifted to 18 to 40 cm/s for PISA measurement during 2D CDE to achieve an optimized PISA shell most representative of a round shape (Figure 6). VC width was obtained from the apical 4-chamber view (A4C). For jet area or PISA radius measurement, additional views were assessed to optimize the visualization of the jet or to align the sample line with the flow. Angle correction for 2D PISA was applied as per the relevant guidelines (3), and low-regurgitant-velocity correction was calculated as in vitro model.
3D echocardiography
3D volumes were acquired from the RV-focused A4C. The patient was positioned in the steep left lateral orientation. Sector size and depth were fine-tuned to encompass the complete RV while a volume rate of 20 to 25 volumes per second was maintained. The dataset was exported for subsequent analysis with dedicated software (4D RV-Function 2.0; TomTec Imaging Systems, Unterschleissheim, Germany) to obtain the RV end-diastolic volume (RVEDV), RV end-systolic volume (RVESV), and RV SV.
The 3D VC area (VCA) was acquired and measured as previously described with minimal color gain (−4 dB, 10–20%) (17). Specifically, the frame closest to the time of peak velocity on CW spectral display was chosen in order to achieve concomitant timing with 2D PISA measurement. The two perpendicular longitudinal planes were aligned to match the color jet’s orientation, and the transverse plane was shifted to the point where the cross-sectional area was minimized. The VCA could then be directly planimetered on the transverse plane (Figure 4).

Reference standard
TR was graded using the guideline-recommended integral approach (3). Specific criteria for mild TR included (I) a thin and small central color jet; (II) a VC width less than 0.3 cm from A4C; (III) a PISA radius less than 0.4 cm at Nyquist 30–40 cm/s; (IV) incomplete or faint CW Doppler jet spectrum; (V) systolic dominant hepatic vein flow; (VI) tricuspid A-wave-dominant inflow, and (VII) a normal RV and right atrium (RA). Criteria for severe TR included (I) dilated annulus with no valve coaptation or flail leaflet; (II) large central jet occupying more than 50% of the RA; (III) a VC width greater than 0.7 cm from A4C; (IV) a PISA radius greater than 0.9 cm at Nyquist 30–40 cm/s; (V) a dense and triangular CW jet or sine wave pattern; (VI) systolic reversal of hepatic vein flow, and (VII) a dilated RV with preserved function. If four or more of the specific criteria were met, TR was graded mild or severe. If fewer than four of the criteria or contradictory measurement values were present, quantitative measurements would be performed including (I) averaged VC width taken from A4C and the RV inflow view with cutoffs of 0.3 and 0.7 cm, respectively; (II) direct-planimetered VCA with cutoffs of 0.2 and 0.4 cm2; and (III) RVol calculated through the volumetric approach with cutoffs of 30 and 45 mL. The severity was determined based on the majority of the three quantitative parameters. The severity grading was performed by Y.L., B.C. and L.D. at least 2 months before comprehensive 2D PISA calculation, with these observers being blinded to the grades when the index 2D PISA parameters were measured.
VCA and volumetric RVol, respectively, were chosen to substitute for EROA and RVol by conventional 2D PISA as recommended by the current guidelines, as the 2D PISA method was the method being evaluated.
The volumetric approach calculated the tricuspid RVol by subtracting the right ventricular outflow tract (RVOT) forward SV from the RV SV (Figure 5). The RVOT SV was calculated as the result of multiplying the cross-sectional area with the VTI of the RVOT. Both the RVOT diameter and the VTI were measured at the pulmonary valve annulus from the parasternal short-axis view on a midsystolic frame. The RV SV was calculated as the difference between the RV EDV and RV ESV, both of which were obtained from 3D echocardiography as described above. The volumetric EROA was then calculated as RVol divided by the VTI of TR. The reference EROA in multilinear regression analysis was calculated as the mean of the VCA and volumetric EROA.

Statistical analysis
The Kolmogorov-Smirnov test for normality was performed on all data sets. Continuous data are expressed as the mean ± standard deviation (SD) or as median (interquartile range) according to data distribution, and categorical data are presented using percentages and frequencies. Continuous data of the baseline characteristics were compared using analysis of variance (ANOVA) with Geisser-Greenhouse correction, post hoc comparisons were made using Dunn-Šidák correction, and frequencies were compared using the chi-squared test. EROAs of different correction algorithms were compared using simple linear regression, and the agreement was tested using Bland-Altman analysis directly or after logarithmic transformation depending on the data distribution. The correlations were reported using the Pearson correlation coefficient (r). Multivariable linear regression analysis was performed to identify the factors associated with the underestimation of conventional 2D PISA method, which was defined as the difference between the reference EROA and that of the uncorrected 2D PISA. Candidate independent variables were selected based on previous studies [systolic pulmonary artery pressure, Vorifice/(Vorifice − Valiasing)] (5,14), clinical considerations in valve regurgitation quantitation (etiology, atrial fibrillation), and the theoretical hydrodynamic model of PISA [reference EROA, RVEDV, the ratio of reference EROA to RVEDV (reference EROA/RVEDV)]. These three candidate types were specifically included because the proximal flow convergence zone would interfere with the ventricle and invalidate the hemispheric assumption when the regurgitant orifice was sufficiently large to approach the ventricular wall. These candidates were entered into the multivariable regression model simultaneously, and the final model excluded the reference EROA due to its colinearity with reference EROA/RVEDV. The units used for per-unit changes in the model were mmHg for RV systolic pressure, mm2 for reference EROA and the dependent variable, and mL for RVEDV. Receiver operating characteristic (ROC) curve analysis was used to determine the grading accuracy of the quantitative parameters. The maximal Youden index (sensitivity + specificity − 1) was used to define the best cutoffs in ROC analysis. 2D PISA-derived EROA, volumetric EROA, and VCA measurements from 10 patients were repeatedly acquired by the same observer (Y.L.) and a different observer (Y.W.) to determine intra- and interobserver variability. Patients were chosen randomly for this test. Both investigators possess specialized expertise in quantifying TR and were unaware of each other’s findings. The repeated measurements were conducted no less than 3 months after the initial measurements were taken.
All statistical tests were 2-tailed, and P values <0.05 were considered to indicate statistical significance. Statistical analysis was performed using GraphPad Prism version 9.4 (GraphPad Software, San Diego, CA, USA) and SPSS version 26.0 (IBM Corp., Armonk, NY, USA).
Results
In vitro model
Figure 7 shows the calculated EROA, either corrected or not, plotted against the true EROA for the three circular orifices (0.20, 0.30, and 0.80 cm2) at various aliasing velocities (0.11, 0.22, 0.32, and 0.43 cm/s). There was good correlation between the calculated EROAs and the true EROA (r=0.85, r=0.88, and r=0.85 for EROAUC, EROAVo-Va, and EROA0.7, respectively; all P values <0.0001). However, EROAUC and EROAVo-Va demonstrated significant underestimation of the true EROA (both P values <0.0001, Friedman test), while EROA0.7 only slightly underestimated the true EROA. Both correction algorithms lessened the magnitude of underestimation and narrowed the limits of agreement compared with the true EROA (Figure 7C-7E).

Figure 8 illustrates the relationship between the calculated EROAs and the true EROA after aliasing velocity optimization (when the proximal flow convergence zone was most representative of a round shape). As the optimization involved one measurement under a certain aliasing velocity over the other three (chosen from 11, 22, 32, and 43 cm/s), the sample size was one-fourth of that presented in Figure 7. The mean and SD of the selected optimized aliasing velocities were 24 and 7 cm/s, respectively. The correlation became better (r=0.98, r=0.97, and r=0.98 for EROAUC, EROAVo-Va, and EROA0.7, respectively; all P values <0.0001), and EROAVo-Va only produced an underestimation mean of 0.02 cm2 compared with the true EROA (P=0.3163, 1-way ANOVA), while EROA0.7 overestimated the true EROA with a mean bias of 0.05 cm2 (P=0.0032, 1-way ANOVA) (Figure 8).

Clinical validation
Patient characteristics
Initially, 150 patients were screened, but 10 were excluded due to incomplete 3D images of the RV, 8 due to a poor acoustic window, and 1 due to severe pulmonary regurgitation. Ultimately, 131 patients were successfully enrolled and studied. Patients’ baseline characteristics and 2D and 3D echocardiographic parameters are shown in Table 1. Among the whole patient population and among those with severe TR, 59.8% and 73.2% were receiving diuretics, respectively.
Table 1
| Variable | Primary TR | Functional TR | P | |||
|---|---|---|---|---|---|---|
| Nonsevere (n=13) | Severe (n=24) | Nonsevere (n=64) | Severe (n=30) | |||
| Age (years) | 61±15 | 60±11 | 61±11 | 62±10 | 0.931 | |
| Gender, male | 7 (54%) | 8 (33%) | 21 (33%) | 10 (33%) | 0.535 | |
| BSA (m2) | 1.51±0.19 | 1.53±0.16 | 1.55±0.15 | 1.60±0.19 | 0.224 | |
| Heart rate (bpm) | 80±14 | 76±14 | 85±18 | 80±15 | 0.096 | |
| Atrial fibrillation | 9 (69%) | 14 (58%) | 41 (64%) | 23 (77%) | 0.516 | |
| CI (mL/min/m2) | 2.09±0.75 | 2.06±0.76 | 1.85±0.54 | 1.94±0.60 | 0.427 | |
| sPAP (mmHg) | 43±14 | 37±11 | 43±16 | 41±16 | 0.386 | |
| TR VTI (cm) | 86.6±20.5 | 74.9±19.2 | 86.6±23.0 | 81.9±18.9 | 0.149 | |
| 2DE quantitative parameters | ||||||
| VCW (mm) | 5.5±1.4 | 8.1±2.3 | 4.1±1.2 | 7.5±2.3 | <0.001* | |
| 2D PISA EROA (mm2) | 19.9±7.9 | 51.6±22.7 | 16.6±9.0 | 40.3±17.6 | <0.001* | |
| 3DE quantitative parameters | ||||||
| RVEF (%) | 53±11 | 54±10 | 50±10 | 55±9 | 0.134 | |
| RVEDV (mL) | 128±42 | 173±56 | 107±33 | 147±40 | <0.001* | |
| RVESV (mL) | 63±33 | 83±40 | 54±21 | 67±24 | <0.001* | |
| VCA (mm2) | 48.2±37.1 | 87.1±39.0 | 23.1±13.2 | 71.2±31.0 | <0.001* | |
| Volumetric EROA (mm2) | 31.4±13.6 | 71.3±30.7 | 22.0±14.2 | 52.2±22.4 | <0.001* | |
*, P value <0.05. Data are presented as mean ± standard deviation and n (%). TR, tricuspid regurgitation; BSA, body surface area; CI, cardiac index; sPAP, systolic pulmonary arterial pressure; VTI, velocity-time integral; 2DE, 2-dimensional echocardiography; VCW, vena contracta width; PISA, proximal isovelocity surface area; EROA, effective regurgitant orifice area; 3DE, 3-dimensional echocardiography; RVEF, right ventricular ejection fraction; RVEDV, right ventricular end-diastolic volume; RVESV, right ventricular end-systolic volume; VCA, vena contracta area.
Comparison of the correction algorithms for the 2D PISA method with the reference methods
The EROAs calculated through 2D PISA method, either corrected or not, correlated well with both the VCA (r=0.74, r=0.73, and r=0.70 for EROAUC, EROAVo-Va, and EROA0.7, respectively; P values <0.0001; Figure 9) and volumetric EROA (r=0.75, r=0.74, and r=0.72 for EROAUC, EROAVo-Va, and EROA0.7, respectively; all P values <0.0001; Figure 10). However, a consistent significant underestimation by the 2D PISA methods was observed as a function of the EROA in both functional and primary TR. Both correction algorithms lessened the systematic underestimation (Figures 11,12, Tables 2,3), but the limits of agreement remained relatively unchanged. It was also observed that the differences between methods were more sparsely distributed and skewed upward as the EROA increased, which suggested that the underestimation by the 2D PISA methods proportionally increased and that the agreement between methods became worse in larger EROAs in both functional and primary TR.

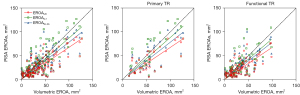
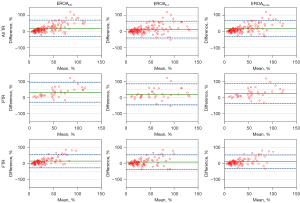

Table 2
| TR etiology | EROAUC | EROA0.7 | EROAVo-Va |
|---|---|---|---|
| All TR | 20 (−21 to 70) | 12 (−41 to 64) | 15 (−35 to 65) |
| Primary TR | 33 (−28 to 94) | 21 (−45 to 86) | 27 (−36 to 89) |
| Functional TR | 14 (−28 to 56) | 8 (−37 to 53) | 11 (−32 to 53) |
PISA, proximal isovelocity surface area; EROA, effective regurgitant orifice area; VCA, vena contracta area; TR, tricuspid regurgitation; UC, uncorrected; Vo, peak regurgitant velocity; Va, color aliasing velocity.
Table 3
| TR etiology | EROAUC | EROA0.7 | EROAVo-Va |
|---|---|---|---|
| All TR | 10 (−26 to 46) | 2 (−38 to 43) | 6 (−32 to 43) |
| Primary TR | 17 (−24 to 58) | 4 (−47 to 56) | 10 (−33 to 54) |
| Functional TR | 7 (−25 to 40) | 1 (−34 to 37) | 4 (−30 to 38) |
PISA, proximal isovelocity surface area; EROA, effective regurgitant orifice area; TR, tricuspid regurgitation; UC, uncorrected; Vo, peak regurgitant velocity; Va, color aliasing velocity.
Table 4 shows the multilinear regression model, in which the dependent variable was defined as the difference between the uncorrected 2D PISA EROA and the reference EROA (the mean of the VCA and volumetric EROA). It was demonstrated that the aliasing velocity-related correction coefficient, Vorifice/(Vorifice − Valiasing), the RVEDV, and the ratio between the reference EROA and RVEDV contributed significantly to the difference between the uncorrected 2D PISA EROA and the reference EROA.
Table 4
| Variable | Unstandardized B | Standardized coefficients beta | |t| | VIF | P value |
|---|---|---|---|---|---|
| Etiology | 1.628 | 0.040 | 0.6184 | 1.330 | 0.5374 |
| Atrial fibrillation | 0.7791 | 0.020 | 0.3559 | 1.012 | 0.7225 |
| RVEDV | 0.1569 | 0.401 | 6.723 | 1.152 | <0.0001* |
| sPAP | −0.1176 | −0.095 | 1.157 | 2.180 | 0.2496 |
| Aliasing correction coefficient | −113.7 | −0.277 | 3.409 | 2.144 | 0.0009* |
| Reference EROA/RVEDV | 63.94 | 0.591 | 9.658 | 1.213 | <0.0001* |
*, P value <0.05. PISA, proximal isovelocity surface area; EROA, effective regurgitant orifice area; VIF, variance inflation factor; RVEDV, right ventricular end-diastolic volume; sPAP, systolic pulmonary artery pressure.
Comparison of severity grading accuracy
In ROC analysis, the accuracies of the 2D PISA methods for differentiating severe TR, as defined using the guideline-recommended integral approach, were similar [area under the curve (AUC): 0.905, 0.903, and 0.893 for EROAUC, EROAVo-Va, and EROA0.7, respectively]. No significant differences were found regarding diagnostic accuracy (all P values >0.05, Z test). The cutoff values for severe TR in EROAUC, EROAVo-Va, and EROA0.7 were 0.26 (83.3% and 84.4% for sensitivity and specificity, respectively), 0.29 (83.3% and 84.4% for sensitivity and specificity, respectively), and 0.39 cm2 (72.2% and 93.5% for sensitivity and specificity, respectively), respectively, as defined by the Youden index. The cutoff values for severe TR stratified by etiology are provided in Table S1.
Intra- and interobserver agreement
The intra- and interobserver repeatability was good for 2D PISA EROA and was modest for volumetric EROA as the confidence intervals were wider (Table S2). The intraobserver agreement was good for VCA, but the interobserver agreement of this parameter was only fair as indicated by the very wide CIs.
Discussion
Current guidelines recommend the use of the 2D PISA method to quantify TR and note the possibility of underestimation (3), which has been substantiated by recent studies (12,13). However, no correction algorithm is recommended for TR, and the different correction methodologies applied across studies have yielded markedly divergent partition values (12,18-20). Computational modeling demonstrates that the effect of low regurgitant velocity accounts for the majority of 2D PISA error (11). Therefore, in this study, we evaluated different correction algorithms, specifically regurgitant-orifice-to-Nyquist-velocity ratio correction and the constant 0.7 correction for low regurgitant velocity both in pulsatile models and in clinic. Our principal findings were as follows: (I) Aliasing velocity optimization combined with the proposed correction factor, Vorifice/(Vorifice − Valiasing), could effectively account for the systematic underestimation by the 2D PISA method under low-regurgitant-velocity conditions in vitro, which confirms the accuracy of the correction when other sources of error are controlled. (II) After the Vorifice/(Vorifice − Valiasing) correction, there remained significant underestimation by 2D PISA EROA clinically, which is concordant with previous studies demonstrating that irregular orifice and varied valve geometry also contribute to the error of 2D PISA method. (III) A constant correction coefficient of 0.7 demonstrated high accuracy in diagnosing severe TR and good agreement with the reference values in clinic. (IV) The absolute size of the EROA and the relative size of the EROA to the RV cavity contributed significantly to the measurement error by 2D PISA method.
The 2D PISA method is based on the hydrodynamic theory which predicts that flow approaches a point-like (infinitesimal) orifice in a flat plate as a series of concentric hemispheric shells of decreasing area and increasing velocity (14). The radius of the shell can be measured to calculate the area of the proximal isovelocity contour based on the hemispheric assumption, and quantitative regurgitant indices can then be derived by the conservation of mass. However, in clinical practice, the prerequisite for the hydrodynamic assumption is often violated. The regurgitant orifice of TR is irregular and larger rather than point-like (orifice shaped) (21), the tricuspid valve is tethered rather than flat (global geometry) (22), and the peak regurgitant velocity is comparatively low rather than almost infinitely large through a point-like orifice (low-velocity flow field), all of which lead to the distortion of the true PISA; thus, the PISA calculated by measuring the radius of the proximal isovelocity contour shell could result in over- or underestimation; the first problem above is addressed in the guidelines of the American Society of Echocardiography developed in collaboration with Society for Cardiovascular Magnetic Resonance, with different cutoffs for severe primary and secondary mitral regurgitation, and the second is addressed via an angle-correction algorithm (3). However, the effect of a low-velocity flow field has only been studied by computational and in vitro modeling, and while different correction algorithms have been proposed, they have not been clinically validated, and guideline recommendations do not yet exist.
Our study confirmed that aliasing velocity optimization combined with the proposed correction factor, Vorifice/(Vorifice − Valiasing), could account for the systematic underestimation by 2D PISA method under low-pressure conditions in vitro, where no other sources of error exist. The 0.7-constant correction overestimates EROA in vitro but shows only marginal systematic bias clinically. This could be explained by its overestimation compensating for other sources of underestimation that were not accounted for in our study. Importantly, the underestimation under low-pressure conditions has been reported to be the major source of error in 2D PISA method, with the underestimation via irregular orifice shape being comparatively marginal (10). On the other hand, as is evidenced by the cutoffs stratified by etiology, with the same reference standard, the cutoffs for functional TR were generally smaller than for primary TR. These findings suggest that 2D PISA tends to underestimate EROA to a greater extent in functional TR than in primary TR, which could be explained as a result of PISA underestimation due to the effect of ellipsoidal regurgitant orifice shape in functional TR (23). This can also be attributed to the limited sample size in the current study. As constant correction provided similar accuracy compared to conventional PISA method with decreased systematic bias, it may be a clinically useful means to quickly estimate TR severity but should be further validated in a larger cohort with balanced etiological groups.
Another important finding of the current study is that the absolute size of the EROA and the relative size of the EROA to the RV cavity contribute significantly to the measurement error of 2D PISA method. This could be explained by the violation of the theoretical assumption of the flow convergence method and the difficulty in determining the regurgitant orifice. Proximal flow convergence method requires a regurgitant orifice present on an infinitely large plane so that the flow accelerates toward the orifice in a predictable manner. However, when a baseline shift is performed at low regurgitant velocities in TR, the aliasing border usually interacts with the ventricular wall before an optimized hemispherical shell of PISA can be obtained. This has been demonstrated in previous studies, which reported that confining wall geometry strained the streamline distribution in the proximal flow field (24,25). Moreover, one previous study indicated that the major source of inconsistency in PISA measurement is the inability to determine the center point of the regurgitant orifice, which is located much farther from either the leaflet tip or the outer margin of VC in the presence of extremely severe TR. This could add to the variability of PISA radius measurement.
Future technical improvements
3D CDE can directly measure the PISA shell without geometric assumptions and is expected to overcome the limitations of the 2D PISA method (26). It has been validated in a group of patients with functional TR and demonstrated improved agreement with the reference method compared with the 2D PISA method (13). However, several problems need to be addressed before wider clinical application of the 3D PISA method. First, 3D PISA is not the actual PISA but the proximal iso-Doppler-velocity surface area (27-30), and this could lead to underestimation. In addition, the limited temporal resolution of 3D CDE makes it hard to select the convergence zone that actually coincides with the peak regurgitant velocity, and thus may cause overestimation of the EROA with the clinically used peak PISA method. Finally, the current 3D PISA method is based on a proprietary vendor platform and software package, which further limits its widespread adoption.
Clinical implications
Quantitative assessment of the severity of TR remains challenging. The 2D PISA method is recommended to quantify TR, but the application of this approach requires the orifice radius to be infinitesimal compared with the PISA radius, which is often hard to achieve with low regurgitant velocities and leads to significant underestimation of TR severity. Two correction proposed algorithms, the regurgitant-orifice-to-Nyquist-velocity ratio correction and the constant 0.7 correction, were tested in this study. The former excellently corrects the error caused by low regurgitant velocities in vitro but still requires correction for other sources of error including valve geometry (angle correction) and irregular orifice when applied clinically; meanwhile, the latter overestimates EROA in vitro but shows good agreement with the reference method and high accuracy in determining severe TR in clinical validation. This represents a valuable clinical tool for quick correction of the underestimation by 2D-the PISA method in TR.
Limitations
Choice of disperse orifice sizes
The plates with orifices were prepared using perforating cutting dies, with the available sizes included being 20, 30, and 80 mm2 and larger or smaller ones. Smaller or larger sizes would either be subject to manufacturing error or change the boundary condition on which PISA method relies. A more granular scale of orifice size would better mimic the clinical scenarios.
Reference standard
As external reference standards for TR quantification are limited, several comparator methods were used in this study, each of which may involve measurement variability (31,32). For VCA, although the temporal resolution of 3D CDE on modern echocardiography machines is not lower than that of 2D CDE, it comes at the price of spatial resolution. The use of VCA as a reference method is thus subject to the error of spatial averaging. TOE was not employed in this study but may provide better definition of VCA with its high spatial resolution.
In the volumetric approach, there is no validation of the RV volume against cardiac magnetic resonance (CMR), and the measurement of RVOT diameter from a 2D perspective might lead to either an over- or underestimation of the RVOT area. A preliminary study comparing CMR-derived RVol to that derived by 3DE also showed slight underestimation (3.6 mL) (32).
Intermodality comparison
CMR is also the recommended modality for quantifying TR and has been increasingly adopted in recent studies (31,33). The reference methods of our study are echocardiography-based and thus were unable to provide information on intermodality agreement, which may significantly affect clinical decision-making. Future studies are expected to validate these proposed PISA correction algorithms against CMR imaging.
Effect of temporal variation
The PISA method is based on single-frame measurements. Previous experience in mitral regurgitation shows that temporal variation of regurgitant flow and orifice area during systole could lead to clinically significant underestimation by the PISA method (34,35). Preliminary evidence has also emerged suggesting the existence of dynamic systolic flow in TR (36), which was not accounted for in the current study. Future studies are expected to validate the existence of temporal variation in TR and its effect on PISA accuracy.
Vendor dependency
For either in vitro or in vivo validation, only 1 ultrasound machine vendor was used. As color Doppler imaging is sensitive to technical settings and as different vendors adopt different rendering strategies and smoothing algorithms, the PISA method might be subject to vendor dependency. The comparison made in this study was based on the same vendor and could still be considered valid; however, the cutoffs reported may not be directly applicable in clinical use or comparison in future studies.
The atrial and ventricular type of functional TR
The atrial and ventricular type of functional TR are associated with different patterns of valve deformation geometry (22,37) and may thus behave differently when the 2D PISA method is applied. However, as most of our patients had a disease origin of the left heart and only concomitantly had atrial fibrillation and as paroxysmal atrial fibrillation was not excluded, it was impossible to differentiate between the atrial or ventricular type of functional TR in this study. Subsequent studies with strict patient selection protocols and a larger sample size to investigate the impact of such subgroups are needed.
Unaccounted sources of error in 2D PISA
Complex valve geometry and variable regurgitant orifice shape were not accounted for in this study. 2D PISA quantification with an extremely eccentric jet is highly challenging, as it would be hard to align the insonation beam for the recording of the Doppler spectrum while the proximal flow field may be largely distorted from the hemispheric assumption. The simple constant correction only provides a tool to avoid underestimation of TR severity. Approaches to addressing all possible sources of error and accurately quantifying valve regurgitation should be developed.
Conclusions
Using a correction factor of 0.7 in quantifying TR provides similar accuracy to that of the conventional method and the complex aliasing velocity-based correction method. This approach lessens the systematic underestimation of the conventional 2D PISA method in a low-velocity flow field in TR compared with other quantitative approaches. This represents a valuable clinical tool for quickly correcting the underestimation of the 2D PISA method in TR and may increase the frequency of applying the correction and earlier recognition of patients with severe TR.
Acknowledgments
We would like to thank all the patients who participated in this study and the engineers from Siemens for their technical assistance. Part of the abstract has been presented during a moderated poster session at the 2023 Congress of the European Society of Cardiology.
Funding: This work was supported by
Footnote
Conflicts of Interest: All authors have completed the ICMJE uniform disclosure form (available at https://qims.amegroups.com/article/view/10.21037/qims-22-1311/coif). The authors have no conflicts of interest to declare.
Ethical Statement: The authors are accountable for all aspects of the work in ensuring that questions related to the accuracy or integrity of any part of the work are appropriately investigated and resolved. The study was conducted in accordance with the Declaration of Helsinki (as revised in 2013) and was approved by the ethics committee of Zhongshan Hospital, Fudan University. Informed consent was obtained from all individual participants.
Open Access Statement: This is an Open Access article distributed in accordance with the Creative Commons Attribution-NonCommercial-NoDerivs 4.0 International License (CC BY-NC-ND 4.0), which permits the non-commercial replication and distribution of the article with the strict proviso that no changes or edits are made and the original work is properly cited (including links to both the formal publication through the relevant DOI and the license). See: https://creativecommons.org/licenses/by-nc-nd/4.0/.
References
- Wang N, Fulcher J, Abeysuriya N, McGrady M, Wilcox I, Celermajer D, Lal S. Tricuspid regurgitation is associated with increased mortality independent of pulmonary pressures and right heart failure: a systematic review and meta-analysis. Eur Heart J 2019;40:476-84. [Crossref] [PubMed]
- Dreyfus J, Ghalem N, Garbarz E, Cimadevilla C, Nataf P, Vahanian A, Caranhac G, Messika-Zeitoun D. Timing of Referral of Patients With Severe Isolated Tricuspid Valve Regurgitation to Surgeons (from a French Nationwide Database). Am J Cardiol 2018;122:323-6. [Crossref] [PubMed]
- Zoghbi WA, Adams D, Bonow RO, Enriquez-Sarano M, Foster E, Grayburn PA, Hahn RT, Han Y, Hung J, Lang RM, Little SH, Shah DJ, Shernan S, Thavendiranathan P, Thomas JD, Weissman NJ. Recommendations for Noninvasive Evaluation of Native Valvular Regurgitation: A Report from the American Society of Echocardiography Developed in Collaboration with the Society for Cardiovascular Magnetic Resonance. J Am Soc Echocardiogr 2017;30:303-71. [Crossref] [PubMed]
- Lancellotti P, Moura L, Pierard LA, Agricola E, Popescu BA, Tribouilloy C, Hagendorff A, Monin JL, Badano L, Zamorano JLEuropean Association of Echocardiography. European Association of Echocardiography recommendations for the assessment of valvular regurgitation. Part 2: mitral and tricuspid regurgitation (native valve disease). Eur J Echocardiogr 2010;11:307-32. [Crossref] [PubMed]
- Deng YB, Shiota T, Shandas R, Zhang J, Sahn DJ. Determination of the most appropriate velocity threshold for applying hemispheric flow convergence equations to calculate flow rate: selected according to the transorifice pressure gradient. Digital computer analysis of the Doppler color flow convergence region. Circulation 1993;88:1699-708. [Crossref] [PubMed]
- Rodriguez L, Thomas JD, Monterroso V, Weyman AE, Harrigan P, Mueller LN, Levine RA. Validation of the proximal flow convergence method. Calculation of orifice area in patients with mitral stenosis. Circulation 1993;88:1157-65. [Crossref] [PubMed]
- Shandas R, Gharib M, Sahn DJ. Nature of flow acceleration into a finite-sized orifice: steady and pulsatile flow studies on the flow convergence region using simultaneous ultrasound Doppler flow mapping and laser Doppler velocimetry. J Am Coll Cardiol 1995;25:1199-212. [Crossref] [PubMed]
- Barclay SA, Eidenvall L, Karlsson M, Andersson G, Xiong C, Ask P, Loyd D, Wranne B. The shape of the proximal isovelocity surface area varies with regurgitant orifice size and distance from orifice: computer simulation and model experiments with color M-mode technique. J Am Soc Echocardiogr 1993;6:433-45. [Crossref] [PubMed]
- Anayiotos AS, Perry GJ, Myers JG, Green DW, Fan PH, Nanda NC. A numerical and experimental investigation of the flow acceleration region proximal to an orifice. Ultrasound Med Biol 1995;21:501-16. [Crossref] [PubMed]
- Lee J, Mitter SS, Van Assche L, Huh H, Wagner GJ, Wu E, Barker AJ, Markl M, Thomas JD. Impact of assuming a circular orifice on flow error through elliptical regurgitant orifices: computational fluid dynamics and in vitro analysis of proximal flow convergence. Int J Cardiovasc Imaging 2023;39:307-18. [Crossref] [PubMed]
- Lee J, Mitter SS, Van Assche L, Huh H, Wagner GJ, Wu E, Barker AJ, Markl M, Thomas JD. Impact of assuming a circular orifice on flow error through elliptical regurgitant orifices: computational fluid dynamics and in vitro analysis of proximal flow convergence. Int J Cardiovasc Imaging 2023;39:307-18. [Crossref] [PubMed]
- Dahou A, Ong G, Hamid N, Avenatti E, Yao J, Hahn RT. Quantifying Tricuspid Regurgitation Severity: A Comparison of Proximal Isovelocity Surface Area and Novel Quantitative Doppler Methods. JACC Cardiovasc Imaging 2019;12:560-2. [Crossref] [PubMed]
- de Agustin JA, Viliani D, Vieira C, Islas F, Marcos-Alberca P, Gomez de Diego JJ, Nuñez-Gil IJ, Almeria C, Rodrigo JL, Luaces M, Garcia-Fernandez MA, Macaya C, Perez de Isla L. Proximal isovelocity surface area by single-beat three-dimensional color Doppler echocardiography applied for tricuspid regurgitation quantification. J Am Soc Echocardiogr 2013;26:1063-72. [Crossref] [PubMed]
- Rodriguez L, Anconina J, Flachskampf FA, Weyman AE, Levine RA, Thomas JD. Impact of finite orifice size on proximal flow convergence. Implications for Doppler quantification of valvular regurgitation. Circ Res 1992;70:923-30. [Crossref] [PubMed]
- Little SH, Igo SR, McCulloch M, Hartley CJ, Nosé Y, Zoghbi WA. Three-dimensional ultrasound imaging model of mitral valve regurgitation: design and evaluation. Ultrasound Med Biol 2008;34:647-54. [Crossref] [PubMed]
- Mitchell C, Rahko PS, Blauwet LA, Canaday B, Finstuen JA, Foster MC, Horton K, Ogunyankin KO, Palma RA, Velazquez EJ. Guidelines for Performing a Comprehensive Transthoracic Echocardiographic Examination in Adults: Recommendations from the American Society of Echocardiography. J Am Soc Echocardiogr 2019;32:1-64. [Crossref] [PubMed]
- Liu Y, Chen B, Zhang Y, Zuo W, Li Q, Jin L, Kong D, Pan C, Dong L, Shu X, Ge J. Sources of Variability in Vena Contracta Area Measurement for Tricuspid Regurgitation Severity Grading: Comparison of Technical Settings and Vendors. J Am Soc Echocardiogr 2021;34:270-278.e1. [Crossref] [PubMed]
- Bartko PE, Arfsten H, Frey MK, Heitzinger G, Pavo N, Cho A, Neuhold S, Tan TC, Strunk G, Hengstenberg C, Hülsmann M, Goliasch G. Natural History of Functional Tricuspid Regurgitation: Implications of Quantitative Doppler Assessment. JACC Cardiovasc Imaging 2019;12:389-97. [Crossref] [PubMed]
- Peri Y, Sadeh B, Sherez C, Hochstadt A, Biner S, Aviram G, Ingbir M, Nachmany I, Topaz G, Flint N, Keren G, Topilsky Y. Quantitative assessment of effective regurgitant orifice: impact on risk stratification, and cut-off for severe and torrential tricuspid regurgitation grade. Eur Heart J Cardiovasc Imaging 2020;21:768-76. [Crossref] [PubMed]
- Muraru D, Previtero M, Ochoa-Jimenez RC, Guta AC, Figliozzi S, Gregori D, Bottigliengo D, Parati G, Badano LP. Prognostic validation of partition values for quantitative parameters to grade functional tricuspid regurgitation severity by conventional echocardiography. Eur Heart J Cardiovasc Imaging 2021;22:155-65. [Crossref] [PubMed]
- Song JM, Jang MK, Choi YS, Kim YJ, Min SY, Kim DH, Kang DH, Song JK. The vena contracta in functional tricuspid regurgitation: a real-time three-dimensional color Doppler echocardiography study. J Am Soc Echocardiogr 2011;24:663-70. [Crossref] [PubMed]
- Topilsky Y, Khanna A, Le Tourneau T, Park S, Michelena H, Suri R, Mahoney DW, Enriquez-Sarano M. Clinical context and mechanism of functional tricuspid regurgitation in patients with and without pulmonary hypertension. Circ Cardiovasc Imaging 2012;5:314-23. [Crossref] [PubMed]
- Song JM, Kim MJ, Kim YJ, Kang SH, Kim JJ, Kang DH, Song JK. Three-dimensional characteristics of functional mitral regurgitation in patients with severe left ventricular dysfunction: a real-time three-dimensional colour Doppler echocardiography study. Heart 2008;94:590-6. [Crossref] [PubMed]
- Anayiotos AS, Fan P, Perry GJ, Myers J, Elmahdi AM, Nanda NC. Analysis of the Proximal Orifice Flowfield Under Pulsatile Flow Conditions and Confining Wall Geometry: Implications in Valvular Regurgitation. Echocardiography 1998;15:219-32. [Crossref] [PubMed]
- Pu M, Vandervoort PM, Greenberg NL, Powell KA, Griffin BP, Thomas JD. Impact of wall constraint on velocity distribution in proximal flow convergence zone. Implications for color Doppler quantification of mitral regurgitation. J Am Coll Cardiol 1996;27:706-13. [Crossref] [PubMed]
- Thavendiranathan P, Liu S, Datta S, Rajagopalan S, Ryan T, Igo SR, Jackson MS, Little SH, De Michelis N, Vannan MA. Quantification of chronic functional mitral regurgitation by automated 3-dimensional peak and integrated proximal isovelocity surface area and stroke volume techniques using real-time 3-dimensional volume color Doppler echocardiography: in vitro and clinical validation. Circ Cardiovasc Imaging 2013;6:125-33. [Crossref] [PubMed]
- Little SH, Igo SR, Pirat B, McCulloch M, Hartley CJ, Nosé Y, Zoghbi WA. In vitro validation of real-time three-dimensional color Doppler echocardiography for direct measurement of proximal isovelocity surface area in mitral regurgitation. Am J Cardiol 2007;99:1440-7. [Crossref] [PubMed]
- Little SH. Is it really getting easier to assess mitral regurgitation using the proximal isovelocity surface area? J Am Soc Echocardiogr 2012;25:824-6. [Crossref] [PubMed]
- Badano LP, Hahn R, Rodríguez-Zanella H, Araiza Garaygordobil D, Ochoa-Jimenez RC, Muraru D. Morphological Assessment of the Tricuspid Apparatus and Grading Regurgitation Severity in Patients With Functional Tricuspid Regurgitation: Thinking Outside the Box. JACC Cardiovasc Imaging 2019;12:652-64. [Crossref] [PubMed]
- deGroot C, Drangova M, Fenster A, Zhu S, Pflugfelder PW, Boughner DR. Evaluation of 3-D colour Doppler ultrasound for the measurement of proximal isovelocity surface area. Ultrasound Med Biol 2000;26:989-99. [Crossref] [PubMed]
- Zhan Y, Debs D, Khan MA, Nguyen DT, Graviss EA, Khalaf S, Little SH, Reardon MJ, Nagueh S, Quiñones MA, Kleiman N, Zoghbi WA, Shah DJ. Natural History of Functional Tricuspid Regurgitation Quantified by Cardiovascular Magnetic Resonance. J Am Coll Cardiol 2020;76:1291-301. [Crossref] [PubMed]
- Utsunomiya H, Harada Y, Susawa H, Takahari K, Ueda Y, Izumi K, Itakura K, Ikenaga H, Hidaka T, Fukuda Y, Shiota T, Kihara Y. Comprehensive Evaluation of Tricuspid Regurgitation Location and Severity Using Vena Contracta Analysis: A Color Doppler Three-Dimensional Transesophageal Echocardiographic Study. J Am Soc Echocardiogr 2019;32:1526-1537.e2. [Crossref] [PubMed]
- Zhan Y, Senapati A, Vejpongsa P, Xu J, Shah DJ, Nagueh SF. Comparison of Echocardiographic Assessment of Tricuspid Regurgitation Against Cardiovascular Magnetic Resonance. JACC Cardiovasc Imaging 2020;13:1461-71. [Crossref] [PubMed]
- Uretsky S, Aldaia L, Marcoff L, Koulogiannis K, Hiramatsu S, Argulian E, Rosenthal M, Gillam LD, Wolff SD. The Effect of Systolic Variation of Mitral Regurgitation on Discordance Between Noninvasive Imaging Modalities. JACC Cardiovasc Imaging 2019;12:2431-42. [Crossref] [PubMed]
- Hung J, Otsuji Y, Handschumacher MD, Schwammenthal E, Levine RA. Mechanism of dynamic regurgitant orifice area variation in functional mitral regurgitation: physiologic insights from the proximal flow convergence technique. J Am Coll Cardiol 1999;33:538-45. [Crossref] [PubMed]
- Li L, Colen TM, Jani V, Barnes BT, Craft M, Tham E, Khoo NS, Smallhorn J, Danford DA, Kutty S. Dynamic Systolic Changes in Tricuspid Regurgitation Vena Contracta Size and Proximal Isovelocity Surface Area in Hypoplastic Left Heart Syndrome: A Three-Dimensional Color Doppler Echocardiographic Study. J Am Soc Echocardiogr 2021;34:877-86. [Crossref] [PubMed]
- Utsunomiya H, Itabashi Y, Mihara H, Berdejo J, Kobayashi S, Siegel RJ, Shiota T. Functional Tricuspid Regurgitation Caused by Chronic Atrial Fibrillation: A Real-Time 3-Dimensional Transesophageal Echocardiography Study. Circ Cardiovasc Imaging 2017;10:e004897. [Crossref] [PubMed]


