
Prior information-guided reconstruction network for positron emission tomography images
Introduction
Positron emission tomography (PET) is a modality used in nuclear medicine which can visualize various functionalities in a living organ and quantitatively estimate radiotracer concentrations. However, the radiotracer concentration image cannot be directly obtained from the PET scanner. An image reconstruction process is required to estimate the distribution of the radiotracer concentrations based on the raw data, which are usually stored in the form of a sinogram.
At present, the traditional reconstruction algorithms mainly include the analytic method and the iterative method. Analytic methods, such as filtered back projection (FBP), are simple and fast but sensitive to high noise and susceptible to producing streak artifacts. The iterative method can obtain much clearer reconstructed images, but the computation is expensive, involving processes such as ordered subset expectation maximization (OSEM). Hence, considerable research attention has been paid to developing a fast and accurate reconstruction method. In recent years, deep learning has demonstrated promising potential in the field of medical image processing (1-5). Thus, many researchers have begun to refine the application of deep learning–based reconstruction methods. Deep learning was first used in nuclear medicine image reconstruction for denoising. After AUTOMAP (automated transform by manifold approximation) was proposed by Zhu et al. (6), research into direct reconstruction with deep learning began to proliferate. AUTOMAP is a unified medical image reconstruction framework, which is able to achieve a transformation directly from the raw data domain to the image domain. Häggström et al. (7) designed a deep encoder-decoder network specifically for PET, named DeepPET. It provides direct reconstruction from the sinogram domain to the image domain. An evaluation of the simulation dataset demonstrated that DeepPET can generate higher image quality in a shorter amount of time compared with traditional methods. However, its performance in a real patient dataset was poorer. A conditional generative adversarial network (cGAN)-based direct network was then proposed by Liu et al. (8); however, its performance with real data was still unsatisfactory. The direct reconstruction methods mentioned above all attempt to learn the mapping from the sinogram domain to the image domain without any additional prior information (PI).
Without constraints, the results are not accurate and often produce nonexistent structures. Hence, several research groups are beginning to study how to incorporate auxiliary information in the process of deep learning to assist in accurate image generation. Two major combination approaches are considered here: (I) combination with other nuclear medical modalities, such as various types of attenuation correction, typically time-of-flight (TOF)-PET data (9-12); and (II) combination with conventional methods of any form, such as FBP and maximum likelihood expectation maximization (MLEM). For non-TOF sinogram data, the combination with conventional methods is usually selected due to the lack of a corresponding attenuation correction map. Gong et al. (13) proposed an unsupervised deep learning framework for direct reconstruction with magnetic resonance (MR) images as PI. Ote et al. (14) developed a deep learning-based reconstruction network with view-grouped histo-images as the input and computed tomography (CT) images as the constraint. Wang et al. (15) designed FBP-Net, which combines the FBP algorithm into the neural network to improve the image quality. Lv et al. (16) proposed a back-projection-and-filtering (BPF)-like reconstruction method based on U-net. The key to this approach also involves back projection and filtering into a deep learning form, with the filter being built with modified U-net architecture. Zhang et al. (17) proposed a cascading back-projection neural network (bpNet) with back-projection operation, which achieved transformation from the sinogram domain to the back-projection image domain. This operation is similar to FBP and can serve as prior knowledge for the whole reconstruction network. Xue et al. (18) described a similar domain transform approach but implemented on a different network. They proposed using a direct reconstruction network with back projection based on a cycle-consistent generative adversarial network (CycleGAN). GapFill-Recon Net (19) is also a domain transform reconstruction network based on CNN, but before reconstruction, it combines the processing to address the sinogram gap. Yang et al. (20) proposed a cycle-consistent, learning-based hybrid iteration reconstruction method which also starts from raw data and then projects to the image domain for reconstruction. The image reconstruction pipeline of all these methods (15-20) begins from the sinogram to the back-projection image and then to the PET image. The sinogram information is not used directly but is projected and filtered into the back-projection domain. If both of the sinogram data and the BP data can be used in a suitable way, the reconstruction image quality might be improved.
Inspired by classic image translation framework, pix2pixHD (21), which obtained excellent results for the image-to-image translation task, we propose a cGAN-based reconstruction network, the prior information-guided reconstruction network (PIGRN), which includes a dual-channel generator and a 2-scale discriminator. The input sources of the two channels are respectively raw data and PI. In this approach, the input of the first channel is the image pairs composed of the sinogram and the corresponding radiotracer concentration images (ground truth). The flow of this channel is downsampling, several residual blocks, and upsampling, after which output images with the same size as the ground truth can be obtained. The input of the second channel is FBP images which act as the PI. After downsampling, the FBP image is the same size as the output of the first channel. Both the outputs are then concatenated and fed into the next residual blocks. The output of the generator is then transposed to the 2-scale discriminator, and the average discriminant score of the fine scale and the coarse scale is the final answer of the total discriminator. The loss function not only includes the classic conditional GAN but also incorporates a perceptual loss on the discriminator, which has been shown to be useful for image processing (22). The ablation experiments on the Zubal phantom datasets have confirmed the effectiveness of dual-channel generator and 2-scale discriminator. The experimental comparisons, in which both simulation and real Sprague Dawley (SD) rat datasets were used to compare PIGRN with classic U-Net (23) and DeepPET, showed substantial advantages in improving the quality and accuracy of the reconstructed images. We also designed an experiment trained with thorax slices of rats and tested with brain slices, with the quantitative results indicating that the proposed method has strong generalization ability.
This paper is organized as follows. In “Methods” section, the proposed method and its supporting theories are introduced in detail; in “Results” section, the ablation experiments, comparison experiments, and generalization experiments are described; in “Discussion” section, the experimental results are reported; and finally, in “Conclusions” section, we discuss our results and draw conclusions concerning our proposed method.
Methods
Problem definition
In PET imaging, the relationships between the sinogram and radioactivity images are normally described as follows:
where denotes the sinogram data which are collected in the PET imaging process, is the unknown activity image that needs to be estimated, is the system matrix (which is needed in the iterative algorithms), I is the number of lines of response, and J is the number of pixels in the image space. In reality, y includes not only the accidental coincidences, and these background events are summarized as e.
Therefore, the task in our project can be defined as a process of generating an activity map x from sinogram data y. This task is an obviously ill-posed optimization problem. Without any prior information, the estimate of x may be out of control. If we can find a that is approximate to x in the activity image domain, the estimate value of x can be within a reasonable range. The activity image xF obtained using FBP produces artifacts and is blurred but does provide the global structure of the activity image. Therefore, xF can be considered as . After removing the noise out of the product term, we can formulate x as follows:
where N(∙) is the proposed neural network architecture, p is the trainable parameters, and [∙] is the concatenated operation which combines both the sinogram and FBP information.
Network structure
Inspired by the pix2pixHD framework applied in the image translation task, we propose the PIGRN for PET images, as shown in Figure 1. The entire network comprises two parts: a 2-channel generator and a 2-scale discriminator. In the generator, we have two input channels: the first is a raw-data channel including the sinogram and radioactivity images which is considered to be the ground truth, and the second is the corresponding preinformation. The outputs of the two channels are concatenated and passed by a series of residual blocks. After these operations, we can obtain the estimate PET images which are then passed to the discriminator. To improve the image quality in detail structure, the discriminator is set to be two scales: a fine scale and a coarse scale. Averaging the scores of the two scale discriminators provides the final results.
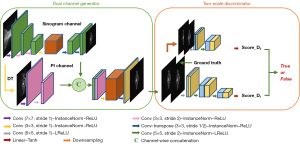
Two-channel generator
The generator has two channels: the first is fed with image pairs, and the second is the PI channel which is fed with the corresponding prior information. We can adopt different information, such as the images generated by traditional methods, the attenuation correction mapping, and even other physical information, into the second channel to improve the reconstruction results. To make the network more universal, FBP was used in this study. For convolution layers, other than the first layer which use 7×7 kernels, all the convolution layers use 3×3 kernels and are followed by instance normalization and Rectified Linear Unit (ReLU) nonlinearities. To reduce boundary artifacts, all the padding layers are reflection padding.
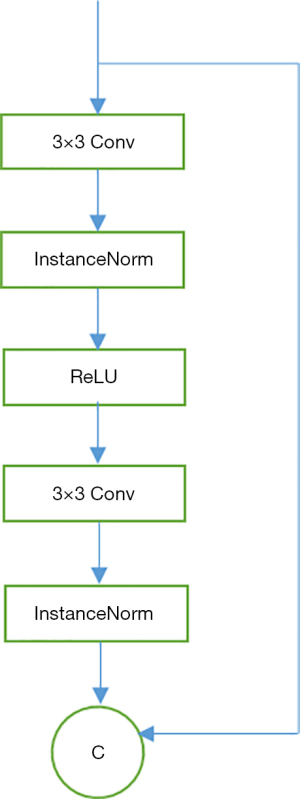
In the first channel, we use a stride of two convolutions to downsample the input, which is followed by a series of residual blocks and then two convolutional layers with a half stride for upsampling. There are two benefits of this downsampling and upsampling operation: reducing the computational cost and obtaining larger effective receptive fields with the same number of layers. In order to avoid the network degradation with the deepening of training, several residual blocks are added. The basic structure is shown in Figure 2. In the second channel, we use the corresponding FBP images as input, which are obtained after domain transformation (DT). In this work, the FBP images are generated using the Michigan Image Reconstruction Toolbox (MIRT) (24). The only task this channel is responsible for is downsampling the input to ensure the results of the two channels have the same shape. Rather than using the element-wise sum of the two outputs, channel-wise concatenation can better retain the features of each channel. The concatenation is followed by a series of residual blocks and upsampling, after which, we can obtain the output of the entire generator that has the same shape as that of the input.
Two-scale discriminator
The input of the discriminator is the concatenation of the ground truth and the estimated images that are generated from generator. In order to obtain both the global view and finer detail features, we use two discriminators that share the same network structure but operate at different image scales. We refer to the coarse scale discriminator as D1 and the fine scale discriminator which downsamples the images by a factor of 2 as D2. D1 and D2 are trained to differentiate the ground truth and estimated images at the coarse and fine scale, respectively. The basic structure of discriminators is Patch GAN (25) which does not score on the whole image, but on small patches. Different from that of the generator, the kernel size of the convolution layers is 5×5. All the convolution layers are followed by instance normalization and leaky ReLU layers.
Loss function
With the multiscale discriminators, the learning problem becomes a multitask problem, which can be expressed as follows:
where G is the generator, and Dk denotes the kth discriminator. The classic condition GAN loss LcGAN is given as follows:
where y is the sinogram, and x is the combination of the corresponding ground truth and FBP images. The loss function not only includes the classic condition GAN but also incorporates a perceptual loss on the discriminator, which has been shown to be useful for image processing (21). The pix2pixHD framework involves a feature matching loss that includes the perceptual loss, which can be described as follows:
where T is the total number of layers of the Patch GAN process, Nidenotes the number of elements in each layer, and denotes the ith layer of Dk. The full loss function then can be described as follows:
where λ controls the weights of the two terms.
Results
Simulation datasets
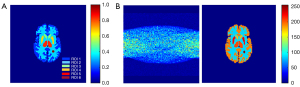
In this study, we built two types of simulation datasets based on the Zubal phantom. The phantom was divided into six regions of interest (ROIs) as shown in Figure 3A. Figure 3B shows the image pair including the sinogram and the corresponding radioactivity image. ROI 6 is a tumor we specifically added. The simulated tracer was [18F]-labeled fluorodeoxyglucose (18F-FDG). All the images were 160×160 pixels in size.
Single-shape dataset and various-shape dataset
The single-shape dataset contained 200 sets of radioactivity images which had the same shape but were filled with different time-activity curves (TACs). The various shape dataset was built on 200 phantoms and was generated by randomly translating, rotating, and scaling the Zubal phantom. The TACs were calculated via the COMKAT toolbox after the kinetic parameters, plasma input function, and sampling protocol were set. The kinetic parameters used in each region in this simulation were from the existing literature on tracer dynamics (15). The sampling protocol was set to 3×60, 9×180, and 6×300 s. Each set thus contained 18 frames. All the true radioactivity images were then projected to the sinogram domain by using MIRT. The number of projection angles and detector bins were 160 and 128, respectively. We also added 20% Poisson random noise to the sinograms. After generating both radioactivity images and sinograms, we spliced them into image pairs. For the corresponding FBP images, they were generated with the MIRT. For the input, each sample needs an image pair and an FBP image. Each dataset consisted of 200 subjects which included 200×18 image pairs and 200 FBP images, and we randomly selected 150 subjects as the training dataset and the others as the testing dataset.
SD rat datasets
Animal experiments were approved by the experimental animal welfare and ethics review committee of Zhejiang University and were performed in compliance with the national guidelines for animal experiments and local legal requirements.
Whole-body dataset and organ-level dataset
We used 12 SD rats with an average age of 9 weeks and a weight of about 300 g with glioma in this experiment. The rats were injected with 18F-FDG and scanned using an Inveon micro-PET scanner (Siemens Healthineers). Each scan lasted 60 minutes, and the tracer dose was injected at about 37 MBq. The sampling protocol was set to 10×60 s, 3×300 s, and 5×420 s. Before scanning, the rats were fasted for at least 8 hours but could drink water. During the scanning, the position of the rats was fixed with adhesive tape, and 1% isoflurane and 1 L/mL oxygen were introduced into the oxygen mask to anesthetize the rats. We first used the single-slice rebinning (SSRB) method to rebin the 3D sinograms and randomly corrected them to obtain the 2D sinograms. For the radioactivity images, they were reconstructed using 3D-OSEM algorithm of the scanner and were subject to random correction, normalization of detection efficiency, and attenuation correction. For FBP images, the generation method was the same as that of the simulation dataset. Each 3D data set contained 159 slices, excluding the slices without effective information in the previous and subsequent position, we finally chose 130 slices of each frame of data. We built two types of datasets in our experiments. The first was built based on the whole body. The second dataset was designed based on the organ level, and we separated the whole body into two parts: the brain and the thorax. We attempted to complete training with thorax part and to complete testing on the brain part to verify the ability of the algorithm to accurately generate unseen structures. The training set and the testing set of the two datasets were all divided on the individual level. For the whole-body dataset, nine rats were randomly selected as the training set, while three rats were used as the testing set. For the organ-level dataset, we trained our network with the head part of the nine rats and tested with the thorax part of the other three rats.
Quantitative analysis
Evaluation of the whole image
We adopted two classic metrics here for the image quality evaluation. The first was peak signal-to-noise ratio (PSNR), with a larger the value indicating a better of the image quality:
where x denotes the ground truth, denotes the reconstructed image, n is the number of all image pixels, and Xmax represents the maximum value of the ground truth.
Considering that PSNR is not very close to the perception of human eyes, we chose structure similarity index measure (SSIM) as the second metrics to reflect the similarity of luminance, contrast, and structure between two images. The range of SSIM is 0 to 1, the larger SSIM, the higher similarity,
where μx and denotes the mean value of x and , respectively; is the variance of x; is the variance of ; and denotes the covariance of x and . The parameters are c1=6.5025 and c2=58.5225.
Evaluation of tumor and ROIs
We calculated the tumor’s bias and variance in the simulation dataset as follows:
where n denotes the overall number of pixels in the ROI, denotes the reconstructed value at voxel i, xi denotes the true value at voxel i, and is the mean value of xi.
Implementation details and convergence of the algorithm
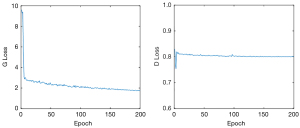
The network was trained for 200 epochs on an Ubuntu 18.04 LTS server with a TITAN RTX 24G (Nvidia). During the experiments, we used the Adam optimizer to optimize the loss function with a learning rate (lr) =0.002, β1=0.5, β2=0.999, batch size =64, and an empirically set λ1=10 in the loss function. The loss function curve in Figure 4 shows the convergence of the generator and discriminator. It can be seen that the change of the generator tends to be flat around 200 epochs, which is also the reason why 200 epochs were selected.
Ablation experiments
We designed two ablation experiments based on simulation datasets to verify the effectiveness of the dual-channel generator and 2-scale discriminator, respectively.
Validation of FBP channel based on the single-shape dataset
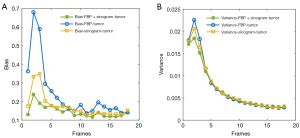
In this experiment, we examined the reconstruction performance based on different input, with the results being shown in Figure 5. Regardless of which input was used, the overall structure of the images was well reconstructed in human vision. However, for small, local ROIs, such as ROI 3, ROI 4, ROI 5, and the tumor, the result generated by two channels (FBP + sinogram) was much closer to the ground truth. As shown in Table 1, the 2-channel input generator obtained the highest PSNR and SSIM with smaller standard deviations, indicating that the network is more stable with the additional FBP channel. For the performance of the reconstruction on finer structures, we calculated the mean of bias and variance of each small ROI as shown in Figure 6. The network with the 2-channel input obtained much better results in detailed reconstruction. We also plotted the reconstruction results of the tumor (ROI 6) by frame as shown in Figure 7. With the FBP channel help, the network with the 2-channel input is highly stable and robust on dynamic PET images.
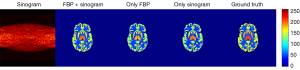
Table 1
| Input | PSNR | SSIM |
|---|---|---|
| FBP | 27.0235±4.4130 | 0.9711±0.0141 |
| Sinogram | 28.3810±3.1649 | 0.9771±0.0061 |
| FBP + sinogram | 29.1670±2.6810* | 0.9789±0.0039* |
Data are shown as mean ± SD. *, the results of the proposed method. PSNR, peak signal-to-noise ratio; SSIM, structure similarity index measure; FBP, filtered back projection; SD, standard deviation.

Validation of 2-scale discriminator based on the various-shape dataset
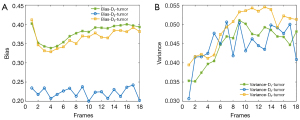
After the first ablation experiment verification, all the subsequent experiments were based on dual-channel input. To validate our network on a more complex dataset, this experiment was carried out on the various-shape dataset. Figure 8 shows the reconstruction results of different discriminators including D3, D2, and D1. D3, D2, and D1 indicate the network is trained with 3-scale, 2-scale, and 1-scale discriminators, respectively. It is obvious that the results trained with D2 provided the best image quality compared with D1 and D3. For the detailed quantitative results, D2 also obtained the highest PSNR and SSIM with lower standard deviations, as shown in Table 2. Although it seems the image obtained using D3 has a much clearer edge structure than does D1, the bias and variance of the 2 are very similar as, shown in Figure 9. We consider the D2 discriminator to have sufficient ability in focusing on both global and detailed structure reconstruction, as our image size is not too large. The D3 discriminator makes the discriminate network so complex that the quantitative results are not satisfactory. For the performance on tumor shown in Figure 10, although the variance of three types of discriminators are very similar, D2 involves a much lower bias than do the other two types. We thus adapted the 2-scale discriminator in the subsequent experiments.
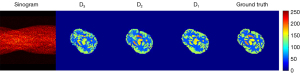
Table 2
| Input | PSNR | SSIM |
|---|---|---|
| D1 | 22.9023±3.9877 | 0.9230±0.0427 |
| D2 | 23.6658±3.2899* | 0.9382±0.0309* |
| D3 | 22.7840±3.9117 | 0.9202±0.0441 |
Data are shown as mean ± SD. *, the results of the adopted structure. PSNR, peak signal-to-noise ratio; SSIM, structure similarity index measure; D1, 1-scale discriminator; D2, 2-scale discriminator; D3, 3-scale discriminator; SD, standard deviation.

Comparison experiments
We compared our method with two classic networks in medical image processing. The first was U-Net, which has demonstrated excellent performance in many medical image reconstruction tasks, not only for PET. The second was DeepPET method, which is a very popular direct reconstruction method proposed for PET images. The learning rate was 0.0001, the batch size was 64, and all the experiments iterated 200 epochs.
Simulation experiments
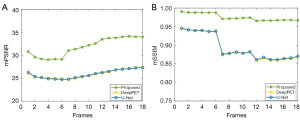
Figure 11 shows the three different kinds of deformation phantoms that were specifically chosen to illustrate the reconstruction results of the comparison methods. In this figure, the red arrows indicate the reconstruction results of the tumor; as shown in the first column, for the scaling transform, our method provides a more approximate global structure and much clearer fine parts compared with the ground truth; as shown in the second column depicting the translating transform phantom, although the three methods are all able to reconstruct the basic structure, the radioactivity information reconstructed by the other two comparison methods is not accurate; in the third column depicting the rotating transform, the quality of the reconstructed images generated by DeepPET and U-Net are so pooled that there is not even a clear global edge. It can be clearly seen that PIGRN has a stronger ability in reconstructing the PET images that have substantial deformation and translation as compared with DeepPET and U-Net. This outstanding performance was also verified from a quantitative perspective, as shown in Table 3. The much smaller standard deviations of the proposed method indicate that our network is extremely stable compared with the other two methods. Although the variance value of the tumor part of PIGRN is slightly higher than that of the other two methods, the bias value is much lower, meaning our method performed better on the small structure. For dynamic PET images, the SSIM value and PSNR value of PIGRN undergoes minimal changes throughout the whole dynamic phase, as shown in Figure 12, which demonstrates our method also has good robustness.
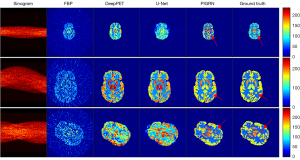
Table 3
| Method | PSNR | SSIM | Bias (tumor) | Variance (tumor) |
|---|---|---|---|---|
| U-Net | 21.0616±6.1045 | 0.8866±0.0645 | 0.3871 | 0.0270 |
| DeepPET | 20.8910±4.1045 | 0.9242±0.0535 | 0.3519 | 0.0340 |
| PIGRN | 24.4137±2.9526* | 0.9492±0.0239* | 0.2224* | 0.0448* |
Data are shown as mean ± SD. *, the results of the proposed method. PSNR, peak signal-to-noise ratio; SSIM, structure similarity index measure; PIGRN, prior information-guided reconstruction network; SD, standard deviation.
Whole-body experiments in SD rats
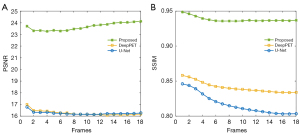
We conducted an experiment to verify the performance of our method on real datasets. We trained on nine SD rats and tested with another 3. Figure 13 presents the reconstruction results of the different methods. In the figure, the red arrows indicate the reconstruction results of some fine structures. It obvious that the proposed method has a much higher degree of reduction in the reconstruction details. The reconstructed image of DeepPET is clear but so smooth that some important tiny structures are lost. U-Net only has an ability to reproduce a rough structure. For both these methods, the shape and concentration of many reconstructed regions are inaccurate (as indicated by the red arrows). The quantitative results of the three methods are summarized in Table 4. For both PSNR and SSIM, the values of PIGRN are much higher than those of DeepPET and U-Net. As the whole-body dataset is dynamic, we could also verify the robustness of our method on different concentration frames, especially the low-concentration frames. As can be seen in Figure 14, the SSIM and PSNR curves varied with frames are stable, indicating that PIGRN is not only more accurate but also has strong robustness.
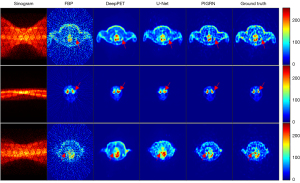
Table 4
| Method | PSNR | SSIM |
|---|---|---|
| U-Net | 26.4909±2.1707 | 0.9063±0.0416 |
| DeepPET | 25.7671±2.2573 | 0.9060±0.0416 |
| PIGRN | 31.8498±3.0512* | 0.9754±0.0127* |
Data are shown as mean ± SD. *, the results of the proposed method. PSNR, peak signal-to-noise ratio; SSIM, structure similarity index measure; PIGRN, prior information-guided reconstruction network; SD, standard deviation.
Network generalization experiments based on the organ-level dataset
In additional to its accuracy and robustness, we also evaluated the generalization ability of our network. An organ level dataset as described in “SD rat datasets” section was specifically built for this experiment. We randomly chose nine rats for training and the other three for testing. In the organ-level experiment, PIGRN was trained with only the thorax slices of nine rats. In the whole-body experiment, PIGRN was trained with the whole-body slices including both the thorax part and the brain part of the same nine rats. For comparison, the two experiments shared the same testing set, which was composed of the brain slices of the other three rats. Figure 15 presents the brain reconstruction results under different training sets. The reconstructed brain images obtained from the whole-body experiment and organ-level experiment are shown in the second column (whole-body) and the third column (organ-level) respectively. Comparing with organ-level column, the brain images in the whole-body column are closer to ground truth. This is due to similar brain slices were used in the training phase of the whole-body experiment. While the brain images obtained in the organ-level experiment are also very close to the ground truth, it suggests that PIGRN has the ability to reconstruct a previously unseen structure. This strong generalization ability was also verified by quantitative results (Table 5), with the PSNR and SSIM value of the two datasets being extremely similar.
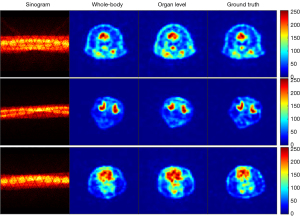
Table 5
| Dataset | PSNR | SSIM |
|---|---|---|
| Whole-body | 30.7769±1.8210 | 0.9647±0.0120 |
| Organ-level | 30.1775±1.5618 | 0.9629±0.0050 |
Data are shown as mean ± SD. PSNR, peak signal-to-noise ratio; SSIM, structure similarity index measure; SD, standard deviation.
Discussion
PIGRN is a novel reconstruction network designed for PET images. The results of the experiments and generalization experiment based on simulation datasets and the SD rat dataset indicate that the proposed PIGRN has the ability to improve image quality with strong generalization ability. In addition to the accuracy and generalization of reconstruction, the reconstruction time of the algorithm is also worth noting, as this is largely determines whether the algorithm is feasible in clinical practice. We list the training times and testing times of the proposed method and the reference deep learning methods in Table 6. For the deep learning methods, the training time is the time spent on training the model. After the model has been trained, there is no need for further training operations, while the testing time is the real time for clinical image reconstruction. Although the training time is longer, the testing time of a single slice is acceptable in clinical experiments and is much faster than that of the traditional method FBP. The proposed algorithm, while ensuring accuracy, involves a reconstruction time that is completely within an acceptable range and is only a quarter of that of the FBP algorithm.
Table 6
| Method | Training time (h) | Testing time (s) |
|---|---|---|
| FBP | – | 0.15 |
| U-Net | 0.5 | 0.008 |
| DeepPET | 2.5 | 0.011 |
| PIGRN | 4.17 | 0.039 |
FBP, filtered back projection; PIGRN, prior information-guided reconstruction network.
In addition to comparing our proposed network with other recently popular deep learning reconstruction algorithms, we also attempted to compare it with the newly proposed FBP-Net. Figure 16 presents the reconstruction results of both FBP-Net and the proposed method based on the various-shape dataset. For the convenience of comparison, we selected the same slices as those in Figure 11, and the corresponding quantitative results are listed in Table 7. Although the quantitative results of the two methods are highly similar, it can be clearly seen that the results from PIGRN are closer to the ground truth to the naked eye. Because PIGRN is not particularly smooth, the PSNR is higher; however, smoothing may not be beneficial for medical images, as this may overlook very small targets. Moreover, PIGRN has stronger portability, and the PI channel can incorporate different PI to assist in reconstruction. We look forward to verifying its other effects if richer data, such as additional CT images, can be obtained. We would like to explore three areas in future PIGRN reconstruction tasks:
- Large size images. The generator can be extended to multiple channels that operate at different scales. All the output then be concatenated and fed into a discriminator. For the matching generator, the discriminator can also be extended to multiple scales.
- Combination of multiple PI sources. For a generator operating on multiple channels, each channel can introduce a type of PI into the network. All the PI can then be combined for reconstruction processing.
- TOF-PET data. For the PET data that are collected from TOF-PET scanner, we can directly treat the attenuation correction images as the PI channel.
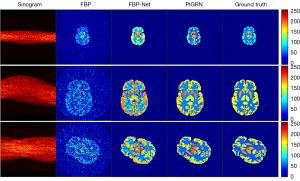
Table 7
| Dataset | PSNR | SSIM |
|---|---|---|
| FBP-Net | 24.6973±1.4913 | 0.9493±0.0127 |
| PIGRN | 24.4137±2.9526* | 0.9492±0.0239* |
Data are shown as mean ± SD. *, the results of the proposed method. PSNR, peak signal-to-noise ratio; SSIM, structure similarity index measure; FBP, filtered back projection; PIGRN, prior information-guided reconstruction network; SD, standard deviation.
Several limitations to our work should be mentioned. First, a true comparison of the training time between PIGRN and DeepPET or U-Net was not possible, as the PIGRN has many more parameters. Second, our real dataset was based on SD rats, which are small and cannot truly reflect the size of the human body. Therefore, we eagerly to seek to evaluate our method using human PET data. Finally, our method only focused on 2D image reconstruction, as 3D projection data has to be rebinned to 2D before training.
Conclusions
We developed a PIGRN based on cGAN for reconstructing PET images from both raw data and PI. PIGRN can ensure good reconstruction accuracy, and the network structure is flexible and has strong portability. The results of the comparison experiments and generalization experiment based on simulation datasets and SD rat dataset demonstrated that the proposed PIGRN has the ability to improve the image quality and has strong generalization ability.
Acknowledgments
Funding: This work was supported in part by
Footnote
Conflicts of Interest: All authors have completed the ICMJE uniform disclosure form (available at https://qims.amegroups.com/article/view/10.21037/qims-23-579/coif). The authors have no conflicts of interest to declare.
Ethical Statement: The authors are accountable for all aspects of the work in ensuring that questions related to the accuracy or integrity of any part of the work are appropriately investigated and resolved. Animal experiments were approved by the experimental animal welfare and ethics review committee of Zhejiang University and were performed in compliance with the national guidelines for animal experiments and local legal requirements.
Open Access Statement: This is an Open Access article distributed in accordance with the Creative Commons Attribution-NonCommercial-NoDerivs 4.0 International License (CC BY-NC-ND 4.0), which permits the non-commercial replication and distribution of the article with the strict proviso that no changes or edits are made and the original work is properly cited (including links to both the formal publication through the relevant DOI and the license). See: https://creativecommons.org/licenses/by-nc-nd/4.0/.
References
- Matsubara K, Ibaraki M, Nemoto M, Watabe H, Kimura Y. A review on AI in PET imaging. Ann Nucl Med 2022;36:133-43. [Crossref] [PubMed]
- Arabi H. AkhavanAllaf A, Sanaat A, Shiri I, Zaidi H. The promise of artificial intelligence and deep learning in PET and SPECT imaging. Phys Med 2021;83:122-37. [Crossref] [PubMed]
- Cheng Z, Wen J, Huang G, Yan J. Applications of artificial intelligence in nuclear medicine image generation. Quant Imaging Med Surg 2021;11:2792-822. [Crossref] [PubMed]
- Zaharchuk G, Davidzon G. Artificial Intelligence for Optimization and Interpretation of PET/CT and PET/MR Images. Semin Nucl Med 2021;51:134-42. [Crossref] [PubMed]
- Wang T, Lei Y, Fu Y, Wynne JF, Curran WJ, Liu T, Yang X. A review on medical imaging synthesis using deep learning and its clinical applications. J Appl Clin Med Phys 2021;22:11-36. [Crossref] [PubMed]
- Zhu B, Liu JZ, Cauley SF, Rosen BR, Rosen MS. Image reconstruction by domain-transform manifold learning. Nature 2018;555:487-92. [Crossref] [PubMed]
- Häggström I, Schmidtlein CR, Campanella G, Fuchs TJ. DeepPET: A deep encoder-decoder network for directly solving the PET image reconstruction inverse problem. Med Image Anal 2019;54:253-62. [Crossref] [PubMed]
- Liu Z, Chen H, Liu H. Deep Learning Based Framework for Direct Reconstruction of PET Images. Medical Image Computing and Computer Assisted Intervention 2019:48-56.
- Arabi H, Bortolin K, Ginovart N, Garibotto V, Zaidi H. Deep learning-guided joint attenuation and scatter correction in multitracer neuroimaging studies. Hum Brain Mapp 2020;41:3667-79. [Crossref] [PubMed]
- Whiteley W, Luk WK, Gregor J. DirectPET: full-size neural network PET reconstruction from sinogram data. J Med Imaging (Bellingham) 2020;7:032503. [Crossref] [PubMed]
- Hashimoto F, Ito M, Ote K, Isobe T, Okada H, Ouchi Y. Deep learning-based attenuation correction for brain PET with various radiotracers. Ann Nucl Med 2021;35:691-701. [Crossref] [PubMed]
- Yang J, Sohn JH, Behr SC, Gullberg GT, Seo Y. CT-less Direct Correction of Attenuation and Scatter in the Image Space Using Deep Learning for Whole-Body FDG PET: Potential Benefits and Pitfalls. Radiol Artif Intell 2021;3:e200137. [Crossref] [PubMed]
- Gong K, Catana C, Qi J, Li Q. Direct Reconstruction of Linear Parametric Images From Dynamic PET Using Nonlocal Deep Image Prior. IEEE Trans Med Imaging 2022;41:680-9. [Crossref] [PubMed]
- Ote K, Hashimoto F. Deep-learning-based fast TOF-PET image reconstruction using direction information. Radiol Phys Technol 2022;15:72-82. [Crossref] [PubMed]
- Wang B, Liu H. FBP-Net for direct reconstruction of dynamic PET images. Phys Med Biol 2020; [Crossref]
- Lv L, Zeng GL, Zan Y, Hong X, Guo M, Chen G, Tao W, Ding W, Huang Q. A back-projection-and-filtering-like (BPF-like) reconstruction method with the deep learning filtration from listmode data in TOF-PET. Med Phys 2022;49:2531-44. [Crossref] [PubMed]
- Zhang Q, Gao J, Ge Y, Zhang N, Yang Y, Liu X, Zheng H, Liang D, Hu Z. PET image reconstruction using a cascading back-projection neural network. IEEE Journal of Selected Topics in Signal Processing 2020;14:1100-11.
- Xue H, Zhang Q, Zou S, Zhang W, Zhou C, Tie C, Wan Q, Teng Y, Li Y, Liang D, Liu X, Yang Y, Zheng H, Zhu X, Hu Z. LCPR-Net: low-count PET image reconstruction using the domain transform and cycle-consistent generative adversarial networks. Quant Imaging Med Surg 2021;11:749-62. [Crossref] [PubMed]
- Huang Y, Zhu H, Duan X, Hong X, Sun H, Lv W, Lu L, Feng Q. GapFill-Recon Net: A Cascade Network for simultaneously PET Gap Filling and Image Reconstruction. Comput Methods Programs Biomed 2021;208:106271. [Crossref] [PubMed]
- Yang B, Zhou L, Chen L, Lu L, Liu H, Zhu W. Cycle-consistent learning-based hybrid iterative reconstruction for whole-body PET imaging. Phys Med Biol 2022; [Crossref]
- Wang TC, Liu MY, Zhu JY, Tao A, Kautz J, Catanzaro B. High-resolution image synthesis and semantic manipulation with conditional GANs. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition 2018:8798-807.
- Ledig C, Theis L, Huszár F, Caballero J, Cunningham A, Acosta A, Shi W. Photo-realistic single image super-resolution using a generative adversarial network. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition 2017:4681-90.
- Ronneberger O, Fischer P, Brox T. U-net: Convolutional networks for biomedical image segmentation. Lecture Notes in Computer Science (including subseries lecture notes in artificial intelligence and lecture notes in bioinformatics) 2015:234-41.
- Fessler JA. Michigan Image Reconstruction Toolbox. Available online: https://web.eecs.umich.edu/~fessler/code/, downloaded on 2018-05.
- Isola P, Zhu JY, Zhou T, Efros AA. Image-to-image translation with conditional adversarial networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition 2017:1125-34.


